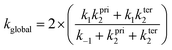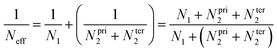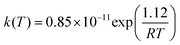Theoretical calculations of the kinetics of the OH reaction with 2-methyl-2-propen-1-ol and its alkene analogue

Abstract

In this work, the first and rate determining steps of the mechanism of the OH addition to 2-methyl-2-propen-1-ol (MPO221) and methylpropene (M2) have been studied at the DFT level, employing the BH and HLYP functional and the cc-pVDZ and aug-cc-pVDZ basis sets. The thermochemical properties of equilibrium (enthalpy, entropy and Gibbs free energies) have been determined within the conventional statistical thermodynamics relations and the rate coefficients have been determined on the basis of the variational transition state theory. The adoption of the microcanonical variational transition state theory was proved to be crucial for the description of the kinetics of OH addition to these unsaturated compounds. The rate coefficients obtained for the OH reactions with MPO221 and M2 at 298.15 K deviate, respectively, 27% and 13% from the experimental rate coefficient available in the literature. A non-Arrhenius profile is observed for the rate coefficients. Moreover, the values of the rate coefficients for the MPO221 + OH reaction are greater than those for the M2 + OH reaction, suggesting that the substitution of the hydrogen atom in an alkene by the –OH functional group increases the reactivity with respect to the hydroxyl radical.

---

1. Introduction

Volatile organic compounds (VOCs) are emitted into the troposphere by both biogenic and anthropogenic sources, playing an important role in atmospheric chemistry. Among these volatile compounds, unsaturated alcohols form a special class of primary pollutants. In the lower atmosphere, the reaction with OH radicals is the most important chemical process related to its removal and, for such a reaction, two basic mechanisms may be expected: the addition of OH to the carbon atoms involved in the double bond¹ and the hydrogen abstraction, although the latter is believed to significantly contribute to the global kinetics only at temperatures much higher than the atmospheric common values.² Among the unsaturated alcohols, the 2-methyl-2-propen-1-ol (MPO221) is of particular interest. It is applied as a monomer for the synthesis of polymers as well as a solvent for several applications and a starting material in the synthesis of pharmaceuticals, pesticides and other allyl compounds.

The temperature and pressure dependence of the rate coefficients for the reaction MPO221 + OH → products has been experimentally determined,³ as well as the rate coefficients for the addition of OH to the analogue alkene (2-methylpropene, M2).⁴ In both cases, the dependence of the rate coefficients with the temperature suggests a non-Arrhenius behavior. In addition, as it was pointed out by Cometto et al.,³ the reactivity of the unsaturated alcohol towards the OH radical is nearly twice higher than the reactivity of the M2 toward the same radical.

For the determination of the rate coefficients for the MPO221 + OH reaction in the range 263–371 K, Cometto and co-workers employed both relative and absolute methods (for the latter, the pulsed laser photolysis-laser induced fluorescence detection, PLP-LIF technique was employed) and their data have been best fitted to the expression: k(T) = 1 × 10⁻¹¹ × exp(652/T) cm³ per molecule per s.³ Atkinson and co-workers have reported rate coefficients for the M2 + OH reaction, using flash-photolysis and resonance fluorescence techniques.⁴ From this work is it possible to obtain the following Arrhenius expression: k(T) = 0.92 × 10⁻¹¹ × exp(503/T) cm³ per molecule per s between 297 and 425 K. Later, using structure–activity relationships, Grosjean and co-workers reported rate coefficients for M2 and a series of unsaturated compounds reactions with OH radicals.⁵

In addition to the experimental papers, a theoretical work by Zhang and co-workers reports a study about the OH addition paths and hydrogen abstraction reactions located on the MPO221 + OH potential energy surface, at the CCSD(T)//MP2/6-311++G(d,p) level.⁶ This work contributes to the knowledge about the atmospheric chemistry of unsaturated alcohols and their reaction with the OH radical, suggesting that the major products from the addition and elimination reactions are HCHO and (CH₃)₂COH, being CH₃OH and CH₃C(OH)CH₃ also expected at minor abundance. Since the abstraction reaction is only expected to contribute to the global kinetics at high temperatures, at atmospheric conditions, the overall reaction kinetics is dominated by the addition steps, for which the transition states are found lower in energy than the isolated reactants, thus justifying the negative temperature dependence of the rate coefficients. These trends are also found for OH reactions with similar unsaturated alcohols.⁷

As suggested in the literature, the OH addition reactions to unsaturated alcohols yield dialcohol radicals via formation of an intermediate, a pre-barrier complex (PC), stabilized by a few kcal mol⁻¹ in relation to the isolated reactants. The saddle point for the PC → radical conversion is located, obviously above the intermediate, but below the isolated reactants leading to a non-Arrhenius behaviour with negative overall activation energies.⁸ This fact itself is considered an instigating kinetic problem in which accurate theoretical methods are necessary for the prompt description of the reaction paths along the potential energy surface. Also, the primary addition of the OH radical to the unsaturated alcohol is expected to be a barrierless reaction for which the conventional transition state theory must not apply and, instead, variational transition state methods are required.⁹

In this work, the addition reactions of OH to MPO221 and M2 are investigated. These reactions can be schematically written as:

MPO221 + OH → HOCH₂C(CH₃)CH₂OH (1a)

MPO221 + OH → HOCH₂C(OH)(CH₃)CH₂ (1b)

M2 + OH → CH₃C(OH)(CH₃)CH₂ (2a)

M2 + OH → CH₃C(CH₃)CH₂OH (2b)

Our main goal is to understand the relative reactivity of the unsaturated alcohol with respect to its alkene analogue, on the basis of the potential energy profiles and rate coefficients, calculated using the canonical variational transition state theory.⁹

2. Computational methods

The MPO221 + OH and M2 + OH reactions have been described at Density Functional Theory (DFT) level,¹⁰ adopting the BHandHLYP functional¹¹ along with the cc-pVDZ and the aug-cc-pVDZ basis sets.¹² Geometry optimizations aiming to the location of all minima and saddle points have been performed and the characterization of these stationary points, after the converged geometry optimization calculations have been done by analysis of the vibrational frequencies, calculated at the same level. Also, in order to guarantee that the optimized structure corresponds to a global or local minimum, relaxed scans along one or more dihedral angles have been calculated. This procedure has been adopted because the potential energy surface is expected to show a high density of minima, due to the combination of some internal rotations, differing one from the other by a few kcal mol⁻¹. Spin contamination has been observed in all DFT calculations and in all cases the value has been greater than 0.754. Theoretical calculations have been performed with the Gaussian 09 program.¹³

The stationary points can be summarized as reactants, pre-barrier complex, saddle point and products. The minimum energy paths connecting the pre-barrier complex and product and passing through the saddle point have been calculated using the intrinsic reaction path (IRC) method.¹⁴ For the description of the minimum energy path connecting the pre-barrier complex and the reactants, scan calculations have been performed by partially optimizing the geometries along a path of increasing C–OH interatomic distances. Thermochemical quantities have been calculated using conventional statistical thermodynamics relations, assuming the harmonic oscillator, rigid rotor and ideal gas models,¹⁵ except for the case of the CH₃ internal rotations, which have been treated as a hindered rotor.¹⁶

Canonical variational transition state rate coefficients have been calculated using the model described elsewhere.¹⁷ Briefly, the vibrationally adiabatic potential energy curve is transformed into a Gibbs free energy curve at each temperature, using the same thermodynamics formulations mentioned above, and then a polynomial of third or fifth order is fitted to this Gibbs free energy function, G(s, T), being s the reaction coordinate. At each temperature, the function G(s, T) is analytically maximized to obtain the s value that corresponds to the location of the generalized transition state and its properties (vibrational frequencies, moments of inertia and critical energy) are interpolated and applied as the input quantities for the conventional Eyring equation¹⁸ over the temperature range 200–400 K.

3. Results and discussion

3.1. The MPO221 + OH reaction

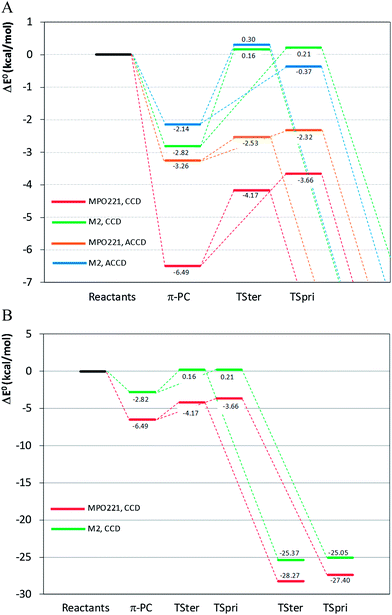
The structures for reactants, pre-barrier complex, saddle points and products are shown in Fig. 1. The most relevant geometric parameters obtained at the BHandHLYP level with both cc-pVDZ and aug-cc-pVDZ basis sets are given as ESI.† The important structural and energetic aspects of the MPO221 + OH reaction obtained at the BHandHLYP/cc-pVDZ level will be discussed in this section. The summarized relative energies, obtained at all theoretical levels explored in this work, are introduced in Table 1.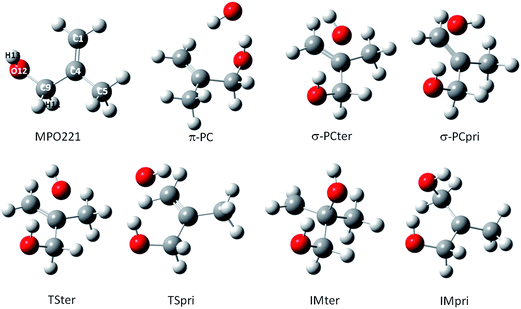

Fig. 1 The structures for reactants, pre-barrier complex, saddle points and products along the MPO221 + OH reaction profile.

Table 1 Electronic energies corrected by zero-point vibrational energy (in kcal mol⁻¹) for the several stationary points involved in the OH + MPO221 reaction, in relation to the isolated reactants

	BHandHLYP
	cc-pVDZ	aug-cc-pVDZ
Reactants	0.00	0.00
σ-PCpri	−5.76	−2.93
σ-PCter	−5.64	−3.35
π-PC	−6.49	−3.26
TSpri	−3.66	−2.32
TSter	−4.17	−2.53
IMpri	−27.40	−25.15
IMter	−28.27	−26.61

---

In order to confirm that the starting geometry is the global minimum, scan calculations were performed over the dihedral angles, at the BHandHLYP/cc-pVDZ level. The global minimum was proved to be the conformer with the oxygen atom almost on the same plane that contains the double bond, showing a dihedral angle OCC=C of −8.1°. The hydrogen atom, bonded to the oxygen with the interatomic distance of 0.957 Å, forming an angle 107.8° with the carbon atom, also showing a dihedral angle of −61.8° with respect to the neighbouring carbon atom. A mirror inversion of this structure reveals a non-superimposable conformer (i.e. an enantiomer). We assume that the global reaction dynamics will follow the minimum energy structures along the reaction path that keep the same geometric and conformational profile of the MPO221 global minimum, respecting the enantiomeric structures.

As mentioned before, literature strongly suggests that a pre-barrier complex plays an important role in the dynamics of the OH addition to unsaturated compounds.^8,19 Hence, starting from the minimum energy geometry of MPO221, new calculations at the UBHandHLYP/cc-pVDZ level were performed with the aim of searching for possible geometries of the pre-barrier complexes which resulted in the different structures, characterized as σ-type (being intermediates in the mechanism of addition of OH to the primary, σ-PCpri, or tertiary carbon atom, σ-PCter) and as π-type (π-PC).

The geometries for the σ-PCter and σ-PCpri suggest that the OH radical interacts with the unsaturated alcohol lying nearly parallel to the plane containing the allylic moiety, with the O–C distances of 2.783 Å and 2.632 Å for O^(OH)–C¹ (σ-PCpri) and O^(OH)–C⁴ (σ-PCter), respectively, and O^(OH)C¹C⁴C⁹ dihedral angles of −53.7° and −74.7°, respectively (note the labels in Fig. 1). The dihedral angles related to the MPO221 moiety on the σ-PCs slightly differ from those of the isolated molecule, being d_(H11C9C4C5) = −76.8° and d_(H13O12C9C4) = −60.9° for the σ-PCter and d_(H11C9C4C5) = −66.2° and d_(H13O12C9C4) = −62.0° for the σ-PCpri, σ pre-complexes. The O^(OH)–H¹³ distances are 2.038 and 1.966 Å for σ-PCter and σ-PCpri, respectively, which are typical hydrogen bond distances. The OH bond distance of the isolated radical is also slightly modified at the pre-barrier complex, being 0.990 Å at the isolated OH radical and approximately 0.968 Å at the complex. No significant change is verified for the C¹C⁴ double bond distance due to the OH interaction, being 1.327 Å at the isolated unsaturated alcohol and 1.335 Å at the σ pre-barrier complexes. The third geometry, referred as a π-type pre-barrier complex, shows the hydrogen atom of the OH radical pointing to the allylic plane, avoiding a perpendicular geometry, showing the dihedral angle d_{(O(OH)C1C4C9)} = 60.9°. The oxygen–carbon bond distances are 3.241 Å O^(OH)–C¹, 3.318 Å O^(OH)–C⁴ and the interatomic hydrogen bond distance, O^(OH)–H¹³, is 2.020 Å.

Both σ-PC and π-PC are stabilized in relation to the isolated reactants by 7.58 kcal mol⁻¹ (σ-PCter), 7.35 kcal mol⁻¹ (σ-PCpri) and 8.24 kcal mol⁻¹ (π-PC), at the BHandHLYP/cc-pVDZ level. Including the vibrational zero-point energies, the corrected relative energies, are 5.64 kcal mol⁻¹, 5.76 kcal mol⁻¹ and 6.49 kcal mol⁻¹, respectively.

The stabilization energies observed for the pre-complexes are probably due to the hydrogen bond. For a thermodynamic discussion, thermal contributions must also be added to calculate the enthalpy difference for the association process, 2-methyl-2-propen-1-ol + OH → PC, which are, at 298.15 K, −6.10 and −6.03 kcal mol⁻¹ (σ-PCter and σ-PCpri) and −6.96 kcal mol⁻¹ (π-PC). Finally, including entropic contributions, the Gibbs free energy differences for the association are 2.29 and 1.48 kcal mol⁻¹ (σ-PCter and σ-PCpri) and 1.28 kcal mol⁻¹ (π-PC).

The π-PC is energetically favoured with respect to the σ complexes, even though the energy differences are lower than 1 kcal mol⁻¹. This observation is supported in the literature^20,21 and justified by the additional stabilization due to the interaction of the H atom (from the OH radical) with the electronic density of the double bond, as well as the hydrogen bond interaction between the O atom (from the OH radical) and the H atom (from the OH group of the alcohol), which is common to both σ and π-type pre-barrier complexes.

Differently from the case of the pre-barrier complexes, the π interaction is not observed at the saddle points and only σ-type saddle points were located for the OH addition to both the terminal carbon atom (C3 addition) and the tertiary carbon atom (C2 addition). These saddle points may lead to tertiary and primary radicals, as the addition products, and could be well characterized by their imaginary frequencies. The geometries obtained at the BHandHLYP level suggest cyclic hydrogen-bonded structures showing an intramolecular interaction between the oxygen atom from the OH radical with the hydrogen atom from the alcohol group at the MPO221. A five or six-membered ring is formed (TSter, being saddle point in the mechanism of addition of OH to the tertiary carbon atom and TSpri, addition of OH to the primary carbon atom, respectively).

The optimized geometries of the saddle points, TSter and TSpri, differ from those obtained for the most stable π-PC, being the C¹C⁴ interatomic distances enhanced at the TSs whereas the C¹O¹⁴ and C⁴O¹⁴ distances show smaller values. The electronic energies of the saddle points are lower than the sum of electronic energies of the isolated reactants at the BHandLYP level, regardless of the basis set. The relative energies at the BHandHLYP/cc-pVDZ level (corrected by vibrational zero point energies) are −4.17 and −5.76 kcal mol⁻¹ for TSter and TSpri, respectively. The TSpri shows the electronic energy lower than the TSter by around 1 kcal mol⁻¹, which is quite a small energy difference and is probably of the same order of magnitude of the expected calculation error. In fact, this result is very sensitive to the basis set and the inverse situation is observed when the aug-cc-pVDZ basis set is adopted, being the TSter more stable by 0.2 kcal mol⁻¹.

Starting from the saddle points, minimum energy paths were calculated by the IRC procedure. At the product region of the reaction path (after the saddle point) of these reaction paths suggests the formation of an O–C bond, while at the reactants region (before the saddle point), the less stable σ-PCs geometries are reached. The reaction profiles lead to the formation of dialcohol radicals resulting from the addition of the hydroxyl radical to either the primary or tertiary carbon atom, yielding the radicals hereafter referred as IMpri and IMter, respectively.

The optimized geometries for IMpri and IMter were obtained and by the calculated vibrational frequencies, these structures could be correctly characterized as stationary points, being located 27.40 and 28.27 kcal mol⁻¹, respectively, below the isolated reactants. Comparing the relative energy (corrected by zero-point energy), it can be noted that the IMter is lower, by 0.87 kcal mol⁻¹.

In order to complete the reaction profile at the BHandHLYP level and connect the pre-complex to the isolated reactants, a potential curve was obtained, with the O–C distance as the scan coordinate, starting from the π-PC, leading to the isolated reactants. The final energy observed on the potential curve well agrees with the sum of the electronic energies of the isolated reactants.

A comparison of our results with other available in the literature is, at this moment, necessary. Our optimized σ and π-type pre-barrier complexes differ from those reported by Zhang and co-workers.⁶ Our geometries are tighter, with O–C distances smaller by 1.7 Å. Worthy of notice is that their geometry predicts an interaction of the hydrogen atom (from the OH radical) with the oxygen atom (from the alcohol group in MPO221), whereas in our geometry the opposite is observed, being the oxygen atom (from the OH radical) interacting with the hydrogen atom (from the alcohol group). In order to understand the differences between the two structures, new calculations were performed searching the minimum energy geometry resembling that previously reported by Zhang and co-workers.⁶ The second π-PC (denoted as 2π-PC) was located at the BHandHLYP/aug-cc-pVDZ level, with geometric parameters comparable to those reported by Zhang and also showing the stabilization energy of −4.74 kcal mol⁻¹, almost 1.5 kcal mol⁻¹ below the π-PC. From the inspection of the optimized geometries of the π-PC and 2π-PC, it can be inferred that each of these geometries represents different pre-barrier complexes resulting from the upward and downward OH attack to MPO221, or the π-PC geometries resulting from the upward OH attack to different conformers of the MPO221 (which are, in fact, mirror images of each other). Thus, the upward and downward OH attack to the MPO221 must result in two different reaction paths.

The π-PC is connected to the TSpri and TSter, as reported above. In order to preserve the conformational patterns of the 2π-PC structure, new saddle points (2TSpri and 2TSter) were located. The barrier heights for the reaction paths followed from the 2π-PC (0.89 and 0.44 kcal mol⁻¹, for 2TSpri and 2TSter, respectively) are higher than those followed from the π-PC. Moreover, the relative energies of the 2TSpri and 2TSter are positive, which should result in an Arrhenius-like temperature dependence of the global rate coefficients (if only these reaction paths were considered, according to the hypothesis of the 2π-PC being the best pre-barrier complex structure along the MPO221 + OH reaction path). Since a non-Arrhenius-like temperature dependence is experimentally observed, it can be assumed that a minor contribution of reaction paths followed by the 2π-PC to the global kinetics is expected. The 2π-PC formation and the reaction paths followed by this structure were, therefore, neglected. A figure showing the different geometries and reaction paths discussed above is given as ESI.†

Besides the comparison of the results available in the literature and ours, an assessment of our DFT data is also important, in order to guarantee the quality of our theoretical description. Therefore, calculations for the MPO221 + OH reaction profile were performed also at other theoretical levels. For example, MP2/cc-pVDZ calculations corroborate the DFT geometric results and suggest the π-PC geometry as a final structure at the IRC, after passing through the σ-PC geometries. Unfortunately, these MP2 calculations could not be considered to further rate coefficients calculations due to the very high spin contamination observed for the saddle points (in the range 0.90–0.94, depending on the basis set). Spin-projected MP2 energies were also observed as a possible solution to the spin contamination problem and the relative electronic energies for the π-PC and TSpri and TSter saddle points (with respect to isolated reactants, without zero point energy corrections) are: −8.02, −5.66 and −6.89 kcal mol⁻¹, respectively, in reasonable agreement with the BHandHLYP results (−8.24, −5.96 and −6.28 kcal mol⁻¹, respectively). Moreover, in order to tentatively validate BHandHLYP/cc-pVDZ electronic energies, CCSD and QCISD calculations were performed for geometry optimizations and vibrational frequencies and further CCSD(T)/cc-pVDZ single point calculations were performed on the basis of the CCSD/cc-pVDZ optimized geometries. At the CCSD(T) level, the relative electronic energies of the π-PC and TSpri and TSter stationary points are: −7.68, −4.07 and −4.90 kcal mol⁻¹, respectively, whereas at the QCISD/cc-pVDZ the corresponding values −7.23, −3.46 and −4.56 kcal mol⁻¹, respectively, are observed.

A comparison of the CCSD(T) and QCISD relative energies with those obtained at the BHandHLYP level shows that the π-PC stabilization energies agree within 1 kcal mol⁻¹, as well as the barrier heights of the TSter (with respect to the π-PC), whereas the barrier height of the TSpri is slightly increased at the QCISD and CCSD(T) in comparison with the BHandHLYP results, differing from 1.5 and 1.3 kcal mol⁻¹. Despite these deviations, a reasonable agreement among all the ab initio and DFT data is observed and the BHandHLYP results are considered satisfactory. The electronic energies of the reactants, π-PC, TSpri and TSter obtained at the PMP2, QCISD and CCSD(T) levels are given as ESI.†

Worthy of attention is that the geometric parameters do not significantly differ, when results from less accurate calculation level are compared with the geometric parameters calculated within a high accuracy calculation level. But, even the minor discrepancies at the optimized geometries may propagate significant errors at the relative energies if these were obtained from single point calculations at a higher sophisticated level on the basis of the optimized geometries located at a less accurate ab initio or DFT level. For example, considering CCSD(T)/cc-pVDZ//BHandHLYP/cc-pVDZ or CCSD(T)/cc-pVDZ//MP2/cc-pVDZ, as tentatively possibilities of improving the electronic energies of the stationary points, results show that the σ-PCs and saddle points are stabilized in respect to the π-PC, suggesting a mechanism which is not passing through the π-PC, but directly from the σ-PCs to the products. This mechanism is quite unexpected and not supported by previous literature reports,²⁰ hence this CCSD(T)//BHandHLYP/cc-pVDZ profile can not be considered in further rate coefficients calculations or discussion. The less satisfactory performance of the CCSD(T) single point corrections for the evaluation of rate coefficients for this kind of reaction has also been observed in previous works²² and may be due to unbalanced energy differences between the stationary points, even though very small if absolute energies are compared, but high enough to modify the reaction profile since the stationary points already show relatively small energy differences. Such problem was also observed when G3 method was attempted for the description of the reaction energy profile, resulting at saddle points (TSter and TSpri) with relative energies smaller than the π-PC stationary point.

As a final test of the BHandHLYP functional, and its applicability to the description of the MPO221 + OH reaction, new calculations employing the M06-2X functional were performed. Although this functional has received great attention at the literature, being suggested to be a particularly accurate and reliable functional for the description of barrier heights,^23–25 some disappointing results were obtained for the MPO221 + OH reaction and the location of the π-PC and σ-PCpri stationary points were not successful, independently of the basis set, even after several attempts. Moreover, the TSpri and TSter saddle points show, at the M06-2X/cc-pVDZ level, −9.76 and −9.96 kcal mol⁻¹, as relative electronic energies with respect to the isolated reactants, which are much smaller than the ab initio and BHandHLYP results, suggesting that these saddle points were over stabilized. The inclusion of diffuse functions at the basis set do not significantly modify these results and the relative energies for the TSpri and TSter saddle points as −8.18 and −8.60 kcal mol⁻¹, respectively, are obtained. Finally, only the BHandHLYP results were considered for further rate coefficients calculations.

For the M2 + OH reaction, the geometries of the stationary points, including the pre-barrier complex and saddle points have been located and validated by analysis of the vibrational frequencies, calculated after the geometry optimization at the same theoretical levels applied for the MPO221 + OH reaction, previously discussed. The optimized geometries are shown in Fig. 2. Interesting to note is that the OH radical lies almost perpendicular to the double bond suggesting a π-like pre-barrier complex stabilized by 2.82 and 2.14 kcal mol⁻¹ with respect to the isolated reactants, at the BHandHLYP/cc-pVDZ and BHandHLYP/aug-cc-pVDZ levels, with zero-point vibrational energy corrections, respectively. The saddle points for the OH addition to the primary and tertiary carbon atoms (TSpri and TSter) are located 0.21 and 0.16 kcal mol⁻¹ above the reactants at the BHandHLYP/cc-pVDZ level, and −0.37 and 0.30 kcal mol⁻¹ with respect to the isolated reactants at the BHandHLYP/aug-cc-pVDZ level. The spin contamination was monitored and the 〈S²〉 value was always less than 0.7504 in all cases. The addition products, IMpri and IMter, are stabilized by 25.05 and 25.37 kcal mol⁻¹, respectively, at the BHandHLYP/cc-pVDZ level and 23.90 and 24.35 kcal mol⁻¹, respectively, at the BHandHLYP/aug-cc-pVDZ level. The energy profile is introduced in Fig. 3A and B and the energy values with respect to the M2 + OH reaction are summarized in Table 2.

Fig. 2 The structures for reactants, pre-barrier complex, saddle points and products along the M2 + OH reaction profile.

Fig. 3 (A) Energy profile for the MPO221 + OH and M2 + OH reactions (zero-point vibrational energies are not included) at the BHandHLYP/cc-pVDZ (CCD) and BHandHLYP/aug-cc-pVDZ (ACCD) levels. Zoom at the pre-complex region. (B) Energy profile for the MPO221 + OH and M2 + OH reactions (zero-point vibrational energies are not included) at the BHandHLYP/cc-pVDZ (CCD) level. Complete energy diagram.

Table 2 Electronic energies corrected by zero-point vibrational energy (in kcal mol⁻¹) for the several stationary points involved in the OH + M2 reaction, in relation to the isolated reactants

	BHandHLYP
	cc-pVDZ	aug-cc-pVDZ
Reactants	0.00	0.00
π-PC	−2.82	−2.14
TSpri	0.21	−0.37
TSter	0.16	0.30
IMpri	−25.05	−23.90
IMter	−25.37	−24.35

---

Potential curves for the dissociation of the π-pre-barrier complex were obtained leading to the isolated reactants. The final electronic energy of this potential curve differs by less than 0.01 kcal mol⁻¹ from the sum of the electronic energies of M2 and OH. Also, starting from the saddle points, intrinsic reaction coordinates were calculated, showing the connection between the pre-barrier complex and the addition products, IMpri and IMter.

3.2. Canonical variational rate coefficients for the MPO221 + OH reaction

Rate coefficients were calculated for the association step and dissociation and addition reactions of the π-PC, represented by the chemical model:

MPO221 + OH → π-PC, k₁

π-PC → MPO221 + OH, k₋₁

π-PC → IMpri, k^pri₂

π-PC → IMter, k^ter₂

The canonical variational transition state method,¹⁸ was adopted, using the theoretical molecular properties calculated at BHandHLYP level with both cc-pVDZ and aug-cc-pVDZ basis sets. For the calculation of the global rate coefficient, the steady-state approximation was assumed, following the expression (the factor 2 accounts for the degeneracy of the reaction path due to stereochemistry):

A total of 20 geometries (and the corresponding molecular properties) along the potential curve representing the dissociation of the π-PC (π-PC → MPO221 + OH) were used in order to evaluate the k₋₁ rate coefficient.

The enthalpy profiles are similar to the vibrationally adiabatic potential curve, increasing along the reaction coordinate, so as the entropy is an increasing function of the reaction coordinate. The enthalpy curves as a function of the reaction coordinate calculated at lower temperature values are located above those calculated at higher temperatures, so as the entropy curves. Considering the Gibbs free energy expression, the entropic contribution term (−TS) as a function of the reaction coordinate calculated at lower temperatures are below those calculated at higher temperatures. Since the dependence of the entropic term on the temperature is higher than that observed for the enthalpic term, a maximum on the Gibbs free energy curve is observed moving towards the reactants region as the temperature increases. In other words, the looseness of the variational transition state decreases as the temperature increases. As these rate coefficients were calculated, the k₁ rate coefficients were evaluated assuming the microscopic reversibility.

The BHandHLYP/aug-cc-pVDZ k₋₁ rate coefficients are higher than those obtained at the BHandHLYP/cc-pVDZ level by factors of approximately 3–1500, depending on the temperature (the factor decreases with the temperature). This observation is justified by the smaller stabilization energy of the π-PC obtained using the diffuse functions (−3.26 kcal mol⁻¹, in comparison with −6.49 kcal mol⁻¹, obtained at the BHandHLYP/cc-pVDZ level). The BHandHLYP/aug-cc-pVDZ k₁ rate coefficients are, nonetheless, slightly lower than those obtained at the BHandHLYP/cc-pVDZ level due to compensation of the Gibbs free energies of reaction thus, the equilibrium constants. The k₁ and k₋₁ rate coefficients calculated at different theoretical levels (and internal rotation model for the torsion) are shown in Table 3.

Table 3 The variational rate coefficients: k₁ (cm³ per molecule per s), k₋₁, k^ter₂ and k^pri₂ (s⁻¹) and k_global (cm³ per molecule per s), calculated for the MPO221 + OH reaction at the BHandHLYP level with different basis sets as a function of the temperature (K)

	Temperature (K)	k1 (cm^3 per molecule per s)	k−1 (s^−1)	k^ter2 (s^−1)	k^pri2 (s^−1)	kglobal (cm^3 per molecule per s)
BHandHLYP/cc-pVDZ	200	7.96 × 10^−11	1.07 × 10^8	1.95 × 10^9	7.14 × 10^8	1.53 × 10^−10
	250	1.42 × 10^−10	4.69 × 10^9	9.08 × 10^9	3.05 × 10^9	2.05 × 10^−10
	300	7.81 × 10^−11	2.74 × 10^10	1.28 × 10^10	7.68 × 10^9	6.69 × 10^−11
	350	7.27 × 10^−11	1.19 × 10^11	2.17 × 10^10	1.46 × 10^10	3.41 × 10^−11
	400	6.62 × 10^−11	3.31 × 10^11	3.20 × 10^10	2.35 × 10^10	1.90 × 10^−11
	450	5.93 × 10^−11	6.92 × 10^11	4.31 × 10^10	3.37 × 10^10	1.19 × 10^−11
	500	5.25 × 10^−11	1.18 × 10^12	5.48 × 10^10	4.48 × 10^10	8.17 × 10^−12
BHandHLYP/aug-cc-pVDZ	200	3.87 × 10^−11	1.62 × 10^11	7.57 × 10^10	6.33 × 10^10	3.58 × 10^−11
	250	4.93 × 10^−11	9.39 × 10^11	1.52 × 10^11	8.14 × 10^10	1.96 × 10^−11
	300	2.14 × 10^−11	1.34 × 10^12	1.22 × 10^11	9.02 × 10^10	5.85 × 10^−12
	350	1.60 × 10^−11	2.06 × 10^12	1.37 × 10^11	9.38 × 10^10	3.22 × 10^−12
	400	1.22 × 10^−11	2.63 × 10^12	1.49 × 10^11	9.43 × 10^10	2.60 × 10^−12
	450	9.59 × 10^−12	2.99 × 10^12	1.58 × 10^11	9.29 × 10^10	1.49 × 10^−12
	500	7.70 × 10^−12	3.15 × 10^12	1.65 × 10^11	9.06 × 10^10	1.16 × 10^−12

---

For the calculation of the k₂ rate coefficient, 21 points along the reaction coordinate (and the corresponding molecular properties) were used for the variational procedure. It is interesting to highlight the profiles of the enthalpy, entropy and Gibbs free energy curves as a function of the reaction coordinate obtained during the variational calculation of the rate coefficients. The entropy curves at any temperature show a decreasing profile, since the reaction proceeds from a looser to a tighter structure. The enthalpy curves, although similar to the IRC curve, show a maximum ΔH value displaced from the s = 0 towards positive values of the reaction coordinate, even at the lowest temperature values. In fact, the vibrationally adiabatic potential curve, resulting from the addition of the zero point vibrational energy to the electronic energy, already shows such displacement from the saddle point. This situation has been previously observed and the reaction is said to be controlled by the vibrational adiabaticity,²⁶ since the variational effect arises from the increase of the values of the vibrational frequencies as the reaction proceeds toward the product region. As the entropy is a decreasing function of the reaction coordinate, the maximum value in the Gibbs free energy function, ΔG(s, T), moves towards the positive reaction coordinate values, and this variational displacement increases with the temperature, suggesting that the entropy contributions are also important to the variational effect. Finally, the k₂ rate coefficients calculated for the π-PC → IMter reaction are systematically higher than those obtained for the π-PC → IMpri reaction, as well as the BHandHLYP/aug-cc-pVDZ k₂ rate coefficients are higher than the BHandHLYP/cc-pVDZ, which is justified by energy barriers. The k₂ rate coefficients calculated in the temperature range from 200 to 500 K are also shown in Table 3.

The resulting global rate coefficients, are also shown in Table 3. Note that this reaction shows a non-Arrhenius behaviour: the values of the rate coefficients decrease as the temperature increases. Our rate coefficients calculated at 298 K are 6.87 × 10⁻¹¹ and 6.00 × 10⁻¹² cm³ per molecule per s, at the BHandHLYP/cc-pVDZ and BHandHLYP/aug-cc-pVDZ levels, respectively. The values show good agreement with the value 9.12 × 10⁻¹¹ cm³ per molecule per s, reported by Cometto and co-workers,³ being the ratios theoretical/experimental equal to 0.75 (BHandHLYP/cc-pVDZ) and 0.06 (BHandHLYP/aug-cc-pVDZ). Comparing the BHandHLYP/cc-pVDZ and experimental rate coefficients,³ at the same temperature range, a root mean square deviation of 2.34 × 10⁻¹¹ cm³ per molecule per s is found.

The BHandHLYP/aug-cc-pVDZ global rate coefficients are systematically lower than the BHandHLYP/cc-pVDZ rate coefficients by a factor of nearly 10. This is a consequence of the lower stabilization energy of the π-PC and saddle-points obtained with the inclusion of diffuse functions to the basis set, despite the structural resemblance of the optimized geometries obtained with the two basis sets. Also, the energy barriers for the π-PC reactions, calculated with diffuse functions, are the lowest.

Even though the deviations observed for the calculated rate coefficients with respect to the experimental values may be considered small and found within the expected theoretical error, the calculated rate coefficients decrease faster than the experimental values. For the BHandHLYP/cc-pVDZ calculations, the Arrhenius parameters (apparent activation energy and pre-exponential factor, in units of kcal mol⁻¹ and cm³ per molecule per s) are −2.51 and 0.10 × 10⁻¹¹, in contrast with the experimental −1.30 and 1.0 × 10⁻¹¹.³ We notice that a small refinement of the kinetic model is still necessary for a precise description of the temperature dependence of the rate coefficients.

3.3. RRKM calculations for the MPO221 + OH reaction

The major uncertainty on the previous CVTST calculations is perhaps due to assuming for the first step, MPO221 + OH = π-PC, that the equilibrium is established at the canonical level. For any weakly bound intermediate, the canonical equilibrium assumption may lead to considerable error, since the canonical partition should not be as fast as the following reaction steps in the mechanism. For such a partition, the intermediate should be trapped time enough at the potential well and suffer several collisions until the thermal equilibrium is achieved.

In this sense, Greenwald and co-workers suggested that even though a canonical equilibrium cannot be achieved, the energy and angular momentum constraints must be respected and a microcanonical partition is expected in a two-transition state model.²⁷ An effective sum of states (N_eff) is calculated taking into account the sums of states, N₁ and N₂, of each outer and inner transition state located for each E and J:

The microcanonical variational transition state theory (mCVTST) was adopted here in order to test the hypothesis of the canonical equilibrium. Restrictions of energy and angular momentum were adopted, assuming a microcanonical ensemble.

In our model, the π-PC reactions forming the radical products are coupled and cannot be considered independently. We thus suggest a slight modification of this two-transition state model to adequate our case:

where N^pri₂ and N^ter₂ are sums of states of the inner transition states for the addition of OH to the primary carbon atom and to the tertiary carbon atom.

In this work, each sum of states was minimized along the reaction path in a variational procedure using the RRKM code.²⁸ Sum of states were calculated considering the ranges of energy up to 50 kcal mol⁻¹ (ΔE = 0.5 kcal mol⁻¹) and J from 0 to 200 (ΔJ = 1) in a total of 20 100 values for each step. The internal rotation model is also assumed for the torsion, in contrast to the harmonic oscillator model. High-pressure limit rate coefficients, k^∞(T), were finally calculated as:

where Q_a, Q_b are partition functions for the reactants (electronic × vibrational × rotational) and Q_rel is the relative translational partition function.

Table 4 introduces the resulting rate coefficients in the range from 200–500 K. The negative temperature dependence is also observed. As expected, from the previous discussion about the CVTST rate coefficients, mCVTST rate coefficients calculated at the BHandHLYP/aug-cc-pVDZ level are lower than those calculated at the BHandHLYP/cc-pVDZ level. But, considering the BHandHLYP/aug-cc-pVDZ results, a substantial improvement is obtained with the microcanonical variational calculations with respect to the canonical rate coefficients. The mCVTST rate coefficients are always higher than the CVTST rate coefficients in accordance to the expectation that the canonical assumption should lead to overestimated rate values.

Table 4 The microcanonical variational rate coefficient, k_global (cm³ per molecule per s) calculated for the MPO221 + OH reaction, as a function of the temperature

Temperature (K)	kglobal (cm^3 per molecule per s)
	BHandHLYP/cc-pVDZ	BHandHLYP/aug-cc-pVDZ
200	8.28 × 10^−10	1.58 × 10^−10
250	6.63 × 10^−10	9.74 × 10^−11
300	4.78 × 10^−10	6.56 × 10^−11
350	3.56 × 10^−10	4.74 × 10^−11
400	2.68 × 10^−10	3.62 × 10^−11
450	2.04 × 10^−10	2.90 × 10^−11
500	1.59 × 10^−10	2.45 × 10^−11

---

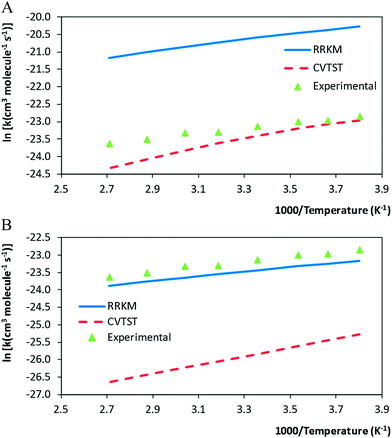
The resulting mCVTST rate coefficients are also worthy of comparison with the experimental data. Fig. 4 shows the CVTST, mCVTST (both obtained from molecular properties and energies predicted at the BHandHLYP/cc-pVDZ level, Fig. 4A and at the BHandHLYP/aug-cc-pVDZ level, Fig. 4B) and the experimental rate coefficients represented in an Arrhenius plot. It can be noted that the BHandHLYP/aug-cc-pVDZ + mCVTST rate coefficients agree very well with the experimental values, with deviations of 30%. The rate coefficient predicted at 298 K is 6.66 × 10⁻¹¹ cm³ per molecule per s. The slopes of the mCVTST and experimental values are also similar. The BHandHLYP/aug-cc-pVDZ + mCVTST rate coefficients can be finally expressed by the equation (the parameters are in units of cm³ per molecule per s and kcal mol⁻¹):

in very good agreement with the experimental Arrhenius equation.³ The same good agreement is not observed for the BHandHLYP/cc-pVDZ values with respect to the experimental and the improvement of the final results is finally observed for the best quality basis set.

Fig. 4 (A) Calculated (canonical and microcanonical variational transition state methods from BHandHLYP/cc-pVDZ molecular properties) and experimental rate coefficients for the MPO221 + OH reaction, as a function of the temperature (K). (B) Calculated (canonical and microcanonical variational transition state methods from BHandHLYP/aug-cc-pVDZ molecular properties) and experimental rate coefficients for the MPO221 + OH reaction, as a function of the temperature (K).

3.4. Comparison with the M2 + OH kinetics

The rate coefficients were calculated following a similar procedure to the formerly adopted for the evaluation of the rate coefficients for the MPO221 + OH reaction. Also, non-Arrhenius behaviour was observed for the M2 + OH reaction. This result is supported by previous experimental data3. CVTST rate coefficients are introduced in Table 5. At 298 K, our CVTST rate coefficient predicted at the BHandHLYP/cc-pVDZ level (4.99 × 10⁻¹³ cm³ per molecule per s) is nearly 100 times lower than the experimental value (4.97 × 10⁻¹¹ cm³ per molecule per s),⁴ while that predicted at the BHandHLYP/aug-cc-pVDZ (2.36 × 10⁻¹² cm³ per molecule per s) is 21 times lower. However, a further improvement of our model is achieved, once more, when the microcanonical variational transition state method is employed. In this case, our predicted value at 298 K is 5.63 × 10⁻¹¹ cm³ per molecule per s, in much better agreement with that reported by Atkinson and co-workers.⁴ The mCVTST rate coefficients are introduced in Table 6 and Fig. 5 compares the CVTST, mCVTST (both calculated from molecular properties predicted at the BHandHLYP/aug-cc-pVDZ level) and experimental rate coefficients. Our mCVTST results also fit to the Arrhenius expression (the parameters are in units of cm³ per molecule per s and kcal mol⁻¹):

Table 5 The variational rate coefficients: k₁ (cm³ per molecule per s), k₋₁, k^ter₂ and k^pri₂ (s⁻¹) and k_global (cm³ per molecule per s), calculated for the M2 + OH, at the BHandHLYP level with different basis sets as a function of the temperature (K)

	Temperature (K)	k1 (cm^3 per molecule per s)	k−1 (s^−1)	k^ter2 (s^−1)	k^pri2 (s^−1)	kglobal (cm^3 per molecule per s)
BHandHLYP/cc-pVDZ	200	1.76 × 10^−11	2.05 × 10^10	2.27 × 10^8	5.42 × 10^8	1.27 × 10^−12
	250	2.73 × 10^−11	1.91 × 10^11	9.65 × 10^8	2.66 × 10^9	1.02 × 10^−12
	300	3.94 × 10^−11	8.60 × 10^11	2.51 × 10^9	7.58 × 10^9	9.15 × 10^−13
	350	5.40 × 10^−11	2.55 × 10^12	4.95 × 10^9	1.59 × 10^10	8.77 × 10^−13
	400	7.13 × 10^−11	5.79 × 10^12	8.21 × 10^9	2.75 × 10^10	8.76 × 10^−13
	450	9.14 × 10^−11	1.10 × 10^13	1.22 × 10^10	4.20 × 10^10	8.97 × 10^−13
	500	1.14 × 10^−10	1.84 × 10^13	1.66 × 10^10	5.86 × 10^10	9.31 × 10^−13
BHandHLYP/aug-cc-pVDZ	200	4.65 × 10^−10	2.43 × 10^12	7.14 × 10^8	7.07 × 10^9	2.96 × 10^−12
	250	4.74 × 10^−10	7.80 × 10^12	2.27 × 10^9	1.84 × 10^10	2.50 × 10^−12
	300	4.43 × 10^−10	1.48 × 10^13	4.86 × 10^9	3.46 × 10^10	2.35 × 10^−12
	350	3.82 × 10^−10	2.02 × 10^13	8.34 × 10^9	5.43 × 10^10	2.36 × 10^−12
	400	3.02 × 10^−10	2.19 × 10^13	1.25 × 10^10	7.61 × 10^10	2.44 × 10^−12
	450	2.21 × 10^−10	1.97 × 10^13	1.70 × 10^10	9.87 × 10^10	2.58 × 10^−12
	500	1.48 × 10^−10	1.53 × 10^13	2.18 × 10^10	1.22 × 10^11	2.76 × 10^−12

---

Table 6 The microcanonical variational rate coefficient, k_global (cm³ per molecule per s) calculated for the M2 + OH reaction, as a function of the temperature

Temperature (K)	kglobal (cm^3 per molecule per s)
	BHandHLYP/cc-pVDZ	BHandHLYP/aug-cc-pVDZ
200	8.10 × 10^−12	1.68 × 10^−10
250	6.94 × 10^−12	8.53 × 10^−11
300	6.48 × 10^−12	5.55 × 10^−11
350	6.34 × 10^−12	4.18 × 10^−11
400	6.36 × 10^−12	3.46 × 10^−11
450	6.49 × 10^−12	3.04 × 10^−11
500	6.69 × 10^−12	2.79 × 10^−11

---

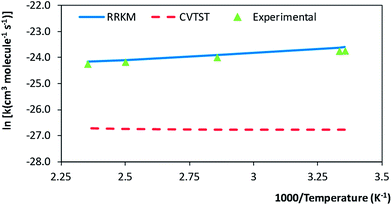Fig. 5 Calculated (canonical and microcanonical variational transition state methods) and experimental rate coefficients for the M2 + OH reaction, as a function of the temperature (K).

For both MPO221 + OH and M2 + OH reactions, the electrophilic addition of the OH radical to the primary and tertiary carbon atoms of the double bond may be observed. The reaction profile suggests the formation of a π-PC, in which the OH radical moiety lies nearly perpendicular to the C=C plane and the transition states always show electronic energies which are lower than the respective sum of electronic energies of the isolated reactants to yield hydroxyalkyl radicals as products. The global rate coefficients show non-Arrhenius behaviour and are comparable to the experimental values.

By comparing the global rate coefficients obtained for each reaction at the same temperature, the rate coefficients for the OH addition to the unsaturated alcohol show higher values, suggesting that the substitution of a hydrogen atom by a OH– group on the alkene causes the OH addition rate coefficient, and thus the reactivity, to increase. A substitution factor, defined as k(OH)/k(H), was shown to vary from 1.5 to 2.0 for this and other similar reactions.³ Our calculated value is 1.18 at 300 K and decreases, as the temperature increases, in agreement with the experimental observation.

The results found in this work can be justified by specific electronic interactions that stabilise the stationary points on the MPO221 + OH potential energy surface compared to those on the M2 + OH surface. The pre-barrier complex is possibly the most affected species in these mechanisms by such interactions. Beyond the PCs, the saddle points located on the MPO221 + OH potential energy surface form five or six-membered rings stabilised also by electronic interactions that are not present in the related M2 + OH saddle points. The electronic interactions that stabilise both PCs and saddle-points are highlighted as the cause of the enhanced reactivity of the unsaturated alcohol with respect to its alkene analogue. Such electronic interactions have probably the contribution of hydrogen bonds, although a more robust investigation is still encouraged.

4. Conclusions

In this work, the rate coefficients for the reactions of OH radical with 2-methyl-2-propen-1-ol and 2-methylpropene have been calculated and compared. This is, to the best of our knowledge, the first theoretical work to address the fundamental structural and energetic aspects of such reactions that explain the different reactivity of the unsaturated alcohol with respect to its alkene analogue. The dynamics of the OH electrophylic addition to the sp² carbon atoms of the unsaturated compounds is initiated by the formation of a pre-barrier complex in which the hydrogen atom of the OH radical interacts with the π-electrons, leading to a stationary point with minimum energy geometry having the H-atom of the OH radical pointing to the double bond. In the alkene, the OH stands almost perpendicular to the plane of the double bond, whereas in the unsaturated alcohol, the radical inclines due to hydrogen bond interactions with the OH– functional group. In fact, our results show that the OH– functional group plays a fundamental role in the reactivity by allowing stabilisation of both pre-barrier complexes, intermediates and saddle points.

The calculated rate coefficient for the 2-methyl-2-propen-1-ol + OH reaction at 298.15 K, adopting the microcanonical variational transition state method, is 6.66 × 10⁻¹¹ cm³ per molecule per s at the BHandHLYP/cc-pVDZ level, which deviates 27% from the experimental result. Arrhenius parameters have also been predicted in good agreement with the experimental data. For the 2-methylpropene, the calculated rate coefficient is 5.63 × 10⁻¹¹ cm³ per molecule per s, 13% higher than the experimental value. Moreover, both reactions show non-Arrhenius behaviour, confirming the experimental observation. The canonical variational transition state method could also predict the rate coefficients in fair agreement with the experimental data (although with a correct temperature dependence profile), but the adoption of the microcanonical variational method has been proved to be crucial for the precise prediction of the rate coefficients for the OH addition to these unsaturated compounds. The good agreement of the results from our theoretical model with the experimental available data represents not only a satisfactory quantitative prediction of rate coefficients but a fundamental contribution to the understanding at the microscopic molecular level of the observed experimental results, which are undoubtedly very important considering the role played by such compounds in atmospheric chemistry.

Acknowledgements

The authors thank the Brazilian National Council for Scientific and Technological Development, CNPq (Universal 2011 and PROSUL, Proc. 490252/2011-7) and CONICET, ANPCyT-FONCyT, MinCyT and SECyT-UNC of Argentina for financial support of this research.

References and notes

1. M. C. Piqueras, R. Crespo, I. Nebot-Gil and F. Tomás, J. Mol. Struct.: THEOCHEM, 2001, 537, 199.
2. C. E. Canosa-Mas, M. D. King, L. McDonnell and R. P. Wayne, Phys. Chem. Chem. Phys., 1999, 1, 2681.
3. P. M. Cometto, P. R. Dalmasso, R. A. Taccone, S. I. Lane, F. Oussar, V. Daële, A. Mellouki and G. Le Bras, J. Phys. Chem. A, 2008, 112, 4444.
4. R. Atkinson and J. N. Pitts, J. Chem. Phys., 1975, 63, 3591.
5. D. Grosjean and E. L. Williams II, Atmos. Environ., 1992, 26, 1395.
6. W. Zhang, B. Du and C. Feng, Theor. Chem. Acc., 2010, 125, 45.
7. B. Du and W. Zhang, Struct. Chem., 2011, 22, 589.
8. M. Francisco-Márquez, J. R. Alvarez-Idaboy, A. Galano and A. Vivier-Bunge, Phys. Chem. Chem. Phys., 2003, 5, 1392.
9. D. G. Truhlar and B. C. Garret, Annu. Rev. Phys. Chem., 1984, 35, 159.
10. I. N. Levine, Quantum Chemistry, Prentice Hall, New Jersey, 2000.
11. A. D. Becke, J. Chem. Phys., 1993, 98, 1372.
12. T. H. Dunning, J. Chem. Phys., 1989, 90, 1007.
13. M. J Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Blondo, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hadsegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kund, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian09, (Revision A.02), Gaussian, Inc., Wallingford, CT, 2009.
14. K. A. Fukui, J. Phys. Chem., 1970, 74, 4161.
15. C. J. Cramer, Essentials of Computational Chemistry Theories and Models, John Wiley and Sons, New York, 2004.
16. P. Y. Ayala and H. B. Schlegel, J. Chem. Phys., 1988, 108, 2314.
17. R. C. M. Oliveira and G. F. Bauerfeldt, Int. J. Quantum Chem., 2012, 112, 3132.
18. J. I. Steinfeld, J. S. Francisco and W. L. Hase, Chemical Kinectics and Dynamics, Upper Saddle River, New Jersey, 1999.
19. M. Francisco-Márquez, J. R. Alvarez-Idaboy, A. Galano and A. Vivier-Bunge, Phys. Chem. Chem. Phys., 2004, 6, 2237.
20. M. C. Piqueras, R. Crespo, I. Nebot-Gil and F. Tomás, J. Mol. Struct.: THEOCHEM, 2001, 537, 199.
21. D. L. Singleton and R. J. Cvetanovic, J. Am. Chem. Soc., 1976, 98, 6812.
22. J. R. Alvarez-Idaboy, N. Mora-Diez and A. Vivier-Bunge, J. Am. Chem. Soc., 2000, 122, 3715.
23. J. Daranlot, K. M. Hickson, J.-C. Loison, R. Méreau, F. Caralp, W. Forst and A. Bergeat, J. Phys. Chem. A, 2012, 116, 10871.
24. J.-C. Loison, M.-T. Rayez, J.-C. Rayez, A. Gratien, P. Morajkar, C. Fittschen and E. Villenave, J. Phys. Chem. A, 2012, 116, 12189.
25. N. D. Vu, V. Khamaganov, V. S. Nguyen, S. A. Carl and J. Peeters, J. Phys. Chem. A, 2013, 117, 12208.
26. J. Zheng, R. J. Rocha, M. Pelegrini, L. F. A. Ferrão, E. F. V. Carvalho, O. Roberto-Neto, F. B. C. Machado and D. G. Truhlar, J. Chem. Phys., 2012, 136, 184310.
27. E. E. Greenwald, S. W. North, Y. Georgievskii and S. J. Klippenstein, J. Phys. Chem. A, 2005, 109, 6031.
28. L. Zhu and W. L. Hase, Chem. Phys. Lett., 1990, 175, 117.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c4ra00695j

---