Friction of aromatic thiol monolayers on silver: SFA and AFM studies of adhesive and non-adhesive contacts†
Y. Yang‡
,
J. Singh§
and
M. Ruths*
Department of Chemistry, University of Massachusetts Lowell, 1 University Avenue, Lowell, MA 01854, USA. E-mail: marina_ruths@uml.edu
First published on 4th April 2014
Abstract
The boundary friction of aromatic thiol (thiophenol, p-phenylthiophenol, and p-terphenylthiol) and octadecanethiol self-assembled monolayers on template-stripped silver was measured under adhesive and non-adhesive conditions with the Surface Forces Apparatus (SFA) and Atomic Force Microscopy (AFM). In non-adhesive contacts, the friction force increased linearly with load. Friction coefficients obtained with the two techniques were in good agreement and decreased with increasing packing density of the aromatic monolayers, but did not reach the low value obtained for octadecanethiol. The sublinear increase in friction force vs. load in adhesive contacts was evaluated as critical shear stresses based on nominal contact areas directly measured with the SFA and calculated using the Thin-Coating Contact Mechanics model for the AFM. The same trend was found in the shear stresses as in the friction coefficients.
Introduction
Friction and lubrication are complex processes where very different responses can be obtained through slight variations of materials and conditions. The fields of nano- and microtribology have been developed to provide a fundamental understanding of friction at the molecular, nanoscopic, and microscopic length scales, with the expectation that macroscopic friction phenomena may eventually be explained and predicted based on this knowledge. In boundary friction, which involves bare or monolayer-covered surfaces in “dry” contact or separated by fluid-like films with a thickness of a few molecular diameters,1 it is known that the chemical properties (molecular structure, conformation, order, interaction, and reactivity) of the surfaces and films and the topology (at the molecular, nanoscopic, and microscopic length scales) play important roles. These parameters can be explored by direct friction force measurements using the Surface Forces Apparatus (SFA) and Atomic Force Microscopy (AFM).The interacting surfaces in the SFA and AFM are typically assumed to form a “single-asperity” contact, where the area of contact is the nominal (apparent) one between a perfectly smooth sphere and a flat surface. The friction force, F, measured with these techniques at low loads, L, in an adhesive contact between surfaces that can be considered “atomically smooth” (mica or other crystalline substrates) or slightly rough at the molecular level (e.g., self-assembled monolayers of different packing density) has been observed to increase sub-linearly with L,1–12 in proportion to the nominal contact area, A (“adhesion-controlled” friction), and thus showing an apparent dependence on the radius of curvature, R, of the SFA surfaces or AFM tip in a manner predicted by contact mechanics models for macroscopic bodies.13–15 In contrast, surfaces with no or very low adhesion have shown a linear dependence of F on L with no apparent dependence on R (“load-controlled” friction).6–12,16–20
These friction responses are not fully explained, although they have been observed for decades and key aspects of them can be reproduced in computer models.21 Recent computer simulations22–24 have suggested that within the nominal contact area, the size of the real, molecular contact area as well as its increase with increasing load are adhesion-dependent, but in a different manner than that observed for nominal or macroscopic contacts.13–15 Molecular scale roughness, real contact areas, and changes therein are difficult to quantify in nanoscale friction experiments, which involve deformable substrates in continuous motion under considerable pressure. In contrast, the nominal contact area can be either directly measured (in the SFA) or estimated from contact mechanics models (for the AFM), although concerns have been raised about the applicability of such models on the nanometer and sub-nanometer scale25 where atomic level roughness causes local changes in the pressure. This influence of the substrate structure was reduced but not removed when a molecularly thin film was present in the contact.24
Here, investigations of the adhesion and load contributions in different systems with roughness at the atomic and molecular levels were extended from nanometer-sized contacts in the AFM to larger areas in the SFA. In the SFA, where the radius of curvature of the surfaces is 5–6 orders of magnitude larger than in the AFM, the nominal contact area is 3–4 orders of magnitude larger and the friction response is thus an average over many more molecules than in the AFM. Aromatic thiol self-assembled monolayers (SAMs) and a close-packed alkanethiol SAM were chosen as model systems to further explore the effects of molecular structure and monolayer packing density and rigidity.26–29 The monolayers were formed on template-stripped silver in order to utilize the optical interferometry technique available for measurements of R and A in the SFA. The adhesion was modified by immersing the contacts in either dry N2 gas or ethanol to obtain van der Waals interactions of different magnitude between the surfaces. Previous work has indicated that ethanol does not remain confined between the surfaces under the chosen conditions,8–10 but some penetration of ethanol into poorly packed monolayers cannot be excluded.
Friction data were acquired in adhesive and in non-adhesive contacts with both techniques, building on previous work involving only one technique or one condition, such as comparing different surface or tip radii or different adhesion strengths within one technique,6–12,16,19 or comparison of AFM and SFA data obtained under non-adhesive conditions (linear friction) only.18 The observed sub-linear and linear F vs. L in adhesive and non-adhesive systems, respectively, were in agreement with the responses predicted by computer simulations of real contact areas.22–24 A good agreement was found between friction coefficients measured with SFA and AFM in non-adhesive contacts. The friction of the aromatic SAMs decreased with increasing packing density but was significantly higher than that of the alkanethiol. The same trend was seen under adhesive conditions in the critical shear stresses calculated from F values obtained with both techniques and the corresponding nominal contact areas A.
Materials and methods
Self-assembled monolayers on silver
Aromatic and polyaromatic thiols are known to form self-assembled monolayers (SAMs) on silver,30–36 although less information is available on the resulting structures than on those formed on gold (cf. ref. 9 and references therein). Schematic molecular structures of the compounds investigated here, thiophenol (TP, Fluka, purity 99.6%), p-phenylthiophenol (PTP, Oakwood Products, West Columbia, SC, 97%), and p-terphenyl thiol (TPT, Frinton Laboratories, Vineland, NJ), are shown in Scheme 1.For the AFM experiments, monolayers of these thiols and of 1-octadecanethiol (ODT, Sigma-Aldrich, 98%) were formed by immersing template-stripped silver substrates overnight in ethanol (Sigma-Aldrich, ≥99.5%) solutions with the concentrations given in Table 1. The 50 nm thick template-stripped silver was prepared analogously to template-stripped gold substrates in ref. 9, i.e., by letting the silvered side of a mica sheet adhere to heated polystyrene, allowing the resulting assembly to cool, and removing the mica right before immersing the substrate in thiol solution. The extent of possible oxidation of the freshly exposed template-stripped silver (previously in contact with the mica) while transferring the substrate into solution was not explored in this study. No differences were observed in the contact angles or friction of monolayers on substrates prepared from silver evaporated the same day or months earlier, provided that the exposure to laboratory air was brief after removing the mica. For the SFA measurements, the template-stripped silver was formed on a half-cylindrical quartz-glass support by gluing the silvered side of a mica sheet down with Norland Optical Adhesive #61, cured with a Pen-Ray lamp (18 W) at a distance of about 2 cm for 1.5 h. This glue does not dissolve and shows minimal swelling when immersed in ethanol during the self-assembly. The opposing surface in the SFA measurements was a bare (unmodified), back-silvered mica surface, whereas in the AFM experiments it was a Si tip (CSC17, MikroMasch) covered with a layer of native oxide.
| SAM | Conc. (mM) | h (nm) | Molec. area (nm2) | θtilt (°) |
|---|---|---|---|---|
| a Estimated from the S2p/Ag3d ratio measured by XPS and the average molecular area of ODT. | ||||
| TP | 0.8–1.0 | 0.6 (ref. 32) | 0.305 (ref. 30) | 24 (ref. 32) |
| 0.7 (ref. 34) | 0.328 (ref. 31) | 29 (ref. 30) | ||
| 37 (ref. 33) | ||||
| PTP | 0.5–0.6 | 1.1 (ref. 32) | 0.27a | 18 (ref. 36) |
| 1.3 (ref. 34) | 0–10 (ref. 35) | |||
| TPT | 0.03–0.05 | 1.5 (ref. 32) | 0.24a | 16 (ref. 32) |
| 1.7 (ref. 36) | ||||
| ODT | 1.0 | 2.41 (ref. 37) | 0.2175 (ref. 37) | 12 (ref. 37) |
| 0.195 (ref. 38) | ||||
Some information on monolayer thicknesses h, molecular areas and tilt angles on silver can be found in the literature (cf. Table 1), and averages of these values of h were used in the contact mechanics model described below. TP is known to form a poorly packed monolayer on gold, whereas PTP and TPT form more close-packed, rigid layers with their molecules in a nearly upright orientation, and qualitative statements in the literature suggest that a similar behavior is expected on silver although values of the molecular area were found only for TP (Table 1). The molecular areas of PTP and TPT on silver were estimated by using X-ray photoelectron spectroscopy (XPS, VG ESCALAB MKII, Mg Kα X-ray, 200 W). Spectra of the SAMs (PTP, TPT and, for comparison, 1-octadecanethiol) on silver were obtained, referenced to C(1s) = 284.6 eV. From the spectra, the sulfur to silver ratio (S2p/Ag3d) was calculated: 1-octadecanethiol (0.093), PTP (0.072), and TPT (0.081). Based on the reported molecular area37,38 of 1-octadecanethiol, (an average value of 0.21 nm2 per molecule, cf. Table 1), the molecular areas of PTP and TPT on Ag were estimated proportionally: 0.27 nm2 (PTP), 0.24 nm2 (TPT). These values are smaller than the literature values for TP (Table 1), which is consistent with the expected more close-packed structure of the PTP and TPT monolayers. For comparison, the area occupied by a vertically oriented benzene ring is 0.21 nm2, based on van der Waals and covalent radii.39,40
Contact angles and surface energies
A Krüss Drop Shape Analysis System 100 (Germany) was used to measure the advancing and receding contact angles of distilled water, and the advancing contact angles of methyl iodide (MI), on the aromatic SAMs (Table 2). The uncertainty in the measurement is about 1°. The values in Table 2 are averages of 2–5 measurements at different positions on several separately prepared samples. The corresponding experimental values of the surface energies, γYD, were calculated using the Young–Dupré equation (cf. ESI†).41,42 The values of γYD = γpS + γdS, where γpS and γdS are the polar and dispersive contributions to the surface energy of the solid, respectively, are given in Table 2, and were around 38 mJ m−2 (for ODT, γYD = 27 mJ m−2). γpS is quite low in all the aromatic systems, i.e., the surface energy of the SAMs arises mainly from dispersive intermolecular interactions as noted previously for monolayers of these compounds and phenyl terminated alkanethiols on gold.9,10| SAM | θadv,H2O (°) | θrec,H2O (°) | θadv,MI (°) | γpS (mJ m−2) | γdS (mJ m−2) | γYD (mJ m−2) | γvdW (mJ m−2) |
|---|---|---|---|---|---|---|---|
| TP | 82 | 77 | 41 | 3.6 | 35.9 | 39.5 | 46 |
| PTP | 94 | 74 | 44 | 0.6 | 37.4 | 38 | 41 |
| TPT | 92 | 74 | 44 | 1.0 | 36.5 | 37.5 | 41 |
These values can be compared to theoretical surface energies, γvdW = AH/(24πD0)2, (Table 2) at a cut-off distance D0 = 0.165 nm.41 The Hamaker constant AH was calculated according to the van der Waals–Lifshitz theory for a symmetrical three-layer system41 SAM/dry N2 gas/SAM, with bulk refractive index and dielectric constant 1.59 and 4.26 for TP, 1.55 and 4.5 for PTP, and 1.55 and 4.2 for TP. Using the corresponding values for ODT, 1.47 and 2.2, one obtains γvdW = 31 mJ m−2. A similar approach can be used to calculate the theoretical interfacial energy in three-layer asymmetric systems, SAM/dry N2 gas or ethanol/mica or SiO2. Such interfacial energies are relevant for comparison with the work of adhesion from the pull-off regime in the friction experiments. The bulk refractive index and dielectric constant 1.6 and 7 for mica and 1.45 and 3.8 for SiO2 were used to calculate the theoretical interfacial energy in dry N2 and in ethanol. These values are given in Table 3 in connection with the discussion of the experimental values.
Friction measurements with SFA
In the SFA,43 normal forces (load, L) and lateral forces (friction force, F) are measured between two macroscopic surfaces placed in a crossed-cylinder configuration, which at small separations is equivalent to the geometry of a sphere near a flat surface. The surfaces form an optical interferometer that permits the determination of gap thickness (film thickness)44 between the facing surfaces with an accuracy of 0.1–0.2 nm. The interference fringe pattern is observed in two perpendicular directions for measurements of the radius of curvature of the surfaces, R, with an accuracy of about 10% (R is typically a few cm). In a similar manner, the diameter of a flattened contact region (for example, surfaces in adhesive or compressive contact during a friction measurement) can be measured with an accuracy of 1–2 μm. This diameter is typically 10–200 μm, depending on the strength of adhesion, applied normal force (load), and deformability of the surfaces and glue layers supporting them. The nominal area of contact between the surfaces is therefore typically found in the range 100–30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 μm2, in good agreement with predictions from contact mechanics models for interacting bulk or layered materials.13,45
000 μm2, in good agreement with predictions from contact mechanics models for interacting bulk or layered materials.13,45
In these experiments, we used an SFA3 (ref. 46) with sliding attachments as described in detail in ref. 47. Compressive or tensile loads were measured and regulated by moving the base of a double cantilever leaf spring (supporting the lower surface) vertically with mechanical stages and detecting its deflection. The spring had a spring constant of 340 N m−1, giving a sensitivity in L of about ca. 5 × 10−8 N. To induce sliding, this lower surface was moved laterally back and forth over a distance of 10–20 μm at a constant velocity of v = 1.6 or 3.2 μm s−1 using a piezoelectric bimorph device.47 The upper surface was mounted on a friction device, on strain gauge-equipped springs (spring constant 650 or 2400 N m−1) whose deflection was proportional to the lateral force between the surfaces (sensitivity in F of a few μN). In cases of very high friction (in the experiments in N2), the range of linear motion of the bimorph device was too small to induce sliding of the surfaces. Then the friction device was used as both an actuator (using a DC motor) and a detector in back-and-forth sliding over a distance of 100–200 μm at a constant speed chosen in the range 3–6 μm s−1. No dependence of the friction force on the sliding velocity was detected in the investigated range.
After mounting the surfaces in the instrument chamber, it was purged with N2 for a few hours to remove water vapor which would otherwise capillary condense when the surfaces were brought into contact. During experiments in dry N2 gas, the chamber was kept dry with P2O5 in a salt boat inserted through its wall. For experiments in ethanol (Sigma-Aldrich, ≥99.5%), a small droplet of ethanol, dried over molecular sieves, was injected between the surfaces through a flush-cleaned PTFE syringe filter (Pall Acrodisc, pore size 0.45 μm). Additional ethanol was placed in the boat (instead of P2O5) to decrease the evaporation from the droplet between the surfaces. In some experiments, several contact positions could be found so that measurements were done first in dry N2 gas and then in ethanol, on the same surfaces but on separate contact positions.
Friction measurements with AFM
Friction forces, F, were also measured with atomic force microscopy (AFM) in lateral or friction mode, using a Multimode AFM with a Nanoscope IIIa controller (Bruker). The experiments were conducted over a scan length of 1 μm with bare Si tips (CSC17, MikroMasch) carrying a native silicon oxide layer. The scan velocity was 2 μm s−1. The dependence of F on velocity was weak in the range 0.4–0.122 μm s−1 and is not reported here. The normal and lateral spring constants were determined from the resonance frequency and quality factor48,49 of the cantilevers and from the dimensions50,51 as measured by scanning electron microscopy. The normal spring constants were in the range 0.16–0.23 N m−1 and the lateral spring constants were 20–30 N m−1. The geometric mean radius of curvature of the tips, R, was determined by reverse imaging of a calibration sample (TGT01, MikroMasch) at scan angles of 0° and 90°, with an uncertainty of ΔR ≈ 3 nm for R < 100 nm and ΔR ≈ 5 nm for larger tips. The tips used here had radii of 56, 69, 159 and 372 nm.As in the SFA experiments, the AFM measurements were performed in ethanol (using a fluid cell) and in dry N2 (in a home-made instrument enclosure). In the experiments in N2, a relative humidity of ≤1.5% (monitored with a Vaisala DM70 dewpoint meter) was reached after purging for 2 h. The statistical error in F (standard deviation of the mean, from averaging the sliding portion of the friction loop) was ca. 0.2 nN at F <+50 nN, and 0.5 nN at higher F, and is not shown in Fig. 2, 5, and 7 below since it is similar to the height of the symbols. As in the experiments with the SFA, in cases where both conditions could be explored in the same experiment, the ones in N2 were done first to reduce the risk of contamination.
Contact mechanics model
The effective Young's modulus of the mica–glue assembly in the SFA is typically a few tens of GPa.52 Deformations due to adhesion and compression occur mainly in the glue layer, so that the maximum pressure in the center of the contact is not more than a few tens of MPa. In contrast, the Young's moduli of the AFM tip and substrate, 70–80 GPa for silver, 70–80 GPa for SiO2,53 and 170 GPa for Si,50,51 are much higher than that of a self-assembled monolayer, which is expected to be only a few GPa (cf. Discussion and ref. 9 and 10). At low L, the radius a of the nominal contact area in the AFM is smaller than or similar to the monolayer thickness h, and the deformations occur mainly within the monolayer. At higher loads, the effective stiffness of such a layered system is still affected by the monolayer and contact mechanics models for homogeneous elastic bodies13–15 are not expected to apply.The extended Thin-Coating Contact Mechanics (TCCM) model was used to estimate the nominal contact areas in the AFM experiments on adhesive systems. Measured F values were compared to calculated curves of F = ScA, where Sc was a constant, the critical shear stress, and A was the nominal contact area at a given load L. The details of this model,54,55 examples of its application to monolayer systems, and evaluations of uncertainties in calculated values are shown elsewhere,56,57 and only selected information needed for the discussion of the present work is shown here. The probe (a spherical indenter) and the flat substrate are assumed to be rigid, which is a reasonable approximation at low load in our systems. The relationship between L, the radius of the contact area, a, and the work of adhesion (W = 2γ) in the extended TCCM model is given in non-dimensional form by54,55
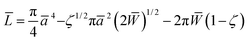 | (1) |
![[L with combining macron]](https://www.rsc.org/images/entities/i_char_004c_0304.gif) = L/(EuRh),
= L/(EuRh), 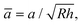 and
and ![[W with combining macron]](https://www.rsc.org/images/entities/i_char_0057_0304.gif) = W/(Euh). The uniaxial strain modulus is given by Eu = E(1 − ν)/[(1 + ν)(1 − 2ν)], where E is Young's modulus, ν is Poisson's ratio (0.4), and h is the film thickness (monolayer thickness in Table 1). ζ = 2Wh/Euδc2 is a transition parameter (0 ≤ ζ ≤ 1), a measure of the ratio of elastic deformation to the effective range of the surface forces. ζ = 0 and ζ = 1 correspond to limits where the range of adhesion forces is large and small compared to the elastic deformations. The critical separation, δc, was assumed to be 1 nm,54,55 as in previous applications of this model to monolayer systems.9,10
= W/(Euh). The uniaxial strain modulus is given by Eu = E(1 − ν)/[(1 + ν)(1 − 2ν)], where E is Young's modulus, ν is Poisson's ratio (0.4), and h is the film thickness (monolayer thickness in Table 1). ζ = 2Wh/Euδc2 is a transition parameter (0 ≤ ζ ≤ 1), a measure of the ratio of elastic deformation to the effective range of the surface forces. ζ = 0 and ζ = 1 correspond to limits where the range of adhesion forces is large and small compared to the elastic deformations. The critical separation, δc, was assumed to be 1 nm,54,55 as in previous applications of this model to monolayer systems.9,10
Previous studies of aromatic and aliphatic monolayers8–10 have indicated that different values of E are needed to describe such systems. Here, E = 7 GPa (Eu = 15 GPa) was used for most of the data on aromatic systems and E = 0.2 or 0.5 GPa (Eu = 0.4 or 1 GPa) for ODT. The uncertainty in Sc mainly arises from propagation of the uncertainties in R, h, Eu, and W in the calculation of A. The uncertainty in Sc can be calculated by differentiating eqn (1) and using ΔR = 3 nm (R < 100 nm) or 5 nm (R ≥ 100 nm), Δh = 0.2 nm, ΔEu = 2 GPa for the aromatic compounds and 0.06 GPa for ODT, and ΔW = 0.002 J m−2. Following the procedure in ref. 9, the relative uncertainty in Sc in the current experiments was estimated to be about 20% for TP, 13% for PTP and TPT, and 10–13% for ODT.
The net displacement U (here, the indentation into the monolayer) can be calculated from54,55
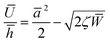 | (2) |
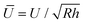 and
and 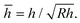 Estimates for the monolayer systems (based on the chosen values of E) suggest that at the monolayer transitions observed in the AFM experiments (indicated in Fig. 2 and 5), the net displacement in the aromatic systems is 10–15% of the monolayer thickness, which is likely to be beyond the linear elasticity regime assumed in the TCCM model. For ODT it is close to 50% at the transition for R = 69 nm and about 20% for R = 372 nm. In each case, the displacement is approximately half that value at loads half-way between the pull-off and the transition points, which is the region where comparison between the model and the experimental data is of greater interest.
Estimates for the monolayer systems (based on the chosen values of E) suggest that at the monolayer transitions observed in the AFM experiments (indicated in Fig. 2 and 5), the net displacement in the aromatic systems is 10–15% of the monolayer thickness, which is likely to be beyond the linear elasticity regime assumed in the TCCM model. For ODT it is close to 50% at the transition for R = 69 nm and about 20% for R = 372 nm. In each case, the displacement is approximately half that value at loads half-way between the pull-off and the transition points, which is the region where comparison between the model and the experimental data is of greater interest.
Results
Friction at low adhesion (in ethanol)
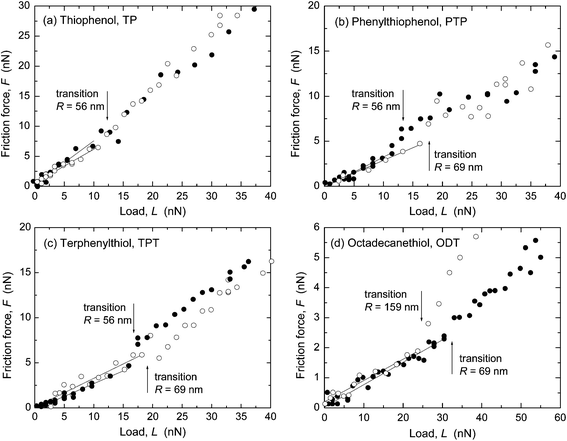
Representative results from SFA and AFM measurements performed in ethanol are shown in Fig. 1 and 2, respectively. The interfacial energy estimated from the pull-off forces with both techniques was low, γ ≤ 2 mJ m−2, in all four systems. The sliding velocity v was a few μm s−1. The radius of curvature, R, of the surfaces in the SFA was in the range 2–5 cm (R was not measured in all SFA experiments, cf. ESI†) and in the AFM experiments the tip radius was 56–159 nm. A linear dependence of the friction force, F, on load, L, was observed, with F → 0 when L → 0. In the AFM experiments (Fig. 2), a transition from the reproducible, linear friction force at low loads to a more scattered and less reproducible regime at higher loads occurred at a pressure of about 1–2 GPa, which has been observed previously in monolayer systems at similar pressures.8–10,18,19 Only the data at low loads, before the transition marked with an arrow in the figures, were included in the linear fit to obtain the friction coefficient μ. Such transitions were not observed in the SFA experiments (Fig. 1) because the pressure was lower due to the larger and more deformable substrates.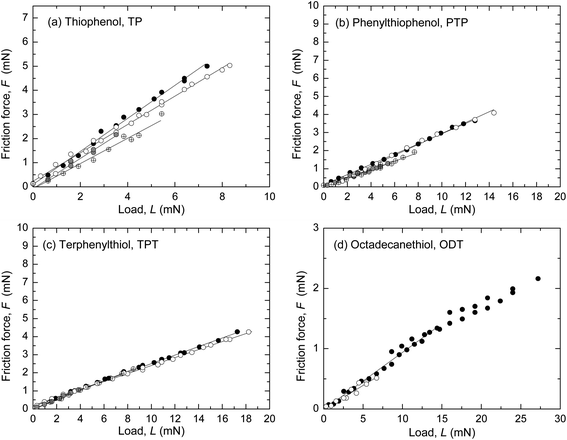 | ||
Fig. 1 Friction force F vs. load L measured in ethanol with the SFA. The upper disk carried a self-assembled monolayer on template-stripped silver and the bottom surface was bare (unmodified) mica. (a) Thiophenol (TP), ( and and  ) v = 3.2 μm s−1, R not measured; (gray circle and ) v = 3.2 μm s−1, R not measured; (gray circle and  ) v = 1.6 μm s−1, R = 2.53 cm and 4.69 cm. μ = 0.52–0.69. (b) p-Phenylthiophenol (PTP), ( ) v = 1.6 μm s−1, R = 2.53 cm and 4.69 cm. μ = 0.52–0.69. (b) p-Phenylthiophenol (PTP), ( and and  ) v = 3.2 μm s−1, R not measured; (gray circle and ) v = 3.2 μm s−1, R not measured; (gray circle and  ) v = 1.6 μm s−1, R = 2.57 cm and 4.41 cm. μ = 0.227–0.298. (c) p-Terphenyl thiol (TPT), ( ) v = 1.6 μm s−1, R = 2.57 cm and 4.41 cm. μ = 0.227–0.298. (c) p-Terphenyl thiol (TPT), ( and and  ) v = 3.2 μm s−1, R not measured; (gray circle and ) v = 3.2 μm s−1, R not measured; (gray circle and  ) v = 1.6 μm s−1, R = 3.13 cm and 2.25 cm. μ = 0.221–0.290. (d) 1-Octadecanethiol (ODT), ( ) v = 1.6 μm s−1, R = 3.13 cm and 2.25 cm. μ = 0.221–0.290. (d) 1-Octadecanethiol (ODT), ( and and  ) v = 3.2 μm s−1, R not measured and R = 2.9 cm. μ = 0.079–0.095. Average μ from these and additional measurements are given in Table 3. ) v = 3.2 μm s−1, R not measured and R = 2.9 cm. μ = 0.079–0.095. Average μ from these and additional measurements are given in Table 3. | ||
Values of μ from several SFA and AFM experiments, including the ones shown in Fig. 1 and 2, are summarized in Fig. 3 and Table 3 (see also ESI†). In Fig. 3, μ is shown as a function of molecular area to illustrate the effect of packing density in the aromatic systems. ODT, which has a different molecular structure, was included in the graph for comparison. Except for in the case of TP, where slightly higher μ were obtained with AFM, the values obtained with the two techniques were very similar and showed the trend μTP > μPTP ≥ μTPT > μODT.
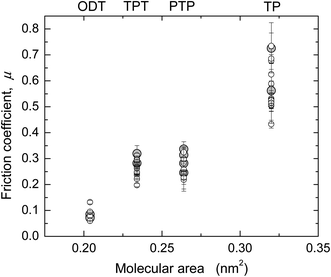 | ||
Fig. 3 Friction coefficients μ for the four monolayer systems, measured in ethanol with SFA ( ) and AFM (larger gray circles). ) and AFM (larger gray circles). | ||
| System | μ | Sc (MPa) | γTCCMa (mJ m−2) | γvdW,AFM (mJ m−2) | ||
|---|---|---|---|---|---|---|
| SFA | AFM | SFA | AFM | |||
| a From the extended TCCM model,54,55 γTCCM = W/2.b E = 3–7 GPa.c E = 0.2–0.5 GPa. | ||||||
| TP | 0.56 ± 0.02 | 0.64 ± 0.08 | ≥20 (estim.) | 683 ± 44b | 26 ± 1 | 36 |
| PTP | 0.26 ± 0.01 | 0.29 ± 0.02 | 7.3 ± 0.6 | 385 ± 18b | 32 ± 3 | 34 |
| TPT | 0.263 ± 0.007 | 0.30 ± 0.02 | 11.5 ± 0.9 | 465 ± 27b | 32 ± 2 | 34 |
| ODT | 0.09 ± 0.01 | 0.077 ± 0.004 | 2.9 ± 0.3 | 20 ± 7c (R = 69 nm) | 28 ± 1 | 30 |
| 5.1 ± 1.1c (R = 372 nm) | ||||||
Friction at higher adhesion (in N2)
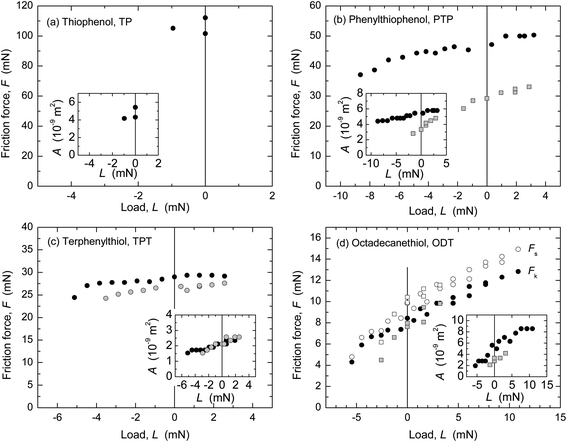
The friction forces of the four monolayer systems were also measured in dry N2 gas (r.h. < 1.5%) with the SFA (Fig. 4) and AFM (Fig. 5). In N2 gas, the adhesion between the surfaces is higher than in ethanol because of the stronger van der Waals forces across dry N2 than across ethanol. Interfacial energies can be calculated from the measured pull-off forces (and, in the case of the AFM data, from the TCCM model) and compared to values for mica–SAM interaction or silica–SAM interaction expected from van der Waals–Lifshitz theory (Table 3). A good agreement was found. Similarly to in many previous studies of adhesive systems, the values of F and the shape of the F vs. L curves in Fig. 4 and 5 were quite different from the data at low adhesion shown in Fig. 1 and 2.In the SFA experiments, the nominal contact area A can be directly measured (cf. inserts in Fig. 4) and the critical shear stress Sc directly calculated as F/A. Within experimental uncertainty (note that the relative uncertainty in A is higher than that in F, cf. Materials and methods), Sc was a constant for each F vs. L curve and reproducible from experiment to experiment. The Sc values from several experiments (cf. ESI†) are shown in Fig. 6a and an average for each monolayer system is given in Table 3.
 | ||
| Fig. 6 Critical shear stresses Sc for the four monolayer systems from (a) SFA and (b) AFM experiments in dry N2. | ||
The friction force in the TP system was very high and the template-stripped silver surface was easily damaged when sliding commenced. Only an estimate of Sc is given for this system. The other monolayers protected the silver surface much better and damage only appeared after prolonged sliding, as a small roughening of the surface (not the large failure commonly seen if a mica surface becomes damaged). ODT exhibited stick-slip sliding at the investigated sliding speeds and loads, shown as static (Fs) and kinetic friction (Fk) values in Fig. 4d. The calculation of Sc for ODT is based on Fk. The other three systems occasionally showed stick-slip at the lowest loads, which changed into to smooth kinetic sliding after a few back-and-forth passes over the sliding range.
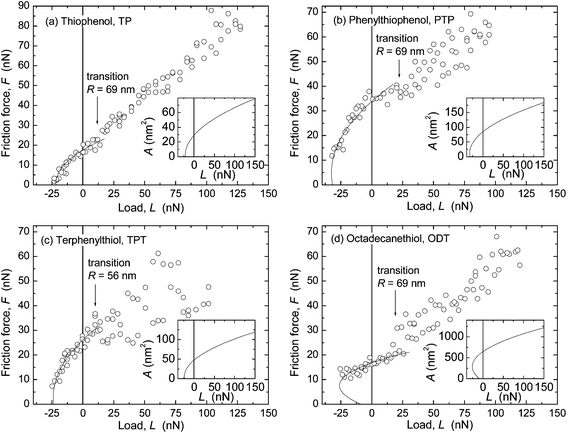
AFM data from adhesive contacts cannot be analyzed in such a direct manner, since the nominal contact area cannot be directly measured. The solid curves in the main panels of Fig. 5 are intended to describe the low load regime of the data only (below the transition regimes indicated by arrows), and represent F = ScA, where Sc is a constant and the contact area A (A = πa2) was calculated from a using a uniaxial elastic modulus of Eu = 15 GPa (E = 7 GPa, ν = 0.4) for the aromatic monolayers and E = 0.2 or 0.5 GPa (Eu = 0.4 or 1 GPa) for ODT. The resulting values of critical shear stress, Sc, from these and other experiments (cf. ESI†) are summarized in Fig. 6b and Table 3. The highest friction is obtained with TP, and that of the more closely packed systems is lower. In each system, the interfacial energy γTCCM (=W/2) used in the calculated curves to reproduce the pull-off regime is in good agreement with the interfacial energy γvdW,AFM calculated from bulk dielectric properties (Table 3).
Discussion
Surface and interfacial energies
The advancing and receding contact angles of water were similar on the PTP and TPT monolayers on silver, and slightly lower values were found for TP (Table 2). They were in good agreement with literature values in cases where these can be found30,32,34,36 and similar to values obtained for these thiols on gold, where it has been concluded that the flat side of the terminal aromatic ring is partly accessible to the water.9,10 The contact angle hysteresis (θadv − θrec ≈ 5–20°) was consistent with a similar chemical structure at the uppermost part of the three aromatic monolayers, and also similar to that found for these compounds on Au.The experimental surface energy values γYD obtained from the contact angle measurements were in good agreement with surface energies γvdW (Table 2) calculated using van der Waals–Lifshitz theory. Except for in the case of TP, there was also a good agreement between the interfacial energies γTCCM (=W/2), obtained from the comparison of curves calculated with the contact mechanics model to the pull-off region of AFM data (Fig. 5) and the interfacial energies γvdW,AFM calculated for the three-layer system SAM/N2 gas/SiO2 (Table 3). A similar calculation of interfacial energy can be done for the three-layer system SAM/ethanol/SiO2, giving values of about 2 mJ m−2, which is in good agreement with those obtained in the experiments in ethanol.
Friction measured with the SFA versus the AFM
An important issue in experiments with the SFA and AFM is the difference in contact area and pressure. Within the load range that can be conveniently reached in the SFA, the maximum pressure in the contact area is generally less than 50 MPa, whereas the contact pressures in the AFM, even at very low loads, are already close to the GPa range. In the very first systematic comparison of friction measurements with SFA and AFM, large differences were observed in the measured friction of confined polymer melts.58 This was most likely due to different film thicknesses and AFM probe penetration of the confined films. One previous study has shown that quantitatively comparable friction results could be obtained with these techniques in non-adhesive systems where one or both surfaces were covered with a self-assembled aromatic silane monolayer,18 as a way to provide a confined film (boundary lubricant layer) with similar thickness and structure in the different pressure ranges investigated.The thiol monolayers in this study were chosen with this criterion in mind, and only the low-load data from AFM was evaluated, putting aside data from higher loads/different monolayer conformations expected after the monolayer transitions. Very similar values of the friction coefficients were consistently found with the two different methods for non-adhesive contact (Fig. 1 and 2). There was a systematic decrease in μ with increasing packing density (Table 3), i.e., μ was highest for TP, and lower for PTP and TPT, but still higher than μ of close-packed ODT monolayers under similar conditions. The values were lower than those measured with AFM in systems where both surfaces carried an aromatic thiol monolayer.9
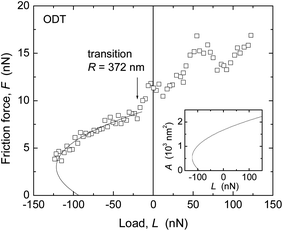
Similar trends were found in the critical shear stresses, and within the accuracy of our experiments, Sc appeared to be a constant over the load range investigated in each experiment (for example, within each data set shown in Fig. 4 and 5). However, a direct comparison between values obtained with the two techniques was complicated by the different methods by which the Sc values were obtained (from directly measured versus inferred contact areas where the choice of E strongly affects A and thus Sc), and by the observation of different results when a tip with much larger radius (R = 372 nm) was used for measurements on ODT (Fig. 7) than that used in Fig. 5d (69 nm).
When using R = 372 nm, a value of Sc = 5.1 ± 1.1 MPa was found (cf. tabulated values in ESI†), in closer agreement with the values measured with the SFA for ODT (2.9 ± 0.3 MPa, Table 3) and other close-packed alkane-based systems.20,59,60 In contrast, in AFM measurements in N2 on aromatic thiols on gold, good agreement was found between Sc values obtained with R = 53–300 nm.9 An important difference between these systems is the larger stiffness of the aromatic monolayers, as mentioned in the estimate of displacement in the section on the contact mechanics model. The effects of different displacement or penetration with different techniques in films thinner and stiffer than polymer melts (where this issue was first documented58) deserve further consideration.
Summary
The Surface Forces Apparatus (SFA) technique and Atomic Force Microscopy (AFM) in friction mode were used to study the effects of adhesion strength and probe size on the friction forces in a series of self-assembled monolayer systems with different rigidity and packing density on silver substrates. A linear dependence of the friction force on load (F = μL) was found at low adhesion (measurements performed in ethanol). In the aromatic systems, μ was found to decrease with increasing packing density of the monolayers with both SFA and AFM. Higher adhesion (in N2 gas) gave an apparent dependence on the nominal contact area of the form F = ScA, where Sc is the critical shear stress. Sc can be calculated directly from the SFA data. In the cases of AFM, Sc values were obtained at low load in the adhesive systems by using the extended TCCM model for layered systems to calculate A vs. L. Sc was found to decrease with increasing molecular packing density. A Young's modulus of E ≈ 7 GPa was needed to reproduce the F vs. L curves in these adhesive systems, whereas octadecanethiol (ODT) monolayers were described by E ≈ 0.2 GPa and an Sc value closer to that obtained in the SFA experiments. Possible effects of displacement are discussed.Acknowledgements
The assistance of Jisun Im with XPS measurements is gratefully acknowledged. J. Mead is thanked for access to the contact angle analysis system and T. Pettersson is thanked for software used to analyze the AFM data. This work was supported by NSF CAREER award CMMI-0645065 and through the NSF-funded Nanoscale Science and Engineering Center – Center for High-Rate Nanomanufacturing (CHN) (award NSF-0425826).References
- J. N. Israelachvili and A. D. Berman, in Handbook of Micro/Nanotribology, ed. B. Bhushan, CRC Press, Boca Raton, FL, 2nd edn, 1999, pp. 371–432 Search PubMed.
- R. W. Carpick and M. Salmeron, Chem. Rev., 1997, 97, 1163–1194 CrossRef CAS PubMed.
- R. W. Carpick, N. Agraït, D. F. Ogletree and M. Salmeron, Langmuir, 1996, 12, 3334–3340 CrossRef CAS.
- G. Bogdanovic, F. Tiberg and M. W. Rutland, Langmuir, 2001, 17, 5911–5916 CrossRef CAS.
- S. Ecke and H.-J. Butt, J. Colloid Interface Sci., 2001, 244, 432–435 CrossRef CAS.
- C. R. Hurley and G. J. Leggett, Langmuir, 2006, 22, 4179–4183 CrossRef CAS PubMed.
- T. J. Colburn and G. J. Leggett, Langmuir, 2007, 23, 4959–4964 CrossRef CAS PubMed.
- M. Ruths, S. Lundgren, K. Danerlöv and K. Persson, Langmuir, 2008, 24, 1509–1516 CrossRef CAS PubMed.
- Y. Yang and M. Ruths, Langmuir, 2009, 25, 12151–12159 CrossRef CAS PubMed.
- Y. Yang, A. C. Jamison, D. Barriet, T. R. Lee and M. Ruths, J. Adhes. Sci. Technol., 2010, 24, 2511–2529 CrossRef CAS PubMed.
- K. Busuttil, N. Nikogeorgos, Z. Zhang, M. Geoghegan, C. A. Hunter and G. J. Leggett, Faraday Discuss., 2012, 156, 325–341 RSC.
- N. Nikogeorgos, C. A. Hunter and G. J. Leggett, Langmuir, 2012, 28, 17709–17717 CrossRef CAS PubMed.
- K. L. Johnson, K. Kendall and A. D. Roberts, Proc. R. Soc. London, Ser. A, 1971, 324, 301–313 CrossRef CAS.
- B. V. Derjaguin, V. M. Muller and Y. P. Toporov, J. Colloid Interface Sci., 1975, 53, 314–326 CrossRef CAS.
- R. W. Carpick, D. F. Ogletree and M. Salmeron, J. Colloid Interface Sci., 1999, 211, 395–400 CrossRef CAS PubMed.
- M. Ruths, J. Phys. Chem. B, 2006, 110, 2209–2218 CrossRef CAS PubMed.
- A. Berman, C. Drummond and J. Israelachvili, Tribol. Lett., 1998, 4, 95–101 CrossRef CAS.
- M. Ruths, N. A. Alcantar and J. N. Israelachvili, J. Phys. Chem. B, 2003, 107, 11149–11157 CrossRef CAS.
- M. Ruths, Langmuir, 2003, 19, 6788–6795 CrossRef CAS.
- M. Ruths and J. N. Israelachvili, in Springer Handbook of Nanotechnology, ed. B. Bhushan, Springer-Verlag, Berlin & Heidelberg, 3rd edn, 2010, pp. 857–922 Search PubMed.
- J. Gao, W. D. Luedtke, D. Gourdon, M. Ruths, J. N. Israelachvili and U. Landman, J. Phys. Chem. B, 2004, 108, 3410–3425 CrossRef CAS.
- Y. Mo, K. T. Turner and I. Szlufarska, Nature, 2009, 457, 1116–1119 CrossRef CAS PubMed.
- Y. Mo and I. Szlufarska, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 035405 CrossRef.
- S. Cheng, B. Luan and M. Robbins, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 016102 CrossRef.
- B. Luan and M. O. Robbins, Nature, 2005, 435, 929–932 CrossRef CAS PubMed.
- M. Salmeron, Tribol. Lett., 2001, 10, 69–79 CrossRef CAS.
- P. T. Mikulski and J. A. Harrison, J. Am. Chem. Soc., 2001, 123, 6873–6881 CrossRef CAS.
- B. Bhushan and H. Liu, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 245412 CrossRef.
- S. Lee, Y.-S. Shon, R. Colorado, Jr, R. L. Guenard, T. R. Lee and S. S. Perry, Langmuir, 2000, 16, 2220–2224 CrossRef CAS.
- J. Y. Gui, D. A. Stern, D. G. Frank, F. Lu, D. C. Zapien and A. T. Hubbard, Langmuir, 1991, 7, 955–963 CrossRef CAS.
- M. C. Schalnat and J. E. Pemberton, Langmuir, 2010, 26, 11862–11869 CrossRef CAS PubMed.
- S. Frey, V. Stadler, K. Heister, W. Eck, M. Zharnikov and M. Grunze, Langmuir, 2001, 17, 2408–2415 CrossRef CAS.
- A. A. Mani, Z. D. Schultz, B. Champagne, C. Humbert, L. Dreesen, A. A. Gewirth, J. O. White, P. A. Thiry, A. Peremans and Y. Caudano, Appl. Surf. Sci., 2004, 237, 444–449 CrossRef CAS PubMed.
- A. Shaporenko, A. Terfort, M. Grunze and M. Zharnikov, J. Electron Spectrosc. Relat. Phenom., 2006, 151, 45–51 CrossRef CAS PubMed.
- U. Weckenmann, S. Mittler, K. Naumann and R. A. Fischer, Langmuir, 2002, 18, 5479–5486 CrossRef CAS.
- A. Shaporenko, M. Brunnbauer, A. Terfort, M. Grunze and M. Zharnikov, J. Phys. Chem. B, 2004, 108, 14462–14469 CrossRef CAS.
- P. E. Laibinis, G. M. Whitesides, D. L. Allara, Y.-T. Tao, A. N. Parikh and R. G. Nuzzo, J. Am. Chem. Soc., 1991, 113, 7152–7167 CrossRef CAS.
- J. P. Folkers, J. A. Zerkowski, P. E. Laibinis, C. T. Seto and G. M. Whitesides, in ACS Symposium Series No. 499, ed. T. Bein, American Chemical Society, Washington, DC, 1992, pp. 10–23 Search PubMed.
- Y.-T. Tao, C.-C. Wu, J.-Y. Eu, W.-L. Lin, K.-C. Wu and C.-h. Chen, Langmuir, 1997, 13, 4018–4023 CrossRef CAS.
- H. H. Jung, Y. D. Won, S. Shin and K. Kim, Langmuir, 1999, 15, 1147–1154 CrossRef CAS.
- J. N. Israelachvili, Intermolecular and Surface Forces, Elsevier, Amsterdam, 3rd edn, 2011 Search PubMed.
- H. Y. Erbil, Surface Chemistry of Solid and Liquid Interfaces, Blackwell, Oxford, 2006 Search PubMed.
- J. N. Israelachvili and G. E. Adams, J. Chem. Soc., Faraday Trans. 1, 1978, 74, 975–1001 RSC.
- J. N. Israelachvili, J. Colloid Interface Sci., 1973, 44, 259–272 CrossRef CAS.
- I. Sridhar, K. L. Johnson and N. A. Fleck, J. Phys. D: Appl. Phys., 1997, 30, 1710–1719 CrossRef CAS.
- J. N. Israelachvili and P. M. McGuiggan, J. Mater. Res., 1990, 5, 2223–2231 CrossRef CAS.
- G. Luengo, F.-J. Schmitt, R. Hill and J. N. Israelachvili, Macromolecules, 1997, 30, 2482–2492 CrossRef CAS.
- J. E. Sader, J. W. M. Chon and P. Mulvaney, Rev. Sci. Instrum., 1999, 70, 3967–3969 CrossRef CAS PubMed.
- C. P. Green, H. Lioe, J. P. Cleveland, R. Proksch, P. Mulvaney and J. E. Sader, Rev. Sci. Instrum., 2004, 75, 1988–1996 CrossRef CAS PubMed.
- Y. Liu, T. Wu and D. F. Evans, Langmuir, 1994, 10, 2241–2245 CrossRef CAS.
- Y. Liu, D. F. Evans, Q. Song and D. W. Grainger, Langmuir, 1996, 12, 1235–1244 CrossRef CAS.
- H. K. Christenson, Langmuir, 1996, 12, 1404–1405 CrossRef CAS.
- R. G. Munro, Elastic Moduli Data for Polycrystalline Oxide Ceramics, NISTIR 6853, National Institute of Standards and Technology, Gaithersburg, Maryland, 2002 Search PubMed.
- E. D. Reedy, Jr, J. Mater. Res., 2006, 21, 2660–2668 CrossRef.
- E. D. Reedy, Jr, J. Mater. Res., 2007, 22, 2617–2622 CrossRef.
- E. D. Reedy, Jr, M. J. Starr, R. E. Jones, E. E. Flater and R. W. Carpick, in Proceedings of the 28th Annual Meeting of the Adhesion Society, Mobile, AL, 2005, pp. 366–368 Search PubMed.
- M. Chandross, C. D. Lorenz, M. J. Stevens and G. S. Grest, Langmuir, 2008, 24, 1240 CrossRef CAS PubMed.
- P. M. McGuiggan, J. Zhang and S. M. Hsu, Tribol. Lett., 2001, 10, 217–223 CrossRef CAS.
- A. I. Bailey and J. S. Courtney-Pratt, Proc. R. Soc. London, Ser. A, 1955, 227, 500–515 CrossRef CAS.
- B. J. Briscoe and D. C. B. Evans, Proc. R. Soc. London, Ser. A, 1982, 380, 389–407 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Calculation of surface energy. Friction coefficients. Critical shear stresses. See DOI: 10.1039/c4ra01803f |
| ‡ Current address: Lubrizol Advanced Materials, Inc., Brecksville, OH 44141, USA. Email: E-mail: yutao.yang@lubrizol.com |
| § Current address: domnick hunter Process Filtration, Oxnard, CA 93030, USA. Email: E-mail: jagdeep.singh@parker.com |
| This journal is © The Royal Society of Chemistry 2014 |