Tuning the reactivity of Ru nanoparticles by defect engineering of the reduced graphene oxide support

Abstract

We systematically investigated the electronic structure of Ru nanoparticles supported on various local structures on reduced graphene oxide (rGO) by first-principles-based calculations. We showed that Ru nanoparticles prefer to nucleate at these localized defect structures on rGO, which act as strong trapping sites for Ru nanoparticles and inhibit their aggregation. The binding of Ru nanoparticles to rGO, which is dependent on these local defect structures and correlates with the interfacial charge transfer, determines the electronic structure of the composites. Further study reveals that the performance of these composites against oxygen adsorption changes proportionally with the shift of the d-band center of the nanoparticles. The correlation between the defect structures on rGO and the reactivity of the composites suggests that controlled modification of the graphenic support by defect engineering would be an efficient way to fabricate new transition metal/rGO composites with high stability and desired reactivity.

---

Introduction

As a unique two-dimensional carbon material, graphene has been predicted to be an excellent support for dispersion of transition metal nanoparticle (TM NP) catalysts, due to its large surface area, outstanding electronic and thermal conductivity, as well as the high mechanical strength and potentially low production cost.^1–3 The graphene samples used as support materials for catalytic applications are commonly synthesized by oxidative exfoliation of graphite, followed by reduction and the product is called rGO.⁴ Depending on the conditions of exfoliation and subsequent reduction,⁵ the reported surface area of rGO is 600–900 m² g⁻¹, which is already comparable with or even higher than that of bundle of carbon nanotube (CNT) grown by chemical vapour deposition⁶ or mesoporous carbon⁷ and can be further increased by introduction of various defects.⁸

In contrast to conventional support materials in most of the supported-metal–NP composites for catalytic applications, which are catalytically inert and only provide a large surface area for the dispersion of TM NPs and keep them well-separated for reuse, some support materials, including rGO, have shown synergetic effects with the metal NPs and effectively enhance/modulate their activity or selectivity.^9–12 Various rGO supported TM NP composites, such as Pt,^13–15 Pd,¹⁶⁻¹⁸ Au,¹⁹ Ag,²⁰ Fe,²¹ Cu,^22,23 Ru,²⁴ Rh²⁵ and etc., have been fabricated and showed excellent catalytic performance in some important reactions including oxygen reduction, hydrodesulfurization, CO adsorption/desorption, methanol oxidation and etc.^13–25 Due to the localized nature of TM d-states and their dominant contribution to the reactivity of these TM–rGO composites, the electronic structure of these composites has already converged to the bulk limit²⁶ and the renown contribution of the quantum size effect to the reactivity and activity of these composites would be less significant.²⁷ Most of the TM–rGO composites outperform NPs of the same TM with similar size and morphology deposited on support materials other than rGO, showing that the enhanced catalytic performances of these TM–rGO composites should be mainly contributed by the strong interactions between the TM NPs and the graphenic support that interfere the electronic structure of the composites.^12,28–33 For example, Oh et al. investigated CO adsorption on Fe and Pt NPs deposited on graphenic carbon and they attributed the weakening of the CO–TM interaction to the formation of TM-carbon contact.^15,21 Similarly, small Pt NPs deposited on graphenic support have been proved to be CO tolerant when used as the electrode material for fuel cells.³⁴ Ru NPs of 2–3 nm in size supported on rGO also showed extraordinary high activity as compared with Ru NPs of similar size deposited on mesoporous carbon foam in catalytic hydrogenation of arene and the enhanced catalytic performance was explained with the intimate TM–rGO contact and the synergetic effect of the rGO support.^24,29 These findings further suggested the possibility of manipulating the catalytic activity of the deposited TM NPs by using rGO as the support material, though the detailed contribution of the TM NP–rGO interface to the performance of these composites has seldom been visited.

Recently, Ru and Ru alloy NPs deposited on carbon materials have drawn considerable attention for their outstanding catalytic performance. Ru NPs supported on active carbon showed high catalytic activity in hydrogenation of lactic acid, arene and ketone, and hydrolysis of NaBH₄.^35–38 Ru NPs embedded in ordered mesoporous carbon material also demonstrated a higher activity in Fischer–Tropsch synthesis,³⁹ hydrogenation of glucose,⁴⁰ and partial hydrogenation of dinitrobenzene into nitroanilines,⁴¹ owing to the intimate contact of Ru NP with the carbon support that improves hydrogen dissociation on the catalyst surface and facilitates the transfer of spilled-over hydrogen.³⁷ Similarly, the strong interfacial interaction also accounts for the high activity of the Ru/NH₂-functionalized graphite composites in hydrolysis of NaBH₄ to produce H₂.⁴² Ru NPs located on the exterior surface of CNT exhibit superior catalytic reactivity for N₂ dissociation as compare to those located inside CNT clearly demonstrating the impact of the support.^43,44

One of the key problems in practical applications of Ru NPs is their poor stability against sintering. For example, the carbon-supported Ru NP exhibits an outstanding performance in low-temperature direct methanol fuel cell, but suffers from the particle sintering that leads to less active large particles over a short period of time.⁴⁵ In principle, this issue could be also overcome by choosing appropriate support material that can form suitable interaction with Ru NPs to make them more tolerant to the reaction environment.⁴⁶ Unlike pristine graphene, where the TM atoms diffuse very fast resulting in the renowned problem of particle aggregation and sintering, rGO has abundant types of defects that will act as anchor points for the nucleation and growth of TM NPs. With the help of high-resolution transmission electron microscope (TEM), Gomez-Navarro et al. identified the presence of various types of defects in rGO samples synthesized with Hummers method,⁴ including clustered pentagons and heptagons, vacancies, edges and contaminations.⁴⁷ Theoretically, Wang et al. also showed that electron beam irradiation can serve as a useful tool to modify the defect morphology in a controllable manner and to tailor the physical properties of defective graphene as well as rGO.⁴⁸ The existence of these defects and their interconversion provide a solution to enhance the TM NP-support interaction and to tune the reactivity of the fabricated composites.^49,50 Combining theoretical and experimental efforts, we recently showed that Ru NPs can be stabilized by single vacancies on graphenic support, due to hybridization between the dsp states of Ru NPs and the sp² dangling bonds at the defect sites. As the electronic structure of Ru NPs is strongly interfered by the interfacial Ru–C interaction, the adsorption of hydrogen, benzene, toluene and the reaction intermediates is also enhanced, giving rise to superior catalytic performance of these composites in benzene and toluene hydrogenation.^24,28–30 However, the impact of these defects on the reactivity and stability of deposited TM NP hasn't been rationalized.

Inspired by previous efforts and to rationalize the design of new and efficient Ru/rGO composite catalysts, we present a systematic investigation on the electronic structure of Ru NPs deposited on various local structures on rGO support by first-principles-based calculations. We showed that Ru NPs prefer to bind directly with the localized defective structures on the graphenic support, which act as strong trapping sites for Ru NPs and inhibit their aggregation. We also showed that this interaction, which correlates with the interfacial structures and charge transfer, tunes averaged d-band center of the composites and contributes to improved reactivity of these composites. Further study reveals that the performance of the composites against oxygen adsorption correlates well with the shift of the d-band center of the NPs. These findings further suggest that controlled modification of the rGO support would be a feasible way for the developments of new TM–rGO composites with high stability and desired catalytic performance. The remaining of the paper is organized as the following: the theoretical methods and computational details are described in Section 2, the results are presented and discussed in Section 3 and concluded in Section 4.

Theoretical methods

The electronic structure of Ru NP–rGO composites was studied with projector-augmented wave (PAW) pseudopotential and spin-polarized Perdew–Burke–Ernzerhof (PBE) functional as implemented in the Vienna ab-initio Simulation Package (VASP).^51–57 A kinetic energy cutoff of 400 eV was used for the rGO support, the Ru NPs and the composites. The rGO and Ru NP–rGO composites were explored within the c(4 × 8) supercell of graphene with the defect generated at the cell center, while the free standing Ru NPs were studied in a 25.10 × 25.20 × 25.30 ų orthogonal cell. The integration of the Brillouin zone was conducted with a 2 × 2 × 1 Monkhorst–Pack grid centered at Γ-point for the support and composites, and with a Γ-point only grid for the Ru NPs.⁵⁸ The defective support, the Ru NPs and the composites were preoptimized with empirical potential,^59,60 and were then fully relaxed within the ab-initio scheme until the residue forces were reduced below 1 × 10⁻² eV Å⁻¹. The bulk lattice parameters of Ru were reproduced as a = 2.73 Å, c = 4.31 Å, while the minimum C–C distance in pristine graphene was calculated as 1.42 Å.^61,62 The Ru₁₃ particle of icosahedral symmetry was found to be stable and its spin momentum was reproduced as 11.51 μ_B.⁶³

The binding energy (E_b) is calculated as the energy difference between the Ru NP–rGO composite and the separated rGO support plus the freestanding Ru NP or Ru atom, following eqn (1).

E_b = E_{Ru NP/rGO} − (E_rGO + E_{Ru NP}) (1)

For the study concerning O adsorption, we focused on those adsorption structures with O adsorbed far from the interface to avoid overestimation of the impact of the interface. These adsorption structures were fully optimized until the residue forces were reduced below 1 × 10⁻² eV Å⁻¹ and the adsorption energy (E_ad) was calculated as the energy difference between the O absorbed Ru–rGO composite and the free gas molecule plus the bare composite, following eqn (2).

E_ad = E_{O+Ru NP/rGO} − (E_O2/2 + E_{Ru NP/rGO}) (2)

Bader analysis was employed to get a quantitative description of the charge transfer in the Ru NP/rGO composites.⁶⁴ The formation energy of defect is defined in the ESI.†

Results and discussion

The rGO support

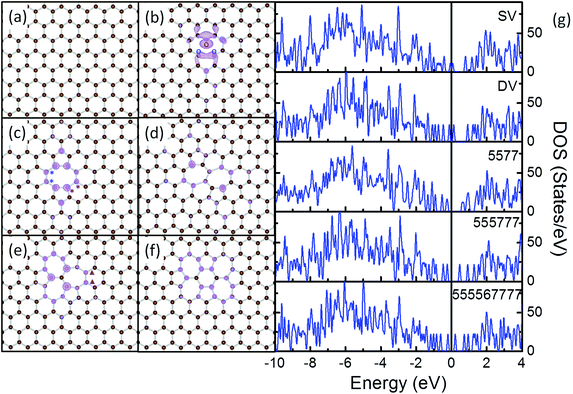
Most of the rGO samples used for catalytic applications are synthesized through Hummers method, i.e. through oxidative exfoliation of graphite and subsequent reduction.⁴ Recent TEM experiments identified the presence of various types of defects in rGO including point defects (such as single vacancies, double vacancies, haeckelite structures and etc.), line defects (such as edges), and contaminations.⁴⁷ Further IR, Raman and temperature programmed desorption (TPD) and theoretical results verified that on the final TM–rGO composites, most of the oxygen containing groups and surface contaminations on rGO were removed chemically to a large extent during the reduction, the activation of the composites or the thermal treatments.^65–68 To this end, pristine graphene (PG), single vacancy (SV), double vacancy (DV) and several haeckelite structures, namely 5577, 555 777 and 55 556 777 defects (Fig. 1), are selected as the typical local structures to mimic the electronic basic of the rGO support in Ru NP/rGO composites.

Fig. 1 Structures of PG (a), SV (b), DV (c), 5577 (d), 555 777 (e), 555 567 777 (f) and their density of states (DOS) curves (g). The charge densities of defective states at the Fermi level in (g) are shown in purple in (b)–(f) with an isovalue of ±0.003 a.u.

Removing 1 C atom from PG (Fig. 1a) yields SV (Fig. 1b). Due to the removal of C atom, dangling bonds are formed at the 3 C atoms around the vacancy. To stabilize the vacancy, 2 of the three C atoms bond together forming a C₅ ring, while the other C atoms adjacent to the vacancy constitute a C₉ ring. The C–C distance between the 2 newly bonded atoms is shortened from 2.46 Å in the graphene lattice to 2.01 Å, but is still longer than the nearest C–C distance of 1.42 Å in PG. The remaining C atom with dangling bond is repelled 0.21 Å out of the basal plane of the graphene.^69,70 The formation energy of SV is calculated as 7.69 eV, which compares well with the experimental value of 7.0 ± 0.5 eV (ref. 71) and the DFT results of 7.7 eV.⁷⁰ The calculated magnetic momentum is 1.14 μ_B, corresponding to the delocalized dangling bond at the vacant site (see Fig. 1 and S1† for details).⁶⁷

The subsequent removal of the C atom associated with the dangling bond in SV will generate a DV (Fig. 1c). The 2 newly generated dangling bonds on the neighbouring C atoms recombine as another elongated C–C bond, which divides the C₉ ring in SV to 1 C₅ ring and 1 C₈ ring. Previously, the formation of DV by coalescence of two SVs has also been reported.^72,73 The 2 C–C bonds formed by reconstruction are both 1.76 Å in length, which are about 0.25 Å shorter than the one in SV. This will cause tension vertical to the direction connecting the centres of the 2 C₅ rings. Similar to the case of CNT,⁷⁴ to release the tension in DV and to gain additional stability, all the C–C bonds on the C₈ ring are elongated from the 1.42 Å in PG to above 1.45 Å and a curvature, though less significant, is observed along the graphene plane. The calculated formation energy of DV is 7.63 eV, suggesting that the stability of DV is similar to that of SV.⁷⁵

Further rearrangements of C atoms at DV may help to release the tension and stabilize the defective rGO support. The rotation of the bond marked with red “*” in the C₈ ring of DV (Fig. 1c) leads to the conversion of two C₆ rings next to the DV to 1 C₅ ring and 1 C₇ ring. In this way, the C₅ ring next to the rotated bond in DV is transformed to a distorted C₆ ring. In the final structure, 2 C₇ rings sharing a C–C bond are formed with a C₅ ring neighboring to each of them (5577, Fig. 1d). To satisfy the requirements for formation of C₇ and C₅ rings, the 2 C₆ rings neighboring both 1 C₅ and 2 C₇ rings are significantly distorted with the neighboring C–C–C angles vary in the range from 115° to 121°. The distance of the C–C bond shared by the 2 C₇ rings is elongated from 1.42 Å in PG by 0.05 Å, while that of the 2 C–C bonds separating the C₇ and C₆ rings are elongated to 1.90 Å. The distortion and elongation of C–C bond to this scale is not energetically preferable in conjugated carbon materials, so the calculated formation energy of 5577 is 3.40 eV less stable than DV.

The rotation of the C–C bond marked with blue “*” in Fig. 1c leads to the arrangement of three C₅ rings and three C₇ rings, forming a 555 777 defect (Fig. 1e). In this DV variant, the 3 C₇ rings are separated by 3 C–C bonds sharing the same C atom. Each C₇ ring is surrounded by 2C₅, 2 C₇ and 3 C₆ rings, while each C₅ ring is surrounded by 2 C₇ and 3 C₆ rings. As in this structure, the angle and bond length requirements for formation of C₅ and C₇ rings are satisfied by the arrangement of the rings, the 555 777 maintains nearly a planar structure. Distortion can be observed in the C₆ rings neighbouring both the C₅ and C₇ rings, but is less pronounced as compared with those in 5577 and DV. The calculated formation energy for this defect is 0.98 eV more stable as compared with DV.⁷⁴

A further rotation of the bond indicated by purple “▲” in Fig. 1e results in a more complex 555 567 777 defect structure, which is comprised of 4 C₅ rings, 1 C₆ ring and 4C₇ rings (Fig. 1f). With the bond rotation, the C₇ ring, where the rotated bond exists, is transformed to a C₆ ring, while the 2 distorted C₆ rings adjacent to the C₅ and C₇ rings are deformed to C₇ rings and the less distorted C₆ ring next to the deformed C₇ ring is converted to a C₅ ring. In this way, in the final structure, the 4C₇ rings and 2C₅ rings are each sharing 1 edge with the central C₆ ring and the remaining 2 C₅ rings reside far from the central C₆ ring and are sharing edges with 2 adjacent C₇ rings. To release the tension, curvature is formed within the 555 567 777. According to the calculated formation energies, 555 567 777 is 0.43 eV more stable as compared with DV and is 0.55 eV less stable as compared with 555 777.

Our calculations show that the stability of these defects follows the order of 555 777 > 555 567 777 > DV > 5577, while that of SV is similar to DV. The high energies required for the conversion among them suggest that these defects would be stable in conventional reaction environments.⁴⁸ DOS analysis was carried out to examine the electronic structure of these defects (Fig. 1g). It is apparent that there are sharp spikes within 0.5 eV from the Fermi level on the DOS curves of all these defects. The charge densities of these states were extracted (Fig. 1b–f) which further prove that these spikes are the defect states localized on the carbon atoms at the defect sites. Previously, these defects were studied in CNT systems, where the changes in electron transport and electronic properties were discussed. Defects like these have also been predicted to alter the electronic properties of graphene and modify the chemical reactivity toward adsorbates.^48,74–81 In this sense, we expect these defects would provide reactive anchoring points to bind strongly with the Ru NPs and the interfacial interactions will further tune the electronic structure of the formed composites.

The Ru–rGO composites

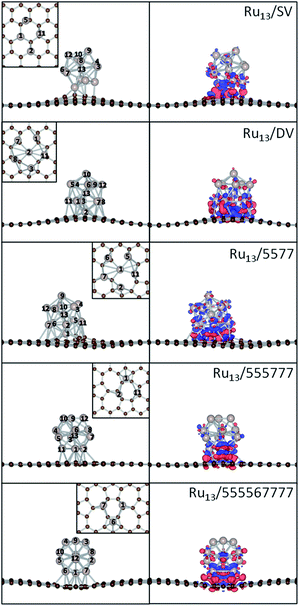
First-principles-based calculations were performed to illuminate the electronic structures of Ru/SV, Ru/DV, Ru/5577, Ru/555 777 and Ru/555 567 777 composites. In the calculations, the Ru₁₃ particle, PG, SV, DV, 5577, 555 777 and 555 567 777 were used as the models for Ru NPs and the supports. As the optimized Ru₁₃ particle has every surface Ru atom equivalent in the icosahedral symmetry, these composites were constructed by defining the interaction between Ru₁₃ and supports with either 1 single Ru atom, 1 edge (2 adjacent Ru atoms) or 1 surface (3 adjacent Ru atoms) of the Ru₁₃ NP, with respect to the atomic symmetry of the supports. All these possible structures of the composites were fully optimized as described in Theoretical methods to calculate the E_b. The most stable structures of these composites are shown in Fig. 2, with their magnetic, structural and energetic properties summarized in Table 1. As the three dimensional growth of Ru NPs has already been reported over rGO, the models used here would in principle be able to mimic the chemistry and interfacial interaction of Ru/rGO composites.

Fig. 2 The optimized structures and the corresponding contour plots of the differential charge density of Ru/SV, Ru/DV, Ru/5577, Ru/555 777 and Ru/55 556 7777 composites. The interfacial Ru atoms with Ru–C distances less than 3.00 Å are shown as the insets in the left panel. The contour level for the differential charge density is ±0.005 a.u.

Table 1 Structural, magnetic and energetic properties of Ru₁₃/rGO composites

Composites	E b ^a(eV)	μ ^b (μB)	Min Ru–C^c (Å)	Min/max Ru–Ru^d (Å)
a The binding energy of Ru13 NP on various rGO structures. b Magnetic momentum of the composites. The magnetic momentum for freestanding Ru13 particle is 11.51 μB. c The minimum Ru–C distance at the Ru NP–rGO interface. d The minimum and maximum Ru–Ru distance inside the Ru NPs. For freestanding Ru13 particle, the maximum Ru–Ru distance is 2.49 Å, and the minimum Ru–Ru distance is 2.70 Å.
Ru13/SV	−7.40	5.27	1.97	2.46/2.86
Ru13/DV	−9.01	15.82	2.02	2.49/2.78
Ru13/5577	−8.72	15.68	1.97	2.48/2.78
Ru13/555 777	−4.25	11.09	2.14	2.49/2.85
Ru13/555 567 777	−4.34	12.00	2.13	2.49/2.79

---

The π conjugation among C atoms makes the PG highly inert in its planar structure, so the Ru₁₃ particle can only donate its dsp hybridized states to interact with these π states to form weak coordinative interfacial interaction. The calculated E_b of a Ru₁₃ particle onto PG is only −1.32 eV. In that configuration, Ru₁₃ binds with 3 C=C of the same C₆ ring on the graphene through 3 Ru atoms. If the Ru₁₃ particle is deformed, the E_b can be enhanced to −2.45 eV.^30,68 As the E_b of a single Ru atom on PG is −3.26 eV and the calculated diffusion barrier of Ru atoms on PG is only 0.86 eV, it is reasonable to believe that the diffusion of Ru atoms at the edge of deformed particles will be much easier. In this sense, PG will not be able to stabilize the Ru particles from aggregation through Ostwald ripening mechanism and is less eligible for application as support material for Ru NP based catalysts.⁴⁶

When defect states and dangling bonds are introduced, significant enhancements in E_b of Ru atoms over these local defects can be observed. The E_b of a Ru atom on SV is significantly enhanced to −7.55 eV from −3.26 eV over PG, while the E_b on DV is also strengthened to −6.82 eV. Similar enhancement of E_b of single Ru atom at 5577, 555 777 and 555 567 777 can also be observed. Considering the fast diffusion of TM atoms on PG, these highly mobile Ru atoms will be trapped at these defects first and then nucleate to form Ru NPs.⁷³

The introduction of defects also significantly enhances the interaction between Ru₁₃ particles with the rGO support. Even on 555 777, the most stable defective rGO structure considered, the E_b is nearly doubled to −4.25 eV as compared to −2.45 eV over PG. The Ru₁₃ particle binds most strongly on DV and the corresponding E_b is −9.01 eV, which is enhanced by about 3 times. The stability of these composites follows the order Ru₁₃/DV > Ru₁₃/5577 > Ru₁₃/SV > Ru₁₃/555 777 > Ru₁₃/555 567 777. It is apparent that there is a strong dependence of the E_b on the structure of rGO support. It is also notable that the E_b of Ru₁₃/555 567 777 differs with that on Ru₁₃/555 777 by only 0.09 eV, while they differ by about 4.0 eV when compared with those of Ru₁₃/SV, Ru₁₃/DV and Ru₁₃/5577. This can be understood by the different interfacial structures formed and the amount of charge transfer from the Ru NP to the support.

Unlike Pt₁₃ NP supported on graphene, which demonstrates severe morphological change and adapts low symmetry open structures upon deposition due to the low Pt–Pt cohesive energy and large Pt-graphene interfacial lattice mismatch,^32,33 the deposited icosahedral Ru₁₃ particle is only deformed slightly to form plausible interaction with the rGO support when monitored by the minimum and maximum Ru–Ru distance.⁶⁸ The elongation of Ru–Ru distance in the deposited NPs is within 0.16 Å, while there is no observable change in the minimum Ru–Ru distance. Even for the most stable Ru/DV composite, the variation of Ru–Ru distance upon deposition is within 0.08 Å. This implies that the deposition will not significantly alter the structure of the Ru NPs. while the large E_b of Ru NPs on the defective graphene will further contribute to the additional stability of the NPs electronically. This is also supported by the high stability of Ru NPs of less than 2 nm in size supported on rGO can survive after heat treatment at 973 K.⁶⁸

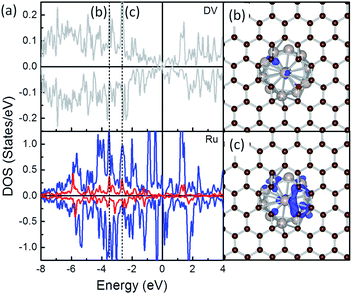
To highlight how the rGO support, or more specific, the interfacial structures promote the stability of these composites, further analysis was carried out. The electronic structure of the interfacial atoms was explored first to evidence the nature of the interaction among them. Among the most plausible structures of these composites, the minimum Ru–C distance falls in the range from 1.97 to 2.14 Å, which is typical for the formation of Ru–C bonds. Taking the Ru/DV as an example, DOS analysis was performed to investigate the interaction among the interfacial Ru and C atoms (Fig. 3). The DOS curves of the interfacial Ru atom and C atoms overlap over a large energy range, from ∼−8.0 eV to the Fermi level (E_F). In particular, strong resonance peaks are found among the C-sp states and Ru-sp and Ru-d states at ∼−3.8 eV (Fig. 3b) and −2.eV (Fig. 3c). These, together with localized wavefunctions on the interfacial atoms in the contour plots of the wavefunction in these energy ranges (in Fig. 3b and c), indicate the interaction among these states. Further differential charge density analysis shows that there are localized charge accumulation regions formed between the interfacial Ru and C atoms (Fig. 2, right panel), proving the covalent character these Ru–C interactions. Therefore, the strong E_b of Ru NP over rGO can be partially attributed to the covalent interfacial Ru–C interaction, but will also be strongly dependent on the Ru/rGO interfacial structure.

Fig. 3 DOS (a) and contour plots of bonding states (b and c) among interfacial C and Ru atoms of Ru/DV composite. In (b) and (c), defective graphene is in front of the Ru NP to show the interfacial interaction.

For the Ru/SV, Ru/DV and Ru/5577 composites, one of the Ru atoms is embedded into the carbon lattice and the interfacial structures are different from those of Ru/555 777 and Ru/555 567 777. Driven by the exothermic formation of the new Ru–C bonds and to gain additional stability, the barrier for reconstruction of the rGO support will be significantly lowered in existence of deposited Ru atoms. Consequently, the elongated C–C bonds in SV, DV and 5577 to minimize the number of dangling bonds around the defects are further distorted to accommodate Ru atoms and stabilize them by formation of plausible Ru–C bonds in the final deposition structures. At the Ru/SV interface, except the embedded one, 2 of the 4 interfacial Ru atoms take the C=C bridge site while the remaining one stands right above a C atom at the defect site. The Ru1–Ru11 distance is found elongated by 0.16 Å to match the interaction (Fig. 2). As for Ru/DV, there are 6 interfacial atoms, one is embedded to interact with 4C atoms at the defect, while 2 of the remaining sit on C=C bridge sites and the others form shared interactions with at least 3 adjacent C atoms surrounding the defect sites. The breaking of 1 additional C–C bond and formation of more Ru–C interactions make Ru/DV more stable than Ru/SV. Similar reconstruction is also observed in Ru/5577, where one of the C₅ rings and one distorted C₆ ring on the opposite direction are broken to minimize the tension at the defect sites. In this way, 1 C₇ ring, 1 C₅ ring and 2 C₆ rings act as the edge of the defect for embedding of Ru atom within a 4-coordinated site. Due to the differences in structure, or more specific, the difference in bond angle between the combination of a C₅ ring and C₇ ring and 2 C₆ rings that constrains the formation of Ru–C bonds, the Ru/5577 composite is less stable by 0.29 eV than Ru/DV, but is still more stable than Ru/SV by about 1.32 eV.

In contrast to SV, DV and 5577, there is no such significant reconstruction of the support or embedding of Ru atom over 555 777 and 555 567 777. At the interface, one of the 3 Ru atoms sits above the center of the C₅ ring and the remaining 2 Ru atoms occupies 2 C=C bridge sites of the same C₆ ring (555 567 777) or C₇ ring (555 777) to balance the Ru–Ru and the Ru–C interactions (Fig. 2). As the C₇ ring is charge depleting, the C₆ ring is charge neutral and the C₅ ring is charge accumulating when embedded in graphenic lattice, the Ru particle binds more strongly by 0.09 eV on 555 567 777 than 555 777. To this end, the large binding of Ru NP over SV, DV and 5577 supports can be attributed to the different Ru–C interaction formed between the Ru NPs and the C atoms around the local defect site, involving the cleavage of C–C bond and formation of the new Ru–C bonds and is strongly dependent on the interfacial structures.

The formation of the Ru–C bonds is also accompanied with charge transfer. The Bader analysis was performed to quantify the total charge transfer at the Ru NP-support interface. As for the freestanding Ru₁₃ particle, charge is transferred from the center Ru atom to the surface atoms, and the Bader charge on outermost Ru atoms differs slightly. In contrast, the formation of new Ru–C bonds upon deposition leads to obvious charge accumulation region at the interface and charge redistribution inside the particle, as evidenced by the contour plots of the differential charge density (Fig. 2) and the Bader analysis (Table 2). Regardless of the support, the direction of charge transfer is from the Ru₁₃ particle to the support. The amounts of charge transfer also shows a strong dependence on the rGO supports and are more significant over those composites with Ru atom embedded into the graphene basal lattice. In Ru₁₃/SV, the amount of charge transfer from Ru₁₃ to SV is 1.05 |e| and is 0.55 |e| less than that of the Ru₁₃/DV. The amounts of charge transfer between Ru NP and other rGO support fall in the range from 0.97 |e| to 1.60 |e|. The lowest amount of charge transfer of 0.97 |e| is observed on Ru/555 777, which is also of the least E_b. It is also immediately apparent that there is a positive correlation between the E_b of the composites and the Δq_B. The higher the stability of composites, the larger the amounts of interfacial charge transfer. (Fig. 4) In this sense, the differences in the amount of charge transfer among these Ru/rGO composites can be ascribed to the different interfacial structures and interactions formed upon Ru NP deposition.

Table 2 The Bader charge (q_B) and excess Bader charge (Δq_B) over the isolated Ru₁₃ NP and the composites

No^a	Isolated	SV		DV		555 777		555 567 777		5577
	q B ^b (e)	q B ^b (e)	ΔqB^c (e)	q B ^b (e)	ΔqB^c (e)	q B ^b (e)	ΔqB^c (e)	q B ^b (e)	ΔqB^c (e)	q B ^b (e)	ΔqB^c (e)
a Please see Fig. 2 for the numbering of Ru atoms. b Only the 4d and 5s electrons of Ru atoms are considered as valence electrons, so the qB is 8.00 e for an isolated Ru atom. As charge transfer among Ru atoms is normal in small NPs, the qB is not 8 even in isolated Ru13. c The amount of charge transfer on individual Ru atom is calculated as the difference in qB before and after deposition. A negative ΔqB means charge transfer from the Ru atom and a positive ΔqB implies the Ru atom gains charge.
1	8.03	7.51	−0.52	7.82	−0.21	7.74	−0.29	7.72	−0.30	7.44	−0.59
2	8.03	7.88	−0.14	7.42	−0.60	7.75	−0.28	7.94	−0.08	7.82	−0.21
3	7.96	8.02	0.06	7.77	−0.20	7.98	0.01	8.05	0.09	8.05	0.09
4	8.08	8.06	−0.02	8.03	−0.05	8.00	−0.08	7.98	−0.09	8.03	−0.05
5	8.02	7.83	−0.20	8.03	0.00	7.97	−0.05	7.95	−0.07	7.87	−0.16
6	8.03	8.02	−0.01	8.01	−0.01	8.03	0.00	7.78	−0.24	7.85	−0.18
7	8.03	7.99	−0.04	7.86	−0.17	7.98	−0.05	7.72	−0.30	7.81	−0.22
8	8.04	8.04	0.00	7.82	−0.22	8.02	−0.02	8.01	−0.02	8.02	−0.02
9	8.04	8.01	−0.04	8.03	−0.02	8.04	−0.01	8.03	−0.01	8.03	−0.01
10	8.02	8.05	0.03	8.03	0.00	8.01	−0.01	8.01	−0.02	8.04	0.01
11	8.09	7.82	−0.27	7.82	−0.27	7.79	−0.30	8.02	−0.07	7.84	−0.25
12	8.06	8.00	−0.06	8.05	−0.01	8.03	−0.03	8.01	−0.05	8.04	−0.02
13	7.57	7.73	0.16	7.71	0.15	7.71	0.14	7.72	0.15	7.68	0.11
Ru NP	104.00	102.95	−1.05	102.40	−1.60	103.03	−0.97	102.95	−1.05	102.50	−1.50

---

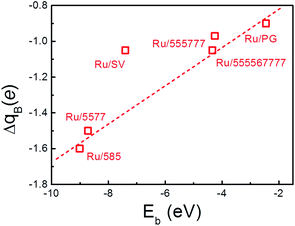Fig. 4 The correlation between the amount of charge transfer from Ru NP to the rGO support (Δq_B) and the binding energy of the Ru NPs onto support (E_b). The dashed line is guide to the eye.

Due to the formation of the interfacial Ru–C interactions, the slight distortion in Ru NP is observed with the maximum value only at the interface while the level of distortion decreases quickly with the distance of Ru atoms from the surface. Our recent findings showed that Ru NPs can be stabilized by SV due to hybridization the between the dsp states of Ru NPs and the dangling bonds at the graphene defect sites.^29,30 As the interfacial structures of the considered composites are similar to those of Ru/SV and Pd/SV, the previously discussed stabilization mechanism by controlled TM atomic diffusion facilitated by the interfacial electronic structure can be expected to hold.^12,30,68

The electronic structure and reactivity of Ru/rGO composites

The electronic structure of these Ru/rGO composites was further analyzed to highlight the interference of interfacial interaction (Fig. 5). It is immediately apparent that the DOS peaks of Ru-d states are broadened upon deposition and those of Ru-d, Ru-sp and C-sp states resonance strongly within the range from −6.0 eV to E_F showing the new interactions are formed among them. At the same time, the sharp spikes in the vicinity around the E_F in Fig. 1, arising from the localized dangling bonds or defect states on the C atoms at the defect sites, disappear upon deposition of the Ru NP. At the same time, the broadening of the DOS of C-sp states is obvious, which is a sign for the enhanced hybridization among the states of interfacial C and Ru atoms. This is also consistent with the Bader and differential charge density analysis. The distribution of DOS of Ru-d states is dependent on the rGO supports, which is the consequence of the differences in the formed interfacial interaction.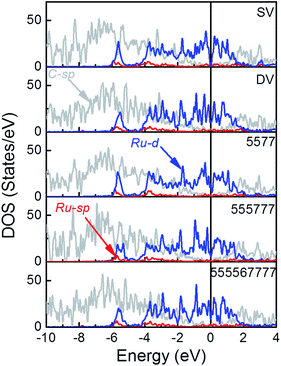

Fig. 5 The PDOS of Ru/SV, Ru/DV, Ru/5577, Ru/555 777 and Ru/555 567 777 composites (see Fig. S2† for DOS projected to different spins).

A more quantitative analysis on the shift of the d-band center of the deposited Ru NPs with respect to the freestanding NP was performed to investigate the impact of the interfacial interaction on the electronic structure of the deposited Ru NPs. The energy levels of d-states were aligned by the vacuum levels of the corresponding NP/composites and the results were compared directly to those of the freestanding NP to determine the shift of the d-band of Ru NPs upon deposition. (Table 3) The averaged ε_d values of the Ru particles on SV, 555 777, DV, 555 576 666 and 5577 are −5.35, −5.40 eV, −5.25 eV, −5.42 eV and −5.33 eV with respect to the vacuum, respectively. In contrast to the averaged ε_d of the freestanding Ru NP of −5.45 eV, the ε_d of the deposited Ru NPs are all shifted upward, showing the impact of supports on the electronic structure of the composites. Taking the Ru/5577 as an example, the shift of ε_d of each Ru atoms fall in the range from −0.80 eV to 0.15 eV while the largest shift appears on the embedded Ru atom, which is downshifted by 0.80 eV from the E_F. This is a sign of weakening of the interaction among Ru atoms as new Ru–C bonds are formed at the interface by the transfer of Ru-dsp electrons of the NPs surface into the dangling bonds or defective states of the rGO support. As this charge transfer process is thermodynamically driven and new bonds are formed at lower energy levels among the interfacial atoms, the d-band of the embedded Ru atom is shifted downward. Consequently, interactions among the Ru atoms are altered, which makes the interactions among Ru atoms far from the interface stronger than those of Ru atoms around the interface. To catch up with this change, the Ru atoms are deformed slightly to balance the Ru–Ru and Ru–C interactions and gain additional stability. This will induce further charge transfer among Ru atoms and change their d-band levels. Therefore, except the embedded atom, ε_d of the other Ru atoms retain or become even shifted upward, while the averaged ε_d of the Ru NPs is also upshifted as compared with the freestanding counterpart. The calculated ε_d was plotted vs. the binding of Ru NP onto various rGO supports to highlight the important contribution of the interfacial interaction on the electronic structure of deposited Ru NPs. (Fig. 6) It is immediately apparent that there is also a positive correlation between the E_b of the composites and the ε_d. The higher the E_b of composites, the higher the energy level of ε_d. The important role of the interfacial interaction on tuning the electronic properties of the deposited Ru NPs is thus visualized. Furthermore, the differences in electronic structure of these Ru/rGO composites can be ascribed to the different interfacial structures and interactions formed upon Ru NP deposition.

Table 3 Electronic structures of Ru₁₃/rGO composites

	ε d′^a (eV)	E F ^b (eV)	E VAC ^c (eV)	W f ^d (eV)	ε d ^e (eV)	Δεd^f (eV)
a Calculated averaged d-band center of the freestanding Ru NP and composites with respect to the corresponding Fermi level. b Calculated Fermi levels of the freestanding Ru NP and composites with respect to the vacuum level. c Calculated vacuum levels of the freestanding Ru NP and composites. d The workfunction of the Ru NP or composites calculated as the difference between the Fermi level and the corresponding vacuum level. e The averaged d-band centers of the Ru NP or Ru/rGO composites aligned by the vacuum levels. f The change of averaged d-band centers of Ru/rGO composites respect to the freestanding Ru NP, aligned by the vacuum levels.
Ru13	−1.41	−3.56	0.49	4.04	−5.45
Ru13/SV	−1.17	−1.83	2.34	4.18	−5.35	0.10
Ru13/555 777	−1.06	−1.94	2.41	4.34	−5.40	0.05
Ru13/DV	−1.09	−1.82	2.34	4.16	−5.25	0.20
Ru13/555 567 777	−1.08	−1.94	2.40	4.34	−5.42	0.03
Ru13/5577	−1.12	−1.89	2.32	4.21	−5.33	0.12

---

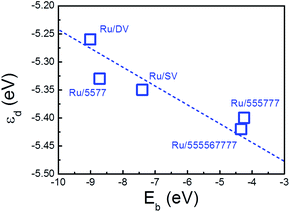Fig. 6 Calculated averaged d-band center of the deposited Ru NPs (ε_d) plotted versus the and the binding energy of the Ru NPs onto supports (E_b). The dashed line is guide to the eye.

It has already been proved that energy level of the d-band center of ultrafine TM NPs is an effective indicator for the reactivity and can be compared directly with those of the bulk truncated surfaces.^29,82 According to the “d-band model” of Hammer and Norskov et al. that correlates the reactivity and catalytic activity to ε_d, this upshifted d-band center suggests a higher activity of Ru/rGO composites as compared with the freestanding Ru NPs.⁸³ To visualize the promotion effect of the rGO supports on reactivity of these composites, the O adsorption, which is essential for various reactions including oxygen reduction, hydrogen evolution and etc., was selected as the model reaction. As it has already been shown over extended surface of transition metals⁸⁴ and alloys⁸⁵ that the O E_ad will decreases linearly with the increasing O coverage due to repulsive interaction among absorbed negatively charged O atoms, we focused on the initial O atomic adsorption over these composites. In the most plausible O adsorption structure, the O stands on the bridge site between 2 adjacent Ru atoms. To avoid the potential interference and involvement of the states of the support and set the lower bound of the promotion effect, we only consider the O adsorption on the bridge site that is far from the interface.

The calculated E_ad of a single O atom is −3.55 eV over freestanding Ru NP. As the d-band center of the composites is shifted after deposition, the O E_ad is further enhanced by −0.23 eV and −0.32 eV to −3.78 eV and −3.87 eV over Ru/SV and Ru/DV composites, respectively. Similar enhancement of O adsorption is also observed on Ru/5577, Ru/555 777, Ru/555 567 777 composites, while the O E_ad all falls in the range from −3.55 eV to −3.87 eV. The calculated E_ad were plotted versus ε_d in Fig. 7, demonstrating a clear linear relationship. In this sense, the enhanced E_ad can be directly correlated with the shift of ε_d that originates from the different type of interfacial interactions formed within these composites. As the O E_ad is all enhanced over these Ru/rGO composites, these composites are expected to show improved catalytic activity and excellent environmental tolerance in those reactions requires adsorbed O atom as an intermediate. The strong dependence of the O E_ad on the shift of ε_d, which originates from the different interfacial interaction formed, also demonstrates the effectiveness of manipulating defect structures on rGO in tuning the electronic structure of the deposited TM particles, and the possibility of improving the catalytic performance of rGO supported TM nanocatalysts through defect engineering of the support material.

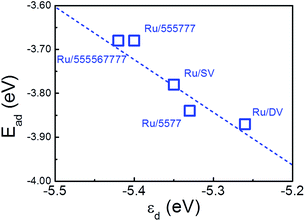Fig. 7 Calculated O adsorption energies (E_ad) over Ru/rGO composites plotted versus d-band center with respect to vacuum (ε_d). The dashed line is to guide the eye.

Conclusions

We systematically investigated the electronic structure of Ru NPs deposited on various local structures on rGO support by first-principles-based calculations. We showed that Ru prefers to bind directly with the graphenic support and various defective structures on rGO can act as strong trapping sites for Ru NPs and inhibit their aggregation. We also showed that this interaction, which correlates with the interfacial structures and the charge transfer, tunes averaged d-band center of the composites and contributes to improved reactivity of these composites. Further study reveals that the performance of the composites against oxygen adsorption correlates well with the shift of the d-band center of the deposited Ru NPs, which originates from the covalent interfacial Ru–C interaction and is determined by the defect structures on rGO support. These findings paved the way for developments of new transition metal/rGO composites with high stability and superior catalytic performance by defect engineering of the support materials through controlled modification. These TM/rGO composites can be fabricated, in principle, by co-reduction of the electron-beam radiated rGO sample in aqueous solution of TM cations, during which the newly generated defects will first react to get passivated with O-containing functional groups to anchor TM ions and then get reduced to form mature interaction with the TM NPs right at the defect sites. The size of TM NPs will not change the dominating role of support and the interfacial interaction. Unlike NPs of sp metals, where the impact of quantum size effect would be significant due to free-electron like behaviour of s and p electrons, the reactivity of TM NPs are determined by their localized d states. Various experimental works have shown that the support material and the interfacial interaction can significantly impact the catalytic performance of the TM NPs. For example, Ru NPs of similar size distribution (2–15 nm) and morphology supported on different support materials showed different catalytic performance in NH₃ decomposition and this difference can only be attributed to the support materials and the interfacial interaction.⁸⁶ In this sense, the impact of defective rGO support would be still significant when the size of TM NP goes up.

Acknowledgements

The work was supported by NSFC (21373036, 21103015, 21271037 and 11174045), the Fundamental Research Funds for the Central Universities (DUT14LK09), the Key Laboratory of Coastal Zone Environmental Processes YICCAS (201203) and the Special Academic Partner GCR Program from King Abdullah University of Science and Technology. Y. H. would also thank Dalian University of Technology for the Seasky Professorship.

Notes and references

1. A. K. Geim and K. S. Novoselov, Nat. Mater., 2007, 6, 183–191.
2. A. K. Geim, Science, 2009, 324, 1530–1534.
3. M. Inagaki, Y. A. Kim and M. Endo, J. Mater. Chem., 2011, 21, 3280–3294.
4. W. S. Hummers and R. E. Offeman, J. Am. Chem. Soc., 1958, 80, 1339–1340.
5. Y. W. Zhu, S. Murali, W. W. Cai, X. S. Li, J. W. Suk, J. R. Potts and R. S. Ruoff, Adv. Mater., 2010, 22, 3906–3924.
6. R. R. Bacsa, C. Laurent, A. Peigney, W. S. Bacsa, T. Vaugien and A. Rousset, Chem. Phys. Lett., 2000, 323, 566–571.
7. Y. Han, S. S. Lee and J. Y. Ying, Chem. Mater., 2007, 19, 2292–2298.
8. H. K. Chae, D. Y. Siberio-Perez, J. Kim, Y. Go, M. Eddaoudi, A. J. Matzger, M. O'Keeffe and O. M. Yaghi, Nature, 2004, 427, 523–527.
9. Y. X. Yao, X. Liu, Q. Fu, W. X. Li, D. L. Tan and X. H. Bao, ChemPhysChem, 2008, 9, 975–979.
10. J. Z. Zhang, X. Liu, M. N. Hedhili, Y. H. Zhu and Y. Han, ChemCatChem, 2011, 3, 1294–1298.
11. X. Chen, X. Liu, L. Wang, M. Li, C. T. Williams and C. Liang, RSC Adv., 2013, 3, 1728–1731.
12. X. Liu, L. Li, C. G. Meng and Y. Han, J. Phys. Chem. C, 2012, 116, 2710–2719.
13. E. Yoo, T. Okada, T. Akita, M. Kohyama, I. Honma and J. Nakamura, J. Power Sources, 2011, 196, 110–115.
14. Y. C. Si and E. T. Samulski, Chem. Mater., 2008, 20, 6792–6797.
15. J. Oh, T. Kondo, D. Hatake, Y. Iwasaki, Y. Honma, Y. Suda, D. Sekiba, H. Kudo and J. Nakamura, J. Phys. Chem. Lett., 2010, 1, 463–466.
16. W. Y. Xu, X. Z. Wang, Q. Zhou, B. Meng, J. T. Zhao, J. S. Qiu and Y. Gogotsi, J. Mater. Chem., 2012, 22, 14363–14368.
17. X. M. Chen, G. H. Wu, J. M. Chen, X. Chen, Z. X. Xie and X. R. Wang, J. Am. Chem. Soc., 2011, 133, 3693–3695.
18. Z. Jin, D. Nackashi, W. Lu, C. Kittrell and J. M. Tour, Chem. Mater., 2010, 22, 5695–5699.
19. F. A. He, J. T. Fan, F. Song, L. M. Zhang and H. L. W. Chan, Nanoscale, 2011, 3, 1182–1188.
20. L. Zheng, G. N. Zhang, M. Zhang, S. H. Guo and Z. H. Liu, J. Power Sources, 2012, 201, 376–381.
21. J. Oh, T. Kondo, D. Hatake, K. Arakawa, T. Suzuki, D. Sekiba and J. Nakamura, J. Phys. Chem. C, 2012, 116, 7741–7747.
22. X. W. Liu, J. J. Mao, P. D. Liu and X. W. Wei, Carbon, 2011, 49, 477–483.
23. M. Cattelan, S. Agnoli, M. Favaro, D. Garoli, F. Romanato, M. Meneghetti, A. Barinov, P. Dudin and G. Granozzi, Chem. Mater., 2013, 25, 1490–1495.
24. K. X. Yao, X. Liu, Z. Li, C. C. Li, H. C. Zeng and Y. Han, ChemCatChem, 2012, 4, 1938–1942.
25. M. Giovanni, H. L. Poh, A. Ambrosi, G. J. Zhao, Z. Sofer, F. Sanek, B. Khezri, R. D. Webster and M. Pumera, Nanoscale, 2012, 4, 5002–5008.
26. L. Li, A. H. Larsen, N. A. Romero, V. A. Morozov, C. Glinsvad, F. Abild-Pedersen, J. Greeley, K. W. Jacobsen and J. K. Norskov, J. Phys. Chem. Lett., 2013, 4, 222–226.
27. X. Liu, S. B. Zhang, X. C. Ma, J. F. Jia, Q. K. Xue, X. H. Bao and W. X. Li, Appl. Phys. Lett., 2008, 93, 093105.
28. X. Liu, C. Meng and Y. Han, Phys. Chem. Chem. Phys., 2012, 14, 15036–15045.
29. X. Liu, C. Meng and Y. Han, Nanoscale, 2012, 4, 2288–2295.
30. X. Liu, K. X. Yao, C. G. Meng and Y. Han, Dalton Trans., 2012, 41, 1289–1296.
31. X. Liu, C. Meng and Y. Han, J. Phys. Chem. C, 2013, 117, 1350–1357.
32. I. Fampiou and A. Ramasubramaniam, J. Phys. Chem. C, 2012, 116, 6543–6555.
33. I. Fampiou and A. Ramasubramaniam, J. Phys. Chem. C, 2013, 117, 19927–19933.
34. G. Kim and S.-H. Jhi, ACS Nano, 2011, 5, 805–810.
35. A. Primo, P. Concepcion and A. Corma, Chem. Commun., 2011, 47, 3613–3615.
36. C. Crisafulli, S. Scire, M. Salanitri, R. Zito and S. Calamia, Int. J. Hydrogen Energy, 2011, 36, 3817–3826.
37. F. B. Su, F. Y. Lee, L. Lv, J. J. Liu, X. N. Tian and X. S. Zhao, Adv. Funct. Mater., 2007, 17, 1926–1931.
38. M. Gopiraman, S. Ganesh Babu, Z. Khatri, W. Kai, Y. A. Kim, M. Endo, R. Karvembu and I. S. Kim, J. Phys. Chem. C, 2013, 117, 23582–23596.
39. W. Chen, N. B. Zuckerman, X. W. Kang, D. Ghosh, J. P. Konopelski and S. W. Chen, J. Phys. Chem. C, 2010, 114, 18146–18152.
40. J. J. Liu, P. Bai and X. S. Zhao, Phys. Chem. Chem. Phys., 2011, 13, 3758–3763.
41. J. Hou, Y. Ma, Y. Li, F. Guo and L. Lu, Chem. Lett., 2008, 37, 974–975.
42. Y. Liang, H. B. Dai, L. P. Ma, P. Wang and H. M. Cheng, Int. J. Hydrogen Energy, 2010, 35, 3023–3028.
43. S. J. Guo, X. L. Pan, H. L. Gao, Z. Q. Yang, J. J. Zhao and X. H. Bao, Chem.–Eur. J., 2010, 16, 5379–5384.
44. H. L. Gao and J. J. Zhao, J. Chem. Phys., 2010, 132, 234704.
45. T. Kawaguchi, W. Sugimoto, Y. Murakami and Y. Takasu, J. Catal., 2005, 229, 176–184.
46. R. Borup, J. Meyers, B. Pivovar, Y. S. Kim, R. Mukundan, N. Garland, D. Myers, M. Wilson, F. Garzon, D. Wood, P. Zelenay, K. More, K. Stroh, T. Zawodzinski, J. Boncella, J. E. McGrath, M. Inaba, K. Miyatake, M. Hori, K. Ota, Z. Ogumi, S. Miyata, A. Nishikata, Z. Siroma, Y. Uchimoto, K. Yasuda, K. I. Kimijima and N. Iwashita, Chem. Rev., 2007, 107, 3904–3951.
47. C. Gomez-Navarro, J. C. Meyer, R. S. Sundaram, A. Chuvilin, S. Kurasch, M. Burghard, K. Kern and U. Kaiser, Nano Lett., 2010, 10, 1144–1148.
48. Z. Wang, Y. G. Zhou, J. Bang, M. P. Prange, S. B. Zhang and F. Gao, J. Phys. Chem. C, 2012, 116, 16070–16079.
49. F. Banhart, J. Kotakoski and A. V. Krasheninnikov, ACS Nano, 2010, 5, 26–41.
50. A. Hashimoto, K. Suenaga, A. Gloter, K. Urita and S. Iijima, Nature, 2004, 430, 870–873.
51. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561.
52. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251–14269.
53. G. Kresse and J. Furthmuller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
54. G. Kresse and J. Furthmuller, Comput. Mater. Sci., 1996, 6, 15–50.
55. P. E. Blochl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
56. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
57. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
58. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192.
59. X. Liu, C. G. Meng and C. H. Liu, Phase Transitions, 2006, 79, 249–259.
60. X. Liu, C. G. Meng and C. H. Liu, Acta Phys.–Chim. Sin., 2004, 20, 280–284.
61. V. A. Finkel, G. P. Kovtun and M. I. Palatnik, Phys. Met. Metallogr., 1971, 32, 231–235.
62. A. H. Castro Neto, F. Guinea, N. M. R. Peres, K. S. Novoselov and A. K. Geim, Rev. Mod. Phys., 2009, 81, 109–162.
63. D. W. Boukhvalov and M. I. Katsnelson, ACS Nano, 2011, 5, 2440–2446.
64. R. F. W. Bader, Chem. Rev., 1991, 91, 893–928.
65. C. Xu, X. Wang and J. W. Zhu, J. Phys. Chem. C, 2008, 112, 19841–19845.
66. G. M. Scheuermann, L. Rumi, P. Steurer, W. Bannwarth and R. Mulhaupt, J. Am. Chem. Soc., 2009, 131, 8262–8270.
67. X. F. Gao, J. Jang and S. Nagase, J. Phys. Chem. C, 2010, 114, 832–842.
68. B. F. Machado, M. Oubenali, M. Rosa Axet, T. Trang Nguyen, M. Tunckol, M. Girleanu, O. Ersen, I. C. Gerber and P. Serp, J. Catal., 2014, 309, 185–198.
69. O. V. Yazyev and L. Helm, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 125408.
70. Y. Ma, P. O. Lehtinen, A. S. Foster and R. M. Nieminen, New J. Phys., 2004, 6, 68.
71. P. A. Thrower and R. M. Mayer, Phys. Status Solidi A, 1978, 47, 11–37.
72. G. D. Lee, C. Z. Wang, E. Yoon, N. M. Hwang and K. M. Ho, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 245411.
73. L. Wu, T. Hou, Y. Li, K. S. Chan and S.-T. Lee, J. Phys. Chem. C, 2013, 117, 17066–17072.
74. R. G. Amorim, A. Fazzio, A. Antonelli, F. D. Novaes and A. J. R. da Silva, Nano Lett., 2007, 7, 2459–2462.
75. J. M. Carlsson and M. Scheffler, Phys. Rev. Lett., 2006, 96, 046806.
76. J. Kotakoski, A. V. Krasheninnikov, U. Kaiser and J. C. Meyer, Phys. Rev. Lett., 2011, 106, 105505.
77. R. Y. Oeiras, F. M. Araujo-Moreira and E. Z. da Silva, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 073405.
78. J. Kang, J. Bang, B. Ryu and K. J. Chang, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 115453.
79. D. W. Boukhvalov and M. I. Katsnelson, Nano Lett., 2008, 8, 4373–4379.
80. D. Ghosh, G. Periyasamy and S. K. Pati, J. Phys. Chem. C, 2013, 117, 21700–21705.
81. P. A. Denis and F. Iribarne, J. Phys. Chem. C, 2013, 117, 19048–19055.
82. Q. Fu, X. R. Cao and Y. Luo, J. Phys. Chem. C, 2013, 117, 2849–2854.
83. B. Hammer and J. K. Norskov, in Advances in Catalysis, Academic Press Inc, San Diego, 2000, pp. 71–129.
84. W. X. Li, J. Phys.: Condens. Matter, 2008, 20, 184022.
85. X. Liu, H. Guo and C. Meng, J. Phys. Chem. C, 2012, 116, 21771–21779.
86. S. F. Yin, Q. H. Zhang, B. Q. Xu, W. X. Zhu, C. F. Ng and C. T. Au, J. Catal., 2004, 224, 384–396.

---

Footnote

† Electronic supplementary information (ESI) available: The definition of the formation energy of defects, and the DOS of SV, Ru₁₃, Ru/SV, Ru/DV, Ru/5577, Ru/555 777 and Ru/555 567 777 composites projected to different spins. See DOI: 10.1039/c4ra02900c

---