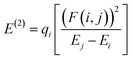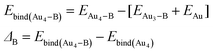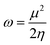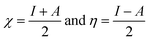DOI:
10.1039/C4RA03753G
(Paper)
RSC Adv., 2014,
4, 29642-29651
Modulation of structural, energetic and electronic properties of DNA and size-expanded DNA bases upon binding to gold clusters†
Received
24th April 2014
, Accepted 20th June 2014
First published on 23rd June 2014
Abstract
Gold cluster–nucleobase complexes have potential applications in designing and fabrication of novel electronic nano-devices, and there has been a surge in research activities in this area recently. Binding of gold clusters (Au3 and Au4) with DNA bases and size-expanded DNA bases (x-bases) have been studied using density functional theory employing high quality basis set. A comprehensive attempt has been made to examine several gold–nucleobase complexes with respect to change in the orientation of Au clusters with respect to all the titratable sites of the bases. Geometric and electronic features of these complexes provided evidences for existence of non-conventional hydrogen bonds, which was further substantiated via vibrational frequency and natural bond orbital (NBO) analysis. The nucleobases, both canonical and size-expanded forms, form stable complexes with both the gold clusters considered here. The natural population analysis (NPA) and NBO analysis indicated that complexation greatly affects the charge distribution on the DNA bases due to charge transfer between base and gold cluster. Upon complexation, a marked decrease in the HOMO–LUMO gaps and ionization potentials was observed, which was more profound in case of x-bases due to the extended π-conjugation of the fused benzene rings. Such electronic effects driven by structural perturbations in nucleobases are expected to provide a better test bed for designing charge transfer driven nano-devices. This study demonstrates that combining structural modifications to DNA bases and subsequent binding to gold nanoparticles can be effectively used to modulate and design materials with desired optico-electronic properties.
Introduction
Gold nanoparticles have potential applications in wide spectrum of areas from material science to medicine, and it is possible to alter their optical, catalytic and electronic properties by tagging with biomolecules.1,2 An added interest in gold nanoclusters is due to the recent discoveries of unprecedented large planar gas-phase gold clusters.2–5 Tagging of nanoparticles to biomolecules is well investigated both theoretically and experimentally.6 Modifications in DNA involving metals has drawn special attention as recent experimental results indicate a metallic behaviour of such complexes.7 Several studies have appeared on the alteration in the photochemical properties of nucleic acids on being tagged with gold clusters.8–11 These features facilitate detection of extremely small concentrations of analyte, serve as platforms for 2- and 3-dimensional constructs, and behave as real-time observable nodes in imaging studies.12 Most of these studies have focused on understanding the influence of metal complexation on hydrogen bonding patterns of the canonical base pairs. Meyong et al. have reported that a guanidinium ion and guanine nucleobase when forming hydrogen bonded base pair via a gold electrode with deoxycytidine-monophosphate (dCMP), exhibit ballistic electron conductivity through a molecular junction giving rise to an effective electric circuit which may act as a possible device for sequencing unmodified single-stranded DNA.13 It is expected that such modifications would yield potential molecular wires. Fuentes-Cabrera et al. have investigated the coupling of Zn ions to natural bases.14 The role of transition metals in metalated DNAs has been extensively addressed at the ab initio level by investigating the interaction of transition metals with natural bases.15
In spite of the wide applications of metal-conjugated nucleobases, their inherent property of low conductivity and thermal stability does not allow us to achieve the long standing goal of designing a genetic system with enhanced information storage and transmission capability beyond the natural DNA limits. Designing synthetic analogues of natural DNA bases, like size-expanded DNA bases, possibly realize more thermally stable and conductive molecular wires and, suggest ways to go beyond the limits of natural DNA in nanotechnological applications and might eventually lead to entirely new genetic systems.9–11,16,17 Kool et al. synthesized size-expanded oligomers of DNA which are known to possess high thermal stability due to better stacking interactions when compared to native DNA base pairs.17,18 Both theoretical and experimental studies have suggested that larger base size yields a fluorescent character to the base pairs that can be practically exploited in the detection of natural DNA and RNA.17–21 Recently, it has also been reported that the modified bases show significantly different photophysical and photochemical properties, although the basic structural and bonding aspects remain similar.22 This is driven by the presence of an aromatic ring that causes an alteration of electronic distribution over the frontier molecular orbitals thereby causing the optical response to be diverging in comparison to the natural bases.23 Some theoretical studies have been reported addressing the interaction of these size-expanded bases and bases pairs with small metal clusters. Brancolini et al. have studied the interaction of size-expanded bases with copper and silver metal atoms and suggest that these complexes are the most assuring materials to be used as nanowires with enhanced electron transfer and also for signal detection via modified DNA helix.10 Binding of gold nano clusters with size-expanded bases has also been studied, and it has been shown that the modification of electronic structure leads to some interesting properties such as high conductivity and charge transfer.24 Recently, the interaction between size-expanded guanine and small gold clusters has been investigated which suggests that the introduction of an aromatic ring in guanine reduces the HOMO–LUMO gap and delocalizes the spatial distribution of electrons, making it ideal for charge transfer performance.25 Although, few studies on size-expanded guanine interactions with gold clusters have been published, a comparative study of complexes with all the four size-expanded bases is expected to further our understanding.
In this work, we have made a comparative study on interaction of small gold clusters with natural and size-expanded nucleobases. In our previous work, we have mentioned that among the Aun (n = 3–13) clusters, Au3 and Au4 show maximum interaction with biomolecules.26 Here, we chose these two clusters which also serve as the catalytic models for Au(111) and Au(110) surfaces.27 In order to model the bases, both natural as well as size-expanded, the sugar-phosphate backbone of these structures originally present is replaced by a methyl group in order to remove the complexity. Since the primary aim of the paper is to investigate gold cluster interaction with nucleobases, this truncation is deemed adequate. It has been previously shown that methyl substitution reduces the computational effort without significantly affecting the properties of the real systems.28 Our study focuses on how the insertion of benzene ring in the natural bases alters the energy levels and gaps, thereby justifying the suitability of the newly designed size-expanded DNA base analogues tagged on gold clusters for molecular conduction applications. Geometrical features, binding energy trends, modifications in electric properties and natural orbital populations have been analysed to understand the nature of interaction present in the complexes.
Methodology
The electronic properties of several nucleobase (natural/size-expanded)–cluster complexes were investigated by means of DFT calculations. To choose the initial structures for geometric relaxation, coordinates of DNA bases were generated using GaussView05.29 The coordinates of x-DNA bases were extracted from the nuclear magnetic resonance (NMR) models of xDNA deposited in the Protein Data Bank (PDB ID:2ICZ).30 Benchmark studies by Wu et al. on transition elements suggested that PBE0, the generalized-gradient-approximation exchange-correlation functional of Perdew, Burke, and Ernzerhof31 reproduces the experimental dissociation energies reasonably well.32 Knal et al. have shown PBE0 to be the best functional in describing the ground state thermodynamic stabilities of intermolecular charge transfer complexes.33 Based on these studies, we have used the PBE0 functional for all the calculations reported here. Stuttgart-Dresden 19 electron (SDD) effective core potential (ECP) has been used for gold.34 These energy-consistent ECPs work within the relativistic Dirac–Fock theory and significantly remove the spin contamination. Split valence double-ζ functions with polarization functions, d type for all non-hydrogen atoms and p type for hydrogen atoms, including a s–p and a p–d diffusion function, 6-311G++(2d,2p), formed the basis set for the optimization of the bases.35 Initial neutral geometries of complexes were generated by placing the gold cluster at active (electronegative) sites of the base and were subjected to geometry optimization. The interaction was studied for: N1, N3, N6 and N7 sites of adenine, N1, N2, N3, O6, N7 of guanine, N3 and N4 of cytosine and O2, N3 and O4 sites of thymine. The same sites were considered for their size-expanded (x) analogues. All possible orientations of gold clusters (Au3 and Au4) with respect to the base at above mentioned titratable sites were considered and the geometry optimizations resulted in more than one stationary points. We are reporting only the most stable ones here. Real vibrational frequencies were obtained for all the optimized structures, indicating that they lie on the minima on the respective potential energy surfaces. The interaction energies (Eint) were calculated using the following equation:| | |
Eint = Ecomplex,n − [Ebase + EAu,n]
| (1) |
where, Ecomplex is the zero-point vibrational energy (ZPVE) corrected electronic energy of the complex, Aun (n = 3, 4), and Ebase and EAu,n are the ZPVE corrected electronic energies of uncomplexed base and cluster, respectively. Analysis of charge distribution was carried out based on (i) electrostatic potential (ESP) surfaces (mapped with the total electron density) and (ii) natural population analysis (NPA). The vertical ionization potential (IPvertical) was calculated as:| | |
IPvertical = Ecation − Eneutral
| (2) |
where, Ecation is the energy of the complex when one electron is removed from the system corresponding to the neutral geometry and Eneutral is the energy of the neutral complex. The NBO analysis,36 was performed on these complexes to examine all possible stabilizing interactions. Second order stabilization energy, E(2), due to interactions between filled Lewis (NBO(i)) and empty non-Lewis orbitals (NBO(j)), is obtained as37| |
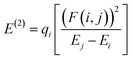 | (3) |
where qi is donor orbital occupancy, Ei and Ej are energies of the orbitals i, j respectively, and F(i,j) is the off diagonal NBO Fock matrix element. All the calculations were performed using the Gaussian 09 suite of programs.38
Results and discussion
Structure and stability
The results of geometry optimizations corresponding to the complexes showing maximum interaction are presented in Fig. 1 and 2. The data for all the optimizations carried out can be found in the ESI.† It is observed that all the complexes investigated in this work possess a charge transfer type interaction.
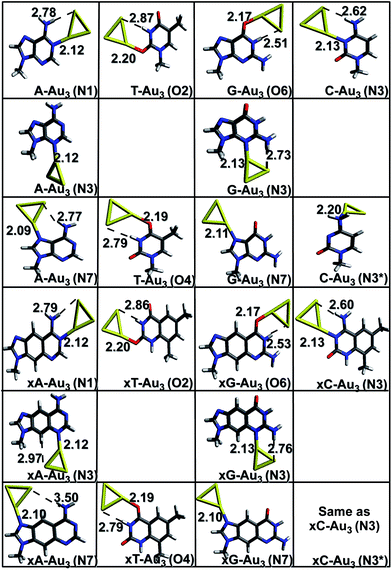 |
| | Fig. 1 Gas phase optimized geometries of natural/modified nucleobases formed with Au3 at the PBE0/SDD∪6-311++G(2d,2p). The bond lengths are in Å. Blue color refers to N, grey represents C, red represents O, yellow represents Au and white represents H. The non-conventional hydrogen bonds are represented with a dotted line. | |
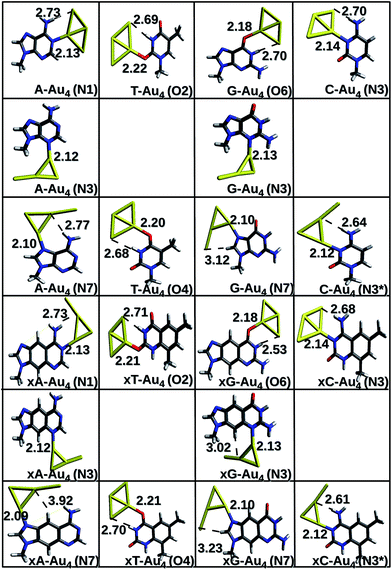 |
| | Fig. 2 Gas phase optimized geometries of natural/modified nucleobases formed with Au4 at the PBE0/SDD∪6-311++G(2d,2p). The bond lengths are in Å. Blue color refers to N, grey represents C, red represents O, yellow represents Au and white represents H. The non-conventional hydrogen bonds are represented with a dotted line. | |
Complexes with Au3. The initial geometries for optimization were generated by placing the gold clusters near the active (titratable) sites of the bases/x-bases. These sites constitute electron-rich atoms: nitrogen and oxygen, which can easily donate the electron density to the empty 5d and 6s orbitals of gold. Owing to relativistic effects, gold has a high electron affinity which explains its high propensity to accept the electrons.4,39 Gold has also been found to act as a proton acceptor and forms non-conventional hydrogen bonds (N–H⋯Au and C–H⋯Au).25,40 These two factors are responsible for a stable complex formation. As depicted in Fig. 1, the Au3 cluster preferentially binds to the N1, N3, N6, N7 sites of adenine and x-adenine; N3, N4 sites of cytosine and x-cytosine; N1, N3, O6, N7 of guanine and x-guanine; O2, O4 sites of thymine and x-thymine. A non-conventional hydrogen bond is formed between amino/imino hydrogen and gold (N–H⋯Au) in most of the cases. In case of Au3 complexed with x-cytosine (N3 and N3* site of interaction), both initial structures considered, optimized to the same minimum (Fig. 1). The most stable complexes are planar and are formed via Au–N or Au–O anchor (coordinative) bonds. This result is in agreement with the earlier reported result of Kryachko et al.8,25 The anchoring bond lengths are shown in Fig. 1. As can be seen from the figure, the Au–N bond length is shorter than Au–O. The Au–N distance falls in the range of 2.09–2.13 Å which is close to the sum of covalent radii of nitrogen 0.75 Å and gold 1.44 Å. As a result, a strong covalent contribution can be expected. The higher basicity of nitrogen makes it a better electron donor and hence a stronger bond is formed on Au–N interaction. In the case of Au–O, where the carbonyl oxygen is rather acidic in nature, oxygen becomes a comparatively poor electron donor, resulting in a weak interaction. The strength of the non-conventional hydrogen bonds is analysed in terms of the Au⋯H bond lengths and ∠N−H−Au or ∠C−H−Au (Table S1 (a)†). It is noticed that on complexation, the vibrational frequency corresponding to N–H stretching mode is red shifted. This shift is higher for imino N–H bonds than that for amino N–H bonds. The corresponding intensity values increase 1–2 orders of magnitude on complexation.
Complexes with Au4. Both rhombic and y-shaped clusters were considered for interaction. In most of the cases, the rhombic form interacts strongly with the base. The anchor bond lengths are larger for complexes with Au4; N–Au falls in the range of 2.13–2.18 Å whereas Au–O bond length falls in the range of 2.18–2.34 Å. This suggests a weaker interaction with Au4 in comparison to that of Au3 cluster. The non-conventional hydrogen bonds are also comparatively weaker in this case, as depicted by the longer bond lengths of N–H⋯Au bonds (Table S1 (b)†).
Energetics
The binding energy of bare Au3 cluster (−25.9 kcal mol−1) is much lower than that of bare Au4 cluster (−51.2 kcal mol−1) in magnitude as calculated using the equation,2,4| | |
Ebind = Ecluster,n − [Ecluster,n−1 + EAu]
| (4) |
where, Ecluster is the ZPVE corrected electronic energy of the cluster, ‘n’ refers to number of Au atoms and EAu refers to the energy of one gold atom. This indicates that Au4 cluster is more stable than Au3. Contrary to this, the interaction energy of Au3 gold cluster to DNA bases is comparatively higher than that of Au4 (Table 1). This is explained on the basis of the stabilization provided by electron pairing effects in case of even membered complexes.2,4,41 Au3 with unpaired electron is more reactive leading to higher affinity towards nucleobases compared to Au4 where all electrons are paired. This also explains the longer anchor bond lengths for Au4. The only exception to this is C(N3*) where the planarity of the system and an additional N–H–Au bond formation for the complex with Au4 is providing it more stability. The interaction with x-bases is found to be stronger in comparison to their corresponding natural bases for complexes with Au3. However, in case of complexes with Au4, there are some cases where natural bases show more affinity towards gold than their x-counterpart, but the differences are marginal (Table 1). A comparison of interaction energies of all the base–Au3/4 complexes gives the following order of affinity towards gold: C > A > G > T. The order for x-bases also follows the same trend. This result is in line with earlier reported results of Kryachko et al.8 Where interaction occurs in the same plane as the base, the complexes show higher interaction energy; for instance, A–Au3(N1) has an interaction energy of −32.3 kcal mol−1, whereas for A–Au3(N6), it is only −17.9 kcal mol−1 (Fig. 1 and 2). The N3 site of cytosine/x-cytosine shows maximum affinity towards gold, whereas thymine shows minimum interaction with gold cluster. This result is in agreement with some of the earlier reported works, where cluster interactions with DNA bases have been studied.8,42,43 The low affinity of thymine with gold clusters can be explained on the basis of the delocalization of electrons on the carbonyl oxygen with the electron cloud of aromatic ring, thus making it less capable of donating electrons to the metal cluster. There are two such carbonyl oxygen present in thymine. This further prevents the nitrogen atom from being a hydrogen bond donor. The Pearson product moment correlation coefficient (PPMCC), which is a measure of linear dependence between two variables was calculated to find out the linear dependence between the anchor bond lengths and binding energies. The details of this calculation are available in the supporting information (Table S5†). Excellent negative value was obtained for all the cases (−0.92 for Au3 and −0.93 for Au4) indicating that the two quantities are negatively correlated, i.e., smaller the bond length, stronger is the complex.
Table 1 Interaction energies calculated at the PBE0/SDD∪6-311++G(2d,2p) level of theory
| Complex |
Energy (kcal mol−1) |
| Au3 |
Au4 |
| A (N1) |
−32.3 |
−25.0 |
| A (N3) |
−29.6 |
−25.4 |
| A (N7) |
−32.2 |
−27.6 |
| xA (N1) |
−33.3 |
−29.8 |
| xA (N3) |
−33.6 |
−26.8 |
| xA (N7) |
−32.3 |
−30.1 |
| C (N3) |
−33.9 |
−25.3 |
| C (N3*) |
−18.4 |
−31.6 |
| xC (N3) |
−34.1 |
−25.4 |
| xC(N3*) |
— |
−32.0 |
| G (O6) |
−27.7 |
−17.8 |
| G (N3) |
−28.8 |
−21.7 |
| G (N7) |
−29.4 |
−26.6 |
| xG (O6) |
−26.3 |
−17.2 |
| xG (N3) |
−32.8 |
−27.1 |
| xG (N7) |
−30.5 |
−26.7 |
| T (O2) |
−17.1 |
−11.1 |
| T (O4) |
−20.3 |
−13.0 |
| xT (O2) |
−18.4 |
−11.2 |
| xT (O4) |
−19.3 |
−12.1 |
We have calculated the effect of binding on the binding energies of Au4–B complex (B = C, A, T, G and the x-analogues), using the equation,
| |
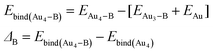 | (5) |
In most cases, ΔB is insignificant (<±4 kcal mol−1). There is one case with much larger value, namely, ΔC(N3*) = −18.7 kcal mol−1. This corresponds to major structural changes in the cluster when binding with the base takes place.
Fig. 3 clearly indicates a sharp decrease in the HOMO–LUMO gaps on complexation with cluster in both cases (Au3 and Au4). This feature may enhance the capability of gold clusters to act as vehicle for transferring mobile charges, a useful feature in nanoelectronic applications. It is observed that complexation results in the alteration of the HOMO orbitals of the base which causes this marked reduction of the gap. The HOMO and LUMO natural orbitals of purine bases are π orbitals where as in case of pyrimidines, HOMO has a σ character (Fig. 4). These observations are in line with the earlier reported results of Varsano et al.44 For x-bases, the HOMO and LUMO orbitals have a π character where the π orbitals of benzene ring are also found to contribute.25 When the complexation takes place, in most of the cases it is observed that the HOMO shifts towards the metal accompanied by a rise in its energy reducing the gap. Though, DFT is known to underestimate the HOMO–LUMO gaps, the systematic decrease on complexation seems reliable.
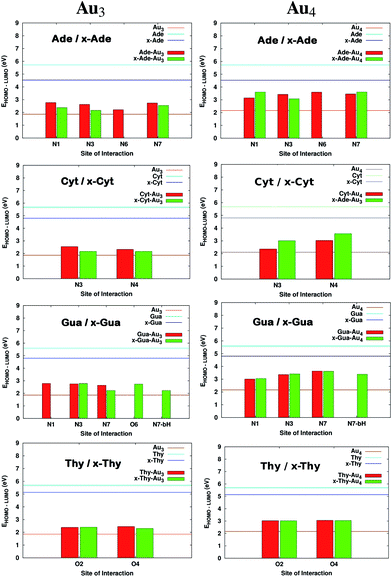 |
| | Fig. 3 Comparison of HOMO–LUMO gaps before and after complexation for complexes of DNA and x-DNA bases with Au3 and Au4. The values that are missing do not have a corresponding interaction from that site. | |
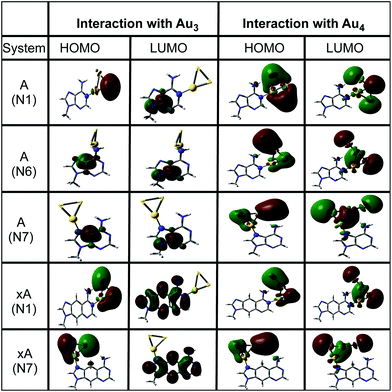 |
| | Fig. 4 The natural orbital plots corresponding to the HOMO and LUMO orbitals of adenine and x-adenine complexes as calculated in gas phase at the PBE0/SDD∪6-311++G(2d,2p) level of theory. | |
It has been reported earlier that gold clusters have higher ionization potential (IP) values than DNA bases41 which are in the range of 8.2–9.5 eV among which guanine is found to have the lowest value.45–47 Earlier works indicated that long-distance transfer of electrons through molecules aid in the function of DNA during oxidative stress and is also a key feature in designing novel molecular devices.48–51 This can be well accomplished by designing complexes having reduced IPvertical values. It is clear from Fig. 5 that on complexation, IPvertical is reduced and for the aromatic expansion of the base the reduction is even larger in many cases. It is observed that the reduction is site specific only for complexes with guanine and x-guanine. This may be because of different atoms involved in the formation of the anchor bond (O(6)–Au and N(7)–Au). We also observe that the extent of decrease in IPvertical is higher for complexes formed with Au3.
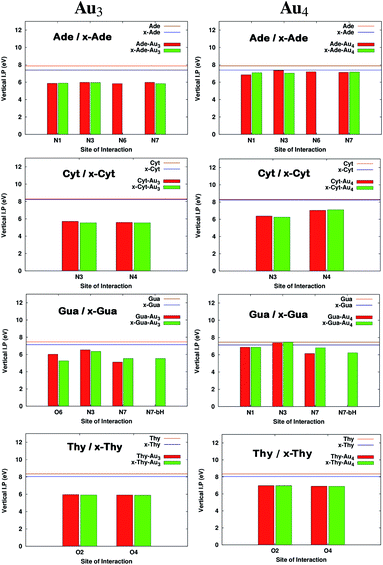 |
| | Fig. 5 Comparison of Ionization potentials before and after complexation for complexes with Au3 and Au4. All the calculations have been performed at the PBE0 level of theory using the SDD∪6-311++G(2d,2p) basis set. The values that are missing do not have a corresponding interaction from that site. | |
Electric properties
The dipole moments (μ), polarizabilities (α) and first-order hyperpolarizbilities (β) were computed to monitor the impact of complexation on the electric properties of the bases/x-bases. The values are given in Table S4.† It is observed that μ increases on complexation implying a greater charge separation. Owing to the collapse of symmetry of the gold cluster on complexation, the values of α and β also increase. Increase in polarizability causes the dispersion forces to increase, resulting in an increase in the melting and boiling points of the complex.52 Hence, we expect these complexes to be thermally more stable than their uncomplexed counterparts. Higher values of β indicate that these complexes might possess good non-linear optical properties. It is observed that x-adenine shows the maximum β value for interaction with both Au3 and Au4 when it is interacting at the N7 site.
Electrophilicity index
Global electrophilicity index (ω) defined in terms of the chemical potential (μ) and chemical hardness (η) is a measure that quantifies the electrophilic nature of molecules.53 This is given as:| |
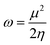 | (6) |
where μ = −χ, the electronegativity of the system. The quantities χ and η are defined within the conceptual DFT frame work as:54,55| |
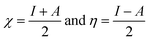 | (7) |
where I is the ionization potential and A is the electron affinity of the system. The parameter ω in quantitative structure–activity relationships (QSAR),56 is a measure of the propensity of the molecule to act as a nucleophile. It is known from previous studies that DNA acts as a nucleophile and tends to react with certain water soluble epoxides that are carcinogenic.57 This results in damage to DNA. The increase in electrophilicity index values suggests that the tendency to react with epoxides would possibly reduce. The values of ω for the complexed systems are reported in Table S4† and Fig. 6 shows the variation in ω. It is clear from the figure that the electrophilicity index values increase on size-expansion which is further enhanced on complexation reducing the toxicity.58
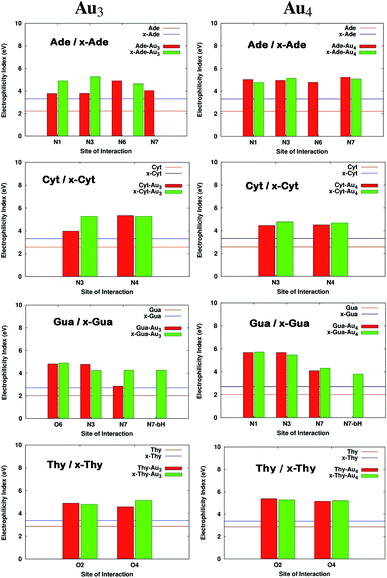 |
| | Fig. 6 Electrophilicity index values on complexation of bases with Au3 and Au4. All the calculations have been performed at the PBE0 level of theory using the SDD∪6-311++G(2d,2p) basis set. The values that are missing do not have a corresponding interaction from that site. | |
Natural population analysis (NPA)
NPA enables the evaluation of ‘natural’ orbital population and atomic charge at the atomic centre.59 The advantage of NPA populations over others is that, it satisfies the important physical constraints of Pauli principle and charge additivity. These features, in particular, guarantees the overall conservation of probability.59 We have calculated the natural charges in order to quantify the charge transfer between the base/x-base and metal cluster. Also the charges at the titratable sites are compared with those of the uncomplexed bases. Fig. 7 shows the charges on the atoms involved in the formation of anchor bonds. In most of the cases, atoms forming the anchor bonds have opposite charges reflecting the ionic nature of the anchoring bond. The more is the ionic character, the higher is the interaction energy. Table 2 represents the charge gained by cluster (Δq) on complexation, suggesting that the cluster oxidises the coordinated base/x-base. The charge transfer is slightly higher for x-bases and also in complexes with Au4.
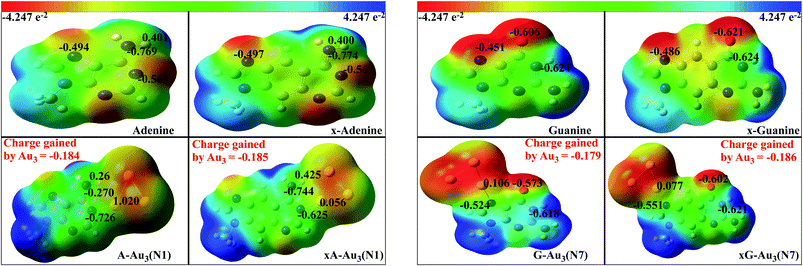 |
| | Fig. 7 Electrostatic potential surface mapped over isodensity surface for complexed (with Au3) and uncomplexed purines in gas phase. The isovalue for these images is 0.0004 a.u. The numbers in black represent the natural charges on the respective atoms. The total charge gained by the cluster is represented in red. | |
Table 2 Magnitude of charge transfer where qcluster = 0 calculated using the natural charge data. Δq refers to the excess charge on the cluster when complexed to the base
| Complex |
Δq |
| Au3 |
Au4 |
| A (N1) |
−0.184 |
−0.202 |
| A (N3) |
−0.195 |
−0.207 |
| A (N6) |
−0.158 |
−0.197 |
| A (N7) |
−0.177 |
−0.193 |
| xA (N1) |
−0.185 |
−0.201 |
| xA (N3) |
−0.193 |
−0.211 |
| xA (N7) |
−0.176 |
−0.184 |
| C (N3) |
−0.175 |
−0.199 |
| C (N3*) |
−0.161 |
−0.195 |
| xC (N3) |
−0.172 |
−0.195 |
| xC(N3*) |
— |
−0.196 |
| G (O6) |
−0.100 |
−0.146 |
| G (N3) |
−0.192 |
−0.217 |
| G (N7) |
−0.179 |
−0.184 |
| xG (N3) |
−0.192 |
−0.221 |
| xG (N7) |
−0.186 |
−0.192 |
| xG (O6) |
−0.100 |
−0.124 |
| xG (N7-bH) |
−0.186 |
−0.194 |
| T (O2) |
−0.114 |
−0.121 |
| T (O4) |
−0.121 |
−0.129 |
| xT (O2) |
−0.114 |
−0.178 |
| xT (O4) |
−0.116 |
−0.127 |
Natural bond orbital analysis (NBO)
NBO methods involve the expression of molecular properties in terms of a ‘Natural Lewis structure’ (NLS) depiction of wave function.59 NBO allows wave function to be expressed in terms of Lewis (one-centre lone-pair or two-centre bond-pair) and non-Lewis type (all remaining orbitals) contributions, allowing the use of elementary valence bond concepts. NBOs describe the residual resonance delocalization effects giving an insight to the existing inter- and intramolecular interactions in the system. Second-order perturbation theory analysis is done to gauge the donor–acceptor interactions within the NBO framework. This gives a quantitative view of the charge transfer interactions existing between the donor and the acceptor species. Table 3 shows the stabilization energy (E(2)) values for some of the complexes. In case of anchoring bonds, the lone pair of the donor (N,O) is transferred to the antibonding orbitals of Au. It is also observed that lone pair on Au donates electron density to the anti-bonding orbital of N–H substantiating the formation of non-conventional hydrogen bonds. In case of xA–Au3 (N7) we observe a C–H–Au interaction with an E(2) value of 2.38 kcal mol−1, which is indicative of a weak hydrogen bonding type interaction between benzylic carbon and gold. Our results conform to a recent work of Sun et al. who have also identified similar interactions in case of guanine complexed with gold.25 The E(2) values clearly indicate that charge transfer plays an important role in stabilizing the interaction between base and cluster. Higher E(2) for x-bases complexes indicates higher charge transfer in those systems.
Table 3 Second order perturbation theory analysis of Fock matrix in NBO basis for Au3 cluster
| Base |
Site |
Donor |
Acceptor |
E(2) (kcal mol−1) |
| Adenine |
N1 |
nN6 |
σ*Au−Au |
11.75 |
| N7 |
nN7 |
σ*Au−Au |
11.99 |
| |
nAu |
σ*N6−H |
4.86 |
| x-Adenine |
N1 |
nN6 |
σ*Au−Au |
17.64 |
| |
nAu |
σ*N6−H |
5.63 |
| N7 |
nN7 |
σ*Au−Au |
17.04 |
| |
nAu |
σ*bC−H |
2.38 |
| Guanine |
O6 |
nO6 |
σ*Au−Au |
8.59 |
| N7 |
nN7 |
σ*Au−Au |
11.17 |
| x-Guanine |
O6 |
NO6 |
σ*Au−Au |
11.81 |
| |
nAu |
σ*N1−H |
4.53 |
| N7 |
nN7 |
σ*Au−Au |
18.18 |
| Cytosine |
N3 |
nN3 |
σ*Au−Au |
10.47 |
| |
nAu |
σ*N4−H |
4.00 |
| N4 |
nN4 |
σ*Au−Au |
9.64 |
| x-Cytosine |
N3 |
nN3 |
σ*Au−Au |
15.47 |
| |
nAu2 |
σ*N4−H |
3.83 |
| Thymine |
O2 |
nO2 |
σ*Au−Au |
5.95 |
| |
nAu |
σ*N3−H |
1.71 |
| O4 |
nO4 |
σ*Au−Au |
7.82 |
| |
nAu |
σ*N3−H |
0.50 |
| x-Thymine |
O2 |
nO2 |
σ*Au−Au |
6.87 |
| |
nAu |
σ*N3−H |
1.03 |
| O4 |
nO4 |
σ*Au−Au |
9.68 |
Conclusion
In this work, density functional theory has been applied to examine the geometries, electronic structures, charge populations and interaction energies of DNA bases/x-bases tagged with Au3 and Au4 clusters. The calculations showed that gold nano clusters form stable complexes with natural as well as x-bases. The interactions are stronger with Au3 clusters. The affinity of x-bases for gold is found to be higher. Highest interaction energy is found for xC–Au3(N3) (−34.14 kcal mol−1). The major bonding factors found to govern this interaction are the anchoring bonds between Au–N(O) and the non-conventional hydrogen bonding between N–H⋯Au. Following the gold binding, a redistribution of electronic charge around the Watson–Crick edge takes place, suggesting a modification in hydrogen bonding patterns on base pair formation. The role of gold cluster binding on the ability of nucleobases to form base pair interactions is being investigated.
The electronic coupling between the metal atoms and nucleic acid bases results in the reduction of HOMO–LUMO gaps suggesting that these systems might behave as good conductors. It is also found that on complexation, a considerable amount of electronic charge is being transferred from base/x-base to gold cluster. Thus, the gold clusters oxidise the base/x-base. The reduction in ionization potential suggests an ease in hole transfer through these systems, while the increase in polarizability values indicates more thermal stability. Increased values of first order hyperpolarizabity suggest that these complexes might possess non-linear optical properties. Hence a strong modulation of the electronic structure, energy levels and band gaps is observed on complexation, indicating that such systems can be potentially used as building blocks for making nano electronic devices.
Acknowledgements
We thank Department of Science and Technology for financial support. S. R. acknowledges support from CSIR for SRF fellowship.
References
-
(a) T. H. Lee and K. M. Ervin, J. Phys. Chem., 1994, 98, 10023–10031 CrossRef CAS;
(b) I. L. Garzón, C. Rovira, K. Michaelian, M. R. Beltrán, P. Ordejón, J. Junquera, D. Sánchez-Portal, E. Artacho and J. M. Soler, Phys. Rev. Lett., 2000, 85, 5250–5251 CrossRef.
- H. Häkkinen, M. Moseler and U. Landman, Phys. Rev. Lett., 2002, 89, 033401–033404 CrossRef.
- F. Furche, R. Ahlrichs, P. Weis, C. Jacob, S. Gilb, T. Bierweiler and M. M. Kappes, J. Chem. Phys., 2002, 117, 6982–6990 CrossRef CAS PubMed.
- P. Pyykkö, Chem. Rev., 1988, 88, 563–594 CrossRef.
- P. Pyykkö, Angew. Chem., Int. Ed., 2004, 43, 4412–4456 CrossRef PubMed.
-
(a) R. Jin, Y. Cao, C. A. Mirkin, K. L. Kelly, G. C. Schatz and J. G. Zheng, Science, 2001, 294, 1901–1903 CrossRef CAS PubMed;
(b) C. A. Mirkin, R. L. Letsinger, R. C. Mucic and J. J. Storhoff, Nature, 1996, 382, 607–609 CrossRef CAS PubMed;
(c) X.-J. Chen, B. L. Sanchez-Gaytan, Z. Qian and S.-J. Park, Wiley Interdiscip. Rev.: Nanomed. Nanobiotechnol., 2012, 4, 273–290 CrossRef CAS PubMed;
(d) S. J. Oldenburg, J. B. Jackson, S. L. Westcott and N. J. Halas, Appl. Phys. Lett., 1999, 75, 2897–2899 CrossRef CAS PubMed;
(e) G. S. Shafai, S. Shetty, S. Krishnamurty, V. Shah and D. G. Kanhere, J. Chem. Phys., 2007, 126, 014704–014712 CrossRef PubMed;
(f) M. Haruta, T. Kobayashi, H. Sano and N. Yamada, Chem. Lett., 1987, 16, 405–408 CrossRef;
(g) L. Zhang, F. X. Gu, J. M. Chan, A. Z. Wang, R. S. Langer and O. C. Farokhzad, Clin. Pharmacol. Ther., 2007, 83, 761–769 CrossRef PubMed;
(h) P. Chen, S. Mwakwari and A. Oyelere, Nanotechnol., Sci. Appl., 2008, 1, 45–66 CAS;
(i) M. De, C.-C. You, S. Srivastava and V. M. Rotello, J. Am. Chem. Soc., 2007, 129, 10747–10753 CrossRef CAS PubMed.
-
(a) P. Aich, S. L. Labiuk, L. W. Tari, L. J. Delbaere, W. J. Roesler, K. J. Falk, R. P. Steer and J. S. Lee, J. Mol. Biol., 1999, 294, 477–485 CrossRef CAS PubMed;
(b) K. Tanaka, A. Tengeiji, T. Kato, N. Toyama and M. Shionoya, Science, 2003, 299, 1212–1213 CrossRef CAS PubMed;
(c) K. Tanaka, G. H. Clever, Y. Takezawa, Y. Yamada, C. Kaul, M. Shionoya and T. Carell, Nat. Nanotechnol., 2006, 1, 190–194 CrossRef CAS PubMed.
- E. S. Kryachko and F. Remacle, Nano Lett., 2005, 5, 735–739 CrossRef CAS PubMed.
- D. Porath, G. Cuniberti and R. Felice, Charge Transport in DNA-Based Devices, Springer, Berlin Heidelberg, 2004, vol. 237, pp. 183–228 Search PubMed.
- G. Brancolini and R. D. Felice, J. Chem. Phys., 2011, 134, 205102–205114 CrossRef PubMed.
- M. Nagatori, M. Ojima, Y. Ibuki, H. Sakamoto and K. Mizoguchi, J. Phys. Soc. Jpn., 2011, 80, 114803–114805 CrossRef.
-
(a) R. Elghanian, J. J. Storhoff, R. C. Mucic, R. L. Letsinger and C. A. Mirkin, Science, 1997, 277, 1078–1081 CrossRef CAS;
(b) R. Shenhar and V. M. Rotello, Acc. Chem. Res., 2003, 36, 549–561 CrossRef CAS PubMed;
(c) J. Cheon and J.-H. Lee, Acc. Chem. Res., 2008, 41, 1630–1640 CrossRef CAS PubMed.
- M. H. Lee and O. F. Sankey, J. Phys.: Condens. Matter, 2009, 21, 351101–3511011 Search PubMed.
- M. Fuentes-Cabrera, B. G. Sumpter, J. E. Šponer, J. Šponer, L. Petit and J. C. Wells, J. Phys. Chem. B, 2007, 111, 870–879 CrossRef CAS PubMed.
-
(a) A. Vazquez-Mayagoitia, O. Huertas, G. Brancolini, A. Migliore, B. G. Sumpter, M. Orozco, F. J. Luque, R. Di Felice and M. Fuentes-Cabrera, J. Phys. Chem. B, 2009, 113, 14465–14472 CrossRef CAS PubMed;
(b) L. Guo, N. Yin and G. Chen, J. Phys. Chem. C, 2011, 115, 4837–4842 CrossRef CAS;
(c) T. Matsui, H. Miyachi, T. Sato, Y. Shigeta and K. Hirao, J. Phys. Chem. B, 2008, 112, 16960–16965 CrossRef CAS PubMed.
-
(a) C. Brotschi and C. J. Leumann, Angew. Chem., Int. Ed., 2003, 42, 1655–1658 CrossRef CAS PubMed;
(b) M. Kaufmann, M. Gisler and C. Leumann, Angew. Chem., Int. Ed., 2009, 48, 3810–3813 CrossRef CAS PubMed.
-
(a) H. Liu, J. Gao, S. R. Lynch, Y. D. Saito, L. Maynard and E. T. Kool, Science, 2003, 302, 868–871 CrossRef CAS PubMed;
(b) D. W. Kang, X. P. Hao, X. Z. Li, L. B. Li and S. J. Xie, Appl. Phys. Lett., 2013, 102, 072410–072414 CrossRef PubMed;
(c) M. Zwolak and M. D. Ventra, Appl. Phys. Lett., 2002, 81, 925–927 CrossRef CAS PubMed.
- S. R. Lynch, H. Liu, J. Gao and E. T. Kool, J. Am. Chem. Soc., 2006, 128, 14704–14711 CrossRef CAS PubMed.
- M. Fuentes-Cabrera, X. Zhao, P. R. C. Kent and B. G. Sumpter, J. Phys. Chem. B, 2007, 111, 9057–9061 CrossRef CAS PubMed.
- A. Migliore, S. Corni, D. Varsano, M. L. Klein and R. Di Felice, J. Phys. Chem. B, 2009, 113, 9402–9415 CrossRef CAS PubMed.
- J. R. Blas, O. Huertas, C. Tabares, B. G. Sumpter, M. Fuentes-Cabrera, M. Orozco, P. Ordejón and F. J. Luque, J. Phys. Chem. A, 2011, 115, 11344–11354 CrossRef CAS PubMed.
- P. K. Samanta and S. K. Pati, New J. Chem., 2013, 37, 3640–3646 RSC.
- D. Varsano, A. Garbesi and R. Di Felice, J. Phys. Chem. B, 2007, 111, 14012–14021 CrossRef CAS PubMed.
-
(a) P. Sharma, S. Sharma, A. Mitra and H. Singh, J. Biomol. Struct. Dyn., 2009, 27, 65–81 CrossRef CAS PubMed;
(b) P. Sharma, H. Singh, S. Sharma and H. Singh, J. Chem. Theory Comput., 2007, 3, 2301–2311 CrossRef CAS.
-
(a) W. Sun and R. Di Felice, J. Phys. Chem. C, 2012, 116, 24954–24961 CrossRef CAS;
(b) L. Zhang, T. Ren, X. Yang, L. Zhou and X. Li, Int. J. Quantum Chem., 2013, 113, 2234–2242 CrossRef CAS.
- S. Rai and H. Singh, J. Mol. Model., 2013, 19, 4099–4109 CrossRef CAS PubMed.
- P. J. Mohan, A. Datta, S. S. Mallajosyula and S. K. Pati, J. Phys. Chem. B, 2006, 110, 18661–18664 CrossRef CAS PubMed.
- D. Bhattacharyya, S. C. Koripella, A. Mitra, V. B. Rajendran and B. Sinha, J. Biosci., 2007, 32, 809–825 CrossRef CAS PubMed.
- R. Dennington, T. Keith and J. Millam, GaussView Version 5, Semichem Inc., Shawnee Mission KS, 2009 Search PubMed.
- S. R. Lynch, H. Liu, J. Gao and E. T. Kool, J. Am. Chem. Soc., 2006, 128, 14704–14711 CrossRef CAS PubMed.
-
(a) E. M. Fernández, J. M. Soler, I. L. Garzón and L. C. Balbás, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 165403–165417 CrossRef;
(b) J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS;
(c) J. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Phys. Rev. Lett., 2003, 91, 146401–146405 CrossRef.
-
(a) Z. J. Wu, J. S. Shi, S. Y. Zhang and H. J. Zhang, Phys. Rev. A: At., Mol., Opt. Phys., 2004, 69, 064502–064506 CrossRef;
(b) Y. Zhao and D. G. Truhlar, Phys. Chem. Chem. Phys., 2005, 7, 2701–2705 RSC;
(c) Y. Zhao and D. G. Truhlar, J. Chem. Theory Comput., 2007, 3, 289–300 CrossRef CAS.
- A. Knal and N. Acar, J. Mol. Struct.: THEOCHEM, 2010, 949, 36–40 CrossRef PubMed.
-
(a) A. Ehlers, M. Bhme, S. Dapprich, A. Gobbi, A. Hllwarth, V. Jonas, K. Khler, R. Stegmann, A. Veldkamp and G. Frenking, Chem. Phys. Lett., 1993, 208, 111–114 CrossRef CAS;
(b) M. Dolg, U. Wedig, H. Stoll and H. Preuss, J. Chem. Phys., 1987, 86, 866–872 CrossRef CAS PubMed;
(c) D. Andrae, U. Huermann, M. Dolg, H. Stoll and H. Preu, Theor. Chim. Acta, 1990, 77, 123–141 CrossRef CAS;
(d) E. M. Fernández, J. M. Soler and L. C. Balbás, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 235433–235441 CrossRef.
-
(a) P. Hariharan and J. Pople, Mol. Phys., 1974, 27, 209–214 CrossRef CAS;
(b) P. Hariharan and J. Pople, Chem. Phys. Lett., 1972, 16, 217–219 CrossRef CAS;
(c) V. A. Rassolov, M. A. Ratner, J. A. Pople, P. C. Redfern and L. A. Curtiss, J. Comput. Chem., 2001, 22, 976–984 CrossRef CAS;
(d) W. J. Hehre, R. Ditchfield and J. A. Pople, J. Chem. Phys., 1972, 56, 2257–2261 CrossRef CAS PubMed.
- E. D. Glendening, A. E. Reed, J. E. Carpenter and F. Weinhold, NBO Version 3.1, Gaussian, Inc., Wallingford, CT, 2004 Search PubMed.
- F. Weinhold and C. R. Landis, Chem. Educ. Res. Pract., 2001, 2, 91–104 RSC.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09 Revision C.01, Gaussian Inc., Wallingford CT, 2009 Search PubMed.
- M. C. Gimeno, in The Chemistry of Gold, Wiley-VCH Verlag GmbH & Co. KGaA, 2009, pp. 1–63 Search PubMed.
- A. H. Pakiari and Z. Jamshidi, J. Phys. Chem. A, 2007, 111, 4391–4396 CrossRef CAS PubMed.
- P. Pyykkö, Chem. Soc. Rev., 2008, 37, 1967–1997 RSC.
- H. Kimura-Suda, D. Y. Petrovykh, M. J. Tarlov and L. J. Whitman, J. Am. Chem. Soc., 2003, 125, 9014–9015 CrossRef CAS PubMed.
- L. M. Demers, M. Östblom, H. Zhang, N.-H. Jang, B. Liedberg and C. A. Mirkin, J. Am. Chem. Soc., 2002, 124, 11248–11249 CrossRef CAS PubMed.
- D. Varsano, R. Di Felice, M. A. L. Marques and A. Rubio, J. Phys. Chem. B, 2006, 110, 7129–7138 CrossRef CAS PubMed.
- N. A. Richardson, S. S. Wesolowski and H. F. Schaefer, J. Am. Chem. Soc., 2002, 124, 10163–10170 CrossRef CAS PubMed.
- T. Caruso, M. Carotenuto, E. Vasca and A. Peluso, J. Am. Chem. Soc., 2005, 127, 15040–15041 CrossRef CAS PubMed.
- D. M. Close, J. Phys. Chem. A, 2004, 108, 10376–10379 CrossRef CAS.
- B. Giese, J. Amaudrut, A.-K. Kohler, M. Spormann and S. Wessely, Nature, 2001, 412, 318–320 CrossRef CAS PubMed.
- A. Heller, Faraday Discuss., 2000, 116, 1–13 RSC.
- H. W. Fink and C. Schonenberger, Nature, 1999, 398, 407–410 CrossRef CAS PubMed.
- D. Porath, A. Bezryadin, S. De Vries and C. Dekker, Nature, 2000, 403, 635–638 CrossRef CAS PubMed.
- P. W. Atkins, Atkins' Physical chemistry, Oxford University Press, Oxford New York, 2010 Search PubMed.
- R. G. Parr, L. v. Szentpály and S. Liu, J. Am. Chem. Soc., 1999, 121, 1922–1924 CrossRef CAS.
- R. G. Parr and R. G. Pearson, J. Am. Chem. Soc., 1983, 105, 7512–7516 CrossRef CAS.
- H. Chermette, J. Comput. Chem., 1999, 20, 129–154 CrossRef CAS.
- P. Thanikaivelan, V. Subramanian, J. R. Rao and B. U. Nair, Chem. Phys. Lett., 2000, 323, 59–70 CrossRef CAS.
- B. N. Ames and L. S. Gold, Mutat. Res., Fundam. Mol. Mech. Mutagen., 2000, 447, 3–13 CrossRef CAS.
- P. K. Chattaraj, U. Sarkar and D. R. Roy, Chem. Rev., 2006, 106, 2065–2091 CrossRef CAS PubMed.
- E. D. Glendening, C. R. Landis and F. Weinhold, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 1–42 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Structures, Cartesian coordinates, atomic energies, HOMO–LUMO energy gaps, IPvertical, dipole moments, polarizability, hyperpolarizability values, natural orbital plots for all the systems. See DOI: 10.1039/c4ra03753g |
|
| This journal is © The Royal Society of Chemistry 2014 |
Click here to see how this site uses Cookies. View our privacy policy here.