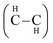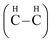Electronic and optical properties of chair-like and boat-like graphane
A. H. Reshak*ab and
S. Auluckc
aNew Technologies – Research Centre, University of West Bohemia, Univerzitni 8, 306 14 Pilsen, Czech Republic. E-mail: maalidph@yahoo.co.uk
bCenter of Excellence Geopolymer and Green Technology, School of Material Engineering, University Malaysia Perlis, 01007 Kangar, Perlis, Malaysia
cCouncil of Scientific and Industrial Research – National Physical Laboratory Dr K S Krishnan Marg, New Delhi 110012, India
First published on 6th August 2014
Abstract
We have studied two favorable conformations of graphane, the chair-like graphane and boat-like graphane. In the chair-like, the H atoms attached to the C atoms alternate on both sides of the sheet while in the boat-like, the C bonded H atoms alternate in pair. Both conformations of graphane have a 2D puckered honeycomb like structure with one hydrogen atom bonded covalently (sp3) to each carbon atom. The chair-like belongs to the P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1 (164) space group and the boat-like belongs to the Pmmn (59) space group. We have used the state-of-the-art full potential linear augmented plane wave (FPLAPW) method with different possible approximations for the exchange–correlation (XC) potential. The XC potential was described by the local density approximation (LDA) of Ceperley–Alder (CA), the generalized gradient approximation (GGA) of Perdew–Becke–Ernzerhof (PBE) and the Engel–Vosko generalized gradient approximation (EVGGA). The calculated partial density of states for both configurations, show that there exists a strong hybridization between C and H orbitals which confirms the existence of the covalent bonds. The electronic charge density distribution of both configurations (chair-like and boat-like) has been calculated, the charge accumulates along C–C and C–H bonds. According to the electro-negativity values of C (2.55) and H (2.1), it is clear that there is strong covalent bonding between C and H atoms. The linear optical properties give a deep insight into the electronic structure. The calculated values of the energy gap and the bond lengths show good agreement with previous results.
m1 (164) space group and the boat-like belongs to the Pmmn (59) space group. We have used the state-of-the-art full potential linear augmented plane wave (FPLAPW) method with different possible approximations for the exchange–correlation (XC) potential. The XC potential was described by the local density approximation (LDA) of Ceperley–Alder (CA), the generalized gradient approximation (GGA) of Perdew–Becke–Ernzerhof (PBE) and the Engel–Vosko generalized gradient approximation (EVGGA). The calculated partial density of states for both configurations, show that there exists a strong hybridization between C and H orbitals which confirms the existence of the covalent bonds. The electronic charge density distribution of both configurations (chair-like and boat-like) has been calculated, the charge accumulates along C–C and C–H bonds. According to the electro-negativity values of C (2.55) and H (2.1), it is clear that there is strong covalent bonding between C and H atoms. The linear optical properties give a deep insight into the electronic structure. The calculated values of the energy gap and the bond lengths show good agreement with previous results.
1. Introduction
Recently a new two dimensional honeycomb lattice material of a monolayer of carbon atoms was discovered. It was called graphene.1,2 Graphene is a hexagonal lattice consisting of a single atomic layer of sp2 hybridized carbon atoms. Around each carbon atom, three strong σ bonds are established with the other three surrounding carbon atoms.3 This two dimensional lattice of monolayer carbon atoms opened a new era in nanotechnology. The outstanding mechanical,4 electrical5 and physical properties6,7 of graphene warrants its use in a variety of areas such as hydrogen technology,8 electronics,5 sensing9 and drug delivery,10,11 among many others. After this discovery several researches focused on modifying graphene for further applications in nanoelectronics. Researchers modified several graphene based materials among them the hydrogenated graphene (called graphane).12–19 In 2003, Sluiter and Kawazoe12 suggested the existence graphane and in 2009, Elias et al.,14 synthesized graphane by exposure the graphene sheet to the hydrogen plasma. Since then, the researchers proposed several new configurations for the newly discovered graphane.Leenaerts et al.20 investigated the different stoichiometric configurations of graphane and graphene fluoride within density functional theory (DFT). They found large differences between graphane and graphene fluoride which are caused by the presence of charges on the fluorine atoms. Authors also perform GW calculations for the electronic band gap of both graphene derivatives. These band gaps and also the calculated Young's moduli are at variance with available experimental data. Duminda et al.21 have studied the stability of chair, boat, and twist-boat graphane structures using first-principles calculations. Their results indicate that locally stable twist-boat membranes significantly contribute to the experimentally observed lattice contraction. They found that the band gaps of graphane nanoribbons decrease monotonically with the increase of the ribbon width and are insensitive to the edge structure.
Shkrebtii et al.22 proved the possibility of electron gap tuning of graphene-based materials, using extensive first principles modeling of the structural, electronic and optical properties of partially hydrogenated graphene. Zhu and Li23 reported that the malleable nature of atomically thin graphene makes it a potential candidate material for nanoscale origami, a promising bottom-up nanomanufacturing approach to fabricating nanobuilding blocks of desirable shapes. Klimov et al.24 have determined the electromechanical properties of a suspended graphene layer by scanning tunneling microscopy (STM) and scanning tunneling spectroscopy (STS) measurements, as well as computational simulations of the graphene-membrane mechanics and morphology. Lee et al.25 measured the elastic properties and intrinsic breaking strength of free-standing monolayer graphene membranes by nanoindentation in an atomic force microscope. The force–displacement behavior is interpreted within a framework of nonlinear elastic stress–strain response, and yields second- and third-order elastic stiffnesses of 340 newtons per meter (N m−1) and −690 N m−1, respectively.
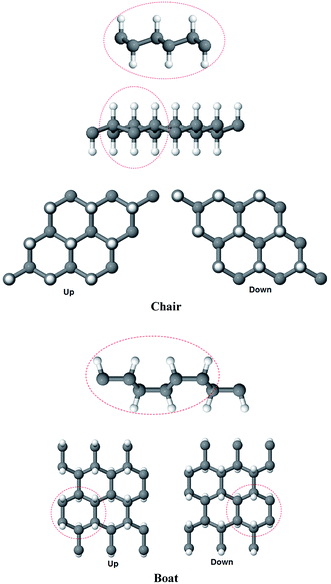
Recently, a fully hydrogenated graphene sheet, called graphane, which is an ‘extended two dimensional covalently bonded hydrocarbon’, having a formula unit CH, was predicted by Sofo et al.13 Sluiter et al.,12 and Sofo et al.,13 suggest that among the many configurations (stirrup, boat-1, boat-2, twisted-boat, chair) graphane is most stable in the chair-like configuration. Graphane could have potential applications as a hydrogen storage material and in two dimensional electronics. Chaoyu He et al.,26 reported that the hexagonal hydrocarbon rings in the most stable of the five graphane allotropes are equivalent. Therefore in this study we will focus on the comparison between the most stable configuration (chair) and one of the not so stable configurations. For the latter we have selected the boat-1 configuration.
We think that it is timely to perform first-principles calculations on these two configurations to investigate the electronic structure, electronic charge density distribution, chemical bonding and the optical properties, using the state of-the-art full-potential augmented plane wave plus local orbitals approach (FP-LAPW + lo) based on the density functional theory (DFT). As first-principles' method is a useful tool for predicting physical properties of materials, it has been widely used in the calculation of physical properties of material.27–32 We should emphasize that we did not aware of any theoretical or experiment work on the optical properties of these materials. This motivated us to calculate the optical properties of chair-like and boat-like graphane. Future experimental work will testify our calculated results. The optical properties can provide detailed information about the electronic structure of the materials. The optical properties of solids are a major topic, both in basic research as well as for industrial applications. While for the former the origin and nature of different excitation processes is of fundamental interest, the latter can make use of them in many optoelectronic devices.
2. Details of calculations
We selected to study two conformations of graphane, the chair-like graphane and boat-like graphane as illustrated in Fig. 1. In the chair-like graphane, the H atoms attached to the C atoms alternates on both sides of the sheet (Fig. 1a) while in the boat-like graphane, the C bonded H atoms alternates in pair (Fig. 1b). Chair-like and boat-like have 2D puckered honeycomb like structure with one hydrogen atom bonded covalently (sp3) to each carbon atom of the sheet. The chair-like conformer has P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1 (164) space group with unit cell a = 2.516 Å, b = 2.516 Å and c = 4.978 Å. Whereas the boat-like conformer has Pmmn (59) space group with unit cell a = 4.272 Å, b = 2.505 Å and c = 4.976 Å. In this calculation we have used the state-of-the-art full potential linear augmented plane wave (FPLAPW) method in a scalar relativistic version as embodied in the WIEN2k code.33 This is an implementation of the density functional theory (DFT) with different possible approximations for the exchange-correlation (XC) potential. The XC potential was described by the local density approximation (LDA) of Ceperley–Alder (CA)34 and the generalized gradient approximation (GGA) of Perdew–Becke–Ernzerhof (PBE),35 which is based on exchange–correlation energy optimization to calculate the total energy. In addition, we have used Engel–Vosko generalized gradient approximation (EVGGA)36 which optimizes the corresponding potential for electronic band structure calculations. The Kohn–Sham equations are solved using a basis of linear APW's. The potential and charge density in the muffin-tin (MT) spheres are expanded in spherical harmonics with lmax = 8 and nonspherical components up to lmax = 6. In the interstitial region the potential and the charge density are represented by Fourier series. The structure is fully relaxed until the forces on the atoms reach values less than 1 mRy per a.u. Once the forces are minimized in this construction one can then find the self-consistent density at these positions by turning off the relaxations and driving the system to self-consistency. From the obtained relaxed geometry the electronic structure and the chemical bonding can be determined and various spectroscopic features can be simulated and compared with experimental data. Self-consistency is obtained using 5000
m1 (164) space group with unit cell a = 2.516 Å, b = 2.516 Å and c = 4.978 Å. Whereas the boat-like conformer has Pmmn (59) space group with unit cell a = 4.272 Å, b = 2.505 Å and c = 4.976 Å. In this calculation we have used the state-of-the-art full potential linear augmented plane wave (FPLAPW) method in a scalar relativistic version as embodied in the WIEN2k code.33 This is an implementation of the density functional theory (DFT) with different possible approximations for the exchange-correlation (XC) potential. The XC potential was described by the local density approximation (LDA) of Ceperley–Alder (CA)34 and the generalized gradient approximation (GGA) of Perdew–Becke–Ernzerhof (PBE),35 which is based on exchange–correlation energy optimization to calculate the total energy. In addition, we have used Engel–Vosko generalized gradient approximation (EVGGA)36 which optimizes the corresponding potential for electronic band structure calculations. The Kohn–Sham equations are solved using a basis of linear APW's. The potential and charge density in the muffin-tin (MT) spheres are expanded in spherical harmonics with lmax = 8 and nonspherical components up to lmax = 6. In the interstitial region the potential and the charge density are represented by Fourier series. The structure is fully relaxed until the forces on the atoms reach values less than 1 mRy per a.u. Once the forces are minimized in this construction one can then find the self-consistent density at these positions by turning off the relaxations and driving the system to self-consistency. From the obtained relaxed geometry the electronic structure and the chemical bonding can be determined and various spectroscopic features can be simulated and compared with experimental data. Self-consistency is obtained using 5000 points in the irreducible Brillouin zone (IBZ). We have calculated the linear optical susceptibilities using 10
points in the irreducible Brillouin zone (IBZ). We have calculated the linear optical susceptibilities using 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000 points in the IBZ. The FPLAPW method has proven to be one of the most accurate methods for calculating the electronic structure of solids within DFT.37,38
points in the IBZ. The FPLAPW method has proven to be one of the most accurate methods for calculating the electronic structure of solids within DFT.37,38
3. Results and discussion
3.1. Electronic band structure, density of states and electronic charge density
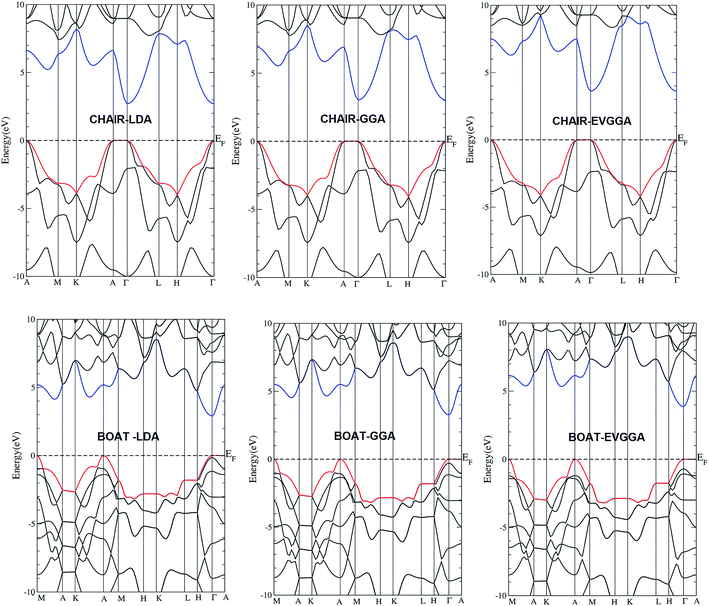
The electronic band structure along the high symmetry directions for the chair-like graphane and boat-like graphane, calculated using three types of exchange correlations mentioned above, are shown in Fig. 2. In all cases and for both configurations the conduction band minimum (CBM) and the valence band maximum (VBM) are located at Γ point the center of the BZ, resulting in a direct band gap. The values of the energy gap for both configurations using different exchange and correlation potentials in comparison to the previous theoretical work are listed in Table 1. Following Table 1, one can see that the values of the energy gap increases when we move from LDA to GGA then to EVGGA. To the best of our knowledge, there are no experimental data for the energy band gaps available in literature to make a meaningful comparison. One can see that the values of energy gap obtained by EVGGA show good agreement with previous theoretical results.13,26 This is mainly due to the fact that LDA and GGA have simple forms that are not sufficiently flexible to accurately reproduce both the exchange–correlation energy and its charge derivative. Engel and Vosko considered this shortcoming and constructed a new functional form of GGA that is able to better reproduce the exchange potential at the expense of less agreement in the exchange energy. Thus, EVGGA, yields better band splitting and some other properties that mainly depend on the accuracy of the exchange–correlation potential.Due to different configurations the boat-like graphane exhibits extra bands in the CB and VB in comparison to chair-like graphane. The total density of states (TDOS) along with the C-s/p and H-s partial density of states (PDOS) of both configurations are shown in Fig. 3a–f. Fig. 3a and b shows the TDOS of chair-like graphane and boat-like graphane using three kinds of exchange correlations. We find that moving from LDA to GGA to EVGGA confirms our previous finding regarding that increase in the band gaps. As the gap obtained with EVGGA agrees best with other workers,13,26 we decided to show the results obtained by EVGGA only. Fig. 3c shows the TDOS of both configurations using EVGGA. We find that the calculated TDOS shows the general structure of both configurations. However the boat-like graphane exhibits more structure with higher amplitudes in comparison to chair-like graphane, which confirm our previous finding that boat-like has more bands than chair-like.
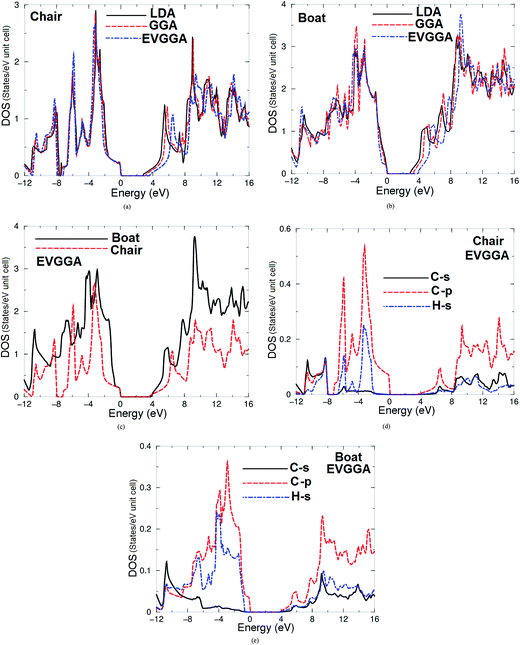 | ||
| Fig. 3 Calculated total and partial density of states for chair-like/boat-like graphane using LDA, GGA and EVGGA. | ||
Fig. 3d and e, illustrates the C-s/p and H-s partial density of states for both configurations. We notice that for chair-like there exists a strong hybridization between C-s and C-p states in the energy range between −11.0 and −7.0 eV and around 7.5 eV. In the energy range extended from −9.0 till −7.0 eV and also around 6.5 eV the C-s/p states strongly hybridized with H-s state. The C-s state hybridized with H-s state between 4.0 and 6.0 eV, 7.0 and 8.5 eV, 10.5 and 11.5 eV, and around 15.0 eV. While for boat-like, C-s/p states hybridized with H-s state around −11.0 eV, C-p state hybridized with H-s states around −4.5 eV, whereas C-s state hybridized with H-s state between 4.0–8.0 eV, 8.5–9.5 eV and 14.0–15.0 eV. In the chair-like graphane the strong hybridization between C-s/p and H-s states at the VB and the CB resulting in very strong covalent bonds, the may be one reason for the high stability of this configuration, while boat-like exhibit strong hybridization between C-s/p and H-s only around −11.0 eV that means the covalent bonds is concentrated only in this energy region. For both configurations it is clear that the VBM and the CBM is mainly formed by C-p states.
From the PDOS-VB one can elucidate the origin of chemical bonding following the same method we used in our previous work.39 One should emphasize that for the chair-like the PDOS-VB located between −8.0 eV and EF is larger compared to C-p state (0.55 electron per eV), H-s state (0.22 electron per eV) and C-s states (0.02 electron per eV), while for boat-like it is for C-p state (0.37 electron per eV), H-s state (0.24 electron per eV) and C-s states (0.04 electron per eV). Therefore some electrons from C and H atoms are transferred into valence bands and contribute in covalence interactions. The interaction due to the strong hybridization and the covalent bonds is defined by the degree of hybridization. Hence, there is a strong covalent bonding between the atoms which exhibit strong hybridization. The PDOS helps to analyze the nature of the bonds according to a classical chemical concept. This concept is very useful to classify compounds into different categories with respect to different chemical and physical properties. To support this statement we have taken a more careful look at the bonding situation since the existence of real hybridization between states of atoms should lead to covalent bond's origin between these atoms.
The electronic charge density distribution of both configurations (chair-like and boat-like) has been calculated in the (1 1 0) and (−1 0 1) crystallographic plane, respectively as shown in Fig. 4a and b. One can see that the charge accumulates around C–C and C–H along the bonds. According to the electro-negativity values of C (2.55) and H (2.1), it is clear that there is a strong covalent bonding between C and H atoms. This can be seen easily by color charge density scale where blue color (+1.00) corresponds to the maximum charge accumulation site. Also one can see that there is a strong covalent bonding between the C–C and C–H atoms. We should emphasize that in the centre of the honeycomb the charge is zero as can be seen by red color (+0.00) corresponds to the minimum charge accumulation site. The bond lengths and angles are listed in Table 2. Following this table one can see that the chair-like graphane has only one type of C–C bond, while boat-like have two types of C–C bonds. The bond length of C–C which are attached to H on the same side is longer (due to H–H repulsion) than that which H attached in opposite sides.
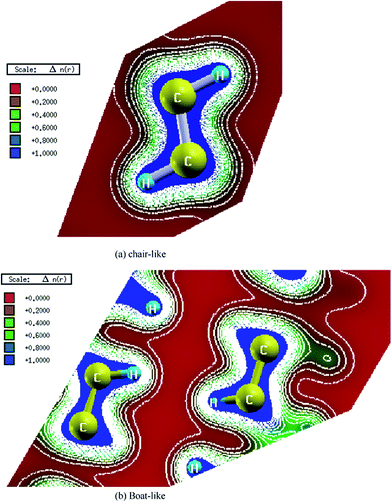 | ||
| Fig. 4 Calculated electronic charge density distribution for chair-like graphane in the (1 1 0) crystallographic plane and boat-like graphane in the (−1 0 1) crystallographic plane. | ||
3.2. Optical properties
The optical properties can provide detailed information about the electronic structure of the materials. The optical properties of solids are a major topic, both in basic research as well as for industrial applications. While for the former the origin and nature of different excitation processes is of fundamental interest, the latter can make use of them in many optoelectronic devices. The chair-like conformer is belong to P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1 (164) space group, this symmetry allows two non-zero components of the complex second-order dielectric (optical) tensor corresponding to the electric field
m1 (164) space group, this symmetry allows two non-zero components of the complex second-order dielectric (optical) tensor corresponding to the electric field ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) being directed along a and c-crystallographic axes, these are εxx(ω) and εzz(ω). While for boat-like conformer (Pmmn (59)) the symmetry allows three non-zero components of the complex second-order dielectric tensor corresponding to the electric field
being directed along a and c-crystallographic axes, these are εxx(ω) and εzz(ω). While for boat-like conformer (Pmmn (59)) the symmetry allows three non-zero components of the complex second-order dielectric tensor corresponding to the electric field ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) being directed along a, b, and c-crystallographic axes, these are εxx(ω), εyy(ω) and εzz(ω). We identify these with the x, y and z Cartesian directions. The imaginary part of the two/three complex tensor components completely defines the linear optical properties. The imaginary part of the optical function's dispersion originates from inter-band transitions between the valence and conduction bands. According to the dipolar selection rule only transitions changing the angular momentum quantum number l by unity are allowed. The imaginary parts of the optical function's dispersion were calculated using the following expression40
being directed along a, b, and c-crystallographic axes, these are εxx(ω), εyy(ω) and εzz(ω). We identify these with the x, y and z Cartesian directions. The imaginary part of the two/three complex tensor components completely defines the linear optical properties. The imaginary part of the optical function's dispersion originates from inter-band transitions between the valence and conduction bands. According to the dipolar selection rule only transitions changing the angular momentum quantum number l by unity are allowed. The imaginary parts of the optical function's dispersion were calculated using the following expression40
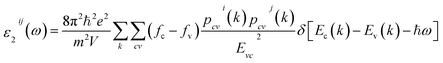 | (1) |
The two components of the imaginary part of the dielectric functions εxx2(ω) and εzz2(ω) for chair-like graphane are shown in Fig. 5a. The edges of the optical absorption (threshold) for these two components are situated at 3.60 eV. Two fundamental peaks were located at around 11.0 eV for εxx2(ω) and 13.0 eV for εzz2(ω). One can see that the fundamental peak of εxx2(ω) is situated between two humps, while that of εzz2(ω) are located between the small peak (around 8.0 eV) from the left hand side and several humps on the right hand side. There exists a considerable anisotropy between εxx2(ω) and εzz2(ω).
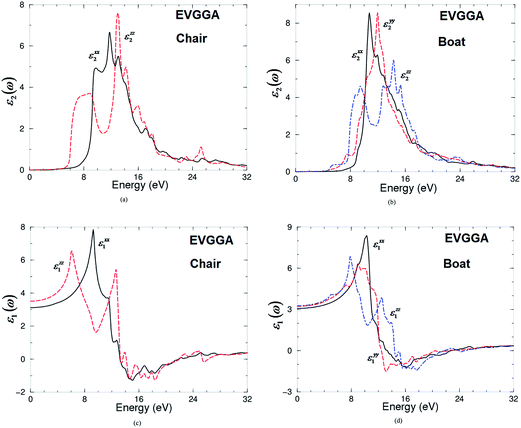 | ||
| Fig. 5 Calculated imaginary and real parts of the optical dielectric function for chair-like/boat-like graphane using EVGGA. | ||
In Fig. 5b, we show the three tensor components of boat-like graphane εxx2(ω), εyy2(ω) and εzz2(ω). The threshold of the optical absorption for the three components εxx2(ω), εyy2(ω) and εzz2(ω) are located at 3.2 eV. εxx2(ω) and εyy2(ω) displays one principal peak situated around 11.0 and 12.0 eV, while εzz2(ω) displays two principal peaks located around 8.0 and 16.0 eV. The first peak consists of one small hump while the second peak is situated between two humps. One can see a considerable anisotropy between the three components. Knowing the imaginary part of the dielectric function's dispersions εxx2(ω), εyy2(ω) and εzz2(ω) the real part εxx1(ω), εyy1(ω) and εzz1(ω) can be obtained following Kramers–Kronig relations. These are shown in Fig. 5c and d. Again it shows a considerable anisotropy. The calculated εxx1(0), εyy1(0) and εzz1(0) are presented in Table 3.
| Component | Chair-like | Boat-like |
|---|---|---|
| εxx1(0) | 3.1 | 3.08 |
| εyy1(0) | — | 3.23 |
| εzz1(0) | 3.3 | 3.27 |
4. Conclusions
The state-of-the-art full potential linear augmented plane wave (FPLAPW) method as embodied in the WIEN2k code with three different possible approximations for the exchange–correlation (XC) potential were used to calculate the electronic and optical properties of two conformations of graphane, the chair-like graphane and boat-like graphane. The three XC potentials used are local density approximation (LDA) of Ceperley–Alder (CA), gradient approximation (GGA) of Perdew–Becke–Ernzerhof (PBE), and Engel–Vosko generalized gradient approximation (EVGGA). For chair-like graphane and boat-like graphane the conduction band minimum (CBM) and the valence band maximum (VBM) are located at Γ point the center of the BZ, resulting in a direct band gap of about 2.69/3.02 eV (LDA), 3.02/3.37 eV (GGA) and 3.60/3.90 eV (EVGGA) for chair-like/boat-like. Our calculated energy gap for chair-like/boat-like using EVGGA show good agreement with the previous theoretical results 3.47 eV and 3.5 eV/3.37 eV and 3.7 eV. The calculated partial density of states exhibits a strong hybridization between the orbitals which shows the existence of the covalent bonds. In additional we have calculated the electronic charge density distribution of chair-like/boat-like graphane which confirms the existence of the covalent bonds. The linear optical properties are presented and discussed in details. The optical properties exhibit considerable anisotropy, from the optical properties we can get deep insight the electronic structure, therefore the calculated optical function's dispersion confirm increasing the energy gap when we move from chair-like to boat-like graphane also it confirm the complicated structure of boat-like graphane. The calculated values of the bond lengths obtained using EVGGA show good agreement with pervious results.Acknowledgements
The result was developed within the CENTEM project, reg. no. CZ.1.05/2.1.00/03.0088, co-funded by the ERDF as part of the Ministry of Education, Youth and Sports OP RDI program. Computational resources were provided by MetaCentrum (LM2010005) and CERIT-SC (CZ.1.05/3.2.00/08.0144) infrastructures. S.A. thanks Council of Scientific and Industrial Research (CSIR) – National Physical Laboratory for financial support.References
- K. Nakada, M. Fujita, G. Dresselhaus and M. S. Dresselhaus, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 17954 CrossRef CAS
.
- S. Okada, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 041408 CrossRef
.
- R. Lv and M. Terrones, Mater. Lett., 2012, 78, 209–218 CrossRef CAS PubMed
.
- C. Gomez-Navarro, M. Burghard and K. Kern, Nano Lett., 2008, 8, 2045 CrossRef CAS PubMed
.
- Y.-H. Lin, K. A. Jenkins, A. Valdes-Garcia, J. P. Small, D. B. Farmer and P. Avouris, Nano Lett., 2009, 9, 422 CrossRef CAS PubMed
.
- C. L. Kane and E. J. Mele, Phys. Rev. Lett., 2005, 95, 226801 CrossRef CAS
.
- A. H. Reshak, S. A. Khan and S. Auluck, J. Mater. Chem. C, 2014, 2, 2346–2352 RSC
.
- A. Ferre-Vilaplana, J. Chem. Phys., 2005, 122, 104709 CrossRef CAS PubMed
.
- I. Zanella, S. B. Fagan, R. Mota and A. Fazzio, J. Phys. Chem. C, 2008, 112, 9163 CAS
.
- Z. Liu, J. T. Robinson, X. Sun and H. Dai, J. Am. Chem. Soc., 2008, 130, 10876 CrossRef CAS PubMed
.
- A. de Leon and A. F. Jalbout, Chem. Phys. Lett., 2008, 457, 179 CrossRef CAS PubMed
.
- M. H. F. Sluiter and Y. Kawazoe, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 085410 CrossRef
.
- J. O. Sofo, A. S. Chaudhari and G. D. Barber, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 153401 CrossRef
.
- D. C. Elias, R. R. Nair, T. M. G. Mohiuddin, S. V. Morozov, P. Blake and M. P. Halsall, et al., Science, 2009, 323, 610 CrossRef CAS PubMed
.
- D. K. Samarakoon and X. Q. Wang, ACS Nano, 2009, 12, 4017 CrossRef PubMed
.
- O. Leenaerts, H. Peelaers, A. D. Hernández-Nieves, B. Partoens and F. M. Peeters, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 195436 CrossRef
.
- A. Bhattacharya, S. Bhattacharya, C. Majumder and G. P. Das, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 033404 CrossRef CAS
; A. Bhattacharya, S. Bhattacharya, C. Majumder and G. P. Das, J. Phys. Chem. C, 2010, 114, 10299 Search PubMed
; S. Bhattacharya, C. Majumder and G. P. Das, J. Phys. Chem. C, 2009, 113, 15783 Search PubMed
.
- X. D. Wen, L. Hand, V. Labet, T. Yang, R. Hoffmann, N. W. Ashcroft, A. R. Oganov and O. Lyakhov, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 6833 CrossRef CAS
.
- D. K. Samarakoon, Z. F. Chen, C. Nicolas and X. Q. Wang, Small, 2011, 7, 965 CrossRef CAS PubMed
.
- O. Leenaerts, H. Peelaers, A. D. Hernández-Nieves, B. Partoens and F. M. Peeters, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 195436 CrossRef
.
- D. K. Samarakoon and X.-Q. Wang, ACS Nano, 2009, 3(12), 4017–4022 CrossRef CAS PubMed
.
- A. I. Shkrebtii, E. Heritage, P. McNelles, J. L. Cabellos and B. S. Mendoza, Phys. Status Solidi C, 2012, 9(6), 1378–1383 CrossRef CAS PubMed
.
- S. Zhu and T. Li, ACS Nano, 2014, 8(3), 2864–2872 CrossRef CAS PubMed
.
- N. N. Klimov, S. Jung, S. Zhu, T. Li, C. Alan Wright, S. D. Solares, D. B. Newell, N. B. Zhitenev and J. A. Stroscio, Science, 2012, 336, 1557 CrossRef CAS PubMed
.
- C. Lee, X. Wei, J. W. Kysar and J. Hone, Science, 2008, 321, 385 CrossRef CAS PubMed
.
- C. He, L. Z. Sun, C. X. Zhang, N. Jiao, K. W. Zhang and J. Zhong, arXiv:1204.6621v1 [cond-mat.mtrl-sci] CrossRef CAS PubMed; C. He, C. X. Zhang, L. Z. Sun, N. Jiao, K. W. Zhang and J. Zhong, Phys. Status Solidi RRL, 2012, 6(11), 427–429 CrossRef CAS PubMed
.
- A. H. Reshak, S. Auluck and I. V. Kityk, J. Phys.: Condens. Matter, 2008, 20, 145209 CrossRef
.
- A. H. Reshak, S. Auluck and I. V. Kityk, J. Solid State Chem., 2008, 181, 789–795 CrossRef CAS PubMed
.
- A. H. Reshak, J. Chem. Phys., 2006, 124, 104707 CrossRef CAS PubMed
; A. H. Reshak, Eur. Phys. J. B, 2005, 47, 503–508 CrossRef
.
- A. H. Reshak, I. V. Kityk and S. Auluck, J. Phys. Chem. B, 2010, 114, 16705–16712 CrossRef CAS PubMed
.
- A. H. Reshak, S. Auluck, D. Stys, I. V. Kityk, H. Kamarudin, J. Berdowski and Z. Tylczynskif, J. Mater. Chem., 2011, 21, 17219 RSC
.
- A. H. Reshak, M. Piasecki, S. Auluck, I. V. Kityk, R. Khenata, B. Andriyevsky, C. Cobet, N. Esser, A. Majchrowski, M. S'wirkowicz, R. Diduszko and W. Szyrski, J. Phys. Chem. B, 2009, 113(46), 15237 CrossRef CAS PubMed
.
- P. Blaha, K. Schwarz, G. K. H. Madsen, D. Kvasnicka and J. Luitz, WIEN2k, An augmented plane wave plus local orbitals program for calculating crystal properties, Vienna University of Technology, Austria, 2001 Search PubMed
.
- D. M. Ceperley and B. I. Ader, Phys. Rev. Lett., 1980, 45, 566–569 CrossRef CAS
parametrized in J. P. Perdew and A. Zunger, Phys. Rev. B: Solid State, 1973, 8, 4822–4832 CrossRef
.
- J. P. Perdew, S. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS
.
- E. Engel and S. H. Vosko, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 13164 CrossRef CAS
.
- S. Gao, Comput. Phys. Commun., 2003, 153, 190 CrossRef CAS
.
- K. Schwarz, J. Solid State Chem., 2003, 176, 319 CrossRef CAS
.
- A. H. Reshak, D. Stys, S. Auluck and H. Kamarudin, Mater. Chem. Phys., 2011, 130, 458 CrossRef CAS PubMed
.
- F. Bassani and G. P. Parravicini, Electronic States and Optical Transitions In Solids, Pergamon Press Ltd, Oxford, 1975, pp. 149–154 Search PubMed
.
| This journal is © The Royal Society of Chemistry 2014 |