Local chirality measures in QSPR![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h2_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h2_char_2009.gif) IR and VCD spectroscopy†
IR and VCD spectroscopy†
Piotr F. J. Lipiński*a and
Jan Cz. Dobrowolskibc
aDepartment of Neuropeptides, Mossakowski Medical Research Center, Polish Academy of Sciences, 02-106 Warsaw, Poland. E-mail: plipin@icm.edu.pl
bNational Medicines Institute, 00-725 Warsaw, Poland
cInstitute of Nuclear Chemistry and Technology, 03-195 Warsaw, Poland
First published on 15th September 2014
Abstract
The paper presents the first successful attempt at obtaining Quantitative Structure–Property Relationships (QSPR) of vibrational spectra parameters with chirality measures. The local chirality measures defined based on the Sinister–Rectus Chirality and Continuous Chirality approaches were calculated and intercompared for selected fragments of 28 5-substituted 1-cyano-1H-indenes. It appeared that there is no correlation between global and local variants of the chirality measures which additionally are less linearly interdependent than the global ones. The obtained local chirality measures were correlated with the frequency, IR and VCD intensity of the ν(CN) and ν(C*H) stretching modes. It was proven that vibrational spectroscopy gives some information on the local chirality of molecules. Especially, some well-isolated VCD bands could be a proper experimental, physical measure of local chirality. It was also demonstrated that some local chirality measures are highly collinear with the substituent effect descriptors σp and pEDA(I), showing that the electronic properties of a substituent may significantly influence the chirality of an aromatic system.
Introduction
Most chemists think of chirality as a zero-one property: a molecule can be either achiral or chiral – it means the molecule is either superimposable or non-superimposable on its mirror image. There is however quite well developed theory and practice of quantitative chirality and several groups introduced their quantitative descriptors of chirality (chirality measures) of different types. The descriptors assign a positive real number to a molecule if it is chiral and zero otherwise. The magnitude of the chirality measure reflects to what degree a molecule is chiral.The two most important approaches to measuring chirality stem directly from the IUPAC Gold Book definition of chirality. According to it, chirality is such a property of a rigid molecule that the molecule is non-superposable on its mirror image.1 The definition translates then the non-superposability criterion into the language of molecular symmetry, stating that such a molecule has neither a mirror plane, nor a center of inversion, nor a rotation-reflection axis. The criteria: molecular symmetry and non-superposability, gave rise to two distinct types of chirality measures2 determining: distance between a molecule and an achiral reference or distance between enantiomers. Chirality can also be defined operationally by its elements: chirality center, chirality axis and chirality plane.1 Thus yet another type of chirality measures originates therefrom: their presence (especially the presence of a chirality center) is at the core of graph-theory chirality measures.3 If atom properties are considered, additional types of chirality measures can be introduced.4–8 For non-rigid molecules, unforeseen by the IUPAC definition,1 a good practice in calculating chirality measures is to perform the Boltzmann averaging over conformer population.7
The Continuous Chirality Measure (CCM) by the Avnir group is the chirality measure of the first type, i.e. refers a chiral molecule to an achiral reference, whereas the Sinister–Rectus Chirality Measure (SRCM) introduced by our group is the measure of the second type, i.e. refers a chiral molecule to its enantiomer and additionally can include some properties of atoms (the measure of the fourth type). The various types of chirality measures were reviewed by Avnir et al.,9 Petitjean,10 Casanova i Casas11 or Natarajan and Basak,3 and Zhang et al.12
The chirality measures were shown to be useful reaction coordinates13 and Quantitative Structure–Activity–Property Relationship (QSAR/QSPR) descriptors in modeling phenomena like asymmetric catalysis14 or receptor binding and biological activity.7,15 Nevertheless, the representation of quantitative chirality in QSAR modeling still seems much too low, if we look at the importance of chirality in all areas of modern chemistry, especially in medicinal chemistry. One of the reasons behind it may be due to the fact that so far the quantitative chirality was mainly investigated in the global context of whole molecules, while in most interactions it is properties of functional groups or molecular fragments that are responsible for the presence and strength of an interaction. The local chirality that might play role here should be then described by local chirality measures. The most facile way to obtain them seems by dissecting molecules into fragments and calculating the chirality measures of these fragments.
Such an idea was presented and tentatively tested by Alvarez et al. in modeling of enantioselevtive catalytic activity of bis(oxazoline)copper(II) complexes.16 The authors calculated CCM for both full molecules as well as their subunits, and successfully correlated them with the enantiomeric excess induced by a given catalyst. Aside from this paper, the local chirality in chemistry was considered chiefly descriptively in connection with molecular stereoisomerism,17,18 materials chemistry19,20 or molecular spectroscopy.21,22 Finally, there are also papers by Janssens et al. who dealt with local chirality within molecular quantum similarity,23 and by Moreau who proposed a measure of the chirality of an atom's environment.24
Following the concept by Alvarez et al. for obtaining local chirality measures, we report here the CCM and SRCM local chirality measures of 28 chiral 1-cyano-1H-indenes and demonstrate their usefulness as descriptors in Quantitative Structure–Property Relationship modeling of infrared (IR) and vibrational circular dichroism (VCD) spectral parameters.
Theory
Chirality measures
The algorithm calculating Continous Chirality Measures, CCM, generates a series of structures with the same atoms and vertex labeling but of different symmetry (achiral references) and evaluates the distance to the original structure according to the equation:25
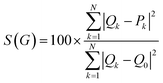 | (1) |
For calculating Sinister–Rectus Chirality Measures, a mirror image of a molecule is generated and then optimally superposed on the original structure. The distance between them serves as a Sinister–Rectus Chirality Measure:6,7
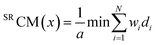 | (2) |
The superposition can be purely geometrical, however as SRCMs are evaluated in a property space, each atom may bear some property included in weights (e.g. a label, mass, charge etc.). For a given molecule considered in different property spaces, the respective superpositions are different and it gives rise to several types of SRCMs.
Local chirality measures and their notation
In the paper we introduce local variants of the two chirality measures. They are calculated with the procedures described above but applied to only selected parts of the molecule. Note that the local CCM proposed by Alvarez et al.16 use whole original molecule as an achiral reference, while in our approach it is only the very considered fragment that serves to this aim.We denote the Continuous Chirality Measures CCM, and Sinister–Rectus Chirality Measures SRCM. A property that defines a property space in which SRCM is evaluated, is given in the subscript: e.g. SRCM0 (the pure geometrical SRCM), SRCML (the labeled SRCM), SRCMM (the mass-weighted SRCM), SRCMq (the charge-weighted SRCM). The fragment on which a local chirality measure is calculated is denoted in parentheses, e.g. CCM (a) or SRCMq (a).
Methods
Molecules and fragments chosen for calculation of local chirality measures
The investigated molecular system is 5-substituted 1-cyano-1H-indene (Scheme 1). It consists of two fused, planar and rigid rings A and B, attached with a substituent in the C5 position. The chiral center is located at the A ring. It seems then natural to calculate three variants of the chirality measures (Scheme 1):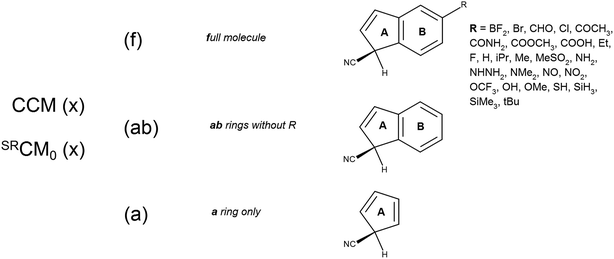 | ||
| Scheme 1 The model system under the study and its cut-off variants considered for calculation of local chirality measures. | ||
(a) global chirality measures of full molecules (f)
(b) chirality measures of the system remaining after the cut-off of a substituent, containing rings A and B (ab)
(c) chirality measures of the system remaining after the cut-off of the ring B (a).
Quantum chemical calculations
The molecules were optimized using Gaussian 09 (ref. 26) at the B3LYP/aug-cc-pvDZ level. We inspected their harmonic frequencies for absence of imaginary values to ascertain they are true minima on the potential energy surface. Also the VCD spectra were simulated at the same level. When a substituent was flexible, we generated all conformers of the molecule and calculated their population factors, which served for weighted-averaging of all considered properties, be they chirality measures or spectral parameters.Chirality measures calculation
The four types of Sinister–Rectus Chirality Measures (SRCM) measures were calculated using CHIMEA software.27 These were: pure, labeled, mass-weighted and charge-weighted SRCMs: SRCM0, SRCML, SRCMM and SRCMq, respectively.7 The Continous Chirality Measures (CCMs) were obtained from an online service provided by the Avnir lab.14 All they were calculated in the three variants mentioned.Results and discussion
Chirality measures
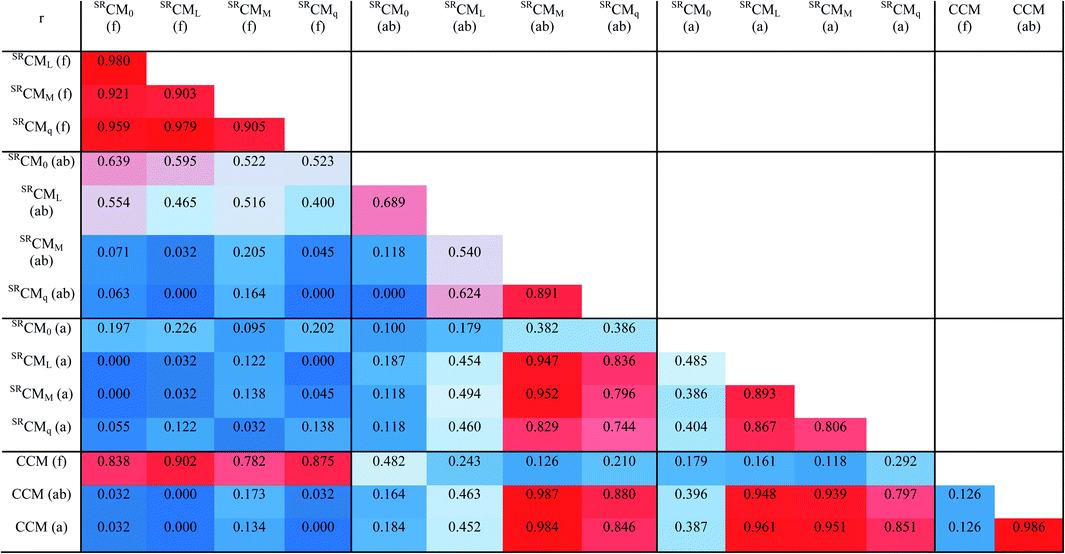
In total, we obtained 15 sets of values of different chirality measures: four types of SRCMs and CCM, each in three variants (a global one and two local ones). They are presented in Table S2 in the ESI.†The first question to be put is whether these variables are linearly independent. Table 1 presents their correlation matrix. (An exhaustive collection of 225 scatter plots showing relationships between all the considered measures is given in the ESI, with their list in Table S3.†) The set of SRCMs (f) is indeed strongly intercorrelated. The pure SRCM0 (f) is highly collinear with the labeled SRCML (f) (correlation coefficient r = 0.980) and the charge SRCMq (f) (r = 0.929), and to a significant extent with the mass SRCMM (f) (r = 0.921). Interestingly, there is no correlation between global SRCMs (f) and its local counterparts SRCMs (ab) or SRCMs (a). When comparing SRCMs (f) with CCM (f) one observes clear tendencies, however with much scatter (r = 0.782 − 0.902).
The local SRCMs (ab) do not intercorrelate, only the charge SRCMq (ab) and the mass SRCMM (ab) exhibit some colinearity (r = 0.891). The (a) variant SRCMs also do not intercorrelate, although some tendencies can be observed.
Comparing distinct local variants of SRCMs, one has to note that the pure SRCM0 (ab) and SRCM0 (a) do not correlate with each other neither with any other local chirality measure. The only significant correlation here is between the mass SRCMM (ab) and its (a) counterpart SRCMM (a) (r = 0.952) or the labeled SRCML (a) (r = 0.947).
The CCM (f) also does not correlate with its local variants CCM (ab) and CCM (a), while the two latter are highly collinear (r = 0.986). The global CCM (f) is not correlated with any SRCMs (although global SRCMs (f) are to some extent collinear with it). One should also note high correlations between local CCMs and SRCMM (ab), SRCML (a) or SRCMM (a) (r > 0.950).
From the above, it is seen that in the case of the considered indene system SRCMs and CCMs describe different aspects of quantitative chirality. The similar weak correlations were found in α-amino acids (r2 = 0.789), however in a set of rigid androgen steroids SRCML correlated perfectly with CCM with r2 = 0.996.7
Another important conclusion is that the quantitative local and global chirality are indeed different magnitudes. All types of SRCM (f) are to some extent intercorrelated and might be sometimes represented by only one variable. In local SRCMs, their various types are generally independent. In the case of local chirality measures, it is also not without significance, which fragment will be chosen for the calculation, as it yields different values in SRCMs (what however is not the case with CCM).
The fact that the global measures are more intercorrelated than are the local measures is a consequence of summation operations performed in the numerator of eqn (1) and (2). The truncation operation producing a local measure from a global one means cancellation of all the summed distances connected with the cut fragment(s). If the properly chosen fragment is large enough, it dominates the value of the measure, and if it is cancelled, the local measure may reveal specificity of the chosen chiral fragment and shows very distinctive values originating from strong differences between converging geometries, depending on the type of physical property taken as the weight.7
Correlations of spectral parameters with chirality measures
Vibrational spectroscopy represents a branch of physicochemical methods very important from the point of view of many basic and applied domains of chemistry. It is then crucial to develop its interpretational basis, including QSPR modeling of spectral parameters. Quantitative relationships give here meaningful insights into the mechanisms behind the changes in the parameters.In the case of the IR spectroscopy, a lot of research was done in the past, since it is now an established and routine method, however VCD spectroscopy still requires solving of most basic issues concerning the effects of solvents, conformations, substituents28 and other variations in a molecular structure or environment on the spectral parameters. This is the more important if we keep in mind that VCD is a promising tool of chiral chemistry, useful for characterization and analysis of chiral compounds.29–32
A VCD measurement consists in detecting differences in absorption of left- and right-circularly polarized light in the infrared region by a sample. As the handedness of a molecule is sensitive towards circularly polarized light, enantiomers of a chiral molecule yield VCD spectra with exactly the same frequencies and absolute values of intensity, however the intensity signs are opposite. At the same time, an achiral molecule gives no VCD signal. Thus, a VCD spectrum bears information about the configuration of a molecule (its chiral centers or other chirogenic elements), but is it able to tell us anything about quantitative chirality of a molecule or its parts? Or to put it other way: might quantitative chirality be useful in predicting VCD spectral parameters?
Correlational analysis in the field of vibrational spectroscopy is a challenging task, mainly because of numerous knotty couplings between the vibrational modes. Usually a proper approach would require a meticulous working out of potential energy distribution.33 Here, for the sake of simplicity, we took into account only two best isolated and well-uncoupled modes: ν(CN) and ν(C*H) stretchings. The choice of the modes was done on the basis of a high-throughput scan of possible correlations between the spectral and chirality parameters by an in-house script. The selection allowed to avoid complications arising from vibrational coupling and problems in recognizing identity of modes. Other vibrations, even though appeared to exhibit some kind of correlation with the chirality measures, were omitted due to the complexity of interpretation.
The ν(CN) stretching mode in 1-cyano-1H-indenes is located in the range of 2335–2343 cm−1, while ν(C*H) stretching of methine in the chirality center spans in the region of 3004–3012 cm−1. The spectral parameter values for these two modes are given in the Tables S4–S5 in ESI.† In the previous study,28 we reported strong linear and non-linear models for the frequencies (ν), infrared intensities (IIR) and VCD intensities (IVCD) of ν(CN) and ν(C*H) stretching modes, demonstrating that the spectral parameters of these vibrational modes depend on the substituent effect. At the same time the properties can be unexpectedly correlated with the here reported local chirality measures. To mention only the statistically best relationships, we can list the following equations (the coefficients were rounded to express statistically significant values):
for ν(CN):
| ν = −800.0(±60.0) × SRCMM (ab) − 2800.0(±35.0), r = 0.93, n = 28 | (3) |
| IIR = 930.0(±50.0) × SRCMM (ab) − 520.0(±50.0), r = 0.91, n = 26 | (4) |
| IVCD = −155.0(±9.5) × SRCMM (ab) + 86.0(±5.5), n = 26, r = 0.96 | (5) |
ν = −560.0(±90.0)CCM (a)2 + 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500.0(±1800.0)CCM (a) − 56 500.0(±1800.0)CCM (a) − 56![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000.0(±9500.0), r = 0.91, n = 27 000.0(±9500.0), r = 0.91, n = 27
| (6) |
IIR = 250.0(±20.0)CCM (a)2 − 5150.0(±450.0)CCM (a) + 26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000.0(±2250.0), r = 0.94, n = 27 000.0(±2250.0), r = 0.94, n = 27
| (7) |
IVCD = −110.0(±25.0)CCM (a)2 + 2200.0(±550.0)CCM (a) − 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 350.0(±2750.0), r = 0.92, n = 27 350.0(±2750.0), r = 0.92, n = 27
| (8) |
As we reported previously,28 in the ν(CN) stretching, as we reported previously, the frequency, infrared intensity and VCD intensity are intercorrelated. The mode frequency decreases when the chirality measured by SRCMM (ab) increases. At the same time, the infrared intensity rises. As shown in Fig. 1c, the VCD intensity decreases. However, note that an IVCD decrease for one series of enantiomers means an increase for the series of opposite enantiomers. It is then proper to say that the more chiral is the fragment of a molecule, the more intense (in the terms of absolute values) is the ν(CN) stretching in the VCD spectrum.
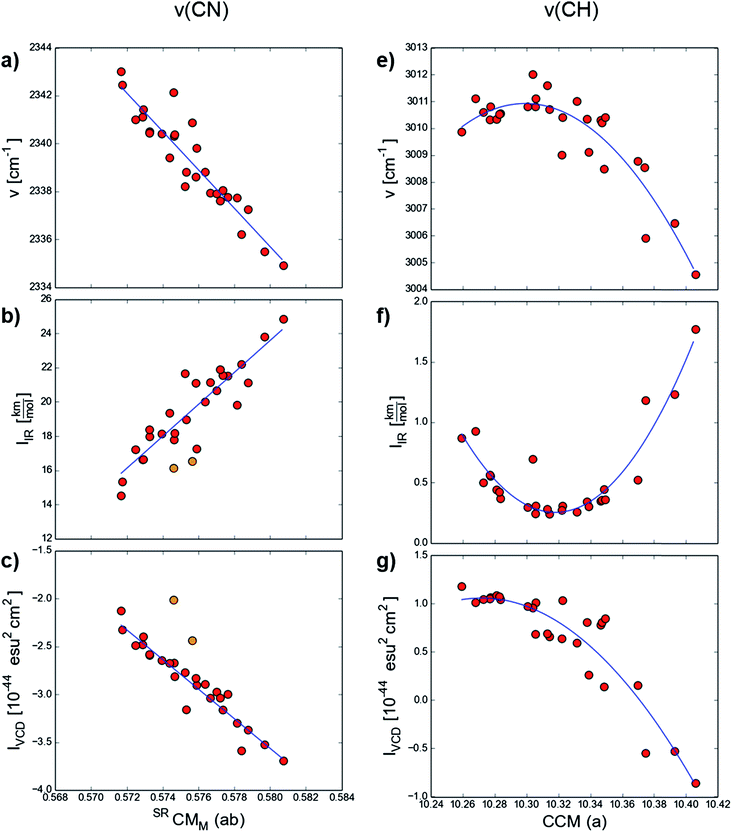 | ||
| Fig. 1 Correlations of the spectral parameters of ν(CN) (a) eqn (3), (b) eqn (4), (c) eqn (5)) and ν(C*H) (d) eqn (6), (e) eqn (7), (f) eqn (8)) with local chirality measures. | ||
In the case of the methine stretching in the chirality center ν(C*H), the relationships between the spectral parameters and the quantitative chirality measured by CCM (a) are nonlinear. The correlations with the mode frequency and infrared intensity seem parabolic with the most and less chiral fragments lying on the parabola slopes (here e.g. NH2, NMe2, NHNH2 and NO, NO2 substituted indenes). As more extreme chirality cases are lacking, the curves cannot be drawn long enough to judge whether we have here a truly parabolic relationship or not. The ν(C*H) VCD intensity decreases as the chirality goes up.
It seems interesting why the correlations for frequencies and IR intensities are so similar to the ones for VCD intensity. VCD intensity is a scalar product of two vectors: electric-dipole transition moment (EDTM) and magnetic dipole transition moment (MDTM) and thus it is a product of their values multiplied by the cosine of the angle between them. IR intensity is proportional to the EDTM value. In some cases, when the product of two VCD factors is approximately constant and the variation of the third one is similar to that of IIR, the VCD intensity follows the same trend.28 This is why the correlations for ν, IIR, IVCD look so similar.
Note that instead of SRCMM (ab) or CCM (a), in the eqn (3)–(8) one could use other local chirality measures (look up Table 1), obtaining similar equations with different factors and slightly lower correlation coefficients or even statistically equal.
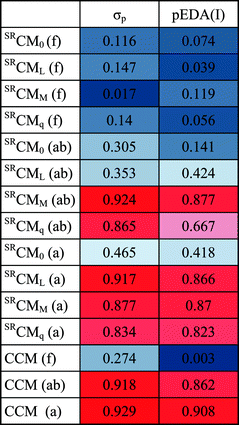
As the considered spectral parameters are correlated with both substituent effect descriptors and the local chirality measures, it turns out that the here reported chirality measures correlate with substituent effect descriptors Hammet σp constants and pEDA(I) (Table 2 and Fig. 2). Thus 1-cyano-1H-indenes form an unprecedented case where electronic properties of a substituent directly influence chirality of the ring system or its part. Various substituents exert distinct changes in the electronic structure of the ring system, both donating or withdrawing electrons from it as well as causing shifts in electron density between ring positions. It is reflected in changes in spectral parameters, but also in slight, yet significant variations in molecular geometry (e.g. bonds or angles). These variations on the other hand modify quantitative chirality of fragments, and thus substituent effect descriptors can be linked to the local chirality measures in this very case. It seems very interesting whether for molecules of more complex shapes, such a correlation would still be observed. This, however, will be tested in further studies.
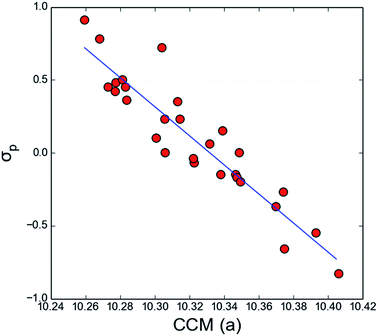 | ||
| Fig. 2 Correlation of CCM (a) with Hammett σp substituent effect descriptor. CCM (a) = −0.09(±0.01)σp + 10.33(±0.00), n = 28, r = 0.93. | ||
Conclusions
In the paper we applied our Sinister–Rectus Chirality Measures (SRCMs) and Continuous Chirality Measures (CCMs) by the Avnir group to calculate the chirality measures of selected fragments of 28 5-substituted 1-cyano-1H-indenes and thus to obtain local chirality measures. The 10 obtained local measures were compared to 5 global ones and between each other and the analysis showed that there is no correlation between global and local variants of the chirality measures. The local measures are less linearly interdependent than the global are, which is a consequence of the summation operations used in the definitions of SRCMs and CCMs and the cancellation of a large part of the measure (responsible for co-linearity) when the local one is determined.The paper presents the first successful attempt at obtaining quantitative structure–property relationships of vibrational spectra parameters with the chirality measures. We managed to correlate the obtained local chirality measures with spectral parameters of the ν(CN) and ν(C*H) stretching modes such as frequency, infrared intensity and VCD intensity. Thus we prove that vibrational spectroscopy (IR or VCD) bear some information on the local chirality of molecules. It can be hypothesized that e.g. VCD intensities of selected, well-isolated bands could be (at least in some cases) an experimental, physical measure of local chirality/asymmetry, similarly to 19F NMR shifts that serve to measure the resonance effect.34
Some local chirality measures of the 5-substituted 1-cyano-1H-indenes are highly collinear with the substituent effect descriptors σp and pEDA(I), showing that the electronic properties of a substituent may significantly influence the chirality of an aromatic system. The donating or withdrawing electrons from the system modifies electron density in the aromatic ring and affects spectral parameters through the molecular geometry. These variations modify quantitative chirality of the fragments as revealed in local chirality measures. The model molecule is hence an interesting case of a system where a change of electronic properties of a substituent can be directly translated into a change in the ring local chirality.
Conflict of interest
The authors declare no competing financial interests.Abbreviations
| Aug-cc-pvDZ | Correlation-consistent double-zeta type of Dunning basis set augmented by diffuse functions |
| B3LYP | Becke three parameter Lee-Yang-Parr DFT functional |
| CCM | Continous Chirality Measures |
| CN-IND | 1-Cyano-1H-indene |
| EDTM | Electric-dipole transition moment |
| IIR | Infrared intensity |
| IR | Infrared spectroscopy |
| IVCD | Rotational strength |
| ν(.) | Stretching vibration |
| NMR | Nuclear magnetic resonance spectroscopy |
| MDTM | Magnetic-dipole transition moment |
| pEDA(I) | π electron donor–acceptor descriptor of the substituent effect |
| QSAR | Quantitative Structure–Activity Relationship |
| QSPR | Quantitative Structure–Property Relationship |
| r | Correlation coefficient |
| σp | Hammett σp descriptor of the substituent effect |
| SRCM | Sinister–Rectus Chirality Measure |
| VCD | Vibrational Circular Dichroism |
Acknowledgements
The study was supported by National Science Centre in Poland (NCN, Grant 2012/05/N/NZ7/01952). Computational Grant G19-4 from the Interdisciplinary Centre of Mathematical and Computer Modelling (ICM) at Warsaw University is gratefully acknowledged.References
- Chirality. IUPAC. Compendium of Chemical Terminology. XML on-line corrected version, http://goldbook.iupac.org, 1997.
- A. B. Buda, T. A. der Heyde and K. Mislow, On Quantifying Chirality, Angew. Chem., Int. Ed. Engl., 1992, 31, 989–1007 CrossRef
.
- R. Natarajan and S. C. Basak, Numerical Characterization of Molecular Chirality of Organic Compounds, Curr. Comput.-Aided Drug Des., 2009, 5, 13–22 CrossRef CAS
.
- A. Pyka, A New Optical Topological Index (Iopt) for Predicting the Separation of D and L Optical Isomers by TLC. Part III, J. Planar Chromatogr.--Mod. TLC, 1993, 282–288 CAS
.
- I. Gutman and A. Pyka, New Topological Indices for Distinguishing between Enantiomers and Stereoisomers: A Mathematical Analysis, J. Serb. Chem. Soc., 1997, 62, 261–265 CAS
.
- S. Ostrowski, M. H. Jamróz, J. E. Rode and J. C. Dobrowolski, On Stability, Chirality Measures, and Theoretical VCD Spectra of the Chiral C58X2 Fullerenes (X = N, B), J. Phys. Chem. A, 2012, 116, 631–643 CrossRef CAS PubMed
.
- M. H. Jamróz, J. E. Rode, S. Ostrowski, P. F. J. Lipiński and J. C. Dobrowolski, Chirality Measures of α-Amino Acids, J. Chem. Inf. Model., 2012, 52, 1462–1479 CrossRef PubMed
.
- S. Ostrowski, M. H. Jamróz and J. C. Dobrowolski, A Study on the Stability, Chirality, and Theoretical Spectra of the Heterofullerenes C69X (X = N, P, As, B, Si, Ge), Tetrahedron: Asymmetry, 2013, 24, 1097–1109 CrossRef CAS PubMed
.
- D. Avnir, H. Hel-Or and P. Mezey, Symmetry and Chirality: Continuous Measures, in The Encyclopedia of Computational Chemistry, ed. P. V. Schleyer, N. L. Allinger, T. Clark, J. Gasteiger, P. A. Kollman, H. F. Schaefer III and P. R. Schreiner, Wiley, Chichester, 1998, pp. 2890–2901 Search PubMed
.
- M. Petitjean, Chirality and Symmetry Measures: A Transdisciplinary Review, Entropy, 2003, 5, 271–312 CrossRef CAS PubMed
.
- D. Casanova i Casas, Mesures de Forma I Simetria En Química: Algorismes I Aplicacions, Universitat de Barcelona, 2006 Search PubMed
.
- Q.-Y. Zhang, L.-Z. Xu, J.-Y. Li, D.-D. Zhang, H.-L. Long, J.-Y. Leng and L. Xu, Methods of Studies on Quantitative Structure–Activity Relationships for Chiral Compounds, J. Chemom., 2012, 26, 497–508 CrossRef CAS
.
- J.-W. Handgraaf, J. N. H. Reek, L. Bellarosa and F. Zerbetto, Continuous Chirality Measure in Reaction Pathways of Ruthenium-Catalyzed Transfer Hydrogenation of Ketones, Adv. Synth. Catal., 2005, 347, 792–802 CrossRef CAS
.
- A. Zayit, M. Pinsky, H. Elgavi, C. Dryzun and D. Avnir, A Web Site for Calculating the Degree of Chirality, Chirality, 2011, 23, 17–23 CrossRef CAS PubMed
.
- S. Keinan and D. Avnir, Quantitative Chirality in Structure–Activity Correlations. Shape Recognition by Trypsin, by the D 2 Dopamine Receptor, and by Cholinesterases, J. Am. Chem. Soc., 1998, 120, 6152–6159 CrossRef CAS
.
- S. Alvarez, S. Schefzick, K. Lipkowitz and D. Avnir, Quantitative Chirality Analysis of Molecular Subunits of bis(oxazoline)copper(II) Complexes in Relation to Their Enantioselective Catalytic Activity, Chemistry, 2003, 9, 5832–5837 CrossRef CAS PubMed
.
- K. Mislow and J. Siegel, Stereoisomerism and Local Chirality, J. Am. Chem. Soc., 1984, 106, 3319–3328 CrossRef CAS
.
- S. Fujita, Chirality Fittingness of an Orbit Governed by a Coset Representation. Integration of Point-Group and Permutation-Group Theories to Treat Local Chirality and Prochirality, J. Am. Chem. Soc., 1990, 112, 3390–3397 CrossRef CAS
.
- V. Humblot, M. O. Lorenzo, C. J. Baddeley, S. Haq and R. Raval, Local and Global Chirality at Surfaces: Succinic Acid versus Tartaric Acid on Cu110, J. Am. Chem. Soc., 2004, 126, 6460–6469 CrossRef CAS PubMed
.
- N. Katsonis, E. Lacaze and B. L. Feringa, Molecular Chirality at Fluid/solid Interfaces: Expression of Asymmetry in Self-Organised Monolayers, J. Mater. Chem., 2008, 18, 2065 RSC
.
- C. Herrmann, K. Ruud and M. Reiher, Can Raman Optical Activity Separate Axial from Local Chirality? A Theoretical Study of Helical Deca-Alanine, ChemPhysChem, 2006, 7, 2189–2196 CrossRef CAS PubMed
.
- C. R. Jacob, S. Luber and M. Reiher, Calculated Raman Optical Activity Signatures of Tryptophan Side Chains, ChemPhysChem, 2008, 9, 2177–2180 CrossRef CAS PubMed
.
- S. Janssens, C. Van Alsenoy and P. Geerlings, Molecular Quantum Similarity and Chirality: Enantiomers with Two Asymmetric Centra, J. Phys. Chem. A, 2007, 111, 3143–3151 CrossRef CAS PubMed
.
- G. Moreau, Atomic Chirality, a Quantitative Measure of the Chirality of the Environment of an Atom, J. Chem. Inf. Model., 1997, 37, 929–938 CrossRef CAS
.
- H. Zabrodsky and D. Avnir, Continuous Symmetry Measures. 4. Chirality, J. Am. Chem. Soc., 1995, 117, 462–473 CrossRef CAS
.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox. Gaussian 09, Revision B.01, 2009 Search PubMed
.
- M. H. Jamróz, CHIMEA — Program Calculating Discrete Chirality Measures of Molecules, 2010 Search PubMed
.
- P. F. J. Lipiński and J. C. Dobrowolski, Substituent Effect in Theoretical VCD Spectra, RSC Adv., 2014, 4, 27062 RSC
.
- T. B. Freedman, X. Cao, R. K. Dukor and L. A. Nafie, Absolute Configuration Determination of Chiral Molecules in the Solution State Using Vibrational Circular Dichroism, Chirality, 2003, 15, 743–758 CrossRef CAS PubMed
.
- O. McConnell, Y. He, L. Nogle and A. Sarkahian, Application of Chiral Technology in a Pharmaceutical Company. Enantiomeric Separation and Spectroscopic Studies of Key Asymmetric Intermediates Using a Combination of Techniques. Phenylglycidols, Chirality, 2007, 19, 716–730 CrossRef CAS PubMed
.
- P. J. Stephens, F. J. Devlin and J.-J. Pan, The Determination of the Absolute Configurations of Chiral Molecules Using Vibrational Circular Dichroism (VCD) Spectroscopy, Chirality, 2008, 20, 643–663 CrossRef CAS PubMed
.
- T. Kuppens, P. Bultinck and W. Langenaeker, Determination of Absolute Configuration via Vibrational Circular Dichroism, Drug Discovery Today: Technol., 2004, 1, 269–275 CrossRef CAS PubMed
.
- M. H. Jamróz, Vibrational Energy Distribution Analysis (VEDA): Scopes and Limitations, Spectrochim. Acta, Part A, 2013, 114, 220–230 CrossRef PubMed
.
- C. Hansch, A. Leo and R. W. Taft, A Survey of Hammett Substituent Constants and Resonance and Field Parameters, Chem. Rev., 1991, 91, 165–195 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available: Substituents used in the study with the values of their substituent effect descriptors, values of the calculated chirality measures, scatter plots of relationships between the chirality measures, detailed spectral parameters of all considered modes, energetics of examined conformers and coordinates of optimized structures. This material is available free of charge via the Internet at http://pubs.acs.org. See DOI: 10.1039/c4ra08434a |
| This journal is © The Royal Society of Chemistry 2014 |