Stabilizing reconstruction induced by O protrusions of the ZnO (0001) polar surface

Abstract

The stability of the ZnO polar surfaces which is crucial for their applications is still being debated intensely. Here, we demonstrate that O extrusion outside the outermost bilayer is a universal reconstruction behavior of the Zn-terminated (0001) surface (with or without terraces) to compensate the well-known instability of such polar surfaces. The study is based on first-principles energetics of several atomic reconstruction configurations that emerge spontaneously in ab initio molecular dynamics simulations, including on-site O extrusions, O interstitials and O extrusions as adatoms at hollow sites, compared with previously proposed O-rich compensation models with O adatoms and Zn vacancies. The O extrusion process is specifically favored for Zn-rich environments, which provides a theoretical support for investigating the defect-process of a ZnO polar surface.

---

1. Introduction

Zinc oxide (ZnO) is a transparent semiconductor with a wide band gap of about 3.2–3.44 eV.^1,2 It has a wide range of applications, such as chemical sensors,³ catalysts,^4–7 optoelectronics,⁸ nanowire lasers,⁹ diodes¹⁰ and solar cells.¹¹ Meanwhile, low-dimensional ZnO nanostructures also have a number of applications due to their promising electronic and electromechanical properties^12–14 and can be utilized as piezoelectric sensors and electronic devices.¹⁵ To further understand and develop these applications, controllable synthesis and growth of ZnO is a prerequisite; this in turn requires understanding the stability and driving force towards stabilization of its polar surfaces.

ZnO is an ionic crystal with hexagonal wurtzite structure, whose space group is P6₃mc. Clean and unreconstructed (i.e. bulk-like) surfaces of polar ionic crystal materials possess an intrinsic instability, since their successive layers have opposite charges arranged in bilayers: these bilayers collectively create a net dipole moment perpendicular to the surface, resulting in an unsustainable electrostatic energy which is in direct proportion to the macroscopic sample thickness if the opposite surfaces are not suitably restructured from their bulk-like form.^16,17 A metallization of the surface¹⁸ has been used and expected by a rearrangement of charges between the O- and the Zn-terminated surfaces. However, theoretical studies^16,19,20 concluded a contraction of the first Zn–O double layer from this metallization, which can be ruled out from experimental observation.²¹ To stabilize such polar surfaces, relevant theoretical studies have shown that, apart from situations where the adsorption of charged particles (e.g. H-passivation) occurs,^18.19,22,23 stabilization is predominantly driven by surface reconstructions.^4,24–28 For example, an outward relaxation of the topmost Zn layer is found and a 0.75 occupancy of the topmost Zn layer could best fit surface X-ray diffraction experiments for the ZnO (0001) surface.^31,32 Unfortunately, the experiments gave no indication on how the removal of Zn atoms occurs. Following this, a theoretical prediction proposed that a 25% charge modification on both the O-terminated surface and the Zn-terminated surface can quench the overall dipole, independent of the slab thickness.³³

Other structures are also consistent with this compensation mechanism, such as existence of O adatoms and terraces and steps.^25,34 However, the most recent published models based on STM results and calculations^4,24–30 do not enable us to understand the process of the dynamic surface reconstruction itself. In particular, it is difficult to identify experimentally whether the O adatoms come from environmental adsorption, from molecular dissociation or from the ZnO system itself. A recent model, consistent with the observations, proposes a high density of cavities of various sizes on the surface, with Zn and O atoms leaving lattice sites, while the Zn atoms migrate freely on the surface and many O atoms are trapped at surface hollow sites forming adatoms.³⁵ Nonetheless, other stabilization mechanisms remain possible and need to be studied, which is the purpose of this work: we explore both stoichiometric and non-stoichiometric models using ab initio molecular dynamics (MD) to “automatically” generate new possible structures and use these structures to reflect the stabilization mechanism from the aspects of dipole compensation and formation energies.

Furthermore, to our knowledge, no ab initio dynamic investigation of a clean and ideal ZnO (0001) polar surface has been undertaken. The ab initio study from an ideally truncated surface may shed light on the essential dynamic mechanisms of reconstruction which are out of reach through current experimental approach. By contrast, multiple experimental processes can introduce dramatic defects and disorder on the otherwise regular surface, making the actual surface confusing to study in terms of its intrinsic driving force of stabilization. The fundamental structures observed in the ab initio MD simulations may be considered to be typical and frequent in real complex experimental conditions, despite the intrinsic simulation limitations compared to real experimental conditions, such as time scale and system size. The O-extrusion reconstruction which we predict in this work coincides with certain features of the adatom-cavity (ADC) structure recently proposed by Xu et al.,³⁵ which is based on a combination of low-temperature Scanning Tunnelling Microscopy (STM) and Low-Energy Electron Diffraction (LEED) experiments with static Density Functional Theory (DFT) calculations. Hence, our study can be the key to understanding and predicting the fundamental compensation mechanisms.

2. Computational details

To illustrate the potential reconstruction and its influence on the surface stabilization, we carried out ab initio MD simulations in this work. We used the Troullier–Martins pseudopotential³⁶ with the generalized gradient approximation (GGA) (Perdew–Burke–Ernzerhof functional^37,38) for DFT as implemented in the SIESTA package.^39,40 A linear combination of numerical localized atomic orbitals (split-valence double-ζ basis set with polarization orbitals) was used as the basis representation of the Kohn and Sham wavefunctions.⁴² In the MD calculations, an energy mesh cutoff of 200 Ry was used to calculate the charge density on a real-space grid mesh and only the Gamma point in k-space was calculated. The convergence criterion for the forces was set to be 0.02 eV Å⁻¹.

All surfaces were modelled by periodically repeated slabs with a thickness of four bilayers, separated by a vacuum layer of more than 15 Å, using a (4 × 4) two-dimensional unit cell. A dipole correction within the SIESTA code was used to prevent artificial electrostatic interactions between the repeated units and to compensate the electric field at the vacuum created by the dipole moment of the system. In our calculations, the dipole correction showed no noticeable influence on the structures generated by the MD simulations, but was necessary for static energy determination.

In order to study the stabilization behavior of the Zn-terminated surface, we build slab models for which the O-terminated back surface is stabilized according to electrostatic arguments.³³ A 0.5 monolayer (ML) of H is added as terminal hydroxyl (OH) groups on the unreconstructed O-terminated ZnO surface to stabilize this surface as previously proposed.⁴² Calculations presented in this paper were performed by applying this compensation mechanism on the O surface. The MD simulations were performed under the conditions of a constant temperature and constant volume (NVT) ensemble using the Nosé–Hoover algorithm, with the two bilayers of the O-terminated surface (including the H atoms) held fixed with the bulk structure. A time step of 3 fs was used to integrate Newton's equation of motion and a smaller time step of 1 fs has also been tested and showed consistent results.

More importantly, there are two questions to which we have given special attention: (1) the reliability of the computational method, and (2) the Pulay force problem. Regarding the computational reliability: in the first-principles calculations, the SIESTA code uses localized basis sets to calculate the ZnO (0001) surface system (e.g. atomic coordinates, eigenvalues, atomic forces, etc.). Especially in the finite temperature MD simulations by first principles, the accuracy of the ion–ion and ion–electron interaction calculations will directly influence the MD results, as well as the accuracy of optimizations with total energy calculations. To prove the reliability of our work, we further used CASTEP,⁴³ which is DFT software based on a pseudopotential method using plane wave basis sets, to implement the first-principles MD simulations with a high level of computation quality.

We found that the results show great similarity between these two methods. In this complementary work, whether CASTEP uses density mixing or ensemble DFT (EDFT)⁴⁴ for electronic minimization and force optimization together with the BFGS algorithm for structural relaxation, the results objectively confirm the reliability of the work done with the SIESTA code. Regarding the Pulay force problem: based on the Hellman–Feynman theorem, the force calculations in DFT are directly related to the ground state energy calculated using eigenstate wavefunctions expanded in a complete set of fixed basis functions. Meanwhile the basis set depends upon the ionic positions. The localized basis sets will contribute artificial so-called Pulay forces or stresses. Ideally, the Pulay forces will be minimized to zero in the limit of a complete basis set, but this is never realized in practice, or if position independent basis functions, such as plane-waves, are used. Therefore, the plane wave method can effectively solve this problem, as CASTEP does. However, regarding question (1) above, this shows that CASTEP also gives similar results, which confirms our findings. Therefore, the Pulay forces have a minor impact on our MD simulations, especially if we choose relatively large cut-off energy in the energy mesh for describing the charge density.

3. Results and discussion

3.1. MD on pure Zn-terminated ZnO (0001)

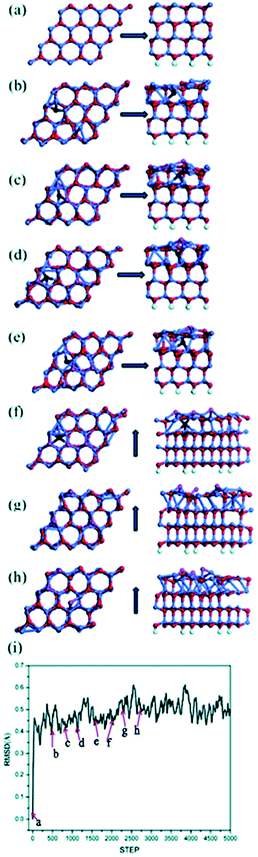
As we will exhibit next, multiple types of surface reconstruction are observed in our MD simulations in a wide range of temperatures, including formation of adatoms, vacancies and interstitial defects. Coexistence and interaction among them are revealed. Interestingly, the Zn and O atoms show quite different dynamic behaviors, due to their different chemical bonding. A larger (6 × 6) unit cell with the same thickness also exhibits similar dynamic behaviors, while addition of a dipole moment correction in the calculation does not change the results, only increasing the accuracy of total energies.

Fig. 1 shows MD snapshots of typical reconstructions of a Zn-terminated ZnO (0001) surface at nominally 1600 K within the first 3 ps of a single MD run. The bulk-like starting structure (Fig. 1a) is a stack of identical bilayers (viewed sideways in the right-hand panel of Fig. 1a), each consisting of one Zn layer and one deeper O layer. We observe intrusion of O atoms into interstitial sites (hereafter labeled “O_in structure”, and colored dark red in Fig. 1b–g) and onsite extrusion (without lateral displacement) of O atoms to positions outside the outermost bilayer (hereafter labeled “O_ex structure”, and colored purple in Fig. 1c–h). Thus, one oxygen atom (dark red in Fig. 1b) has moved from the outermost bilayer into an interstitial site between the first and second bilayers as an interstitial defect (“O_in structure”). Soon after this intrusion of an O atom, the three Zn atoms adjacent to its initial site (now a vacancy) make new bonds with each other, forming a small Zn cluster (with Zn–Zn bond lengths between 2.4 and 2.6 Å, relatively short compared to 2.67 Å for pure bulk Zn), as shown in Fig. 1c. Concurrently, another nearby oxygen atom has moved outward as an extrusion, as shown in purple in Fig. 1c (thus forming an “O_in–O_ex pair structure”). This outward movement may be due to local stress induced by the O_in and to O_in–O_ex repulsion.

Fig. 1 Snapshots of typical reconstructed geometries in a MD run at 1600 K (O: red; Zn: gray; each left/right pairs show top and side views, resp., of a single (4 × 4) unit cell; as indicated by the arrows: (a) initial bulk-like structure at t = 0 ps, (b) O_in structure (dark red) at t = 0.6 ps, (c) O_ex–O_in structure at t = 0.75 ps, (d) one O_in and two O_ex (light red) structures at t = 1.2 ps, (e) diffusion of O_ex at t = 1.65 ps, (f) one O_in and three O_ex structures at t = 1.95 ps, (g) three O_ex at t = 2.25 ps, and (h) three O_ex, among which one has diffused to a hollow site, at t = 2.7 ps. In (i) the RMSD of this trajectory is equilibrated after about 2000 steps (6 ps).

After another 450 fs (see Fig. 1d), the O_ex feature appears at another O site of the same hexagonal ZnO ring: this is not an atomic O shift (which would also need an O–O exchange), but a wave-like propagation of the extrusion between neighboring oxygen sites. At another random position (see Fig. 1d), a second O atom has also been extruded directly at its own site (“O_ex structure”), without nearby O_in, concurrently with the formation of an in-plane Zn–Zn bond. Fig. 1d and e also clearly show propagation of this O_ex feature, during which the first O_ex feature (see Fig. 1e) propagates back to its initial O_ex site of Fig. 1c. In Fig. 1f, a second O_ex has formed near O_in, increasing the concentration of O_ex further from 12.5% to 18.75% (from two to three O_ex per (4 × 4) unit cell). This concentration of O_ex is equilibrated after 6 ps as shown in the RMSD curve (Fig. 1i). It is also noted that during the process described in Fig. 1f–h, the sites of the three O_ex features propagate easily across the surface and one of the O atoms diffuses to a hollow site (“the O_hollow structure”) while the O_in atom returns to a normal lattice position in the first bilayer. This process seems to play a role as an easy route for the appearance of O_ex structures.

Multiple MD simulations have been conducted at temperatures within the range 400–1300 K. They all reveal similar characteristics: random O_ex and O_in structures sometimes combined as O_in–O_ex pair structures, in a dynamic concentration from 1 to 4 such structures per (4 × 4) supercell. Such reconstruction occurs frequently already at relatively low temperatures, indicating a relatively small barrier. These reconstruction configurations have been confirmed to be local minima based on energy optimization, which will be discussed separately further below.

Besides the temperature, the initial model in MD simulations may also play an important role in determining the dynamic behavior. Apart from the bulk-like model containing equal numbers of Zn atoms and O atoms, the existence of Zn vacancies, O adatoms and steps are alternative reconstructions that might enhance the stability of the surface. Therefore, MD simulations starting from these specific models were performed using the same settings of computation parameters. Based on the compensation mechanism with 25% depletion of surface charges, the initial number of Zn vacancies and O adatoms was set between 1 and 4 (corresponding to a concentration of 25%) within a (4 × 4) supercell, corresponding to going from partial to complete compensation in principle.³³ These MD results confirm the existence of all the four typical local structures that we described above (O_ex, O_in, O_hollow and O_ex–O_in pair shown in Fig. 1) and we accept them as universal reconstructions on the Zn-terminated polar surface of ZnO. Moreover, our MD results on the clean Zn-terminated ZnO (0001) surface show that the local structures of O_ex and O_in variations and propagations below the topmost Zn–O bilayer drive the rearrangement and flattening of sub-surface Zn–O structures.

3.2. MD on O-terminated nano-steps on ZnO (0001)

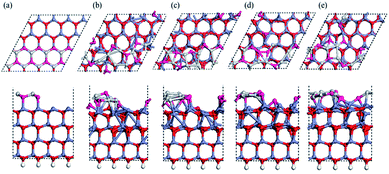
A previous Monte Carlo simulation has revealed possible surface reconstructions on the polar ZnO (0001) surface based on triangular islands and pits.²⁸ To understand the role of general nano-steps on the (0001) ZnO surface, we used a (4 × 4) supercell containing steps with a height corresponding to adding one Zn–O bilayer. Snapshots of our MD simulation at 1600 K are shown in Fig. 2, starting again from a bulk-like surface. Fig. 2b presents a rather chaotic situation, indicating intense mobility and reconstruction at the terrace after 0.9 ps (Fig. 2b). An overall tendency appears whereby the O atoms at the terrace gradually move outward to form O-rich step edges, leaving Zn-rich regions within the upper terraces (see Fig. 2c–e). The diffusion process is through onsite extrusion and diffusion of O (to hollow sites), from the outer step edges to the concave in-step regions. This reconstructed O terminated step edge is similar to previous results²⁸ for triangular terraces.

Fig. 2 Snapshots of an MD simulation for the Zn-terminated surface with a bilayer-high step at 1600 K, in top and side views in top and bottom panels, respectively (the latter looking from the right side in the top view): (a) at 0 ps, (b) at 8.7 ps, (c) at 11.7 ps, (d) at 14.7 ps, (e) at 16.8 ps (on the terraces, the Zn atoms are colored light grey and the O atoms purple to distinguish from others).

Based upon our MD simulations, we conclude that the O_ex reconstruction can be considered as a universal feature on this polar surface, even in the presence of available Zn vacancies, O adatoms, or nano-steps. Admittedly, the relative total energies of these reconstructed configurations cannot be obtained through MD simulations. Therefore, we optimized these specific models with DFT, using improved parameters compared to the MD simulation, consistent with previous reports.³⁸ An energy mesh cutoff of 300 Ry and a 6 × 6 × 1 k-sampling generated by the Monkhorst–Pack scheme for the first Brillouin zone were used after testing convergence.

3.3. Modification by reconstructions

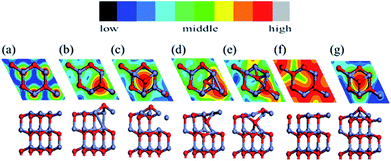
We used a (2 × 2) slab model (corresponding to a 1/4 ratio of defects; we also tested a (4 × 4) unit cell to prove sufficiency of size) with a vacuum region of more than 15 Å to represent the reconstructed surfaces observed in the MD simulation (see Fig. 3). Here the thickness of the slab was increased to eight Zn–O double layers. All slabs were optimized at 0 K with the back four double layers and H atoms fixed. A perfectly ordered, defect-free surface (as shown in Fig. 3a) was also relaxed as a reference. We will discuss the compensation preferences of various reconstruction mechanisms by comparison between those structures in terms of stability and polarity.

Fig. 3 Top and side views of optimized structures at 0 K for bulk-like and reconstructed models of Zn-terminated ZnO (0001), in top and side views in the top and bottom panels, respectively (showing only the outermost 3 of 8 bilayers and one (2 × 2) unit cell): (a) the bulk-like surface; (b) the O_ex structure; (c) the O_hollow structure; (d) the O_in structure; (e) the O_ex–O_in pair structure; (f) the Zn vacancy structure, (g) the O adatom structure at the hollow site. All the relaxed structures are overlaid on top of simulated scanning tunneling microscopy (STM) images in constant current mode (showing the isosurface of constant charge density ρ = 0.002 e/Bohr³, with heights colored according to the color bar).

The calculated interlayer distances for the bulk-like surface show similar tendencies as in previous reports:^9,10,16,38 the interlayer spacing d₁₂ (within the outermost ZnO bilayer) is clearly reduced by 26% from the bulk value, while the next spacing d₂₃ (between the outermost two ZnO bilayers) shows a 4.2% expansion vs. the bulk. In fact, for all the reconstructed structures, the average spacing within the outermost bilayer is significantly reduced relative to the bulk, while the average spacing between the outermost two bilayers also increases. The energetic results and electric dipole moments (perpendicular to the surface) of these structures are listed in Table 1, with the energy of the optimized bulk-like structure of Fig. 3a as reference.

Table 1 Relative energies and electric dipole moments of different models of the ZnO (0001) surface. The total energy of the optimized bulk-like ZnO model of Fig. 3a is set as reference (0 eV)

Structure	Bulk-like	Oex	Ohollow	Oin	Oex–Oin
Relative energy (eV)	0	−0.18	0.08	0.44	0.65
Electric dipole moment (a.u.)	0.67	−0.04	−0.43	0.02	−0.23

---

We find that the O_ex structure is more favorable than the bulk-like model by 0.18 eV and also has a negligible dipole moment. In contrast, the other reconstructions have unfavorable energies, though all exhibit a quenched dipole moment in the z direction. We even find overcompensation (negative dipole) for the O_hollow and O_ex–O_in structures. Though such overcompensation does not exist for the O_in structure, the strong stress induced by the O_in atom increases the total energy. This suggests a competition between bonding character and polarity for the final stability of these structures, which shows agreement with recent calculations by Xu et al.³⁵

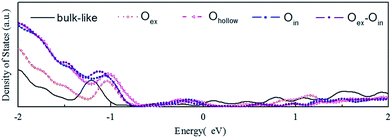
In Fig. 4 we display the density of states (DOS) calculated for the initial bulk-like model and the reconstructed models illustrated in Fig. 1. The main change of the DOS curve occurs at the localized peak around −1 eV, which corresponds to the outermost O atoms. Another electronic modification is found around the Fermi energy, indicating the existence of dangling bond electronic states on the surface. Both of the two variations are expected and proved to come from the surface reconstructions based on a localized density of states (LDOS) analysis. All the models show metallic properties, due to the limited thickness of the slab. Besides, the different O-complex structures on the surface show variations of the DOS spectra near −1 eV compared to the DOS spectra of the bulk-like structure, which represents modification of the electronic structure by local reconstructions.

Fig. 4 Total density of states (TDOS, in arbitrary unit) of (a) the optimized bulk-like ZnO surface, (b) the optimized O_ex model, (c) the optimized O_hollow model, (d) the optimized O_in model and (e) the optimized O_in–O_ex model.

We now focus on the O_ex structure since it is a potential stabilizing mechanism for this polar surface of ZnO. The extruded O breaks a bond with a deeper Zn atom while it maintains three O–Zn bonds closer to the surface plane. To saturate the valence electrons, the Zn atom beneath the extruded O makes new bonds with Zn atoms of the outermost layer. The outward displacement of the O atom is able to quench the overall dipole moment (in the +z direction), by inducing an opposing electric dipole in the −z direction. The concentration of O_ex as well as its effect on the overall dipole moment has been tested. A density of defects higher than the 25% shown in Fig. 3b is energetically unstable, indicating a strong repulsion between neighboring O_ex atoms. Such an upper concentration limit also exists for the other structures. In contrast, any lower concentration of O_ex structures will not compensate the dipole moment completely, e.g. 12.5% of O_ex will leave a dipole moment of 0.27 a.u. per unit cell higher than 25% of O_ex (whose dipole is set as 0 in Table 2). As a result, the favorable concentration of 25% is in agreement with the former experimental^31,32 and theoretical results³³ of charge transfer. Experimentally, the source of the observed O adatoms is unclear. Our findings suggest that the O_ex is a potential source of an O adatom, which escapes from ZnO surface layers and diffuses to the hollow site. In Fig. 3, we present simulated STM images of all the candidate reconstructions for comparison with experimental observations. The STM simulations were determined with a constant current mode using the Tersoff–Hamann approximation.

Table 2 Total energies of various compensation systems, relative to the optimized bulk-like ZnO model of Fig. 3a. The O₂ gas and Zn gas correspond to the O-rich/Zn-poor limit; Zn bulk corresponds to the Zn-rich/O-poor limit, indicating a clustering of abundant Zn atoms

Structure	Total energy (Zn rich: Zn bulk)	Total energy (O rich: O2 gas)	Total energy (O rich: Zn gas)
Bulk-like	0.18	0.18	0.18
Oex	0	0	0
Znvac + Zn	0.35	—	3
Oadatom–O	—	−3.76	—

---

A comparison of formation energies has also been conducted between this stabilization mechanism and two earlier compensation models: the isolated O-adatom and the Zn-vacancy models. To this end, the chemical potentials of O₂ gas, Zn gas and Zn bulk were involved, corresponding to various experimental conditions. The chemical potential of “O₂ gas” as a reference implies that oxygen is abundantly available in the gas phase, while “Zn gas” is used to represent the absence of Zn atoms from the surface. Both of these imply an O-rich limit, while “Zn bulk” indicates abundant Zn atoms clustering on the ZnO surface as the Zn-rich limit. Table 2 summarizes the total energies of various compensation models, for these experimental limits. The total energy of O_ex is set as the energy reference (0 eV) and a negative energy indicates a higher stability. As Table 2 indicates, the O_ex structure is favorable compared to the other stability mechanisms for the Zn-rich condition as well as the Zn-poor condition referenced to Zn gas. On the contrary, for the O-rich condition referenced to the O₂ gas, the O adatom model is much better than the others. This result also confirms the feasibility of O_ex as a stability mechanism.

4. Conclusions

In conclusion, we have studied the dynamic behavior of the Zn-terminated polar surface ZnO (0001) by ab initio MD simulations, which reveal several atomic reconstructions at elevated temperatures. O atoms tend to be pushed out from the surface as extrusions. These extrusions may be the main source of O adatoms at the top sites or hollow sites, leaving vacancies at the initial O sites. Based on our MD simulations, reliable optimization and energy analysis support these O extrusions as a stabilizing reconstruction mechanism, especially in the Zn-rich limit. Our work reveals novel defects such as the O_ex and O_in structures and predicts their ability to compensate for the intrinsically destabilizing dipole moments of bulk-like surface structures.

Acknowledgements

The work described in this paper is supported in part by a grant from the Research Grants Council of Hong Kong SAR [Project no. CityU 103511], by the State Key Development Program for Basic Research of China (Grant no. 2012CB215405), by the National Natural Science Foundation of China (Grant no. 11374272), by the Natural Science Foundation of SZU (grant no. 836-000064), by the Hong Kong Baptist University Strategic Development Fund and by the High Performance Cluster Computing Centre, Hong Kong Baptist University, which receives funding from the Research Grants Council, University Grants Committee of the HKSAR and Hong Kong Baptist University.

Notes and references

1. F. Fuchs, J. Furthmüller, F. Bechstedt, M. Shishkin and G. Kresse, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 115109.
2. J. Wróbel, K. J. Kurzydłowski, K. Hummer, G. Kresse and J. Piechota, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 155124.
3. W. Göpel, Prog. Surf. Sci., 1985, 20(1), 9.
4. O. Dulub, L. A. Boatner and U. Diebold, Surf. Sci., 2002, 519(3), 201.
5. T. S. Askgaard, J. K. Nørskov, C. V. Ovesen and P. Stoltze, J. Catal., 1995, 156(2), 229.
6. I. Nakamura, T. Fujitani, T. Uchijima and J. Nakamura, J. Vac. Sci. Technol., A, 1996, 14(3), 1464.
7. M. Bowker, H. Houghton and K. C. Waugh, J. Chem. Soc., Faraday Trans. 1, 1981, 77, 3023.
8. L. J. Brillson and Y. C. Lu, J. Appl. Phys., 2011, 109(12), 121301.
9. D. Vanmaekelbergh and L. K. van Vugt, Nanoscale, 2011, 3(7), 2783.
10. D. M. Bagnall, Y. F. Chen, Z. Zhu, T. Yao, S. Koyama, M. Y. Shen and T. Goto, Appl. Phys. Lett., 1997, 70(17), 2230.
11. J. S. Wu and D. F. Xue, Sci. Technol. Adv. Mater., 2011, 3, 127.
12. X. Wang, J. Song, J. Liu and Z. L. Wang, Science, 2007, 316(5821), 102.
13. J. Zhou, Y. Gu, P. Fei, W. Mai, Y. Gao, R. Yang, G. Bao and Z. L. Wang, Nano Lett., 2008, 8(9), 3035.
14. J. H. He, C. L. Hsin, J. Liu, L. J. Chen and Z. L. Wang, Adv. Mater., 2007, 19(6), 781.
15. H. Xue, N. Pan, M. Li, Y. Wu, X. Wang and J. Hou, Nanotechnology, 2010, 21(21), 215701; X. Wang, J. Zhou, J. Song, J. Liu, N. Xu and Z. L. Wang, Nano Lett., 2006, 6, 2768.
16. C. Noguera, J. Phys.: Condens. Matter, 2000, 12(31), R367.
17. J. Goniakowski, F. Finocchi and C. Noguera, Rep. Prog. Phys., 2008, 71(1), 016501.
18. A. Wander, F. Schedin, P. Steadman, A. Norris, R. McGrath, T. S. Turner, G. Thornton and N. M. Harrison, Phys. Rev. Lett., 2001, 86, 3811.
19. A. Wander and N. M. Harrison, J. Chem. Phys., 2001, 115, 2312.
20. J. M. Carlsson, Comput. Mater. Sci., 2001, 22(1–2), 24.
21. M. Sambi, G. Granozzi, G. A. Rizzi, M. Casarin and E. Tondello, Surf. Sci., 1994, 319(1–2), 149.
22. M. Valtiner, M. Todorova, G. Grundmeier and J. Neugebauer, Phys. Rev. Lett., 2009, 103, 065502.
23. M. Valtiner, M. Todorova and J. Neugebauer, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 165418.
24. O. Dulub, U. Diebold and G. Kresse, Phys. Rev. Lett., 2003, 90, 016102.
25. G. Kresse, O. Dulub and U. Diebold, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 245409.
26. F. Ostendorf, S. Torbrügge and M. Reichling, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 041405(R).
27. S. Torbrügge, F. Ostendorf and M. Reichling, J. Phys. Chem. C, 2009, 113, 4909.
28. J. V. Lauritsen, S. Porsgaard, M. K. Rasmussen, M. C. R. Jensen, R. Bechstein, K. Meinander, B. S. Clausen, S. Helveg, R. Wahl, G. Kresse and F. Besenbacher, ACS Nano, 2011, 5, 5987.
29. H. Meskine and P. A. Mulheran, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 165430.
30. S. Pal, T. Jasper-Tönnies, M. Hack and E. Pehlke, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 085445.
31. H. Maki, N. Ichinose, N. Ohashi, H. Haneda and J. Tanaka, Surf. Sci., 2000, 457(3), 377.
32. N. Jedrecy, M. Sauvage-Simkin and R. Pinchaux, Appl. Surf. Sci., 2000, 162, 69.
33. B. Meyer and D. Marx, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67(3), 035403.
34. S. Torbrugge, F. Ostendorf and M. Reichling, J. Phys. Chem. C, 2009, 113(12), 4909.
35. H. Xu, L. Dong, X. Q. Shi, M. A. Van Hove, W. K. Ho, N. Lin, H. S. Wu and S. Y. Tong, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 235403.
36. N. Troullier and J. L. Martins, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 43(3), 1993.
37. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77(18), 3865.
38. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78(7), 1396.
39. P. Ordejon, E. Artacho and J. M. Soler, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 53(16), 10441.
40. J. M. Soler, E. Artacho, J. D. Gale, A. Garcia, J. Junquera, P. Ordejon and D. Sanchez-Portal, J. Phys.: Condens. Matter, 2002, 14(11), 2745.
41. W. Kohn and L. J. Sham, Phys. Rev., 1965, 140(4A), A1133.
42. B. Meyer, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69(4), 045416.
43. S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. J. Probert, K. Refson and M. C. Payne, Z. Kristallogr., 2005, 220, 567.
44. N. Marzari, D. Vanderbilt and M. C. Payne, Phys. Rev. Lett., 1997, 79, 1337.

---