Do spin state and spin density affect hydrogen atom transfer reactivity?
Caroline T.
Saouma
and
James M.
Mayer
*
Department of Chemistry, University of Washington, Campus Box 351700, Seattle, WA, USA. E-mail: mayer@chem.washington.edu
First published on 22nd October 2013
Abstract
The prevalence of hydrogen atom transfer (HAT) reactions in chemical and biological systems has prompted much interest in establishing and understanding the underlying factors that enable this reactivity. Arguments have been advanced that the electronic spin state of the abstractor and/or the spin-density at the abstracting atom are critical for HAT reactivity. This is consistent with the intuition derived from introductory organic chemistry courses. Herein we present an alternative view on the role of spin state and spin density in HAT reactions. After a brief introduction, the second section introduces a new and simple fundamental kinetic analysis, which shows that unpaired spin cannot be the dominant effect. The third section examines published computational studies of HAT reactions, which indicates that the spin state affects these reactions indirectly, primarily via changes in driving force. The essay concludes with a broader view of HAT reactivity, including indirect effects of spin and other properties. It is suggested that some of the controversy in this area may arise from the diversity of HAT reactions and their overlap with proton-coupled electron transfer (PCET) reactions.
I. Introduction
Hydrogen atom transfer (HAT, eqn (1)) is one of the most fundamental chemical reactions.1 It is central to combustion,| X + H–Y → X–H + Y | (1) |
A much-debated issue in HAT is the importance of unpaired spins: does the spin state of the abstractor and/or the amount of unpaired spin density on the abstracting atom affect reactivity? This is part of a broad discussion of the influence of spin states and spin state changes on transition metal reactivity, as stated in a recent commentary by Costas and Harvey: “Properties of different spin states will surely continue to serve… as a guiding principle for molecular design by computational and experimental chemists.”8
Traditionally, HAT reactions were the province of organic radical chemistry, and unpaired spin is present in all of the classical abstractors, such as halogen atoms, oxyl radicals, and alkyl radicals. There is a common intuition that HAT must be related to spin because so many facile HAT reactions involve radical reactants. The issue of spin has come to the fore as it has been recognized that transition metal species often react by HAT, or more generally by proton-coupled electron transfer (PCET). These transition metal active-sites, catalysts, and reagents can exist in spin states from singlet to septet, and can exhibit multi-[spin]-state reactivity. It has been suggested that open-shell metal oxidants are inherently better hydrogen atom abstractors, and that singlet ground state molecules need to react via higher spin states. The literature contains many statements such as “From these combined experimental/computational studies, the crucial role of unpaired spin density at the abstracting atom becomes clear.”7 From a paper about a manganese(V) oxo species: “Oxyl character, found only in the triplet and quintet states, is thus essential for efficient C–H activation”.9 The arguments for spin playing a key role come from analyses of gas-phase reactions, from computational studies, and from valence-bond analyses.6,7
In contrast, extensive studies by Rüchardt have shown that simple closed-shell organic molecules (singlet, S = 0) can react by HAT, albeit usually at elevated temperatures. This work is described in an excellent 1997 review.10 Singlet metal complexes including d0 permanganate and chromium(VI) compounds have also been shown, in studies starting in the 1960s, to abstract H˙ from hydrocarbon substrates.11,12 A number of recent reports describe H-atom abstractions by a variety of dn metal species (n > 0) with singlet ground states, including Goldberg's MnV(O),13 Kojima's 7-coordinate RuIV(O),14 and Tolman's CuIII(OH)15 complexes.16
The motivation for this essay is to clarify how spin state and spin density affect HAT reactivity. This understanding should be valuable from the design of new catalysts to studies of metalloenzyme biochemistry. The simple arguments advanced here should be of fundamental interest and of value to experimental chemists in the bioinorganic, inorganic, and organometallic communities.
The next section of this essay uses a simple kinetic/thermodynamic argument to prove that open-shell species cannot in general be intrinsically more reactive than closed-shell species. The common correlation of HAT with free radical chemistry is not a causation. The larger third section presents an analysis of published computational studies of HAT reactions, showing that reactivity correlates better with driving force than with spin state. It provides a context to understand why higher-spin forms often are faster H-atom abstractors and enables predictions of cases where lower spin states should be more reactive. The essay concludes by bringing together disparate perspectives, including the suggesting that some of the controversy in this area relates to the diversity of HAT processes. These vary from traditional cases in which the e− and H+ originate in the same bond to reactions in which there is significant separation between the two particles.
II. A simple kinetic demonstration that unpaired spin cannot be a requirement for HAT reactivity
There are a number of examples of HAT reactions between two closed-shell species, such as MnO4− + Ph2CH2 (ΔG°HAT ≅ −1 kcal mol−1)12c,17 and α-methylstyrene + 9,10-dihydroanthracene (ΔH°HAT = +39 kcal mol−1).10 Such reactions can be written schematically as in eqn (2), in which X: and H–Y are both closed-shell, singlet (S = 0) reactants. Neither X: nor H–Y have any significant unpaired spin density on any atom. H-atom transfer gives two doublet (S = 1/2) products, indicated by dots in the equation.| X: + H–Y ⇆ X–H˙ + Y˙ | (2) |
The reaction in the forward direction is HAT with a closed-shell abstractor. The reaction in the reverse direction is HAT by the radical species Y˙.
The hypothesis that reagents with unpaired spins are intrinsically better HAT abstractors requires that the reaction of Y˙, the reverse of eqn (2), be more facile than the forward reaction, which has a closed-shell species as the abstractor. However, when the free energy of reaction (2) (ΔG°2) is zero, the barriers ΔG‡ are the same for radical species Y˙ as for the non-radical species X:. The rate constants for HAT by Y˙ and by X: must be identical (Keq = 1). There can be no kinetic advantage for Y˙ over X: due to the former having an unpaired spin. It should be emphasized that in comparing different reactions in which ΔG°2 = 0, the barrier ΔG‡2 may differ (e.g., comparison of X: + H–Y → X–H˙ + Y˙ with Z: + H–Y → Z–H˙ + Y˙). The key point is that for any such reaction with ΔG° = 0, the barrier must be the same for X: and Y˙.
In the more general case when ΔG°2 ≠ 0, the barriers to the forward and reverse HAT reactions differ only by ΔG°2 (eqn (3) and Fig. 1). If the reaction of Y˙ is faster (lower barrier) than that of X:, it is due only to the reaction of Y˙ being more thermodynamically favorable. There cannot be any intrinsic kinetic advantage for Y˙ vs. X:. In this context, an intrinsic kinetic effect is something that affects the kinetic barrier independent of the net thermochemistry of reaction.18
| ΔG‡2r (HAT by Y˙) = ΔG‡2f (HAT by X:) – ΔG°2 | (3) |
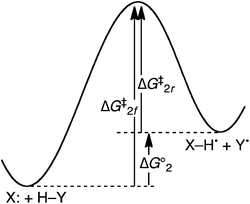 | ||
| Fig. 1 Schematic free energy surface for the HAT reaction of two closed-shell species X: + H–Y ⇆ X–H˙ + Y˙ (eqn (2)), indicating the free energy barriers (ΔG‡) for the forward and reverse reactions and the driving force (ΔG°2). | ||
This simple analysis comparing the forward and reverse reaction rates for eqn (2) shows that the spin state or spin density of an active site cannot be the direct determinant of hydrogen atom abstraction reactivity.19 In general, HAT reaction barriers ΔG‡1 can be understood in various ways. From a Marcus theory perspective, the key parameters are the reaction free energy ΔG°1 and the reorganization energy λ.5,20 The related valence bond analysis uses the reaction energy, the resonance energy stabilization of the transition state (B) and the energies required to bring the reactants into resonance with the products at the crossing point (foGo).6 As emphasized by Shaik,6 the spin state of a reactant can affect all of these parameters and therefore indirectly affect the rate of an HAT reaction. For instance, within some sets of radicals those with the larger spin density at the abstracting atom may have decreased reorganization energies.6 In sum, Fig. 1 shows that the intrinsic barriers for HAT by X: and Y˙ in eqn (2) must be the same, but the size of this barrier is determined by the properties of the reagents, including the spin on Y˙.
It should be noted that the arguments here and below apply only to HAT reactions that occur in a single kinetic step. Different issues arise for net H-atom transfers that occur in multiple steps, for instance electron-then-proton, or proton-then-electron transfer. Additionally, it is assumed that HAT steps are spin-allowed, that they occur without change in the overall spin state of the system.21 Our recent study of the spin-forbidden HAT reaction converting a quartet cobalt(II) complex to a singlet Co(III) product, [CoII(H2L)3]2+ (S = 3/2) + XO˙ (S = 1/2) → [CoIII(H2L)2(HL)]2+ (S = 0) + XOH (S = 0), concluded that the reaction occurs in two steps. Pre-equilibrium spin isomerization to the singlet surface occurs prior to HAT.22
III. Effects of spin state
If the spin state cannot be the primary determinant of HAT reactivity, why is it that reagents with higher spin states are frequently found to be more reactive toward HAT than related species with lower spin states? A complication in such comparisons is that they usually involve different chemical species. For instance, gas-phase studies in the Schwarz laboratory show CaO+˙ to be much more reactive than neutral, closed-shell CaO.7 The HAT rate for a dimeric FeIV(O)(μ-O)FeIII complex with an S = 2 FeIV(O) unit is larger than that of a different [Fe3.5(μ-O)]2 compound.23 In these and other examples, the species being compared have different ligands, geometries, electronic structures, and/or charges, so it is difficult to extract solely the effects of the spin state.A more direct comparison is the HAT reactivity of the same complex in different spin states. Many computational studies of metal-mediated HAT reactions report energy surfaces for multiple spin states, at the same level of theory. While distinct spin states of the same complex have different calculated structures and thermochemistry for HAT, they are more directly comparable than two different species.
A. Barrier and driving force as a function of spin state
A typical example of the many computational studies of transition metal HAT reactions is the energy profile for HAT from cyclohexane to the iron(IV)-oxo complex [(N4Py)Fe(O)]2+, reproduced in Fig. 2 (N4Py = N,N-bis(2-pyridylmethyl)-N-(bis-2-pyridylmethyl)amine, R–H = C6H12).24 As is often found, the higher spin state is higher in energy in the reactant but has a lower barrier to reaction. Thus it would be easy to conclude that the higher spin state is the origin of the higher reactivity. However, as the authors of this study point out,24,25 it is also valuable to examine the product energies in addition to those of the reactants and transition states.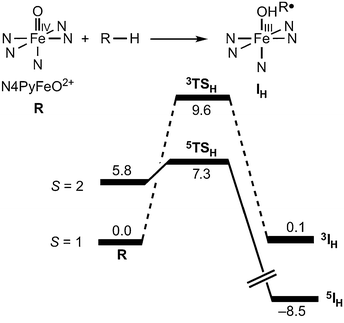 | ||
| Fig. 2 From Fig. 1b of ref. 24. “Gas-phase energy profiles [kcal mol−1] calculated with B3LYP.” N4Py = N,N-bis(2-pyridylmethyl)-N-(bis-2-pyridylmethyl)amine, R–H = C6H12. Reprinted by permission from Macmillan Publishers Ltd: [Nat. Chem.] (ref. 24), copyright (2011). | ||
Following the Hammond postulate, the position and energy of the transition state usually reflects the free energy change (ΔG°) for that single reaction step.26 For two similar reactions, the more exoergic reaction usually has a transition state that is more reactant-like, a barrier that is earlier along the reaction coordinate, and a barrier that is lower in energy. For the case illustrated in Fig. 2,24 HAT on the triplet surface is calculated to have ΔE = +0.1 kcal mol−1, while the reaction on the quintet surface has ΔE = −14.3 kcal mol−1. The Hammond postulate then implies – as noted in this study25 – that the quintet surface has an earlier transition state and a lower HAT barrier. The lower barrier on the quintet surface occurs even if the intrinsic reactivity of the quintet and triplet states are the same. In this case, the 14.4 kcal mol−1 greater exoergicity of the reaction on the quintet surface more than compensates for the 5.8 kcal mol−1 higher energy of the reactant quintet state.
The preceding example illustrates the importance of driving force (G°HAT) on HAT reactions. This is not a new conclusion, as it has been well established in the organic radical literature for decades and long been a key part of Shaik's valence bond analyses of radical reactivity.6,27 The correlation of barrier height with driving force is sometimes called the Bell-Evans-Polanyi (BEP) principle (from 1938).28 While the BEP correlation does not hold for all chemical reactivity, it has been found to work well for many kinds of HAT reactions (and was cited in the report of the results in Fig. 224,25).
Our laboratory has further shown that most HAT reactions are well described by a Marcus-theory approach, with rate constants typically well predicted by the Marcus cross relation.5,20b When comparing two similar reactions (reactions with the same intrinsic barrier λ), this approach predicts that the change in the barrier height ΔΔG‡, upon a change in driving force ΔΔG°, is given by eqn (4a). For the large majority of HAT reactions that are in the ΔG° ≪ 4λ regime, the Marcus approach predicts that the slope of the BEP correlation, ΔΔG‡/ΔΔG°, sometimes referred to as the Brønsted α, will be close to 0.5. In other words, roughly half of the change in ΔG° will appear in ΔG‡.29 This is typical of free energy relationships for solution phase reactions.26,30 Though this expression was derived using Marcus theory, a very similar expression is obtained from VB theory, following Shaik (eqn (4b); Erp = driving force, ΔGo = promotion energy gap).6
| ΔΔG‡/ΔΔG° = 0.5 + ΔΔG°/4λ | (4a) |
| ΔΔE‡VB/ΔΔErp = 0.5 + ΔΔErp/ΔGo | (4b) |
Applying this analysis to the case shown in Fig. 2, the 14.4 kcal mol−1 greater exoergicity for the quintet state over the triplet state predicts a 7.2 kcal mol−1 lower barrier. The reported calculated difference in barriers is 8.1 kcal mol−1, in quite good agreement with the prediction from eqn (4). While there could be other differences between the quintet and triplet states that affect the barrier, the primary effect is that the different spin states have different driving forces for H-atom abstraction.
B. A meta-analysis of 13 computational studies
We have analyzed 13 computational papers on HAT reactions iron and manganese oxo complexes from different laboratories to explore the generality of the conclusion that driving force is the major contributor to the observed spin effects. This is a sort of chemical meta-analysis.31 These 13 are all of the papers found in an initial literature search for studies with the data necessary for the analysis; while this is not a comprehensive set, no active selection was done. The studies are from different laboratories and use a variety of related methods. These papers report the barriers and energetics for H-atom transfers of the same species in different spin states, typically as energies ΔE‡ and ΔE° (rather than free energies). Some of the papers also compare σ and π transition state energies of the same spin multiplicity. Only in a few cases was the driving force emphasized as a primary determinant of differences between spin states.25,32,33These 13 papers report calculations for 31 reactions which can be analyzed to give 59 different comparisons of the same chemical process on two different spin surfaces. Each comparison is summarized as a row in Table 1. The ΔE‡ and ΔE° for both spin isomers are given, as are the differences, ΔΔE‡ and ΔΔE°, between the higher and lower spin state. The ratio ΔΔE‡/ΔΔE° (Fig. 3) then provides a test of the relationship between barrier and driving force (eqn (4)).
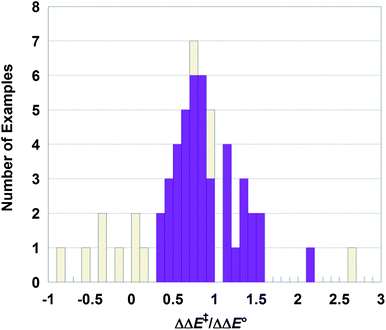 | ||
| Fig. 3 Histogram of ΔΔE‡/ΔΔE° values from Table 1. The solid purple bars are for cases with confident predictions, while the gold hashed bars have |ΔΔE‡| and/or |ΔΔE°| < 2.5 kcal mol−1. Five gold cases are not shown, at ΔΔE‡/ΔΔE° = +14, 6.7, 4.5, −1.8 and −3.5. | ||
In 52 of the 59 comparisons, the isomer with the more favorable driving force (ΔE°) has the lower barrier (ΔE‡), as indicated by a positive value of ΔΔE‡/ΔΔE°. Seventeen of these cases have computed magnitudes of |ΔΔE‡| and/or |ΔΔE°| of less than 2.5 kcal mol−1 and therefore significant uncertainty in the sign of ΔΔE‡/ΔΔE°. DFT calculations are known to have difficulty in accurately reproducing the relative energies of spin states.22 Omitting these 17 cases leaves 42 comparisons, all of which have ΔΔE‡/ΔΔE° > 0. In all of the cases where the calculations give a confident prediction, the spin isomer with the greater driving force has the lower barrier.
The histogram of ΔΔE‡/ΔΔE° in Fig. 3 shows the 42 more confident values in solid purple and the more uncertain ones in hashed gold (five of the latter are off the scale in Fig. 3 and not shown). The 42 values form a reasonable distribution, with a median value of ΔΔE‡/ΔΔE° of 0.8 and a mean (standard deviation) of 0.9 (0.4). The complete dataset has a similar median (0.7) but a much larger standard deviation about the mean, 1.0 (2.1), presumably due to the uncertainties in the small values of the ΔΔE° denominator. These values are in modest agreement with the prediction that ΔΔE‡/ΔΔE° ≅ 0.5 from eqn (4). The distribution is fairly scattered, as expected for a meta-analysis of a diverse set of data with significant uncertainties. Still, the median and mean values indicate that the barriers are strongly correlated with the driving forces. In fact, ΔE‡ may be even more sensitive to ΔE° than predicted by eqn (4), as most of the ΔΔE‡/ΔΔE° values are larger than 0.5.
Of the 59 comparisons, 16 have a lower barrier on the lower-spin surface, ΔE‡(lower spin) < ΔE‡(higher spin). These 27% are thus opposite to the hypothesis that higher spin states favor HAT. There is a bias towards lower barriers for higher spin isomers, but not a very strong one.
Singlet states are involved in 15 of the 59 comparisons. In four of these cases (27%), the singlet is calculated to have the lower barrier. Thus, a non-zero spin ground state does not appear to be required for HAT or even a guarantee of a lower barrier for HAT.34
In sum, while there is significant scatter in the data, this meta-analysis indicates that driving force is a primary determinant of HAT barrier. Higher spin states are usually more reactive, but only in ∼70% of the cases. Singlet spin states are usually less reactive, but only in ∼75% of the cases. It should be noted that some of these comparisons are from studies that focus on the importance of spin states35 or spin density36b,37 and do not discuss driving force. We emphasize that the driving force is not the sole determinant of reactivity, as has been concluded in a number of studies.5,18,32a,37 Still, the meta-analysis indicates that the driving force is the largest single determinant of HAT reactivity. We strongly encourage all studies of this kind to start their analyses a discussion of differences in reaction driving force, before looking for other causes for differences in HAT barriers.
C. Low-spin species are typically more reactive when ΔG° is more favorable
The correlation of barrier with driving force gives predictions and explanations for cases where low-spin states are more reactive. Fig. 4 shows the calculated energies for HAT from cyclohexane to [(N4Py)Fe(O)]2+ on three different spin surfaces.25 (A selected portion of this surface, from a later review,24 was shown above as Fig. 2.) Overall, the quintet surface has the lowest energy transition state. This 5TSH is 5.9 kcal mol−1 above the reactant cluster on the quintet surface, 5RC (the values quoted here include solvation energies, from the numbers in square brackets in Fig. 4). It should be noted that the singlet state here is an open shell singlet.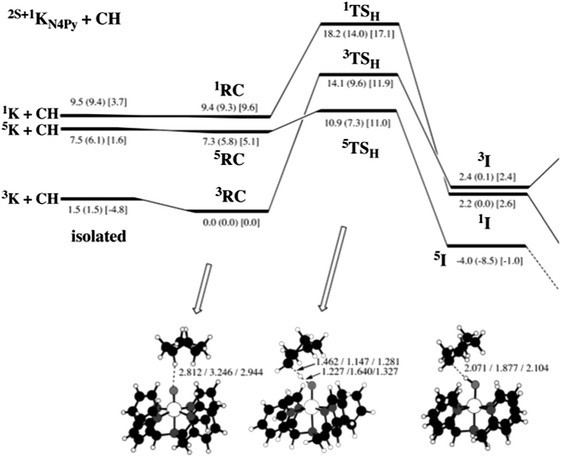 | ||
| Fig. 4 Fig. 2 from ref. 25. “Energy profile for the reaction of 2S+1KN4Py (S = 0, 1, 2) with cyclohexane (C6H12). Relative energies are indicated in the order: B2//B1 (B2//B1 + ZPE) [B2//B1 + ZPE + Esolv].” Abbreviations: K = [(N4Py)Fe(O)]2+, CH = cyclohexane, RC = reactant cluster (the precursor to the H-atom transfer), TSH = the HAT transition state, and I = the immediate product of HAT, which is one intermediate along the complete reaction pathway. Energies quoted in the text are differences between RC, TSH, and I (for a particular spin state), using values that correspond to B2//B1 + ZPE + Esolv (in brackets). Reprinted with permission from the American Chemical Society: [J. Am. Chem. Soc.] (ref. 25), copyright (2006). | ||
On the singlet surface, the computed barrier is 7.5 kcal mol−1 (E[1TSH] – E[1RC]), significantly smaller than the 11.9 kcal mol−1 barrier on the triplet surface. Why is the singlet state of [(N4Py)Fe(O)]2+ more reactive than the triplet state? A primary reason appears to be that HAT on the singlet surface is more exoergic. HAT by the singlet is downhill, with ΔE = −7.0 kcal mol−1 while HAT on the triplet surface is uphill, by +2.4 kcal mol−1. The 9.4 greater exoergicity on the singlet surface correlates with a 4.6 kcal mol−1 lower barrier, close to the 4.7 kcal mol−1 predicted by eqn (4) (0.5 × ΔΔE°).
Comparing the solvated singlet and quintet surfaces, the driving force is slightly less favorable on the higher spin surface (−6.1 vs. –7.0 kcal mol−1), yet the barrier is lower for the higher spin species. While the differences are small, this is not as predicted by eqn (4). We discuss this case here to emphasize that eqn (4) will not hold in all cases. Deviations from eqn (4) may be due to differences in reorganization energy for the different spin states, to other contributions to HAT reactivity (see Sections IV.A. and IV.B.), or to uncertainties in the computations.
The quintet surface in Fig. 4 has the lowest calculated barrier and forms the most stable product, 5I. The 5I state is the most stable product because it contains the preferred high-spin sextet (S = 5/2) iron(III) hydroxide product, antiferromagnetically coupled to the carbon radical [6FeIII(OH) + 2R˙]. Thus our general prediction is that the quintet state of an FeIV(O) complex will be the most reactive when the FeIII(OH) product is high-spin. Of the 39 comparisons involving quintet FeIV(O) states in Table 1, all but four have lower barriers than related triplet or singlet states.
For reactions where the product is much more stable in a low-spin state, the opposite prediction is made: lower spin isomers of the reactant should typically have lower barriers. For instance lower-spin FeIV(O) compounds should be more reactive when the product is low-spin (S = 1/2) L5FeIII(OH). A related example of this could be HAT by 4-coordinate C3v symmetric L3FeIV(N) species to form L3FeIII(NH) products; this process should be favored to occur for S = 0 nitrido species,38 as the resulting iron(III) imido species in this geometry are known to be S = ½.39 The relationship between spin state and driving force in metal complexes will likely vary from system to system, as factors such as geometry at the metal and d-electron count will modulate the spin selectivity.
IV. A broader view
A. Other contributions to HAT reactivity
This short essay emphasizes the reaction driving force because this is usually the largest single contributor to the HAT reaction barrier. However, other factors clearly contribute to HAT reactivity, which should be considered when comparing similar reactions with different species. This was emphasized long ago in the organic radical literature and in the valence-bond analyses by Shaik and others.6,18,27b,32a,40 Our more recent Marcus approach has noted the importance of reorganization energies (λ).5,20b,41 Detailed theories of proton-coupled electron transfer (PCET), of which HAT is one type, include λ as well vibronic overlaps and donor–acceptor motions.42In addition to these fundamental issues, a number of studies have indicated that steric effects can substantially reduce HAT rate constants.43 In an early example, Groves and Nemo suggested in 1983 that steric influences on hydroxylation by iron-oxo-porphyrin complexes were due to a stereoelectronic effect on HAT.44 This is closely related to the current discussions of σ vs. π mechanisms for H-atom transfer to metal oxo sites.37,45 Very recently, stereochemical effects were suggested to account for the slower HAT reactions of [FeIV(NTs)(N4Py)]2+ (NTs = tosylimido2−) compared to that of [FeIV(O)(N4Py)]2+ with C–H bonds; the BDE(NH) and BDE(OH) of the respective product iron(III) species is very similar, and hence so is the driving force.46 Steric interactions could, in principle, preclude HAT reactions to occur in systems that have a favorable driving force.
B. Spin density vs. spin states
Spin states are in most cases a clear experimental observable. Molecules in singlet states, for instance, are diamagnetic and have sharp NMR spectra. Most computations, as shown above, have been sorted by spin state.21 The section above has analyzed reactions as if they proceed only on one spin surface, the triplet surface for example, for the entire HAT step. It should be noted, however, that there is typically rapid interconversion of spin states for transition metal complexes, faster than microseconds for thermodynamically favored processes.48 Thus most thermal solution reactions that can access multiple spin states will be under Curtin–Hammett conditions49 of rapid equilibration of the reactant and product spin states prior to and subsequent to HAT reaction. Under these conditions, reactions will usually proceed over the lowest barrier regardless of spin state.22,25 This is likely to be a part of the influential “two state reactivity” (TSR) advanced most notably by Shaik.47 Thus, when multiple spin states are thermally accessible, correlations between spin state and reactivity are not simple.An alternative perspective is that spin density on the abstracting atom, not spin state, is key to HAT reactivity. Spin density at a particular atom need not correlate with spin state. As a general statement, spin density reflects electronic structure and will influence barrier heights. Spin density is difficult to measure experimentally (cf., ref. 50), and is not usually reported in computational studies. So this suggestion is difficult to address, at least at the moment. Correlating spin density with HAT reactivity for simple organic radicals such as oxyl radicals is complicated by the rough correlation of spin density at O and the O–H bond strength.51 Still, it is difficult to reconcile this spin density hypothesis with the HAT reactivity of closed-shell singlets, such as permanganate and α-methylstyrene, that have essentially no spin density on any atom. We return to this issue in the next section.
It has recently been suggested that the key parameter is spin density at the abstracting atom at the transition state.52 Thus a closed-shell singlet reactant could develop spin density at the abstracting atom along the reaction coordinate. In our view, this proposal provides limited insight. HAT is by definition a one-electron process, so the H donor and acceptor each change spin state by 1/2. Since the transition state is in some ways an interpolation between reactants and products, it is difficult to imagine an HAT reaction in which there isn't some spin density on both reactants at the transition state. There could be more or less spin density at the specific atom that accepts the H, as discussed in the next section. Measuring spin density at a transition state appears to be very difficult, and computing this parameter requires a complete calculation that gives the barrier height, so it is not clear that this perspective has substantial predictive value.
C. Hydrogen atom transfer vs. “proton-coupled electron transfer”
Throughout this essay, “hydrogen atom transfer” (HAT) has been defined as a process that transfers H˙ from one reagent X–H to another reagent Y (eqn (1)). This is the typical usage.A narrower view is that HAT refers only to reactions in which the proton and electron originate and terminate in the same bond (eqn (5)).53 For reactions that fit this narrow definition, the presence of spin density at the abstracting atom may often be a useful heuristic for predicting HAT reactivity. This is frequently the case for reactions of simple p-block radicals, such as the series of oxyl radicals HO˙, RO˙, PhO˙, and HOO˙. In such cases, the spin density at Y often parallels the Y–H bond strength, and therefore spin density parallels the HAT driving force and rate constant. One could argue that in these situations the spin density is the fundamental property, leading to the higher Y–H bond strength and reactivity.6
The narrow definition, however, excludes many reactions generally called HAT. A variety of HAT reactions – especially those involving metal complexes – involve spatial and/or orbital separation of the e− and H+. The most famous example is from the catalytic cycle of cytochrome P450 (eqn (6)). The e− and H+ are removed from the same C–H bond but transfer to quite separated sites: the proton to the oxo group and the electron to a hole on the porphyrin and thiolate ligands.54 Another example is the phenol-phenoxyl self-exchange reaction.55 In the extreme case in eqn (7), long-range electron transfer from X to Y is concerted with short-range proton transfer from AH to :B. Some studies have termed reactions such as eqns (6)–(8) “proton-coupled electron transfer” (PCET)6,55 and we will use that terminology here for consistency, although PCET is increasingly used as a much broader “catch-all” term. One specific example of eqn (7) is the self-exchange reaction between iron–biimidazoline complexes, the core of which is shown in eqn (8).56
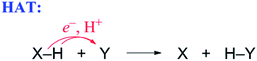 | (5) |
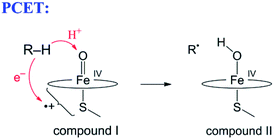 | (6) |
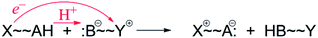 | (7) |
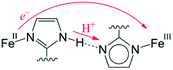 | (8) |
It should be emphasized that there is a continuum of reactions from “same-bond HAT” to PCET, which adds to the controversy in the role of spin on these reactions. Shaik has referred to these cases as “blended HAT/PCET” or “variable HAT/PCET mixing.”57 Reactions of phenols are a good example, because the SOMO in the product phenoxyl radicals is at least as much on the aromatic ring as the oxygen. So does the removed electron “come from” the phenol O–H bond or from the π system? In eqn (6), the e− and H+ “come from” the same bond but transfer to different places in the product – is this “same-bond HAT” or PCET?
We believe that this continuum between “same-bond HAT” and PCET is at the heart of some of the confusion over the relationship of spin and reactivity. Consider a reaction involving addition of e− and H+ (H˙) to an atom X that obeys the octet rule in the product: X + H˙ → XH. The atom X would therefore typically need to have an accessible 7-electron configuration in the reactant or at the transition state, and thus some unpaired spin density. However, if the e− is transferring to a site that is distant from the proton accepting atom, as in the PCET reactions (6)–(8), then the proton-accepting atom need not have any unpaired spin density. In this situation, the proton-accepting atom acts only as a base. The electron transfer (ET) portion of the PCET process resembles a pure ET step, without any specific spin requirements other than that the overall reaction be spin-allowed.
The self-exchange reaction of ketones and ketyl radicals (eqn (9)) is an interesting example. These occur with bimolecular rate constants of ∼5 × 103 M−1 s−1 (ΔG‡ = 12 kcal mol−1).58 In this process, the singlet ketone is the H-atom acceptor, and its oxygen atom that accepts the H obeys the octet rule. Triplet excited states are not thermally accessible. A purist might argue that this is not a true “same-bond HAT” process, that it occurs only because it is a PCET process with the unpaired electron being primarily on the ketyl carbon. In our view such distinctions are not helpful. These reactions – and many like them – occur readily. The electron and proton find their way to the appropriate sites.
 | (9) |
Many 1e−/1H+ transfer reactions involving transition metals have substantial PCET character, and therefore do not require unpaired spin at the abstracting atom, like the ketone in eqn (9). We note again that the discussion here is limited to reactions in which the e− and H+ transfer in a single concerted step; different issues arise when the transfer occurs via a stepwise ET-PT or PT-ET mechanisms.
Conclusions
A very recent review by Shaik asks and then answers: “‘is there a need to have a radical center at the abstractor in order to abstract a hydrogen atom?’ The answer to this question is, ‘of course not’, but if the abstractor is a closed-shell molecule then in the normal HAT event, this will require a high barrier.”6 This appears to contradict the simple kinetic argument in Section II, which demonstrates that open-shell reactants cannot be intrinsically more reactive for hydrogen-atom abstraction than closed-shell ones. But the Shaik review is not discussing intrinsic barriers in that quote, but rather absolute barriers. It states soon after that: “the BDEOH [bond dissociation energy] quantity for the closed-shell abstractors already incorporates the cost of decoupling the bonds of the closed-shell abstractors and preparing them for abstracting an H atom.” In other words, the difference between open and closed-shell reactants is manifest in the bond strength and therefore in the driving force for HAT. This difference in driving force then affects the transition state energy. Thus that review and this essay agree in important ways, despite the apparently contradictory language. The indirect effects of spin appear to be more important for the very narrowly defined “same bond” HAT processes. In “same bond” HAT, closed-shell abstractors have a “cost” to “prepare them for abstracting an H atom,” in Shaik's VB language. In contrast, in PCET reactions where the e− and H+ are well separated, there is no such cost.The common intuition that HAT is facilitated by the presence of unpaired spin at the abstracting atom derives from organic radical chemistry. For main-group compounds, an open-shell reactant is usually needed in order to have sufficient thermodynamic driving force for HAT. However, unpaired spin is not required for HAT even in organic chemistry, as shown by Rüchardt's reverse radical disproportionation reactions and the ketone reaction 9.10,58 For HAT reactions involving transition metal ions, where there is often substantial separation of the e− and the H+, spin states and spin density are more distantly connected to reactivity.
This essay shows, through simple kinetic argument (Section II) and a meta-analysis of computational studies (Section III) that HAT reactivity is best understood starting from the driving force for the HAT step. Barrier heights sometimes parallel spin multiplicities, but almost always correlate with reaction energy. The effects of spin state on HAT are indirect, mostly through the reaction driving force.
| Reactants | Spin statesa (mechanism)b | ΔE≠ (hs) | ΔE≠ (ls) | ΔΔE≠ (hs–ls) | ΔE° (hs) | ΔE° (ls) | ΔΔE° (hs-ls) | ΔΔE≠/ΔΔE° | Ref. |
|---|---|---|---|---|---|---|---|---|---|
| a Listed as [higher energy spin state]/[lower energy spin state] for the reactants. b A π mechanism denotes transfer of a β electron from the nucleophile into a π* orbital of the metal oxo reagent. A σ mechanism denotes transfer of a β electron from the nucleophile into a σ* orbital of the metal oxo reagent. c Calculated gas phase energies. d Calculated energies in acetonitrile solvent. e TMG3tren = 1,1,1-tris{2-[N2-(1,1,3,3-tetramethylguanidino)]ethyl}amine. f N4Py = N,N-bis(2-pyridylmethyl)-N-(bis-2-pyridylmethyl)amine. g TMC = 1,4,8,11-tetramethyl-1,4,8,11-tetraazacyclotetradecane. h The reactant energies are calculated to be equivalent in both spin states. i Tp = (3,5-diphenylpyrazolyl)hydroborate. j OBz = benzylformate. k Calculated energies in benzene solvent. l Bn-TPEN = N-benzyl-N,N′,N′-tris(2-pyridylmethyl)ethane-1,2-diamine. m Energies calculated with coupled-cluster theory. n tHp = tetrahydrogenporphyrin. o Cpd I(CcP) = compound I model for cytochrome c peroxidase. p tpp = tetraphenylporphyrin. q DHP = 9,10-dihydrophenanthroline. r Cz = corrolazinato3−. s DHA = 9,10-dihydroanthracene. t Calculated energies with chlorobenzene solvent. u Two low-lying triplet states are present in this system: in triplet A, the unpaired electrons are located in a MnO π* orbital and a ligand a1u orbital, while in triplet B, the unpaired electrons are located in a MnO π* orbital and the Mn δ orbital. v TBC = 1,4,8,11-tetrabenzyl-1,4,8,11-tetraazacyclotetradecane. | |||||||||
| [FeIIIO]+ + C2H6c | Quartet/sextet | 23.2 | 16.2 | 7.0 | −0.1 | −3.5 | 3.4 | 2.1 | 59 |
| [FeIIIO]+ + C2H6d | Quartet/sextet | 21.2 | 14.5 | 6.7 | 6.3 | −2.1 | 8.4 | 0.8 | 59 |
| [(TMG3tren)FeIVO]2+ + C6H8de | Triplet(π)/quintet(σ) | 15.6 | 12.3 | 3.3 | −12.3 | −22.1 | 9.8 | 0.3 | 35a |
| [(N4Py)FeIVO]2+ + C6H8df | Quintet(σ)/triplet(π) | −1.4 | 13 | −14.4 | −25.8 | −15.5 | −10.3 | 1.4 | 35a and 60 |
| [(TMC)(MeCN)FeIVO]2+ + C6H8dg | Triplet(π)/quintet(σ)h | 7.1 | 18.8 | −11.7 | −15.9 | −8.1 | −7.8 | 1.5 | 35a |
| (Tp)(OBz)FeIVO + C6H8ijk | Triplet(π)/quintet(σ) | 6.3 | 12.5 | −6.2 | −28.7 | −20.1 | −8.6 | 0.7 | 35a |
| [(N4Py)FeIVO]2+ + C6H12df | Quintet(σ)/triplet(π) | 5.9 | 11.9 | −6.0 | −6.1 | 2.4 | −8.5 | 0.7 | 25 |
| Singlet/triplet(π) | 11.9 | 7.5 | 4.4 | 2.4 | −7.0 | 9.4 | 0.5 | 25 | |
| Singlet/quintet(σ) | 5.9 | 7.5 | −1.6 | −6.1 | −7.0 | 0.9 | −1.8 | 25 | |
| [(N4Py)FeIVO]2+ + toluenedf | Quintet(σ)/triplet(π) | 3.7 | 11.4 | −7.7 | −11.8 | −4.7 | −7.1 | 1.1 | 25 |
| Singlet/triplet(π) | 11.4 | 13.8 | −2.4 | −4.7 | −10.3 | 5.6 | −0.4 | 25 | |
| Singlet/quinteth | 3.7 | 13.8 | −10.1 | −11.8 | −10.3 | −1.5 | 6.7 | 25 | |
| [(Bn-TPEN)FeIVO]2+ + C6H12dl | Quintet(σ)/triplet(π) | 7.1 | 12.5 | −5.4 | −5.6 | 0.9 | −6.5 | 0.8 | 25 |
| Singlet/triplet(π) | 12.5 | 9.4 | 3.1 | 0.9 | −8.2 | 9.1 | 0.3 | 25 | |
| Singlet/quintet(σ) | 7.1 | 9.4 | −2.3 | −5.6 | −8.2 | 2.6 | −0.9 | 25 | |
| [(TMC)(MeCN)FeIVO]2+ + C6H12dg | Quintet(σ)/triplet(π) | 10.8 | 23.2 | −12.4 | −0.4 | 9.4 | −9.8 | 1.3 | 25 |
| Singlet/triplet(π) | 23.2 | 17.6 | 5.6 | 9.4 | 1.1 | 8.3 | 0.7 | 25 | |
| Singlet/quintet(σ) | 10.8 | 17.6 | −6.8 | −0.4 | 1.1 | −1.5 | 4.5 | 25 | |
| [(TMC)(OTf)FeIVO]+ + C6H12dg | Quintet(σ)/triplet(π) | 9.8 | 22.8 | −13.0 | −0.7 | 9.1 | −9.8 | 1.3 | 25 |
| Singlet/triplet(π) | 22.8 | 17.0 | 5.8 | 9.1 | −0.2 | 9.3 | 0.6 | 25 | |
| Singlet/quintet(σ) | 9.8 | 17.0 | −7.2 | −0.7 | −0.2 | −0.5 | 14.4 | 25 | |
| [(N4Py)FeIVO](ClO4)2 + C6H12df | Quintet(σ)/triplet(π) | 7.8 | 23.2 | −15.4 | −2.4 | 11.4 | −13.8 | 1.12 | 60 |
| [(N4Py)FeIVO](ClO4)2 + C6H8df | Quintet(σ)/triplet(π) | 2.8 | 14.4 | −11.6 | −28.1 | −14.0 | −14.1 | 0.82 | 60 |
| Quintet(π)/triplet(σ) | 13.1 | 20.2 | −7.1 | −28.1 | −14.0 | −14.1 | 0.5 | 60 | |
| Quintet(π)/triplet(π) | 13.1 | 14.1 | −1.3 | −28.1 | −14.0 | −14.1 | 0.09 | 60 | |
| Quintet(σ)/triplet(σ) | 2.8 | 20.2 | −17.4 | −28.1 | −14.0 | −14.1 | 1.23 | 60 | |
| [(TMC)(MeCN)FeIVO]2+ + PhC2H5dg | Quintet(σ)/triplet(π) | 11.2 | 24.7 | −13.5 | −4.9 | 4.3 | −9.2 | 1.47 | 61 |
| [(TBC)(MeCN)FeIVO]2+ + PhC2H5dv | Quintet(σ)/triplet(π) | 8.7 | 25.0 | −16.3 | −7.5 | 3.3 | −10.8 | 1.51 | 61 |
| [(NH3)5 FeIVO]2+ + C2H6d | Quintet(σ)/triplet(σ) | 9.7 | 20.3 | −10.6 | −1.3 | 14.1 | −15.4 | 0.7 | 36 |
| Quintet(π)/triplet(π) | 17.1 | 16.3 | 0.8 | 6.9 | 6.0 | 0.9 | 0.9 | 36 | |
| Quintet(σ)/triplet(π) | 9.7 | 16.3 | −6.6 | −1.3 | 6.0 | −7.3 | 0.9 | 36 | |
| Quintet(π)/triplet(σ) | 17.1 | 20.3 | −3.2 | 6.9 | 14.1 | −7.2 | 0.4 | 36 | |
| Triplet(π)/quintet(π)m | 19.7 | 14.4 | 5.3 | 18 | 5.3 | 12.7 | 0.4 | 36 | |
| Triplet(π)/quintet(σ)m | 3.1 | 14.4 | −11.3 | −11.4 | 5.3 | −16.7 | 0.7 | 36 | |
| [(OH)(axial)(NH3)4 FeIVO]+ + C2H6d | Triplet(π)/quintet(π) | 20.4 | 20.5 | −0.1 | 7.2 | 10.6 | −3.4 | 0.0 | 36 |
| Triplet(π)/quintet(σ) | 16.3 | 20.5 | −4.2 | 3.5 | 10.6 | −7.1 | 0.6 | 36 | |
| Triplet(π)/quintet(σ)m | 9.9 | 24.5 | −14.6 | −7.7 | 11.5 | −19.2 | 0.8 | 36 | |
| [(OH)2(equatorial)(NH3)3 FeIVO]+ + C2H6d | Triplet(π)/quintet(π)h | 19.3 | 24.5 | −5.2 | 9.7 | 13.8 | −4.1 | 1.3 | 36 |
| Triplet(π)/quintet(σ)h | 11.8 | 24.5 | −12.7 | −0.9 | 13.8 | −14.7 | 0.9 | 36 | |
| Triplet(π)/quintet(π)m | 23.9 | 32.1 | −8.2 | 15.7 | 23.2 | −7.5 | 1.1 | 36 | |
| Triplet(π)/quintet(σ)m | 4.1 | 32.1 | −28.0 | −12.8 | 23.2 | −36.0 | 0.8 | 36 | |
| [(TMC)(OTf)FeIVO]+ + C6H8dg | Quintet(σ)/triplet(π) | 4.8 | 15.8 | −11.0 | −21.5 | −11.3 | −10.2 | 1.1 | 33 |
| (tHp˙+)(OH)FeIVO + C3H6n | Doublet/quartet | 5.7 | 2.9 | 2.9 | −16.4 | −17.5 | 1.1 | 2.6 | 32a |
| Cpd I(CcP) + C3H6o | Doublet/quartet | 18.4 | 17.8 | 0.6 | 2.6 | 1.7 | 0.9 | 0.7 | 32a |
| (tHp)(Cl)MnVO + toluenen | Quintet/triplet | 3.6 | 2.7 | 0.9 | −10.9 | −4.2 | −6.7 | −0.4 | 9 |
| [(tHp)(H2O)MnVO]+ + toluenedn | Quintet/triplet | 2.2 | 0.4 | 1.8 | −8.6 | −5.7 | −2.9 | −0.6 | 9 |
| (tHp)(OH)MnVO + toluenedn | Quintet/triplet | −0.7 | 4.3 | −5.0 | −17.5 | −4.2 | −13.3 | 0.4 | 9 |
| [(tHp)(O)MnVO]− + toluenedn | Quintet/triplet | 2.0 | 8.0 | −6.0 | −19.4 | −6.3 | −13.1 | 0.5 | 9 |
| (tpp)(Cl)MnVO + DHPdpq | Quintet/triplet | 1.8 | 0.9 | 0.9 | −15.1 | −9.7 | −5.4 | −0.2 | 62 |
| (Cz)MnVO + DHArst | Triplet Bu/singlet | 6.1 | 22.8 | −16.7 | −13.9 | 14.9 | −28.8 | 0.6 | 35b |
| Triplet Au/singlet | 15.7 | 22.8 | −7.1 | 0.3 | 14.9 | −14.6 | 0.5 | 35b | |
| [(Cz)(F)MnVO]− + DHArst | Triplet Bu/singlet | 2.5 | 14.6 | −12.1 | −23.0 | −4.3 | −18.7 | 0.6 | 35b |
| Triplet Au/singlet | 4.9 | 14.6 | −9.7 | −14.8 | −4.3 | −10.5 | 0.9 | 35b | |
| [(Cz)(CN)MnVO]− + DHA | Triplet Bu/singlet | −0.6 | 10.7 | −11.3 | −23.9 | −5.9 | −18.0 | 0.6 | 35b |
| Triplet Au/singlet | 18.4 | 10.7 | 7.7 | −8.1 | −5.9 | −2.2 | −3.5 | 35b | |
| (tHp)FeIVO + CH4nt | Quintet(σ)/triplet(π) | 11.7 | 27.2 | −15.5 | 3.7 | 24.2 | −20.5 | 0.76 | 63 |
| Quintet(σ)/triplet(σ) | 11.7 | 23.0 | −11.3 | 3.7 | 17.3 | −13.6 | 0.83 | 63 | |
| [(tHp)(SH)FeIVO]− + CH4nt | Quintet(σ)/triplet(π) | 22.8 | 22.9 | −0.1 | 16.2 | 17.0 | −0.8 | 0.13 | 63 |
| Quintet(π)/triplet(π) | 25.0 | 22.9 | 2.1 | 19.3 | 17.0 | 2.3 | 0.91 | 63 | |
Acknowledgements
The authors gratefully acknowledge the U.S. National Institutes of Health, GM50422 to JM and 1F32 GM099316 to CS, for financial support. We dedicate this manuscript to Dr. Keith Ingold and Prof. Dr. Christof Rüchardt, our mentors in organic radical chemistry.Notes and references
- Hydrogen-Transfer Reactions, ed. J. T. Hynes, J. P. Klinman, H.-H. Limbach and R. L. Schowen, Wiley-VCH, Weinheim, 2007 Search PubMed.
- (a) M. Costas, M. P. Mehn, M. P. Jensen and L. Que, Chem. Rev., 2004, 104, 939–986 CrossRef CAS PubMed; (b) B. F. Gherman, S. J. Lippard and R. A. Friesner, J. Am. Chem. Soc., 2005, 127, 1025–1037 CrossRef CAS PubMed; (c) J. Stubbe and W. A. van der Donk, Chem. Rev., 1998, 98, 705–762 CrossRef CAS PubMed; (d) S. V. Kryatov, E. V. Rybak-Akimova and S. Schindler, Chem. Rev., 2005, 105, 2175–2226 CrossRef CAS PubMed; (e) C. Krebs, D. Galonić Fujimori, C. T. Walsh and J. M. Bollinger, Acc. Chem. Res., 2007, 40, 484–492 CrossRef CAS PubMed.
- (a) J. T. Groves and Y.-Z. Han, in Cytochrome P450: Structure, Mechanism, and Biochemistry, ed. P. R. Ortiz de Montellano, Plenum Press, New York, NY, 1995, pp. 3–48 Search PubMed; (b) J. T. Groves, J. Inorg. Biochem., 2006, 100, 434–447 CrossRef CAS PubMed.
- D. R. Weinberg, C. J. Gagliardi, J. F. Hull, C. F. Murphy, C. A. Kent, B. C. Westlake, A. Paul, D. H. Ess, D. G. McCafferty and T. J. Meyer, Chem. Rev., 2012, 112, 4016–4093 CrossRef CAS PubMed.
- J. M. Mayer, Acc. Chem. Res., 2011, 44, 36–46 CrossRef CAS PubMed.
- W. Lai, C. Li, H. Chen and S. Shaik, Angew. Chem., Int. Ed., 2012, 51, 5556–5578 CrossRef CAS PubMed.
- N. Dietl, M. Schlangen and H. Schwarz, Angew. Chem., Int. Ed., 2012, 51, 5544–5555 CrossRef CAS PubMed.
- M. Costas and J. N. Harvey, Nat. Chem., 2013, 5, 7–9 CrossRef CAS PubMed.
- D. Balcells, C. Raynaud, R. H. Crabtree and O. Eisenstein, Inorg. Chem., 2008, 47, 10090–10099 CrossRef CAS PubMed.
- C. Rüchardt, M. Gerst and J. Ebenhoch, Angew. Chem., Int. Ed., 1997, 36, 1406–1430 CrossRef.
- (a) K. B. Wiberg, in Oxidation in Organic Chemistry Part A, ed. K. B. Wiberg, Academic Press, New York, 1965, pp. 69–184 Search PubMed; (b) R. Stewart, Oxidation Mechanisms, Benjamin, New York, 1964 Search PubMed; (c) K. B. Wiberg and G. Foster, J. Am. Chem. Soc., 1961, 83, 423–429 CrossRef.
- (a) G. K. Cook and J. M. Mayer, J. Am. Chem. Soc., 1995, 117, 7139–7156 CrossRef CAS; (b) G. K. Cook and J. M. Mayer, J. Am. Chem. Soc., 1994, 116, 1855–1868 CrossRef CAS; (c) K. A. Gardner, L. L. Kuehnert and J. M. Mayer, Inorg. Chem., 1997, 36, 2069–2078 CrossRef CAS PubMed; (d) K. Gardner and J. Mayer, Science, 1995, 269, 1849–1851 CAS; (e) For a vanadium(V) example, see: C. Waidmann, et al. , J. Am. Chem. Soc., 2009, 131, 4729–4743 CrossRef CAS PubMed; (f) W. W. Y. Lam, S.-M. Yiu, J. M. N. Lee, S. K. Y. Yau, H.-K. Kwong, T.-C. Lau, D. Liu and Z. Lin, J. Am. Chem. Soc., 2006, 128, 2851–2858 CrossRef CAS PubMed.
- (a) K. A. Prokop, S. P. de Visser and D. P. Goldberg, Angew. Chem., Int. Ed., 2010, 49, 5091–5095 CrossRef CAS PubMed; (b) D. E. Lansky, B. Mandimutsira, B. Ramdhanie, M. Clausén, J. Penner-Hahn, S. A. Zvyagin, J. Telser, J. Krzystek, R. Zhan, Z. Ou, K. M. Kadish, L. Zakharov, A. L. Rheingold and D. P. Goldberg, Inorg. Chem., 2005, 44, 4485–4498 CrossRef CAS PubMed.
- (a) S. Ohzu, T. Ishizuka, Y. Hirai, H. Jiang, M. Sakaguchi, T. Ogura, S. Fukuzumi and T. Kojima, Chem. Sci., 2012, 3, 3421–3431 RSC; (b) T. Kojima, Y. Hirai, T. Ishizuka, Y. Shiota, K. Yoshizawa, K. Ikemura, T. Ogura and S. Fukuzumi, Angew. Chem., Int. Ed., 2010, 49, 8449–8453 CrossRef CAS PubMed.
- P. J. Donoghue, J. Tehranchi, C. J. Cramer, R. Sarangi, E. I. Solomon and W. B. Tolman, J. Am. Chem. Soc., 2011, 133, 17602–17605 CrossRef CAS PubMed.
- The conclusions in ref. 13 and 14 have been questioned: (a) D. Schröder and S. Shaik, Angew. Chem., Int. Ed., 2011, 50, 3850–3851 CrossRef PubMed; (b) T. Kojima and S. Fukuzumi, Angew. Chem., Int. Ed, 2011, 50, 3852–3853 CrossRef CAS; (c) D. Janardanan, D. Usharani and S. Shaik, Angew. Chem., Int. Ed., 2012, 51, 4421–4425 CrossRef CAS PubMed.
- J. J. Warren, T. A. Tronic and J. M. Mayer, Chem. Rev., 2010, 110, 6961–7001 CrossRef CAS PubMed.
- P. Su, L. Song, W. Wu, P. C. Hiberty and S. Shaik, J. Am. Chem. Soc., 2004, 126, 13539–13549 CrossRef CAS PubMed.
- Fig. 1, and this essay as a whole, assume the applicability of a transition state theory (TST) model, so that rate constants are determined solely by barrier height (ΔG‡). Such a model is used in essentially all of the literature on spin effects on solution hydrogen atom transfer reactions, both experimental and computational. There are more sophisticated models of HAT and PCET kinetics, which can include tunneling of the electron and/or the proton, non-adiabiticity in the e− and/or H+ transfers, and dynamical effects see: S. Hammes-Schiffer and A. A. Stuchebrukhov, Chem. Rev., 2010, 110, 6939–6960 CrossRef CAS PubMed . By the principle of detailed balance, that the ratio of the forward and reverse rate constants must be e−ΔG°/RT(http://en.wikipedia.org/wiki/Detailed_balance), such non-TST effects would not change the conclusion from Fig. 1.
- (a) R. A. Marcus and N. Sutin, Biochim. Biophys. Acta, 1985, 811, 265–322 CrossRef CAS; (b) J. P. Roth, J. C. Yoder, T.-J. Won and J. M. Mayer, Science, 2001, 294, 2524–2526 CrossRef CAS PubMed.
- Spin-orbit coupling has not played a major role in HAT discussions.
- V. W. Manner, A. D. Lindsay, E. A. Mader, J. N. Harvey and J. M. Mayer, Chem. Sci., 2012, 3, 230–243 RSC.
- G. Xue, R. De Hont, E. Münck and L. Que, Nat. Chem., 2010, 2, 400–405 CrossRef CAS PubMed.
- S. Shaik, H. Chen and D. Janardanan, Nat. Chem., 2011, 3, 19–27 CrossRef CAS PubMed.
- H. Hirao, D. Kumar, L. Que and S. Shaik, J. Am. Chem. Soc., 2006, 128, 8590–8606 CrossRef CAS PubMed.
- (a) A. Pross, in Theoretical & Physical Principles of Organic Reactivity, Wiley-Interscience, New York, 1995, pp. 136–155 Search PubMed; (b) T. H. Lowry and K. S. Richardson, in Mechanism anf Theory in Organic Chemistry, Harper & Row, New York, 3rd edn, 1987, pp. 211–229 Search PubMed.
- (a) J. M. Tedder, Angew. Chem., Int. Ed., 1982, 21, 401–410 CrossRef; (b) K. U. Ingold and G. A. Russell, in Free Radicals, ed. J. K. Kochi, Wiley, New York, 1973, pp. 283–293, ch. 7 Search PubMed; (c) K. U. Ingold and G. A. Russell, in Free Radicals, ed. J. K. Kochi, Wiley, New York, 1973, p. 69, ch. 2 Search PubMed.
- M. G. Evans and M. Polanyi, Trans. Faraday Soc., 1938, 34, 11–24 RSC.
- This follows from the Marcus equation, ΔG‡ = (ΔG° + λ)2/4λ, taking the partial derivative of ΔG‡ with respect to ΔG° (∂ΔG‡/∂ΔG°).22.
- This conclusion may not apply to gas-phase ion molecule reactions, where the long-range attraction of the ion and molecule and lack of thermal equilibration of the reactant complex with solvent lead to different kinetic properties. Cf., M. L. Chabinyc, S. L. Craig, C. K. Regan and J. I. Brauman, Science, 1998, 279, 1882–1886 CrossRef CAS PubMed.
- Meta-analysis, in Wikipedia, http://en.wikipedia.org/wiki/Meta-analysis.
- (a) S. P. de Visser, J. Am. Chem. Soc., 2010, 132, 1087–1097 CrossRef CAS PubMed; (b) Y. Kang, H. Chen, Y. J. Jeong, W. Lai, E. H. Bae, S. Shaik and W. Nam, Chem.–Eur. J., 2009, 15, 10039–10046 CrossRef CAS PubMed.
- H. Hirao, L. Que, W. Nam and S. Shaik, Chem.–Eur. J., 2008, 14, 1740–1756 CrossRef CAS PubMed.
- Most of these studies do not discuss the computed spin densities at the abstracting oxygen, so it is possible that the singlet state could be an open-shell singlet with significant unpaired spin density at oxygen.
- (a) D. Janardanan, Y. Wang, P. Schyman, L. Que and S. Shaik, Angew. Chem., Int. Ed., 2010, 49, 3342–3345 CrossRef CAS PubMed; (b) D. Janardanan, D. Usharani and S. Shaik, Angew. Chem., Int. Ed., 2012, 51, 4421–4425 CrossRef CAS PubMed.
- C. Geng, S. Ye and F. Neese, Angew. Chem., Int. Ed., 2010, 49, 5717–5720 CrossRef CAS PubMed.
- A. R. McDonald, Y. Guo, V. V. Vu, E. L. Bominaar, E. Munck and L. Que, Chem. Sci., 2012, 3, 1680–1693 RSC.
- (a) T. A. Betley and J. C. Peters, J. Am. Chem. Soc., 2004, 126, 6252–6254 CrossRef CAS PubMed; (b) C. Vogel, F. W. Heinemann, J. Sutter, C. Anthon and K. Meyer, Angew. Chem., Int. Ed., 2008, 47, 2681–2684 CrossRef CAS PubMed; (c) J. J. Scepaniak, M. D. Fulton, R. P. Bontchev, E. N. Duesler, M. L. Kirk and J. M. Smith, J. Am. Chem. Soc., 2008, 130, 10515–10517 CrossRef CAS PubMed.
- (a) C. T. Saouma and J. C. Peters, Coord. Chem. Rev., 2011, 255, 920–937 CrossRef CAS PubMed; (b) S. D. Brown, T. A. Betley and J. C. Peters, J. Am. Chem. Soc., 2003, 125, 322–323 CrossRef CAS PubMed; (c) J. J. Scepaniak, J. A. Young, R. P. Bontchev and J. M. Smith, Angew. Chem., Int. Ed., 2009, 48, 3158–3160 CrossRef CAS PubMed.
- (a) S. Shaik, W. Wu, K. Dong, L. Song and P. C. Hiberty, J. Phys. Chem. A, 2001, 105, 8226–8235 CrossRef CAS; (b) C. Isborn, D. A. Hrovat, W. T. Borden, J. M. Mayer and B. K. Carpenter, J. Am. Chem. Soc., 2005, 127, 5794–5795 CrossRef CAS PubMed.
- C. R. Waidmann, X. Zhou, E. A. Tsai, W. Kaminsky, D. A. Hrovat, W. T. Borden and J. M. Mayer, J. Am. Chem. Soc., 2009, 131, 4729–4743 CrossRef CAS PubMed.
- S. Hammes-Schiffer, Acc. Chem. Res., 2009, 42, 1881–1889 CrossRef CAS PubMed.
- (a) N. A. Eckert, S. Vaddadi, S. Stoian, R. J. Lachicotte, T. R. Cundari and P. L. Holland, Angew. Chem., Int. Ed., 2006, 45, 6868–6871 CrossRef CAS PubMed; (b) A. Gunay and K. H. Theopold, Chem. Rev., 2010, 110, 1060–1081 CrossRef CAS PubMed; (c) J. England, M. Martinho, E. R. Farquhar, J. R. Frisch, E. L. Bominaar, E. Münck and L. Que, Angew. Chem., Int. Ed., 2009, 48, 3622–3626 CrossRef CAS PubMed; (d) R. E. Cowley and P. L. Holland, Inorg. Chem., 2012, 51, 8352–8361 CrossRef CAS PubMed.
- J. T. Groves and T. E. Nemo, J. Am. Chem. Soc., 1983, 105, 6243–6248 CrossRef CAS.
- (a) A. Decker, J.-U. Rohde, E. J. Klinker, S. D. Wong, L. Que and E. I. Solomon, J. Am. Chem. Soc., 2007, 129, 15983–15996 CrossRef CAS PubMed; (b) S. Ye and F. Neese, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 1228–1233 CrossRef CAS PubMed.
- A. K. Vardhaman, P. Barman, S. Kumar, C. V. Sastri, D. Kumar and S. P. de Visser, Angew. Chem., Int. Ed., 2013, 52 DOI:10.1002/anie.201305370.
- S. Shaik, H. Hirao and D. Kumar, Acc. Chem. Res., 2007, 40, 532–542 CrossRef CAS PubMed.
- (a) P. Gütlich, A. Hauser and H. Spiering, Angew. Chem., Int. Ed., 1994, 33, 2024–2054 CrossRef; (b) M. Besora, J.-L. Carreón-Macendo, Á. Cimas and J. N. Harvey, in Advances in Inorganic Chemistry, ed. E. Rudi and D. H. Colin, Academic Press, 2009, vol. 61, pp. 573–623 Search PubMed; (c) M. Besora, J.-L. Carreón-Macedo, A. J. Cowan, M. W. George, J. N. Harvey, P. Portius, K. L. Ronayne, X.-Z. Sun and M. Towrie, J. Am. Chem. Soc., 2009, 131, 3583–3592 CrossRef CAS PubMed.
- J. I. Seeman, Chem. Rev., 1983, 83, 83–134 CrossRef CAS.
- R. Gupta, D. C. Lacy, E. L. Bominaar, A. S. Borovik and M. P. Hendrich, J. Am. Chem. Soc., 2012, 134, 9775–9784 CrossRef CAS PubMed.
- (a) Along the series HO–H, CH3O–H, HOO–H, PhO–H, the decreasing bond strengths17 are accompanied by increasing delocalization of the radical by hyperconjugation or conjugation; (b) J. S. Wright and K. U. Ingold, J. Chem. Educ., 2000, 77, 1062 CrossRef; (c) K. U. Ingold and G. A. DiLabio, Org. Lett., 2006, 8, 5923–5925 CrossRef CAS PubMed.
- (a) M. L. Neidig, A. Decker, O. W. Choroba, F. Huang, M. Kavana, G. R. Moran, J. B. Spencer and E. I. Solomon, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 12966–12973 CrossRef CAS PubMed; (b) J. S. Woertink, P. J. Smeets, M. H. Groothaert, M. A. Vance, B. F. Sels, R. A. Schoonheydt and E. I. Solomon, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 18908–18913 CrossRef CAS PubMed; (c) S. Ye and F. Neese, Curr. Opin. Chem. Biol., 2009, 13, 89–98 CrossRef CAS PubMed.
- There is also an HAT definition that requires only that e− and H+ be in the same bond in the reactant, see: M.-H. V. Huynh and T. J. Meyer, Chem. Rev., 2007, 107, 5004–5064 CrossRef CAS PubMed . This would make eqn (6) HAT in the forward direction but not in the reverse direction.
- (a) J. Rittle and M. T. Green, Science, 2010, 330, 933–937 CrossRef CAS PubMed; (b) S. Shaik, W. Lai, H. Chen and Y. Wang, Acc. Chem. Res., 2010, 43, 1154–1165 CrossRef CAS PubMed.
- (a) J. M. Mayer, D. A. Hrovat, J. L. Thomas and W. T. Borden, J. Am. Chem. Soc., 2002, 124, 11142–11147 CrossRef CAS PubMed; (b) G. A. DiLabio and E. R. Johnson, J. Am. Chem. Soc., 2007, 129, 6199–6203 CrossRef CAS PubMed.
- (a) J. P. Roth, S. Lovell and J. M. Mayer, J. Am. Chem. Soc., 2000, 122, 5486–5498 CrossRef CAS; (b) N. Iordanova, H. Decornez and S. Hammes-Schiffer, J. Am. Chem. Soc., 2001, 123, 3723–3733 CrossRef CAS PubMed.
- C. Li, D. Danovich and S. Shaik, Chem. Sci., 2012, 3, 1903–1918 RSC.
- P. J. Wagner, Y. Zhang and A. E. Puchalski, J. Phys. Chem., 1993, 97, 13368–13374 CrossRef CAS.
- X.-L. Sun, X.-R. Huang, J.-L. Li, R.-P. Huo and C.-C. Sun, J. Phys. Chem. A, 2012, 116, 1475–1485 CrossRef CAS PubMed.
- D. Janardanan, D. Usharani, H. Chen and S. Shaik, J. Phys. Chem. Lett., 2011, 2, 2610–2617 CrossRef CAS.
- S. A. Wilson, J. Chen, S. Hong, Y.-M. Lee, M. Clémancey, R. Garcia-Serres, T. Nomura, T. Ogura, J.-M. Latour, B. Hedman, K. O. Hodgson, W. Nam and E. I. Solomon, J. Am. Chem. Soc., 2012, 134, 11791–11806 CrossRef CAS PubMed.
- J. F. Hull, D. Balcells, E. L. O. Sauer, C. Raynaud, G. W. Brudvig, R. H. Crabtree and O. Eisenstein, J. Am. Chem. Soc., 2010, 132, 7605–7616 CrossRef CAS PubMed.
- A. Rosa and G. Ricciardi, Inorg. Chem., 2012, 51, 9833–9845 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2014 |
