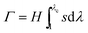Multi-scale multi-mechanism design of tough hydrogels: building dissipation into stretchy networks
Xuanhe
Zhao
*
Soft Active Materials Laboratory, Department of Mechanical Engineering and Materials Science, Duke University, Durham, North Carolina 27708, USA. E-mail: xz69@duke.edu
First published on 29th October 2013
Abstract
As swollen polymer networks in water, hydrogels are usually brittle. However, hydrogels with high toughness play critical roles in many plant and animal tissues as well as in diverse engineering applications. Here we review the intrinsic mechanisms of a wide variety of tough hydrogels developed over the past few decades. We show that tough hydrogels generally possess mechanisms to dissipate substantial mechanical energy but still maintain high elasticity under deformation. The integrations and interactions of different mechanisms for dissipating energy and maintaining elasticity are essential to the design of tough hydrogels. A matrix that combines various mechanisms is constructed for the first time to guide the design of next-generation tough hydrogels. We further highlight that a particularly promising strategy for the design is to implement multiple mechanisms across multiple length scales into nano-, micro-, meso-, and macro-structures of hydrogels.
1. Introduction
As aggregations of polymer networks and water, hydrogels are abundant in plant and animal tissues, with examples ranging from xylems and phloems to muscles and cartilages.1,2 Owing to their unique integration of solid and liquid properties, hydrogels are also extensively explored and widely used in diverse applications such as contact lenses, wound dressings, cosmetics, absorbents in waste managements, media for electrophoresis, scaffolds for tissue engineering, vehicles for drug delivery, coatings for medical devices, extracellular matrices for biological studies, packers in oilfields, and sensors and actuators in soft machines.3–16Natural hydrogels in plant and animal tissues usually need to be sufficiently robust to support mechanical loads from surrounding components. Similarly, many applications of hydrogels require them to maintain physical integrity over time, such as in contact lenses, wound dressings, drug delivery, and coatings; other applications even require hydrogels to carry significant mechanical loads and/or accommodate substantial deformation, such as in artificial load-bearing tissues, oilfield packers, and hydrogel-based actuators and soft machines.
Swelling of polymer networks in water usually reduces their mechanical strengths, leading to relatively brittle hydrogels. However, due to tremendous demands for tough hydrogels in various applications, intensive research has been going on to improve mechanical strengths of hydrogels over the last few decades. Many hydrogels have shown significant enhancements of fracture toughness over their conventional counterparts (Fig. 1). Examples include poly(vinyl alcohol) hydrogels with crystalline domains,17–19 double-network hydrogels,20,21 hydrogels with hybrid chemical and physical crosslinkers,21–27 hydrogels with crosslinkers of high functionalities,28–32 hydrogels with transformable domains,33,34 topological hydrogels with sliding crosslinkers,35–37 and tetra-arm polymer hydrogels.38,39 Many tough hydrogels have also been made biocompatible for biomedical applications40–44 or responsive to external stimuli for actuators and soft machines.45–48 A number of review articles have summarized the progress of various types of tough hydrogels.45,49–57
 | ||
| Fig. 1 Examples of hydrogels with enhanced mechanical strengths: (a) double-network hydrogel, reproduced with permission,20 (b) topological hydrogel with sliding crosslinkers, reproduced with permission,35 (c) hydrogel with nano-clay crosslinkers, reproduced with permission,32 (d) hydrogel with micro-sphere crosslinkers, reproduced with permission,31 (e) fibrin hydrogel with folded protein domains, reproduced with permission,33 (f) hydrogel with hybrid physical and chemical crosslinkers, reproduced with permission,21 and (g) fiber-reinforced hydrogel, reproduced with permission.130 | ||
Despite these successes, the developments of tough hydrogels have generally relied on an empirical and trial-and-error approach, whereas the intrinsic relations between various mechanisms for toughness enhancements have not been systematically discussed or explored.54,55,58 For instance, hydrogels with microscopic interpenetrating polymer networks20 and hydrogels with macroscopic fiber-reinforcements59 have both achieved impressive levels of fracture toughness. These hydrogels have very different compositions and structures and therefore different toughness-enhancement mechanisms at different length scales. However, it is not clear whether there exists a general principle underlying various toughness-enhancement mechanisms for hydrogels. Furthermore, the mechanical properties of existing tough hydrogels may still suffer from limitations. For example, some double-network hydrogels are susceptible to fatigue under cyclic loadings, due to the damage of polymer networks under large deformation, and there are substantial demands for new hydrogels with further enhanced mechanical properties, such as anti-fatigue hydrogels. Therefore, a general principle together with practical guidelines for the design of tough hydrogels will be of critical importance to the development of next-generation hydrogels as well as the fundamental understanding of soft materials.
The objectives of the current review are to: (i) present a general principle that underlies various toughness-enhancement mechanisms in existing tough hydrogels, (ii) provide a matrix of guidelines for the design of tough hydrogels, and (iii) propose new strategies for the development of next-generation hydrogels with extraordinary mechanical properties. Using the theory of dissipation-induced toughening,60–63 we will demonstrate that a general principle for the design of tough hydrogels is to implement mechanisms into hydrogels to dissipate significant amounts of mechanical energy under large deformation and to maintain their original configurations after deformation. While the developments of various tough hydrogels have indeed followed this general principle, we will show that different hydrogels have resorted to different mechanisms to dissipate mechanical energy or to maintain high elasticity. Consequently, a combination of the mechanisms for dissipating energy and maintaining elasticity naturally provides a matrix that can guide the design of nano-, micro-, meso-, and macro-structures of hydrogels to achieve high toughness. Thereafter, we will show that many possible combinations on the design matrix have not been explored for tough hydrogels. We will finally propose that integrating different mechanisms across multiple length scales represents a particularly promising strategy for the design of next-generation hydrogels with extraordinary mechanical properties.
2. General principle for the design of tough hydrogels
2.1. Fracture energy to characterize toughness of hydrogels
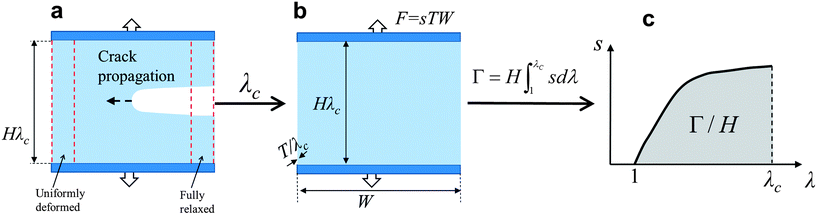
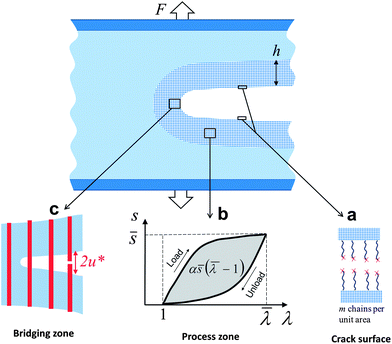
Since hydrogels generally undergo nonlinear and large deformation, the commonly used fracture toughness for linear elastic materials is generally not applicable to hydrogels. As a result, the toughness of hydrogels has been traditionally measured with a number of parameters, including Young's and shear modulus, swelling ratio, fracture stress in tension, compression and shear, fracture strain in tension, compression and shear, and fracture energy. A tough hydrogel should be able to sustain relatively high levels of both mechanical load (i.e., stress) and deformation (i.e., strain), regardless of defects in it. However, modulus only characterizes stiffness of hydrogels under small deformation; swelling ratio only gives hydrogels' water-retaining capacity; and fracture stress or strain only reflects the hydrogels' capability of sustaining either mechanical load or deformation, respectively. In addition, the measured values of fracture stress and strain usually depend on the nature of defects in hydrogels. In this regard, fracture energy is a more adequate parameter to characterize fracture toughness of hydrogels than others.64To clearly illustrate the importance of fracture energy, let us consider the classical pure-shear test for measuring fracture energy of soft materials such as elastomers and gels.65–68 As illustrated in Fig. 2, two identical pieces of a hydrogel are fabricated with the same thickness T, width W and height H, where W ≫ H ≫ T. Both pieces of samples are clamped along their long edges (i.e., along the width direction) with rigid plates. A notch with a length of ∼0.5W is introduced into the first sample, which is then gradually pulled to a stretch of λc times of its undeformed length until a crack begins to propagate from the notch (Fig. 2a). Thereafter, the second sample without notch is uniformly stretched to the same critical stretch λc, with the applied force F recorded as a function of the stretch λ (Fig. 2b). Since W ≫ H in the first sample, regions of the hydrogel far away from the crack tip are either fully relaxed or uniformly deformed. Therefore, propagation of the crack can be regarded as transition of a uniformly deformed region into a fully relaxed region with the same width (Fig. 2a). The energy required to advance the notch by a unit area at the undeformed state (i.e., the fracture energy) can be calculated as 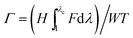 , where F and λ have been measured in the second sample (Fig. 2b). Furthermore, since the nominal stress along the applied force in the second sample is s = F/(WT), we can express the measured fracture energy of the hydrogel as65,66
, where F and λ have been measured in the second sample (Fig. 2b). Furthermore, since the nominal stress along the applied force in the second sample is s = F/(WT), we can express the measured fracture energy of the hydrogel as65,66
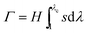 | (1) |
From eqn (1), it can be seen that a hydrogel with higher fracture energy tends to be able to sustain higher levels of both stress and strain, and therefore has a higher toughness. Furthermore, the measured fracture energy is independent of defects in hydrogels, because the size of the notch is much larger than any defect in the samples. Owing to these merits, fracture energy has been widely used as a critical parameter to characterize fracture toughness of hydrogels. It should be noted that many other methods can also be used to measure fracture energies of gels such as the trouser tear test65 and single-edge notch test,69 and the measured fracture energies with different methods are generally consistent with one another.21
Further considering the mechanistic origins of fracture energy, we can generally divide the fracture energy of a hydrogel into two parts, i.e.
| Γ = Γ0 + ΓD | (2) |
 | ||
| Fig. 3 The fracture energy of a hydrogel can be divided into two parts: (a) the intrinsic fracture energy for rupturing polymer chains along the crack plane and (b) the mechanical energy dissipated by loading and unloading the hydrogel in the process zone and (c) by pullout of fibers and fillers in the bridging zone.70 | ||
2.2. Intrinsic fracture energy of hydrogels
The intrinsic fracture energy is the energy required to break polymer chains lying across the crack plane by a unit area (Fig. 3a).66 According to the Lake–Thomas theory, the intrinsic fracture energy of a hydrogel can be calculated as66| Γ0 = Ufm | (3) |
| m = mdryC2/3 | (4) |
The intrinsic fracture energy for common elastomers (i.e., Ufmdry) is ∼50 J m−2.66 Therefore, for corresponding hydrogels with ∼90% water, the intrinsic fracture energy can be evaluated to be ∼10 J m−2, which is a relatively low value. Furthermore, since hydrogels are usually fabricated with dilute polymers which can rarely be crosslinked as tightly as in elastomers, eqn (4) tends to overestimate the intrinsic fracture energy of hydrogels. Therefore, hydrogels with only intrinsic fracture energy are usually very brittle.
2.3. Fracture energy due to mechanical dissipation
In many hydrogels, particularly tough hydrogels, the propagation of a crack will not only break polymer chains lying across the crack plane, but also induce dissipation of mechanical energy in regions around the crack. As illustrated in Fig. 3b, when a hydrogel with a notch is stretched, the region around the crack tip will be first loaded and then unloaded as the crack propagates. In addition, for hydrogels reinforced with meso-/macro-scale fibers or fillers, the fibers or fillers behind the crack tip will be fractured and pulled out upon crack extension (Fig. 3c). During these processes, mechanical dissipation may result from different mechanisms such as rupture of polymer chains or crosslinkers, transformation of chains or crosslinkers, fracture of fillers and fibers, and friction of fillers and fibers with hydrogel matrices. These mechanisms will be discussed in detail in Section 3.Inspired by previous studies on high-toughness ceramics,70 we divide the dissipation mechanisms of tough hydrogels into two categories: (i) stress–strain hysteresis of hydrogels deformed and undeformed in a process zone around the crack (Fig. 3b) and (ii) pullout of meso/macro-scale fibers or fillers in a bridging zone behind the crack tip (Fig. 3c).
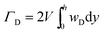 | (5) |
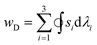 | (6) |
To illustrate the physical ideas of mechanical dissipation from the process zone, we will not carry out the numerical calculations in the current paper. Instead, we denote a typical hydrogel element at location yD of the process zone, so that 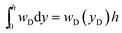 . Since the hydrogel around the crack tip is dominantly stretched in the direction along the applied force in pure shear tests, we further denote
. Since the hydrogel around the crack tip is dominantly stretched in the direction along the applied force in pure shear tests, we further denote ![[small lambda, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cc.gif) as the maximum stretch along the applied force in the typical hydrogel element (at yD) and
as the maximum stretch along the applied force in the typical hydrogel element (at yD) and ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) as the corresponding nominal stress in the typical element (Fig. 3b). Therefore, we can approximately express the fracture energy due to mechanical dissipation in the process zone as
as the corresponding nominal stress in the typical element (Fig. 3b). Therefore, we can approximately express the fracture energy due to mechanical dissipation in the process zone as
ΓD ≈ 2Vα![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) ( (![[small lambda, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cc.gif) − 1)h − 1)h | (7) |
![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) (
(![[small lambda, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cc.gif) − 1)].
− 1)].
From eqn (7), it is clear that a hydrogel that can sustain higher levels of stress and strain with larger stress–strain hysteresis and process zone will lead to higher fracture energy. For example, a hydrogel with V = 1, α ≈ 50%, ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) ≈ 1 MPa,
≈ 1 MPa, ![[small lambda, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cc.gif) ≈ 2 (i.e., 100% strain), and h ≈ 100 μm can readily achieve fracture energy ∼100 J m−2, much higher than the intrinsic fracture energy of hydrogels. Indeed, the fracture energies of many tough hydrogels have far exceeded 100 J m−2, due to higher values of
≈ 2 (i.e., 100% strain), and h ≈ 100 μm can readily achieve fracture energy ∼100 J m−2, much higher than the intrinsic fracture energy of hydrogels. Indeed, the fracture energies of many tough hydrogels have far exceeded 100 J m−2, due to higher values of ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) ,
, ![[small lambda, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cc.gif) , α and/or h.20,21,54,59
, α and/or h.20,21,54,59
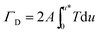 | (8) |
![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) as a typical value of the normal stress in the fiber or filler, we can approximately express the fracture energy due to mechanical dissipation in a bridging zone as
as a typical value of the normal stress in the fiber or filler, we can approximately express the fracture energy due to mechanical dissipation in a bridging zone asΓD ≈ 2A![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) u* u* | (9) |
Using typical values of A = 10%, ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) = 1 MPa, and u* = 500 μm–1 mm, we can evaluate the fracture energy from the bridging zone to be on the order of 100 J m−2, which is also much larger than the intrinsic fracture energy of hydrogels.
= 1 MPa, and u* = 500 μm–1 mm, we can evaluate the fracture energy from the bridging zone to be on the order of 100 J m−2, which is also much larger than the intrinsic fracture energy of hydrogels.
Notably, the simultaneous operation of the process zone and the bridging zone may generate fracture energy much higher than the summation of fracture energy from either zone individually, due to the coupling effects between the process zone and the bridging zone.70 We will discuss the coupling effects in Section 6.
2.4. Design principle for tough hydrogels: energy dissipation and high stretchability
Since the intrinsic fracture energies of hydrogels are relatively low (i.e., ∼10 J m−2) and almost impossible to be significantly increased, the enhancement of hydrogels' fracture energy will basically rely on mechanical energy dissipated in regions around the cracks. Therefore, in order to design a tough hydrogel, we need to implement one or multiple mechanisms into the hydrogel to dissipate a substantial amount of mechanical energy in the process and/or bridging zones upon crack propagation. From eqn (7) and (9), we can see that the mechanical dissipation requires the hydrogel's process zone to have high levels of stress (![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) ) and strain (
) and strain (![[small lambda, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cc.gif) ), large stress–strain hysteresis (α), and substantial size (h) (Fig. 3b), and/or requires its bridging zone to accommodate high traction (
), large stress–strain hysteresis (α), and substantial size (h) (Fig. 3b), and/or requires its bridging zone to accommodate high traction (![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) ) and large crack opening (u*) for pulling out fibers or fillers (Fig. 3c).
) and large crack opening (u*) for pulling out fibers or fillers (Fig. 3c).
Evidentially, the typical strain (![[small lambda, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cc.gif) ) and size (h) of the process zone and the crack opening (u*) in the bridging zone will monotonically increase with the stretchability of the hydrogel. Therefore, to achieve substantial mechanical dissipation, it is also critical for the hydrogel in the process and bridging zones to be able to sustain relatively high levels of deformation while maintaining integrity. In particular, since the stress levels in hydrogels usually cannot exceed a few megapascals, enhancing the stretchability of hydrogels is an effective way to increase their fracture energy and toughness. For example, the tough polyacrylamide-alginate hydrogel developed by Sun et al. can sustain a stretch of ∼17 even with a notch in the sample and therefore gives a fracture energy as high as ∼9000 J m−2.21 Besides the requirement of high stretchability in the process and bridging zones, the bulks of tough hydrogels also need to maintain their original shape and geometry after large deformation. Otherwise, the hydrogels can develop plastic deformation under loads (Fig. 4b), which is undesirable in applications of tough hydrogels. For example, many tough hydrogels have demonstrated full recovery of their original configurations after compressive strains over 90% (e.g., Fig. 1). Based on the above analyses, we can conclude that the general principle for the design of tough hydrogels is two-fold:
) and size (h) of the process zone and the crack opening (u*) in the bridging zone will monotonically increase with the stretchability of the hydrogel. Therefore, to achieve substantial mechanical dissipation, it is also critical for the hydrogel in the process and bridging zones to be able to sustain relatively high levels of deformation while maintaining integrity. In particular, since the stress levels in hydrogels usually cannot exceed a few megapascals, enhancing the stretchability of hydrogels is an effective way to increase their fracture energy and toughness. For example, the tough polyacrylamide-alginate hydrogel developed by Sun et al. can sustain a stretch of ∼17 even with a notch in the sample and therefore gives a fracture energy as high as ∼9000 J m−2.21 Besides the requirement of high stretchability in the process and bridging zones, the bulks of tough hydrogels also need to maintain their original shape and geometry after large deformation. Otherwise, the hydrogels can develop plastic deformation under loads (Fig. 4b), which is undesirable in applications of tough hydrogels. For example, many tough hydrogels have demonstrated full recovery of their original configurations after compressive strains over 90% (e.g., Fig. 1). Based on the above analyses, we can conclude that the general principle for the design of tough hydrogels is two-fold:
i. to dissipate significant amounts of mechanical energy in hydrogels upon crack propagation and
ii. to retain original configurations of hydrogels after large deformation.
While the developments of tough hydrogels have followed the general principle, different tough hydrogels have nevertheless relied on different mechanisms to dissipate mechanical energy and to maintain high elasticity. In Section 3 and 4, we will discuss various mechanisms for energy dissipation (Fig. 5) and maintaining elasticity (Fig. 6) in hydrogels, respectively.
In addition, it should be noted that if a hydrogel decreases its stress–strain hysteresis after the first or first few loading–unloading cycles, it will reduce the capability of energy dissipation (i.e., reduce α in eqn (7)) and decrease fracture energy over multiple cycles of large deformation (Fig. 4c). Therefore, in order to develop tough hydrogels that are also anti-fatigue under large deformation, the stress–strain hysteresis of the hydrogels need to be repeatable over multiple loading–unloading cycles (Fig. 4a).
3. Mechanisms for dissipating energy in tough hydrogels
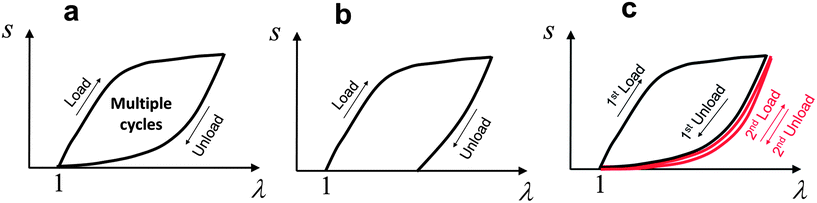
3.1. Fracture of polymer chains
Following the pioneering work by Gong et al. on double-network hydrogels,20,43,54,55,64,79–90 fracture of polymer chains has been widely used as a mechanism to dissipate mechanical energy in hydrogels (Fig. 5a). As a polymer chain is fractured, the mechanical energy stored in the chain is dissipated. According to the Lake–Thomas theory, the fracture energy due to rupture of polymer chains in a process zone can be evaluated as66| ΓD = 2UfNfh | (10) |
The chain-fracture mechanism requires that polymer chains in process zones can be effectively fractured. In order to promote fracture, a large number of polymer chains with relatively short lengths are usually incorporated into hydrogels. Even when the hydrogel is undeformed, these short chains can be highly stretched due to swelling of the hydrogel.72,91 As the hydrogel is deformed, the short chains can be ruptured to dissipate mechanical energy. Previous studies have shown that the chain-fracture mechanism can be implemented with a wide variety of highly crosslinked polymers, such as poly(2-acrylamido-2-methylpropanesulfonic acid),20 glycidyl methacrylated hyaluronan,92 poly(acrylic acid),93 agarose,94 poly(vinyl alcohol),95 gellan gum methacrylate,42 and methacrylated chondroitin sulfate.96 For example, Fig. 7a shows a damage zone around the crack in the poly(2-acrylamido-2-methylpropanesulfonic acid)–polyacrylamide double-network hydrogel, due to the fracture of polymer chains in the short-chain network of poly(2-acrylamido-2-methylpropanesulfonic acid).97,98
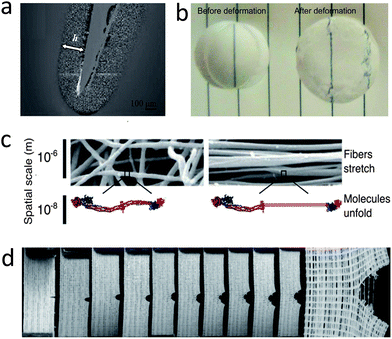 | ||
| Fig. 7 Examples of mechanisms for energy dissipation in tough hydrogels: (a) damage zone around a crack in a double-network hydrogel due to the fracture of the short-chain network, reproduced with permission,97 (b) plastic deformation in an ionically crosslinked hydrogel under compression due to reversible crosslinking of polymer chains from ionic crosslinkers, reproduced with permission,102 (c) unfolding of folded domains in a fibrin hydrogel under deformation, reproduced with permission,33 and (d) fracture and pullout of fibers upon crack propagation in a fiber-reinforced hydrogel, reproduced with permission.59 | ||
It should also be noted that fracture of polymer chains usually induces irreversible damage of polymer networks in hydrogels. As a result, the stress–strain hysteresis loops generally decrease over repeated deformation in tough hydrogels that use the chain-fracture mechanism (Fig. 4c).20 Therefore, tough hydrogels relying on the chain-fracture mechanism will be susceptible to fatigue under multiple cycles of large deformation, unless other mechanisms are introduced to heal the ruptured polymer chains.99–101
3.2. Reversible crosslinking of polymer chains
Physical crosslinkers in polymer networks are generally weaker than chemical crosslinkers based on covalent bonds. Polymer chains can be detached from physical crosslinkers under mechanical loads and/or agitations from environments such as temperature, pH, and ionic strength (Fig. 5b). The detachment relaxes stretched polymer chains, and therefore dissipates mechanical energy in the polymer network. Furthermore, these physical crosslinkers in hydrogels can usually be recovered after decrosslinking. The reversible crosslinking of polymer chains has been widely used as a mechanism to induce mechanical dissipation in hydrogels (Fig. 5b). The mechanical energy dissipated due to decrosslinking of polymer chains in a process zone can be evaluated as| ΓD = 2UdcNdch | (11) |
Physical crosslinkers commonly used for the reversible-crosslinking mechanism in hydrogels include ionic interaction,21,102–106 ligand–receptor interaction,107,108 hydrogen bond,31,109–115 and hydrophobic interaction.116–122 Since these physical crosslinkers in hydrogels can usually be recovered after decrosslinking, it is possible to maintain the stress–strain hysteresis of hydrogels the same over cyclic loadings, potentially leading to anti-fatigue hydrogels (Fig. 4a).26,115,123–126 On the other hand, since the recovered crosslinkers are usually not at their original locations, hydrogels that only use the reversible-crosslinking mechanism can deform plastically under loads (Fig. 4b). For example, Zhao et al. observed plastic deformation in ionically crosslinked alginate hydrogels under compression, but not in the covalently crosslinked ones (Fig. 7b).102 Therefore, when the reversible-crosslinking mechanism is used, it is critical to introduce another mechanism to maintain elasticity of hydrogels, which will be discussed in Section 4.
In addition, the reversible crosslinking of different types of crosslinkers usually occurs at different time scales. Therefore, hydrogels that use the reversible-crosslinking mechanism usually demonstrate rate-dependent viscoelasticity, which is commonly associated with the mechanical dissipation and toughening of these hydrogels.26 However, so far only a few measurements on fracture energies of tough hydrogels were carried out at different strain rates. Therefore, it is still a critical task to measure the capacity of existing reversible crosslinkers in dissipating mechanical energy under different strain rates. Such information will guide the design of viscoelastic hydrogels that can maintain high toughness under a required range of strain rates.
3.3. Transformation of domains in polymer chains or crosslinkers
Polymer chains and crosslinkers may contain certain domains that transform between different configurations under mechanical loads (Fig. 5c).127 During the transformation, mechanical energy can be dissipated. Furthermore, the transformation may also change the lengths of polymer chains and crosslinkers, and induce effects such as variation of swelling ratio or color change of the hydrogels.33,34 Examples of transformable domains include folded proteins and polysaccharides in biological polymers and mechanophores – molecular units that can be chemically activated by mechanical forces – in synthetic polymers.127–129 For example, Brown et al. demonstrated that fibrin hydrogels can sustain high stretches up to 2.7, owing to protein unfolding in fibrin fibers (Fig. 7c).33 The protein unfolding also induces expulsion of water, varying the swelling ratio of the hydrogel. As another example, Gossweiler et al. incorporated spiropyran mechanophores into polydimethylsiloxane elastomer matrices.34 Although elastomers instead of hydrogels were tested, Gossweiler et al. showed that mechanical deformation can activate spiropyran mechanophores, which not only dissipate mechanical energy but also change the elastomer's color from transparent into pure.Interestingly, while transformable domains are rarely incorporated into synthetic polymers, they exist in a wide variety of biological polymers, such as fibrin, collagen, silk, keratin, and polysaccharides.127 Although the fracture energy of biological hydrogels can reach relatively high values (e.g., 1000 J m−2 for cartilage), only a few tough hydrogels have been developed with biological polymers. Nevertheless, designing hydrogels based on biological polymers with transformable domains indeed represents a promising approach in the development of tough hydrogels.
3.4. Fracture and pullout of fibers or fillers
The dissipation mechanisms discussed above generally depend on molecular-scale nano-/micro-structures of polymer networks, and are generally applied in process zones of hydrogels. On the other hand, meso-/macro-scale fibers and fillers can also be embedded in a hydrogel matrix. Fracture and pullout of the fibers and fillers in a bridging zone in front of the crack can significantly dissipate mechanical energy in the hydrogel (see Fig. 5d and eqn (8) and (9)).59,75,130Examples of fibers and hydrogel matrices that use the fiber-pullout mechanism include polyurethane-fiber reinforced epoxy-amine hydrogel (Fig. 7d);59 polycaprolactone-fiber reinforced poly(ethylene glycol),75 agarose,76 and alginate–polyacrylamide130 hydrogels; and polyglycolic-acid-fiber reinforced agarose and fibrin hydrogels.77
4. Mechanisms for maintaining elasticity of tough hydrogels
In addition to energy dissipation, high stretchability is another critical property for hydrogels to achieve high fracture energy and toughness. In this section, we will discuss various mechanisms that enable stretchability and elasticity of hydrogels. The stretch limit of a polymer chain with n monomers is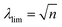 .131–133 Swelling a polymer network in water or polymer solution will pre-stretch polymer chains in the network. The effective stretch limit of a polymer chain in a hydrogel from the swollen state (as the reference state) to a deformed state can be expressed as131–133
.131–133 Swelling a polymer network in water or polymer solution will pre-stretch polymer chains in the network. The effective stretch limit of a polymer chain in a hydrogel from the swollen state (as the reference state) to a deformed state can be expressed as131–133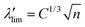 | (13) |
4.1. Interpenetration of long-chain networks
Polymer networks with relatively long polymer chains can be interlaced with other networks with relatively short chains on a molecular scale to form interpenetrating polymer networks. While the short-chain networks may be fractured or physically decrosslinked under deformation, the long-chain networks can still maintain high elasticity of the interpenetrating networks (Fig. 6a). Since 2003, Gong's group has interpenetrated different types of polymer networks, and found that long-chain networks are indeed critical components for various double-network hydrogels to achieve high toughness.20,43,54,55,64,79–88 Owing to the broad choices of polymers, interpenetration of long-chain networks has been widely used as a mechanism to achieve high elasticity of tough hydrogels. The most common candidates for the long-chain polymer networks include polyacrylamide,20,111 poly(N-isopropylacrylamide),112 poly(ethylene glycol),116 poly(N,N′-dimethylacrylamide),92,114 poly(acrylic acid),134,135 and gelatin.20,424.2. Hybrid physical and chemical crosslinkers
While decrosslinking of physically crosslinked networks dissipates mechanical energy, hydrogels with only physical crosslinkers can develop irreversible plastic deformation under mechanical loads (Fig. 4b and 7b). To maintain elasticity of hydrogels, chemical crosslinkers based on covalent bonds or other strong crosslinkers such as crystalline domains can be used to loosely crosslink polymers to give long-chain networks. Meanwhile, physical crosslinkers can be incorporated into the same polymer networks to increase the overall crosslinking density. The resultant hybrid-crosslinked networks enable hydrogels to maintain high elasticity when the networks are partially decrosslinked under large deformation (Fig. 6b).Owing to its simple fabrication, hybrid crosslinking has been widely used as a mechanism to maintain high elasticity of tough hydrogels (Fig. 6b). Polymer networks that enable the hybrid-crosslinking mechanism usually can be crosslinked both chemically and physically. Examples of polymer networks with hybrid crosslinkers for tough hydrogels include alginate,25,102 chitosan,22 and polyacrylamide with hydrophobic modification.117,119,136
4.3. High-functionality crosslinkers
Following Flory, we define the number of polymer chains that can be crosslinked by a crosslinker as the functionality of the crosslinker.131 Common physical and chemical crosslinkers usually have relatively low functionalities (e.g., less than 10), and there is usually a single polymer chain bridging between two adjacent common crosslinkers. When polymer chains are ruptured under deformation, the connections between crosslinkers are eliminated, potentially leading to fracture of the network. In order to achieve high elasticity of hydrogels, large crosslinkers with very high functionality (e.g., over 100) can be incorporated into polymer networks. In these networks, there are multiple polymer chains that connect two adjacent high-functionality crosslinkers, and these chains usually have non-uniform lengths. Therefore, as the polymer networks are deformed, relatively short chains may be ruptured or detached from the high-functionality crosslinkers but the long chains can still maintain the elasticity of the hydrogels (Fig. 6c).Examples of high-functionality crosslinkers used in tough hydrogels include crystalline domains in polymer networks such as poly(vinyl alcohol);17,18 exfoliated nano-clays that can crosslink various polymers such as polyacrylamide, poly(N-isopropylacrylamide) and poly(ethylene glycol);28–30 glassy spheres of poly(methyl methacrylate) that crosslink poly(methyl methacrylate)–poly(n-butyl acrylate) copolymers;137 microspheres made from mixtures of styrene, butyl acrylate, and acrylic acid;31 chitosan nanofibers that crosslink polyacrylamide;138 graphene oxide that crosslinks polyacrylamide;139,140 and lamellar bilayer structures of surfactants that crosslink polyacrylamide.124
4.4. Networks with long monodisperse polymer chains
Polymer networks are usually constituted of polydisperse polymer chains, due to the nature of polymerization. When such a polymer network is deformed, the shorter chains are more susceptible to rupture, which can initiate damage in the network. Although polymer networks with long polydisperse chains may still give relatively high stretchability, it may be more desirable to use networks with monodisperse chains to design tough hydrogels (Fig. 6d).To achieve polymer networks with monodisperse chains, Sakai et al. crosslinked tetrahedron-like macromonomers of poly(ethylene glycol) with well-defined sizes.38,39 The resultant poly(ethylene glycol) networks were proven to be extremely uniform by small-angle neutron scattering and light scattering measurements.141,142 As another example, Okumura and Ito developed a special crosslinker with the shape of eight, which not only interlocks two polymer chains but also can slide along the chains.35 When a polymer network with the sliding crosslinkers is deformed, polymer chains can automatically adjust their lengths due to relocation of crosslinkers to give relatively homogeneous networks under loads (Fig. 6d). Poly(ethylene glycol) hydrogels with sliding crosslinkers indeed gave very high swelling ratio and stretchability.
Notably, mechanisms for energy dissipation have not been implemented into polymer networks with monodisperse chains developed so far, as indicated by the negligible stress–strain hysteresis loops of these hydrogels.35–39
4.5. Meso-/macro-scale composites
The mechanisms discussed above generally rely on nano-/micro-structures of polymer networks to maintain high elasticity of hydrogels. On the other hand, meso-/macro-scale fibers and fillers can also be embedded in hydrogel matrices to form composites. As discussed in Section 3.4, the fracture and pullout of the fibers or fillers can dissipate mechanical energy in hydrogels. Furthermore, if the fibers or fillers are interwoven into three-dimensional networks, they can also maintain the elasticity of hydrogel composites under deformation (Fig. 6e).59 In addition, since the networks of fibers or fillers constrain the swelling or deswelling of hydrogels, they can also control water concentration in hydrogel composites.59 Examples of tough fiber-reinforced hydrogel composites have been discussed in Section 3.4.5. A design matrix for tough hydrogels
As discussed above, the general principle for the design of tough hydrogels is to implement mechanisms into hydrogels to dissipate mechanical energy and to maintain high elasticity. We have discussed various mechanisms for dissipating energy and maintaining elasticity of hydrogels in Sections 3 and 4, respectively. Combinations of the two sets of mechanisms naturally provide a matrix that guides the design of tough hydrogels (Table 1). A number of combinations on the design matrix have been intensively explored over the past few decades, which will be discussed in this section.5.1. Chain fracture/reversible crosslinking plus interpenetration of long-chain networks
From the design matrix (Table 1), it is clear that one common strategy to develop a tough hydrogel is to interpenetrate polymer networks with relatively short and long polymer chains. Under deformation, the short-chain networks can be fractured and/or physically decrosslinked to dissipate mechanical energy (Sections 3.1 and 3.2), while the long-chain networks will maintain the high elasticity of the hydrogels (Section 4.1).Gong et al. carried out pioneering work in developing various tough hydrogels by combining mechanisms of chain fracture and interpenetration of long-chain networks.20 For example, they interpenetrated a short-chain network of poly(2-acrylamido-2-methylpropanesulfonic acid) with a long-chain network of polyacrylamide. The resultant hydrogel gave a fracture energy over 1000 J m−2, owing to the rupture of poly(2-acrylamido-2-methylpropanesulfonic acid) and the high elasticity of polyacrylamide (Fig. 1a).20,54 Recently, Sun et al. combined mechanisms of reversible crosslinking and interpenetration of long-chain networks by interpenetrating ionically crosslinked alginate and covalently crosslinked polyacrylamide networks. Reversible crosslinking of the short-chain alginate and high elasticity of the long-chain polyacrylamide lead to a tough hydrogel with a fracture energy over 9000 J m−2 and a uniaxial stretch over 21 (Fig. 1f). Remarkably, the alginate–polyacrylamide hydrogel can partially recover its stress–strain hysteresis after large deformation, due to the recovery of ionic crosslinkers in alginate. Furthermore, a number of theoretical and computational models have been developed for tough hydrogels using combined mechanisms of chain fracture/reversible crosslinking and interpenetration of long-chain networks.61,62,72,143–145
5.2. Reversible crosslinking plus hybrid crosslinkers
Another commonly used strategy to design a tough hydrogel is based on hybrid physical and chemical crosslinkers. The chemical crosslinkers alone give relatively long polymer chains that maintain high elasticity of hydrogels (Section 4.2), while the physical crosslinkers enable reversible crosslinking of polymer chains to dissipate mechanical energy (Section 3.2).For example, Kong et al. compared the fracture toughness of ionically and covalently crosslinked alginate hydrogels, and found that the ionic hydrogel has much higher toughness than the covalent one.25 Zhao et al. later observed plastic deformation in ionic alginate hydrogels under compression, validating the reversible crosslinking of ionic crosslinkers which dissipated mechanical energy in the hydrogel (Fig. 7b).102 Kersey et al. incorporated metal–ligand complexes as weak reversible crosslinkers into a covalently crosslinked hydrogel, which significantly improved the fracture toughness of the hydrogel.24 Miquelard-Garnier et al. introduced hydrophobic groups into hydrogels to form weak crosslinkers, and found that the hydrogels' mechanical dissipation under deformation increased due to the dissociation of hydrophobic groups.146–148 Hybrid crosslinking based on hydrophobic interactions was also investigated by Abdurrahmanoglu et al. for tough hydrogels.117,119,136 Henderson et al. introduced ionic crosslinkers into a triblock copolymer hydrogel that was strongly crosslinked by glassy spheres.23 They found that ionic crosslinkers significantly increased fracture stress as well as stress–strain hysteresis of the hydrogel. Recently, Hui and Long have developed a theoretical model for tough and self-healable hydrogels that use combined mechanisms of reversible crosslinking and hybrid crosslinkers.149
5.3. Chain fracture/reversible crosslinking plus high-functionality crosslinkers
Another strategy to design a tough hydrogel is based on large crosslinkers with high functionalities. Multiple polymer chains can be attached to a high-functionality crosslinker via covalent bonds and/or physical interactions. Furthermore, the lengths of polymer chains connecting two adjacent crosslinkers are generally non-uniform. As the hydrogel is deformed, relatively short chains across crosslinkers can be ruptured or physically decrosslinked to dissipate mechanical energy (Sections 3.1 and 3.2), while relatively long chains can still bridge between the crosslinkers to maintain high elasticity of the hydrogel (Section 4.3).For example, in the pioneering work by Peppas, crystalline domains were introduced into poly(vinyl alcohol) using the freeze–thaw method to form high-functionality crosslinkers, which significantly enhance the toughness of hydrogels.17,18 Haraguchi and Takehisa and others used exfoliated nano-clays as high-functionality crosslinkers, on which multiple types of polymers such as polyacrylamide, poly(N-isopropylacrylamide), poly(ethylene glycol) can be crosslinked through hydrogen bonds, ionic interactions, or covalent bonds.28–30 Seitz et al. developed tough hydrogels based on poly(methyl methacrylate)–poly(n-butyl acrylate) copolymers, where the poly(methyl methacrylate) segments aggregate into glassy spheres as high-functionality crosslinkers.137
5.4. Pullout of fibers plus meso-/macro-scale composites
Fiber reinforcement is an emerging strategy to design tough hydrogels. Stretchy fiber networks embedded in hydrogel matrices can maintain the elasticity of hydrogels under deformation (Section 4.5), while the fracture and pullout of fibers in bridging zones of the hydrogels can dissipate mechanical energy (Section 3.4).For example, Agrawal et al. used a rapid prototyping technique to print polyurethane fibers into three-dimensional networks to reinforce an epoxy-amine hydrogel. The fracture energy of the fiber-refined hydrogel was measured to range from 3 to 12 kJ m−2, as the fiber density increased from 100 to 200 per inch.59 Moutos et al. weaved polyglycolic-acid fibers into three-dimensional networks to reinforce agarose and fibrin hydrogels.77 Thereafter, Liao et al. used woven polycaprolactone-fiber networks to reinforce an interpenetrating-network hydrogel based on alginate and polyacrylamide. Notably, multiple combinations of mechanisms were employed in Liao et al.'s hydrogel, including reversible crosslinking of alginate plus hybrid crosslinkers and pullout of fibers plus meso-scale composites.130
6. Future directions
6.1. New combinations of mechanisms
While a number of combinations on the design matrix have been intensively explored over the past few decades, there are still promising combinations that have not been well studied (Table 1). For example, Brown et al. showed that a combination of domain transformation and hybrid crosslinking improved the mechanical strength and stretchability of fibrin hydrogels.33 Since a wide variety of biological polymers can give domain transformations for mechanical dissipation, interpenetrating these polymers with long-chain networks or crosslinking them with high-functionality crosslinkers may result in tough hydrogels, which may also possess bioactivities due to the biopolymers used.As another example, polymer networks with long monodisperse polymer chains may be further crosslinked with reversible physical crosslinkers or interpenetrated with short-chain polymer networks. In this way, the uniform long-chain polymer networks will lead to high stretchability of the hydrogels while the reversible crosslinking or chain fracture dissipates mechanical energy, potentially resulting in tough hydrogels.
In addition, new mechanisms are being intensively developed for dissipating energy and maintaining high elasticity of hydrogels. These new mechanisms in combination with each other or with existing mechanisms can provide promising strategies for the design of future tough hydrogels (Table 1).
6. 2. Multi-scale multi-mechanism design for next-generation tough hydrogels
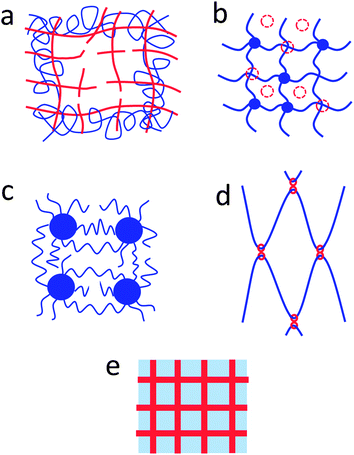
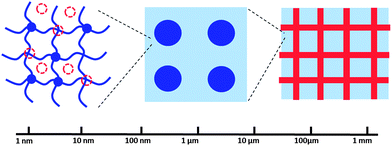
The mechanisms discussed in Sections 3, 4 and 5 are based on nano-, micro-, meso-, and macro-structures of hydrogels, which span length scales over multiple orders of magnitude (Fig. 8). The mechanisms of chain fracture, reversible crosslinking, interpenetration of long-chain networks, hybrid crosslinkers, and monodisperse chains are generally implemented at length scales between 1 nm and 100 nm. The size of transformable domains ranges from 10 nm to 1 μm, and that of high-functionality crosslinkers from 100 nm to 100 μm. Furthermore, fiber or filler reinforcements of hydrogels usually rely on meso-/macro-structures of hydrogels with length scales ranging from 1 μm to 1 mm (Fig. 8).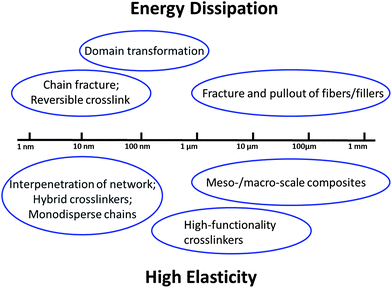 | ||
| Fig. 8 The mechanisms for dissipating mechanical energy and maintaining high elasticity of hydrogels span over multiple length scales ranging from nanometers to millimeters. | ||
Despite the diverse mechanisms discussed above (Table 1), tough hydrogels developed so far usually use a single pair of mechanisms to dissipate mechanical energy and maintain high elasticity of hydrogels. However, these mechanisms may become ineffective in many situations, deteriorating the hydrogels' toughness. For example, double-network hydrogels usually rely on the fracture of a short-chain network for energy dissipation and the interpenetration of a long-chain network for maintaining elasticity. However, if the short-chain network is already ruptured, the hydrogels' fracture energy can be significantly reduced. In fact, the toughness of poly(2-acrylamido-2-methylpropanesulfonic acid)–polyacrylamide hydrogel decreases drastically, as the poly(2-acrylamido-2-methylpropanesulfonic acid) network is ruptured. As another example, hydrogels with hybrid crosslinkers usually rely on reversible crosslinking of physical crosslinkers for energy dissipation and the chemically crosslinked networks to maintain elasticity. However, if the change of a solution's pH or ionic strength has eliminated those physical crosslinkers, the hybrid hydrogels will cease to be tough. Indeed, the alginate–polyacrylamide hydrogel with hybrid crosslinkers will significantly reduce its toughness, if the Ca2+ crosslinkers for alginate is chelated by EDTA.
The next-generation tough hydrogels should be able to maintain high toughness in various environments and under various loading conditions. However, as discussed above, hydrogels that rely on a single pair of mechanisms may lose their toughness due to environmental and loading effects. A promising strategy to design next-generation tough hydrogels is to integrate multiple pairs of mechanisms across multiple length scales into a hydrogel (Fig. 9). In this way, if one pair of mechanisms becomes ineffective, other pairs can still maintain high toughness of the hydrogel. For example, a tough hydrogel that integrates fiber-reinforcement at the macro-/meso-scale, high-functionality crosslinkers at the micro-scale, and hybrid crosslinkers at the nano-scale may give consistently high fracture energy in various environments and under various loading conditions (Fig. 9). Recently, Liao et al. integrated meso-scale fiber-reinforcement and nano-scale hybrid crosslinkers into a tough hydrogel. Despite the great promise, the multi-scale multi-mechanism strategy for the design of tough hydrogels is still in its initial stage and requires further research.
Furthermore, the fracture energy of a hydrogel based on multiple mechanisms may also be much higher than the summation of fracture energy for individual mechanisms, due to the coupling between different mechanisms. For example, the pullout of fibers can significantly deform a hydrogel along the fibers, potentially dissipating more mechanical energy in the hydrogel matrix than in the same hydrogel without fibers. In fact, the coupling effects between process zones and bridging zones have been widely used to enhance toughness of ceramics.70 Similarly, the coupling between various mechanisms in hydrogels may play an important role in the design of next-generation tough hydrogels.
Last but not least, in contrast to the extensive experimental work on various types of tough hydrogels (Table 1), theoretical models developed so far for tough hydrogels have been limited to those with interpenetrating networks61,62,72,143–145 and hybrid crosslinkers.149 However, multi-scale predictive models can greatly facilitate the design and development of next-generation tough hydrogels based on various mechanisms. For example, atomistic or molecular-dynamic models may be used to predict the values of physical parameters such as Uf in eqn (10) and Udc in eqn (11). Based on these parameters predicted by the nano/micro-scale models, meso/macro-scale models such as finite-element models72 can be used to further predict the energy dissipation and fracture process of tough hydrogels by calculating parameters such as α and h in eqn (7). Furthermore, mechanism-based physical models can also provide a fundamental understanding of the coupling effects between different pairs of mechanisms in tough hydrogels, rationally guiding the multi-scale multi-mechanism design of next-generation tough hydrogels.
7. Summary
While hydrogels have promising applications in diverse fields, the scope of hydrogel applications is often severely limited by their relatively low mechanical strengths. Over the last few decades, substantial progress has been made to develop hydrogels with high mechanical toughness. As a result, the fracture energy of various hydrogels has been enhanced from tens to thousands of joules per meter square, potentially excelling the fracture energy of tough natural hydrogels such as cartilage.This review is aimed at elucidating the fundamental principle and mechanisms for toughness enhancement in various hydrogels, and proposing strategies for the design of future tough hydrogels. A general principle that underlies the development of tough hydrogels is to implement mechanisms into hydrogels to dissipate significant amounts of mechanical energy under large deformation and to maintain their original configurations after deformation. The mechanisms for dissipating mechanical energies in hydrogels include fracture of polymer chains, reversible crosslinking of polymer chains, domain transformation in polymers or crosslinkers, and pullout of fibers or fillers, and the mechanisms for maintaining high elasticity of hydrogels include interpenetration of long-chain networks, hybrid crosslinkers, high-functionality crosslinkers, networks with long monodisperse chains, and meso-/macro-scale composites. Combinations of the two sets of mechanisms provide a matrix that can guide the design of next-generation tough hydrogels. A particularly promising strategy for the design is to implement multiple pairs of mechanisms across multiple length scales into nano-, micro-, meso-, and macro-structures of hydrogels.
Acknowledgements
The work was supported by NSF CAREER Award (CMMI-1253495), NSF Triangle MRSEC (DMR-1121107), NIH Grant (UH2 TR000505), NSF Grant (CMMI-1200515), and ONR Grant (N000141310828).References
- M. A. Zwieniecki, P. J. Melcher and N. M. Holbrook, Science, 2001, 291, 1059–1062 CrossRef CAS PubMed.
- V. C. Mow, S. C. Kuei, W. M. Lai and C. G. Armstrong, J. Biomech. Eng., 1980, 102, 73–84 CrossRef CAS.
- N. A. Peppas, J. Z. Hilt, A. Khademhosseini and R. Langer, Adv. Mater., 2006, 18, 1345–1360 CrossRef CAS.
- K. Y. Lee and D. J. Mooney, Chem. Rev., 2001, 101, 1869–1879 CrossRef CAS PubMed.
- J. L. Drury and D. J. Mooney, Biomaterials, 2003, 24, 4337–4351 CrossRef CAS.
- J. Kopecek, J. Polym. Sci., Part A: Polym. Chem., 2009, 47, 5929–5946 CrossRef CAS PubMed.
- R. Yoshida, Curr. Org. Chem., 2005, 9, 1617–1641 CrossRef CAS.
- J. J. Schmidt, J. Rowley and H. J. Kong, J. Biomed. Mater. Res., Part A, 2008, 87, 1113–1122 CrossRef PubMed.
- P. Calvert, MRS Bull., 2008, 33, 207–212 CrossRef.
- T. Murosaki, T. Noguchi, K. Hashimoto, A. Kakugo, T. Kurokawa, J. Saito, Y. M. Chen, H. Furukawa and J. P. Gong, Biofouling, 2009, 25, 657–666 CrossRef CAS PubMed.
- D. Seliktar, Science, 2012, 336, 1124–1128 CrossRef CAS PubMed.
- P. Calvert, Adv. Mater., 2009, 21, 743–756 CrossRef CAS.
- L. Dong, A. K. Agarwal, D. J. Beebe and H. Jiang, Nature, 2006, 442, 551–554 CrossRef CAS PubMed.
- S. Cai, Y. Lou, P. Ganguly, A. Robisson and Z. Suo, J. Appl. Phys., 2010, 107, 103535 CrossRef PubMed.
- G. Lewis, J. Biomed. Mater. Res., Part B, 2012, 100, 1702–1720 CrossRef PubMed.
- W. Hong, X. Zhao, J. Zhou and Z. Suo, J. Mech. Phys. Solids, 2008, 56, 1779–1793 CrossRef CAS PubMed.
- N. A. Peppas and E. W. Merrill, J. Polym. Sci., Part A: Polym. Chem., 1976, 14, 441–457 CAS.
- N. A. Peppas and E. W. Merrill, J. Biomed. Mater. Res., 1977, 11, 423–434 CrossRef CAS PubMed.
- S. R. Stauffer and N. A. Peppas, Polymer, 1992, 33, 3932–3936 CrossRef CAS.
- J. P. Gong, Y. Katsuyama, T. Kurokawa and Y. Osada, Adv. Mater., 2003, 15, 1155–1158 CrossRef CAS.
- J.-Y. Sun, X. Zhao, W. R. K. Illeperuma, O. Chaudhuri, K. H. Oh, D. J. Mooney, J. J. Vlassak and Z. Suo, Nature, 2012, 489, 133–136 CrossRef CAS PubMed.
- J. Berger, M. Reist, J. M. Mayer, O. Felt, N. A. Peppas and R. Gurny, Eur. J. Pharm. Biopharm., 2004, 57, 19–34 CrossRef CAS.
- K. J. Henderson, T. C. Zhou, K. J. Otim and K. R. Shull, Macromolecules, 2010, 43, 6193–6201 CrossRef CAS.
- F. R. Kersey, D. M. Loveless and S. L. Craig, J. R. Soc., Interface, 2007, 4, 373–380 CrossRef CAS PubMed.
- H. J. Kong, E. Wong and D. J. Mooney, Macromolecules, 2003, 36, 4582–4588 CrossRef CAS.
- T. L. Sun, T. Kurokawa, S. Kuroda, A. B. Ihsan, T. Akasaki, K. Sato, M. A. Haque, T. Nakajima and J. P. Gong, Nat. Mater., 2013, 12, 932 CrossRef CAS PubMed.
- K. R. Shull, Nature, 2012, 489, 36–37 CrossRef CAS PubMed.
- K. Haraguchi and T. Takehisa, Adv. Mater., 2002, 14, 1120–1124 CrossRef CAS.
- Q. Wang, J. L. Mynar, M. Yoshida, E. Lee, M. Lee, K. Okuro, K. Kinbara and T. Aida, Nature, 2010, 463, 339–343 CrossRef CAS PubMed.
- K. Haraguchi and H. J. Li, Angew. Chem., Int. Ed., 2005, 44, 6500–6504 CrossRef CAS PubMed.
- T. Huang, H. Xu, K. Jiao, L. Zhu, H. R. Brown and H. Wang, Adv. Mater., 2007, 19, 1622–1626 CrossRef CAS.
- K. Haraguchi, T. Takehisa and S. Fan, Macromolecules, 2002, 35, 10162–10171 CrossRef CAS.
- A. E. X. Brown, R. I. Litvinov, D. E. Discher, P. K. Purohit and J. W. Weisel, Science, 2009, 325, 741–744 CrossRef CAS PubMed.
- G. Gossweiler, Q. Wang, X. Zhao and S. Craig, 2013, in preparation.
- Y. Okumura and K. Ito, Adv. Mater., 2001, 13, 485–487 CrossRef CAS.
- K. Ito, Polym. J., 2007, 39, 489–499 CrossRef CAS.
- K. Ito, Curr. Opin. Solid State Mater. Sci., 2010, 14, 28–34 CrossRef CAS PubMed.
- T. Sakai, T. Matsunaga, Y. Yamamoto, C. Ito, R. Yoshida, S. Suzuki, N. Sasaki, M. Shibayama and U. I. Chung, Macromolecules, 2008, 41, 5379–5384 CrossRef CAS.
- T. Sakai, Y. Akagi, T. Matsunaga, M. Kurakazu, U. Chung and M. Shibayama, Macromol. Rapid Commun., 2010, 31, 1954–1959 CrossRef CAS PubMed.
- Y. Tanabe, K. Yasuda, C. Azuma, H. Taniguro, S. Onodera, A. Suzuki, Y. M. Chen, J. P. Gong and Y. Osada, J. Mater. Sci.: Mater. Med., 2008, 19, 1379–1387 CrossRef CAS PubMed.
- K. Yasuda, N. Kitamura, J. P. Gong, K. Arakaki, H. J. Kwon, S. Onodera, Y. M. Chen, T. Kurokawa, F. Kanaya, Y. Ohmiya and Y. Osada, Macromol. Biosci., 2009, 9, 307–316 CrossRef CAS PubMed.
- H. Shin, B. D. Olsen and A. Khademhosseini, Biomaterials, 2012, 33, 3143–3152 CrossRef CAS PubMed.
- K. Yasuda, J. P. Gong, Y. Katsuyama, A. Nakayama, Y. Tanabe, E. Kondo, M. Ueno and Y. Osada, Biomaterials, 2005, 26, 4468–4475 CrossRef CAS PubMed.
- H. Yin, T. Akasaki, T. L. Sun, T. Nakajima, T. Kurokawa, T. Nonoyama, T. Taira, Y. Saruwatari and J. P. Gong, J. Mater. Chem. B, 2013, 1, 3685–3693 RSC.
- A. Bin Imran, T. Seki and Y. Takeoka, Polym. J., 2010, 42, 839–851 CrossRef CAS.
- L. Tang, W. G. Liu and G. P. Liu, Adv. Mater., 2010, 22, 2652–2656 CrossRef CAS PubMed.
- R. C. Fei, J. T. George, J. Park, A. K. Means and M. A. Grunlan, Soft Matter, 2013, 9, 2912–2919 RSC.
- M. A. C. Stuart, W. T. S. Huck, J. Genzer, M. Mueller, C. Ober, M. Stamm, G. B. Sukhorukov, I. Szleifer, V. V. Tsukruk, M. Urban, F. Winnik, S. Zauscher, I. Luzinov and S. Minko, Nat. Mater., 2010, 9, 101–113 CrossRef PubMed.
- D. Myung, D. Waters, M. Wiseman, P. E. Duhamel, J. Noolandi, C. N. Ta and C. W. Frank, Polym. Adv. Technol., 2008, 19, 647–657 CrossRef CAS PubMed.
- J. A. Johnson, N. J. Turro, J. T. Koberstein and J. E. Mark, Prog. Polym. Sci., 2010, 35, 332–337 CrossRef CAS PubMed.
- K. Haraguchi, Polym. J., 2011, 43, 223–241 CrossRef CAS.
- M. Shibayama, Soft Matter, 2012, 8, 8030–8038 RSC.
- M. A. Haque, T. Kurokawa and J. P. Gong, Polymer, 2012, 53, 1805–1822 CrossRef CAS PubMed.
- J. P. Gong, Soft Matter, 2010, 6, 2583–2590 RSC.
- Y. Tanaka, J. P. Gong and Y. Osada, Prog. Polym. Sci., 2005, 30, 1–9 CrossRef CAS PubMed.
- S. Naficy, H. R. Brown, J. M. Razal, G. M. Spinks and P. G. Whitten, Aust. J. Chem., 2011, 64, 1007–1025 CrossRef CAS.
- C. W. Peak, J. J. Wilker and G. Schmidt, Colloid Polym. Sci., 2013, 291, 2031–2047 CAS.
- C. M. Hassan and N. A. Peppas, in Biopolymers/Pva Hydrogels/Anionic Polymerisation Nanocomposites, ed. A. Abe, 2000, vol. 153, pp. 37–65 Search PubMed.
- A. Agrawal, N. Rahbar and P. D. Calvert, Acta Biomater., 2013, 9, 5313–5318 CrossRef CAS PubMed.
- R. M. McMeeking and A. G. Evans, J. Am. Ceram. Soc., 1982, 65, 242–246 CrossRef.
- H. R. Brown, Macromolecules, 2007, 40, 3815–3818 CrossRef CAS.
- Y. Tanaka, Europhys. Lett., 2007, 78, 56005 CrossRef.
- G. R. Irwin, J. Appl. Mech., 1957, 24, 361 Search PubMed.
- Y. Tanaka, R. Kuwabara, Y. H. Na, T. Kurokawa, J. P. Gong and Y. Osada, J. Phys. Chem. B, 2005, 109, 11559–11562 CrossRef CAS PubMed.
- R. S. Rivlin and A. G. Thomas, J. Polym. Sci., 1953, 10, 291–318 CrossRef CAS.
- G. J. Lake and A. G. Thomas, Proc. R. Soc. London, Ser. A, 1967, 300, 108–119 CrossRef CAS.
- T. Baumberger, C. Caroli and D. Martina, Nat. Mater., 2006, 5, 552–555 CrossRef CAS PubMed.
- T. Baumberger, C. Caroli and D. Martina, Eur. Phys. J. E: Soft Matter Biol. Phys., 2006, 21, 81–89 CrossRef CAS PubMed.
- W. C. Lin, W. Fan, A. Marcellan, D. Hourdet and C. Creton, Macromolecules, 2010, 43, 2554–2563 CrossRef CAS.
- A. G. Evans, J. Am. Ceram. Soc., 1990, 73, 187–206 CrossRef CAS.
- W. Hong, Z. Liu and Z. Suo, Int. J. Solids Struct., 2009, 46, 3282–3289 CrossRef CAS PubMed.
- X. Zhao, J. Mech. Phys. Solids, 2012, 60, 319–332 CrossRef CAS PubMed.
- X. Wang and W. Hong, Soft Matter, 2012, 8, 8171–8178 RSC.
- W. Hong and X. Wang, J. Mech. Phys. Solids, 2013, 61, 1281–1294 CrossRef CAS PubMed.
- J. Coburn, M. Gibson, P. A. Bandalini, C. Laird, H. Q. Mao, L. Moroni, D. Seliktar and J. Elisseeff, Smart Structures and Systems, 2011, 7, 213–222 CrossRef.
- J. Jang, H. Oh, J. Lee, T. H. Song, Y. H. Jeong and D. W. Cho, Appl. Phys. Lett., 2013, 102, 211914 CrossRef PubMed.
- F. T. Moutos, L. E. Freed and F. Guilak, Nat. Mater., 2007, 6, 162–167 CrossRef CAS PubMed.
- A. G. Evans and R. M. McMeeking, Acta Metall., 1986, 34, 2435–2441 CrossRef.
- Y. H. Na, T. Kurokawa, Y. Katsuyama, H. Tsukeshiba, J. P. Gong, Y. Osada, S. Okabe, T. Karino and M. Shibayama, Macromolecules, 2004, 37, 5370–5374 CrossRef CAS.
- A. Nakayama, A. Kakugo, J. P. Gong, Y. Osada, M. Takai, T. Erata and S. Kawano, Adv. Funct. Mater., 2004, 14, 1124–1128 CrossRef CAS.
- D. Kaneko, T. Tada, T. Kurokawa, J. P. Gong and Y. Osada, Adv. Mater., 2005, 17, 535–538 CrossRef CAS.
- H. Tsukeshiba, M. Huang, Y. H. Na, T. Kurokawa, R. Kuwabara, Y. Tanaka, H. Furukawa, Y. Osada and J. P. Gong, J. Phys. Chem. B, 2005, 109, 16304–16309 CrossRef CAS PubMed.
- Y. H. Na, Y. Tanaka, Y. Kawauchi, H. Furukawa, T. Sumiyoshi, J. P. Gong and Y. Osada, Macromolecules, 2006, 39, 4641–4645 CrossRef CAS.
- M. Huang, H. Furukawa, Y. Tanaka, T. Nakajima, Y. Osada and J. P. Gong, Macromolecules, 2007, 40, 6658–6664 CrossRef CAS.
- R. E. Webber, C. Creton, H. R. Brown and J. P. Gong, Macromolecules, 2007, 40, 2919–2927 CrossRef CAS.
- T. Tominaga, V. R. Tirumala, S. Lee, E. K. Lin, J. P. Gong and W.-L. Wu, J. Phys. Chem. B, 2008, 112, 3903–3909 CrossRef CAS PubMed.
- T. Nakajima, H. Furukawa, Y. Tanaka, T. Kurokawa, Y. Osada and J. P. Gong, Macromolecules, 2009, 42, 2184–2189 CrossRef CAS.
- T. Tominaga, V. R. Tirumala, E. K. Lin, J. P. Gong, H. Furukawa, Y. Osada and W. L. Wu, Polymer, 2007, 48, 7449–7454 CrossRef CAS PubMed.
- T. Nakajima, Y. Fukuda, T. Kurokawa, T. Sakai, U.-i. Chung and J. P. Gong, ACS Macro Lett., 2013, 2, 518–521 CrossRef CAS.
- T. Nakajima, T. Kurokawa, S. Ahmed, W.-l. Wu and J. P. Gong, Soft Matter, 2013, 9, 1955–1966 RSC.
- D. Myung, W. Koh, J. Ko, Y. Hu, M. Carrasco, J. Noolandi, C. N. Ta and C. W. Frank, Polymer, 2007, 48, 5376–5387 CrossRef CAS PubMed.
- L. Weng, A. Gouldstone, Y. Wu and W. Chen, Biomaterials, 2008, 29, 2153–2163 CrossRef CAS PubMed.
- T. Y. Dai, X. T. Qing, Y. Lu and Y. Y. Xia, Polymer, 2009, 50, 5236–5241 CrossRef CAS PubMed.
- B. J. DeKosky, N. H. Dormer, G. C. Ingavle, C. H. Roatch, J. Lomakin, M. S. Detamore and S. H. Gehrke, Tissue Eng., Part C, 2010, 16, 1533–1542 CrossRef CAS PubMed.
- X. Y. Zhang, X. L. Guo, S. G. Yang, S. X. Tan, X. F. Li, H. J. Dai, X. L. Yu, X. L. Zhang, N. Weng, B. Jian and J. Xu, J. Appl. Polym. Sci., 2009, 112, 3063–3070 CrossRef CAS.
- T. C. Suekama, J. Hu, T. Kurokawa, J. P. Gong and S. H. Gehrke, ACS Macro Lett., 2013, 2, 137–140 CrossRef CAS.
- Q. M. Yu, Y. Tanaka, H. Furukawa, T. Kurokawa and J. P. Gong, Macromolecules, 2009, 42, 3852–3855 CrossRef CAS.
- S. M. Liang, Z. L. Wu, J. Hu, T. Kurokawa, Q. M. Yu and J. P. Gong, Macromolecules, 2011, 44, 3016–3020 CrossRef CAS.
- P. Cordier, F. Tournilhac, C. Soulie-Ziakovic and L. Leibler, Nature, 2008, 451, 977–980 CrossRef CAS PubMed.
- S. R. White, N. R. Sottos, P. H. Geubelle, J. S. Moore, M. R. Kessler, S. R. Sriram, E. N. Brown and S. Viswanathan, Nature, 2001, 409, 794–797 CrossRef CAS PubMed.
- A. B. W. Brochu, S. L. Craig and W. M. Reichert, J. Biomed. Mater. Res., Part A, 2011, 96, 492–506 CrossRef PubMed.
- X. Zhao, N. Huebsch, D. J. Mooney and Z. Suo, J. Appl. Phys., 2010, 107, 63509 CrossRef PubMed.
- Z. Zhang, T. Chao and S. Y. Jiang, J. Phys. Chem. B, 2008, 112, 5327–5332 CrossRef CAS PubMed.
- W. Yang, H. Furukawa and J. P. Gong, Adv. Mater., 2008, 20, 4499–4503 CrossRef CAS.
- T. Friedrich, B. Tieke, F. J. Stadler and C. Bailly, Soft Matter, 2011, 7, 6590–6597 RSC.
- J. N. Hunt, K. E. Feldman, N. A. Lynd, J. Deek, L. M. Campos, J. M. Spruell, B. M. Hernandez, E. J. Kramer and C. J. Hawker, Adv. Mater., 2011, 23, 2327–2331 CrossRef CAS PubMed.
- G. I. Bell, Science, 1978, 200, 618–627 CAS.
- K. Y. Lee, H. J. Kong, R. G. Larson and D. J. Mooney, Adv. Mater., 2003, 15, 1828–1832 CrossRef CAS.
- J. K. Hao and R. A. Weiss, Polymer, 2013, 54, 2174–2182 CrossRef CAS PubMed.
- S. M. Liang, J. J. Wu, H. F. Tian, L. N. Zhang and J. Xu, ChemSusChem, 2008, 1, 558–563 CrossRef CAS PubMed.
- Y. Hagiwara, A. Putra, A. Kakugo, H. Furukawa and J. P. Gong, Cellulose, 2010, 17, 93–101 CrossRef CAS.
- C. Y. Chang, K. Han and L. N. Zhang, Polym. Adv. Technol., 2011, 22, 1329–1334 CrossRef CAS.
- S. Naficy, J. M. Razal, P. G. Whitten, G. G. Wallace and G. M. Spinks, J. Polym. Sci., Part B: Polym. Phys., 2012, 50, 423–430 CrossRef CAS.
- C. Azuma, K. Yasuda, Y. Tanabe, H. Taniguro, F. Kanaya, A. Nakayama, Y. M. Chen, J. P. Gong and Y. Osada, J. Biomed. Mater. Res., Part A, 2007, 81, 373–380 CrossRef PubMed.
- J. L. Zhang, N. Wang, W. G. Liu, X. L. Zhao and W. Lu, Soft Matter, 2013, 9, 6331–6337 RSC.
- D. Myung, W. U. Koh, J. M. Ko, Y. Hu, M. Carrasco, J. Noolandi, C. N. Ta and C. W. Frank, Polymer, 2007, 48, 5376–5387 CrossRef CAS PubMed.
- D. C. Tuncaboylu, M. Sari, W. Oppermann and O. Okay, Macromolecules, 2011, 44, 4997–5005 CrossRef CAS.
- J. Yang, F. K. Shi, C. Gong and X. M. Xie, J. Colloid Interface Sci., 2012, 381, 107–115 CrossRef CAS PubMed.
- S. Abdurrahmanoglu, V. Can and O. Okay, Polymer, 2009, 50, 5449–5455 CrossRef CAS PubMed.
- W. B. Li, H. Y. An, Y. Tan, C. G. Lu, C. Liu, P. C. Li, K. Xu and P. X. Wang, Soft Matter, 2012, 8, 5078–5086 RSC.
- S. Abdurrahmanoglu, M. Cilingir and O. Okay, Polymer, 2011, 52, 694–699 CrossRef CAS PubMed.
- G. Q. Jiang, C. Liu, X. L. Liu, Q. R. Chen, G. H. Zhang, M. Yang and F. Q. Liu, Polymer, 2010, 51, 1507–1515 CrossRef CAS PubMed.
- T. Bai, P. Zhang, Y. J. Han, Y. A. Liu, W. G. Liu, X. L. Zhao and W. Lu, Soft Matter, 2011, 7, 2825–2831 RSC.
- M. A. Haque, T. Kurokawa, G. Kamita and J. P. Gong, Macromolecules, 2011, 44, 8916–8924 CrossRef CAS.
- M. A. Haque, T. Kurokawa and J. P. Gong, Soft Matter, 2012, 8, 8008–8016 RSC.
- A. Bin Ihsan, T. L. Sun, S. Kuroda, M. A. Haque, T. Kurokawa, T. Nakajima and J. P. Gong, J. Mater. Chem. B, 2013, 1, 4555–4562 RSC.
- A. Miserez and P. A. Guerette, Chem. Soc. Rev., 2013, 42, 1973–1995 RSC.
- D. A. Davis, A. Hamilton, J. Yang, L. D. Cremar, D. Van Gough, S. L. Potisek, M. T. Ong, P. V. Braun, T. J. Martinez, S. R. White, J. S. Moore and N. R. Sottos, Nature, 2009, 459, 68–72 CrossRef CAS PubMed.
- A. L. Black, J. A. Orlicki and S. L. Craig, J. Mater. Chem., 2011, 21, 8460–8465 RSC.
- I.-C. Liao, F. T. Moutos, B. T. Estes, X. Zhao and F. Guilak, Adv. Funct. Mater., 2013, 47, 5833–5839 CrossRef.
- P. J. Flory, Principles of Polymer Chemistry, Cornell University Press, 1953 Search PubMed.
- P.-G. d. Gennes, Scaling Concepts in Polymer Physics, Cornell University Press, 1979 Search PubMed.
- M. Rubinstein and R. H. Colby, Polymer Physics, Oxford University Press, 2003 Search PubMed.
- H. R. Lin, M. H. Ling and Y. J. Lin, J. Biomater. Sci., Polym. Ed., 2009, 20, 637–652 CrossRef CAS PubMed.
- T. Baskan, D. C. Tuncaboylu and O. Okay, Polymer, 2013, 54, 2979–2987 CrossRef CAS PubMed.
- C. Zhang, A. Aung, L. Q. Liao and S. Varghese, Soft Matter, 2009, 5, 3831–3834 RSC.
- M. E. Seitz, D. Martina, T. Baumberger, V. R. Krishnan, C.-Y. Hui and K. R. Shull, Soft Matter, 2009, 5, 447–456 RSC.
- C. J. Zhou and Q. L. Wu, Colloids Surf., B, 2011, 84, 155–162 CrossRef CAS PubMed.
- R. Q. Liu, S. M. Liang, X. Z. Tang, D. Yan, X. F. Li and Z. Z. Yu, J. Mater. Chem., 2012, 22, 14160–14167 RSC.
- J. Q. Liu, C. F. Chen, C. C. He, L. Zhao, X. J. Yang and H. L. Wang, ACS Nano, 2012, 6, 8194–8202 CrossRef CAS PubMed.
- T. Matsunaga, T. Sakai, Y. Akagi, U.-i. Chung and M. Shibayama, Macromolecules, 2009, 42, 6245–6252 CrossRef CAS.
- T. Matsunaga, T. Sakai, Y. Akagi, U.-i. Chung and M. Shibayama, Macromolecules, 2009, 42, 1344–1351 CrossRef CAS.
- S. Edgecombe and P. Linse, Polymer, 2008, 49, 1981–1992 CrossRef CAS PubMed.
- X. Wang and W. Hong, Soft Matter, 2011, 7, 8576–8581 RSC.
- K. Okumura, Europhys. Lett., 2004, 67, 470–476 CrossRef CAS.
- G. Miquelard-Garnier, D. Hourdet and C. Creton, Polymer, 2009, 50, 481–490 CrossRef CAS PubMed.
- G. Miquelard-Garnier, S. Demoures, C. Creton and D. Hourdet, Macromolecules, 2006, 39, 8128–8139 CrossRef CAS.
- G. Miquelard-Garnier, C. Creton and D. Hourdet, Macromol. Symp., 2007, 256, 189–194 CrossRef CAS.
- C. Y. Hui and R. Long, Soft Matter, 2012, 8, 8209–8216 RSC.
- X. Z. Wang, H. L. Wang and H. R. Brown, Soft Matter, 2011, 7, 211–219 RSC.
- T. Nakajima, N. Takedomi, T. Kurokawa, H. Furukawa and J. P. Gong, Polym. Chem., 2010, 1, 693–697 RSC.
- Q. Wang, R. X. Hou, Y. J. Cheng and J. Fu, Soft Matter, 2012, 8, 6048–6056 RSC.
- T. Nakajima, H. Sato, Y. Zhao, S. Kawahara, T. Kurokawa, K. Sugahara and J. P. Gong, Adv. Funct. Mater., 2012, 22, 4426–4432 CrossRef CAS.
- J. Saito, H. Furukawa, T. Kurokawa, R. Kuwabara, S. Kuroda, J. A. Hu, Y. Tanaka, J. P. Gong, N. Kitamura and K. Yasuda, Polym. Chem., 2011, 2, 575–580 RSC.
- P. Chen, R. L. Wu, J. D. Wang, Y. Liu, C. R. Ding and S. M. Xu, J. Polym. Res., 2012, 19, 9825 CrossRef.
- J. Hu, T. Kurokawa, T. Nakajima, T. L. Sun, T. Suekama, Z. L. Wu, S. M. Liang and J. P. Gong, Macromolecules, 2012, 45, 9445–9451 CrossRef CAS.
- J. Hu, T. Kurokawa, K. Hiwatashi, T. Nakajima, Z. L. Wu, S. M. Liang and J. P. Gong, Macromolecules, 2012, 45, 5218–5228 CrossRef CAS.
- J. Hu, K. Hiwatashi, T. Kurokawa, S. M. Liang, Z. L. Wu and J. P. Gong, Macromolecules, 2011, 44, 7775–7781 CrossRef CAS.
- R. Kishi, K. Hiroki, T. Tominaga, K. I. Sano, H. Okuzaki, J. G. Martinez, T. F. Otero and Y. Osada, J. Polym. Sci., Part B: Polym. Phys., 2012, 50, 790–796 CrossRef CAS.
- K. Harrass, R. Kruger, M. Moller, K. Albrecht and J. Groll, Soft Matter, 2013, 9, 2869–2877 RSC.
- S. E. Bakarich, G. C. Pidcock, P. Balding, L. Stevens, P. Calvert and M. I. H. Panhuis, Soft Matter, 2012, 8, 9985–9988 RSC.
- X. P. Qin, F. Zhao, Y. K. Liu, H. Y. Wang and S. Y. Feng, Colloid Polym. Sci., 2009, 287, 621–625 CAS.
- J. Zhao, K. X. Jiao, J. Yang, C. C. He and H. L. Wang, Polymer, 2013, 54, 1596–1602 CrossRef CAS PubMed.
- C.-W. Chang, A. van Spreeuwel, C. Zhang and S. Varghese, Soft Matter, 2010, 6, 5157–5164 RSC.
- M. Fukasawa, T. Sakai, U. I. Chung and K. Haraguchi, Macromolecules, 2010, 43, 4370–4378 CrossRef CAS.
- K. Shikinaka, Y. Koizumi, Y. Osada and K. Shigehara, Polym. Adv. Technol., 2011, 22, 1212–1215 CrossRef CAS.
- J. Yang, C. R. Han, J. F. Duan, M. G. Ma, X. M. Zhang, F. Xu and R. C. Sun, Cellulose, 2013, 20, 227–237 CrossRef CAS.
- B. Xu, H. J. Li, Y. Y. Wang, G. Z. Zhang and Q. S. Zhang, RSC Adv., 2013, 3, 7233–7236 RSC.
- A. F. Zhu, G. Li and J. M. Jiang, J. Macromol. Sci., Part B: Phys., 2012, 51, 1002–1010 CrossRef CAS.
- A. K. Gaharwar, S. A. Dammu, J. M. Canter, C. J. Wu and G. Schmidt, Biomacromolecules, 2011, 12, 1641–1650 CrossRef CAS PubMed.
- J. C. Fan, Z. X. Shi, M. Lian, H. Li and J. Yin, J. Mater. Chem. A, 2013, 1, 7433–7443 CAS.
- H. Gao, N. Wang, X. F. Hu, W. J. Nan, Y. J. Han and W. G. Liu, Macromol. Rapid Commun., 2013, 34, 63–68 CrossRef CAS PubMed.
- S. Rose, A. Dizeux, T. Narita, D. Hourdet and A. Marcellan, Macromolecules, 2013, 46, 4095–4104 CrossRef CAS.
- J. F. Shen, B. Yan, T. Li, Y. Long, N. Li and M. X. Ye, Composites, Part A, 2012, 43, 1476–1481 CrossRef CAS PubMed.
- A. K. Gaharwar, C. Rivera, C. J. Wu, B. K. Chan and G. Schmidt, Mater. Sci. Eng., C, 2013, 33, 1800–1807 CrossRef CAS PubMed.
- K. Haraguchi and L. Song, Macromolecules, 2007, 40, 5526–5536 CrossRef CAS.
- J. Yang, C. R. Han, J. F. Duan, F. Xu and R. C. Sun, ACS Appl. Mater. Interfaces, 2013, 5, 3199–3207 CAS.
- L. Carlsson, S. Rose, D. Hourdet and A. Marcellan, Soft Matter, 2010, 6, 3619–3631 RSC.
- Z. Y. Li, Y. L. Su, B. Q. Xie, H. L. Wang, T. Wen, C. C. He, H. Shen, D. C. Wu and D. J. Wang, J. Mater. Chem. B, 2013, 1, 1755–1764 RSC.
- F. Zhao, X. P. Qin and S. Y. Feng, Polym. Compos., 2012, 33, 44–51 CrossRef CAS.
- Y. Tan, K. Xu, P. X. Wang, W. B. Li, S. M. Sun and L. S. Dong, Soft Matter, 2010, 6, 1467–1471 RSC.
- Y. Tan, P. X. Wang, K. Xu, W. B. Li, H. Y. An, L. L. Li, C. Liu and L. S. Dong, Macromol. Mater. Eng., 2009, 294, 855–859 CAS.
- Y. T. Wu, Z. Zhou, Q. Q. Fan, L. Chen and M. F. Zhu, J. Mater. Chem., 2009, 19, 7340–7346 RSC.
- W. I. Cha, S. H. Hyon and Y. Ikada, Makromol. Chem., 1992, 193, 1913–1925 CrossRef CAS.
- T. Kaneko, S. Tanaka, A. Ogura and M. Akashi, Macromolecules, 2005, 38, 4861–4867 CrossRef CAS.
- L. Lin, M. Liu, L. Chen, P. Chen, J. Ma, D. Han and L. Jiang, Adv. Mater., 2010, 22, 4826–4830 CrossRef CAS PubMed.
- Y. Liu, M. F. Zhu, X. L. Liu, W. Zhang, B. Sun, Y. M. Chen and H. J. P. Adler, Polymer, 2006, 47, 1–5 CrossRef CAS PubMed.
- S. K. Mujumdar and R. A. Siegel, J. Polym. Sci., Part A: Polym. Chem., 2008, 46, 6630–6640 CrossRef CAS PubMed.
- P. Chen, S. M. Xu, R. L. Wu, J. D. Wang, R. B. Gu and J. Du, Appl. Clay Sci., 2013, 72, 196–200 CrossRef CAS PubMed.
- X. B. Hu, T. Wang, L. J. Xiong, C. Y. Wang, X. X. Liu and Z. Tong, Langmuir, 2010, 26, 4233–4238 CrossRef CAS PubMed.
- S. Abdurrahmanoglu, V. Can and O. Okay, J. Appl. Polym. Sci., 2008, 109, 3714–3724 CrossRef CAS.
- H. Takeno and W. Nakamura, Colloid Polym. Sci., 2013, 291, 1393–1399 CAS.
- M. Zhu, Y. Liu, B. Sun, W. Zhang, X. Liu, H. Yu, Y. Zhang, D. Kuckling and H.-J. P. Adler, Macromol. Rapid Commun., 2006, 27, 1023–1028 CrossRef CAS.
- W. Zhang, Y. Liu, M. Zhu, Y. Zhang, X. Liu, H. Yu, Y. Jiang, Y. Chen, D. Kuckling and H.-J. P. Adler, J. Polym. Sci., Part A: Polym. Chem., 2006, 44, 6640–6645 CrossRef CAS.
- A. F. Zhu, Z. Shi, J. H. Jin, G. Li and J. M. Jiang, J. Macromol. Sci., Part B: Phys., 2012, 51, 2183–2190 CrossRef CAS.
- J. F. Wang, L. Lin, Q. F. Cheng and L. Jiang, Angew. Chem., Int. Ed., 2012, 51, 4676–4680 CrossRef CAS PubMed.
- C. J. Wu, A. K. Gaharwar, B. K. Chan and G. Schmidt, Macromolecules, 2011, 44, 8215–8224 CrossRef CAS.
- J. C. White, W. L. Stoppel, S. C. Roberts and S. R. Bhatia, J. Biomed. Mater. Res., Part A, 2013, 101, 438–446 CrossRef PubMed.
- C. C. He, K. X. Jiao, X. Zhang, M. Xiang, Z. Y. Li and H. L. Wang, Soft Matter, 2011, 7, 2943–2952 RSC.
- J. Yang, C. Gong, F. K. Shi and X. M. Xie, J. Phys. Chem. B, 2012, 116, 12038–12047 CrossRef CAS PubMed.
- J. Yang, L. H. Deng, C. R. Han, J. F. Duan, M. G. Ma, X. M. Zhang, F. Xu and R. C. Sun, Soft Matter, 2013, 9, 1220–1230 RSC.
- G. Q. Jiang, C. Liu, X. L. Liu, G. H. Zhang, M. Yang and F. Q. Liu, Macromol. Mater. Eng., 2009, 294, 815–820 CrossRef CAS.
- D. C. Tuncaboylu, A. Argun, M. Sahin, M. Sari and O. Okay, Polymer, 2012, 53, 5513–5522 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2014 |