 Open Access Article
Open Access ArticleRobustness of synthetic circadian clocks to multiple environmental changes†
Lilia
Gurevich
,
Rivka
Cohen-Luria
,
Nathaniel
Wagner
and
Gonen
Ashkenasy
*
Department of Chemistry, Ben-Gurion University of the Negev, Beer Sheva 84105, Israel. E-mail: gonenash@bgu.ac.il; Tel: +972-8-6461637
First published on 19th February 2015
Abstract
A molecular network that mimics circadian clocks from cyanobacteria is constructed in silico. Simulating its oscillatory behaviour under variable conditions reveals its robustness relative to networks of alternative topologies. The principles for synthetic chemical circadian networks to work properly are consequently highlighted.
Complex networks of bio-molecular interactions and chemical transformations allow living cells to rapidly and simultaneously process multiple extracellular input signals. Arguably, among the most central networking features is the regulation of oscillatory behaviour of circadian clocks, endogenous physiological timing systems that generate 24 hour rhythms in anticipation of dusk and dawn.1 One of the challenges in contemporary Systems Chemistry research is to mimic such complex functionality using synthetic molecular networks.2 However, when looking to fulfil this task, one finds that most currently known biological oscillators are difficult to mimic, due to the complexity of the oscillators themselves and their cellular environments. Yet, it was found nearly a decade ago that the circadian clock of the cyanobacteria Synechococcus elongatus requires neither transcription nor translation,3 and is driven by a rather simple core oscillator consisting of just three proteins: KaiA, KaiB, and KaiC.4 Mixing these three proteins in vitro with ATP resulted in oscillations with a near-24 hour period in the (total) level of KaiC phosphorylation. In this network, schematically shown in Scheme 1a, KaiC is the only protein with enzymatic activity and functions as autokinase, autophosphatase and ATPase, whereas KaiA and KaiB are regulators of KaiC activity. KaiA stimulates KaiC auto-phosphorylation, while a negative feedback mechanism operates by KaiC inactivation of KaiA in a KaiB-dependent manner (Scheme 1a).4b,c
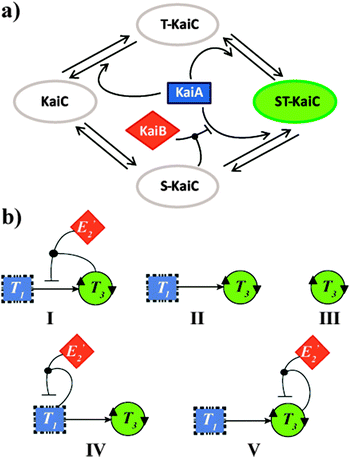 | ||
| Scheme 1 (a) Schematic description of the KaiABC oscillator of the cyanobacteria S. elongatus. Two residues (S431 and T432) in KaiC undergo auto-phosphorylation and auto-dephosphorylation. KaiA shifts the equilibrium toward T-KaiC and ST-KaiC. T432 on ST-KaiC spontaneously dephosphorylates and forms S-KaiC. KaiB binds to S-KaiC and inactivates KaiA to shift the equilibrium towards unphosphorylated KaiC.4b,c (b) Network graph of proposed configurations studied for their potential to reproduce the KaiABC oscillatory behaviour. (I) ‘Native’ configuration, where the oscillatory production of T3, is governed by T3 autocatalysis, T3 production through cross catalysis by T1, and a negative feedback loop due to formation of the E2′NT3T3 inhibitory complex. A more detailed diagram showing all reactants, intermediates and products of this network is shown in Scheme s1 (ESI†). (II) Binary configuration consisting of the T3 autocatalysis and T3 production through cross catalysis by T3. (III) A simple configuration consisting only of T3 autocatalysis. (IV) A ternary configuration consisting of T3 autocatalysis, T3 production through cross catalysis by T3, and an alternate inhibitory pathway due to formation of the E2′NT1T1 complex. (V) A ternary configuration consisting of T3 autocatalysis, T3 production through cross catalysis by T1, and an alternate negative feedback loop due to formation of the E2′NT3T3 complex. | ||
This commonly observed oscillatory behaviour in biology can be mimicked by a small set of chemical reactions that yield oscillations, with the most elaborate systems based on the Belousov–Zhabotinsky (BZ) and similar reactions.5 By means of bio-macromolecules, in vitro nucleic acid oscillators have been realized using molecular networking and transcription regulation strategies.6 Recently, catalytic replication networks have also served to study emergent phenomena in complex mixtures.2b,7 Our studies with peptide networks, for example, have shown how these can function in closed or open environments, performing Boolean logic operations,8 equivalents to a whole range of chemical logic gates,9 and mimicking computational modules and network motifs.8b,c We now argue that studying de novo designed oscillating reaction networks is very timely and of strong current interest. In a very recent paper, we have utilized a ternary network in an open system, driven by realistic peptide replication processes, to simulate in silico the connectivity and network topology of the KaiABC circadian clock from S. elongatus. This network produced rhythms whose constant frequency was independent of the intake and decay rates, and robust towards concentration fluctuations.8g Here, we analyse the potential for this network to function as an effective circadian clock under changing physical (temperature, pH), chemical (reactant, template and salt concentrations) and experimental (reactant and product fluxes) conditions. Using uniform criteria, we quantitatively characterize the robustness of the clock oscillatory periods and their sustainability over time. The network oscillatory behaviour is then compared with the dynamics of alternate networks, in which catalytic and inhibitory pathways were omitted or diverted (Scheme 1b). Remarkably, we find that by better imitating the Kai system, our native-like clock configuration displays robust behaviour under a wider set of conditions. We suggest that disclosing the dynamic characteristics of circadian clocks in this study will help in the design of synthetic oscillatory devices, as well as of additional devices operating via complex network-dependent functions.
The lead network configuration we exploit to mimic the connectivity in the KaiABC system is shown in Scheme 1b (configuration I) and Scheme s1 (ESI†). This ‘native’ network effectively functions as an internal clock, and its rhythm is expressed by the oscillatory production of T3 over time (Fig. 1). T3 is formed auto-catalytically and through cross-catalysis by T1, from nucleophilic (N) and electrophilic (E3) precursors. The negative feedback of the cross-catalytic production by T1 operates via a competing pathway, where a non-functional electrophile (E2′) joins a T1T3 dimer in forming an inhibiting intermediate.8g
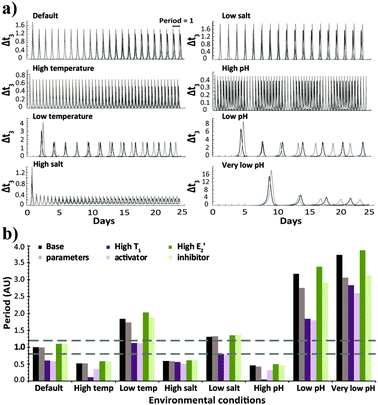 | ||
| Fig. 1 (a) Time-dependent template concentration for the native configuration, simulated with the base parameters under different environmental conditions. Each panel shows two plots obtained for runs with the basic (black) and 20% higher (grey) N and E3 intake and T3 decay rates. (b) Average period values for the native configuration, simulated with the base parameters or when higher amounts of the activator T1 or inhibitor E2′ were introduced. Each set shows bar graphs obtained with the basic (dark colour bars) and 20% higher (light colour) N and E3 intake and T3 decay rates. The horizontal dashed lines emphasize conditions resulting in oscillation periods close to 1. The selection of the relevant parameters that emphasize each of the studied conditions is explained in the ESI† and specified in Table s1. | ||
In order to study the kinetics of this circadian network, as well as the kinetics of the alternative networks discussed below (Scheme 1b, configurations II–V), we apply a second order replication model that describes all parallel reactions of three distinct electrophiles Ei and a common nucleophile N, producing three products/templates Ti (eqn (1)–(3); i, j, k = 1, 2, 3). The i = j = k cases (eqn (2) and (3)) correspond to autocatalysis, while the i ≠ j, k cases describe cross catalytic pathways. Importantly, in order to facilitate the oscillatory behaviour, we implement the model in open systems, where the reactants (N and E3) have a continuous inflow, and the product (T3) decays linearly.10 We have investigated this system by simulating the model in Matlab using kinetic parameters relevant for peptide replication experiments.8b Different network configurations, operating under variable environmental conditions, were assembled by activating, emphasizing and disabling the specific network connections (all together more than 200 different runs; see Table s1 and ESI† for parameter selections).
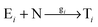 | (1) |
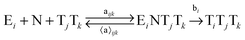 | (2) |
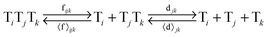 | (3) |
The robustness of the oscillator period is known to be critical for its function. Still, as apparent from the results of Fig. 1, it is difficult to quantify the robustness over an entire range of environmental conditions using a single parameter. We thus evaluate the period robustness under each specific set of environmental conditions (Fig. 2). The calculated robustness, ranging from 0 to 1, is defined as the reciprocal of the product of the three ratios, comparing the periods of the oscillations from different fluxes, for the three sets of initial concentrations. For example, simulating the native clock (I) with fluxes that differ by 20% would be expected to yield significantly different oscillation periods,8g yet the results (Fig. 1 and 2) show that except for running in high temperature or high pH environments, this network maintains almost identical T3 periods.
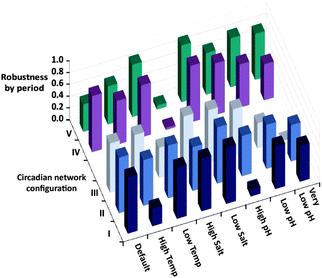 | ||
| Fig. 2 Robustness by period, calculated for the five different configurations shown in Scheme 1b, under eight different sets of environmental conditions. The robustness is defined as the reciprocal of the product of the three ratios, comparing the periods of the T3 oscillations from different fluxes, for the three sets of initial concentrations (base parameters, high T1 activator, high E2′ inhibitor). | ||
Fig. 2 is then further used to compare the period robustness under all eight sets of environmental conditions, for the five network configurations of Scheme 1b. This uniform measure indicates that the native configuration (I) is more robust under a wider set of conditions than both the simple autocatalytic reaction (configuration III), and the alternate ternary network (V) where the negative feedback loop is formed by a direct inhibition of the T3 autocatalysis. The binary network (II) consisting of the T3 autocatalysis and T3 production through cross catalysis but no inhibition, and the ternary network (IV) where T1 activity is auto-inhibited, seem to exhibit similar robustness by period to that of the native system.
In order to further compare the performance of the five studied network configurations, we analyse the sustainability of their oscillations over time for variable conditions (Fig. 3). Here again, after simulating the time-dependent behaviour (e.g., Fig. 3a), a uniform criterion is applied, reflecting the ratio between the amplitude of the oscillations at the beginning of the reaction and at the final stages. Fig. 3b shows that under the base parameter set of concentrations, all configurations will produce sustained oscillations. Yet, under high concentration of the activator T1, the native configuration will still oscillate in a sustainable fashion, while the oscillations of configurations II, IV and V will dampen over time. The oscillations of the alternate configuration (V) also dampen when the system functions under high E2′ inhibitor concentrations.
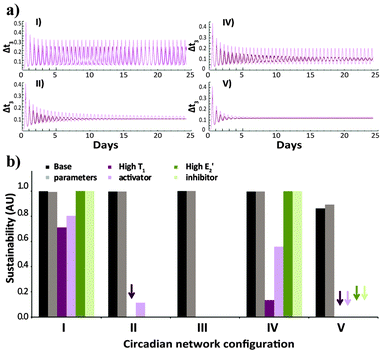 | ||
| Fig. 3 (a) Time-dependent template concentrations obtained for the various network configurations (I, II, IV, V; Scheme 1b), under the default environmental conditions, for the case of high T1 activator concentration. (b) Sustainability values for the different configurations, under default environmental conditions, for the three sets of different concentrations (base parameters, high T1 activator, high E2′ inhibitor). The kinetics (a) and bar graphs (b) show results obtained for the basic (dark colour) and 20% higher (light colour) N and E3 intake and T3 decay rates. Arrows in (b) mark runs that resulted in oscillatory behaviour with sustainability ≤ 0.05. Note that no effect of E2′ increase, or T1 and E2′ increase, is expected for systems II and III, respectively. The selection of the relevant parameters that emphasize each of the studied conditions is explained in the ESI† and specified in Table s1. | ||
Considering both the period robustness and sustainability results under the various conditions, we suggest a mechanism by which our circadian network works properly. Apparently, the fundamental T3 autocatalytic oscillatory behavior due to intake and decay of E3 and T3 is not sufficient for robust and sustained oscillations, and thus needs to be stabilized by cross catalysis from T1. However, for the activator T1 to work properly, a compensation mechanism should be in place in order to keep its concentration low. This is optimally accomplished by the feedback loop, operating via the E2′ association with N and the T1T3 dimer – but not with the homo-dimers T1T1 or T3T3 – which facilitates the siphoning off of excess T1 and thus allows the network to be less sensitive to T1 fluctuations.
In this work we shed light on the design principle and Systems Chemistry of potentially realistic synthetic circadian clocks. While the work is still theoretical in nature, many features of circadian clocks operating under different environmental and experimental conditions were revealed, which would be difficult to predict without the numerical simulation. In that context, it should be noted that no demonstration of a replicating molecular network oscillating out-of-equilibrium has been made available so far. We suggest that this target could be addressed by experimentalists in the near future.
This research is supported by the European Research Council (ERC 259204).
Notes and references
- J. Bass, Nature, 2012, 491, 348 CrossRef CAS PubMed.
- (a) R. F. Ludlow and S. Otto, Chem. Soc. Rev., 2008, 37, 101 RSC; (b) Z. Dadon, N. Wagner and G. Ashkenasy, Angew. Chem., Int. Ed., 2008, 47, 6128 CrossRef CAS PubMed; (c) J. R. Nitschke, Nature, 2009, 462, 736 CrossRef CAS PubMed; (d) L. J. Prins, Chim. Ind., 2010, 92, 126 CAS; (e) K. Ruiz-Mirazo, C. Briones and A. de la Escosura, Chem. Rev., 2014, 114, 285 CrossRef CAS PubMed.
- M. Nakajima, K. Imai, H. Ito, T. Nishiwaki, Y. Murayama, H. Iwasaki, T. Oyama and T. Kondo, Science, 2005, 308, 414 CrossRef CAS PubMed.
- (a) J. S. Markson and E. K. O'Shea, FEBS Lett., 2009, 583, 3938 CrossRef CAS PubMed; (b) G. Dong, Y.-I. Kim and S. S. Golden, Curr. Opin. Genet. Dev., 2010, 20, 619 CrossRef CAS PubMed; (c) P. Lenz and L. Sogaard-Andersen, Nat. Rev. Microbiol., 2011, 9, 565 CrossRef CAS PubMed; (d) M. Egli and C. H. Johnson, Curr. Opin. Neurobiol., 2013, 23, 1 CrossRef PubMed; (e) G. Pattanayak and M. J. Rust, Curr. Opin. Microbiol., 2014, 18, 90 CrossRef CAS PubMed.
- (a) I. R. Epstein and J. A. Pojman, and Editors, An Introduction to Nonlinear Chemical Dynamics: Oscillations, Waves, Patterns, and Chaos, 1998, p. 392 Search PubMed; (b) F. Sagues and I. R. Epstein, Dalton Trans., 2003, 1201 RSC; (c) A. F. Taylor, Prog. React. Kinet. Mech., 2002, 27, 247 CrossRef CAS; (d) R. Yoshida, Adv. Mater., 2010, 22, 3463 CrossRef CAS PubMed.
- (a) E. Franco, E. Friedrichs, J. Kim, R. Jungmann, R. Murray, E. Winfree and F. C. Simmel, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, E784 CrossRef CAS PubMed; (b) K. Montagne, R. Plasson, Y. Sakai, T. Fujii and Y. Rondelez, Mol. Syst. Biol., 2011, 7, 466 CrossRef PubMed; (c) M. Weitz, J. Kim, K. Kapsner, E. Winfree, E. Franco and F. C. Simmel, Nat. Chem., 2014, 6, 295 CrossRef CAS PubMed.
- (a) G. Ashkenasy, R. Jagasia, M. Yadav and M. R. Ghadiri, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 11872 CrossRef PubMed; (b) J. J. P. Peyralans and S. Otto, Curr. Opin. Chem. Biol., 2009, 13, 705 CrossRef CAS PubMed; (c) A. Vidonne and D. Philp, Eur. J. Org. Chem., 2009, 583 CrossRef; (d) O. Taran and G. von Kiedrowski, Chem. Synth. Biol., 2011, 289 CAS; (e) J. Li, P. Nowak and S. Otto, J. Am. Chem. Soc., 2013, 135, 9222 CrossRef CAS PubMed.
- (a) G. Ashkenasy and M. R. Ghadiri, J. Am. Chem. Soc., 2004, 126, 11140 CrossRef CAS PubMed; (b) N. Wagner and G. Ashkenasy, Chem. – Eur. J., 2009, 15, 1765 CrossRef CAS PubMed; (c) N. Wagner and G. Ashkenasy, J. Chem. Phys., 2009, 130, 164907 CrossRef PubMed; (d) Z. Dadon, M. Samiappan, E. Y. Safranchik and G. Ashkenasy, Chem. – Eur. J., 2010, 16, 12096 CrossRef CAS PubMed; (e) M. Samiappan, Z. Dadon and G. Ashkenasy, Chem. Commun., 2011, 47, 710 RSC; (f) G. Ashkenasy, Z. Dadon, S. Alesebi, N. Wagner and N. Ashkenasy, Isr. J. Chem., 2011, 51, 106 CrossRef CAS; (g) N. Wagner, S. Alasibi, E. Peacock-Lopez and G. Ashkenasy, J. Phys. Chem. Lett., 2015, 6, 60 CrossRef CAS PubMed.
- (a) A. P. de Silva and S. Uchiyama, Nat. Nanotechnol., 2007, 2, 399 CrossRef CAS PubMed; (b) E. Katz and V. Privman, Chem. Soc. Rev., 2010, 39, 1835 RSC; (c) K. Szacilowski, Chem. Rev., 2008, 108, 3481 CrossRef CAS PubMed.
- (a) K. M. Beutel and E. Peacock-Lopez, J. Chem. Phys., 2006, 125, 024908 CrossRef PubMed; (b) K. M. Beutel and E. Peacock-Lopez, J. Chem. Phys., 2007, 126, 125104 CrossRef PubMed.
- (a) R. A. Hut and D. G. M. Beersma, Philos. Trans. R. Soc., B, 2011, 366, 2141 CrossRef CAS PubMed; (b) S. Akiyama, Cell. Mol. Life Sci., 2012, 69, 2147 CrossRef CAS PubMed; (c) F. Hussain, C. Gupta, A. J. Hirning, W. Ott, K. S. Matthews, K. Josic and M. R. Bennett, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 972 CrossRef CAS PubMed.
- T. S. Hatakeyama and K. Kaneko, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 8109 CrossRef CAS PubMed.
- (a) P. Ruoff, M. K. Christensen, J. Wolf and R. Heinrich, Biophys. Chem., 2003, 106, 179 CrossRef CAS PubMed; (b) T. Takeuchi, T. Hinohara, G. Kurosawa and K. Uchida, J. Theor. Biol., 2007, 246, 195 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: (i) Detailed description of simulation, parameters and initial conditions, (ii) additional figures. See DOI: 10.1039/c5cc00098j |
| This journal is © The Royal Society of Chemistry 2015 |
