Open Access Article
Open Access ArticleSimulating preferential sorption of tartrate on prismatic calcite surfaces†
Marko
Ukrainczyk
ab,
Maximilian
Greiner
a,
Ekaterina
Elts
a and
Heiko
Briesen
*a
aChair for Process Systems Engineering, Technische Universitat München, Gregor-Mendel-Straße 4, D-85354 Freising, Germany. E-mail: heiko.briesen@wzw.tum.de
bLaboratory for Precipitation Processes, Ruđer Bošković Institute, Bijenička c. 54, HR-10002 Zagreb, Croatia
First published on 7th November 2014
Abstract
Understanding the influence of additives on crystal growth is required to engineer the crystal properties according to their functional applications. In this work, the sorption behavior of tartrate on calcite surfaces is investigated employing molecular dynamics simulations to understand additive-mediated crystal growth. The free energy landscapes for the sorption of tartrate are calculated using metadynamics. The adsorption binding energies of favorable conformations, orientations and positions of tartrate near the (104) and (1−10) calcite surfaces are determined. The obtained results provide a molecular-level explanation of the experimentally observed tartrate-stabilized exposure of prismatic {1−10} faces during calcite growth. The simulations show that tartrate preferentially adsorb directly to the (1−10) calcite surface, whereas tartrate is more loosely adsorbed on the (104) surface, mainly by solvent-mediated binding. The (1−10) geometry of calcite surface sites closely matches the structure of tartrate, with a specific role of carboxylate and hydroxyl groups in recognizing the calcium and carbonate ions, respectively. Two stable adsorption configurations are identified for the (1−10) face: (1) adsorbed tartrate with the effect of surface-induced conformational change and (2) incorporated tartrate into the surface by fitting one of the carboxylate groups into lattice position normally occupied by carbonate ions and additionally stabilized by binding of both hydroxyl groups to neighboring carbonate ions. The results indicate that surface energetics, structural matching and adsorbed water layer play a major role in the strength of the interactions and hence in the expression of calcite morphology. Preferential adsorption of tartrate on {1−10} surfaces could stabilize these otherwise fast-growing faces and thus inhibit crystal growth in {1−10} directions.
1. Introduction
The processing and application of crystalline products strongly depends on their morphology and size distribution. The control and design of a desired crystal morphology and size can be achieved by employing specific additives during crystal growth processes.1,2 In many cases additives are not desired in the crystallization process since they reduce the purity of the crystalline product. It is important to understand how the additives are incorporated into the crystal to control their uptake. A detailed understanding of the influence of additives on crystal growth is required to control the crystallization process and to engineer the crystal properties according to their functional applications. However, the mechanisms of interactions between additives and crystal surfaces are not yet fully understood because of the complexity of the processes occurring at the crystal surface–aqueous solution interface. Once the crystal/solution interface is understood on the atomic resolution, it may be possible to design molecules that have specific interactions with one or more of the crystal faces. Challenges are in the complexity of the process that comprises growth, dissolution and sorption occurring at the solid/liquid interfaces. Given the increasing computational power, molecular dynamics (MD) is emerging as a viable approach toward building a comprehensive picture of molecular phenomena involved in additive-controlled crystallization processes.3–5In recent years, calcium carbonate has been intensively studied to understand how polymorphism, structural features and morphology can be controlled by organic additives.6 Calcium carbonate forms different polymorphs, including calcite, aragonite and vaterite. Among them calcite is the thermodynamically most stable modification under standard conditions and it appears in various morphologies, typically as rhombohedral crystals bounded by the most stable {104} calcite faces. Precipitated calcium carbonate is an important synthetic mineral widely used in various technologies, mainly as multifunctional filler or pigment (paper, plastics, pharmaceuticals, foods).7–9 The organic-mediated crystal growth control of calcium carbonate is also important in biomineralization, where nature engineers materials with substantially enhanced mechanical properties.6 Namely, recent studies showed that calcite has high affinity to incorporate organic molecules into the structure, thereby affecting its composition.10–12 It is believed that the adsorption and incorporation of organic molecules is controlled by the additive recognition for a specific surface structure, and consequently organic additives are selectively incorporated onto specific crystal faces. Some experimental studies showed that inside biogenic calcite crystals, acidic proteins are preferentially incorporated on the set of crystal planes parallel to its crystallographic c-axis.13,14 Ionic interactions are important in the crystallization of mineral compounds. The so-called multifunctional additives, i.e. organic molecules with various functional groups, are capable of forming several bonds with (ionic) surface sites. Calcite exhibits exceptional chemical affinity for organic molecules having polar functional groups, such as carboxylate and hydroxyl groups.6 One of the hypotheses15,16 is that the binding of the acidic macromolecules to calcite surfaces could occur by fitting carboxylate groups into lattice positions occupied by carbonate groups. In order to understand how particular functional groups bind to the surface, breaking down the interactions of these large molecules into more basic units, has shown to be a good strategy.5,17,18 Experimental studies showed that small organic molecules, such as carboxylates or amino acids, can be used as effective regulators of calcite crystal morphology. In particular, dicarboxylates substituted with the amino or hydroxy group on α-carbon has been identified to show high affinity and selectivity for calcite surfaces.17 Previous experimental results indicated specific interactions of tartrate with newly stabilized calcite surfaces, thus modulating the morphology.19 The co-addition of tartrate during steady-state calcite growth system led to a clear selective expression of the prismatic {1−10} side faces, parallel to the c-axis (Fig. 1). This suggests the importance of surface energetics and structural matching in tartrate interactions with calcite surfaces. The prismatic (1−10) surface is of higher energy, than the most stable rhombohedral (104) surface, and if these surfaces are to be expected in the final morphology, they must be significantly stabilized and prevented from growing out. It was suggested that charged carboxylate groups recognize the calcium ions on (1−10) with specific spacing that matches the structure of tartrate. Hydroxyl groups might also have a specific role binding to surface carbonate groups, thus enhancing the adsorption.20 Still, detailed thermodynamic and structural information controlling the growth mechanism, such as the binding energies and sorption modes of organic additives at specific faces and sites are not understood.
MD simulations can provide useful information at molecular level and have already substantially contributed to our understanding of interactions between organics and mineral surfaces. Earlier simulation studies mainly applied simplified approaches, not accounting explicitly for water molecules.16,21,22 However, the effect of water cannot be ignored in studies of additive-controlled crystallization from solution, and recent simulation studies emphasized the importance of structured interfacial water layers on additive adsorption behavior.5,23–25 One of the challenges of classical MD simulations remains in the development of reliable force fields which govern the behavior of solid/liquid interface of a particular system. In the last years there has been considerable effort directed toward the development of force fields for calcium carbonate, capable of describing the bulk crystal as well as interface of this material with water and organics (with the aim to address biomineralization), and to model the nucleation and growth of calcium carbonate.26 MD simulation studies have mainly focused on the most stable rhombohedral (104) calcite surface/liquid interface, obtaining valuable information regarding the structure and dynamics of adsorbed water layers,26,27 but seldom included the presence of organics.5,24 The latest developed calcium carbonate force field28 uses Lennard–Jones potentials which makes the combination with an organic force fields straightforward by applying common combination-rule approach.
Another challenge of the methods based on MD is adequate sampling of the conformational space. Most recent simulations of adsorption indicated that regular MD simulations are often not efficient at overcoming the problem of multiple free energy minima separated by significant barriers which could trap a molecule in one of the local minima. Especially this was shown to be valid for the case of highly-charged mineral surfaces, such as phosphates23 and carbonates.5
In this work, the adsorption behavior of tartrate on calcite surfaces is studied employing MD simulations to understand additive-mediated crystal growth. Tartrate (O2C–CH(OH)–CH(OH)–CO2)2− served as a simple model compound of hydroxy-carboxylates, giving valuable information about basic molecular interactions of these polar functional groups with different calcite surfaces, needed for rational development of novel growth-controlling additives. First, we investigated the energetics and structure of interfacial calcite–water interface for (104) and (1−10) calcite surfaces. Then, free energy landscapes for the adsorption and desorption of tartrate are calculated using metadynamics,29 thus avoiding the pitfalls of MD. Using metadynamics, the adsorption energetics of favorable conformations, orientations and positions of the tartrate molecule near the (104) and (1−10) calcite surfaces are determined. We show the importance of surface energetics, structural matching and preorganization of functional groups as well as structuring of the interfacial water on the adsorption strength, and hence calcite morphology.
2. Simulation methods
2.1. Simulation systems setup
MD simulations were performed with the GROMACS30 software package (version 4.6.3). For the force field parameters of calcite and the calcite/water–organics interactions, CaCO3–TIP3P-solution interfacial model was used, as recently developed by Xiao et al.28 Calcite–tartrate pairwise interaction parameters were deduced from atomwise CaCO3 parameters and atomwise tartrate parameters by applying the geometric mixing rule. The general AMBER force field (GAFF)31 was used to model tartrate. Consistent charges indicated compatibility of GAFF and the chosen calcium carbonate force field.28Tartrate was modeled as a dianion (deprotonated state of both carboxylic groups), since this is the predominant species at experimental conditions19 of calcite crystallization under slightly basic conditions (pH 8). The dihedral parameters were re-parameterized by quantum chemical calculations using the Schrödinger's Jaguar32 software package. Density functional theory (DFT) with B3LYP functional and 6-31G(d,p) basis set was chosen to stay consistent with the GAFF parameterization procedure. The partial atomic charges were derived by the R.E.D Server,33 which implements standard GAFF approach, using Restrained Electrostatic Potential (RESP)34 method taking into account multiple conformations.
Initial structures of the (104) and (1−10) faces were generated using GDIS.35 The resulting hexagonal calcite unit cells were periodically replicated in 3D space, thus generating a crystal slab of approximately 5 × 3 × 2.5 nm3. Extending the simulation box in the direction perpendicular to the surface gave a gap of about 5 nm into which a tartrate molecule and about 2500 water molecules were inserted. To keep the entire system charge-neutral, Na+ counter ions were added in the presence of negatively charged tartrate. Two Na+ ions were initially placed in bulk solution. By doing so, they remained mostly in the solution. Na+ ions might interfere between tartrate and calcite crystal surface, but this was not observed in our performed simulations. Na+ ions were not in close contact with tartrate. This was checked by the convergence test (see the Metadynamics section) and by tracking and inspecting Na+ and tartrate trajectories. Periodic boundary conditions were applied in all directions. Ideal calcite surfaces were assumed: calcium and carbonate ions were position restrained by a harmonic potential with a force constant of 1000 kJ mol−1. Previous simulation studies reported no significant relaxation of surface ions on (104) calcite–water interface,26,27 and only a slight relaxation of (1−10) surface.36 In pure systems (without additives), the (1−10) surface is in contact with water molecules and the top surface ions relax, in order to minimize excess surface free energy. However, in our simulations unrelaxed (1−10) surfaces are assumed, since they are supposed to be stabilized with adsorbed tartrate molecules (adsorbed tartrate layer). All bond lengths of carbonate, water and tartrate were constrained to their equilibrium positions with the LINCS algorithm. Non-bonded interactions were evaluated with a cutoff of 1.0 nm. The Particle Mesh Ewald method (PME) was used to treat long-range electrostatic interactions, with a grid spacing of 0.16 nm and PME order of 4. Simulations were performed using a 2.0 fs time step in the isothermal–isobaric (NPT) ensemble at 300 K and 1 bar. Nose–Hoover temperature coupling was used with a relaxation time of 2.0 ps. Constant pressure was obtained by coupling to a semi-isotropic Parrinello–Rahman barostat, allowing only scaling of the simulation box dimension normal to the surface, with a relaxation time of 2.0 ps. The system was equilibrated by performing 2.0 ns of NPT simulation, before proceeding with production runs or metadynamics. In order to visualize the simulation and to generate molecular snapshots, Visual Molecular Dynamics (VMD)37 was used.
2.2. Metadynamics
Metadynamics applies a time-dependent bias to a predefined set of collective variables (CV) that describe characteristics of a system. A detailed review of metadynamics can be found elsewhere.29,38,39 In short, the algorithm biases a MD simulation through the periodic addition of a small repulsive potential, defined as a sum of Gaussian distributions, to the overall potential energy. By introducing the bias potential it enables escaping the system's free energy minima and simultaneously quantitatively evaluates the free energy landscape. To properly explore and describe the sorption behavior of tartrate on different calcite faces, we selected three CVs: (1) distance from the crystal surface defined as the center of mass of tartrate in the direction orthogonal to the crystal surface, (2) the tartrate orientation represented by the cosine of the angle (cos(θ)) between the tartrate vector, defined by the two carbon atoms to which the polar functional groups are attached, and the axis perpendicular to the surface (3) tartrate molecular conformation, defined as the dihedral angle of the carbon chain. The distance from the surface is defined relative to the average position of the Ca surface sites in the outermost layer. The selected choice of CVs allowed resolving bonded/unbonded states in the CV-space, differently oriented bound configurations and preferred conformations, i.e. the conformational change of tartrate, upon sorption onto the surface. The biasing Gaussian potential functions with a height parameter of 0.05 kJ mol−1 were deposited every 0.5 ps, with a width of 0.01 nm, 0.025 and 5° along CV1, CV2 and CV3, respectively. To ensure the convergence of the system, but not to overfill the free energy landscape in CV-space (oversampling the bulk solution), the simulation run time was optimized to 160 ns. The computational time needed for the simulation on 64 cores was approx. 48 hours. The binding free energy was estimated by reconstructing the free energy landscape using sum_hills utility provided with the PLUMED39 plugin. The free energy difference between the adsorbed state and the desorbed state obtained from the free energy profile is defined as the binding free energy. As a reference level for the binding free energy the most stable trans conformation of the desorbed tartrate in the bulk water was taken. The convergence of simulation was assessed by comparing the reconstructed free energy profiles in the CV space as a function of simulation time. The system was considered to be sampled properly (converged) when the difference between binding energies over time approached zero.3. Results and discussion
3.1. Calcite–water interfaces
Before proceeding to tartrate adsorption behavior on calcite surfaces, we first examine the energetics and structure of calcite interfaces, particularly focusing on the comparison of the (1−10) surface with the most stable (104) surface.Surface free energies, γ, were determined according to the procedure described by de Leeuw et al.40 using the relation, γ = ΔE/(A·Na), where E is the total potential energy, A is the surface area, Na the Avogadro number; the energy difference was calculated as ΔE = Einterface − Ebulk − Ewater. The surface energies of dehydrated surfaces are calculated to be γ(104) = 0.5 J m−2 and γ(1−10) = 0.8 J m−2. The (104) surface is more stable and less reactive than the (1−10) surface. Both surfaces are stabilized when water is introduced, with calculated surface energies γ(104) = 0.1 J m−2 and γ(1−10) = 0.4 J m−2. The fact that the (104) surface is more stable than the (1−10) surface means that the more reactive (1−10) surface should grow more quickly and may well grow out of the thermodynamic crystal morphology altogether, leaving large {104} faces expressed in the crystal morphology. Indeed, the rhombohedral {104} crystal form is the most often experimentally observed in additive-free crystallization systems.17,41 Our calculated surface energies are in good agreement with other theoretical studies36,40 who have demonstrated that this surface is significantly lower in energy (Δγ = 0.3 J m−2) than the (1−10) surface. Thus, if the {1−10} faces are to be expected in the final morphology, it must be significantly stabilized and prevented from growing out.
The higher energy of the (1−10) surface, i.e. higher instability and therefore higher reactivity, can be related in terms of surface structure and electrostatic interactions. Each surface ion, calcium and carbonate, on the (104) face has one broken bond that resulted with the unsaturated coordination and partial charge of z = +1/3 and −1/3 felt in the vacant site above the Ca surface sites and CO3 groups, respectively. On the other hand, the prismatic (1−10) calcite face exhibit three dangling bonds above each surface ion with partial charge of z = ±1. Consequently, the adsorption of charged organic molecules, such as tartrate with polar functional groups, may neutralize partial surface charge, wherein the interactions are stronger with the prismatic faces that are of higher energy due to its three dangling bonds. On contrary, the unsaturated coordination of lattice ions of the rhombohedral {104} calcite surface are mainly stabilized by adsorption of water molecules.
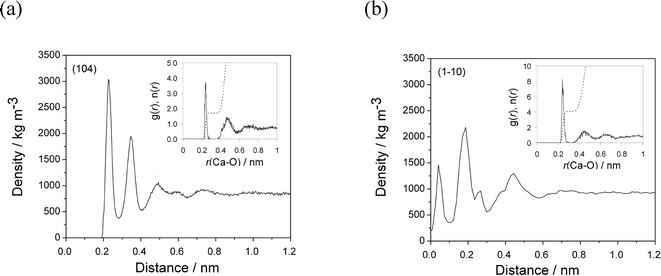
On the most stable calcite (104) surface, water forms several ordered high-density layers, maxima at 0.22, 0.34 and 0.49 nm (Fig. 2(a)), which is consistent with previous simulations5,26 and experimental findings.27 The first stable water layer, with a density of 3000 kg m−3 is formed due to strong interactions between water molecules and calcite surface ions. These water molecules are oriented parallel to the surface, directly bind to the outermost Ca groups, and are also able to form weak hydrogen bonds with the top-surface CO3 groups. The second layer of water molecules are oriented perpendicular to the surface and strictly form hydrogen bonds with the oxygen atoms of the outermost CO3 groups. The radial distribution function of water around the outermost Ca sites showed that in average (simulation time 10 ns) 1.7 water molecules form direct interactions with each of the outermost Ca sites with an average Ca–O distance of 0.238 nm (Fig. 2(a, inset)).
The interfacial water at the (1−10) surface on the other hand is much less structured. Three major water density peaks are located at 0.04, 0.18 and 0.44 nm from the surface (Fig. 2(b)). The density of the first and second water layers are 1500 and 2500 kg m−3, respectively. The water molecules interact directly with the outermost Ca, the underlying Ca layer and outermost CO3 groups. Four water molecules are within the first coordination shell of each outermost Ca site, at an average Ca–O distance of 0.240 nm (Fig. 2(b, inset)). The third water layer interacts mainly with the water molecules in the second layer, additionally neutralizing the high charge of the surface ions, resulting in a density of 1300 kg m−3.
The lower densities of water layers and their less structuring could originate from much lower surface ion density of 2.4 ions nm−2 on the (1−10) face, in comparison to 5.0 ions nm−2 on the (104) calcite face. In addition, the partial surface charge is also higher on the (1−10) face (three dangling bonds), so more water molecules coordinate to highly charged surface ions (z = ±1) leading to less structured layers.
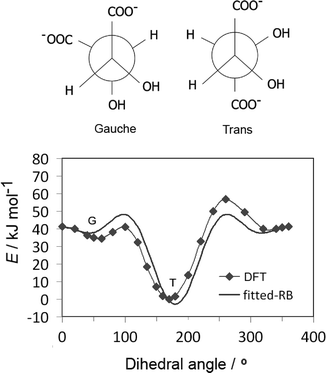
3.2. Tartrate in water
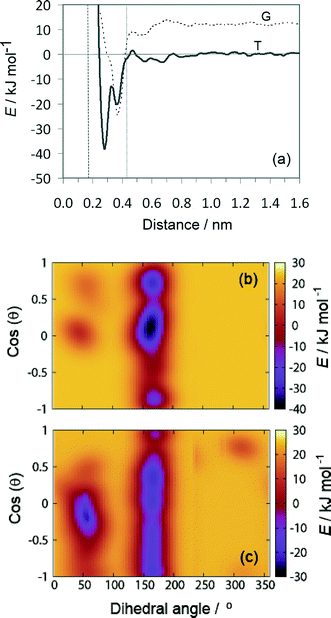
Tartrate forms a number of stable conformations, namely trans and gauche conformers, with the corresponding dihedral angle of about 60° and 180°, respectively (Fig. 3(up)). It is now well established by experimental42 and quantum chemical simulations43 that trans conformation of the carbon chain is the most stable both in vacuum and water, independent of pH conditions. The original GAFF parameters failed to reproduce the right conformation of tartrate in water (missing appropriate dihedral parameters for dioil/dicarboxylate), thus the carbon chain dihedral parameters and partial charges were re-parameterized by quantum chemical calculations, as mentioned in section 2.1. To obtain dihedral parameters, energies of the optimized tartrate structures in vacuum were calculated for the carbon chain dihedral angles within 0–360 degree range (Fig. 3(down)). The Ryckaert–Bellemans (RB) dihedral potential function (Edihedral = ∑Cn(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ − 180°)n) was least-squares fitted to minimize the deviations from DFT energy profile, with the following dihedral parameters obtained: C1 = 47.48 kJ mol−1; C2 = 9.59 kJ mol−1; C3 = 28.46 kJ mol−1; C4 = 31.60 kJ mol−1. The calculated charges are given in ESI.†
φ − 180°)n) was least-squares fitted to minimize the deviations from DFT energy profile, with the following dihedral parameters obtained: C1 = 47.48 kJ mol−1; C2 = 9.59 kJ mol−1; C3 = 28.46 kJ mol−1; C4 = 31.60 kJ mol−1. The calculated charges are given in ESI.†
MD simulation of tartrate in water, using the newly obtained parameters, showed that the most stable tartrate conformation is trans, with carbon chain dihedral angle of 178°, which is in agreement experimental results.42 The relaxed tartrate structure did not significantly differ from the structure in vacuum. One of the hydroxyl groups is bound to form an intramolecular hydrogen bond with the proximal carboxylate oxygen atom while the other hydroxyl group is more free to rotate and more likely to be involved in intermolecular hydrogen bonds, interacting with water molecules (Fig. 4). This relaxed structure of tartrate dianion in aqueous solution is consistent with other DFT simulation study43 which indicated the same non-symmetrically hydration, while preserving the conformation of the carbon skeleton. This indicated the validity of our parameterization for tartrate dianion, which is critical to investigate accurately the interactions of tartrate with calcite surfaces.
To calculate the energy barrier of the conformational change in solution, the metadynamics was employed; the dihedral angle of the carbon chain was used as CV. The change in energy of different conformational states in water was found to be relatively high, about 13 kJ mol−1 between gauche and the most stable trans conformation. This energy difference is significantly higher if compared with the thermal energy barrier, about 2.5 kJ mol−1 at 300 K, so the conformational change could not be seen in unbiased MD simulations.
3.3. Tartrate sorption on calcite surfaces
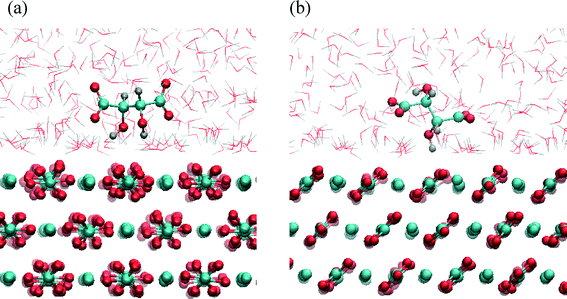
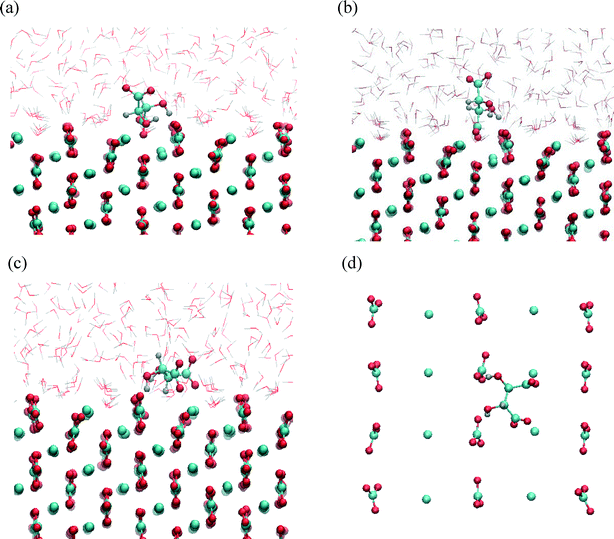
The results of the metadynamics provided the free energy landscape for the sorption of tartrate on different calcite surfaces as a function of the three selected CVs: distance from the surface, molecular orientation (cos(θ)) and conformation (carbon backbone dihedral angle). In addition to the distance from the surface and the molecular orientation we chose the molecular conformation as the third CV, since the conformational change could not be seen in unbiased MD simulations, as mentioned above. At convergence, the four-dimensional (4D) free energy landscape of the system was obtained. This surface was then projected down to a 2D free energy profile, for which the binding free energy is determined (as described in the methods section). The favorable orientation and conformation at discrete positions of tartrate from the surface is explored by the 3D free energy contour plots.The free energy landscape shown for the first energy minimum as a function of molecular orientation and dihedral angle indicates a global minimum at cos(θ) ≈ 0 and dihedral angle of 172° (Fig. 5(b)). In this most stable adsorption configuration, tartrate is oriented parallel to the surface in its trans conformation. The corresponding structure is shown in Fig. 6(a). Both carboxylate groups interact with the interfacial water molecules, located above the two Ca surface sites, whereas hydroxyl groups penetrate the water layer interacting with surface CO3 groups. At the second energy minimum, tartrate is oriented almost perpendicular to the surface (cos(θ) = 0.8), with one of the hydroxyl groups pointing towards the bulk solution (Fig. 6(b)). The hydroxyl group penetrates into the first water layer, however the direct interactions between charged carboxylate groups and surface ions were not observed in any of the identified adsorption configurations for the (104) surface. It seems that the presence of the surface carbonate ions specifically arranged and exposed on the (104) surface makes the direct binding of the carboxylate groups to the calcium ion unfavorable. Nevertheless, stable adsorption of the tartrate molecule to the (104) surface in a water-separated configuration is favored by the possibility to form strong hydrogen bonds between the ordered water molecules and the carboxylate groups. Moreover, hydroxyl groups could form hydrogen bonds with outermost CO3 groups as well as interactions within the first two interfacial water layers.
At the global minimum of −38.25 kJ mol−1, the tartrate molecule lies 0.28 nm from the surface adsorbed only in trans conformation, whereas at the local minima both gauche and trans conformations were observed. Interestingly, for the local minima positioned at 0.38 nm from the surface the gauche conformation is significantly stabilized when adsorbed on the (1−10) calcite surface. The tartrate molecule changes its conformation in order to match the surface geometry. This is clearly evident from the free energy landscape plotted as a function of dihedral angle and molecular orientation at fixed tartrate positions corresponding to the two minima 0.28 nm (Fig. 7(b)) and 0.38 nm (Fig. 7(c)). For the first minimum tartrate lies 0.28 nm with the dihedral angle of 161° indicating trans conformational state when adsorbed. Beside the global minimum at −38.25 kJ mol−1, where the tartrate molecule is oriented parallel to the surface, cos(θ) ≈ 0, two additional local minima exist with tartrate in perpendicular orientation, cos(θ) = 0.8 and −0.9, respectively. However, the surface-induced conformational change is evident for the adsorbed configuration positioned at 0.38 nm, where gauche conformation, with the dihedral angle of 54°, is favored. To closely match the outermost surface ions, the tartrate molecule is oriented parallel to the surface, cos(θ) ≈ 0.
The structures corresponding to the two energy minima are shown in Fig. 8. At the binding configuration closest to the surface, the polar functional groups of tartrate are not only bonded to the outermost surface ions but also to the underlying Ca sites (in the second layer) (Fig. 8(a, b)). In this case we can define tartrate as incorporated into the (1−10) surface since one of the polar functional groups matches the position and orientation of the carbonate lattice ions.44 In the most stable configuration one of the carboxylate groups fits into the (1−10) surface, coordinated by three different Ca surface sites (Fig. 8(b)). Specifically, the incorporated carboxylate group forms a stable interaction with two outermost Ca sites at a Ca–O distance of 0.22 and 0.24 nm, and with one underlying Ca site at a Ca–O distance of 0.23 nm. Both hydroxyl groups interact strongly with oxygen atoms of a two outermost CO3 surface groups at H–OCO2 distances of 0.16 and 0.22 nm. Apart from that, one of the hydroxyl groups additionally binds via oxygen atom with an underlying Ca site with a Ca–O distance of 2.33 nm. Another, similar stable configuration is shown on Fig. 8(b), where one of the carboxylate groups is incorporated in the (1−10) surface. In this state tartrate is oriented parallel to the surface as well, forming strong interactions with each of the hydroxyl groups at H–OCO2 distances of 0.18 and 0.22 nm. The incorporated carboxylate group is coordinated with four Ca sites, two outermost and two underlying, with Ca–O distances 0.24, 0.23 and 0.24, 0.26 nm, respectively. Tartrate incorporation in the surfaces is additionally stabilized by the possible hydrogen bonding between hydroxyl groups and outermost CO3 groups. In both configuration cases described above, the carboxylate group oriented perpendicular to the surface perfectly fits into the lattice positions normally occupied by carbonate ions of (1−10) surface. This finding is in good agreement with the experimental results showing that organic molecules, with carboxylate side groups, could preferentially adsorb and incorporate into (1−10) calcite interfaces.13–16 The incorporation of organic molecules leads to a distortion of the crystal lattice in c-direction, and high resolution powder diffraction studies14 supported the model that the incorporation of acidic macromolecules in biogenic calcite occurs on this specific crystal planes that are parallel to the crystallographic c-axis. It was proposed that this should occur by the specific interaction of the acidic residues, i.e. carboxylate groups that can replace the lattice carbonate ions in these planes. Our simulation results directly support this proposal.
At the local minimum, where tartrate lies 0.38 nm from the surface, the tartrate molecule changes its conformation in order to match the surface geometry to maximize its interactions with the outermost surface ions (Fig. 8(c, d)). In this particular configuration tartrate lies parallel to the surface and forms four stable interactions with the surface. Each of the carboxylate groups interacts strongly with the outermost Ca surface sites; the one in a monodentate mode with Ca–O distance of 0.22 nm and the other in bidentante mode with Ca–O distances of 0.22 and 0.34 nm. Each of the hydroxyl groups directly binds to the oxygen atoms of the outermost CO3 groups at H–OCO2 distances of 0.22 and 0.23 nm. Thus, the (1−10) geometry of the outermost surface sites closely matches the particular gauche conformation of tartrate with the corresponding dihedral angle of 54°. Despite the higher energy of the gauche conformation, adsorption at the (1−10) surface is energetically more favorable than for the otherwise more stable trans conformation in solution, indicating that the close interaction at the surface overcompensates the higher conformational energy. This emphasizes the importance of preorganization of functional groups to closely match the surface structure to stabilize the adsorption. Such mechanism of interaction could also be important for other organic molecules, for examples in the case of highly efficient multifunctional growth-modifiers, such as organic polymers or biomolecules, capable of forming multiple conformations. Similar study simulating tri-peptide adsorption onto hydroxyapatite,45 also pointed to such a possible mechanism of adsorption with the surface-induced conformational change of tri-peptide.
The results of interfacial structure analysis and metadynamics showed that the interactions between tartrate and different calcite faces strongly relate to the structure of (104) and (1−10) calcite–water interfaces. The differences in tartrate adsorption affinities for these two surfaces can be interpreted in terms of surface energetics and differently arranged surface ions. The energy difference between the lowest-energy (104) surface and more reactive (1−10) surface is Δγ = 0.3 J m−2. Thus, the (1−10) surface must be significantly stabilized and prevented from growing out, to be exposed in the final crystal morphology (Fig. 1). Adsorption of the tartrate molecules, could stabilize this otherwise high-energy and fast-growing face. Interactions between tartrate and the (1−10) are stronger with this particular higher energy surface due to special arrangements of the surface ions and their higher reactivity, i.e. higher partial charges. Surface ions specifically arranged and exposed on the (1−10) surface enables the direct binding of carboxylate groups to calcium ions with the simultaneous binding of both hydroxyl groups to neighboring surface carbonate ions. Especially, the position of the surface carbonate group, oriented perpendicular to the surface has a positive effect, where carboxylate functional group fits into the lattice position normally occupied by carbonate ions, and thus coordinate to several calcium ions. On contrary, more than the twice higher surface ion density of the (104) surface (5.0 ions nm−2 > 2.4 ions nm−2) makes the direct binding of the charged carboxylate groups to the calcium ion unfavorable due to the close repulsive interactions with the surface carbonate ions exposed on the (104) surface as well as lower partial charges of surface ions on this stable face.
Moreover, local water density variations at the interface affect the adsorption binding modes of tartrate, which significantly differs for the two surfaces. The structuring of the water is higher for the (104) face, most probably due to the higher density of the surface ions which favors the adsorption of water molecules forming multiple layers above the surface. Within these ordered layers water molecules not only interact with the surface ions but also form strong lateral interactions. Keresit et al.46 demonstrated that water binding energy (−2 kJ mol−1) is small relative to the adsorption energy of water (−45 kJ mol−1) indicating a free-energy loss by an entropic term, i.e. significant structuring at the interface. Thus, tartrate not only competes with water molecules for the biding sites on the (104) surface but can also interact with highly-structured interfacial water. However, the extent of such interactions are significantly lower in comparison to the direct interactions with the highly charged surface ions exposed on the more reactive (1−10) surface. Thus, we confirm that interfacial water is crucial for the tartrate adsorption behavior on calcite surfaces, as it has previously been recognized for selective adsorption of polystyrene sulfonate on calcite5 and citric acid25 and amino acids23,47,48 on hydroxyapatite surfaces.
Growth of calcite is considered to proceed by the movement of steps on the most stable (104) surface. Therefore, the interaction of additive molecules with step sites on the (104) surface should also be considered, as the previous simulations demonstrated that small carboxylated molecules preferentially adsorb along the step sites of the growing (104) surface, rather than on the (104) terraces.6,22,49 Such a selective interaction of the additive with step sites on the (104) surface could be an important mechanism in the early evolution of the morphological change, influencing the topography of the crystal face. Experimental studies indicated that tartrate19 and dicarboxylated amino-acids41,49 exhibit new edges on (104) calcite surface suggesting the formation of specifically oriented steps of the original (104) face. Interactions first occur at the step edges of the {104} surfaces which finally results in the expression of near-{hk0} faces, stabilized by an additive.
The strong preferential binding of tartrate to the (1−10) calcite surface in comparison to weak, water-mediated binding on the (104) surface, explains why tartrate stabilizes the higher energy (1−10) surface and inhibits the growth in this direction. This result agrees well with the experimental observation that tartrate modulates the calcite morphology by exposing the {1−10} faces.19 Thus, the crystal can grow in the direction perpendicular to the (104) face but growth is limited perpendicular to the (1−10) face, resulting in a prismatic morphology combined with two forms, predominantly expressed prismatic {1−10} form and basal {104} faces (Fig. 1).
4. Conclusions
The molecular interactions of tartrate with calcite surfaces in aqueous solution were investigated by molecular dynamics simulations to understand additive-mediated crystal growth. The metadynamics approach was employed to determine the adsorption binding energies as a function of tartrate conformation, orientation and position near (104) and (1−10) calcite surfaces.The results emphasize the importance of the surface energetics, structural matching as well as interfacial water layers in calcite–tartrate interactions. It was found that the adsorption behavior of tartrate is quite different for the two surfaces. Tartrate was more loosely adsorbed on the (104) surface mainly interacting via a water-mediated binding. On the other hand, tartrate was directly and irreversibly bonded to the (1−10) surface with two stable configurations identified: (1) adsorbed tartrate with the effect of surface-induced conformational change, favoring gauche conformation to closely match the geometry of the outermost surface ions; (2) incorporated tartrate into the surface where carboxylate group, oriented perpendicular to the surface, coordinate with outermost and underlying Ca sites, substituting the lattice carbonate ion. Incorporation of tartrate, by fitting the carboxylate group into lattice positions, is additionally stabilized by binding of both hydroxyl groups to neighboring surface carbonate ions. Thus, preorganization of both charged carboxylate functional groups as well as polar hydroxyl groups plays important role in the strength of the interactions.
The large difference in the adsorption modes for these two surfaces are responsible for preferential adsorption on {1−10} faces, which thus become more pronounced in the calcite morphology at the expense of the {104} faces, which are less affected by tartrate. These results indicate that the strong adsorption of tartrate on {1−10} surfaces could stabilize these otherwise fast-growing and higher energy faces and thus inhibit crystal growth in {1−10} directions. The results also supported the hypothesis that incorporation of acidic molecules in calcite could occur on (1−10) faces by fitting side chains carboxylate functional groups into carbonate lattice positions. Our study demonstrated that MD simulations coupled with metadynamics can be used as a powerful tool for free energy sampling of all possible adsorbed states giving valuable insight into mechanisms and modes of molecular interactions on crystal/water-additive interfaces. The obtained results contribute to fundamental understanding of the molecular interactions between different crystal surfaces and organic additives needed for rational development of novel growth-controlling additives. Our future work will focus on simulating the growth from supersaturated solutions of specific fast-growing calcite faces, such as (1−10), in the presence of organic additives.
Acknowledgements
This work was supported by the German Research Foundation (DFG) under project numbers 2035/4-1 and 2035/8-1, and made use of the computer resources provided by the Leibniz Supercomputing Centre. M. Ukrainczyk gratefully acknowledges the support by the TU München Foundation Fellowship.References
- K. Sangwal, Additives and Crystallization Processes: From Fundamentals to Applications, John Willey & Sons, Chichester, 2007 Search PubMed.
- R.-Q. Song and H. Cölfen, CrystEngComm, 2011, 13, 1249–1276 RSC.
- M. Salvalaglio, T. Vetter, F. Gilberti, M. Mazzotti and M. Parrinello, J. Am. Chem. Soc., 2012, 134, 17221–17233 CrossRef CAS PubMed.
- C. Schmidt and J. Ulrich, J. Cryst. Growth, 2012, 353, 168–173 CrossRef CAS.
- J. Shen, C. Li, N. F. A. van Vegt and C. Peter, J. Phys. Chem. C, 2013, 117, 6904–6913 CAS.
- N. A. J. M. Sommerdijk and G. De With, Chem. Rev., 2008, 108, 4499–4550 CrossRef CAS PubMed.
- Industrial Minerals Association, CCA-Europe, http://www.cca-europe.eu/mineral-applications.html, (accessed June 2014).
- M. Ukrainczyk, J. Kontrec and D. Kralj, J. Colloid Interface Sci., 2009, 329, 89–96 CrossRef CAS PubMed.
- J. Kontrec, M. Ukrainczyk, V. Babić-Ivančić and D. Kralj, Croat. Chem. Acta, 2011, 84, 25–32 CrossRef CAS.
- L. Estroff and I. Cohen, Nat. Mater., 2011, 10, 810–811 CrossRef CAS PubMed.
- Y. J. Lee and R. J. Reeder, Geochim. Cosmochim. Acta, 2006, 70, 2253–2263 CrossRef CAS; B. L. Phillips, Y. J. Lee and R. J. Reeder, Environ. Sci. Technol., 2005, 39, 4533–4539 CrossRef PubMed.
- M. Ukrainczyk, M. Gredičak, I. Jerić and D. Kralj, Cryst. Growth Des., 2014, 14, 4335–4346 CAS.
- L. Addadi and S. Weiner, Angew. Chem., Int. Ed. Engl., 1992, 31, 153–169 CrossRef.
- B. Pokroy, A. N. Fitch and E. Zolotoyabko, Adv. Mater., 2006, 18, 2363–2368 CrossRef CAS.
- D. B. De Oliveira and R. A. Laursen, J. Am. Chem. Soc., 1997, 119, 10627–10631 CrossRef CAS.
- A. Wierzbicki, C. S. Sikes, J. D. Madura and B. Drake, Calcif. Tissue Int., 1994, 54, 133–141 CrossRef CAS PubMed.
- S. Mann, J. M. Didymus, N. P. Sanderson, B. R. Heywood and E. J. A. Samper, J. Chem. Soc., Faraday Trans., 1990, 86, 1873–1880 RSC.
- C. L. Freeman, I. Asteriadis, M. Yang and J. H. Harding, J. Phys. Chem. C, 2009, 113, 3666–3673 CAS.
- M. Ukrainczyk, J. Stelling, M. Vucak and T. Neumann, J. Cryst. Growth, 2013, 369, 21–31 CrossRef CAS.
- C. Geffroy, A. Foissy, J. Persello and B. Cabane, J. Colloid Interface Sci., 1999, 211, 45–53 CrossRef CAS PubMed.
- W. Shi, C. Ding, J. Yan, X. Han, Z. Lv, W. Lei, M. Xia and F. Wang, Desalination, 2012, 291, 8–14 CrossRef CAS.
- N. H. de Leeuw and T. G. Cooper, Cryst. Growth Des., 2004, 4, 123–133 CAS.
- Z. Xu, Y. Yang, Z. Wang, D. Mhonoto, C. Shang, Z. Liu, Q. Cui and N. Sahai, J. Comput. Chem., 2014, 35, 70–81 CrossRef CAS PubMed.
- B. Zhu, X. Xu and R. Tang, J. Chem. Phys., 2013, 139, 234705 CrossRef PubMed.
- N. H. de Leeuw and J. A. L. Rabone, CrystEngComm, 2007, 9, 1178–1186 RSC.
- P. Raiteri, J. D. Gale, D. Quigley and P. M. Rodger, J. Phys. Chem. C, 2010, 114, 5997–6010 CAS.
- P. Fenter, S. Keresit, P. Raiteri and J. D. Gale, J. Phys. Chem. C, 2013, 117, 5028–5042 CAS.
- S. Xiao, S. A. Edwards and F. Gräter, J. Phys. Chem. C, 2011, 115, 20067–20075 CAS.
- A. Barducci, M. Bonomi and M. Parrinello, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 826–843 CrossRef CAS.
- D. van der Spoel, E. Lindahl, B. Hess, G. Groenhof, A. E. Mark and H. J. C. Berendsen, J. Comput. Chem., 2005, 26, 1701–1718 CrossRef CAS PubMed.
- J. Wang, R. Wolf, J. Caldwell, P. Kollman and D. Case, J. Comput. Chem., 2004, 25, 1157–1174 CrossRef CAS PubMed.
- A. D. Bochevarov, E. Harder, T. F. Hughes, J. R. Greenwood, D. A. Braden, D. M. Philipp, D. Rinaldo, M. D. Halls, J. Zhang and R. A. Friesner, Int. J. Quantum Chem., 2013, 113, 2110–2142 CrossRef CAS.
- E. Vanquelef, S. Simon, G. Marquant, E. Garcia, G. Klimerak, J. C. Delepine, P. Cieplak and F.-Y. Dupradeau, Nucleic Acids Res., 2011, 39, W511–W517 CrossRef CAS PubMed.
- C. Bayly, P. Cieplak, W. Cornell and P. Kollman, J. Phys. Chem., 1993, 97, 10269–10280 CrossRef CAS.
- S. D. Fleming and A. L. Rohl, Z. Kristallogr., 2005, 220, 580–584 CAS.
- B. Kvamme, T. Kuznetsova and D. Uppstand, J. Math. Chem., 2009, 46, 756–762 CrossRef CAS; M. F. Roberto, B. Marco and A. Dino, Cryst. Growth Des., 2010, 10, 4096–4100 Search PubMed.
- Q. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 CrossRef PubMed.
- A. Laio and F. L. Gervasio, Rep. Prog. Phys., 2008, 71, 126601–126623 CrossRef.
- M. Bonomi, D. Branduardi, G. Bussi, C. Camilloni, D. Provasi, P. Raiteri, D. Donadio, F. Marinelli, F. Pietrucci, R. A. Broglia and M. Parrinello, Comput. Phys. Commun., 2009, 180, 1961–1972 CrossRef CAS.
- N. H. de Leeuw and S. Parker, J. Phys. Chem., 1998, 102, 2914–2922 CrossRef CAS.
- M. Ukrainczyk, M. Gredičak, I. Jerić and D. Kralj, J. Colloid Interface Sci., 2012, 365, 296–307 CrossRef CAS PubMed.
- M. Hoffmann, J. Grajewski and J. Gawronski, New J. Chem., 2010, 34, 2020–2026 RSC.
- J. Gawronski, K. Gawronska, O. Skowronek, U. Rychlewska, B. Warzajtis, J. Rychlewski, M. Hoffmann and A. Szarecka, Tetrahedron, 1997, 53, 6113–6144 CrossRef CAS.
- E. Elts, M. Greiner and H. Briesen, J. Chem. Theory Comput., 2014, 10, 1686–1697 CrossRef CAS.
- N. Almora-Barrios and N. H. de Leeuw, CrystEngComm, 2009, 12, 960–967 RSC.
- S. Keresit and S. Parker, J. Am. Chem. Soc., 2004, 126, 10152–10161 CrossRef PubMed.
- J. Tao, H. Pan, Y. Zeng, X. Xu and R. Tang, J. Phys. Chem. B, 2007, 111, 13410–13418 CrossRef CAS PubMed.
- H. Pan, J. Tao, X. Xu and R. Tang, Langmuir, 2007, 23, 8972–8981 CrossRef CAS PubMed.
- C. A. Orme, A. Noy, A. Wierzbicki, M. T. McBride, M. Grantham, H. H. Teng, P. M. Dove and J. J. DeYoreo, Nature, 2001, 411, 775–779 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c4ce01447b |
| This journal is © The Royal Society of Chemistry 2015 |