Solid state structures of p-cresol revisited

Abstract

The two previously reported solid state forms of p-cresol are revisited and detailed structural analysis, thermal analysis, lattice energy calculations and variable temperature powder X-ray diffraction are presented. A possible mechanism for the transformation from form II to form I is proposed.

---

Polymorphism, the ability of a compound to crystallise in different forms, is an interesting phenomenon in solid state chemistry.¹ In the pharmaceutical industry, polymorphism is a key issue since the different forms of a drug can have different physicochemical properties such as melting point, solubility and bioavailability.² Similarly, different forms of pigments have profound impact on the paint and coatings industries. In some cases a mechanism for the transformation of one form to another can be deduced from a consideration of the crystal structures of each.

p-Cresol (4-methylphenol) is extracted from coal tar and is used in chemical synthesis of antioxidants, anisaldehyde, pharmaceuticals and dyes.³ Apart from its uses in the manufacturing industry, p-cresol has also been widely used as a crystallisation solvent. Two solid state structures of p-cresol were reported several years ago on separate occasions. Form I crystallises from a chloroform solution in the monoclinic space group P2₁/n (refcode CRESOL01⁴ and CRESOL10⁵), while the metastable form II crystallises from an acetone solution in the monoclinic space group C2/c (CRESOL02⁶). Both forms are low-melting solids, with melting points of approximately 35 and 36 °C respectively. Polymorphism of organic liquids is not an uncommon occurrence and it has been reported for a number of compounds. In order to investigate the occurrence of polymorphism of organic solvents we identified common organic solvents with melting points in the range of 0 to 35 °C and a Cambridge Structural Database (CSD version 5.35 May 2014)⁷ search on these compounds revealed polymorphism of the following: formamide,⁸ 4-picoline,⁹ benzene,¹⁰ cyclohexane,¹¹ formic acid,¹² 1,4 dioxane,¹³p-xylene,¹⁴ acetic acid,¹⁵ cyclohexanol,¹⁶ tertiary-butyl alcohol¹⁷ and diphenylether.¹⁸ Polymorphs of most of these compounds were prepared by in situ crystallisation at low temperature or high pressure, but there are a few exceptions such as p-cresol and cyclohexanol, where the polymorphs can be obtained at ambient or near ambient conditions respectively.

Because the crystallographic information on p-cresol is limited (the two structures deposited in the CSD are only modestly refined and some hydrogen atoms are missing from the final model) we carried out a polymorphic study of the two forms of p-cresol. We recollected the data at 173 K; the improved refinement allows the hydrogen bonding to be described in detail.‡ In addition, Hirshfeld surface analysis¹⁹ was used to compare the intermolecular interactions in the two forms. Lattice energy calculations, differential scanning calorimetry (DSC) and variable temperature powder X-ray diffraction (VTPXRD) were used to further study the two forms. Finally, we propose a possible mechanism for the transformation of form II to form I.

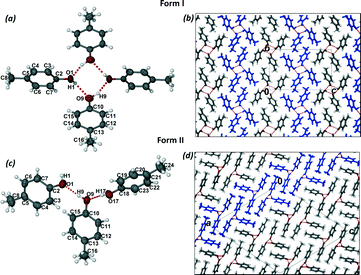
Crystals of form I were grown by dissolving p-cresol in chloroform and allowing the solution to crystallise at room temperature. Form I crystallises in the monoclinic space group P2₁/n with two molecules of p-cresol in the asymmetric unit (Fig. 1a). The methyl groups are disordered in two positions and the p-cresol molecules are connected via two hydrogen bonds (Table 1) to form a hydrogen bonded puckered tetramer which is located on an inversion centre. The hydrogen bonding can be denoted as R⁴₄(8) using the graph set notation.²⁰ The hydrogen bonded tetramers stack in rows parallel to the bc plane and are arranged in an alternating fashion (Fig. 1b). The packing is further stabilised by (i) C–H⋯π interactions between units in the same row and units in consecutive rows which are symmetry related by inversion and (ii) weak C–H⋯O interactions between the disordered methyl groups (–C16H₃) and the neighbouring hydroxyl oxygen (O9).

Fig. 1 (a) The molecular structure of form I showing 70% probability ellipsoids for non-hydrogen atoms. (b) The packing diagram of form I as viewed along the a axis. (c) The asymmetric unit of form II showing 70% probability ellipsoids for non-hydrogen atoms. (d) The packing diagram of form II as viewed along the b axis.

Table 1 Hydrogen bond details for form I and form II

D–H⋯A	D–H^a (Å)	H⋯A (Å)	D⋯A (Å)	∠DHA (°)
Symmetry operators: (i) −x, −y + 1, −z + 1; (ii) 1/2 − x, y − 1/2, 3/2 − z and (iii) x, y − 1, z.a Adjusted according to Lusi and Barbour's distance-dependant neutron-normalised method.^21
Form I
O1–H1⋯O9	0.95	1.97	2.719(2)	134.1
O9–H9⋯O1^i	0.95	1.79	2.673(2)	153.8
C16–H16C⋯O9^ii	0.98	2.42	3.370(2)	152.0
Form II
O1–H1⋯O17^iii	0.95	1.73	2.674(1)	169.7
O9–H9⋯O1	0.96	1.69	2.630(1)	166.7
O17–H17⋯O9	0.95	1.72	2.656(1)	168.2

---

Crystals of form II were grown from an acetone solution of p-cresol at room temperature. Form II crystallises in the monoclinic space group C2/c with three molecules of p-cresol in the asymmetric unit (Fig. 1c). The hydrogen atoms of the methyl groups are disordered over two positions similarly to form I. The p-cresol molecules interact with each other via three hydrogen bonds (Table 1) resulting in a pseudo threefold helical chain running parallel to the b axis (Fig. 1d). The graph set notation for the hydrogen bonding motif is C³₃(6). The 1D chains are paired up in the ac plane (Fig. 1d) and the two chains interact with each other as well as with neighbouring chains via C–H⋯π interactions. An interesting packing feature is observed when viewing the structure of form II down the a axis. In this direction the p-cresol molecules are packed in a fashion that can be perceived as the ‘Zöllner illusion’ (Fig. 2). In this illusion the parallel lines appear to converge or diverge from each other.

Fig. 2 The packing diagram of form II as viewed down the a axis showing the Zöllner illusion.

p-Cresol may be described as an aromatic alcohol thus its interactions can be compared to secondary monoalcohols which most commonly form rings or chains of hydrogen bonds in approximately equal numbers. Thus the observation of the puckered tetramer and the pseudo threefold helical hydrogen bond motifs are rare for alcohols and their occurrence can be explained by steric effects.²² In this regard, p-cresol is somewhat similar to cyclohexanol, a secondary monoalcohol with a bulky substituent. In the stable form of cyclohexanol^16a (form II) a planar four-membered ring motif was observed while one of the metastable forms (form III′) contains threefold helical chains. It was concluded that the formation of the tetramer relieves the strain of the shorter hydrogen bonds of the chain structure leading to the formation of the more stable phase. A similar conclusion may be drawn for the p-cresol structures as the hydrogen bonds are slightly shorter in the metastable form (II) than in the stable form (I).

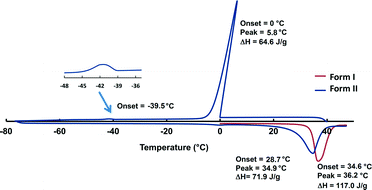
DSC was conducted on the crystals of form I as well as the neat liquid (Fig. 3, original DSC data are deposited into the ESI,† Fig S1 and S2). The DSC trace of crystals of form I in the range of 0–50 °C (heating rate of 10 °C min⁻¹) shows an endothermic event at 36.2 °C corresponding to the melting of the crystals (T_on = 34.6 °C, ΔH = 117.0 J g⁻¹). In order to determine the melting point of the metastable form II, the DSC trace was cycled by heating the crystals of form I to 50 °C followed by cooling to −80 °C then heating back to 50 °C with a heating rate of 10 °C min⁻¹. The DSC trace shows an exothermic event at 0 °C corresponding to the freezing of the liquid to amorphous phase (T_peak = 5.8 °C, ΔH = 64.6 J g⁻¹). Crystallisation to form II is observed at ca. −39 °C as a broad exotherm. The melting of form II in the subsequent heating cycle is seen as an endothermic event at 34.9 °C (T_on = 28.7 °C, ΔH = 71.9 J g⁻¹). The enthalpy difference between the structures derived from the heat of melting was 1.1 kcal mol⁻¹ and this value is typical for polymorphs. The observed significant hysteresis between the cooling (liquid freezes to amorphous and later crystallises) and the heating cycle (crystalline material melts) can be explained by the difference between the amorphous and crystalline nature of the sample. A similar thermal behaviour was described for tertiary-butyl alcohol,^17a however the first large exotherm was defined as a crystallisation while in our case this peak is clearly related to the freezing of the liquid to an amorphous phase.

Fig. 3 The DSC trace (endo down) of form I (red) and form II (blue). Crystallisation of form II is observed at −39.5 °C. Peak temperature for form I is 36.2 °C and peak temperature for form II is 34.9 °C.

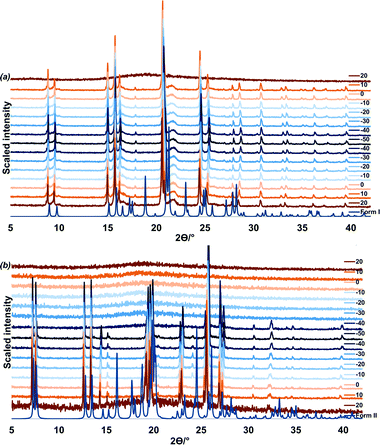
A VTPXRD study (Fig. 4) was conducted on the liquid p-cresol in order to verify the DSC results. Two experiments were carried out and for each experiment the liquid was loaded into a capillary and patterns were recorded at 10 °C intervals for 7.5 min scanning time.

Fig. 4 VTPXRD study for in situ crystallisation of (a) from top: form I recorded at 10 °C intervals, ten minute equilibration was allowed after every temperature change and (b) from top: form II recorded at 10 °C intervals, one minute equilibration was allowed after every temperature change.

In the first experiment, liquid p-cresol was first heated to 50 °C, cooled to −50 °C and heated back to 50 °C (Fig. 4a). The sample was allowed 5 minutes equilibration after every temperature change. In the cooling cycle, the sample is amorphous from 50 to 20 °C; form I crystallises at 10 °C. This phase persists through cooling to −50 °C and heating to 20 °C after which melting commences.

In the second experiment, the liquid was cooled from 20 °C to −50 °C and heated back to 20 °C. One minute equilibration was allowed after every temperature change (Fig. 4b). From 20 °C to −30 °C the sample remains amorphous. At −40 °C form II crystallises. This corresponds to the event on the DSC at −39.1 °C. Form II persists until 20 °C after which melting commences. (Additional VTPXRD data is presented in Fig. S3 and S4 of ESI.†) We may conclude that the fast freezing method leads to the formation of the less stable polymorph, form II.

According to the rules developed by Burger and Ramberger, the thermodynamic relationship between polymorphic forms can be classified as either monotropic or enantiotropic.²³ A monotropic relationship occurs when one polymorph is stable below the melting point and conversion from the metastable to stable form is irreversible. In an enantiotropic relationship, polymorphs interconvert reversibly below their melting point.²⁴ We therefore postulate that the relationship between the two polymorphs of p-cresol is monotropic. This is in agreement with the calculated density of form I (1.193 g cm⁻³), which is higher than that of form II (1.130 g cm⁻³).

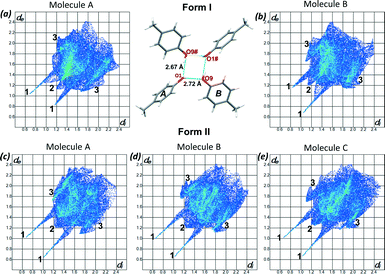
To understand the differences between the thermal behaviour of the polymorphs a detailed structural study was conducted by using the programme Crystal Explorer.¹⁹ Hirshfeld surfaces and 2D fingerprint plots were generated for each molecule in the asymmetric unit of both form I and form II to compare the intermolecular interactions as well as their contributions in the two structures. Fig 5(a) and (b) show the fingerprint plots for the two molecules of form I and Fig 5c–e presents the 2D plots for the three molecules of form II. As expected the main interactions in the two structures are the O⋯H, and H⋯H and C⋯H, labelled as 1, 2 and 3 respectively. In form I the two symmetrically independent molecules have significantly different fingerprint plots. The spikes related to the O⋯H interactions are asymmetric and molecule A presents more hydrogen bond donor properties (longer upper spike) while molecule B acts more like an acceptor (longer lower spike) (Fig. 5a and b). In form II the interactions of the three symmetrically independent molecules are similar and this can be seen on their comparable fingerprint plots (Fig. 5c–e). This statement is also supported by the observed hydrogen bonds of form I and II. However the percentage contributions of each of the interactions are different in the two structures as shown in Table 2. On average H⋯H interactions (generally defined as repulsive) contribute more in form II than in form I while more of the O–H⋯O and C–H⋯C interactions were observed in form I than in form II. The higher percentage contribution of the O–H⋯O and the C–H⋯C in form I contributes to the higher melting point and consequently its stability. Lattice energy calculations²⁵ revealed only a 0.34 kcal mol⁻¹ energy difference between the two polymorphs favouring the formation of form I. The fact that the standard deviation (typically 0.5 kcal mol⁻¹) is greater than the calculated value does not detract from the significance of the result, as discussed below.

Fig. 5 2D fingerprint plots of (a) form I – molecule A, (b) form I – molecule B, (c) form II – molecule A, (d) form II – molecule B and (e) form II – molecule C. The close contacts are labelled 1–3 where 1 is H⋯O, 2 is H⋯H and 3 is C⋯H.

Table 2 Percentage contributions of the main interactions in form I and form II

	H⋯H (%)		C⋯H (%)		O⋯H (%)
Form I		Average		Average		Average
Molecule A	58.0	57.3	25.3	28.4	16.5	14.0
Molecule B	56.6		31.1		11.6
Form II
Molecule A	55.3		29.6		12.7
Molecule B	58.8	59.5	27.8	26.2	13.1	12.8
Molecule C	64.6		21.2		12.2

---

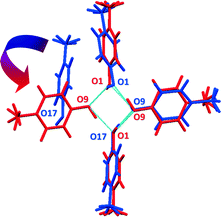
Form I can be obtained readily when a chloroform solution of p-cresol or the neat liquid is cooled at 4 °C; form II on the other hand, is difficult to reproduce and once it is formed it readily converts to form I when allowed to stand at room temperature for several days. Indeed DSC and the lattice energy calculations support the stability of form I over form II. However, we did not observe any phase changes in the PXRD or the DSC; also we were not able to induce the phase change (this is consistent with our suggestion of a monotropic relationship between the two forms). We suggest a transformation mechanism for the change from form II to form I. The two structures contain a common motif which consists of three hydrogen bonded p-cresol molecules. By overlaying these two motifs,²⁶ it can be seen that rotation of the fourth molecule in the helix of form II brings it into position to form a hydrogen bond to complete the tetramer in form I (Fig. 6).

Fig. 6 Overlay of form I (red) and form II (blue) showing the common motif in the two structures. The fourth molecule in form II can rotate and form hydrogen bonding to O1 in order to form the tetramer in form I.

In summary, we have reconsidered the two solid state structures of p-cresol. The stability of form I has been confirmed by DSC as well as lattice energy calculations. We have also shown that both forms can be grown in a capillary by controlling the cooling rate. Crystal structure analysis indicated that the two structures have different hydrogen bond motifs: a puckered tetramer and a pseudo threefold helical chain. The transformation from form II to form I requires substantial changes in the intermolecular bonding but the lattice energy calculations revealed only a 0.34 kcal mol⁻¹ energy difference.

The discovery of polymorphism is, no doubt, important in solid state chemistry. However, equally important is the study of structure–property relationships in these systems. Since the only difference between two polymorphs is structural, any differences in the properties can then be directly related to the structure.

Acknowledgements

We would like to thank the National Research Foundation of South Africa and Cape Peninsula University of Technology for financial support. Authors thank Prof. Jacco van de Streek (University of Copenhagen) for the lattice energy calculations. Authors also thank Prof. Consiglia Tedesco (University of Salerno) for her assistance with the PXRD analysis while she was visiting South Africa with the aid of the People Programme (Marie Curie Actions) of the European Union's Seventh Framework Programme (FP7/2007-2013/ under REA grant agreement no. PIRSES-GA-2012-319011).

Notes and references

1. (a) W. C. McCrone, Polymorphism in Physics and Chemistry of the Organic Solid State, ed. D. Fox, M. M. Labes and A. Weissberger, Interscience, New York, 1965, vol. II, p. 725; (b) J. Bernstein, Polymorphism in Molecular Crystals, Clarendon Press, Oxford, 2002.
2. J. D. Dunitz and J. Bernstein, Acc. Chem. Res., 1995, 28, 193.
3. H. Fiegein, Cresols and Xylenols, in Ullmann's Encyclopedia of Industrial Chemistry, Wiley-VCH, Weinheim, 2007.
4. P. C. Bois, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1970, 26, 2086.
5. P. C. Bois, Bull. Soc. Chim. Fr., 1966, 4016.
6. M. Perrin and A. Thozet, Cryst. Struct. Commun., 1974, 3, 661.
7. F. H. Allen, Acta Crystallogr., Sect. B: Struct. Sci., 2002, 58, 380.
8. (a) R. Gajda and A. Katrusiak, Cryst. Growth Des., 2011, 11, 4768; (b) J. Ladell and B. Post, Acta Crystallogr., 1954, 7, 559.
9. (a) M. Born, D. Mootz and S. Schaefgen, Z. Naturforsch., B: J. Chem. Sci., 1995, 50, 101; (b) U. Ohms, H. Guth, W. Treutmann, H. Dannohl, A. Schweig and G. Heger, J. Chem. Phys., 1985, 83, 273.
10. (a) A. Katrusiak, M. Podsiadlo and A. Budzianowski, Cryst. Growth Des., 2010, 10, 3461; (b) A. Budzianowski and A. Katrusiak, Acta Crystallogr., Sect. B: Struct. Sci., 2006, 62, 94; (c) E. G. Cox, D. W. J. Cruickshank and J. A. S. Smith, Proc. R. Soc. London, Ser. A, 1958, 247, 1; (d) G. E. Bacon, N. A. Curry and S. A. Wilson, Proc. R. Soc. London, Ser. A, 1964, 279, 98; (e) G. J. Piermarini, A. D. Mighell, C. E. Weir and S. Block, Science, 1969, 165, 1250.
11. (a) R. Kahn, R. Fourme, D. Andre and M. Renaud, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1973, 29, 131; (b) N. B. Wilding, J. Crain, P. D. Hatton and G. Bushnell-Wye, Acta Crystallogr., Sect. B: Struct. Sci., 1993, 49, 320.
12. (a) D. R. Allan and S. J. Clark, Phys. Rev. Lett., 1999, 82, 3464; (b) I. Nahringbauer, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1978, 34, 315; (c) F. Holtzberg, B. Post and I. Fankuchen, Acta Crystallogr., 1953, 6, 127.
13. (a) A. Olejniczak, A. Katrusiak and A. Vij, CrystEngComm, 2009, 11, 1240; (b) T. Koritsanszky, M. K. Strumpel, J. Buschmann, P. Luger, N. K. Hansen and V. Pichon-Pesme, J. Am. Chem. Soc., 1991, 113, 9148; (c) J. Buschmann, E. Muller and P. Uger, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1986, 42, 873.
14. (a) B. F. Mentzen and P. Gelin, Mater. Res. Bull., 1995, 30, 373; (b) H. van Koningsveld, A. J. van den Berg, J. C. Jansen and R. de Goede, Acta Crystallogr., Sect. B: Struct. Sci., 1986, 42, 491.
15. (a) A. Dawson, D. R. Allan, S. Parsons and M. Ruf, J. Appl. Crystallogr., 2004, 37, 410; (b) R. Boese, D. Blaser, R. Latz and A. Baumen, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1999, 55, 9900001.
16. (a) R. M. Ibberson, S. Parsons, D. R. Allan and A. M. T. Bell, Acta Crystallogr., Sect. B: Struct. Sci., 2008, 64, 573; (b) E. Sciesinska, J. Mayer, I. Natkaniec and J. Sciesinski, Acta Phys. Pol., A, 1989, 76, 617; (c) J. R. Green and D. R. Wheeler, Mol. Cryst. Liq. Cryst., 1969, 6, 13.
17. (a) P. A. McGregor, D. R. Allan, S. Parsons and S. J. Clark, Acta Crystallogr., Sect. B: Struct. Sci., 2006, 62, 599; (b) R. Steininger, J. H. Bilgram, V. Gramlich and W. Petter, Z. Kristallogr., 1989, 187, 1.
18. A. R. Choudhury, K. I. Slam, M. T. Kirchner, G. Mehta and T. N. Guru Row, J. Am. Chem. Soc., 2004, 126, 12274.
19. (a) M. A. Spackman and D. Jayatilaka, CrystEngComm, 2009, 11, 19; (b) S. K. Wolff, D. J. Grimwood, J. J. McKinnon, M. J. Turner, D. Jayatilaka and M. A. Spackman, CrystalExplorer (Version 3.1), University of Western Australia, 2010; (c) M. J. Turner, J. J. McKinnon, D. Jayatilaka and M. A. Spackman, CrystEngComm, 2011, 13, 1804.
20. J. Bernstein, R. E. Davis, L. Shimoni and N. L. Chang, Angew. Chem., Int. Ed. Engl., 1995, 34, 1555.
21. M. Lusi and L. J. Barbour, Cryst. Growth Des., 2011, 11, 5515.
22. R. Taylor and C. F. Macrae, Acta Crystallogr., Sect. B: Struct. Sci., 2001, 57, 815.
23. A. Burger and R. Ramberger, Microchim. Acta, 1979, 2, 273.
24. K. Park, J. M. B. Evans and A. S. Myerson, Cryst. Growth Des., 2003, 3, 991.
25. Private communication of Prof. Jacco van de Streek, University of Copenhagen, Denmark. For more information see ESI†.
26. Mercury CSD 3.3.1 - New Features for the Visualization and Investigation of Crystal Structures, C. F. Macrae, I. J. Bruno, J. A. Chisholm, P. R. Edgington, P. McCabe, E. Pidcock, L. Rodriguez-Monge, R. Taylor, J. van de Streek and P. A. Wood, J. Appl. Crystallogr., 2008, 41, 466.
27. COLLECT Data Collection Software, 1999, Nonius, Delft, The Netherlands.
28. R. Z. Otwinowski and W. Minor, Processing of X-ray Diffraction Data Collected in Oscillation Mode, Methods in Enzymology, Macromolecular Crystallography, part A, ed. C. W. Carter and R. M. Sweet, Academic Press, 1997, vol. 276, pp. 307–326.
29. G. M. Sheldrick, 1997, SHELXS-97 and SHELXL-97 programs for crystal structure determination and refinement, University of Gottingen, Germany.
30. L. J. Barbour, J. Supramol. Chem., 2000, 1, 86.

---

Footnotes

† Electronic supplementary information (ESI) available. CCDC 1026352, 1026353. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c4ce02334j

‡ Intensity data were collected on a Nonius Kappa CCD Single Crystal X-ray Diffractometer, using graphite monochromated MoKα radiation (λ = 0.7107 Å, T = 173 K) generated by a Nonius FR590 generator at 50 kV and 30 mV. A series of frames were recorded, each of width 1° in ø or in ω to ensure completeness of the data collected to θ > 28°. The unit cell was indexed from the first ten frames, and positional data were refined along with diffractometer constants to give the final cell parameters. The strategy for data collection was evaluated using COLLECT²⁷ software. Integration and scaling (DENZO and SCALEPACK)²⁸ resulted in unique data sets corrected for Lorentz polarization effects and for the effects of crystal decay and absorption by a combination of averaging of equivalent reflection and overall volume and scaling correction. Accurate unit cell parameters were refined on all data. The structure was solved using SHELXS-97²⁹ and refined using full-matrix least squares methods in SHELXL-97, within the X-Seed³⁰ graphical user interface. Non-hydrogen atoms were refined anisotropically. OH distances were calculated using the distance-dependent neutron-normalised method by Lusi and Barbour²¹ and appropriate constrains were applied during the refinement process. The hydrogen atoms bound to carbon atoms were placed at idealized position and refined as riding atoms. CCDC deposit numbers contain the supplementary crystallographic data for this paper. Crystal data for form I: CCDC 1026352, C₇H₈O, M = 108.13, 0.20 × 0.20 × 0.20 mm³, monoclinic, space group P2₁/n (no. 14), a = 5.6775(3), b = 11.7141(7), c = 18.3172(11) Å, β = 98.8320(10)°, V = 1203.77(12) ų, Z = 8, D_c = 1.193 g cm⁻³, F₀₀₀ = 464, MoKα radiation, λ = 0.71073 Å, T = 173(2) K, 2θ_max = 53.0°, 8636 reflections collected, 2479 unique (R_int = 0.0197). Final GooF = 1.054, R₁ = 0.0589, wR₂ = 0.1472, R indices based on 2143 reflections with I > 2sigma(I) (refinement on F²), 147 parameters, 0 restraints. Lp and absorption corrections applied, μ = 0.078 mm⁻¹. Crystal data for form II: CCDC 1026353, C₇H₈O, M = 108.13, 0.10 × 0.10 × 0.10 mm³, monoclinic, space group C2/c (no. 15), a = 26.2548(16), b = 6.0047(4), c = 27.3511(17) Å, β = 117.786(2)°, V = 3814.8(4) ų, Z = 24, D_c = 1.130 g cm⁻³, F₀₀₀ = 1392, MoKα radiation, λ = 0.71073 Å, T = 173(2) K, 2θ_max = 53.0°, 12 863 reflections collected, 3933 unique (R_int = 0.0230). Final GooF = 1.020, R₁ = 0.0377, wR₂ = 0.0936, R indices based on 3201 reflections with I > 2sigma(I) (refinement on F²), 220 parameters, 0 restraints. Lp and absorption corrections applied, μ = 0.074 mm⁻¹.

---