A backside fluorine-functionalized graphene layer for ammonia detection†
M. V.
Katkov
ab,
V. I.
Sysoev
a,
A. V.
Gusel'nikov
a,
I. P.
Asanov
ab,
L. G.
Bulusheva
ab and
A. V.
Okotrub
*ab
aNikolaev Institute of Inorganic Chemistry SB RAS, 3 Acad. Lavrentiev Ave., 630090 Novosibirsk, Russian Federation. E-mail: spectrum@niic.nsc.ru
bNovosibirsk State University, 2 Pirogova Str., 630090 Novosibirsk, Russian Federation
First published on 27th October 2014
Abstract
Graphene is a remarkable material with the best surface to volume ratio as a result of its 2D nature, which implies that every atom can be considered as a surface one. These features make graphene attractive for use as a sensing material; however, the limiting factor is the chemical inertness of pristine graphene. Here we propose a method to create reactive centers by removal of fluorine atoms from the outer surface of fluorinated graphene while preserving the backside fluorination. Such partially recovered graphene layers were produced by the action of hydrazine-hydrate vapor on initially non-conducting fluorinated graphite. The reduction degree of the material and its electrical response revealed upon ammonia exposure were controlled by measuring the surface conductivity. We showed experimentally that the sensing properties depend on the reduction degree and found the correlation of the adsorption energy of ammonia with the number of residual fluorine atoms by the use of quantum-chemical calculations.
1. Introduction
Graphene is a two-dimensional material considered as a single layer of graphite. Its unique electronic properties, supported by numerous physical measurements, have been of great interest in terms of both fundamental and practical aspects.1 Right after publishing the first studies on graphene demonstrating the change in the electronic state under the influence of an electric field,2 the idea of its use as a molecular sensor attracted much attention from sensor researchers.3 It was shown that interaction of a graphene surface with molecules in a gas phase produces a change in the surface electronic state.4–6 Moreover, the surface conductivity change can be induced by an electric field or charge transfer from/to an adsorbed molecule. These graphene properties allow using the material as a molecular sensor.7 The sensing properties of graphene structures obtained by mechanical cleavage,8 CVD synthesis9–12 and chemical exfoliation15–21 have been investigated over the past few years. However, it was figured out that pristine graphene is not a good sensing material because of the chemical inertness of its surface. In addition, it is not possible to produce graphene samples of more than several tens of microns in a plane dimension using the traditional exfoliation method, which limits the overall sensitivity. Graphene synthesized using the CVD method shows good sensing properties,11 which is probably due to a higher defect level of CVD graphene in comparison with exfoliated one. In general, the properties of graphene depend on the degree of its chemical modification. It was also shown that the deposition of semiconductor nanoparticles on a graphene surface could create selective gas sensors.13 Theoretical studies confirm that the presence of defects in a graphene lattice, for example, replacement of carbon atoms with silicon ones, enhances the sensing properties of the material.5,14The greatest number of research activities has been conducted the study of sensors based on graphite oxide. Recovered graphene oxide layers exhibit sensing properties towards nitrogen dioxide,15–18,19 ammonia,18 explosives,19,20 and vapor of organic solvents.21 This type of structure should be considered as the most effective for applications such as the manufacture of printed sensor samples. However, graphite oxide, particularly in the form of films made of separate overlapping particles with the size of about 10 μm, may not be the best sensor contender. It is known that oxygen atoms are arranged irregularly on the graphene planes forming different types of chemical bonds with the oxygen functional groups such as epoxy, hydroxyl, and carboxyl.22
Fluorinated graphite can be considered as an alternative to graphite oxide. Fluorination at room temperature results in fluorine bonding with approximately half the carbon atoms, the bare atoms forming the chains of conjugated carbon–carbon bonds.23 Previously, we proposed the design of a graphene layer on the surface of fluorinated graphite C2F by water24 or hydrazine25 vapor exposure and revealed an increase of the layer resistance upon ammonia adsorption. We expect that in such a reaction chemical bonds C–F remain on the inner side of the graphene. Electrical and sensing properties of such a one-side fluorinated graphene sheet will differ significantly from that of graphene. Being electrically conductive, the graphene sheet will have a significant positive charge due to the transfer of electron density to attached fluorine atoms. Here we demonstrate that the sensing properties of such a layer can be controlled by reduction time and invoke calculations within density functional theory (DFT) for understanding the nature of reduced graphene–ammonia interaction. Hydrazine-hydrate was used as a reductant, and changes in the structure and chemical composition of the surface layers of fluorinated graphite were monitored using the methods of Raman scattering and X-ray photoelectron spectroscopy (XPS).
2. Experimental
2.1. Materials and characterization
A plate of highly ordered pyrolytic graphite (HOPG) was fluorinated using saturated vapors of BrF3 and Br2 during 30 days.26 As the result of covalent attachment of fluorine atoms to both sides of a graphene sheet, the plate thickness increased by at least two times.27 For the sensor preparation, the plate was split into flakes with a typical size of about 2.5 × 5 mm2. Optical microscopy analysis showed that the detached flakes have multilayered structure and uniform bronze coloring (Fig. 1). A large number of wrinkles seen in the image indicates disturbance of initially planar graphene sheets with fluorination.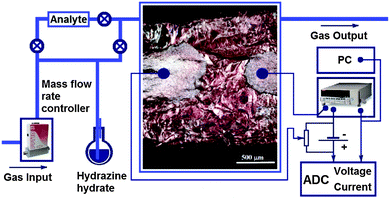 | ||
| Fig. 1 Experimental setup for the electrical measurements. An optical image of a fluorinated graphite C2Fx sample (x < 1) with applied silver contacts is shown in the center. | ||
A flake of fluorinated graphite (FG) was fixed on a Teflon plate, and two gold wire contacts were attached to the flake surface by a silver glue, which formed two silver terminals with a distance of about 0.5 mm between them. A glass cell with a volume of 25 mL was used for chemical reduction of the sample surface and for the sensor measurements as well. Argon with a flow rate of 10 mL min−1 was bubbled through a flask with hydrazine-hydrate and directed into the glass cell. A conductive layer on the flake surface was produced by the following reaction:28
| C2Fx + N2H4 → C + HF + N2 | (1) |
The measurements of the conducting properties of the sample were carried out using a picoammeter KEITHLY 6485. The change in resistance was observed by applying a DC voltage bias of 1 V to the sample contacts and registering the current flowing through the sensor. The schematic view of the experimental setup is shown in Fig. 1. By varying the recovery time, we obtained samples with different reduction degrees, which were controlled by measuring the sample conductivity. Depending on the treatment time (30, 45, 60, and 120 min), the samples were denoted as FG30, FG45, FG60, and FG120, respectively. The conductivity of the top layer was described by at least three exponential functions, indicating a rapid process of fluorine removal from the surface and diffusion of the reducing compound to the deeper layers of fluorinated graphite.25
The change in the structure and surface composition of the samples after exposure to NH3 was examined using Raman scattering and XPS. The Raman spectra were obtained on a Triplemate SPEX spectrometer using a 488 nm excitation source. The XPS spectra were recorded on a Phoibos 150 Specs spectrometer using a monochromatized Al Kα radiation source (Ehv = 1486.6 eV). The pass energy of the electron energy analyzer was set at 20 eV. The angle between the excitation beam and the entrance of the electron detector was 55°. The analyzed area was about 1 mm × 2 mm. Because of the dielectric properties of the initial sample, a charging effect was observed during the measurements, which was compensated by low-energy electron irradiation. The binding energies were internally calibrated to the energy of 285 eV due to surface carbon contamination.
2.2. Gas sensing measurements
The sensing properties of reduced fluorinated graphite were characterized under ambient conditions (room temperature and atmospheric pressure) by exposing to ammonia vapor mixed with an inert gas (argon) using the test installation schematically shown in Fig. 1. The measuring cell had two gas flow connectors (input and output). The gas flow rate in all experiments was 10 mL min−1. Analyzed gas premixed with pure Ar to a required concentration was released into the chamber. Gas flow rates were manipulated using mass flow controllers. A standard test cycle comprised three main steps, which included (1) exposing pure Ar to determine a baseline, (2) exposing the target gas mixed with Ar for response registration, and (3) regenerating the sensor to its original state using pure Ar (Fig. S1, ESI†). The relative response of the sensor was defined as the following: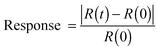 | (2) |
2.3. Quantum chemical calculations
Theoretical modelling of the adsorption of ammonia molecules on the partially fluorinated graphene surface was carried out within DFT using the three-parametrical hybrid functional of Becke29 and Lee–Yang–Parr correlation functional30 with a pair correction31,32 accounting for dispersion interactions (B3LYP-D3 method) as implemented in Jaguar 7.9 program package.33 Atomic orbitals were described using a 6-31G*+ basis set, including polarization and diffuse functions for all atoms except hydrogen. Fluorinated graphene models were constructed based on the C73H21 fragment, where hydrogen atoms saturate the dangling bonds of the boundary carbon atoms. The models of the following compositions C73FH21, C73F3H21, and C73F5H21 were obtained by adding one, three, and five fluorine atoms, correspondingly, to the basal plane of the model fragment. Fluorine atoms were arranged on one side of the fragment with the assumption that incomplete reduction occurs on the internal side of the fluorinated graphite layer after treatment with hydrazine-hydrate. An ammonia molecule was oriented in such a way that the hydrogen atoms or nitrogen atoms were directed to the central part of the non-fluorinated (external) model side. The geometry of the models was optimized completely using an analytical method to the gradient of 5 × 10−4 atomic units for taking into account the shift of the atomic position. The ultrafine grid was used for gradient calculations. The absence of imaginary frequencies indicated that the predicted configurations of ammonia correspond to the local minima on potential energy surfaces.The adsorption energy of NH3 on the reduced surface of fluorinated graphene was calculated as:
| Eads = ECFx + ENH3 − Ecomplex | (3) |
3. Results and discussion
The initial resistance of FG samples is several GΩ at room temperature. Exposing the samples to hydrazine vapor can remove fluorine atoms. That restores sp2 carbon bonds making the sample surface conductive. The longer the reduction time the lower the resistance, which decreased by more than 3 orders of magnitude while reducing a fluorinated graphite flake for tens of minutes (Table 1).| Sample | Reduction time (min) | Resistance (kΩ) |
|---|---|---|
| FG30 | 30 | 300 |
| FG45 | 45 | 90 |
| FG60 | 60 | 30 |
| FG120 | 120 | 5 |
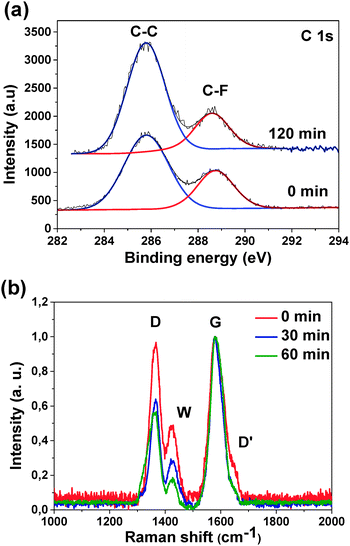
XPS C 1s spectra obtained at the excitation energy of 1486 eV, which allows X-rays to penetrate about three layers of fluorinated graphite, consist of two lines at 286 and 288.7 eV (Fig. 2(a)). The line at the higher binding energy comes from carbon atoms forming a C–F bond while carbon atoms that are not bonded to fluorine atoms contribute to the lower energy component. XPS data show an increase of the concentration of bare carbon atoms upon hydrazine-hydrate treatment, while the relative intensity of the C–F spectral component demonstrates an opposite behaviour. After the sample exposure for 120 min fluorine concentration reduces by half from 22 at% in the initial sample to 12 at% in the treated one. This fact indicates that after exposure to hydrazine-hydrate fluorine atoms leave the sample surface. The optimal exposure time is 30–45 min within our experimental conditions.
Fig. 2(b) compares the Raman scattering spectra of the samples FG, FG30 and FG60 after subtracting the fluorescent background and normalizing to the height of peak G. The spectra have two peaks at 1580 and 1360 cm−1 and a weak shoulder at 1640 cm−1 corresponding to the G, D and D′ vibration modes in graphite. The G mode corresponds to the vibrations of conjugated bonds, and the D and D′ modes are related to Raman scattering on the defects of the hexagonal graphite lattice. The C–F regions in fluorinated graphite can play the role of such defects. An additional pronounced peak (W) is observed at 1425 cm−1. The nature of this peak in the samples of fluorinated HOPG is not clear. As previously mentioned, the lines in the interval between D and G peaks can be attributed to distortions of carbon hexagons as a result of functionalization and formation of conjugated chains.34 As discussed in that work, the band at 1425 cm−1 is related to distortions on the boundaries between flat carbon areas and fluorinated carbon regions in a layer. The relative intensity ratio ID/IG was found to decrease from 1 for the original FG sample to 0.5 for the samples exposed to hydrazine-hydrate vapor. Besides, the D′ peak drops with increase in the exposure time. This indicates an increase of the crystallinity area in the graphene layer and decrease of imperfection related to the attachment of fluorine atoms. It is worth noting that after an exposure time of 60 min the relative intensity of the W peak drops faster than D and D′ peaks. This may stem from the fact that the hydrolysis process mentioned before forms defects in a graphite lattice, which slows down the growth of the crystalline size despite the removal of fluorine atoms.
One evidence of the removal of fluorine atoms is the increase of conductivity. However, the specific conductivity does not reach the typical values known for graphene (1 kΩ). Note that fluorine atoms located on the surface are much easily accessed by the hydrazine reagent and they reacted with a significantly higher probability compared to those inside during reduction.
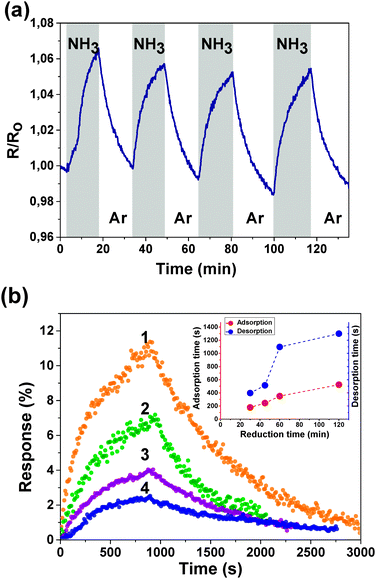
Fig. 3(a) shows the sensing properties of a reduced fluorinated graphite surface by demonstrating the change in the sensor resistance to the cyclic effect of 1% NH3 with the corresponding partial pressure at room temperature. When the adsorption of NH3 on the surface occurs, the electron density transfers from a NH3 molecule to the fluorinated graphene layer. That reduces the concentration of the major charge carriers and increases the resistance. Fig. 3(b) presents a single cycle of the sensor response when exposed to 1% of NH3 for samples FG30, FG45, FG60, and FG120. The maximum relative response is 11% for the sensor with 30 min reduction time. The relative response is dropped to 3% for the sensor with 120 min reduction time. That happens due to the removal of fluorine atoms from the internal surface of the first (the most active) layer of fluorinated graphite, which leads to a decrease in the number of reactive centers. Characteristic reaction times were calculated by fitting the experimental curves of adsorption and desorption with exponential functions and plotted against the reduction time (inset in Fig. 3(b)).
Both adsorption and desorption times increase with an increase in the reduction time. The response of the sensor to 1% NH3 which was directly exposed to an ammonia atmosphere (first cycle) and when it was exposed in flow using the gas system (second cycle) is shown in ESI† (Fig. S2). For the first cycle, the characteristic absorption time is ∼50 s and that for the second one is ∼300 s. In the latter case, the response time corresponds to the following two processes: establishing a constant concentration in the flask and adsorption of NH3 on the sample surface. The first characteristic time may be used to describe the sensor material itself, while the gas system setup is used for the precise concentration control.
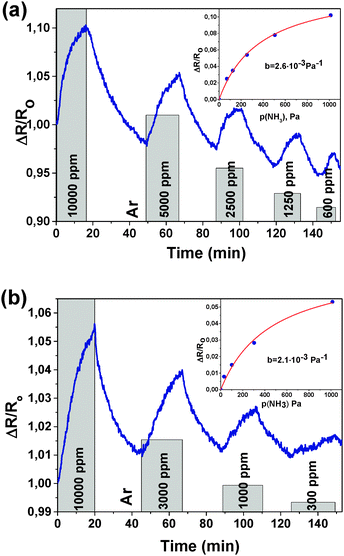
Experiments with different concentrations of NH3 were performed for samples FG30 and FG60 (Fig. 4). Sample FG30 with a reduction time of 30 min showed a response (resistance increase) of 10.2% to 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ppm with the initial resistance of 300 kΩ. The sample FG60 with a reduction time of 60 min showed 5.3% response to 10
000 ppm with the initial resistance of 300 kΩ. The sample FG60 with a reduction time of 60 min showed 5.3% response to 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ppm with the initial resistance of 30 kΩ. The relative response value decreases from about 10 to 2% with a NH3 concentration decrease from 10
000 ppm with the initial resistance of 30 kΩ. The relative response value decreases from about 10 to 2% with a NH3 concentration decrease from 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 to 600 ppm for sample FG30 (Fig. 4(a)). Sensor FG60 has a lower sensitivity in the concentration range from 10
000 to 600 ppm for sample FG30 (Fig. 4(a)). Sensor FG60 has a lower sensitivity in the concentration range from 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 to 300 ppm with a drop in the relative response from 5 to 1% (Fig. 4(b)).
000 to 300 ppm with a drop in the relative response from 5 to 1% (Fig. 4(b)).
To describe the adsorption kinetics, we employ the Langmuir theory, which assumes that adsorption occurs at specific sites with a constant number, one site binds only one molecule, and the molecules do not interact with each other.35 To calculate the adsorption equilibrium constant b, we use the following equation:
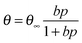 | (4) |
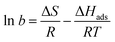 | (5) |
| ΔS = R·ln(RT) | (6) |
Fitting our experimental curves showing the relative resistance as a function of partial ammonia pressure (Fig. 4(a) and (b), insets) with the Langmuir isotherm, we get the absorption constants b equal to 0.0027 and 0.0022 for samples FG30 and FG60, correspondingly, with the assumption that the number of occupied adsorption sites θ is proportional to the resistance change. Then, with the help of eqn (4), we calculate the ammonia adsorption energy for samples FG30 and FG60 that yields the values of 0.227 and 0.233 eV. To compare the obtained values with the absorption energy of NH3 on graphene, we used the experimental data for CVD-graphene (Fig. 2(a) in ref. 10) for plotting the dependence of the sensor response on the NH3 pressure (Fig. S3, ESI†). The adsorption energy of NH3 estimated from the dependence with the help of eqn (4)–(6) is 0.12 ± 0.01 eV, which is consistent with the theoretical value of ∼0.11 eV.36 Our sensor interacts with the adsorbate twice stronger, and we believe that the main reason is that fluorine atoms remain in the sample after the hydrazine hydrate treatment.
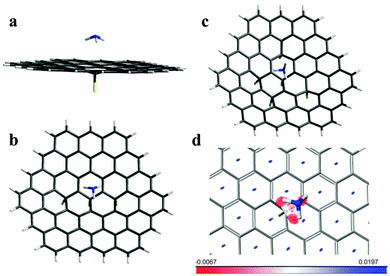
We further use these obtained energies to support the structure model, where the top (working) graphene surface is free of fluorine, while the backside has some fluorine atoms attached. For the C73FH21 model with a single fluorine atom attached, we found the only stable ammonia molecule position when all three hydrogen atoms get as close as possible to carbon atoms surrounding the CF group (Fig. 5(a)). There are many possibilities for the mutual distribution of several fluorine atoms on graphene. The simulation of X-ray emission and absorption spectra of fluorinated graphite C2F obtained under the same conditions as the original samples used in this study revealed that fluorine atoms prefer to form chains on the basal plane sequentially linking with the opposite sides.27,34 Removal of fluorine atoms from one side leaves three backside fluorine atoms in the meta-position of two adjacent hexagons as presented in the C73F3H21 model. The relative arrangement of five fluorine atoms in the C73F5H21 model was set to occupy the para- or meta-positions in relation to each other.
Geometry optimization of the C73F3H21 and C73F5H21 models with the adsorbate showed that ammonia tends to be located over the central CF group and there are two energetically favorable orientations. The calculated absorption energies are listed in Table 2. In the former case a greater energy gain is achieved when ammonia “sits” on the top surface of fluorinated graphene by hydrogen atoms (Fig. 5(b)), while in the latter case the orientation by two “N–H” bonds is more preferable (Fig. 5(c)). The other positions of ammonia found relative to the surface of the C73F3H21 and C73F5H21 models are shown in Fig. S4 (ESI†). The short distances between atoms in the ammonia and fluorinated graphene surface are collected in Table S1 (ESI†). The calculations show that the adsorption energy of NH3 varies from 0.236 to 0.275 eV depending on the orientation of the molecule relative to the graphene surface and the backside fluorination degree. The values are slightly over the experimental energy, which is between 0.227 and 0.233 eV, as determined for samples FG30 and FG60, respectively. The overestimation may arise from the chosen fluorination pattern as well as the theoretical approach. Moreover, the experimental sample can be considerably more complicated than the considered models. Actually, we cannot exclude penetration of NH3 molecules between fluorinated layers when the sensor is tested. Our calculations show that NH3 readily interacts with fluorine via hydrogen bonding similar to that predicted for graphene oxide.37 A fluorine atom is lifted over the graphene sheet and stabilizes at a distance of ∼2.4 Å (Fig. S5, ESI†). The F–HNH2 species forms a charge-transfer complex with graphene, accepting about 0.93e. Since diffusion of the NH3 molecules through the surface microcracks and sample sides should be restricted, we expect inducing a charge only on some areas of the graphene layer. Such positive charging could reduce the adsorption energy of NH3 on the sensor surface in line with the experimental observation. The calculated binding energy of NH3 in the complex is ∼0.623 eV which is considerably higher than the values determined from the sensor measurements. The irreversible reaction of NH3 molecules with fluorine in the depths of the flake is likely responsible for a trend of conductivity increase observed with the sensor cycling (Fig. 3(a)).
| Model | C73FH21 | C73F3H21 (H3N) | C73F3H21 (NH3) | C73F5H21 (H3N) | C73F5H21 (NH3) |
|---|---|---|---|---|---|
| E ad | 0.2364 | 0.2749 | 0.2636 | 0.2455 | 0.2621 |
To reveal the character of noncovalent interactions between ammonia and backside fluorinated graphene we used an approach based on the electron density and its derivatives.38 The result of the calculation for the C73FH21 model is presented in Fig. 5(d). The gradient isosurface is colored in accordance with the sign of the Laplacian and the strength of interaction. Large negative values (in red) correspond to strong attractions, and large positive values (in blue) indicate that the interactions are nonbonding. Areas of nonbonding overlapping are located at the center of each hexagonal ring, while a triangular-shaped surface between the ammonia molecule and fluorographene is deeply red at the edges and weakly red-colored in the center. Thus, there is a slight attraction between the nitrogen atom and carbon atom of the CF group despite the large distance between them, although the greatest contribution to the adsorption energy comes from the attraction between hydrogen atoms and carbon atoms surrounding the CF group.
In all considered complexes, the NH3 molecule interacts stronger with bare carbon atoms surrounding the CF group. Because these carbon atoms are in the sp2-hybridization state, adsorption of NH3 on backside fluorinated graphene occurs via the H–π type interactions.39 Such interactions are dominated by dispersion energies.40 In the case of graphene, the adsorption energy is slightly changed with the NH3 orientation and the adsorption site.41 The theoretical values may vary from 0.016 eV42 to 3.58 eV43 depending on the used approximation level. Fluorination of graphene induces a charge alternation on carbon atoms. For example, in the C73FH21 model with one attached fluorine atom, the magnitudes of Mulliken charges on a carbon atom in the CF group and on adjacent atoms are about +0.32e and −0.03e. Hence, electrostatic interaction between negatively charged bare carbon atoms of fluorinated graphene and hydrogen atoms of the NH3 molecule should additionally contribute to the adsorption energy. Similar results have been obtained when graphene was doped with boron and nitrogen.36 The adsorption energy obtained in our work is between 0.236 and 0.275 eV (Table 2). The weakest NH3 bonding is realized in the model with the lowest fluorination level. The energy increases with fluorine remaining on the inner graphene side, and similar values for the C73F3H21 and C73F5H21 models are explained by a similar local environment of the central CF group, which produces adsorption sites for the NH3 molecule.
4. Conclusions
Graphene layers were recovered by treating fluorinated HOPG with hydrazine hydrate vapor, and a residual fluorine content was controlled by reduction time as indicated by Raman scattering and XPS spectroscopy. Restoring sp2 hybridization (π-type bonding) leads to a crucial enhancement in the material electrical transport. On the one hand, the restored graphene layer retains the majority of the properties of pristine graphene because of the integrity of its hexagonal lattice; on the other hand, it has reactive centers making it not that inert to molecules in the gas phase. The flakes of the fluorinated HOPG with a partially reduced surface were examined as a sensor of NH3 and both the response amplitude and response time were found to be dependent on the recovery degree of the sample. To restore the sensor to its initial state, only air purging at room temperature is required. The resistance as a function of NH3 concentration (pressure) follows a general form of the Langmuir isotherm. Comparing the adsorption energy extracted from our experimental data with the quantum-chemical analysis, we conclude that the backside of the graphene layer has some fluorine atoms attached chemically, which create reactive centers on top of the fluorine-free graphene surface. These centers attract the NH3 molecules through noncovalent bonding, and interaction strength depends on the population density of fluorine atoms remaining on the backside of the graphene layer.Acknowledgements
This research was supported by the Russian Scientific Foundation (Grant #14-13-00813) in the part of sensor measurements and by the FP7-PEOPLE-2013-IRSES #612577 (NanoCF) grant in the part of sample preparation.Notes and references
- A. H. Castro Neto, F. Guinea, N. M. R. Peres, K. S. Novoselov and A. K. Geim, Rev. Mod. Phys., 2009, 81, 109 CrossRef CAS.
- K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666 CrossRef CAS PubMed.
- F. Schedin, A. K. Geim, S. V. Morozov, E. W. Hill, P. Blake, M. I. Katsnelson and K. S. Novoselov, Nat. Mater., 2007, 6, 652 CrossRef CAS PubMed.
- T. S. Sreeprasad and V. Berry, Small, 2013, 9, 341 CrossRef CAS PubMed.
- H. Liu, Y. Liu and D. Zhua, J. Mater. Chem., 2011, 10, 3253–3496 Search PubMed.
- L. Yan, Y. B. Zheng, F. Zhao, S. Li, X. Gao, B. Xu, P. S. Weiss and Y. Zhao, Chem. Soc. Rev., 2012, 41, 97–114 RSC.
- J. D. Fowler, M. J. Allen, V. C. Tung, Y. Yang, R. B. Kaner and B. H. Weiller, ACS Nano, 2009, 3, 301 CrossRef CAS PubMed.
- F. Schedin, A. K. Geim, S. V. Morozov, E. W. Hill, P. Blake, M. I. Katsnelson and K. S. Novoselov, Nat. Mater., 2007, 6, 652–655 CrossRef CAS PubMed.
- M. G. Chunga, D. H. Kimb, H. M. Leec, T. Kima, J. H. Choia, D. K. Seoa, J.-B. Yooc, S.-H. n. Hong, T. J. Kanga and Y. H. Kima, Sens. Actuators, B, 2012, 166–167, 172–176 CrossRef PubMed.
- F. Yavari, E. Castillo, H. Gullapalli, P. M. Ajayan and N. Koratkar, Appl. Phys. Lett., 2012, 100, 203120 CrossRef PubMed.
- A. Inaba, K. Yoo, Y. Takei, K. Matsumoto and I. Shimoyama, Sens. Actuators, B, 2014, 195, 15–21 CrossRef CAS PubMed.
- M. Gautam and A. H. Jayatissa, Mater. Sci. Eng., C, 2011, 31, 1405–1411 CrossRef CAS PubMed.
- S. Mao, S. Cui, G. Lu, K. Yu, Z. Wen and J. Chen, J. Mater. Chem., 2012, 22, 11009 RSC.
- Y. Zou, F. Li, Z. H. Zhu, M. W. Zhao, X. G. Xu and X. Y. Su, Eur. Phys. J. B, 2011, 81, 475 CrossRef CAS.
- W. Li, X. Geng, Y. Guo, J. Rong, Y. Gong, L. Wu, X. Zhang, P. Li, J. Xu, G. Cheng, M. Sun and L. Liu, ACS Nano, 2011, 5(9), 6955–6961 CrossRef CAS PubMed.
- S. Prezioso, F. Perrozzi, L. Giancaterini, C. Cantalini, E. Treossi, V. Palermo, M. Nardone, S. Santucci and L. Ottaviano, J. Phys. Chem. C, 2013, 117(20), 10683–10690 CAS.
- P.-G. Su and H.-C. Shieh, Sens. Actuators, B, 2014, 190, 865–872 CrossRef CAS PubMed.
- Q. T. Trana, H. T. M. Hoaa, D.-H. Yoob, T. V. Cuonga, S. H. Hurc, J. S. Chungc, E. J. Kimc and P. A. Kohld, Sens. Actuators, B, 2014, 194, 45–50 CrossRef PubMed.
- J. D. Fowler, M. J. Allen, V. C. Tung, Y. Yang, R. B. Kaner and B. H. Weiller, ACS Nano, 2009, 3(2), 301–306 CrossRef CAS PubMed.
- J. Huanga, L. Wanga, C. Shia, Y. Daia, C. Gua and J. Liub, Sens. Actuators, B, 2014, 196, 567–573 CrossRef PubMed.
- V. Dua, S. P. Surwade, S. Ammu, S. R. Agnihotra, S. Jain, K. E. Roberts, S. Park, R. S. Ruoff and S. K. Manohar, Angew. Chem., Int. Ed., 2010, 49, 2154–2157 CrossRef CAS PubMed.
- D. R. Dreyer, S. Park, C. W. Bielawski and R. S. Ruoff, Chem. Soc. Rev., 2010, 39, 228–240 RSC.
- L. G. Bulusheva, A. V. Okotrub and N. F. Yudanov, Phys. Low-Dimens. Struct., 2002, 7/8, 1 Search PubMed.
- A. V. Okotrub, I. P. Asanov, N. F. Yudanov, K. S. Babin, A. V. Gusel'nikov, T. I. Nedoseikina, P. N. Gevko, L. G. Bulusheva, Z. Osvath and L. P. Biro, Phys. Status Solidi B, 2009, 246, 2545 CrossRef CAS.
- A. V. Okotrub, K. S. Babin, A. V. Gusel'nikov, I. P. Asanov and L. G. Bulusheva, Phys. Status Solidi B, 2010, 247, 3039 CrossRef CAS.
- N. F. Yudanov and L. I. Chernyavskii, J. Struct. Chem., 1990, 28, 534 CrossRef.
- A. V. Okotrub, N. F. Yudanov, I. P. Asanov, D. V. Vyalikh and L. G. Bulusheva, ACS Nano, 2013, 7, 65 CrossRef CAS PubMed.
- J. T. Robinson, J. S. Burgess, C. E. Junkermeier, S. C. Badescu, T. L. Reinecke, F. K. Perkins, M. K. Zalalutdniov, J. W. Baldwin, J. C. Culbertson, P. E. Sheehan and E. S. Snow, Nano Lett., 2010, 10, 3001 CrossRef CAS PubMed.
- D. Becke, J. Chem. Phys., 1993, 98, 5648 CrossRef PubMed.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- L. Goerigk and S. Grimme, Phys. Chem. Chem. Phys., 2011, 11, 6670 RSC.
- Jaguar, version 7.9, Schrodinger, LLC, New York, NY, 2012 Search PubMed.
- I. P. Asanov, L. G. Bulusheva, M. Dubois, N. F. Yudanov, A. V. Alexeev, T. L. Makarova and A. V. Okotrub, Carbon, 2013, 59, 518 CrossRef CAS PubMed.
- I. Langmuir, J. Am. Chem. Soc., 1918, 40, 1361 CrossRef CAS.
- Y. H. Zhang, Y. B. Chen, K. G. Zhou, C. H. Liu, J. Zeng, H. L. Zhang and Y. Peng, Nanotechnology, 2009, 20, 185504 CrossRef PubMed.
- S. Tang and Z. Cao, J. Phys. Chem. C, 2012, 116, 8778–8791 CAS.
- E. R. Johnson, S. Keinan, P. Mori-Sanchez, J. Contreras-Garsia, A. J. Cohen and W. Yang, J. Am. Chem. Soc., 2010, 132, 6498 CrossRef CAS PubMed.
- V. Georgakilas, M. Otyepka, A. B. Bourlinos, V. Chandra, N. Kim, K. C. Kemp, P. Nobza, R. Zboril and K. S. Kim, Chem. Rev., 2012, 112, 6156–6214 CrossRef CAS PubMed.
- S. Vaupel, B. Brutschy, P. Tarakeshwar and K. S. Kim, J. Am. Chem. Soc., 2006, 128, 5416–5426 CrossRef CAS PubMed.
- O. Leenaerts, B. Partoens and F. M. Peeters, Microelectron. J., 2009, 40, 860–862 CrossRef CAS PubMed.
- R. O. Leenaerts, B. Partoens and F. M. Peeters, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 125416 CrossRef.
- M. Ribeiro, N. M. R. Peres, J. Coutinho and P. R. Briddon, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 075442 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c4cp03552f |
| This journal is © the Owner Societies 2015 |