Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Models of charge pair generation in organic solar cells
Sheridan
Few
*a,
Jarvist M.
Frost
ab and
Jenny
Nelson
*a
aCentre for Plastic Electronics, Department of Physics, Imperial College London, London SW7 2AZ, UK. E-mail: sheridan.few10@imperial.ac.uk; jenny.nelson@imperial.ac.uk
bDepartment of Chemistry, University of Bath, Bath BA2 7AY, UK
First published on 25th November 2014
Abstract
Efficient charge pair generation is observed in many organic photovoltaic (OPV) heterojunctions, despite nominal electron–hole binding energies which greatly exceed the average thermal energy. Empirically, the efficiency of this process appears to be related to the choice of donor and acceptor materials, the resulting sequence of excited state energy levels and the structure of the interface. In order to establish a suitable physical model for the process, a range of different theoretical studies have addressed the nature and energies of the interfacial states, the energetic profile close to the heterojunction and the dynamics of excited state transitions. In this paper, we review recent developments underpinning the theory of charge pair generation and phenomena, focussing on electronic structure calculations, electrostatic models and approaches to excited state dynamics. We discuss the remaining challenges in achieving a predictive approach to charge generation efficiency.
1 Introduction
Organic heterojunction devices have attracted intense interest for low cost photovoltaic applications, with record power conversion efficiencies for a single junction device rising from ∼3% in 2001 to 11.1% in 2011.1 Their function differs from that of inorganic p–n or p–i–n structures in that photocurrent generation depends on two stages: the separation of a photogenerated exciton into independent charge carriers, in addition to the successful transport of independent charge carriers to the electrodes. We do not attempt to give a comprehensive review of experimental literature here, as that would be beyond the scope of a single paper. Comprehensive and up-to-date reviews of experimental studies can be found in ref. 2–4.The process of charge generation is widely believed to consist of the dissociation of the exciton to form an intermediate state involving bound charges at the interface between donor and acceptor materials, sometimes referred to as a charge transfer (CT) state, followed by separation into independent charges. One surprising observation is that, even though a simple coulombic treatment, assuming electrons and holes are point charges, a relative dielectric constant (εr) of 3–4, and a separation (reh) of 1–2 nm at the interface, results in a coulombic binding energy of ∼0.1–0.5 eV (eqn (1)), significantly above the average thermal energy at room temperature, EThermal ∼ 0.025 eV, many experimental studies have found charge separation efficiencies approaching 100%.5,6
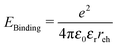 | (1) |
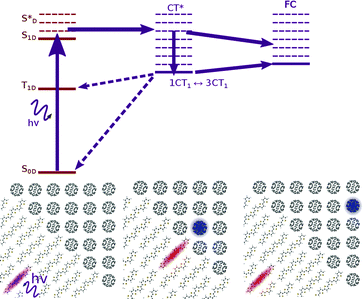
In modelling the process of charge separation, it has been common to distinguish the processes of exciton dissociation, and charge pair separation. The first part concerns the nature of the transition from photoexcited exciton (S*) to the CT state (Fig. 1), and how this is controlled by energy levels of different blend components, while the second part concerns the nature of the transition from CT state to a charge separated state (CS, Fig. 1), and the material parameters that are important for determining this. In this section we introduce, and collect experimental evidence for, a number of proposed mechanisms for these processes.
It is widely held that the offset in energy levels between donor and acceptor material provides the driving force for the S* → CT process,7–10 but there is some uncertainty around the energies and spatial extents of states involved, the sequence of transfer processes, and their dynamics.
A number of works have suggested that there is a threshold in this energy offset, ΔECS, between the singlet and CT state for efficient charge generation to occur. This concept is supported by work by Ohkita et al. showing a correlation between charge generation efficiency and free energy in a series of thiophene based polymers blended with PCBM,11 Veldman et al.9 on a series of polymer:polymer and polymer:small molecule blends, and Faist et al.10 on a series of conjugated polymers blended with fullerenes of different acceptor strength. A number of low bandgap isoindigo12,13 and diketopyrollopyrolle14 containing polymers have subsequently been reported, which exhibit high charge separation efficiencies when blended with fullerene despite small energy level offset. It may be important that the low bandgap component is the polymer, rather than the fullerene, in these latter cases.
Driving forces for charge separation may also result from factors associated with the change in medium.
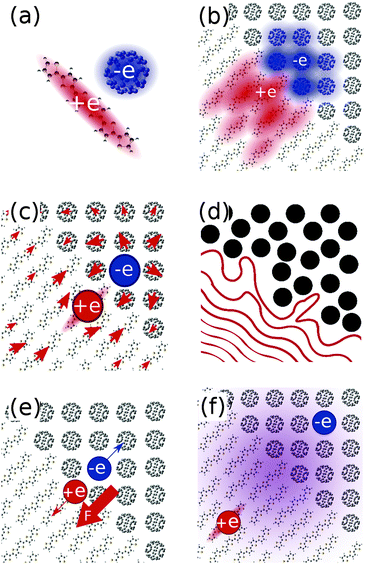
The delocalisation of charge carriers over a molecule (Fig. 2a) or a number of molecules (Fig. 2b) may be important in driving charge separation. Measurements on polycrystalline octothiophenes films by Knupfer et al. suggests a hole delocalisation over four to five thiophene units (∼2 nm),15 and earlier work on P3HT in solution by Holdcroft estimates delocalisation over at least ten units (∼4 nm).16 Shimoi et al. conclude from theoretical and experimental studies that hole polarons delocalise over 4 repeat units (∼2–3 nm) in MDMO-PPV.17 If these polaron sizes are representative of charge distributions close to the interface, then this would result in a large effective separation of electron and hole, and have a significant impact on the coulombic barrier to charge separation. Recent studies by Bernardo et al.,18 and Savoie et al.19 also suggest delocalisation of the electron over multiple fullerenes may be important in determining the dependence of charge transfer state energies on fullerene content.
Another consideration is the possible involvement of electronically or vibronically excited charge transfer states (CT* in Fig. 1), whereby any additional electronic and/or vibrational energy that an exciton possesses above the energy of the lowest CT state (ECT, energy of CT1 in Fig. 1) may be important in bringing about charge separation. A potential mechanism is the coupling of higher lying excitons to more delocalised, higher energy charge transfer states. The existence of such delocalised excited CT states is supported by infrared (IR) pump-push measurements, showing generation of additional charges when a device containing relaxed CT states is excited with an IR pulse.20 This concept is also supported by electroabsorption studies showing a rising electroabsorption signal over tens of femtoseconds to hundreds of picoseconds following photonic excitation. This rise is attributed to a growing electric field due to the separation of interfacial charge pairs, via charge transfer states with increasing degrees of charge delocalisation.21,22 However, recent studies show that the internal quantum efficiency of photocurrent generation is insensitive to photon energy over the range of photon energies spanning CT and single molecule excitations.6 Thus the importance of hot excitations for photocurrent generation is in dispute.
Microscopic treatments of electrostatics of the medium, which account for the effects of chemical structure, position and orientation of molecules at the interface (Fig. 2c), show that these can have a large impact on the magnitude and separation dependence of the charge pair binding energy in ways not captured by a linear dielectric constant (eqn (1)). This is largely due to anisotropic polarisabilities and charge distributions of considered molecules.
Disorder at the interface may give rise to a gradient in the energies of available electron or hole states, promoting charge separation (Fig. 2d). This concept is supported by a number of theoretical studies.23–25 Related to this is the role of entropy in driving separation of charges. There exist many states in which polaron pairs are well separated, and relatively few interfacial charge transfer states. As such, the separation of charges is entropically favourable.4
The built in electric field in a device at short circuit may influence charge separation efficiency, by driving both electron and hole toward opposite electrodes, and, in some cases, away from the interface (Fig. 2e). Experimental studies of devices using measurements of charge density and lifetime26 or using a time delayed collection method27,28 show that charge pair generation can be enhanced by an applied electric field in the case of some relatively amorphous polymer:fullerene blends, though not in other blends. Another study by Veldman et al. found a slightly enhanced dissociation probability in PF10TBT:PCBM devices at typical operating voltages over short circuit.8
Another possible mechanism is the direct generation of free charge carriers from excitons located deep in the polymer domain, without proceeding via an intermediate interfacial CT state (Fig. 2f, bypassing the intermediate CT state in the central panel of Fig. 1), relying on a relatively slow decay of the excitonic wavefunction through the polymer domain.29 A different mechanism which may avoid trapping at the CT state is direct photonic excitation to a superposition of energy eigenstates of different degrees of charge transfer, which, through lattice interactions, may couple directly to charge separated states.30 This concept is supported by the ultrafast (∼100 fs) generation of charges reported in transient absorption studies on a range of polymer:fullerene blends (P3OT:C60,31 P3HT:PCBM,32–35 MDMO-PPV:PCBM,34–36 PFODTBT:PCBM,37 PCPDTBT:PCBM,38–40 PCDTBT:PCBM34,35,41–43), and in time-resolved resonance-Raman showing hole polarons generated far from corresponding electron polarons on timescales of 300 fs in PCDTBT:PCBM.44
Experimental studies have yet to determine which mechanism is, or combination of mechanisms are, dominant in the generation of charges following photoexcitation. In the following section, we describe a number of phenomenological models which have been developed in an effort to understand and model the processes driving charge generation in OPVs. These studies contain little or no chemical information which can help us to differentiate between different materials systems. They do, however, motivate the study of these phenomena in specific material systems. The remainder of this review describes attempts to calculate the parameters relevant to different charge separation models, organised around three key themes: electronic states at the interface and delocalisation of charge carriers, electrostatic effects, and dynamics of charge pair generation.
2 Early models
During the early stages of the development of theory for OPV device function, a number of phenomenological models were developed in an effort to represent the processes driving charge generation in OPVs.One benchmark is Onsager's analytic model for ionic separation in weak electrolytes,45 as adapted by Braun for the study of organic solids containing donor and acceptor units.46 Mihailetchi et al. adapt this model to consider charge generation in organic photovoltaics. They are able to reproduce current density–voltage curves for polymer:fullerene solar cells of different composition, but only using an unphysically slow charge recombination rate of 1 μs−1.47
To explain realistic charge yields, this model has been extended in a variety of ways. Peumans and Forrest's model considers the possible implications of the conversion of excess electrical energy of an exciton incident on the interface to kinetic energy, resulting in an initial separation of electron and hole at the interface.48 This approach reproduces current–voltage curves, but only if assuming a large (48 Å) initial electron–hole separation, and a high attempt-to-jump frequency relative to charge recombination rates.
Deibel et al.49 use a kinetic Monte Carlo device model to consider the impact of reduction in Coulomb barrier associated with a hole whose charge is delocalised over a number of monomer units, similar to the situation in Fig. 2a. They find a large increase in dissociation yield on increasing conjugation length between 1 and 10 monomer units, indicating that charge carrier delocalisation could have a very significant effect on dissociation probability.
In a contrasting approach, Arkhipov et al. consider the increase in the kinetic energy of the hole when coulombically localised by an electron on a fullerene, and positive charges on surrounding donor units (resulting from ground state partial electron transfer between molecules along the heterojunction).50 This model relies on a large degree of groundstate electron transfer from polymer to fullerene (∼0.1e per fullerene) and a very small effective mass of ≤0.3 me along the polymer chain, thought to be inconsistent with small electronic bandwidth in organic materials. More recently, Nenashev et al. combined the models of Deibel and Arkhipov, concluding that both effects may play an important role in determining charge dissociation probability.51
Offermans et al. study the impact of disorder in site energies on charge separation in a kinetic Monte Carlo simulation, finding that a difference in levels of disorder between the two materials could be important in driving separation of charges, via relaxation of hot charges near the interface into deeper energy sites that generally lie further away.52 A recent study by van Eersel et al. similarly concludes that disorder may play an important role in dissociation of charges at the interface.53
Whilst many of the physical factors that may influence the rate of charge separation are invoked in these models, the models cannot relate processes in different materials to their chemical structure. For this, a means to calculate the electronic structure of the materials is required.
3 Electronic states at the interface
Most theoretical efforts to understand the process of charge separation have focussed on the energy and nature of the electronic states at the donor:acceptor interface. Electronic structure calculations of donor:acceptor combinations have the potential to relate observations to the specific chemical and physical structure of the molecules concerned. In most cases quantum chemical methods are used to study a single oligomer or molecule of the donor material and a single molecule of the acceptor. Properties of the electronic states of these molecule pairs are taken to be representative of states at the interface in a continuous system. These may play a role in the charge generation process, either as intermediaries between the exciton and free charges, or as trap sites at which excitons may recombine.We will discuss the development of appropriate electronic structure methods separately to results on specific systems.
3.1 Electronic structure calculation methods
Calculations on excited interfacial states exhibiting charge transfer present theoretical and computational challenges. A balance must be struck between using sufficiently high levels of theory to correctly describe physical processes, and choosing system sizes which are large and detailed enough to be representative of relevant parts of an organic photovoltaic device. In this section, we give a brief summary of the challenges and methods involved. Factors which tend to increase and decrease calculated excitation energies to states exhibiting significant electron–hole separation are summarised in Fig. 3. | ||
| Fig. 3 Factors which will tend to increase and decrease calculated charge transfer excitation energies. | ||
Density functional theory (DFT), whereby the interacting array of electrons are represented by a single electron density function, has enjoyed a great deal of success in reproducing properties of systems in which electrons are relatively delocalised. The Hartree–Fock method represents an alternative approach to electronic structure calculations, whereby exchange interaction between electron states is explicitly considered, but coulombic interactions are only considered via the mean field approximation. For organic systems, in which electrons are relatively tightly bound to molecules, hybrid functionals such as B3LYP,54 containing an empirical mixing of DFT and Hartree–Fock, have been very widely used.
Whilst methods for calculating ground state properties of chemical systems are relatively mature, the development of methods for calculating their excited states remains very much an active field.
A popular method for calculation of excited states is linear response time dependent density functional theory (TDDFT), which has been widely used to model excited states of organic molecules,55 and is attractive for its computational efficiency and availability as part of many quantum chemical packages.
Unfortunately, when used with standard functionals, linear response TDDFT does not reproduce sufficient electron–hole binding energy.56–58 This results in an improper delocalisation of the excited state, and spuriously low charge transfer state excitation energies. These problems may be alleviated by the mixing of a larger component of Hartree–Fock (HF) exchange into the functional, but this will result in an improper description of local excitations, due to a lack of dynamic correlation.
In response to this problem, a number of long-range corrected functionals have been developed, in which the mix of HF and DFT depends upon the spatial separation.59–62 Yanai et al.'s Coulomb attenuating method (CAM-B3LYP),62 has proved popular, and has been shown by Peach et al. to well reproduce high level theory calculations for a series of small molecules exhibiting varying degrees of charge transfer.63 More recently, tuned range separated hybrid functionals such as the Baer–Neuhauser–Livshits functional (BNL) have been developed,64,65 whereby the form of the attenuation factor is explicitly tuned to the system (or systems) under consideration.
Many-body methods beyond linear response and density functional theory should offer greater predictive power, but are currently only tractable for relatively small systems, or in conjunction with other broad approximations. An example of such an approach is the use of Green's functions equations of motion, containing both the nonlocal, energy-dependent electronic self-energy, and the electron–hole interaction leading to the formation of excitons, described by the Bethe–Salpeter equation (BSE).66–71
The delta-SCF method, in which the HOMO of the donor is fit to the ionisation potential (IP(D)) and the LUMO of the acceptor to the electron affinity (EA(A)), represents another method of calculating accurate excited state orbitals, but is also relatively expensive.72
Singles configuration interaction (SCI) represents a method of accurately calculating excited state energies, but is prohibitively expensive when used with standard functionals. SCI has, in a number of studies, has been used with intermediate neglect of differential overlap (INDO) in order to study larger systems.73 As charge is likely to delocalise between molecules, the neglected differential overlap between electron wavefunctions localised on different atoms implicit in INDO may be important in defining characteristics of CT states.
Constrained density functional theory (CDFT) represents another method of accessing charge transfer state properties at reasonable computational cost.74 Here, donor and acceptor molecules are confined to have charges of +e and −e, and an excess spin of ±½, and a self-consistent ground state DFT calculation is made. This allows the CT ground state to be engineered from a functional that would mispredict the charge localisation due to self-interaction error. CDFT is unable to predict states exhibiting partial electron transfer, and offers no direct route to higher excited states of the system.
Irrespective of functional, correct description of long range charge transfer requires a sufficient basis set to allow for orbital density at intermediate locations in space.75
When calculations on a donor:acceptor molecular pair are to be used to represent the extended binary film, the electrostatic response of the surrounding medium needs to be accounted for. The surrounding molecules will, in general, become polarised by the charge pair and may contribute to the barrier to charge separation. Including the detailed response of the medium is a complex problem. A simple approach is to treat the medium as a continuum and carry out an electronic structure calculation in a spherical cavity within a continuous polarisable medium.76
Going beyond the linear response of a dielectric, the surroundings can be modelled at the level of a polarisable empirical force field. Here a full self-consistent calculation of the electronic structure and microscopic polarisation of the medium is needed (potentially even including molecular reorientation).76,77 Such approaches, in which a quantum mechanical (QM) calculation is calculated, embedded within a classical molecular mechanical (MM) surroundings, are often referred to as QM/MM calculations.
There exists no gold standard of calculation which can describe the energies and nature of excited states in the donor:acceptor blend correctly in all cases. However, a number of studies have been carried out using subsets of these methods in order to address various aspects of charge generation in organic photovoltaics. Results of such studies are reviewed in the next two sections.
3.2 Bimolecular interfacial electronic states
First, we review studies that have used the electronic states of donor:acceptor molecular pairs as a model of the OPV charge separating interface.An early work by Kanai and Grossman studied P3HT:C60 with periodic boundary conditions, with four thiophene units and one fullerene molecule in each unit cell.78 Kanai and Grossman use pure DFT for this study, and take unoccupied Kohn–Sham orbitals to represent excited states. The method is flawed because pure DFT is known to delocalise charge to an unrealistic extent in conjugated organic materials,79 and because the Kohn–Sham orbitals are not formally connected to the excited states.80 Nonetheless, the ideas and results presented have stimulated and informed further study in this area. The study found excited electron states localised on P3HT, fullerene, and ‘bridge’ states delocalised over both molecules, resulting from the hybridisation of a P3HT π* state with a triply degenerate unoccupied state of the fullerene. Kanai and Grossman propose that such states may act as intermediate states to facilitate the observed ultrafast charge transfer in this system.
Huang et al.73 used hybrid DFT (B3LYP/6-31g) ground states, with excited states by INDO/SCI to probe excitation energies, Coulomb interaction energies, radiative lifetimes, degree of charge transfer, and magnitude and orientation of the transition dipole moment of PFB:F8BT and TFB:F8BT monomer pairs.
This study found a strong dependence of excited state properties on alignment of the monomer pair. The authors report an attractive configuration in which electron accepting benzothiadiazole (BT) units of F8BT are aligned with electron donating triarylamine groups of PFB, resulting in an excited state of charge transfer character, and a repulsive configuration in which these units are no longer aligned, resulting in a state of excitonic character on the F8BT acceptor, in which the excited state is calculated to have a significantly shorter radiative lifetime. They also find intermediate ‘exciplex’ configurations, in which excitations exhibit a mixed charge transfer and excitonic character, with intermediate radiative lifetimes. This study has been reviewed in detail elsewhere.81
For some systems, in which energy levels of donor and acceptor LUMO are well separated, a spectrum of charge transfer states have been calculated at energies below that of the first single molecule excitation. These include higher charge transfer states in which the hole is more delocalised, resulting in a weaker Coulomb binding between electron and hole. Bakulin et al. have found such states in P3HT:PCBM and P3HT:F8TBT, where the polymers are modelled as oligomers using INDO/SCI.20 Few et al.82 observed a similar trend in the excited states of dodecothiophene:PCBM pairs using TDDFT with B3LYP/6-31g*. The relative delocalisation of higher lying CT states supports the notion that excess exciton energy may help drive charge separation.
Due to the improper treatment of Coulomb interaction exhibited by TDDFT, this method cannot be used to study separation dependence of CT state properties. Whilst Coulomb's law will be reproduced by INDO/SCI, the neglected differential overlap of wavefunctions may be important in determining CT state properties.
We discuss two approaches that are capable of probing separation and orientation dependent properties. These works use a high level of theory to calculate properties of relatively small systems. Isaacs et al. use BNL, a tuned range separated hybrid functional, to calculate excited state properties of molecule pairs of C60 with a series of boron(subphthalocyanine) molecules.72 Range separation parameters are tuned to fit the HOMO of the donor to the ionisation potential, and the LUMO of the acceptor to the electron affinity, as calculated by delta-SCF. Baumeier et al. use many-body Green's functions with the BSE to examine the excited state spectrum of a dicyanovinyl-substituted quaterthiophene:C60 molecule pair.69
In the work of Isaacs et al., energetics of CT states are dominated by electrostatics, with low energy CT states where fullerene localises close to the positively charged thiophene unit in the CT state, and higher energies when the fullerene localises further from this unit. They find a difference in Coulomb binding for different molecular configurations of between 0.2 and 0.6 eV for fullerene with differently functionalised boron(subphthalocyanine) molecules. Baumeier et al. find a similar position dependence of CT state energetics (Fig. 4), with ECT lower by ∼1 eV when the fullerene is localised close to the thiophene compared to when the fullerene is localised close to the terminal dicyanovinyl group. Changes in Coulomb binding energy of electron and hole in the CT state, calculated by summing intermolecular Coulomb interactions between atomic partial charges, do not exactly match changes in ECT. This is attributed largely to the role of molecular polarisation in distorting orbitals in response to the presence of a charged molecule. In the DN configuration, a state is calculated in which 0.75 electrons are transferred from donor to acceptor, attributed to the proximity of C60 to the strongly electronegative dicyanovinyl group, and to the close proximity of two units with acceptor character, making it an outlier in Fig. 4.
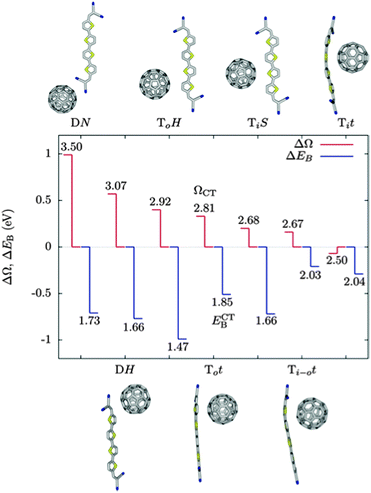 | ||
| Fig. 4 GW-BSE calculations carried out by Baumeier et al.69 on C60:terminally substituted quarterthiophene molecule pairs. Difference between excitation energy to the CT state and S0 → S1 of the donor, ΔΩ = ΩCT − ΩD, in red, and reduction in binding Coulomb binding energy of the CT state relative to the ionisation potential of the donor, ΔEB = ECTB − EDB, in blue. The numbers are the excitation energies, ΩCT, to the CT state, and the Coulomb binding energies, ECTB, of the CT state. All energies in eV. Molecular arrangements with higher excitation energies tend to have a lower ECTB, and more negative values of ΔEB, indicating a larger reduction in the Coulomb barrier to charge separation relative to the ionisation potential of the donor. | ||
These studies suggest that the role of electrostatic interaction is more important than the overlap of orbitals in defining the energetics of interfacial excited states. This suggests that the influence of the environment could be very important in determining charge transfer state energetics. However, in cases where LUMO energies of the two materials are quasi-degenerate, differences in coupling between different molecular arrangements can have a large impact on interfacial states, and potentially on charge generation efficiency. In such cases, small changes in chemical structure can also have a dramatic effect on the energy and nature of calculated excitations.
Use of a lower level of theory allows the calculation of electronic states of larger molecule pairs at reasonable computational cost. Few et al. apply linear response TDDFT with the global hybrid functional B3LYP/6-31g* in vacuo to the calculation of excited states of a wide range of similarly oriented conjugated oligomer:fullerene molecule pair. They show this method to well reproduce trends in electroluminescence energies from corresponding polymer:fullerene blends (Fig. 5a). The success can be partly attributed to the cancellation of errors due to the use of linear response TDDFT (tending to reduce the calculated excitation energy to charge transfer excitations, Fig. 3), and the lack of polarisable medium, relatively small basis sets, and lack of Stokes shift (tending to increase the calculated excitation energy to charge transfer excitations, Fig. 3), and these errors being sufficiently consistent between similar materials to establish meaningful trends.
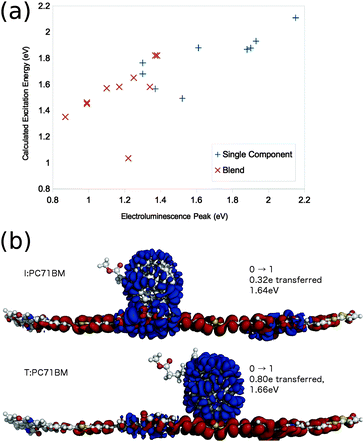 | ||
| Fig. 5 Few et al.'s82 TD-B3LYP/6-31g* results on oligomer:fullerene pairs. (a) Calculated molecule pair, and single molecule excitation energies, plotted against electroluminescence energies measured for corresponding polymer or polymer:fullerene blend. (b) Calculated first excitation of a 33TI:PC71BM molecule pair. Electron density moves from red to blue regions in going from the ground to the excited state. | ||
Few et al.82 apply the same calculation method to a range of polymer:fullerene systems, and investigate the effect of ring alignment (along a few central oligomer units) of the fullerene on the nature and energetic of the excited state spectra of the molecule pairs. CT state properties exhibit only a weak dependence on ring alignment of the fullerene and oligomer for pairs of molecules with well separated LUMO levels, but a much stronger dependence for molecule pairs with near degenerate LUMO levels. In particular, in P3TI:PC71BM, a system in which efficient charge generation is reported despite very close lying LUMO levels of donor and acceptor,12,13 the degree of electron transfer from donor to acceptor molecule varies from 0.32e to 0.80e for a fullerene aligned with different subunits on the central monomer (Fig. 5b). This is attributed to hybridisation of orbitals when fullerene is located close to units on the oligomer where the LUMO is heavily localised. For a number of chemical analogues of PDPP-TT-T alongside PC71BM, another molecule pair with a small LUMO–LUMO offset,14 small changes in chemical structure have a large impact on charge generation efficiency. Few et al. calculate the degree of electron transfer exhibited in the first excited state for oligomers of these analogs with PC71BM, and a correlation is found between systems calculated to exhibit a large degree of electron transfer in the first excited state, and those which efficiently generate charges in a device.
In summary, the energies and nature of excited states at the donor:acceptor interface can be explored with reasonable accuracy using available quantum chemical methods. The cheapest methods are based on DFT, and whilst these methods suffer from known limitations, the methods have proved useful in probing effects of the chemical structure, separation and orientation of molecular pairs on interfacial states. Probing the electronic structure of states that are delocalised over the molecular assembly is more expensive, and whilst experimental evidence suggests the delocalisation of states is important, only limited computational studies have been made so far.
3.3 Electronic states in larger arrays of molecules
The studies discussed in the previous section concern excited states of an individual donor:acceptor molecule pair. Such studies cannot evaluate the role of intermolecular delocalisation on charge separation. The concept of delocalised states is relevant to a number of studies that have shown that the well established redshift of CT state emission with increasing fullerene content in organic solar cells,18,83–85 can be explained partly in terms of fullerene crystallisation. Higher ratios of fullerene have also been shown to correlate with higher charge generation yield, and with a larger photocurrent and PCE in devices.18,84,86,87Though clearly important to study the effect of state delocalisation for these reasons, calculating the degree of charge delocalisation over assemblies of molecules requires a large system size (to allow the charge to be non-local), and is a challenge for DFT due to the self-interaction error. Use of more coarse-grained semi-empirical methods can allow the study of such systems.
One such approach is taken by Cheung and Troisi, in order to study the electrical properties of an assembly of PCBM molecules in the absence of a molecular donor.88 They carry out molecular dynamics on a 3 × 3 × 3 supercell, initially in the PCBM structure crystallised from oDCB solution, as reported by Rispens et al.89 Electronic structure calculations are then carried out on two thousand simulation snapshots. Fullerene molecules are coarse grained. ZINDO is used to calculate the first three quasi-degenerate LUMOs of a single PCBM molecule in vacuum. A rigid structure as used in the ZINDO calculation is superimposed onto each molecule from the MD snapshot, and reference molecular orbitals are imposed onto this molecule. The overlap of the degenerate LUMOs of the PCBM molecules is calculated instead of directly evaluating the electronic coupling, and overlap is only considered between atomic orbitals within 7.2 Å. Electronic states of the system are then calculated using a tight binding model, with molecular orbital site energies, and transfer integrals as calculated by orbital overlap.
Cheung and Troisi define a localisation length as twice the standard deviation of the orbital density with distance from the expectation position for the orbital. The lowest excitations of the system are found to be localized on one or two fullerene molecules (localisation length ∼12 Å), and stabilised by 0.08 eV relative to the single molecule LUMO. Higher states are delocalised over a large number of molecules, and some over the entire simulation space (localisation lengths ∼30–50 Å), many of which are thermally accessible from the lowest excitations.
Savoie et al. apply a similar method to calculate electronic states of crystallites of PCBM of sizes ranging from 1 × 1 × 1 to 4 × 4 × 4 unit cells (4 to 256 molecules),19 also prepared in Rispens et al.'s crystal structure from oDCB solution.89 Savoie et al. calculate electronic states for the crystallite in isolation (Fig. 6a and b), and when a positive point charge is placed alongside the crystallite (Fig. 6c and d). Whilst the lowest excited state is localised close to the positive charge (Fig. 6c), many thermally accessible states are calculated which are delocalised over a large number of fullerene molecules (Fig. 6d). In the case of the 4 × 4 × 4 supercell, the effect of delocalising the positive charge uniformly in one or two dimensions is also considered, yielding a qualitatively similar set of electronic states.
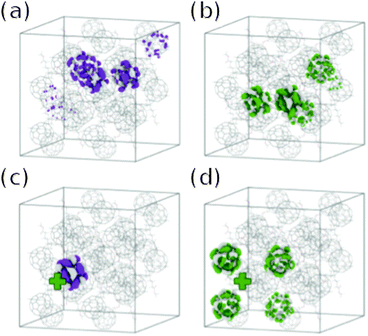 | ||
| Fig. 6 States calculated by Savoie et al.19 in a 2 × 2 × 2 crystallite of PCBM. (a) more localised, and (b) thermally accessible more delocalised electron state in the absence of a positive charge; and (c) more localised, and (d) thermally accessible more delocalised electron state in the presence of a positive point charge. | ||
This is interpreted as offering a possible pathway for efficient charge separation via higher lying, delocalised charge transfer states. Savoie et al. find that the average state localisation is mostly unaffected by rotational and translational disorder of PCBM molecules, attributing this to the spherical symmetry and resulting near-isotropic electronic coupling of the PCBM molecule. They ascribe the dominance of fullerene based acceptors in organic photovoltaics to this robustness of the fullerene electronic structure to structural disorder, a factor previously suggested to explain high mobilities in disordered C60 films.90 A comparative study on non-fullerene acceptors would therefore be interesting.
An interesting approach is taken by Raos et al.,91 who coarse grain the donor:acceptor interface as an regular grid of donor and acceptor molecules on a regular lattice. Each molecule is assigned only HOMO and LUMO orbitals, and transfer integrals with neighbouring molecules taken from a Gaussian distribution, weighted by an factor that decays exponentially with molecular separation distance. All values required as inputs to the Hamiltonian can be obtained from the ionisation energy, electron affinity, and singlet and triplet excitation energies of the molecule under consideration, which could be obtained from accurate gas phase measurements, or ab initio quantum chemical calculations.92
Raos et al. apply this method to two-dimensional model heterojunctions of 15 donor and 15 acceptor sites. In the first excited singlet state of the ordered system, electron and hole are delocalised over several molecules (Fig. 7a). In the first excited singlet states with disorder in coupling (Fig. 7b) or disorder in both site energy and coupling (Fig. 7c), charge is transferred chiefly from molecules which are not directly adjacent to the interface. Similar results are obtained for a larger assembly of 66 donor and 66 acceptor sites.
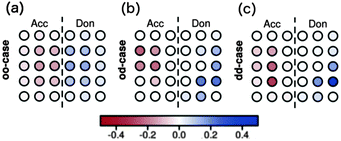 | ||
| Fig. 7 Charges in the first excited singlet states from the CIS calculations on the two-dimensional hetero-junctions as calculated by Raos et al.91 for (a) no disorder, (b) disorder in couplings, but not in site energies, and (c) disorder in both couplings and in site energies. | ||
The results of Raos et al. are obtained from only one system, using one set of site energies and transition integrals. Studies of sensitivity of results to parameter values and system configuration would be required in order to draw general conclusions.
4 Electrostatic effects
As mentioned in the introduction, one proposed explanation for efficient charge generation in organic photovoltaics is a classical screening effect, brought about by induced polarisation in molecules surrounding the CT state. This effectively reduces the Coulomb interaction between electron and hole, and so possibly facilitates charge separation. In the limit of a homogeneous continuous medium, this screening of the Coulomb interaction via polarisation is included in eqn (1) through the εr term. However, a constant εr is only appropriate for materials whose electronic response can reasonably be considered linear, isotropic, and homogeneous. Whilst this may be a fair approximation for large scale systems such as capacitors where bulk effects are important, it does not accurately describe the polarisation of the medium surrounding a charge transfer state, which takes place on a molecular scale (Fig. 2c). The positions and orientations of molecules, along with their charge distributions and polarisabilities, can have a large impact on the energetic landscape for charge separation.24,93Such effects are extremely challenging to probe experimentally. This is, in part, due to differences in dielectric constant when probed at different frequencies. At high frequencies, nuclei may be assumed to be static, and the freedom of electron orbitals to rearrange in response to applied field will be the main factor defining the dielectric response. At lower frequencies, this assumption breaks down, and the reorientation of nuclei in response to applied field will typically result in a higher value for dielectric constant. Values for bulk permittivity at low frequencies can be deduced using capacitance measurements, but can be very sensitive to device architecture. Values of εr at optical frequencies can be obtained using ellipsometry, sometimes in different crystal directions.94–97 Which of these values is relevant to the screening experienced when charges separate, or indeed whether a single number (or tensor) dielectric constant is sufficient to describe this process, is unclear.
Still more challenging to probe are dielectric effects at the interface between two material systems. Permanent interfacial dipoles, either resulting from molecules with an intrinsic ground state dipole, or via ground state partial electron transfer between donor and acceptor molecules, may also play an important role in defining the energetic landscape for charges at the interface. Ultraviolet photoemission spectroscopic studies have been carried out measuring shifts in ionisation potential in a sample with a controlled number of molecular monolayers, suggesting some ground state charge transfer in a number of organic:organic systems relevant to organic photovoltaics.98–102
Determining dielectric effects in general systems is a challenging problem, and not a new one. The Clausius–Mossotti relation, published in 1879, gives an exact expression for the dielectric constant of a simple cubic lattice of point dipoles of a given isotropic polarisability. This has been successful in describing some simple systems, but breaks down when considering disordered systems, systems in other crystal structures, or molecules whose polarisability is not well reproduced by an isotropic polarisability tensor. A number of schemes have been developed based upon the generalised Clausius–Mossotti (GCM) relation, whereby the system is modelled as a finite set of interacting polarisable dipoles, in the presence of an externally applied electric field (representing applied field and/or permanent charges and multipoles in the system).103
The polarisable dipoles in the GCM equation have be chosen to represent units of different size in different schemes. A number of schemes exist whereby molecules are broken down into atomic points, each of which is assigned a polarisability, and atomic polarisabilities are calibrated in order to reproduce those of molecules.104–109 These approaches use various forms of smearing of dipoles and/or separation cutoffs for dipole–dipole interaction to avoid infinite polarisation by the cooperative (head to tail) interaction between induced dipoles.
Polarisabilities of single molecules can sometimes be inferred from optical properties using the Clausius–Mosotti relations,104,105 or may be calculated using quantum chemical methods, although a careful choice of functional must be made when calculating polarisabilities of long conjugated molecules.65,110–114
Electrostatic effects particular to interfaces may influence the energetic landscape for charge carriers in a number of ways, some of which are presented in Fig. 8.24 Changes in dielectric constant will tend to stabilise charges in the εlow domain close to the interface, while driving charges deeper in the εhigh domain (Fig. 8a). Poor packing may effectively result in a lower dielectric constant at the interface, driving charge carriers away (Fig. 8b). A static interfacial electric field due to multipole moments of organic semiconductors will result in a bending of bands close to the interface (Fig. 8c). Structural disorder at the interface, depending on its nature, may result in a range of effects. The impact on energy levels of disorder, whilst significant, is thus not easy to quantify (Fig. 8d).
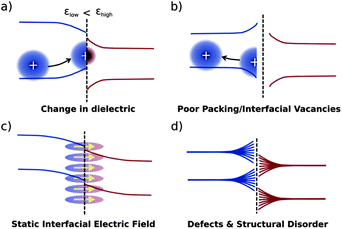 | ||
| Fig. 8 Yost et al.'s24 schematic representation of four different environmental effects on the organic/organic band structure: (a) a difference in dielectrics, (b) poor molecular packing at the interface, (c) a molecular multipole moment creating an electric field at the interface, and (d) a rough depiction of general disorder at the interface. | ||
Verlaak et al. use a GCM-like approach to probe an interface of C60 with the [0,0,1], and [0,1,−1] faces of a pentacene crystal.93 Molecules are given molecular polarisability tensors, αmol, and permanent quadrupole moments Θmol split between a number of sites, s, on the molecule each with polarisability αmol/s, and quadrupole moment Θmol/s. The polarisation of each molecule is calculated in response to an electron–hole pair (represented as point charges) on various molecules in the system, and a value is obtained for the net electrostatic energy due to interactions of charges, induced dipoles, and quadrupoles is calculated.
By comparison of the energies of systems with electrons and holes close to and far from the interface, Verlaak et al. determine a barrier of only 0.04 eV for a pentacene [0,1,−1]:C60 interface, and 0.44 eV for a pentacene [0,0,1]:C60 interface. This is despite a closer approach of nearest neighbour molecules on the interface in the [0,1,−1]:C60 case. This is attributed to a greater stabilising interaction with induced dipoles for electron and hole further from the interface, coupled with a large driving force associated with changes in interactions between charges and permanent quadrupoles on the pentacene molecule. Linares et al. carry out further work on the pentacene:C60 junction using this approach,115 as reviewed elsewhere.81
These results are certainly interesting, however, there are some features of the model which warrant attention. The molecular polarisability tensor is split by simple division, resulting, in the case of pentacene, in atomic or ring polarisabilities which are far from isotropic. In reality, the anisotropic polarisability of pentacene must be due to the anisotropic arrangement of atoms and electrons, and heavily anisotropic polarisability tensors on each individual site may not give an accurate representation of the polar response on a submolecular scale. Secondly, electron and hole polarons are represented as point charges. Baumeier et al.69 find very different energetic landscapes for interfacial charge pairs when considering charges as molecule centred points, and explicitly considering charge distributions.
Chia et al.116 model the dielectric response of crystallites of ∼1000 fullerenes, in which each molecule is treated as a single polarisable point. A direction dependent dielectric constant is obtained by considering the energy surface associated with separation of charges along one or other of the crystal axes Despite the simplicity of this approach, it has been able to well reproduce mean polarisabilities of C60 and PCBM.
QM/MM calculations also help to elucidate the role of electrostatics in determining behaviour of charges at the interface, by providing an estimate of the energetics of single QM molecules at different positions within an assembly of MM molecules, arranged to form a heterojunction.
Yost et al. apply such an approach to a number of organic semiconductor interfaces. They find an energy profile akin to Fig. 8a for a Rubrene (epsilon ∼2.7):C60 (epsilon ∼3.8). Pulling CuPc:PTCBI apart at an interface, they find an energy profile akin to Fig. 8b. Yost et al. examine an interface between C60 and a half unit cell of (dicyanomethylene)-2-methyl-6-(4-dimethylaminostyryl)-4H-pyran (DCM), which exhibits a significant dipole moment. They find a large bending of bands, similar to that shown in Fig. 8c, but to a greater magnitude such that the HOMO and LUMO orbitals of DCM are pushed below those of C60 close to the interface.
Poelking et al. find that long range interactions play a decisive role in the electrostatic landscape of a dicyanovinyl-substituted oligothiophene (DCVnT):C60 device.117 They perform an Ewald split, superimposing a non-periodic foreground onto a periodic, neutral background. They use Thole's model, based upon an interacting set of atomic polarisabilities, to model their foreground. They find that the inclusion of this background changes the energetic landscape from one which does not allow charge separation, to one which favours charge separation.
The geometrical relaxation of surrounding molecules may also play a role in determining the energetic landscape for charge carriers, and may be probed using molecular dynamics simulations. de Gier et al. study the stabilisation of a monomer:fullerene charge transfer state when surrounded by monomers with sidechains of various dipole moment, using molecular dynamics for initial configurations, and allowing sidechains to respond to the presence of the charge transfer state.118 They find a stabilisation of their charge pair by as much as 0.8 eV associated with sidechain orientation in the system with most polar sidechains, compared to 0.3 eV or less for less polar sidechains. This implies that the reorientation of sidechains could play a significant role in stabilising separated charges. However, it is not clear whether such processes could take place on the ultrafast (∼100 fs) timescales associated with the onset of polaron absorption in spectroscopic studies. Such reorganisation may still impact the later generation of charges, or reduce nongeminate recombination.
In summary, it is widely accepted that the treatment of the dielectric environment as a homogenous material of known permittivity is a crude approximation that may lead to inaccurate estimates of the binding energy of charge pairs at the donor:acceptor interface. Microscopic electrostatic approaches, where individual molecules or parts of molecules are represented by polarisable units and the electrostatic energy calculated using a classical sum of coulombic, dipolar and quadrupolar interactions, have been used to investigate the situation at a variety of donor:acceptor interfaces. The resulting interaction energy depends strongly on molecular organisation at the interface as well as on chemical structure, and may differ in magnitude and sign from estimates based on the bulk εr. Attempts to include the effect of molecular dynamics on electrostatic binding energy have been made, though the relevance of these to charge separation depends on the relative rates of the electronic and molecular motions.
5 Dynamics of charge pair generation
All the works mentioned so far have focussed on modelling the energetic landscapes within an organic photovoltaic device. Whilst energetic landscapes are clearly important for defining characteristics favourable to charge generation, the process of generating charges is a dynamic one, and we are ultimately concerned with rates at which different processes take place. There exists no one accepted methodology for the calculation of rate processes in OPVs, but there have been a number of relevant publications calculating rates of processes on a bimolecular, and multimolecular scale.In order for efficient charge generation, the rate of energy transfer from S1D to CT1 or CT* must compete with spontaneous emission from S1D back to S0D, and the rate of separation of charges from CT1 or CT* to CS must compete with recombination rates from CT back to the ground state S0D (Fig. 1).
Spontaneous emission rates may be computed directly from excitation energies and transition dipole moments of excited states using Fermi's golden rule. These rates will give an indication of the recombination timescales with which charge separation must compete. Huang et al. take this approach in studying oligomer pairs.73 They find spontaneous emission rates from states of chiefly single molecule excitation character on the order of 1 ns, and from states of exciplex or polaron pair character of ∼0.1–10 μs.
Under the frozen orbital approximation, rates for hopping between states on different molecules may be calculated from the coupling of orbitals, and the reorganisation energy associated with the movement of the charge by use of Marcus theory. Marcus theory is also based upon Fermi's Golden Rule, and, as such, is only valid under the approximation of weak coupling between states, which may not be valid for excited state dynamics in organic systems. It is also limited by limited by difficulties in knowing the appropriate reorganisation energy for excited state transitions. By comparing transfer rates between calculated CT states, and ground and excited states on donor and acceptor, it may be possible to predict how electron transfer processes at the interface proceed.
An example of such an approach is Yi et al.'s119 calculations of couplings and hopping rates between a sexithiophene (6T) donor molecule, and C60 or perylenetetracarboxydiimide (PDI) acceptor molecule. Yi et al. represent the CT states of the donor:acceptor complex as a linear combination of ground states of the individual donor cation and acceptor anion, and calculate couplings with neutral ground and excited states (calculated using TDDFT) of each single molecule.
Yi et al. find that couplings are strongly dependent on mutual position of molecules. In most positions, couplings between CT state and ground state are stronger, and resultant recombination rates faster, for PDI (∼109–1012 s−1) than C60 (∼108–1010 s−1). This may be an important factor in explaining the more efficient charge generation in polythiophene:fullerene devices than polythiophene:PDI devices.
Difley et al. also use Marcus theory to calculate transition rates two donor:acceptor small molecule pairs, using TDDFT for single molecule states, but CDFT, in which donor and acceptor molecules are confined to have charges of +e and −e, and an excess spin of ±½, to calculate charge transfer states, allowing electron and hole wavefunctions to be influenced by the presence of charges on the opposite molecule.
Use of molecular dynamics simulations allows comparison of relative rates for molecules pairs in a range of geometries. Liu et al. apply a Marcus rate approach to the calculation of charge separation and recombination rates for a P3MT (modelled as a hexamer):PCBM interface, finding charge separation rates on the order of 1010–1012 s−1, and charge recombination rates between 106–109 s−1, strongly dependent on mutual position of molecules. These results are comparable to experimentally reported charge separation rates faster than 4 × 1011 s−1, and recombination rates between 108 and 109 s−1.120 These results suggest that the rate of charge transfer from the CT state to neighbouring units (CT to CS in Fig. 1) is faster than the relaxation from the CT state back to the ground state for a thiophene donor and PCBM acceptor. However, the relative rates of these processes are very dependent upon mutual position and orientation of donor and acceptor molecules at the interface, and recombination rates from the CT state are sufficiently high that this could act as significant loss pathway, especially if charges are unable to escape from the vicinity of the interface.
It is also possible to go beyond rate based approaches, and perform quantum dynamics calculations. This approach requires solving the time dependent Hamiltonian for evolving states. An example of such an approach is Tamura et al.'s121 work, using the multiconfiguration time dependent Hartree (MCTDH) method to calculate dynamics of excited species in a quaterthiophene:C60 molecule pair. They find that spatial separation of molecules has a large influence on dynamics at the interface, with the excitation oscillating between single molecule exciton and charge transfer state for a separation of 3.5 Å, and exciton/CT state population ratio settling down around one quarter after the rapid exciton decay at a separation of 3.0 Å, albeit still with large temporal fluctuations. Tamura et al. take this as evidence that the CT state has a degree of excitonic character, allowing a radiative decay to the ground state. Tamura and Burghardt have also applied this approach to larger assemblies of thiophene:C60 pairs, finding charge separation to occur from an exciton close to the interface on a ∼100 fs timescale (Fig. 9).122
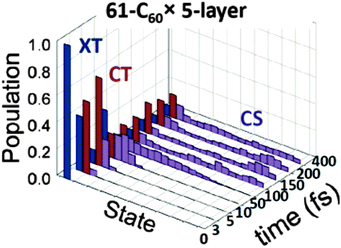 | ||
| Fig. 9 Excitation dynamics from Tamura et al.'s122 MCTDH simulations of a stack of thirteen thiophene oligomers alongside five layers of 61 C60 molecules. The initial excitation (XT), rapidly migrates to the interface to form a CT state, which decays to separated charges (CS) on a ∼100 fs timescale. | ||
Some dynamic models are based on the possible generation of free charges without proceeding via intermediate interfacial states. This may occur either via long-range hopping following the localisation of the excitation on a single molecule, or due to an initially well delocalised state, or superposition of states, which directly decomposes into a state involving well separated charges. Both rely on the idea that photoexcited states, which may already be spatially delocalised, are coupled to charge separated states.
The case of long-range charge separation from a localised exciton has been modelled by Caruso and Troisi using a Marcus-based hopping model. This model is used to compare hopping rates from excited states deep within the donor domain to neighbouring donor molecules, and directly to charge-separated states. They assume an exponential decay of electron wavefunction over space, with a range of decay rates, justified by comparison with those reported for donor–bridge–acceptor molecules. Caruso and Troisi conclude that, for an exponential decay rate of the exciton wavefunction of less than 0.6 Å−1, the majority of electron–hole pairs are generated without the exciton reaching the interface. This decay length is, however, longer than values found even for intramolecular charge transfer in many systems.123–125
The case of charge separation without prior localisation of the exciton has been modelled by Bittner and Silva.30 Here, the initial photoexcitation is to either an energy eigenstate, or a coherent superposition of energy eigenstates of the system, which evolve with time according to the time dependent Schrodinger equation. Decoherence is driven by interaction with a time dependent coupling between orbitals, brought about by environmental fluctuations. Bittner and Silva apply this model to a donor oligomer:acceptor oligomer heterojunction, each domain containing four oligomers with five possible electron sites, and add energetic disorder, in one case close to the interface, and in another, far from the interface. Calculated state energies versus charge separation distance are shown in Fig. 10. They find a fast transfer rate from initial excitation to free polaron states, suggesting that electron or hole could tunnel 12–15 Å from the site of the initial excitation within 35 fs. This is assigned to strong resonance between high oscillator strength excitons, and near-degenerate free polaron states, which are almost always present given a sufficient level of energetic disorder in the simulation space.
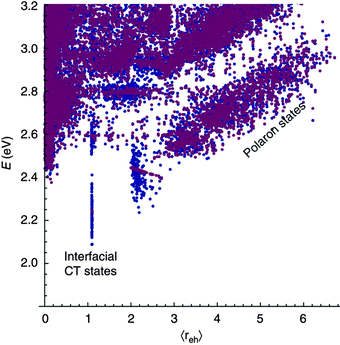 | ||
| Fig. 10 Bittner and Silva's30 calculated state energy versus charge separation distance, for energetic disorder close to the interface and order in regions away from the interface (blue), and energetic order close to the interface and disorder in regions away from the interface (purple). High oscillator strength excitonic states are calculated to exhibit resonance and fast transfer rates to near-degenerate (but low oscillator strength) polaron states. | ||
Compared to the theoretical study of the energies of states at the donor:acceptor interface, the theoretical treatment of transitions between such states is much less well developed. Approaches based upon Fermi's Golden Rule have been used to quantify the rates of transitions between excitonic states, charge transfer states and ground, but are limited by the validity of the weak coupling approximation. More powerful approaches are based on the evolution of states within the time dependent Schrodinger equation and allow multiple state configurations to be studied. These approaches are promising, but still under development, and are likely to require large approximations, or be computationally expensive for representative systems.
6 Summary and concluding remarks
Whilst there is as yet no complete theory of charge generation at organic heterojunctions, different parts of the problem have been addressed and significant progress has been made in building theoretical tools and in rationalising experimental results. The work has clarified the directions for development of more powerful models.High level calculations of molecule pairs in vacuo indicate that mutual position of donor and acceptor molecules is very important in defining the energies of CT states. The nature and energy of excited states are particularly sensitive to molecular alignment when the LUMO of donor and acceptor are close in energy. Semi-empirical calculations of states in larger arrays of molecules indicate that the states involved in charge transfer may delocalise over many molecules. This work indicates that more efficient treatments of excited states in multi-molecular systems are needed. However, this capability will also require improved experimental probes of the physical structure of interfacial regions.
Studies on electrostatics show that changes in dielectric constant, poor packing, static internal electric fields, and structural disorder can all influence the energetic landscape close to the heterojunction. The orientation of molecules, and alignment of crystals at the interface, can be decisive in determining this landscape, in a manner which could not be captured with a bulk dielectric constant. Long range interactions, and edges of the device can also play a defining role in the energetic landscape for charge separation. The significance of local structural detail again indicates the need for improved structural probes in order to apply the models usefully to practical situations.
Calculated transition rates on molecule pairs agree reasonably well with the range of those reported experimentally, and studies on the impact of mutual position and orientation of molecules may provide insights into favourable orientations for separation of charges. Explicit calculations on the evolution of states in larger arrays of molecules indicate the possibility of ultrafast separation, which may proceed via the CT state or directly to charge separated states. On longer timescales, the dynamics of molecules close to the interface may influence charge separation efficiency, but little progress has been made in this area so far.
Whilst these studies do not provide a unique mechanism for charge separation, they help to inform the roles that molecular properties may play in these mechanisms. They provide a greater understanding of the importance of orbital energies and polarisabilities of molecules, ways in which molecules may be arranged in order for couplings and energetics favourable for charge separation, the possible role of disorder, and relevant timescales for this process. Through further study, and with the aid of more detailed information on the structure and the ultrafast dynamics of charge transfer processes, the roles of these different mechanisms in driving the efficient charge separation observed in many OPV material systems may be better understood, and design rules developed for OPV structures of improved performance.
Acknowledgements
JN and SF acknowledge the support of the UK Engineering and Physical Sciences Research Council through the Plastic Electronics Doctoral Training Centre (EP/G037515), the Supergen Supersolar Hub (EP/J017361), and grants EP/J500021 and EP/K030671. JMF also acknowledges EPSRC grant EP/K016288. JN thanks the Royal Society for a Wolfson Merit Award. We are grateful to James Kirkpatrick for stimulating and useful discussions.References
- National Renewable Energy Laboratory, Best research cell efficiencies, 2014.
- M. Antonietta and A. Troisi, Phys. Chem. Chem. Phys., 2014, 16, 20277–20278 RSC.
- F. Gao and O. Inganäs, Phys. Chem. Chem. Phys., 2014, 20291–20304 RSC.
- T. M. Clarke and J. R. Durrant, Chem. Rev., 2010, 110, 6736–6767 CrossRef CAS PubMed.
- S. H. Park, A. Roy, S. Beaupre, S. Cho, N. Coates, J. S. Moon, D. Moses, M. Leclerc, K. Lee and A. J. Heeger, Nat. Photonics, 2009, 3, 297–303 CrossRef CAS.
- K. Vandewal, S. Albrecht, E. T. Hoke, K. R. Graham, J. Widmer, J. D. Douglas, M. Schubert, W. R. Mateker, J. T. Bloking, G. F. Burkhard, A. Sellinger, J. M. J. Fréchet, A. Amassian, M. K. Riede, M. D. McGehee, D. Neher and A. Salleo, Nat. Mater., 2014, 13, 63–68 CrossRef CAS PubMed.
- M. A. Loi, S. Toffanin, M. Muccini, M. Forster, U. Scherf and M. Scharber, Adv. Funct. Mater., 2007, 17, 2111–2116 CrossRef CAS.
- D. Veldman, O. Ipek, S. C. J. Meskers, J. Sweelssen, M. M. Koetse, S. C. Veenstra, J. M. Kroon, S. S. van Bavel, J. Loos and R. a. J. Janssen, J. Am. Chem. Soc., 2008, 130, 7721–7735 CrossRef CAS PubMed.
- D. Veldman, S. C. J. Meskers and R. A. J. Janssen, Adv. Funct. Mater., 2009, 19, 1939–1948 CrossRef CAS.
- M. A. Faist, T. Kirchartz, W. Gong, R. S. Ashraf, I. McCulloch, J. C. de Mello, N. J. Ekins-Daukes, D. D. C. Bradley and J. Nelson, J. Am. Chem. Soc., 2012, 134, 685–692 CrossRef CAS PubMed.
- H. Ohkita, S. Cook, Y. Astuti, W. Duffy, S. Tierney, W. Zhang, M. Heeney, I. McCulloch, J. Nelson, D. D. C. Bradley and J. R. Durrant, J. Am. Chem. Soc., 2008, 130, 3030–3042 CrossRef CAS PubMed.
- E. Wang, Z. Zhang, K. Vandewal, P. Henriksson, F. Zhang, M. R. Andersson, Z. Ma and O. Inganäs, J. Am. Chem. Soc., 2011, 133, 14244–14247 CrossRef CAS PubMed.
- F. Z. Koen Vandewal, Z. Ma, J. Bergqvist, Z. Tang, E. Wang, P. Henriksson, K. Tvingstedt, M. R. Andersson, O. Inganäs, O. Inganäs, K. Vandewal, Z. Ma, J. Bergqvist, Z. Tang, E. Wang, P. Henriksson, K. Tvingstedt, M. R. Andersson and F. Zhang, Adv. Funct. Mater., 2012, 22, 1–38 CrossRef.
- H. Bronstein, E. Collado-Fregoso, A. Hadipour, Y. W. Soon, S. D. Dimitrov, R. S. Ashraf, B. P. Rand, S. E. Watkins, S. Tuladhar, I. M. Meager, J. R. Durrant, I. McCulloch, Z. Huang and P. S. Tuladhar, Adv. Funct. Mater., 2013, 23, 5647–5654 CrossRef CAS.
- M. Knupfer, J. Fink and D. Fichou, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 1–4 CrossRef.
- S. Holdcroft, Macromolecules, 1991, 24, 4834–4838 CrossRef CAS.
- Y. Shimoi, A. Shuji, K. Shin-ichi and M. Kazuhiro, Solid State Commun., 1995, 95, 137–141 CrossRef CAS.
- B. Bernardo, D. Cheyns, B. Verreet, R. D. Schaller, B. P. Rand and N. C. Giebink, Nat. Commun., 2014, 5, 3245 CAS.
- B. M. Savoie, A. Rao, A. A. Bakulin, S. Gelinas, B. Movaghar, R. H. Friend, T. J. Marks and M. A. Ratner, J. Am. Chem. Soc., 2014, 136, 2876–2884 CrossRef CAS PubMed.
- A. A. Bakulin, A. Rao, V. G. Pavelyev, P. H. M. van Loosdrecht, M. S. Pshenichnikov, D. Niedzialek, J. Cornil, D. Beljonne and R. H. Friend, Science, 2012, 1340, 1–13 Search PubMed.
- D. Amarasinghe Vithanage, a. Devižis, V. Abramavičius, Y. Infahsaeng, D. Abramavičius, R. C. I. MacKenzie, P. E. Keivanidis, a. Yartsev, D. Hertel, J. Nelson, V. Sundström and V. Gulbinas, Nat. Commun., 2013, 4, 2334 CAS.
- S. Gélinas, A. Rao, A. Kumar, S. L. Smith, A. W. Chin, J. Clark, T. S. van der Poll, G. C. Bazan and R. H. Friend, Science, 2014, 343, 512–516 CrossRef PubMed.
- T. Liu, D. L. Cheung and A. Troisi, Phys. Chem. Chem. Phys., 2011, 13, 21461–21470 RSC.
- S. R. Yost and T. Van Voorhis, J. Phys. Chem. C, 2013, 117, 5617–5625 CAS.
- Y.-T. Fu, C. Risko and J.-L. Brédas, Adv. Mater., 2013, 25, 878–882 CrossRef CAS PubMed.
- G. F. a. Dibb, F. C. Jamieson, A. Maurano, J. Nelson and J. R. Durrant, J. Phys. Chem. Lett., 2013, 4, 803–808 CrossRef CAS.
- J. Kniepert and M. Schubert, J. Phys. Chem. Lett., 2011, 2, 700–705 CrossRef CAS.
- S. Albrecht and W. Schindler, J. Phys. Chem. Lett., 2012, 640–645 CrossRef CAS.
- D. Caruso and A. Troisi, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 13498–13502 CrossRef CAS PubMed.
- E. R. Bittner and C. Silva, Nat. Commun., 2014, 5, 3119 Search PubMed.
- B. Kraabel, C. Lee, D. McBranch, D. Moses, N. Sariciftci and A. J. Heeger, Chem. Phys. Lett., 1993, 213, 389–394 CrossRef CAS.
- I. Hwang, D. Moses and A. Heeger, J. Phys. Chem. C, 2008, 112, 4350–4354 CAS.
- C.-X. Sheng, T. Basel, B. Pandit and Z. Vardeny, Org. Electron., 2012, 13, 1031–1037 CrossRef CAS PubMed.
- L. G. Kaake, D. Moses and A. J. Heeger, J. Phys. Chem. Lett., 2013, 4, 2264–2268 CrossRef CAS.
- S. Mukamel, J. Phys. Chem. A, 2013, 117, 10565 CrossRef PubMed.
- C. Brabec, G. Zerza, G. Cerullo, S. Di Silvestri, S. Luzzati, J. C. Hummelen and S. Sariciftci, Chem. Phys. Lett., 2001, 340, 232–236 CrossRef CAS.
- F. Zhang, K. Jespersen, C. Björström, M. Svensson, M. Andersson, V. Sundström, K. Magnusson, E. Moons, a. Yartsev and O. Inganäs, Adv. Funct. Mater., 2006, 16, 667–674 CrossRef CAS.
- I.-W. Hwang, C. Soci, D. Moses, Z. Zhu, D. Waller, R. Gaudiana, C. Brabec and A. J. Heeger, Adv. Mater., 2007, 19, 2307–2312 CrossRef CAS.
- F. Etzold, I. a. Howard, N. Forler, D. M. Cho, M. Meister, H. Mangold, J. Shu, M. R. Hansen, K. Müllen and F. Laquai, J. Am. Chem. Soc., 2012, 134, 10569–10583 CrossRef CAS PubMed.
- G. Grancini, M. Maiuri, D. Fazzi, A. Petrozza, H.-J. Egelhaaf, D. Brida, G. Cerullo and G. Lanzani, Nat. Mater., 2013, 12, 29–33 CrossRef CAS PubMed.
- N. Banerji, S. Cowan, M. Leclerc, E. Vauthey and A. J. Heeger, J. Am. Chem. Soc., 2010, 132, 17459–17470 CrossRef CAS PubMed.
- N. Banerji, J. Mater. Chem. C, 2013, 1, 3052 RSC.
- M. Tong, N. E. Coates, D. Moses, A. J. Heeger, S. Beaupré and M. Leclerc, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 125210 CrossRef.
- F. Provencher, N. Bérubé, A. W. Parker, G. M. Greetham, M. Towrie, C. Hellmann, M. Côté, N. Stingelin, C. Silva and S. C. Hayes, Nat. Commun., 2014, 5, 4288 Search PubMed.
- L. Onsager, J. Chem. Phys., 1934, 2, 599 CrossRef CAS PubMed.
- C. L. Braun, J. Chem. Phys., 1984, 80, 4157 CrossRef CAS PubMed.
- V. Mihailetchi, L. Koster, J. Hummelen and P. Blom, Phys. Rev. Lett., 2004, 93, 19–22 CrossRef.
- P. Peumans and S. R. Forrest, Chem. Phys. Lett., 2004, 398, 27–31 CrossRef CAS PubMed.
- C. Deibel, T. Strobel and V. Dyakonov, Phys. Rev. Lett., 2009, 103, 1–4 CrossRef.
- V. I. Arkhipov, P. Heremans and H. Baìŝsler, Appl. Phys. Lett., 2003, 82, 4605 CrossRef CAS PubMed.
- A. V. Nenashev, S. D. Baranovskii, M. Wiemer, F. Jansson, R. Österbacka, a. V. Dvurechenskii and F. Gebhard, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 035210 CrossRef.
- T. Offermans, S. C. J. Meskers and R. a. J. Janssen, Chem. Phys., 2005, 308, 125–133 CrossRef CAS PubMed.
- H. van Eersel, R. a. J. Janssen and M. Kemerink, Adv. Funct. Mater., 2012, 22, 2700–2708 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 1372 CrossRef CAS PubMed.
- G. Zhang and C. B. Musgrave, J. Phys. Chem. A, 2007, 111, 1554–1561 CrossRef CAS PubMed.
- A. Dreuw and M. Head-Gordon, J. Am. Chem. Soc., 2004, 126, 4007–4016 CrossRef CAS PubMed.
- D. J. Tozer, J. Chem. Phys., 2003, 119, 12697 CrossRef CAS PubMed.
- T. Ziegler, M. Seth, M. Krykunov, J. Autschbach and F. Wang, THEOCHEM, 2009, 914, 106–109 CrossRef CAS PubMed.
- P. M. W. Gill, R. D. Adamson and J. a. Pople, Mol. Phys., 1996, 88, 1005–1009 CrossRef CAS.
- T. Leininger, H. Stoll, H.-J. Werner and A. Savin, Chem. Phys. Lett., 1997, 275, 151–160 CrossRef CAS.
- H. Iikura, T. Tsuneda, T. Yanai and K. Hirao, J. Chem. Phys., 2001, 115, 3540 CrossRef CAS PubMed.
- T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS PubMed.
- M. J. G. Peach, P. Benfield, T. Helgaker and D. J. Tozer, J. Chem. Phys., 2008, 128, 044118 CrossRef PubMed.
- R. Baer and D. Neuhauser, Phys. Rev. Lett., 2005, 94, 2–5 CrossRef.
- E. Livshits and R. Baer, Phys. Chem. Chem. Phys., 2007, 9, 2932–2941 RSC.
- L. Hedin, Phys. Rev., 1965, 139, 796–823 CrossRef CAS.
- E. Salpeter and H. Bethe, Phys. Rev., 1951, 84, 1232–1242 CrossRef.
- Y. Ma, M. Rohlfing and C. Molteni, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 241405 CrossRef.
- B. Baumeier, D. Andrienko and M. Rohlfing, J. Chem. Theory Comput., 2012, 8, 2790–2795 CrossRef CAS.
- B. Baumeier, D. Andrienko, Y. Ma and M. Rohlfing, J. Chem. Theory Comput., 2012, 8, 997–1002 CrossRef CAS.
- D. Niedzialek, I. Duchemin, T. B. D. Queiroz, S. Osella, A. Rao, R. Friend, X. Blase, S. Kümmel and D. Beljonne, 2014, DOI:10.1002/adfm.201402682.
- E. B. Isaacs, S. Sharifzadeh, B. Ma and J. B. Neaton, J. Phys. Chem. Lett., 2011, 2, 2531–2537 CrossRef CAS.
- Y.-S. Huang, S. Westenhoff, I. Avilov, P. Sreearunothai, J. M. Hodgkiss, C. Deleener, R. H. Friend and D. Beljonne, Nat. Mater., 2008, 7, 483–489 CrossRef CAS PubMed.
- S. Difley and T. V. Voorhis, J. Chem. Theory Comput., 2011, 7, 594–601 CrossRef CAS.
- K. E. Riley, B. T. Op't Holt and K. M. Merz, J. Chem. Theory Comput., 2007, 3, 407–433 CrossRef CAS PubMed.
- M. Swart, L. Jensen and P. Van Duijnen, Solvation Effects on Molecules and Biomolecules, Springer, Netherlands, Dordrecht, 2008, pp. 39–102 Search PubMed.
- S. Difley, L.-P. Wang, S. Yeganeh, S. R. Yost and T. Van Voorhis, Acc. Chem. Res., 2010, 43, 995–1004 CrossRef CAS PubMed.
- Y. Kanai and J. C. Grossman, Nano Lett., 2007, 7, 1967–1972 CrossRef CAS PubMed.
- I. H. Nayyar, E. R. Batista, S. Tretiak, A. Saxena, D. L. Smith and R. L. Martin, J. Phys. Chem. Lett., 2011, 2, 566–571 CrossRef CAS.
- R. M. Martin, Electronic structure: basic theory and practical methods, Cambridge University Press, 2004 Search PubMed.
- D. Beljonne, J. Cornil, L. Muccioli, C. Zannoni, J.-L. Breìdas and F. Castet, Chem. Mater., 2011, 23, 591–609 CrossRef CAS.
- S. Few, J. M. Frost, J. Kirkpatrick and J. Nelson, J. Phys. Chem. C, 2014, 16, 8253–8261 Search PubMed.
- M. a. Loi, S. Toffanin, M. Muccini, M. Forster, U. Scherf and M. Scharber, Adv. Funct. Mater., 2007, 17, 2111–2116 CrossRef CAS.
- D. Veldman, O. Ipek, S. C. J. Meskers, J. Sweelssen, M. M. Koetse, S. C. Veenstra, J. M. Kroon, S. S. van Bavel, J. Loos and R. A. J. Janssen, J. Am. Chem. Soc., 2008, 130, 7721–7735 CrossRef CAS PubMed.
- A. A. Y. Guilbert, M. Schmidt, A. Bruno, J. Yao, S. King, M. Sachetan, T. Kirchartz, M. I. Alonso, A. R. Goñi, N. Stingelin, A. Saif, M. Campoy-quiles and J. Nelson, Adv. Funct. Mater., 2014, 24, 6972–6980 CrossRef.
- B. A. C. Mayer, M. F. Toney, S. R. Scully, J. Rivnay, C. J. Brabec, M. Scharber, M. Koppe, M. Heeney, I. Mcculloch and M. D. Mcgehee, Adv. Funct. Mater., 2009, 1173–1179 CrossRef.
- W. L. Rance, A. J. Ferguson, T. McCarthy-Ward, M. Heeney, D. S. Ginley, D. C. Olson, G. Rumbles and N. Kopidakis, ACS Nano, 2011, 5, 5635–5646 CrossRef CAS PubMed.
- D. L. Cheung and A. Troisi, J. Phys. Chem. C, 2010, 114, 20479–20488 CAS.
- M. T. Rispens, A. Meetsma, R. Rittberger, C. J. Brabec, N. S. Sariciftci and J. C. Hummelen, Chem. Commun., 2003, 2116–2118 RSC.
- J. J. Kwiatkowski, J. M. Frost and J. Nelson, Nano Lett., 2009, 9, 1085–1090 CrossRef CAS PubMed.
- G. Raos, M. Casalegno and J. Ide, J. Chem. Theory Comput., 2013, 10, 364–372 CrossRef.
- I. Dabo, A. Ferretti, C.-H. Park, N. Poilvert, Y. Li, M. Cococcioni and N. Marzari, Phys. Chem. Chem. Phys., 2013, 15, 685–695 RSC.
- S. Verlaak, D. Beljonne, D. Cheyns, C. Rolin, M. Linares, F. Castet, J. Cornil and P. Heremans, Adv. Funct. Mater., 2009, 19, 3809–3814 CrossRef CAS.
- P. C. Eklund, A. M. Rae, Y. Wang, P. Zhou, K.-a. Wang, J. M. Holden, M. S. Dresselhaus and G. Dresselhaus, Thin Solid Films, 1995, 257, 211 CrossRef CAS.
- M. Alonso, M. Garriga, N. Karl, J. Ossó and F. Schreiber, Org. Electron., 2002, 3, 23–31 CrossRef CAS.
- M. Campoy-Quiles, M. I. Alonso, D. D. C. Bradley and L. J. Richter, Adv. Funct. Mater., 2014, 24, 2116–2134 CrossRef CAS.
- M. Campoy-Quiles, C. Müller, M. Garriga, E. Wang, O. Inganäs and M. Alonso, Thin Solid Films, 2014 DOI:10.1016/j.tsf.2014.02.096.
- H. Ishii, K. Sugiyama, E. Ito and K. Seki, Adv. Mater., 1999, 11, 605–625 CrossRef CAS.
- S. C. Veenstra and H. T. Jonkman, J. Polym. Sci., Part B: Polym. Phys., 2003, 41, 2549–2560 CrossRef CAS.
- O. Molodtsova, T. Schwieger and M. Knupfer, Appl. Surf. Sci., 2005, 252, 143–147 CrossRef CAS PubMed.
- Y. Ge and J. E. Whitten, Chem. Phys. Lett., 2007, 448, 65–69 CrossRef CAS PubMed.
- W. Osikowicz, M. deJong and W. Salaneck, Adv. Mater., 2007, 19, 4213–4217 CrossRef CAS.
- P. B. Allen, J. Chem. Phys., 2004, 120, 2951 CrossRef CAS PubMed.
- J. Applequist, J. R. Carl and K.-k. Fung, J. Am. Chem. Soc., 1972, 261, 2952–2960 CrossRef.
- B. Thole, Chem. Phys., 1981, 59, 341–350 CrossRef CAS.
- P. P. T. van Duijnen and M. Swart, J. Phys. Chem. A, 1998, 102, 2399–2407 CrossRef CAS.
- H. a. Stern, G. a. Kaminski, J. L. Banks, R. Zhou, B. J. Berne and R. A. Friesner, J. Phys. Chem. B, 1999, 103, 4730–4737 CrossRef CAS.
- E. Tsiper and Z. Soos, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 085301 CrossRef.
- M. Swart and P. van Duijnen, Mol. Simul., 2006, 32, 471–484 CrossRef CAS.
- V. Lacivita, M. Rèrat, R. Orlando, M. Ferrero and R. Dovesi, J. Chem. Phys., 2012, 136, 114101 CrossRef PubMed.
- M. van Faassen, P. de Boeij, R. van Leeuwen, J. Berger and J. Snijders, Phys. Rev. Lett., 2002, 88, 186401 CrossRef CAS.
- D. S. Sabirov, R. R. Garipova and R. G. Bulgakov, Chem. Phys. Lett., 2012, 523, 92–97 CrossRef CAS PubMed.
- K. Kowalski, J. R. Hammond, W. a. de Jong and A. J. Sadlej, J. Chem. Phys., 2008, 129, 226101 CrossRef PubMed.
- M. Huzak and M. S. Deleuze, J. Chem. Phys., 2013, 138, 024319 CrossRef CAS PubMed.
- M. Linares, D. Beljonne, K. Lancaster, J.-l. Bre, S. Verlaak, A. Mityashin, P. Heremans, A. Fuchs, C. Lennartz, P. Aurel and L. Ducasse, J. Phys. Chem. C, 2010, 3215–3224 CAS.
- C. Chia, D. Teo, S. Few and J. Nelson, 2014, manuscript in preparation.
- C. Poelking, M. Tietze, C. Elschner, S. Olthof, D. Hertel, W. Frank, K. Meerholz, K. Leo and D. Andrienko, under review.
- H. D. de Gier, R. Broer and R. W. Havenith, Phys. Chem. Chem. Phys., 2014, 16, 12454–12461 RSC.
- Y. Yi, V. Coropceanu and J.-L. Brédas, J. Mater. Chem., 2011, 21, 1479 RSC.
- T. Liu and A. Troisi, J. Phys. Chem. C, 2011, 115, 2406–2415 CAS.
- H. Tamura, I. Burghardt and M. Tsukada, J. Phys. Chem. C, 2011, 115, 10205–10210 CAS.
- H. Tamura and I. Burghardt, J. Am. Chem. Soc., 2013, 135, 16364–16367 CrossRef CAS PubMed.
- C. Moser, J. Keske, K. Warncke, R. Farid and P. Dutton, Nature, 1992, 355, 796–802 CrossRef CAS PubMed.
- J. N. Clifford, E. Palomares, M. K. Nazeeruddin, M. Grätzel, J. Nelson, X. Li, N. J. Long and J. R. Durrant, J. Am. Chem. Soc., 2004, 126, 5225–5233 CrossRef CAS PubMed.
- B. Albinsson and J. Martensson, J. Photochem. Photobiol., C, 2008, 9, 138–155 CrossRef CAS PubMed.
| This journal is © the Owner Societies 2015 |