Proton dynamics in oxides: insight into the mechanics of proton conduction from quasielastic neutron scattering
Maths
Karlsson
Department of Applied Physics, Chalmers University of Technology, SE-412 96 Göteborg, Sweden. E-mail: maths.karlsson@chalmers.se; Fax: +46 31 772 2090; Tel: +46 31 772 8038
First published on 29th October 2014
Abstract
This article is concerned with the use of quasielastic neutron scattering as a technique for investigation of the dynamical properties of proton conducting oxides. Currently, the main interest in these materials comes from their promise as electrolytes in future electrochemical devices and particularly through their use as electrolytes in next-generation, intermediate-temperature, fuel cells. However, the realization of such devices depends critically on the development of new, more highly proton conducting oxides. Such a development depends on increasing the current understanding of proton conduction in oxides and for this purpose quasielastic neutron scattering is an important mean. The aim of this article is to introduce the non-specialist reader to the basic principles of quasielastic neutron scattering, its advantages and disadvantages, to summarize the work that has been done on proton conducting oxides using this technique, as well as to discuss future opportunities within this field of research.
1 Introduction
Neutron scattering is now a well-established technique in the field of solid state ionics, i.e. the study of solid electrolytes and their uses, and has played a crucial role in contributing to the current understanding of ion conducting solids. This encompasses studies of both crystal structures, via neutron diffraction (ND), surface and near-surface phenomena via neutron reflectivity (NR), as well as of the dynamical nature of materials via inelastic and quasielastic neutron scattering (INS and QENS). Whereas the majority of previous neutron work has focussed on structural investigations using ND techniques, less work has been directed towards dynamical studies using INS and QENS.This article is specifically concerned with the application of QENS for dynamical studies of proton conducting oxides. The primary interest in these materials, which may be classified according to their structure type, comes from their potential to contribute to a sustainable future, in particular through their use as electrolytes in next-generation, intermediate-temperature (≈200–500 °C) solid oxide fuel-cell (SOFC) technology,1–3 as well as through their use as electrolytes in hydrogen sensors and through their relatively unexplored potential as catalytic materials.4
A particularly promising class of proton conducting oxides are ABO3-type perovskites, where A is a relatively large cation, with an oxidation state commonly +2, and B is a cation with an oxidation state commonly +4.2 The incorporation of protons into these structures relies on acceptor doping to the B site, such as Y3+ substituted for Ce4+ in BaCeO3, followed by hydration. The acceptor doping creates oxygen vacancies, which can be subsequently filled with oxygens during the hydration procedure.2 The hydration is usually performed by heat treatment of the sample in a humid atmosphere; a process during which the water molecules in the gaseous phase dissociate into hydroxyl groups (–OH−) and protons (H+) on the surface of the sample. The –OH− groups then stick to oxygen vacancies, whereas the (other) protons bind to lattice oxygens of the oxide host lattice. In the Kröger–Vink notation5 this reaction may be written as
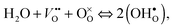 | (1) |
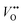 denotes an oxygen vacancy,
denotes an oxygen vacancy, 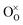 denotes a lattice oxygen, and
denotes a lattice oxygen, and 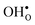 denotes a proton bound to a lattice oxygen (the superscripts ˙ and × denote positive and neutral charges, respectively).
denotes a proton bound to a lattice oxygen (the superscripts ˙ and × denote positive and neutral charges, respectively).
The protons are not stuck to any particular oxygen, but are rather free to move from one oxygen to another one and with time they will therefore diffuse into the bulk of the material. At the same time as protons diffuse into the bulk, the counter diffusion of oxygen vacancies from the bulk to the surface allows the dissociation of other water molecules on the surface of the sample. This leads to an increase of the proton concentration in the material, and so it is believed that the process continues until most, if not all, of the (bulk) oxygen vacancies are filled.
The incorporation of protons during hydration in itself means that the protons have to be mobile. The mobility of protons is routinely characterized by impedance spectroscopy techniques, with which the conductivity of protons can be determined on a macroscopic length-scale. In the case of polycrystalline samples, the impedance spectra may allow the separation of bulk conductivity from contributions from the grain boundaries (GBs). The conductivity in GBs is lower than in the bulk. This is thought to be due to either a structural misalignment in the GB region, leading to lower proton conductivity, or the appearance of a space-charge layer around the GB core, which leads to Schottky barriers and the depletion of mobile protons. At present the latter explanation is the predominating one,6,7 but the details of the GB core are not fully understood.
The connection between macroscopic proton conductivity, σ, and proton diffusion coefficient, Dσ, is given by the Nernst–Einstein equation
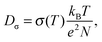 | (2) |
The aim of this article is to introduce the non-specialist reader to the basic concepts of QENS, its advantages and disadvantages, and to review the QENS studies that have been done on proton conducting oxides so far, as well as to discuss the state of the art and prospects and importance for future work in this field. Articles concerned with the use of neutron scattering techniques for studies of solid state ionics in a wider context and not specialized on QENS, are reported elsewhere.8,9
2 Neutron scattering experiments
2.1 Neutron sources and the production of free neutrons
Neutron scattering experiments are performed at large-scale neutron scattering facilities, where neutrons are produced either by nuclear fission or by spallation. In nuclear fission, certain isotopes of very heavy elements, such as uranium or plutonium, are bombarded with neutrons during which other neutrons, as well as a great deal of energy, are released from the nuclei of the isotopes. If the free neutrons are let to react with other atoms, then even more neutrons are released and as a consequence a self-sustaining chain reaction is created. In spallation sources, on the other hand, neutrons are released (spallated) by the bombardment of protons on a heavy metal target. In both types of neutron sources, the produced neutrons are of very high energy (MeV), much higher than what is useful for neutron scattering experiments. The neutrons are therefore slowed down in a, so called, moderator, before they are guided to large instrument halls containing instruments designed for certain types of experiments. The type and temperature of the moderator determine the energy of the neutrons. Generally, neutron energies in the range 0.1–10 meV refer to cold neutrons, neutron energies in the range 10–100 meV refer to thermal neutrons, and neutron energies in the range 100–1000 meV refer to hot neutrons. Cold and thermal neutrons are particularly useful in QENS experiments, since their energies and wavelengths match the energies of relevant dynamical processes and interatomic distances in condensed matter. The implication of this is two-fold: firstly, it implies that the scattered neutrons may take up or loose a large part of their incoming energy, which means that dynamics can be measured with high accuracy; secondly, it implies that interference effects of the scattered neutrons occur, which give structural information. Furthermore, the interaction of neutrons with matter is for most materials weak, which ensures that the bulk sample is being probed and not just surface or near-surface states that may behave differently from the bulk.Examples of state of the art neutron research reactors are the Institut Laue–Langevin (ILL) in France, the NIST Centre for Neutron Research (NCNR) in the US, the Laboratoire Léon Brillouin (LLB) in France, the FRM-II facility in Germany, and the OPAL neutron source of the Australian Nuclear Science and Technology Organisation (ANSTO), which are all continuous neutron sources, whereas the IBR-2M reactor of the Frank Laboratory of Nuclear Research in Russia is a pulsed source. Examples of spallation sources are the ISIS neutron facility in the UK, the Spallation Neutron Source (SNS) in the US, and the Japan Proton Accelerator Research Complex (J-PARC) in Japan, which are pulsed sources, and the Swiss Spallation Neutron Source (SINQ) in Switzerland which is a continuous source. The next-generation neutron source is the European Spallation Source (ESS), a pulsed source which is being constructed in Sweden and that will come into operation around 2020.
2.2 Scattering theory and scattering cross sections
As in all scattering experiments, the energy and momentum are conserved during a neutron scattering event. The energy of a neutron is given by E = ℏ2k2/2m, where m is the neutron's mass and k is the magnitude of the associated wave vector, |k| = k = 2π/λ, and λ is the wavelength of the neutron. Expressions for the momentum and energy transferred from the sample to the neutron during the scattering event may then be written as| ℏQ = ℏ(k0 − k1), | (3) |
|Q|2 = |k0|2 + |k1|2 − 2|k0||k1|cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2θ, 2θ, | (4) |
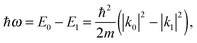 | (5) |
The measured quantity in most experiments is the double differential scattering cross section, d2σ/dΩdE, which represents the number of neutrons scattered into the solid angle dΩ with energy in the range dE. The amplitude of the scattered wave depends on the type of nuclei on which the neutrons are scattered and is also isotope and spin dependent, thus averages have to be taken for each element. The total cross section per scatterer, σ, reflects the effective areas of nuclei as seen by the incident neutrons and is obtained by integrating over all energies and solid angles,
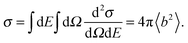 | (6) |
The total scattering cross section can be split into coherent and incoherent parts. The coherent part, σcoh, corresponds to an average over all isotopes and nuclear spin states and may be written as
| σcoh = 4π〈b〉2 = 4πbcoh2. | (7) |
| σinc = 4π(〈b2〉 − 〈b〉2). | (8) |
As in the case of the scattering cross sections, the measured quantity in neutron scattering experiments, i.e. the double differential scattering cross section, can be separated into one coherent and one incoherent part according to
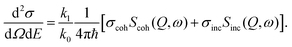 | (9) |
2.3 Quasielastic neutron scattering
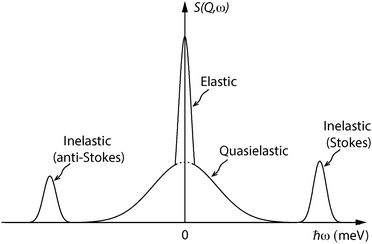
QENS refers to those inelastic processes that are almost elastic. The term is usually considered to mean a broadening of the elastic line in the neutron energy spectrum, S(Q,ω), rather than the appearance of discrete peaks associated with inelastic scattering.† This is illustrated schematically in Fig. 1. The elastic component is due to scattering from atoms which are localized in space, or in other words move too slowly to be resolved within the resolution of the instrument. The inelastic peaks arise from scattering from atoms which vibrate in a periodic manner and with a fixed frequency. Analogously to inelastic light scattering (by Raman spectroscopy), the inelastically scattered neutrons can either loose energy (Stokes scattering) or gain energy (anti-Stokes scattering), respectively, however, in comparison to its optical counterpart, INS does not rely on any selection rules.‡ The QENS broadening is due to scattering from atoms that are moving in a stochastic manner.Just as for other kinds of neutron scattering, QENS contains both coherent and incoherent scattering contributions. As mentioned above, the coherent scattering yields information about interference phenomena between atoms, which in QENS measurements means that information about collective dynamics, e.g. transport properties, may be obtained. The incoherent scattering, on the contrary, relates to scattering from individual atoms, thus providing information about single-particle motions, also known as self-dynamics.
2.4 QENS techniques
QENS techniques can be largely grouped into time-of-flight, backscattering, and neutron spin-echo (NSE) spectroscopy. The majority of previous QENS studies on proton conducting oxides have been performed by the use of time-of-flight and backscattering techniques, which give access to the time-scale of picoseconds, extended up to ≈1 ns in some cases, whereas even slower time-scales can be accessed with the NSE technique. Fig. 2 shows, as an example, approximate (Q,ℏω) domains as covered by the various spectrometers at the ILL. Included in the figure are the (Q,ℏω) ranges of relevance for diffusional dynamics in proton conducting oxides, as will be discussed further below.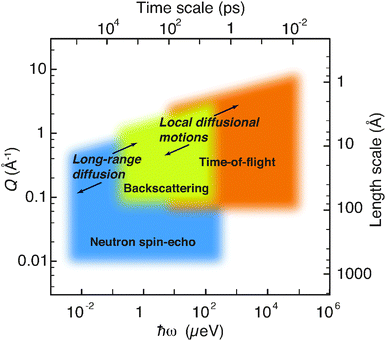 | ||
| Fig. 2 Neutron spectroscopy methods at the ILL encompass a large range of time- and length-scales. The (Q,ℏω) ranges of relevance for dynamical processes in proton conducting oxides are indicated. The figure has been modified after Jobic et al.10 | ||
A brief description of the various QENS techniques, emphasizing the essentials of each method, is presented in the following. A comprehensive description of the techniques can be found elsewhere.11–13
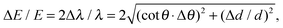 | (10) |
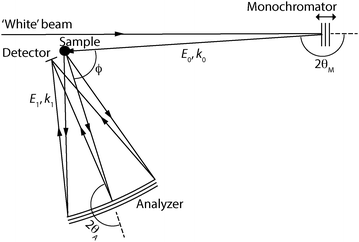
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ·Δθ. It follows that the highest energy resolution is achieved when the Bragg angle approaches 90°, since then cot
θ·Δθ. It follows that the highest energy resolution is achieved when the Bragg angle approaches 90°, since then cot![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ tends to zero, and therefore these spectrometers are also called backscattering spectrometers. In Fig. 3 is shown schematic illustrations of the major components of the two types of instruments. An overview of the beam trajectories by means of distance–time diagrams is also shown.
θ tends to zero, and therefore these spectrometers are also called backscattering spectrometers. In Fig. 3 is shown schematic illustrations of the major components of the two types of instruments. An overview of the beam trajectories by means of distance–time diagrams is also shown.
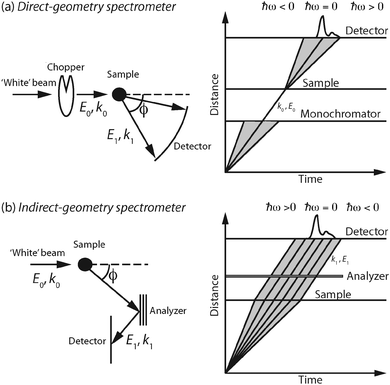 | ||
| Fig. 3 Schematic illustrations of direct-geometry (a) and indirect-geometry (b) spectrometers, together with their corresponding distance–time diagrams for single pulses of neutrons. | ||
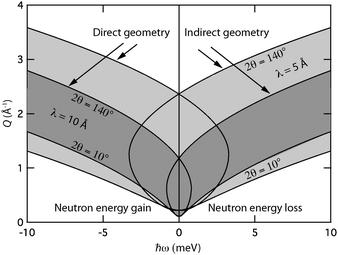
When planning an experiment on a time-of-flight spectrometer, the interplay of instrumental energy resolution and signal intensity is an important concern. Generally, the resolution increases with the use of longer neutron wavelengths, however the intensity is then usually decreased; for instruments on guide tubes the intensity varies as λ−3 at long wavelengths. A further disadvantage of increasing the neutron wavelength is that the accessible region in (Q,ℏω) space gets reduced. This is determined by the laws of conservation of energy and momentum in the scattering process [eqn (4) and (5)] and depends on the particular values of neutron energy and the scattering angle. For a direct-geometry spectrometer, it follows that the accessible region is limited by
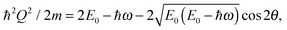 | (11) |
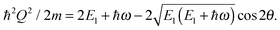 | (12) |
Fig. 4 shows the accessible regions for the two types of spectrometers and two choices of neutron energy. Note that for fixed incident energy (as in direct-geometry spectrometers) and for fixed analyzed energy (as in indirect-geometry spectrometers), the curves that define the measurable (Q,ℏω) region are identical in shape but are each other's mirror image. Furthermore, one should note that direct-geometry spectrometers cannot measure neutron energy losses that are larger than the value of the incident neutron energy, since the final neutron energy can never be less than zero. Similarly, inverted-geometry spectrometers cannot measure neutron energy gains larger than the value of the neutron energy measured by the analyzer. Examples of currently operational time-of-flight spectrometers include: IN4 (ILL), IN5 (ILL), IN6 (ILL), TOFTOF (FRM-II), FOCUS (PSI), MAPS (ISIS), MARI (ISIS), MERLIN (ISIS), LET (ISIS), DCS (NCNR), ARCS (SNS), CNCS (SNS), SEQUOIA (SNS), PELICAN (OPAL), and HRC and AMATERAS (J-PARC).
Backscattering spectrometers are characterized by a higher energy resolution than time-of-flight spectrometers. Typical energy resolutions are between 0.3 µeV and 1 µeV. This translates into the time-scale of nanoseconds, which is much slower than the time-scales probed by most time-of-flight spectrometers. Although most backscattering spectrometers have been built on neutron research reactors and use a monocrystal monochromator, backscattering spectrometers built on spallation sources do not use such monochromators, but instead the incident neutron energy is determined from the overall time-of-flight between the neutron source and the detectors. A dynamical range of several hundred µeV is achievable. Currently operational backscattering spectrometers include: IN10 (ILL), IN13 (ILL), IN16B (ILL), SPHERES (FRM-II), IRIS (ISIS), OSIRIS (ISIS), HFBS (NCNR), and BASIS (SNS).
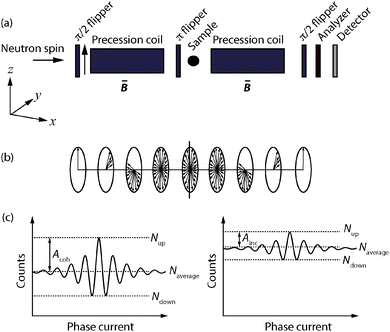
The basic principle of NSE is as follows. First, neutrons from a cold moderator are monochromized with the use of a neutron velocity selector, which gives a relatively wide range of neutron wavelengths (Δλ/λ ≈ 15% FWHM). These neutrons are then polarized along their velocity direction (x), before their spins are rotated to a direction perpendicular to the velocity direction (z) by the use of a π/2 spin flipper, see Fig. 6(a). Then, the neutrons travel in the first precession coil through a magnetic field aligned along the x direction. Here, the neutrons undergo a specific number of Larmor precessions in the yz plane, determined by the neutron velocity (v), the length of the coil (L), and the magnetic field strength (B). Accordingly, the total precession angle (in radians) over the length of the first solenoid can be expressed as
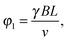 | (13) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 precessions. It is clear that the relatively wide range of neutron wavelengths is rapidly dephased and the final net polarization at the end of the first solenoid will be zero. Before the neutrons are scattered by the sample, the neutron spins are rotated by 180 degrees around the z axis by a π spin flipper. After the scattering event, the neutrons travel through the second solenoid, which is identical to the first one, with the consequence being that the neutrons now precess in the opposite direction.
000 precessions. It is clear that the relatively wide range of neutron wavelengths is rapidly dephased and the final net polarization at the end of the first solenoid will be zero. Before the neutrons are scattered by the sample, the neutron spins are rotated by 180 degrees around the z axis by a π spin flipper. After the scattering event, the neutrons travel through the second solenoid, which is identical to the first one, with the consequence being that the neutrons now precess in the opposite direction.
If the scattering is purely elastic, the neutron spin direction at the end of the second coil will equal that at the beginning of the first coil and the total precession angle is then zero, φ = φ1 − φ2 = 0, irrespective of the spread of neutron velocities, see Fig. 6(b). The final neutron polarization is measured by flipping the neutron spins back into the longitudinal x-direction using a π/2-flipper and finally analyzing it with an array of supermirrors in front of the detector that transmits only neutrons of one polarization direction. Since the angle between the neutron polarization and the analyzer direction is φ, the probability that a neutron is transmitted is cos(φ). What is measured experimentally is the expectation value (average) over all the scattered neutrons, i.e. 〈cos(φ)〉.
If the scattering is quasielastic, the situation is different since the energy and hence the velocities of the neutrons will change at the scattering event, and the neutron spins will therefore not return to their initial state. Accordingly, the accumulated precession angle will be
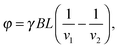 | (14) |
 | (15) |
| Px = 〈cos(tω)〉 ∝ ∫cos(tω)S(Q,ω)dω. | (16) |
| Px = 〈cos(tω)〉 ∝ I(Q,t). | (17) |
As in all types of neutron scattering experiments, the I(Q,t) can be divided into coherent and incoherent parts, I(Q,t) = Icoh(Q,t) + Iinc(Q,t). Incoherent scattering is featured by a 2/3 probability of flipping the spins of the neutrons, effectively reducing the incoherent NSE signal by 2/3, and, in addition, contributing to a background [Fig. 6(c)].19 Hence, the intermediate scattering function measured by NSE can be expressed as
| INSE(Q,t) = Icoh(Q,t) − ⅓Iinc(Q,t). | (18) |
Generally, NSE provides the normalized intermediate scattering function obtained as
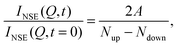 | (19) |
As it has been highlighted before, a wealth of information is obtained by analyzing the Q-dependence of the QENS component. Whereas time-of-flight and backscattering instruments allow the collection of data in the whole accessible range of Q-values in ones, NSE spectrometers, generally, collect data from a limited range of Q-values for each configuration. This is a big hindrance for all NSE experiments in which the signal of interest is not concentrated in a limited Q-range. The availability of a detector covering 30° of the scattering angle on IN11-C at the ILL, partially overcomes this disadvantage, although at the expense of a limitation in the maximum Fourier time achieved. The WASP instrument, which is currently being built at the ILL and which will allow to collect data over even larger scattering angle ranges should allow in the future for a much more efficient data collection in many chemical physics experiments, including investigations of proton conduction. Currently operational NSE spectrometers include: IN11 and IN11-C (ILL), IN15 (ILL), J-NSE and RESEDA (FRM-II), NSE (NCNR), NSE (SNS) and MUSES (LLB).
3 QENS on proton conducting oxides
QENS has played a central role in the field of proton conducting oxides and provided important information about the dynamics of protons in this class of technologically important materials. The usefulness of QENS for studies of proton conducting oxides comes from the fact that it gives access to the relevant time- and length-scales on which the atomic-scale dynamics of protons occur. In addition, the very large incoherent neutron scattering cross section of protons of 80.26 barns (1 barn = 10−24 cm2), far larger than all other nuclei (<10 barns), and relatively small coherent scattering cross section (1.76 barns), enables one to observe protons essentially free from constructive interference, i.e. information about proton self-diffusion can be obtained, whereas the correlation between the dynamical behavior of an ensemble of protons can be neglected.¶ Furthermore, the strong scattering signal from protons provides a good contrast in experiments and enables studies of proton self-diffusion in systems containing only relatively small amounts of protons. It follows that the total dynamical structure factor, S(Q,ω), can, in most cases, be approximated with the incoherent dynamical structure factor, i.e. S(Q,ω) ≈ Sinc(Q,ω). The measured structure factor is a convolution of Sinc(Q,ω) and the resolution function of the instrument, R(Q,ω), that is| Smeas(Q,ω) = Sinc(Q,ω) ⊗ R(Q,ω). | (20) |
The resolution function is usually determined by a measurement of the sample at very low temperature (<10 K), where the diffusional dynamics is frozen-in, or on a `perfectly' elastic, incoherent, scatterer, such as vanadium, of the same geometry as the sample.
When the QENS is accompanied by an elastic component, which is the case for localized motions, the dynamical structure factor may be expressed as
| Sinc(Q,ω) = e−〈u2〉Q2{Selinc(Q)δ(ω) + Sinelinc(Q,ω)}. | (21) |
3.1 Diffusion models
Theoretical models are based on the van Hove correlation function formalism and they predict the profile of S(Q,ω) and I(Q,t), according to the kind of dynamics in the system. Generally, the quasielastic part of S(Q,ω) can be described by one or more Lorentzian functions, related to one or more dynamical processes, i.e.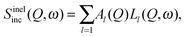 | (22) |
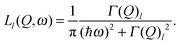 | (23) |
| Γ(Q) = ℏDsQ2, | (24) |
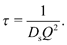 | (25) |
Random translational diffusion, also known as continuous diffusion, is, however, only observed at small Q-values, which correspond to large distances in real space. At larger Q-values, the motion is no more continuous and underlaying microscopic mechanisms are at play. To describe such mechanistic details, several types of jump-diffusion models have been developed. These all describe long-range diffusion as a series of successive jumps and contain as parameters the characteristic jump length and time between successive jumps (the latter is referred to as residence or relaxation time). One of the most used models is that developed by Chudley and Elliott,21 which assumes a constant jump length, r, a residence (relaxation) time, τ, and a negligible jump time. At sufficiently small Q-values, the Γ(Q) still follows a Q2-behavior, as in the case for continuous diffusion, but at larger Q-values Γ(Q) follows an oscillatory behavior according to
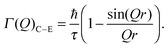 | (26) |
Related jump-diffusion models are the Hall–Ross model,22 which is characterized by a Gaussian distribution of jump lengths, and the Singwi–Sjölander model,23 which is characterized by an exponential distribution of jump lengths. However, one should note that diffusion processes are often more complicated and cannot always be categorized into these relatively simple cases, hence more sophisticated models must be developed. A detailed description and survey of different models can be found in several text books or review articles, see e.g.ref. 12 and 24.
4 Overview of QENS studies
This section reviews the literature on QENS studies on proton conducting oxides. The aim is not to give an exhaustive account for all the work that has been done in this field, but to illustrate different uses of QENS and to summarize some of the key results obtained so far. This is followed by my critical remarks as well as a discussion about the prospects for future studies in this area of research.4.1 Perovskite structured oxides
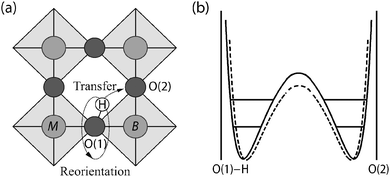
The majority of previous QENS studies on proton conducting oxides have been performed using time-of-flight and backscattering methods and on perovskite structured materials, such as doped variants of BaZrO3 and BaCeO3 based compounds; these studies are here summarized briefly. The initial studies were performed by Hempelmann et al.25 and Matzke et al.26 in the mid nineties on a hydrated sample of SrCe0.95Yb0.05O2.975. Fig. 7 shows the QENS spectra measured at different temperatures. From the low-Q data, it was possible to extract the proton self-diffusion constant as a function of temperature and this was found to be comparable to the bulk proton conductivity measured by impedance spectroscopy.25 The high-Q data was also analyzed and this contains information about the mechanistic detail of the proton conduction. Analysis showed that the QENS spectra could be reproduced by two quasielastic components, corresponding to two different localized proton motions with different activation energies, suggesting the existence of two different structural sites occupied by the protons. More detailed analysis showed that the QENS data was in agreement with a two-state model superimposed on the Chudley–Elliott model. The Chudley–Elliott model suggests in this case that the proton conduction occurs as a series of proton jumps (transfers) between neighboring oxygens, O(1) and O(2), and rotational diffusion of the –OH group between such transfers, see Fig. 8(a), whereas the two-state model indicates that the proton diffusion consists of some sort of trapping and release events.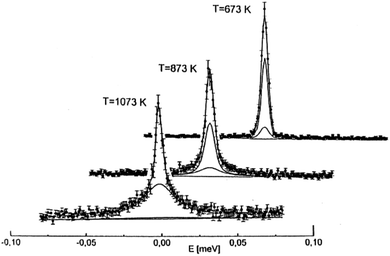 | ||
| Fig. 7 Neutron scattering spectra, S(Q,ω) of SrCe0.95Yb0.05H0.02O2.985 for different temperatures at momentum transfer Q = 0.29 Å−1. The solid lines show the total scattering function as well as the two components of the two-state model. Reprinted with permission from ref. 25, copyright Elsevier, 1995. | ||
The O(1)–H⋯O(2) transfer direction may be modeled by a double Morse type potential, with a barrier height dependent on the separation distance between O(1) and O(2) and on the vibrational level of the O–H stretch mode, which is illustrated in Fig. 8(b). Thus, the rate of proton diffusion is believed to be strongly coupled to the vibrational dynamics of the system. In particular, the proton performs localized O–H stretch and wag modes, which may be seen as precursors to the transfer and reorientational step, respectively, and moreover the dynamics of the oxygen sub-lattice induce large fluctuations in the distances between O(1) and O(2) with time.27,28
Such a proton conduction mechanism in perovskites has later found support from several computer simulations and experiments on different proton conducting oxide systems ever since. In particular, muon spin-relaxation experiments29 and several simulations30–33 have indicated that the dopant atoms are responsible for the trapping effect in these materials, thus decreasing the overall proton conductivity. Simulations have for example reproduced the experimental trend in proton conductivity in the BaZr0.9M0.1O2.95 (M = Y, In, Sc and Ga) series for which the conductivity differs several orders of magnitude depending on the type of dopant atom.34 More recently, the trapping view was further supported by combined thermogravimetric and a.c. impedance spectroscopy data on BaZr0.8Y0.2O3H0.2.35 However, converse to the view that dopant atoms act as localized trapping centers for the proton diffusion, it has also been proposed that the dopant atoms may affect the proton transport in a more nonlocal manner.36,37
Following the pioneering work by Hempelmann et al.25 and Matzke et al.,26 Karmonik et al.38 investigated the proton dynamics in the double perovskite structured material Ba[Ca0.39Nb0.61]O2.91 which, similarly to the previous studies on SrCe0.95Yb0.05O2.975, gave support for a proton conduction mechanism divided into proton jumps and reorientational motions. Subsequently, Pionke et al.39 reported on the proton self-diffusion constant for protons in the same material. Later, Groß et al.40 and Beck et al.41 investigated the influence of the particle size on the atomic-scale proton diffusion in BaZr0.85M0.15O2.925 (M = Y, In, and Ga). A key result is that only the microcrystalline samples showed a clear quasielastic signal related to proton motions. It was imagined that in the nanocrystalline samples, the protons are concerted mainly to the GB regions or to the surface of the crystallites. More recently, Wilmer et al.42 investigated the proton dynamics in BaZr0.90Y0.10O2.95. Attempts to interpret the data in the framework of the two-state model yielded unconvincing results. A simpler approach using the isotropic Chudley–Elliott model yielded reasonable values for the proton self-diffusivities but also unusually high values for the jump distance which was found to be close to the mean distance between dopants of approximately 9 Å. Furthermore, Malikova et al.43 performed a simultaneous structural and dynamic study on BaCe0.90Y0.10O2.95, by combining neutron diffraction with QENS. A key result was that the dehydration occurs over a large temperature range (from 500 °C to 800 °C), providing evidence for the presence of proton sites with a variable degree of hydrogen bonding strengths to the perovskite lattice. Slodczyk et al.44 investigated proton dynamics in Yb-doped BaZrO3, and they observed the onset of proton diffusion at a temperature of approximately 600 °C, whilst Karlsson et al.45 reported on a QENS study of BaZr0.90M0.10O2.95 (M = Y and Sc). In the latter study, the authors revealed a localized proton motion on the ps time-scale and with a small activation energy of 10–30 meV, for both materials. Comparison of the QENS results to density functional theory calculations suggests that for both materials this motion may be ascribed to intra-octahedral proton transfers occurring close to a dopant atom. Braun et al.46 reported on the Y-doped material, BaZr0.90Y0.10O2.95, and found two different activation energies for proton diffusion at different ranges of temperature. Colomban et al.47 reported on a change in local proton dynamics across a structural phase transition in (Ba/Sr)Zr1−xLnxO3−δ, whilst Slodczyk et al.48 investigated proton dynamics in SrZr0.90Yb0.10O2.95 and BaZr0.90Yb0.10O2.95. Measurements taken in the temperature range from 400 °C to 700 °C showed a peak in the mean square displacement of the protons at around 500 °C, suggesting a maximum in proton diffusivity around this temperature. Most recently, Chen et al.49 measured simultaneously macroscopic proton conductivity and atomic-scale proton diffusivity in BaCe0.8Y0.2O2.9, by means of an in situ impedance spectroscopy cell in combination with the QENS measurements. A key result was that the QENS data could be interpreted in terms of inter-octahedral proton transfer.
Whereas all the above mentioned work was done with the use of time-of-flight and backscattering methods, there are only three reports50–52 on the use of NSE spectroscopy for studies on proton conducting oxides, despite its unique benefits. The initial work was done by Karlsson et al.50 on a hydrated sample of BaZr0.90Y0.10O2.95. A key result was that the protonic self-diffusion constant, measured over a length scale of 5–8 unit cell lengths, is comparable with that as extracted from conductivity experiments. This suggests that already on a length-scale as short as ≈20 Å the effect of potential local traps or other “imperfections” in the structure that can be expected to affect the proton dynamics, has averaged out. That is, there are no features on a larger length-scale that have not been experienced by the proton on the shorter length-scale probed by NSE.
More recently, Karlsson et al.51 investigated the dopant concentration dependence of the local proton dynamics in BaZr1−xInxO3−x/2 (x = 0.10 and 0.50). Fig. 9 shows the normalized intermediate scattering function, I(Q,t)/I(Q,0), for the two materials at 500 K and Q = 1.05 Å−1. The relaxational decay with increasing Fourier time relates to dynamics of the protons. A key result is that the shape of the I(Q,t)/I(Q,0)s differs significantly for the two materials. For x = 0.10, the I(Q,t)/I(Q,0) is reflected by a single exponential decay and a constant, I(Q,t)/I(Q,0) = [1 − c(Q)]e−t/τ(Q) + c(Q), where τ = 60 ps is interpreted as the characteristic relaxation time for a localized proton motion, whereas the plateau at long time-scales (c = 0.32) relates to the scattering from protons that are essentially immobile within the experimental NSE time-window. For x = 0.50, on the other hand, the I(Q,t)/I(Q,0) is stretched in time and fits much better to a Kohlrausch–Williams–Watts (KWW) stretched exponential function,53,54I(Q,t)I(Q,0) = e−[t/τKWW(Q)]β(Q) where τKWW(Q) ≈ 4 ns is a characteristic time of a relaxational process and β(Q) ≈ 0.42 is the, so called, stretching parameter. The authors interpreted the stretched relaxational decay in terms of a large distribution of diffusional rates for the protons as due to many different local structural environments around the protons in the material. This is physically reasonable since the high concentration of In is known to induce strong short-range structural perturbations of the longer-range, average, cubic perovskite structure. The structural distortions become more and more pronounced with an increasing dopant level and it has been suggested that they are related to tilting of the (In/Zr)O6 octahedra due to the size difference between the In3+ and Zr4+ ions.55 Furthermore, it has been suggested that there is a compositional “threshold” between x = 0.10 and x = 0.25 above which the dopant induced structural distortions distribute throughout the entire perovskite structure, although with no long-range coherence in terms of the length-scales typically probed by diffraction.55 Thus, the more well-defined time-scale of the proton motion observed for x = 0.10 is likely to result from the more ordered local structure of the material. Interestingly, the idea of a compositional “threshold” between x = 0.10 and x = 0.25, compares to a rise in conductivity from 2.9 × 10−5 S cm−1 for x = 0.10 to 2.6 × 10−4 S cm−1 for x = 0.25, which may indicate that some structural disorder is favorable for high proton conduction in perovskite type oxides.55
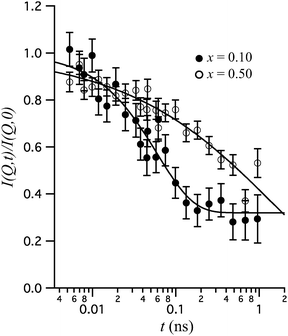 | ||
| Fig. 9 I(Q,t)/I(Q,0) of BaZr1−xInxO3−x/2 (x = 0.10 and 0.50) at 500 K and Q = 1.05 Å−1. The lines represent fits with a single exponential plus a constant (x = 0.10) and a KWW stretched exponential function (x = 0.50), respectively. Reprinted with permission from ref. 51, copyright American Chemical Society, 2010. | ||
4.2 Novel structure types
Clearly, ABO3-type perovskites continue to be the materials that are accumulating the largest interest within the solid state ionics community. However, there is a growing interest in alternative, more complicated, structure types and particularly in structure types containing tetrahedral moieties, such as lanthanum barium gallates, i.e. LaBaGaO4-based compounds.56 The structure of LaBaGaO4 consists of discrete GaO4 tetrahedra, which are charge balanced by the Ba/La ions [Fig. 10(a)]. Increasing the Ba:La ratio results in the formation of oxygen vacancies, La1−xBa1+xGaO4−x/2, and similarly to perovskite type oxides such oxygen vacancies can be filled with hydroxyl groups during a hydration procedure. The presence of oxygen vacancies leads to considerable relaxation of neighboring GaO4 tetrahedra, resulting in the formation of Ga2O7 units so that the Ga retains tetrahedral coordination, however the hydration can lead to the breaking up of such units.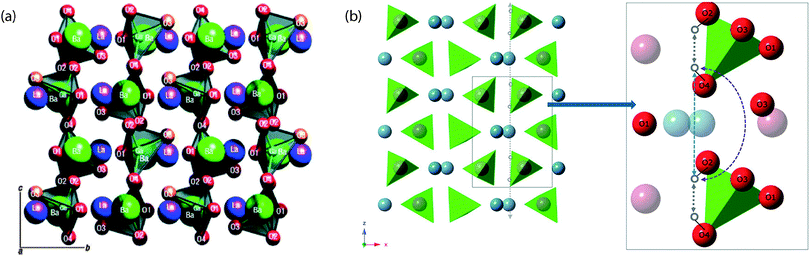 | ||
| Fig. 10 (a) Crystal structure of LaBaGaO4, which is comprised of GaO4 distorted tetrahedra and ordered alternating layers of lanthanum and barium ions. The GaO4 tetrahedra are isolated from one another (with an elongated Ga–O3 bond). (b) Protons are represented as small grey-colored circles bound to particular corners of the GaO4 tetrahedra. The proton migration takes place along the c axis, shown as a gray dashed arrow. The inset shows a slice parallel to the ac plane with the elementary steps: the intratetrahedron path is represented with gray arrows and two possibilities for intertetrahedra paths are represented with (i) blue and (ii) purple arrows. Reprinted with permission from ref. 52, copyright American Chemical Society, 2013, and from ref. 56, copyright Nature Publishing Group, 2007. | ||
Recently, Jalarvo et al.52,57 investigated atomic-scale dynamics of protons in a hydrated sample of La0.8Ba1.2GaO3.9, using neutron backscattering and NSE spectroscopy. The backscattering spectra were fitted to two Lorentzian components; one narrow and one broader one, representing proton dynamics on different time-scales. The analysis of the narrow component showed that it can be related to continuous proton diffusion with an activation energy of 0.44 eV. This activation energy is somewhat smaller than that extracted from conductivity experiments (0.56 eV), but in perfect agreement with the activation energy for intratetrahedron proton jumps as determined by calculations that suggest this process to be rate-limiting for the longer-range proton diffusion.57 The analysis of the broader component shows that this is related to localized proton motions with an activation energy of 0.068 eV, which is similar to the calculated intertetrahedra proton transfer value. On the basis of these results it was suggested that the proton conduction occurs as a series of intratetrahedron proton jumps between the O2 and O4 sites, and intertetrahedron proton jumps from O4 to O2 [cf.Fig. 10(b)]. The intertetrahedron proton jumps are suggested to take place either directly along the c axis, or via the O3 site of a neighboring GaO4 tetrahedron, whereas the overall long-range proton transport takes place along the c axis. The proton conduction mechanism is thus so-called Grotthuss-like, which means that the protons diffuse stepwise throughout the structure of the material. Between each proton jump, the proton is covalently bound to an oxygen and performs O–H stretch and wag vibrational motions, superimposed by the vibrational dynamics of the oxygen lattice. These motions induce fluctuations in the distance between the proton and a neighboring oxygen to which the proton may jump, thus creating transient hydrogen bonds that affect strongly the probability of proton transfer.
5 Critical remarks and outlook
It has been shown that the majority of QENS studies has been performed on classic proton conducting perovskites, in particular on materials based on BaZrO3 and BaCeO3, whereas only a few studies have been performed on other structure types. Although, clearly, these studies have provided important information about the dynamical behavior of protons in oxides, several of them have suffered from either a weak scattering signal or from the limited (Q,ω) range as accessed with the variety of instruments that have been used. As a consequence, it has often been difficult or impossible to find models that reliably describe the data and therefore to draw any firm conclusions on what type of motions that were observed. Furthermore, there are, in some cases, disagreements between the results obtained in different studies, even when the same material was investigated. However, in view of the different types of instruments and instrumental settings that have been used, some reproducibility problems may be expected. In addition, the structural and physiochemical details of the investigated samples, as partly related to the details of the sample preparation, are of important concern.|| In this context, the studies by Groß et al.40 and Beck et al.41 already highlighted the importance of the particle size, hence the synthesis route, on the atomic-scale proton diffusion in BaZr0.85M0.15O2.925 (M = Y, In, and Ga) proton conductors, but many more factors may be at play. Therefore, there is a need to perform systematic investigations, under the same experimental conditions and on well characterized samples, in order to be able to make good comparisons between different measurements. Such studies should include systematic investigations on the effect of type and concentration of dopant atoms, crystal structure, and the level of hydration, on the atomic-scale proton dynamics, for example.Although this article has highlighted the advantages of neutron scattering for research on proton conducting oxides, as with all techniques, QENS has its disadvantages. The primary drawback of QENS is that neutron scattering is an intensity-limited technique. In studies of proton conducting oxides, typically at least 10 grams of the sample is needed to obtain data of sufficient quality. These are very large samples for most other analytical techniques and obtaining a sufficient quantity can be problematic, particularly for new, complex, materials that may only be available in much smaller quantities. On the positive side, the large sample size does mean that concerns about representative sampling are much less severe than for techniques that operate on the milligram or smaller scale. Moreover, measuring times are at least a few hours per instrumental setting, thus kinetic measurements by QENS are generally not feasible. Any instrumental improvements with respect to advances in neutron flux and detector coverage, allowing faster acquisition times and smaller samples, in the form of single crystals or even thin films, to be investigated, are therefore highly welcome. For the future application of proton conducting oxides as fuel-cell electrolytes, one would indeed use a (thin) film of the proton conductor sandwiched between the anode and cathode materials. Other than in powder samples, such films can be highly textured and strained, which may affect significantly the proton conducting properties. Addressing diffusive processes in oxide films is however a lot more challenging than in bulk powder samples due to the heavily reduced sample volume. However, with the vision of the ESS, which, in comparison to present-day neutron sources, will offer considerably higher neutron flux, such experiments might become possible on a routine basis. Increasing the neutron flux may further open up for studies using polarization analysis, for the separation of coherent and incoherent scattering. Such analysis would not only distinguish between collective and self-dynamics but may also give information about proton–proton interactions, for example. Similar information may be obtained by the use of nuclear polarization methods, which offer exciting opportunity to tune continuously the spin-dependent scattering cross section of hydrogen nuclei and thereby the contrast between coherent and incoherent scattering.58 Furthermore, there is a clear trend towards the developments of in situ sample environments, which allow for at least one additional materials property to be measured simultaneously with the collection of the QENS spectra. In this way the inherent uncertainty that comes from correlating separate measurements can be avoided, or allow for measurements which today are not even feasible separately. We have already noted the recent study by Chen et al.,49 who combined QENS with impedance spectroscopy, thus allowing for the direct correlation between proton dynamics on significantly different time- and length-scales. Future work in this direction is likely to expand and will include the development and subsequent use of in situ electrochemical cells, which allow for measurements under conditions that mimic fuel cell operating conditions.
6 Conclusions
To conclude, QENS is an important technique in the field of proton conducting oxides and has already contributed greatly to the understanding of proton dynamics in these materials, nevertheless the technique shows great potential for advancing further this understanding. Future work in this area is likely to comprise systematic investigations of well-characterized samples of both classic proton conducting perovskites as well as of new compounds and will take great advantage of the upgrade of existing neutron spectrometers and from the development of new instrumentation along with the construction of next-generation neutron sources. A better understanding of the mechanism of proton conduction in a wider family of oxide proton conductors is seen as crucial for the development of strategies for developing new materials with higher proton conductivity. This is in turn critical to future breakthroughs in the development of next-generation devices based on proton conducting oxides, such as intermediate-temperature fuel cells, hydrogen sensors, or other electrochemical devices. Even small or gradual advancements of the current understanding of proton conduction mechanisms in oxides may therefore have considerable environmental and economic impact.Acknowledgements
Financial support from the Swedish Research Council (grant nr. 2010-3519 and 2011-4887) is gratefully acknowledged. Finally, many thanks to Antonio Faraone at the NIST Centre for Neutron Research for time and discussions and for valuable comments on the writing of this article.References
- B. C. H. Steele and A. Heinzel, Nature, 2001, 414, 345–352 CrossRef CAS PubMed.
- K. D. Kreuer, Annu. Rev. Mater. Res., 2003, 33, 333–359 CrossRef CAS.
- L. Malavasi, C. A. J. Fisher and M. S. Islam, Chem. Soc. Rev., 2010, 39, 4370 RSC.
- P. J. Gelling and H. J. M. Bouwmeester, Catal. Today, 1992, 12, 1–105 CrossRef.
- F. A. Kröger and H. J. Vink, Solid State Physics: Advances in Research and Applications, Academic Press, 1956 Search PubMed.
- C. T. Chen, C. E. Danel and S. Kim, J. Mater. Chem., 2011, 21, 5435 RSC.
- M. Shirpour, R. Merkle, C. T. Lin and J. Maier, Phys. Chem. Chem. Phys., 2012, 14, 730 RSC.
- I. M. Sosnowska, Solid State Ionics, 1999, 119, 261–268 CrossRef CAS.
- M. Karlsson, Dalton Trans., 2013, 42, 317–329 RSC.
- H. Jobic and D. N. Theodorou, Micropor. Mesopor. Mat., 2007, 102, 21 CrossRef CAS PubMed.
- T. Springer, Quasielastic Neutron Scattering for the Investigation of Diffusive Motions in Solids and Liquids, Springer-Verlag Berlin, Heidelberg, New York, 1972 Search PubMed.
- M. Bée, in Quasielastic Neutron Scattering, ed. D. J. Millen, IOP Publishing, Bristol, 1988 Search PubMed.
- L. Liang, R. Rinaldi and H. Schober, Neutron Applications in Earth, Energy and Environmental Sciences, Springer Science + Business Media, Heidelberg, New York, 2009, ch. 3 Search PubMed.
- M. Birr, A. Heidemann and B. Alefeld, Nucl. Instrum. Methods, 1971, 95, 435 CrossRef CAS.
- J. C. Cook, W. Petry, A. Heidemann and J.-F. Barthelemy, Nucl. Instrum. Methods Phys. Res., Sect. A, 1992, 312, 553 CrossRef.
- F. Mezei, Z. Phys., 1972, 255, 146–160 CrossRef CAS.
- F. Mezei, Neutron Spin Echo: Lecture Notes in Physics, Springer, Heidelberg, 1980, vol. 28 Search PubMed.
- F. Mezei, C. Pappas and T. Gutberlet, Neutron Spin Echo Spectroscopy: Basics, Trends and Applications, Springer, 2003 Search PubMed.
- B. Farago, Neutron Data Booklet, Institut Laue-Langevin, Grenoble, France, 2002, ch. 2.8 Search PubMed.
- V. F. Sears, Neutron News, 1992, 3, 26–37 CrossRef.
- C. T. Chudley and R. J. Elliott, Proc. Phys. Soc., London, 1961, 77, 353 CrossRef.
- P. Hall and D. K. Ross, Mol. Phys., 1981, 42, 673 CrossRef CAS.
- K. Singwi and A. Sjölander, Phys. Rev., 1960, 120, 1093 CrossRef.
- R. Hempelmann, Quasielastic neutron scattering and solid state diffusion, Clarendon Press, Oxford, 2000 Search PubMed.
- R. Hempelmann, C. Karmonik, T. Matzke, M. Cappadonia, U. Stimming, T. Springer and M. A. Adams, Solid State Ionics, 1995, 77, 152–156 CrossRef CAS.
- T. Matzke, U. Stimming, C. Karmonik, M. Soetramo, R. Hempelmann and F. Güthoff, Solid State Ionics, 1996, 86–88, 621–628 CrossRef CAS.
- M. Karlsson, M. E. Björketun, P. G. Sundell, A. Matic, G. Wahnström, D. Engberg, L. Börjesson, I. Ahmed, S. G. Eriksson and P. Berastegui, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 094303 CrossRef.
- M. Karlsson, A. Matic, S. F. Parker, I. Ahmed, L. Börjesson and S. G. Eriksson, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 104302 CrossRef.
- R. Hempelmann, M. Soetratmo, O. Hartmann and R. Wäppling, Solid State Ionics, 1998, 107, 269–280 CrossRef CAS.
- W. Münch, G. Seifert, K. D. Kreuer and J. Maier, Solid State Ionics, 1997, 97, 39–44 CrossRef.
- K. D. Kreuer, W. Münch, U. Traub and J. Maier, Ber. Bunsen-Ges. Phys. Chem., 1998, 102, 552–559 CrossRef CAS.
- W. Münch, G. Seifert, K. D. Kreuer and J. Maier, Solid State Ionics, 1996, 86–88, 647–652 CrossRef.
- F. Shimojo, K. Hoshino and H. Okazaki, J. Phys. Soc. Jpn., 1997, 66, 8–10 CrossRef CAS.
- K. D. Kreuer, S. Adams, W. Münch, A. Fuchs, U. Klock and J. Maier, Solid State Ionics, 2001, 145, 295–306 CrossRef CAS.
- Y. Yamazaki, F. Blanc, Y. Okuyama, L. Buannic, J. C. Lucio-Vega, C. P. Grey and S. M. Haile, Nat. Mater., 2013, 12, 647 CrossRef CAS PubMed.
- K. D. Kreuer, W. Münch, M. Ise, T. He, A. Fuchs, U. Traub and J. Maier, Ber. Bunsen-Ges. Phys. Chem., 1997, 101, 1344 CAS.
- K. D. Kreuer, Solid State Ionics, 1999, 125, 285–302 CrossRef CAS.
- C. Karmonik, R. Hempelmann, J. Cook and F. Güthoff, Ionics, 1996, 2, 69 CrossRef CAS.
- M. Pionke, T. Mono, W. Schweika, T. Springer and H. Schober, Solid State Ionics, 1997, 97, 497–504 CrossRef CAS.
- B. Groß, C. Beck, F. Meyer, T. Krajewski, R. Hempelmann and H. Altgeld, Solid State Ionics, 2001, 145, 325–331 CrossRef.
- C. Beck, S. Janssen, B. Gross and R. Hempelmann, Scr. Mater., 2001, 44, 2309–2313 CrossRef CAS.
- D. Wilmer, T. Seydel and K. D. Kreuer, Mater. Res. Soc. Symp. Proc., 2007, 972, 15 CAS.
- N. Malikova, C. K. Loong, J. M. Zanotti and F. Fernandez-Alonso, J. Phys. Chem. C, 2007, 111, 6574–6580 CAS.
- A. Slodczyk, P. Colomban, D. Lamago, M.-H. Limage, F. Raomain, S. Willemin and B. Sala, Ionics, 2008, 14, 215–222 CrossRef CAS.
- M. Karlsson, I. Ahmed, A. Matic and S. Eriksson, Solid State Ionics, 2010, 181, 126 CrossRef CAS PubMed.
- A. Braun, S. Duval, P. Ried, J. Embs, F. Juranyi, T. Strässle, U. Stimming, R. Hempelmann, P. Holtappels and T. Graule, J. Appl. Electrochem., 2009, 39, 262103 CrossRef PubMed.
- P. Colomban, A. Slodczyk, D. Lamago, G. Andre, O. Zaafrani, O. Lacroix, S. Willemin and B. Sala, J. Phys. Soc. Jpn., 2010, 79, 1 CrossRef.
- A. Slodczyk, P. Colomban, N. Malikova, O. Zaafrani, S. Longeville, J.-M. Zanotti, O. Lacroix and B. Sala, Solid State Ionics, 2013, 252, 7–11 CrossRef CAS PubMed.
- Q. Chen, J. Banyte, X. Zhang, J. P. Embs and A. Braun, Solid State Ionics, 2013, 252, 2–6 CrossRef CAS PubMed.
- M. Karlsson, D. Engberg, M. E. Björketun, A. Matic, G. Wahnström, P. G. Sundell, P. Berastegui, I. Ahmed, P. Falus, B. Farago, L. Börjesson and S. Eriksson, Chem. Mater., 2010, 22, 740–742 CrossRef CAS.
- M. Karlsson, P. Fouquet, I. Ahmed and M. Maccarini, J. Phys. Chem. C, 2010, 114, 3293 Search PubMed.
- N. Jalarvo, L. Stingaciu, D. Gout, Z. Bi, M. P. Paranthaman and M. Ohl, Solid State Ionics, 2013, 252, 12 CrossRef CAS PubMed.
- R. Kolhrausch, Ann. Phys., 1854, 1, 179 CrossRef.
- G. Williams and D. C. Watts, Trans. Faraday Soc., 1970, 66, 80 RSC.
- M. Karlsson, A. Matic, C. S. Knee, I. Ahmed, L. Börjesson and S. G. Eriksson, Chem. Mater., 2008, 20, 3480–3486 CrossRef CAS.
- E. Kendrick, J. Kendrick, K. S. Knight, M. S. Islam and P. R. Slater, Nat. Mater., 2007, 6, 831–835 CrossRef PubMed.
- N. Jalarvo, O. Gourdon, Z. Bi, D. Gout, M. Ohl and M. P. Paranthaman, Chem. Mater., 2013, 25, 2741 CrossRef CAS.
- F. M. Piegsa, M. Karlsson, B. van den Brandt, C. J. Carlile, E. M. Forgan, P. Hautle, J. A. Konter, G. J. McIntyre and O. Zimmer, J. Appl. Crystallogr., 2013, 46, 30–34 CrossRef CAS.
Footnotes |
| † However, in case the intermediate scattering function, I(Q,t), is measured, as is the case in neutron spin-echo experiments, the quasielastic scattering is manifested as a relaxational decay with time. |
| ‡ The activation of Raman scattering relies on changes in polarizability of the vibrating moieties. In INS, all modes are active and in principle measurable. |
| § The proportionality constant originates from instrumental factors which can be accounted for. |
| ¶ For a complete list of the thermal neutron scattering cross sections of all elements and their isotopes, the reader is referred to ref. 20. |
| || This also accounts for the spread in proton conductivities for the same type of systems, as reported in the literature.2 |
| This journal is © the Owner Societies 2015 |