Electronic structure and spectra of (Cu2O)n–H2O complexes†
Ioannis D.
Petsalakis
*ab,
Giannoula
Theodorakopoulos
ab and
Jerry
Whitten
b
aTheoretical and Physical Chemistry Institute, The National Hellenic Research Foundation, 48 Vassileos Constantinou Ave, Athens 116 35, Greece. E-mail: idpet@eie.gr; Fax: +30210 7273794; Tel: +30210 7273807
bDepartment of Chemistry, North Carolina State University, Raleigh, North Carolina 27695, USA. E-mail: whitten@ncsu.edu; Fax: +1 919 515 5079; Tel: +1 919 515 7960
First published on 7th November 2014
Abstract
Density functional theory calculations have been employed to determine optimized geometries for different (Cu2O)n clusters for n = 1 to 6, 12 and 18. The results show the formation of (Cu2O)n rings for n ≥ 2, while (Cu2O)n nanobarrels have been determined for n = 12 and for n = 18. Adsorption of H2O on the (Cu2O)n clusters occurs preferentially by interaction of the water O with outer Cu atoms. Absorption spectra calculated by time dependent density functional theory show that in all cases charge-transfer excitations from occupied orbitals of the (Cu2O)n cluster to a Rydberg orbital of H2O contribute to the character of the singlet excited states calculated at energies starting at about 2.6 eV, with increasing contribution found at higher excitation energies. Configuration interaction calculations on selected (Cu2O)n–H2O complexes determine charge-transfer excitations to contribute significantly to excited states lying at 4.6–6.2 eV above the ground state.
Introduction
Cuprous oxide (Cu2O) is a p-type semiconductor with a high optical absorption coefficient and a bulk band gap of 2.2 eV and it is considered to be an excellent candidate for applications in solar energy photovoltaics and photocatalysis.1–5 The question of Cu2O acting as a photocatalyst for water splitting under visible light irradiation is still open and of particular experimental interest.4–6 Theoretical investigations employing DFT-based and periodic slab methods have been devoted to the investigation of the adsorption and dissociation of H2O on Cu2O surfaces,7 reporting that Cu2O is a promising photocatalyst for water splitting, while ground-state dissociative adsorption of H2O on the Cu2O(110):CuO surface appears to be only slightly endothermic.8 Similarly, the bonding of H2X (for X = O, S) on cluster models of CuO(111) has been investigated by DFT calculations.9Metal oxide nanoparticles have been widely studied as they form an intermediate between the molecular and the bulk state and accordingly may have different properties depending on their size and symmetry.1,2 The possibility of rationally tuning the optical properties of Cu2O through the control over the dimensions and morphologies of Cu2O nanostructures has stimulated a large number of efforts devoted to the fabrication of a range of Cu2O nanostructures,1,2 including nanocubes,3 nanospheres10 and nanorings.11 However, only a few applications of nanoscale Cu2O to water photoelectrochemistry are known.12
The formation of (Cu2O)n clusters has been investigated by DFT calculations on neutral and cationic, hydrated and hydrogenated clusters for n = 1 and 2,13 while DFT and TDDFT calculations have been performed on n = 1, 2 and 3 clusters2 and also on Cu2Om (m = 1, 4) clusters.14 Thus, for (Cu2O)n clusters DFT calculations have been reported only for n up to 3 whereas for CuO larger clusters, including nanotube-analogues with a square unit mesh rather than the hexagonal mesh of carbon nanotubes, have been calculated by DFT.15 It is thus of interest to determine the structure of larger than n = 3 (Cu2O)n clusters and possible stable structures for cuprous oxide nanotubes or nanobarrels.
In the present work the formation of different Cu2O clusters, including nanorings and nanobarrels, has been investigated, as well as the adsorption of H2O on these clusters, by theoretical calculations in an effort to determine their electronic structure and spectra. In this manner, fundamental information of relevance to different applications is determined including the interesting question of the photocatalysis of H2O splitting by Cu2O.
Calculations and results
DFT16 and TDDFT17 calculations have been carried out on different (Cu2O)n clusters for n = 1 to 6, 12 and 18 and (Cu2O)n–H2O complexes for n = 1 to 6. The optimum geometries for all clusters and complexes have been determined using the B3LYP18 functional and LANL2DZ basis set19 and, in addition, for the smaller clusters, i.e. for n = 1 to 6, with the aid of B3LYP and 6-311G(d,p) basis sets. It is not practical to employ the 6-311G(d,p) basis set for the n = 12 and n = 18 clusters as the geometry optimization calculations become extremely time consuming. The excited states of the n = 1 to 6 clusters as well as those of their corresponding complexes with H2O, at the ground state geometries, have been calculated by TDDFT employing the M062X20 functional and the 6-311+G(d,p) basis set, i.e. including diffuse functions, provided in Gaussian 09.21 For charge-transfer type of states, i.e. those involving excitations from (Cu2O)n to H2O, it is not appropriate to employ the B3LYP functional as it would result in underestimation of the excitation energies. For the n = 12 and n = 18 clusters TDDFT calculations employing the 6-311+G(d,p) basis set become too large and not practical. For this reason, configuration interaction calculations have been employed for the excited states of structures involving adsorption of H2O on n = 18 and n = 12 clusters, which pose difficulties to TDDFT and also for H2O on the n = 4 cluster for comparison with TDDFT. Details of the CI calculations have been provided in Section B cf. below and in the ESI.†A. Geometries of (Cu2O)n and (Cu2O)n–H2O, n = 1–6
The coordinates for all the optimum structures determined in the present work are available in the ESI.† The optimized geometries for (Cu2O)n and (Cu2O)n–OH2 clusters for n = 1, 2 and 3 are shown in Fig. 1 and the corresponding structures for n = 4–6 are shown in Fig. 2. In Table 1 the geometrical parameters for the optimized structures for all clusters, n = 1–6 are listed, where average values of the bond lengths and angles are given when there are differences. Further details on the geometries may be generated from the data in the ESI.† In the triatomic Cu2O (cf. a1 in Fig. 1) the Cu–O bond lengths are calculated to be 1.757 Å and the angle ∠CuOCu to be 108.7°. A water molecule is attached to Cu2O, with a binding energy of 0.96 eV, by interaction of the oxygen atom of water with one of the Cu atoms, with a Cu–OH2 distance of 1.904 Å cf. a2 in Fig. 1 and Table 1. Attachment of H2O leads to a slight elongation of the closer O–Cu bond to 1.765 Å, a very slight shortening of the other Cu–O bond to 1.752 Å and a slight opening of the bond angle to 109.1°. The n = 2 cluster, cf. b1 and b2 in Fig. 1, shows the formation of a four-membered ring and two non-ring Cu atoms above and below the plane of the ring, at a dihedral angle of 133.5°. Accordingly, different bond lengths are calculated for O–Cu in the ring, at 1.909 Å, and the O–Cu non-ring at 1.763 Å. The bond angles are different as well, with the ∠CuOCu within the ring at 70.5° and the outer angle at 134.3°. In the ring, the ∠OCuO angles are calculated to be 109.5°. As found for n = 1, a water molecule is attached to the n = 2 cluster, cf. b3, by interaction of the water oxygen with one of the non-ring Cu atoms at a distance of 1.900 Å and a binding energy of 1.06 eV. Similar to n = 2, the n = 3 cluster also favours the formation of a ring, this time a 6-membered ring as shown in c1, with large ∠OCuO ring angles (156.2 ± 0.6°), cf.Fig. 1 and Table 1. It may also be noted that generally the ring Cu–O bond lengths are larger than the outer Cu–O bond lengths, as noted for the n = 2 cluster. Again in the lowest energy structure, H2O attaches by interaction with one of the outer Cu atoms at a Cu–O distance of 1.895 Å and a binding energy of 1.09 eV. As was the case for n = 1, attachment of H2O causes small distortions of the bond lengths and angles of the optimum structures of the clusters, and detailed structures may be generated from the ESI† data. There is good agreement between the present (cf.Fig. 1) and the previously reported structures for a1,2,13,22 a2, b1 and b3 of the present work.13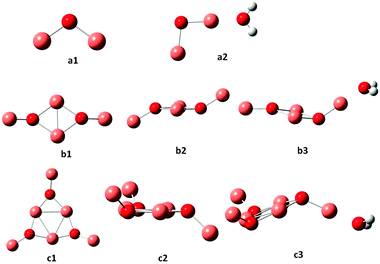 | ||
| Fig. 1 Optimized ground state geometries for (Cu2O)n and (Cu2O)n–OH2, for n = 1, 2 and 3. Small red spheres O, large faded red spheres Cu and small white spheres H atoms. | ||
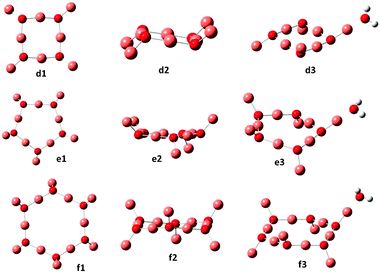 | ||
| Fig. 2 Optimized ground state geometries for (Cu2O)n and (Cu2O)n–OH2, for n = 4, 5 and 6. Small red spheres O, large faded red spheres Cu and small white spheres H atoms. | ||
| n | Cu–O (ring)/Å | Cu–O outer/Å | ∠CuOCu ring/° | ∠OCuO ring/° | Dih. angles Outer Cu/° | Cu–OH2/Å | BE/eV |
|---|---|---|---|---|---|---|---|
| a Average values. b Calculated with B3LYP/LANL2D. | |||||||
| 1 | 1.757 | — | 108.7 | 1.904 | 0.96 | ||
| 2 | 1.909 | 1.763 | 70.5 | 109.5 | 133.5 | 1.900 | 1.06 |
| 3 | 1.843 ± 0.003 | 1.765 ± 0.001 | 83.3 ± 0.3 | 156.2 ± 0.6 | 119.6 ± 2.3 | 1.895 | 1.09 |
| 4 | 1.812 ± 0.003 | 1.7658 | 99.1 ± 0.1 | 171.0 ± 0.3 | 128.1 ± 1.6 | 1.895 | 1.11 |
| 5 | 1.801 ± 0.002 | 1.773 ± 0.001 | 111.3 ± 1.5 | 175.5 ± 1.5 | 131.4 ± 2.3 | 1.896 | 1.09 |
| 6 | 1.797 ± 0.002 | 1.775 ± 0.001 | 119.0 ± 0.8 | 179.6 ± 0.3 | 133.2 ± 1.2 | 1.897 | 1.10 |
| 6b | 1.855 ± 0.002 | 1.836 ± 0.002 | 117.8 ± 1.0 | 177.8 ± 0.5 | 119.2 ±1.2 | — | — |
Previously reported geometries for (Cu2O)n with n = 2 and 32 are found to be higher in energy than the optimum structures b2 and c2 of Fig. 1, where, however, the cis analogues of b2 and c2, i.e., with all singly coordinated Cu atoms in the same direction with respect to the plane of the ring2 are only slightly higher in energy, by 0.03 and 0.1 eV respectively. Geometry optimization of the larger clusters, i.e. for n = 4, 5 and 6, resulted in the structures shown in Fig. 2. As shown, as a rule, rings are formed, where the sides are made up of nearly linear O–Cu–O segments (179°), with another Cu atom at each O atom out of the plane of the ring, cf. also structures b and c for n = 2 and 3 of Fig. 1. The ring Cu–O bond lengths are around 1.800–1.810 Å, with the outer at 1.770–1.776 Å. In the cuprite bulk unit cell of Cu2O, the oxygen atom is surrounded by four Cu atoms, while each Cu atom is coordinated with two O atoms,23 with a Cu–O distance of 1.849 Å. The present results show that in the ring structures of Fig. 1 and 2, O is coordinated with three Cu atoms, ring Cu atoms are coordinated with two O atoms and outer Cu atoms with one O atom. These latter Cu atoms offer the preferable position of attachment of H2O, via interaction with the water oxygen, in all the n = 1–6 clusters calculated in the present work. The resulting structures are denoted as a2, b3 and c3 in Fig. 1 and d3, e3 and f3 in Fig. 2. The O–Cu–OH2 angle is 179° in all cases and the Cu–OH2 distance is about 1.90 Å (cf.Table 1). These structures are the lowest energy structures obtained by optimization calculations, while other types of attachment, e.g. by hydrogen bonding, lead to higher energy structures. The binding energy of adsorbed H2O is around 1 eV for all clusters calculated.
Comparison with the results of B3LYP/LAN2DZ calculations on the n = 1–6 clusters shows that the same basic structure is obtained in each case but with some elongation of the bonds. An example of the results obtained by B3LYP/LAN2DZ is given in the last row of Table 1 for n = 6, showing the differences in the geometrical parameters obtained as compared to those obtained using the 6-311G(d,p) basis set.
B. Cu2O nanobarrels
As noted in the Introduction, different types of nanoclusters of Cu2O have been synthesized1,2 and studied by classical electrodynamics.2 Here different tubes of (Cu2O)n are constructed, and are shown in Fig. 3. Nanobarrels 1a and 1b of Fig. 3, with n = 18 and 12, respectively, have been constructed using the coordination of Cu and O in bulk Cu2O and adsorption of one H2O on these clusters. Determination of the excited states of the n = 18 and 12 clusters and those of their complexes with H2O by TDDFT became very cumbersome because with increasing n the number of low-lying electronic states rapidly increases. Furthermore the calculations on the smaller systems indicated the necessity for diffuse functions in the basis set, making proper TDDFT treatment of the n = 18 and 12 clusters and complexes not practical. Thus for these larger complexes a configuration interaction (CI) method of calculation was employed for the excited charge-transfer states. The CI method employed has been described in a previous work on a (Ti6O12)3 nanotube24 and elsewhere.25 Further details of the CI method and calculations are given in the ESI.† Geometry optimization calculations for structures 1c, 1d, 2a and 2c of Fig. 3 have been carried out by DFT/B3LYP/LAN2LDZ calculations as the clusters are too large for the 6-311G(d,p) basis set. In structures 1a and 1b only the position of H2O has been optimized, with the Cu2O cluster geometry kept frozen in the CI calculations. Structures 1c and 1d result from optimization of the n = 18 1a and n = 12 1b clusters, respectively. Nanobarrels 2a, 2b and 2c have been constructed by stacking d1 and f1 rings (of Fig. 2) and subsequent geometry optimization. Structure 2a is made up by stacking two n = 6 rings, 2b by stacking three n = 6 rings and 2c by stacking three 4-membered rings. Geometry optimization was nearly but not fully converged for the n = 18 structure 2b, of Fig. 3, as the calculation was oscillating between slightly different structures. The results show that in the optimized structures 2a and 2c and also in 2b square surface units are formed, of side O–Cu–O and length at 3.8 Å, resembling the square ring of the n = 4 cluster, cf. d1 of Fig. 2. It should be noted that the optimized structures 1c and 1d of Fig. 3 also have the square surface unit, even though the starting geometries for the optimization are quite different. Square surface units have also been reported for CuO nanotubes,15 whereas in carbon nanotubes the surface units are hexagons. Optimized structures (1d) and (2a) are similar with their main difference being that the outwards pointing Cu atoms in (2a) are pointing inward in (1d). Of the n = 12 structures, (2c) has the lowest energy with structure, (1d) lies higher only by 0.32 eV but (2a) lies at 3.1 eV above 2c. All (Cu2O)n clusters are bound with respect to dissociation to Cu2O units, with each added Cu2O unit to a (Cu2O)n−1 cluster increasing the binding by 2.5–3.6 eV, depending on n. These results show that it is possible to form stable geometries resembling nanotubes, in agreement with experimental reports on the formation of Cu2O nanoclusters of different shapes. The different nanoclusters are bound with respect to dissociation and the relative stability will depend on the size of the clusters.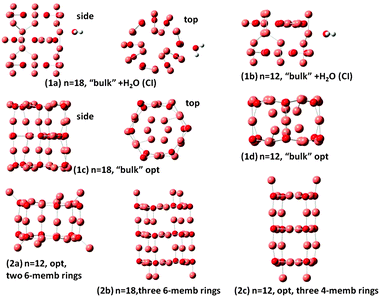 | ||
| Fig. 3 Optimized structures of nanobarrels. Small red spheres O and large faded red spheres Cu atoms. | ||
The present calculations on the structure of two types of clusters namely the n = 1–6 (Cu2O)n clusters and the n = 12 and n = 18 clusters show that formation of such clusters is favorable and the two types are related in the sense that the stacking of the rings determined for the n = 1–6 (Cu2O)n clusters led to stable nanotube or nanobarrel structures, as has been found for structures 2a and 2b of Fig. 3 involving stacking of n = 6 units and for structure 2c of Fig. 3 involving stacking of n = 4 units.
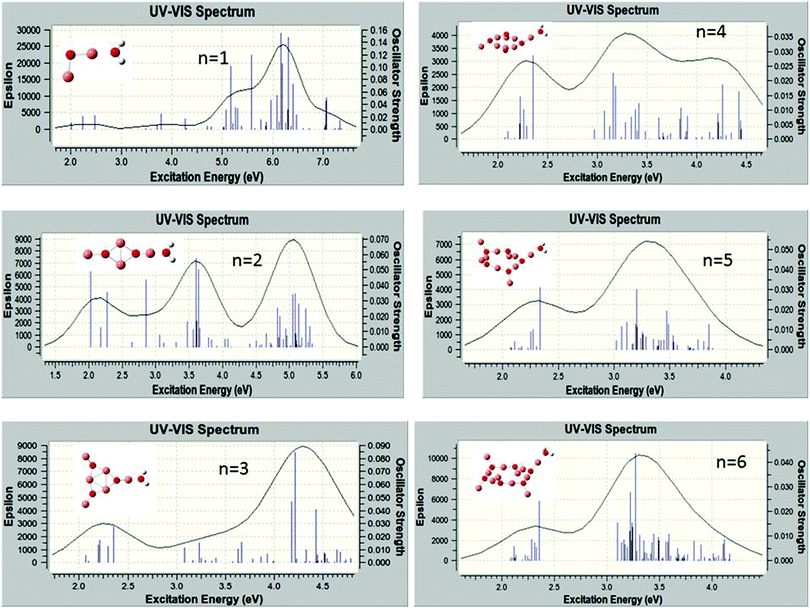
C. Excited states and absorption spectra
The excited electronic states of the (Cu2O)n clusters and the (Cu2O)n–OH2 complexes for n = 1–6 have been calculated by TDDFT/M062X/6-311+G(d,p), for 80–100 roots. The resulting absorption spectra of the (Cu2O)n clusters alone are given in Fig. S1 in the ESI† while spectra of the complexes with water are given in Fig. 4. The lowest singlet excited state of all the clusters lies at an excitation energy of about 2.0 eV with very low oscillator strengths cf.Table 2. Adsorption of H2O does not alter the appearance of the absorption spectra, cf.Fig. 4 and S1 (ESI†). However on closer examination of the excited states it is shown that in the (Cu2O)n–OH2 systems, excitations into an unoccupied Rydberg orbital of H2O contribute to the excited states for all n calculated. For example, for the case of n = 1, the second lowest unoccupied orbital (or LUMO + 1) is a Rydberg orbital of H2O, and even the first excited state at 2.01 eV has a contribution from a charge-transfer excitation, i.e. excitation from an occupied Cu2O orbital to the H2O unoccupied Rydberg orbital, with a coefficient of 0.2. For higher excited states, the charge-transfer contribution increases, e.g. its coefficient becomes 0.81 for an excited state Cu2O–OH2 at 3.48 eV. Similarly, for the higher n clusters, the Rydberg orbital of H2O is one of the lower unoccupied orbitals, cf.Table 2, and charge transfer excitations contribute to the character of the excited states of the complexes starting at the excited state indicated in Table 2. Electron density plots of the two highest occupied and two lowest unoccupied orbitals for the n = 2 complex (cf. b3 in Fig. 1) are plotted in Fig. 5, where it can be seen that the LUMO + 1 is a Rydberg orbital belonging to H2O. This is characteristic of the type of MO electron density plots of all the complexes, for the particular virtual orbital in each case.| n | S1 ΔE (eV), f-value | S Ryd root no., ΔE (eV), f-value | H2O Rydberg orbital |
|---|---|---|---|
| a Corresponding values for (Cu2O)n. | |||
| 1 | 2.01, 0.001/2.00,a 0.015a | (1), 2.01, 0.001 | LUMO + 1 |
| 2 | 2.02, 0.006/1.92,a 0.063a | (4), 2.65, 0.003 | LUMO + 1 |
| 3 | 2.07, 0.005/2.14,a 0.003a | (7), 3.08, 0.011 | LUMO + 2 |
| 4 | 2.07, 0.005/2.12,a 0.002a | (12), 3.07, 0.010 | LUMO + 3 |
| 5 | 2.07, 0.001/2.11,a 0.002a | (15), 3.11, 0.014 | LUMO + 4 |
| 6 | 2.08, 0.001/2.14,a 0.000a | (16), 3.10, 0.015 | LUMO + 5 |
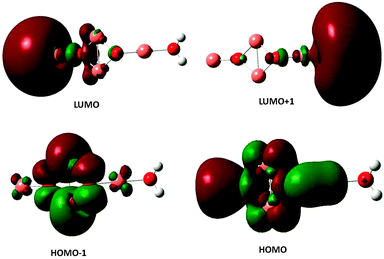 | ||
| Fig. 5 Electron density plots of the two highest occupied and the two lowest unoccupied orbitals of the (Cu2O)2–OH2 complex. | ||
It might be noted that in the absorption spectra of the larger complexes, i.e., for n ≥ 3, cf.Fig. 4, the lowest excited state in which there is H2O contribution occurs at around 3.1 eV, cf.Table 2, with a group of cluster excited states between about 2.0 and 2.4 eV followed by a gap, without any states until 3.0–3.1 eV. In addition, for these complexes the density of states becomes increasingly high and excitation energies over 4.5–5.0 eV are not reached for the calculated roots, which are 80–100, depending on the system.
The lowest excited state of the free H2O molecule is at a vertical excited energy of 7.4 eV from the ground state and although it has Rydberg character at the vertical point, it is in fact dissociating to yield OH + H.26 The possibility of populating a virtual orbital of H2O adsorbed on (Cu2O)n at lower energy than the free water absorption might be of interest for the question of photocatalytic splitting of H2O at clusters of Cu2O. However, geometry optimization of the lowest excited state of Cu2O–H2O, carried out here, resulted in a stable geometry (i.e. not dissociating) for the S1 state of Cu2O–OH2, with the emission spectrum only slightly red shifted with respect to the absorption spectrum. Geometry optimization of higher-lying excited states, with heavier contribution of the charge-transfer excitation, is technically not possible as the density of states is high and there exist many nonadiabatic interactions. The charge-transfer contribution for the higher n complexes starts at higher-lying states, cf.Table 2. Finally, the charge-transfer states of the n = 18 and n = 12 complexes with water, cf. structures 1a and 1b of Fig. 3, and also for the n = 4 cluster, d1 of Fig. 2, have been determined using CI calculations. The CI results show that charge transfer excitations have small contributions to low-lying states while the more significant contributions (coefficients 0.4–0.6) are found for higher lying excited states, for n = 4 at excitation energies from 4.77–4.91 eV, for n = 12 at excitation energies from 4.57–6.14 eV and for n = 18 from 4.52–5.11 eV (cf. ESI†).
The results of the calculations on the excited states, both TDDFT and CI, show that adsorption of a single water molecule on Cu2O clusters induces charge-transfer type excitations contributing to the electronic excited states, at energies well below the lowest singlet excitation energy of free H2O.
Conclusions
Geometry optimization DFT/B3LYP/6-311G(d,p) calculations have been carried out on (Cu2O)n clusters and (Cu2O)n–OH2 complexes for n = 1–6 and DFT/B3LYP/LAN2LDZ calculations on (Cu2O)n clusters with n = 12 and 18. Minimum energy structures have been determined, all bound with respect to dissociation to Cu2O substituent units. The results for n = 2–6 show the formation of rings enabling coordination of the O atoms with three Cu atoms, of which one is coordinated to one O atom and lies above or below the ring. The ring Cu atoms are coordinated to two O atoms in a nearly linear arrangement, when the dimensions of the cluster allow it. trans arrangements of the non-ring Cu atoms are slightly more favourable to cis. In all cases, adsorption of one molecule of H2O occurs by interaction between the water O and one of the non-ring Cu atoms, with a binding energy of about 1.0 eV. Suggestions are made for the formation of (Cu2O)n nanobarrels for n = 12 and 18 and different structures have been determined, showing a square mesh surface structure. Configuration interaction calculations have been carried out on adsorbed H2O on n = 18 and n = 12 nanobarrels.The excited states of (Cu2O)n clusters and (Cu2O)n–OH2 complexes for n = 1, 6 have been calculated by TDDFT/M062X/6-311+G(d,p) calculations at their optimum ground state geometry and for n = 1 at the optimum geometry of the S1 state as well. The results show that the lowest electronic state of these systems lies at an excitation energy from the ground state of about 1.92–2.14 eV and the low energy absorption spectra have generally low oscillator strengths. In all complexes, a Rydberg-type H2O virtual orbital contributes to the character of the excited states, starting at the first excited state (at 2.01 eV) for n = 1, at the fourth excited state (2.65 eV) for n = 2 and at higher excited states (at 3.07–3.11 eV) for the larger complexes. The contribution of charge-transfer excitations becomes significant for higher lying excited states, calculated by CI at excitation energies of 4.5–6.14 eV, for different complexes. The present calculations are consistent with a possible photocatalytic function of Cu2O for water splitting.
Acknowledgements
Support of this research by the U.S. Army Research Office is gratefully acknowledged.Notes and references
- L. Zhang and H. Wang, ACS Nano, 2011, 5, 3257 CrossRef CAS PubMed.
- B. Sinha, T. Goswami, S. Paul and A. Misra, RSC Adv., 2014, 4, 5092 RSC.
- M. Zahmakıran, S. Özkar, T. Kodaira and T. Shiomi, Mater. Lett., 2009, 63, 400 CrossRef PubMed.
- M. Hara, T. Kondo, M. Komoda, S. Ikeda, K. Shinohara, A. Tanaka, J. N. Kondo and K. Domen, Chem. Commun., 1998, 357 RSC.
- P. E. de Jongh, D. Vanmaekelbergh and J. J. Kelly, Chem. Commun., 1999, 1069 RSC.
- P. H. Reddy, H. Sekhar and D. N. Rao, Pramana - Journal of Physics, 2014, 82, 321 CrossRef CAS.
- L. I. Bendavid and E. A. Carter, J. Phys. Chem. B, 2013, 117, 15750 CrossRef CAS PubMed.
- S. A. Saraireh and M. Altarawneh, Can. J. Phys., 2013, 91, 1101 CrossRef CAS.
- M. Casarina, C. Maccato, N. Vigato and A. Vittadini, Appl. Surf. Sci., 1999, 142, 164 CrossRef.
- J. Zhang, J. Liu, Q. Peng, X. Wang and Y. Li, Chem. Mater., 2006, 18, 867 CrossRef CAS.
- R. K. Swarnkar and R. Gopal, Sci. Adv. Mater., 2012, 4, 511 CrossRef CAS PubMed.
- F. E. Osterloh, Chem. Soc. Rev., 2013, 42, 2294 RSC.
- M. Jadraque and M. Martín, Chem. Phys. Lett., 2008, 456, 51 CrossRef CAS PubMed.
- B. Dai, L. Tian and J. Yang, J. Chem. Phys., 2004, 120, 2746 CrossRef CAS PubMed.
- H. F. Farrell and R. D. Parra, J. Vac. Sci. Technol., B: Microelectron. Process. Phenom., 2011, 29, 061806 Search PubMed.
- R. G. Parr and W. Yang, Annu. Rev. Phys. Chem., 1995, 46, 701 CrossRef CAS PubMed.
- M. A. L. Marques and E. K. U. Gross, Annu. Rev. Phys. Chem., 2004, 55, 427 CrossRef CAS PubMed.
- A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098 CrossRef CAS.
- P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 270 CrossRef CAS PubMed.
- Y. Zhao and D. Truhlar, Theor. Chem. Acc., 2008, 120, 215 CrossRef CAS; Y. Zhao and D. Truhlar, Acc. Chem. Res., 2008, 41, 157 CrossRef PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision A.1, Gaussian, Inc., Wallingford CT, 2009 Search PubMed.
- D. A. Dixon and J. L. Gole, Chem. Phys. Lett., 1992, 189, 390 CrossRef CAS.
- A. Soon, M. Todorova, B. Delley and C. Stampfl, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 125420 CrossRef; A. Soon, M. Todorova, B. Delley and C. Stampfl, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 129902(E) CrossRef.
- B. N. Papas and J. L. Whitten, J. Chem. Phys., 2013, 138, 054312 CrossRef CAS PubMed.
- L. S. Sremaniak and J. L. Whitten, Surf. Sci., 2002, 516, 254 CrossRef CAS; L. S. Sremaniak and J. L. Whitten, Surf. Sci., 2007, 601, 3755 CrossRef PubMed; L. S. Sremaniak and J. L. Whitten, Surf. Sci., 2008, 602, 834 CrossRef PubMed.
- G. Theodorakopoulos, I. D. Petsalakis and R. J. Buenker, Chem. Phys., 1985, 96, 217 CrossRef CAS; G. Theodorakopoulos, I. D. Petsalakis and R. J. Buenker, Chem. Phys. Lett., 1987, 138, 71 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c4cp04303k |
| This journal is © the Owner Societies 2015 |