Solvent-mediated molar conductivity of protic ionic liquids†
Received
10th October 2014
, Accepted 4th November 2014
First published on 5th November 2014
Abstract
The molar conductivity, Λm, of protic ionic liquids (PILs) in molecular solvents is measured at 298.15 K. The decrease in the Λm values of PILs is observed with an increase in the concentration of PILs. The limiting molar conductivities, Λ0m, were obtained for each PIL in different molecular solvents using a least squares method. The Λ0m data for PILs were correlated with the structural aspects of PILs and solvent properties. The polar protic solvents show poor ionic association as compared to the polar aprotic solvents, which is discussed on the basis of the hydrogen bond donating (HBD) ability of solvents and PILs. The alkyl chain substitution of anions plays a significant role in the ionic association of the PILs. The diffusion coefficient D0 and the transport number t were determined, which were consistent with the Λ0m values of PILs in water. The Λ0m and D0 values are dependent on the hydrodynamic radius of anions of these ionic liquids. The extent of ionic association for each PIL was discussed using temperature dependent Λm data for aqueous PIL systems in terms of the Walden plot.
1. Introduction
In the last decade, ionic liquids (ILs) have received more and more attention because of their unique interesting physico-chemical properties and have been widely used in chemical reactions, electrochemical, separation, absorption, and transport processes.1–8 Other recent interesting applications are in electrochemical processes, fuel cells, lithium batteries and solar cells.9–12 Interestingly, the properties of ionic liquids can be tuned by the combination of different anions and cations, which provides chances for designing and developing ILs with desired properties1,2 such as catalytic activity, viscosity, ionic conductivity, solubility, polarity, phase behavior, and extraction ability. These properties are influenced by anion–cation and ion–solvent interactions. Many experimental methods like spectroscopic techniques13–18 and isothermal titration calorimetry have been developed to explore the anion–cation and ion–solvent interactions of ILs.19,20 The theoretical studies have been receiving attention because of their advantages of producing electronic structures, anion–cation binding energy, etc.14,21 A study of the conductance of the solutions of ionic liquids is essential for investigating the ionic interactions in these systems. The electrical conductivity of neat ILs is very low due to their high viscosity. To increase the conductivity of ILs, it is necessary to blend these ILs with other molecular solvents.22–25 This is especially important because the addition of molecular solvents dramatically decreases the viscosity of ILs and hence greatly enhances their electrical conductivity.26,27 The literature survey reveals that the data on the electrical conductivity of ILs in molecular solvents are limited.28,29
Zhang et al.30 studied the ionic conductivity of solutions of pyridinium based ionic liquids in different molecular solvents in different temperature ranges of 283.15 to 313.15 K. Buchner et al.31 compared the ionic association behaviour of [BMIM]Cl and [BMIM]BF4 in methanol and dimethyl sulfoxide and used the low concentration chemical model (LcCM) to analyse the conductivity data. The limiting molar conductivities of selected binary mixtures of the imidazolium ILs in molecular solvents show a correlation of solvent properties such as polarity, viscosity, and relative permittivity with the conductivity of ILs. The viscosity and ionic conductivity of binary mixtures of 1-alkyl-3-methylimidazolium tetrafluoroborate [RMIM]BF4 with ethanol32 have also been investigated and the relationship between viscosity and ionic conductivity is obtained from Walden plots.33–35 As such the search of the literature shows that the data are available for aprotic ILs as mentioned above. However no data exist regarding the conductance of protic ionic liquids.
In this article, we report for the first time the molar conductivity, Λm, of three protic imidazolium-based ILs in different molecular solvents at 298.15 K. The molar conductivities were measured for binary mixtures of three PILs, 1-methylimidazolium formate [HmIm][HCOO], 1-methylimidazolium acetate [HmIm][CH3COO], and 1-methyl imidazolium propionate [HmIm][CH3CH2COO], in six molecular solvents, water, methanol, ethanol, dimethyl sulfoxide, nitrobenzene and acetonitrile, at 298.15 K. The effect of molecular solvents on the molar conductivity of PILs was investigated. The experimental molar conductance data for these PILs in different solvents collected at 298.15 K are given in the ESI.† The limiting molar conductivities (Λ0m) are determined for all these systems. These Λ0m are correlated with the properties of ILs and solvents. Further, the transport behaviour of cations and anions is investigated from the transport number and the diffusion coefficient. Walden plots are presented for three PILs in water as a function of temperature to explain the ionicity of PILs.
2. Experimental section
2.1 Chemicals and materials
1-Methylimidazole (99%), acetic acid, formic acid and propanoic acid were purchased from Sigma Aldrich and used as obtained. The solvents dimethyl sulfoxide, nitrobenzene, acetonitrile, ethanol and methanol of high purity grade were purchased from Merck India. Milli-Q water (with a specific conductance of 5.5 × 10−6 S m−1) was used throughout the experiments.
2.2 Synthesis of protic ILs
The protic ionic liquids, [HmIm][HCOO], [HmIm][CH3COO], and [HmIm][CH3CH2COO], were synthesized and purified according to the reported procedure from our research group.36–38 The PILs were synthesized by neutralization reaction of acid and base. Dropwise addition of base to acid was carried out in an ice bath to avoid heat generation due to the exothermic reaction. The reaction mixture of acid and base in the molar ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 was stirred for 6 h at room temperature. Water was removed by using a rotavapour at 80 °C under reduced pressure. These PILs were further dried under vacuum at 70 °C for 10 h. The water content of PILs is analyzed by Karl-Fischer titration and is observed to be 50 ppm. The characterization and determination of purities were performed by 1H NMR spectroscopy in agreement with the reported values.37
1 was stirred for 6 h at room temperature. Water was removed by using a rotavapour at 80 °C under reduced pressure. These PILs were further dried under vacuum at 70 °C for 10 h. The water content of PILs is analyzed by Karl-Fischer titration and is observed to be 50 ppm. The characterization and determination of purities were performed by 1H NMR spectroscopy in agreement with the reported values.37
2.3 Conductivity measurements
The specific conductivities were measured using a Synchrotron 306 conductometer at 1 kHz. The calibration of the conductivity meter was done by using a 0.1 M potassium chloride (KCl) solution. The cell constant was determined with standard aqueous solutions of KCl. Initially, 100 ml of solvent was accurately weighed into the jacket and conductivity measurements were made. A known amount of solution of PILs was added stepwise to the jacket to obtain the required concentration (10−5 to 10−4 mol dm−3) and conductivity was measured after each addition. The molar conductivity was calculated using equation Λm = (k/c) × 1000. The uncertainties were estimated to be ±0.1% for concentration and 1% for conductivity, respectively. The temperature of the jacket was maintained using a JULABO thermostat.
3. Results and discussion
The Λm data for the PILs of interest are given in Tables S1–S6 in the ESI.†Fig. 1 shows comparative plots of the Λm of the imidazolium-based PILs [HmIm][HCOO] with different molecular solvents such as water, methanol, ethanol, dimethyl sulfoxide, acetonitrile and nitrobenzene. The behaviour of Λm of [HmIm][CH3COO] and [HmIm][CH3CH2COO] in the above molecular solvents is shown in Fig. S1 and S2 (ESI†), respectively. The conductivity measurements were carried out for dilute concentrations of the PILs of the range 0.0001 to 0.0007 mol dm−3. There are many reports available in the literature that interpret the molar conductivity data on the basis of the low concentration chemical model (LcCM). Ismail and co-workers have proposed eqn (1) for analyzing conductivity data.39where AΛ, BΛ, and CΛ are the adjustable parameters and c is the molarity of solution expressed in mol dm−3. The values of these parameters were obtained by a least-squares fitting method. In this case, the parameter AΛ is considered to be the limiting molar conductivity denoted as Λ0m. We also applied this eqn (1) to our binary systems of ILs with molecular solvents and compared it with those fitted using the LcCM equation. It was interesting to find that there exists close agreement between values of Λ0m obtained from eqn (1) and from the LcCM. For example, Buchner et al.31 reported a Λ0m of 121.84 S cm2 mol−1 for [BMIM][BF4] at 298.15 K using the LcCM, while using eqn (1)Λ0m is observed to be 117 S cm2 mol−1. However, there is inconsistency in the Λ0m of ILs due to either the use of different conductivity equations to describe the concentration dependence of the molar conductivities or the use of experimental data in a different concentration range to fit the conductivity equations. Our conductivity measurements were carried out in a low dilute concentration range.
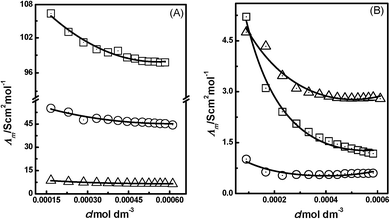 |
| | Fig. 1 The plots of Λmvs. Conc. (A) for [HmIm][HCOO] in water (□), methanol (○), and ethanol (△) and (B) for [HmIm][HCOO] in dimethyl sulfoxide (□), acetonitrile (○), and nitrobenzene (△) at 298.15 K. | |
3.1 Effect of relative permittivity (ε) on limiting molar conductivities
Table 1 shows the Λ0m of all three PILs in polar protic solvents (A) water, methanol, and ethanol, and polar aprotic solvents (B) dimethyl sulfoxide, acetonitrile, and nitrobenzene. The Λ0m values for PILs are higher in polar protic solvents compared to polar aprotic solvents. Fig. 2 shows the plots of Λ0m of PILs [HmIm][HCOO], [HmIm][CH3COO], and [HmIm][CH3CH2COO] vs. relative permittivity (ε) of polar protic solvents. In all the above cases, the Λ0m for PILs in molecular solvents increases with an increase in ε of solvents. This suggests that cations and anions are less associated in the solvent possessing a high dielectric constant due to independent solvation of ions. Thus, both cations and anions do not remain associated in water and hence higher values of Λ0m are seen in water, while in ethanol the ion remains associated and hence shows lower Λ0m values. The difference between Λ0m of water and methanol is high as compared to that between methanol and ethanol. This suggests that relative permittivity plays a significant role in the dissociation of PILs in polar protic solvents. Further, we have also observed a trend in Λ0m of PILs with dielectric medium in polar aprotic solvents dimethyl sulfoxide, acetonitrile, and nitrobenzene as shown in Fig. 3. The Λ0m values for [HmIm][HCOO] in dimethyl sulfoxide, acetonitrile and nitrobenzene are 9.26 S cm2 mol−1, 6.38 S cm2 mol−1 and 1.40 S cm2 mol−1, respectively. These values of Λ0m of PILs in polar aprotic solvents are very small compared to protic solvents even though the relative permittivities are in the comparable range. This may be due to the Grotthuss type mechanism in polar protic solvents.40 Similarly, we have also observed that in other PIL systems, the Λ0m values for [HmIm][CH3COO] are 9.06 S cm2 mol−1, 8.47 S cm2 mol−1 and 2.20 S cm2 mol−1, while for [HmIm][CH3CH2COO] the values are 9.09 S cm2 mol−1, 4.42 S cm2 mol−1 and 3.07 S cm2 mol−1 in dimethyl sulfoxide, acetonitrile and nitrobenzene, respectively. In this case also we have observed that the Λ0m increases with an increase in the dielectric constant of the solvents but to a small extent.
Table 1 The Λ0m of PILs obtained from eqn (1) in different molecular solvents at 298.15 K
| S. No. |
Solvents |
Relative permittivity (ε) |
Λ
0m (S cm2 mol−1) |
| [HmIm][HCOO] |
[HmIm][CH3COO] |
[HmIm][CH3CH2COO] |
| 1 |
Water |
78.00 |
115.06 |
91.12 |
83.24 |
| 2 |
Methanol |
32.70 |
64.71 |
47.55 |
19.66 |
| 3 |
Ethanol |
24.50 |
10.93 |
10.53 |
9.08 |
| 4 |
Dimethyl sulfoxide |
46.70 |
9.26 |
9.06 |
9.09 |
| 5 |
Acetonitrile |
37.50 |
6.38 |
8.47 |
4.42 |
| 6 |
Nitrobenzene |
34.82 |
1.40 |
2.20 |
3.07 |
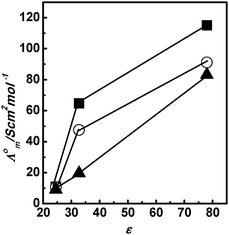 |
| | Fig. 2 Plots of Λ0m with relative permittivity (ε) of water, methanol, and ethanol for [HmIm][HCOO] (■), [HmIm][CH3COO] (○), and [HmIm][CH3CH2COO] (▲) at 298.15 K. | |
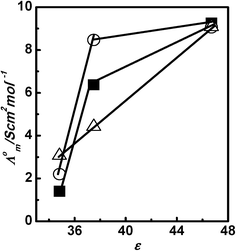 |
| | Fig. 3 Plots of Λ0mvs. relative permittivity (ε) of dimethyl sulfoxide, acetonitrile, and nitrobenzene for [HmIm][HCOO] (■), [HmIm][CH3COO] (○), and [HmIm][CH3CH2COO] (△) at 298.15 K. | |
However, in the case of polar protic solvents, dielectric constant does play a significant role in solvating the cations and anions independently compared to the polar aprotic solvents. This signifies that strong association of cations and anions of PILs is present in the polar aprotic solvents.
The viscosities of water, methanol, ethanol, dimethyl sulfoxide, acetonitrile and nitrobenzene are 0.89, 0.54, 1.10, 2.22, 0.38 and 1.8 mPa s, respectively, at 298.15 K. The examination of the Λ0m values of PILs given in Table 1 did not offer any correlation with viscosities of these solvents.
3.2 Effect of anions on limiting molar conductivity
Comparing the values of Λ0m for [HmIm][HCOO], [HmIm][CH3COO] and [HmIm][CH3CH2COO] in polar protic solvents water, methanol and ethanol reveals an inverse linear relationship between the Λ0m values with an increase in carbon atoms in the alkyl chain of anions of PILs. However, we did not observe any correlation of Λ0m for [HmIm][HCOO], [HmIm][CH3COO] and [HmIm][CH3CH2COO] in polar aprotic solvents dimethyl sulfoxide, acetonitrile, and nitrobenzene.
The representative results for PILs in polar protic solvents are shown in Fig. 4. It is observed that the ionic association of cations and anions for [HmIm][CH3CH2COO] in water and methanol is higher as compared to that in [HmIm][HCOO] and [HmIm][CH3COO]. In ethanol, all three PILs show comparable associations of cations and anions. The decrease in Λ0m for PILs with each methyl group shows associations of cations and anions in water. Further, we have determined Λ0m of cations and anions to study the behaviour and contribution of individual ions in the association process. The individual limiting molar conductivity of ions can be calculated from the total Λ0m. The total Λ0m of PILs is a contribution of individual cations and anions:
where
λ0+m and
λ0−m are the limiting molar conductivities of cations and anions, respectively. The
λ0−m values of [HCOO]
−, [CH
3COO]
− and [CH
3CH
2COO]
− anions in water are 54.6, 40.2 and 35.8 S cm
2 mol
−1, respectively at 298.15 K, which are reported in the literature.
41 The calculated
λ0+m for the [HmIm]
+ cation for each PIL decreases from [HCOO]
− to [CH
3CH
2COO]
− (
Table 2). This is due to an increase in ionic association of cations with anions of PILs. The ionic association is the highest for [HmIm][CH
3CH
2COO] in solvents. It is due to the fact that [CH
3CH
2COO]
− is less stabilised as compared to [HCOO]
− and [CH
3COO]
− anions, as a high inductive effect is observed in the [CH
3CH
2COO]
− anion leading to higher interactions between cations and anions and thus less dissociation.
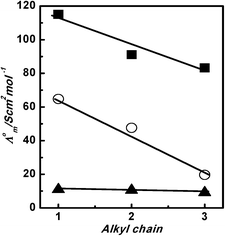 |
| | Fig. 4 Plots of Λ0mvs. alkyl chain length of the anions for [HmIm][HCOO], [HmIm][CH3COO] and [HmIm][CH3CH2COO] in water (■), in methanol (○), and in ethanol (▲) at 298.15 K. | |
Table 2 Limiting molar conductivities Λ0m and transport numbers t+ and t− of cations and anions of PILs in water at 298.15 K
| S. No. |
Protic ionic liquids |
λ
0+m (S cm2 mol−1) |
λ
0−m (S cm2 mol−1) |
t
+
|
t
−
|
| 1 |
[HmIm][HCOO] |
60.46 |
54.60 |
0.53 |
0.47 |
| 2 |
[HmIm][CH3COO] |
50.12 |
40.20 |
0.55 |
0.45 |
| 3 |
[HmIm][CH3CH2COO] |
47.44 |
35.80 |
0.57 |
0.43 |
The transport numbers for cations (t+) and anions (t−) of PILs were calculated using eqn (3) and are tabulated in Table 2.
| | | t+ = λ0+m/Λ0m and t−= λ0−m/Λ0m | (3) |
where
t+ and
t− are cationic and anionic transport numbers, respectively. From
Table 2, it is observed that the
t+ values for all PILs are higher than the
t− values in water. The cationic transport number
t+ for [HmIm]
+ is higher than 0.5, while the anionic transport number is less than 0.5. This indicates that [HmIm]
+ carries more than half of the current and less than half is carried by the anions, as [HmIm]
+ is able to move or diffuse faster than other anions.
The Λ0−m values decrease from [HCOO]− to [CH3CH2COO]− in polar protic solvents. This may be due to the diffusivity of ions of PILs being a function of the ion size and the interactions of ions with the solvents. Thus, [HCOO]− migrates faster as compared to [CH3COO]− and [CH3CH2COO]− and hence shows larger Λ0−m values. This is also reflected in the transport number t− which is noted to be the highest for [HCOO]− and the lowest for [CH3CH2COO]−. This is due to the increase in van der Waals radii of anions from [HCOO]− to [CH3CH2COO]−.
3.3 Effect of hydrogen bonding on the solvation of anions
In Section 3.1, we have discussed the effect of polarity through the relative permittivity of medium on the Λ0m. Polarity is a general term that refers to all the interaction forces between molecules, both specific and nonspecific interactions and is composed of several interacting components, including coulombic interactions, the various dipole interactions, hydrogen-bonding and electron pair donor–acceptor interactions.42,43
The solvatochromic parameter ET(30) or ENT, electronic transition energy, α hydrogen bond donor ability (HBD) and β hydrogen bond acceptor (HBA) parameter explain the solvent dependent phenomenon at the molecular level and give information about the solvation ability of the medium. There are many reports available on the polarity of ILs and molecular solvents which explain the presence of different sites of interactions at the molecular level.44–46 The values of ENT, α and β parameters for PILs and molecular solvents are shown in Table 3. Fig. 5(A) displays the effect of ENT values of molecular solvents on Λ0m of PILs, which shows that the Λ0m of PILs increases with an increase in the ENT value of molecular solvents. The effect is more pronounced in polar protic solvents compared to polar aprotic solvents. The ENT values for polar protic solvents decrease from water to methanol to ethanol as 1 to 0.652, which decrease Λ0m values from 115.06 to 10.93 for [HmIm][HCOO], 91.12 to 10.53 for [HmIm][CH3COO] and 83.24 to 9.09 for [HmIm][CH3CH2COO]. However, the smaller effect is observed in polar aprotic solvents. This is because the ENT of PILs lies between the ENT values of polar protic solvents and polar aprotic solvents. Thus polar protic solvents could strongly solvate the cations and anions of PILs through the hydrogen bond donor (HBD)/acceptor (HBA) ability of solvents. To explain this we have also considered the role of hydrogen bond donor ability HBD (α) of molecular solvents and PILs. The HBD (α) values for [HmIm][HCOO], [HmIm][CH3COO] and [HmIm][CH3CH2COO] are observed to be 0.81, 0.51 and −0.06, respectively,37 which are smaller than the α values for water, methanol and ethanol 1.12, 1.05 and 0.83, respectively. The α values of aprotic solvents such as dimethyl sulfoxide, acetonitrile and nitrobenzene are 0, 0.19 and 0, respectively, which are much smaller than polar protic solvents.43,47 All three PILs show higher values of Λ0m in water. This is because of the highest α of water, which increases the interaction of anions with water through hydrogen bonding, hence causing more dissociation of PILs. Methanol and ethanol possess α values smaller than water. The fact that methanol and ethanol differ from water by the presence of only a methyl and an ethyl group, respectively makes such a difference more relevant. A rational explanation is that the anion is strongly solvated by the hydrogen bonding interactions between the anion and water, methanol, and ethanol. Therefore anions of PILs have more affinity towards polar protic solvents as compared to cations in solutions. Thus, PILs show higher Λ0m in water than methanol and ethanol. The effect of α of each polar protic solvent on Λ0m PILs is of the order of [HmIm][HCOO] > [HmIm][CH3COO] > [HmIm][CH3CH2COO] (Fig. 5(B)). In the case of polar aprotic solvents, dimethyl sulfoxide, acetonitrile and nitrobenzene possess very small α values compared to polar protic solvents leading to lower Λ0m values. However, we did not observe any correlation of Λ0m on the basis of basicity β of molecular solvents. The correlation of α values with Λ0m of PILs in all solvents is similar to ENT which indicates that α is a dominant factor contributing to the solvation dynamics of ions of PILs compared to β. Thus for given PILs, the ionic association was affected significantly by ionic solvation through polarity parameters ENT and α of the molecular solvents. Thus strong solvation of the cation and/or anion weakens the ionic association which is observed in polar protic solvents, whereas weak ionic solvation enhances the ionic association of the PILs in molecular solvents, which is observed in polar aprotic solvents.
Table 3 The ENT, α, and β values of the PILs and molecular solvents at 298.15 K37,42,44
| S. No. |
Protic ionic liquids/solvents |
E
NT
|
α
|
β
|
| 1 |
[HmIm][HCOO] |
0.78 |
0.81 |
0.81 |
| 2 |
[HmIm][CH2COO] |
0.61 |
0.50 |
0.85 |
| 3 |
[HmIm][CH3CH2COO] |
0.50 |
−0.06 |
0.10 |
| 4 |
Water |
1.0 |
1.12 |
0.50 |
| 5 |
Methanol |
0.76 |
1.05 |
0.63 |
| 6 |
Ethanol |
0.65 |
0.83 |
0.75 |
| 7 |
Dimethyl sulfoxide |
0.44 |
0.00 |
0.76 |
| 8 |
Acetonitrile |
0.45 |
0.19 |
0.40 |
| 9 |
Nitrobenzene |
0.32 |
0.00 |
0.39 |
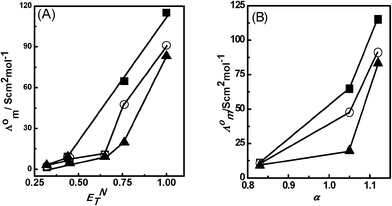 |
| | Fig. 5 Plots (A) Λ0mvs. ENT (B) Λ0mvs. a of solvents for [HmIm][HCOO] (■), [HmIm][CH3COO] (○), and [HmIm][CH3CH2COO] (▲). | |
3.4 Diffusion coefficient and hydrodynamic radius
The diffusion of PIL in water is a combination of diffusion of individual cations and anions and can be determined by applying the Nernst–Haskell equation48 (eqn (4)).| | 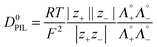 | (4) |
where D0PIL is the diffusion coefficient of PILs in water at infinite dilution, R the gas constant, T the absolute temperature, F the Faraday constant and z+ and z− are the charge numbers on cations and anions, respectively. Λ0+ and Λ0− are the infinite dilution conductivities of the cation and anion, respectively.
The diffusion coefficients for PILs were obtained at infinite dilution in the case of aqueous solutions (Table 4). These values are comparable with the reported values of the diffusion coefficient of PILs [Pyrr][HSO4] and [Pyrr][CF3COO] which were determined from conductivity and NMR studies.49 It is also possible to determine the diffusion coefficient of cations and anions from eqn 5(a) and (b) as
| | 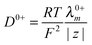 | (5a) |
| | 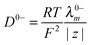 | (5b) |
Table 4 Diffusion coefficient of ILs D0IL and cation D0+ and anion D0− of ILs in aqueous solution and the hydrodynamic radius of the anion RH at 298.15 K
| S. No. |
Protic ionic liquids |
D
0IL (10−5 cm2 s−1) |
D
0+ (10−5 cm2 s−1) |
D
0−(10−5 cm2 s−1) |
R
H (pm) |
| 1 |
[HmIm][HCOO] |
1.527 |
1.609 |
1.453 |
168 |
| 2 |
[HmIm][CH3COO] |
1.187 |
1.334 |
1.070 |
229 |
| 3 |
[HmIm][CH3CH2COO] |
1.086 |
1.263 |
0.953 |
257 |
The diffusion of PILs in water decreases from [HCOO]− to [CH3CH2COO]−. These results are consistent with Λ0m of PILs of the same system. From Table 4, it is observed that the diffusion coefficient for cations is higher than the anions, proving that cations diffuse faster compared to anions. These results are consistent with the transport number. Further we have determined hydrodynamic radii from the Stoke–Einstein equation (eqn (6)).
| | 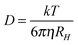 | (6) |
where
D is the diffusion coefficient,
k the Boltzmann constant,
T the temperature in K and
η the viscosity of solvents.
The hydrodynamic radius of anions varies as [HmIm][HCOO] < [HmIm][CH3COO] < [HmIm][CH3CH2COO]. This result is also consistent with molar conductivity of aqueous solution of PIL and diffusion coefficient of anions for each system. Thus lower mobility and diffusion of [CH3CH2COO]− ion are due to the larger hydrodynamic radius of 257 pm than [HCOO]− of 168 pm and [CH3COO]− of 229 pm.
3.5 Ionicity in protic ionic liquids
Ionicity in an electrolytic solution represents free ions present in a system. The Walden plot of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Λmvs. log
Λmvs. log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) η−1 is a suitable method for measuring the ionicity of electrolytic solutions. The Walden rule of relation between conductivity and viscosity is given by eqn (7)where λ, η and k denote the conductivity, viscosity and a temperature dependent constant, respectively. From this, we obtain the formation of free ions, ion pairs and non-charged aggregates in solution. Angell et al.34,35 have described a qualitative approach about the Walden rule for different neat ILs. The plot of log
η−1 is a suitable method for measuring the ionicity of electrolytic solutions. The Walden rule of relation between conductivity and viscosity is given by eqn (7)where λ, η and k denote the conductivity, viscosity and a temperature dependent constant, respectively. From this, we obtain the formation of free ions, ion pairs and non-charged aggregates in solution. Angell et al.34,35 have described a qualitative approach about the Walden rule for different neat ILs. The plot of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Λmvs. log
Λmvs. log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) η−1 predicts a straight line that passes through the origin for ideal solution. The solution of 0.01 M KCl gives a helpful reference line on the Walden plot as shown in Fig. 6.34 Interestingly, a linear relationship exists between the molar conductivities for each of the PILs and the reciprocality of the viscosity (1/η) of water as a function of temperature. This suggests that the fluidity of the medium played a predominant role in the ionic association of the PILs.
η−1 predicts a straight line that passes through the origin for ideal solution. The solution of 0.01 M KCl gives a helpful reference line on the Walden plot as shown in Fig. 6.34 Interestingly, a linear relationship exists between the molar conductivities for each of the PILs and the reciprocality of the viscosity (1/η) of water as a function of temperature. This suggests that the fluidity of the medium played a predominant role in the ionic association of the PILs.
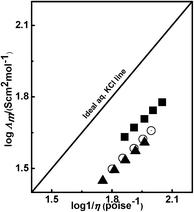 |
| | Fig. 6 The Walden plot of 1 M aqueous solution of [HmIm][HCOO] (■), [HmIm][CH3COO] (○) and [HmIm][CH3CH2COO] (▲) from 293.15 to 313.15 K. | |
The deviation from the ideal line of KCl suggests the extent of ionicity in electrolyte solution. The Walden plot for [HmIm][HCOO], [HmIm][CH3COO] and [HmIm][CH3CH2COO] in water is shown Fig. 6. These binary mixtures of PILs with water show a deviation from the aqueous solution of 0.01 M KCl in which KCl in water is fully dissociated. Angell has explained such deviations by measuring the vertical distance between the KCl line and PILs, denoted by ΔW. Thus the %ionicity can be calculated from ΔW as
| | | %Ionicity = 10(−ΔW) × 100 | (8) |
For example, the value of ΔW = 1 expresses 10% of ionicity of electrolytic solution with respect to the line for 0.01 M KCl. In our system, the ΔW values and % ionicities for three PILs are tabulated in Table 5. The ΔW values for all PILs are less than 1, which significantly indicates that ionicity is very high and a large ΔW indicates incomplete ionic dissociation. The distinction between three PILs assists in understanding the various effects that can be observed from the examination of the Walden plot. [HmIm][HCOO] with an ΔW of 0.23 represents an example of a close-to-ideal KCl. The remaining two [HmIm][CH3COO] and [HmIm][CH3CH2COO] PILs are located at the distance of ΔW of 0.31 and 0.33, respectively. The calculated ionicity for PILs is 58%, 49% and 46% and follows the order [HmIm][HCOO] > [HmIm][CH3COO] > [HmIm][CH3CH2COO]. A similar trend is observed in the case of molar conductivities and the diffusion coefficient of the same PILs. Thus from the data of ionicity, molar conductivity, viscosity, anion size and diffusion coefficient, it is observed that [HmIm][HCOO] is more dissociated as compared to [HmIm][CH3COO] and [HmIm][CH3CH2COO]. The dissociation of PILs is consistent with the hydrogen bonding model described earlier in Section 3.3. Thus from the ΔW, the PILs in water are not fully dissociated like ideal aqueous 0.01 M KCl solution. It may be due to strong ion association in cations and anions in PILs. This study may find applications in the modulation of the conductance performance of the ILs in molecular solvents.
Table 5 Data obtained from the Walden plot of 1 M aqueous solution of PILs at 298.15 K
| S. No. |
Protic ionic liquids |
Λ
m (S cm2 mol−1) |
η (cP) |
ΔW |
Ionicity (%) |
| 1 |
[HmIm][HCOO] |
47.92 |
1.23 |
0.23 |
58 |
| 2 |
[HmIm][CH3COO] |
34.93 |
1.40 |
0.31 |
49 |
| 3 |
[HmIm][CH3CH2COO] |
31.14 |
1.54 |
0.33 |
46 |
Many pure PILs lie below the reference line indicating the incomplete ionization of PILs compared to APILs on the basis of the Walden plot.34 This order of Λ0m for PILs of magnitude lower than APILs is because of more ionic association in PILs.31 The conductivity or ionicity of PILs depends on the transfer of protons from Bronsted acid HA to a Bronsted base B as
The ionicity is adjustable in PILs by the virtue of different driving forces for the proton-transfers. However, the extent of proton transfer in PILs is not yet explained in detail. There are reports available to explain the degree of proton transfer in PILs. First, it is estimated after considering the difference of ΔpKaqa values of the acid and the base. If the ΔpKaqa values are more than 2, it is sufficient to transfer the proton frequently from acid to base.50,51 In our systems, the ΔpKaqa values are 3.34, 2.34 and 2.22 for [HmIm][HCOO], [HmIm][CH3COO] and [HmIm][CH3CH2COO], respectively. These values indicate that proton transfer is effective in the environment of PILs. Also from our conductivity data of PILs, we observed that the cations and anions of PILs exhibit conductivity, which is higher than the neutral species of the acid and the base. Conductivity values also represent the availability of cations and anions in a binary system of water with PILs. From all the above observations and spectral data of 1H-NMR it is clear that the proton is predominately displaced from acid to base. Secondly, PILs form extensive hydrogen bonds, which stabilize both cations and anions, resulting in the probability of reverse proton transfer becoming low. Due to these opposing phenomena, a very small proportion of neutral moiety exists along with the PILs leading to lower α values, which are far beyond the α values for pure HCOOH, CH3COOH and CH3CH2COOH i.e. 1.23, 1.12 and 1.12, respectively. Thus due to the strong columbic interactions between ions, and the long range of the interactions, the vapor pressure over the PILs is much lower than individual vapor pressure of pure acid and base indicating that the free energy change in the proton transfer process is large. It is important to note that a possibility of formation of super anions in pure ionic liquids has been reported.51 The PILs used herein were synthesized with 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 of acid and base. Further, our experiments were performed in very dilute ionic liquid solutions. It is, however, not clear to state whether the formation of super anions is possible in our system unlike those prepared considering the composition of acid in excess compared to base.51
1 of acid and base. Further, our experiments were performed in very dilute ionic liquid solutions. It is, however, not clear to state whether the formation of super anions is possible in our system unlike those prepared considering the composition of acid in excess compared to base.51
4. Conclusions
In this work, we have investigated the ionic association of PILs in different molecular solvents through conductivity measurements. The existence of ion pairing in PILs is observed and depends on the presence of the type of cations and anions and solvent medium. In short, we show that: (1) the limiting molar conductivity Λ0m of PILs is mostly directed by the dielectric properties of the solvents, (2) the solvatochromic parameters ENT and the hydrogen bond donor ability α of solvents dominantly affect the ionic association in PILs as compared to the hydrogen bond acceptor ability β of the solvents, (3) the diffusion coefficients and transport numbers of the individual cations and anions of PILs in aqueous systems can be correlated with solvent properties and the structure of PILs and (4) the ionicity order in PILs was observed to be [HmIm][HCOO] > [HmIm][CH3COO] > [HmIm][CH3CH2COO].
Acknowledgements
The authors thank both the referees for making useful suggestions that led to the improvement of this work. SRT thanks CSIR, New Delhi, for awarding him a Senior Research Fellowship, while A.K. thanks DST, New Delhi, for awarding him a JC Bose National Fellowship (SR/S2/JCB-26/2009).
References
- T. Welton, Chem. Rev., 1999, 99, 2071–2083 CrossRef CAS PubMed.
- J. P. Hallett and T. Welton, Chem. Rev., 2011, 111, 3508–3576 CrossRef CAS PubMed.
- M. J. Earle and K. R. Seddon, Pure Appl. Chem., 2000, 72, 1391–1398 CrossRef CAS.
- R. Sheldon, Chem. Commun., 2001, 2399–2407 RSC.
-
P. Wassercheid and T. Welton, Ionic liquid synthesis, Wiley-VCH Verlag GmbH and Co. KGaA, 2008 Search PubMed.
- V. I. Parvulescu and C. Hardacre, Chem. Rev., 2007, 107, 2615–2665 CrossRef CAS PubMed.
- H. Weingartner, Angew. Chem., Int. Ed., 2008, 47, 654–670 CrossRef PubMed.
- J. Dupont and P. A. Z. Suarez, Phys. Chem. Chem. Phys., 2006, 8, 2441–2452 RSC.
- C. Sirisopanaporn, A. Fernicola and B. Scrosati, J. Power Sources, 2009, 186, 490–495 CrossRef CAS.
- H. Sakable and H. Matsumoto, Electrochem. Commun., 2003, 5, 594–898 CrossRef.
- N. J. Robertson, H. A. Kostalik, T. J. Clark, P. F. Mutolo, H. D. Abruna and G. W. Coates, J. Am. Chem. Soc., 2010, 132, 3400–3404 CrossRef CAS PubMed.
- A. Andriola, K. Singh, J. Lewis and L. Yu, J. Phys. Chem. B, 2010, 114, 11709–11714 CrossRef CAS PubMed.
- J. Jiang, K. Lin, S. Li, P. Shih, K. Hung, S. Lin and C. Chang, J. Chem. Phys., 2011, 134, 044506 CrossRef PubMed.
- T. Koddermann, C. Wertz, A. Heintz and R. Ludwig, ChemPhysChem, 2006, 7, 1944–1949 CrossRef PubMed.
- F. Pierola and Y. Agzenai, J. Phys. Chem. B, 2012, 116, 3973–3981 CrossRef PubMed.
- M. Krell, M. Symons and J. Barthel, J. Chem. Soc., Faraday Trans. 1, 1987, 83, 3419–3427 RSC.
- R. Kotoh, M. Hara and S. Tsuzuki, J. Phys. Chem. B, 2008, 112, 15426–15430 CrossRef PubMed.
- M. Rogac, A. Stoppa, J. Hunger, G. Hefterc and R. Buchner, Phys. Chem. Chem. Phys., 2011, 13, 17588–17598 RSC.
- G. Rai and A. Kumar, Phys. Chem. Chem. Phys., 2011, 13, 14715–14722 RSC.
- G. Rai and A. Kumar, Phys. Chem. Chem. Phys., 2013, 15, 8050–8053 RSC.
- P. A. Hunt and I. R. Gauld, J. Phys. Chem. A, 2006, 110, 2269–2282 CrossRef CAS PubMed.
- A. Pereiro, J. Araujo, F. Oliveira, C. Bernardes, J. Esperanc, J. Lopes, I. Marruchoa and L. Rebelo, Chem. Commun., 2012, 48, 3656–3658 RSC.
- Y. Zhao, X. Zhang, S. Zeng, Q. Zhou, H. Dong, X. Tian and S. Zhang, J. Chem. Eng. Data, 2010, 55, 3513–3519 CrossRef CAS.
- A. Ahmady, M. Hashim and M. Aroua, J. Chem. Eng. Data, 2010, 55, 5733–5738 CrossRef CAS.
- Z. Lei, J. Yuan and J. Zhu, J. Chem. Eng. Data, 2010, 55, 4190–4194 CrossRef CAS.
- A. Kumar, J. Am. Chem. Soc., 1993, 115, 9243–9248 CrossRef CAS.
- N. D. Khupse and A. Kumar, J. Solution Chem., 2009, 38, 589–600 CrossRef CAS.
- M. Anouti, A. Vigeant, J. Jacquemin, C. Brigouleix and D. Lemordant, J. Chem. Thermodyn., 2010, 42, 834–845 CrossRef CAS.
- M. Anouti, M. Caillon-Caravanier, Y. Dridi, J. Jacquemin, C. D. Hardacre and D. Lemordant, J. Chem. Thermodyn., 2009, 41, 799–808 CrossRef CAS.
- Q. Zhang, S. Sun, S. Pitula, Q. Liu, U. WelzBiermann and J. Zhang, J. Chem. Eng. Data, 2011, 56, 4659–4664 CrossRef CAS.
- M. B. Rogac, J. Hunger, A. Stoppa and R. Buchner, J. Chem. Eng. Data, 2010, 55, 1799–1803 CrossRef.
- E. Rilo, J. Vila, M. Garcia, L. M. Varela and O. Cabeza, J. Chem. Eng. Data, 2010, 55, 5156–5163 CrossRef CAS.
- W. Xu, E. I. Cooper and C. A. Angell, J. Phys. Chem. B, 2003, 107, 6170–6178 CrossRef CAS.
- M. Yoshizawa, W. Xu and C. A. Angell, J. Am. Chem. Soc., 2003, 125, 15411–15419 CrossRef CAS PubMed.
- C. A. Angell, N. Byrne and J. P. Belieres, Acc. Chem. Res., 2007, 40, 1228–1236 CrossRef CAS PubMed.
- H. Ohno and M. Yoshizawa, Solid State Ionics, 2002, 154, 303–309 CrossRef.
- S. K. Shukla, N. D. Khupse and A. Kumar, Phys. Chem. Chem. Phys., 2012, 14, 2754–2761 RSC.
- G. Rai and A. Kumar, J. Phys. Chem. B, 2014, 118, 4160–4168 CrossRef CAS PubMed.
- S. Mahiuddin and K. Ismail, J. Phys. Chem., 1984, 88, 1027–1031 CrossRef CAS.
-
S. Glasstone, An Introduction of Electrochemistry, 1942 Search PubMed.
- L. Coury, Curr. Sep., 1999, 18, 91–96 CAS.
- C. Reichardt, Chem. Rev., 1994, 94, 2319–2358 CrossRef CAS.
- M. J. Kamlet, J. M. Abboud, M. H. Abraham and R. W. Taft, J. Org. Chem., 1983, 48, 2877–2887 CrossRef CAS.
- C. Chippe, C. S. Pomelli and S. Rajamani, J. Phys. Chem. B, 2011, 115, 9653–9661 CrossRef PubMed.
- N. D. Khupse and A. Kumar, J. Phys. Chem. B, 2010, 114, 376–381 CrossRef CAS PubMed.
- N. D. Khupse and A. Kumar, J. Phys. Chem. B, 2011, 115, 711–718 CrossRef CAS PubMed.
- A. C. Perej and P. M. Mancini, J. Phys. Org. Chem., 2009, 22, 197–202 CrossRef.
-
R. A. Robinson and R. H. Stokes, Electrolytic solution, Butterworths, London, 1965 Search PubMed.
- M. Anouti, J. Jacquemin and P. Porion, J. Phys. Chem. B, 2012, 116, 4228–4238 CrossRef CAS PubMed.
- J. Stoimenovski, E. I. Izgorodina and D. R. MacFarlane, Phys. Chem. Chem. Phys., 2010, 12, 10341–10347 RSC.
- K. M. Johansson, E. I. Izgorodina, M. Forsyth, D. R. MacFarlane and K. R. Seddon, Phys. Chem. Chem. Phys., 2008, 10, 2972–2978 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: Plots of Λmvs. concentration for [HmIm][CH3OO] and [HmIm][CH3CH2OO] in water, methanol, ethanol, dimethyl sulfoxide, acetonitrile and nitrobenzene. See DOI: 10.1039/c4cp04591b |
|
| This journal is © the Owner Societies 2015 |
Click here to see how this site uses Cookies. View our privacy policy here. ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 was stirred for 6 h at room temperature. Water was removed by using a rotavapour at 80 °C under reduced pressure. These PILs were further dried under vacuum at 70 °C for 10 h. The water content of PILs is analyzed by Karl-Fischer titration and is observed to be 50 ppm. The characterization and determination of purities were performed by 1H NMR spectroscopy in agreement with the reported values.37
1 was stirred for 6 h at room temperature. Water was removed by using a rotavapour at 80 °C under reduced pressure. These PILs were further dried under vacuum at 70 °C for 10 h. The water content of PILs is analyzed by Karl-Fischer titration and is observed to be 50 ppm. The characterization and determination of purities were performed by 1H NMR spectroscopy in agreement with the reported values.37




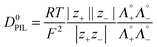
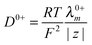
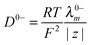
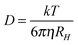
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Λmvs. log
Λmvs. log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) η−1 is a suitable method for measuring the ionicity of electrolytic solutions. The Walden rule of relation between conductivity and viscosity is given by eqn (7)
η−1 is a suitable method for measuring the ionicity of electrolytic solutions. The Walden rule of relation between conductivity and viscosity is given by eqn (7)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Λmvs. log
Λmvs. log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) η−1 predicts a straight line that passes through the origin for ideal solution. The solution of 0.01 M KCl gives a helpful reference line on the Walden plot as shown in Fig. 6.34 Interestingly, a linear relationship exists between the molar conductivities for each of the PILs and the reciprocality of the viscosity (1/η) of water as a function of temperature. This suggests that the fluidity of the medium played a predominant role in the ionic association of the PILs.
η−1 predicts a straight line that passes through the origin for ideal solution. The solution of 0.01 M KCl gives a helpful reference line on the Walden plot as shown in Fig. 6.34 Interestingly, a linear relationship exists between the molar conductivities for each of the PILs and the reciprocality of the viscosity (1/η) of water as a function of temperature. This suggests that the fluidity of the medium played a predominant role in the ionic association of the PILs.

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 of acid and base. Further, our experiments were performed in very dilute ionic liquid solutions. It is, however, not clear to state whether the formation of super anions is possible in our system unlike those prepared considering the composition of acid in excess compared to base.51
1 of acid and base. Further, our experiments were performed in very dilute ionic liquid solutions. It is, however, not clear to state whether the formation of super anions is possible in our system unlike those prepared considering the composition of acid in excess compared to base.51
