Structures of [Li(glyme)]+ complexes and their interactions with anions in equimolar mixtures of glymes and Li[TFSA]: analysis by molecular dynamics simulations†
Seiji
Tsuzuki
*a,
Wataru
Shinoda
b,
Masaru
Matsugami
c,
Yasuhiro
Umebayashi
d,
Kazuhide
Ueno
e,
Toshihiko
Mandai
e,
Shiro
Seki
f,
Kaoru
Dokko
e and
Masayoshi
Watanabe
e
aResearch Initiative of Computational Sciences (RICS), Nanosystem Research Institute, National Institute of Advanced Industrial Science and Technology (AIST), 1-1-1 Umezono, Tsukuba, Ibaraki 305-8568, Japan. E-mail: s.tsuzuki@aist.go.jp
bDepartment of Applied Chemistry, Nagoya University, Furo-cho, Chikusa-ku, Nagoya, 464-8603, Japan
cKumamoto National College of Technology, 2659-2, Suya, Koshi, Kumamoto 861-1102, Japan
dGraduate School of Science and Technology Niigata University 8050, Ikarashi, 2-no-cho, Nishi-ku, Niigata City, 950-2181, Japan
eYokohama National University, 79-5 Tokiwadai, Hodogaya-ku, Yokohama 240-8501, Japan
fCentral Research Institute of Electric Power Industry (CRIEPI), 2-11-1 Iwado-kita, Komae, Tokyo 201-8511, Japan
First published on 11th November 2014
Abstract
Molecular dynamics simulations of equimolar mixtures of glymes (triglyme and tetraglyme) and Li[TFSA] (lithium bis(trifluoromethylsulfonyl)amide) show that the glyme chain length affects the coordination geometries of Li+, which induces the changes in interactions between the [Li(glyme)]+ complex and [TFSA]− anions and diffusion of ions in the equimolar mixtures.
Room temperature ionic liquids (RTILs) have attracted much attention because of their unique physicochemical properties.1 RTILs are expected to be applicable to electrolytes for electric double-layer capacitors, fuel cells, dye-sensitized solar cells and lithium-ion batteries.2 The equimolar mixtures of glymes (oligoethers) and certain Li salts are liquids at room temperature. They have low volatility, high ionic conductivities and high electrochemical stability, which are similar to conventional RTILs.3 The equimolar mixtures are proposed as a new family of RTILs (solvate ionic liquids).4 They have been studied extensively as new electrolyte candidates for lithium–sulfur (Li–S) batteries owing to the low solubility of reaction intermediates (lithium polysulfides, Li2Sm).5
Triglyme and tetraglyme (Fig. 1, G3 and G4) form stable [Li(glyme)]+ complexes in the equimolar mixtures with Li[TFSA].3g The solvate ILs are composed of the [Li(glyme)]+ cations and [TFSA]− anions. The elucidation of the liquid structures of the equimolar mixtures is crucial for understanding the properties of the solvate ionic liquids and for their applications as electrolytes. The structures and stability of the [Li(glyme)]+ complexes and their interactions with anions in the equimolar mixtures play important roles in controlling transport properties of ions and the solubility of Li2Sm, which are important factors in determining the performance of Li–S batteries.5 Unfortunately, however, the liquid structures of solvate ionic liquids have been hardly studied in contrast to extensively studied conventional ionic liquids (aprotic and protic ionic liquids). The stable structures of [Li(G3)]+ and [Li(G4)]+ complexes and their interactions with [TFSA]− anions in the gas phase were studied by ab initio molecular orbital calculations,6 while the coordination structures of [Li(glyme)]+ complexes in the equimolar mixtures are still unclear. We have carried out molecular dynamics simulations of the equimolar mixtures of glymes (G3 and G4) and Li[TFSA] ([Li(glyme)][TFSA]) to reveal the coordination structures of [Li(glyme)]+ complexes in the mixtures. We have discussed the effects of the glyme chain length on the coordination structures of the [Li(glyme)]+ complexes, their interactions with [TFSA]− anions and diffusion of ions in the mixtures.
The MPDyn program7 was used for the molecular dynamics simulations. Molecular dynamics simulations of the mixtures of 125 glymes and 125 Li[TFSA] were carried out in the NPT ensemble. All the C–H bonds were held rigid using the SHAKE algorithm.8 Reversible RESPA was used for multiple time step integration of equations of motion of atoms.9 The time step size for updating interactions in the Ewald reciprocal space was 8 fs, and that for other interactions was 2 fs. Periodic boundary conditions were employed. The nonbonded forces were truncated at 12 Å, while the Coulomb interactions were computed using the Ewald method.10 Constant-temperature and -pressure conditions (0.1 MPa) were maintained by using the Nosé–Hoover chain thermostat11 and the Andersen barostat.12 The time constants for the thermostat and the barostat are 0.5 and 2.0 ps, respectively. The force field parameters for Li+ and the [TFSA]− anion were taken from the literature.13 The parameters for glymes were taken from the literature with some modifications based on ab initio calculations.13d The force field parameters are summarized in Table S1 in the ESI.† Atom types are shown in Fig. S1 and S2 (ESI†). The mixture of Li–glyme complexes and TFSA anions was used for initial geometries of molecular dynamics simulations. The system was equilibrated from low-density conditions. The densities and radial distribution functions of the ionic liquids were evaluated from 12 ns MD trajectories after a 10 ns MD equilibration run at 303 K. The radial distribution functions do not change during the 12 ns production run. After a 4 ns equilibration run, a 30 ns production run was conducted at 403 K to calculate the mean square displacements (MSDs) of the ions. The self-diffusion coefficients were determined by calculating the slopes of the MSDs of the ions versus time in the range between 3 and 4 ns.
The densities of [Li(G3)][TFSA] and [Li(G4)][TFSA] obtained by the molecular dynamics simulation at 303 K are summarized in Table 1. The calculated densities well reproduce the experimental values.3c The errors of the calculated densities are less than 1%.
| d | D sol | D cation | D anion | E bind | |
|---|---|---|---|---|---|
| a Densities (303 K) in g cm−3. b Self-diffusion coefficients in 10−7 cm2 s−1. Calculated values at 403 K and experimental values at 303 K. c Stabilization energies by the formation of [Li(glyme)][TFSA] complexes from [Li(glyme)]+ and [TFSA]−. Ref. 6. d Ref. 3i. | |||||
| Calc. | |||||
| [Li(G3)][TFSA] | 1.43 | 0.43 | 0.43 | 0.24 | −82.8 |
| [Li(G4)][TFSA] | 1.41 | 0.78 | 0.78 | 0.73 | −70.0 |
| Exp.d | |||||
| [Li(G3)][TFSA] | 1.42 | 0.77 | 0.77 | 0.54 | |
| [Li(G4)][TFSA] | 1.40 | 1.26 | 1.26 | 1.22 | |
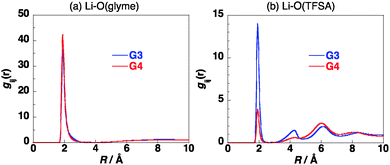
The site–site intermolecular radial distribution functions in [Li(G3)][TFSA] at 303 K were calculated as shown in Fig. 2. The distribution functions between Li+ and oxygen atoms of G3 and that between Li+ and oxygen atoms of [TFSA]− have sharp peaks at about 2 Å, indicating the contact between Li+ and these oxygen atoms in the mixture. The former peak is more than twice as high as that of the latter, which shows that Li+ prefers to have contact with oxygen atoms of G3 in [Li(G3)][TFSA]. The radial distribution functions were calculated by changing temperature from 303 K to 403 K. The effects of temperature on the calculated radial distribution functions are not large as shown in Fig. S3 in the ESI.† The slight broadening of the peaks was observed with the increase of the temperature.
The site–site intermolecular radial distribution functions in [Li(G4)][TFSA] at 303 K were calculated as shown in Fig. 2. The distribution function between Li+ and oxygen atoms of G4 has a sharp peak at about 2 Å, while that between the Li+ and oxygen atoms of [TFSA]− has a low peak at about 2 Å. The height of this peak is about one eighth of that of the former peak, which shows that most of the oxygen atoms which have contact with Li+ in [Li(G4)][TFSA] are the oxygen atoms of G4. The glyme chain length affects the coordination geometry of Li+ significantly. Although the effects of temperature on the calculated radial distribution functions are small, the peak of the radial distribution function between Li+ and oxygen atoms of G4 decreases and that between Li+ and oxygen atoms of [TFSA]− increases slightly with the increase of the temperature as shown in Fig. S4 in the ESI.†
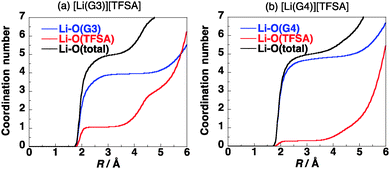
The coordination numbers of Li+ in [Li(G3)][TFSA] and [Li(G4)][TFSA] are shown in Fig. 3. All four oxygen atoms of G3 and one oxygen atom of the [TFSA]− anion have contact with Li+ in [Li(G3)][TFSA]. On the other hand the coordination number of oxygen atoms of G4 is about 4.5 and that of oxygen atoms of [TFSA]− is 0.5 in [Li(G4)][TFSA]. The coordination numbers suggest that two coordination geometries of Li+ exist in [Li(G4)][TFSA]. One is the geometry, where four oxygen atoms of G4 and an oxygen atom of the [TFSA]− anion have contact with Li+. Another is the geometry where all five oxygen atoms of G4 and no oxygen atoms of the [TFSA]− anion have contact with Li+.
The coordination geometry of Li+ in the equimolar mixture ([Li(G3)][TFSA]) is different from the stable geometry of the [Li(G3)][TFSA] complex in the gas phase obtained by ab initio calculations. Ab initio calculations show that the coordination number of Li+ is six in the most stable structure of the [Li(G3)][TFSA] complex (Fig. 4, 1a).6 The four oxygen atoms of G3 and two oxygen atoms of the [TFSA]− anion have contact with Li+ in 1a. The most stable structure, in which an oxygen atom of the [TFSA]− anion has contact with Li+, (Fig. 4, 1b) is 3.5 kcal mol−1 less stable. The stabilization energies by the formation of the complex from isolated ions and glyme (Eform) calculated for 1a and 1b at the MP2/6-311G**//HF/6-311G** level are −178.4 and −174.9 kcal mol−1, respectively.6 Li+ prefers the hexadentate structure in the gas phase, while it prefers the pentadentate structure in the equimolar mixture.
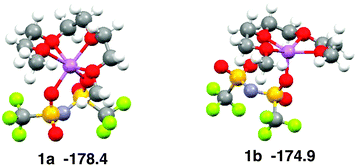 | ||
| Fig. 4 Stable geometries of the [Li(G3)][TFSA] complex and their stabilization energies by formation of complex obtained by ab initio calculations. | ||
Ab initio calculations show that the coordination number of Li+ is five in the most stable structure of the [Li(G4)][TFSA] complex (Fig. 5, 2a).6 The four oxygen atoms of G4 and one oxygen atom of the [TFSA]− anion have contact with Li+ in 2a. The most stable structure, in which no oxygen atom of the [TFSA]− anion has contact with Li+, (Fig. 5, 2b) is 4.0 kcal mol−1 less stable. The five oxygen atoms have contact with Li+ in 2b. The Eform values calculated for 2a and 2b are −177.7 and −173.7 kcal mol−1, respectively.6Fig. 3b shows that both structures exist in the equimolar mixture, although 2b is substantially less stable than 2a in the gas phase.
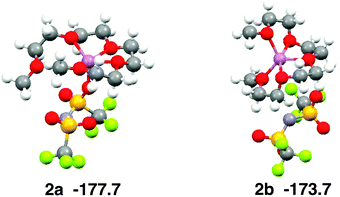 | ||
| Fig. 5 Stable geometries of the [Li(G4)][TFSA] complex and their stabilization energies by formation of complex obtained by ab initio calculations. | ||
The coordination numbers of Li+ in [Li(G3)][TFSA] (Fig. 3a) show that a negatively charged oxygen atom of the [TFSA]− anion has contact with the positively charged Li+. This shows that the [TFSA]− anion interacts with the [Li(G3)]+ cation strongly. On the other hand the coordination number of oxygen atoms of [TFSA]− is 0.5 in [Li(G4)][TFSA]. The interaction of the [TFSA]− anion with the [Li(G4)]+ cation is weaker than that with the [Li(G3)]+ cation. The stabilization energy by the formation of the [Li(glyme)][TFSA] complex from [Li(glyme)]+ and [TFSA]− obtained by ab initio calculations (Ebind) is summarized in Table 1. The calculated Ebind values also show that the interaction of the [TFSA]− anion with the [Li(G3)]+ cation is stronger than that with the [Li(G4)]+ cation. The Ebind values calculated for [Li(G3)][TFSA] and [Li(G4)][TFSA] are −82.8 and −70.0 kcal mol−1, respectively.6 The difference in the coordination geometries affects the magnitude of the interactions.
The self-diffusion coefficients of the ions and glymes in [Li(G3)][TFSA] and [Li(G4)][TFSA] were calculated from the mean square deviations (MSDs) of the ions and glymes, as shown in Table 1. The MSDs of ions and glymes in [Li(G3)][TFSA] and [Li(G4)][TFSA] are shown in Fig. S5 (ESI†). The ratio of self-diffusion coefficients calculated for glymes and Li+ (Dsol/Dcation) in [Li(G3)][TFSA] and [Li(G4)][TFSA] are close to 1.0 as in the cases of experimental self-diffusion coefficients.3c The nearly identical self-diffusion coefficients of Li+ and glymes indicate the formation of the stable [Li(glyme)]+ complexes in the mixtures. The self-diffusion coefficients calculated for Li+ and G3 in [Li(G3)][TFSA] are considerably larger than that for [TFSA]− (Danion), while the self-diffusion coefficients calculated for Li+ and G4 in [Li(G4)][TFSA] are close to that for [TFSA]−. The self-diffusion coefficients calculated for ions and the glyme in [Li(G4)][TFSA] are substantially larger than those in [Li(G3)][TFSA]. The self-diffusion coefficients calculated for the ions and glymes in the [Li(G3)][TFSA] and [Li(G4)][TFSA] accurately describe the experimental trend of the self-diffusion coefficients,3c although the calculated self-diffusion coefficients were smaller than the experimental values as in the cases of other ionic liquids.14
The magnitude of the interactions between cations and anions is one of the important factors controlling the diffusion of ions in ionic liquids.15 The diffusion of ions becomes slow as the interaction between cations and anions becomes strong. The weaker interaction between the [Li(G4)]+ cations and the [TFSA]− anions compared with that between the [Li(G3)]+ cations and the [TFSA]− anions is apparently the cause of the faster diffusion of ions in [Li(G4)][TFSA] compared with that in [Li(G3)][TFSA].
Acknowledgements
This work was supported by the ALCA program of the Japan Science and Technology Agency (JST).Notes and references
- (a) H. L. Chum, V. R. Koch, L. L. Miller and R. A. Oesteryoung, J. Am. Chem. Soc., 1975, 97, 3264 CrossRef CAS; (b) T. Welton, Chem. Rev., 1999, 99, 2071 CrossRef CAS PubMed; (c) P. Wasserscheid and W. Keim, Angew. Chem., Int. Ed., 2000, 39, 3772 CrossRef CAS; (d) D. M. Ryan, T. L. Reichel and T. Welton, J. Electrochem. Soc., 2002, 149, A371 CrossRef CAS PubMed; (e) K. Xu, Chem. Rev., 2004, 104, 4303 CrossRef CAS.
- (a) T. Sato, G. Masuda and K. Takagi, Electrochim. Acta, 2004, 49, 3603 CrossRef CAS PubMed; (b) W. Kubo, S. Kambe, S. Nakade, T. Kitamura, K. Hanabusa, Y. Wada and S. Yanagida, J. Phys. Chem. B, 2003, 107, 4374 CrossRef CAS; (c) P. Wang, S. Zakeeruddin, J.-E. Moser and M. Grätzel, J. Phys. Chem. B, 2003, 107, 13280 CrossRef CAS; (d) B. Garcia, S. Lavalle, G. Perron, C. Michot and M. Armand, Electrochim. Acta, 2004, 49, 4583 CrossRef CAS PubMed; (e) H. Matsumoto, H. Sakaebe and K. Tatsumi, J. Power Sources, 2005, 146, 45 CrossRef CAS PubMed; (f) V. Borgei, E. Markevich, D. Aurbach, G. Semrau and M. Schmidt, J. Power Sources, 2009, 189, 331 CrossRef PubMed.
- (a) T. M. Pappenfus, W. A. Henderson, B. B. Owens, K. R. Mann and W. H. Smyrl, J. Electrochem. Soc., 2004, 151, A209 CrossRef CAS PubMed; (b) T. Tamura, T. Hachida, K. Yoshida, N. Tachikawa, K. Dokko and M. Watanabe, J. Power Sources, 2010, 195, 6095 CrossRef CAS PubMed; (c) T. Tamura, K. Yoshida, T. Hachida, M. Tsuchiya, M. Nakamura, Y. Kazue, N. Tachikawa, K. Dokko and M. Watanabe, Chem. Lett., 2010, 39, 753 CrossRef CAS; (d) K. Yoshida, M. Nakamura, Y. Kazue, N. Tachikawa, S. Tsuzuki, S. Seki, K. Dokko and M. Watanabe, J. Am. Chem. Soc., 2011, 133, 13121 CrossRef CAS PubMed; (e) S. Seki, K. Takei, H. Miyashiro and M. Watanabe, J. Electrochem. Soc., 2011, 158, A769 CrossRef CAS PubMed; (f) N. Tachikawa, K. Yamauchi, E. Takashima, J.-W. Park, K. Dokko and M. Watanabe, Chem. Commun., 2011, 8157 RSC; (g) K. Yoshida, M. Tsuchiya, N. Tachikawa, K. Dokko and M. Watanabe, J. Phys. Chem. C, 2011, 115, 18384 CrossRef CAS; (h) K. Ueno, K. Yoshida, M. Tsuchiya, N. Tachikawa, K. Dokko and M. Watanabe, J. Phys. Chem. C, 2012, 116, 11323 CrossRef CAS PubMed; (i) C. Zhang, K. Ueno, A. Yamazaki, K. Yoshida, T. Mandai, Y. Umebayashi, K. Dokko and M. Watanabe, J. Phys. Chem. B, 2014, 118, 5144 CrossRef CAS PubMed.
- (a) C. A. Angell, Y. Ansari and Z. Zhao, Faraday Discuss., 2012, 154, 9 RSC; (b) T. Mandai, K. Yoshida, K. Ueno, K. Dokko and M. Watanabe, Phys. Chem. Chem. Phys., 2014, 16, 8761 RSC.
- (a) X. Ji, K. T. Lee and L. F. Nazar, Nat. Mater., 2009, 8, 500–506 CrossRef CAS PubMed; (b) S. Evers and L. F. Nazar, Acc. Chem. Res., 2012, 46, 1135 CrossRef PubMed; (c) P. G. Bruce, S. A. Freunberger, L. J. Hardwick and J.-M. Tarascon, Nat. Mater., 2012, 11, 19 CrossRef CAS PubMed; (d) K. Dokko, N. Tachcikawa, K. Yamauchi, M. Tsuchiya, A. Yamazaki, E. Takashima, J. W. Park, K. Ueno, S. Seki, N. Serizawa and M. Watanabe, J. Electrochem. Soc., 2013, 160, A1304 CrossRef CAS PubMed; (e) J.-W. Park, K. Yamauchi, E. Takashima, N. Tachikawa, K. Ueno, K. Dokko and M. Watanabe, J. Phys. Chem. C, 2013, 117, 4431 CrossRef CAS; (f) K. Ueno, J. W. Park, A. Yamazaki, T. Mandai, N. Tachikawa, K. Dokko and M. Watanabe, J. Phys. Chem. C, 2013, 117, 20509 CrossRef CAS; (g) J.-W. Park, K. Ueno, N. Tachikawa, K. Dokko and M. Watanabe, J. Phys. Chem. C, 2013, 117, 20531 CrossRef CAS.
- S. Tsuzuki, W. Shinoda, S. Seki, Y. Umebayashi, K. Yoshida, K. Dokko and M. Watanabe, ChemPhysChem, 2013, 14, 1993 CrossRef CAS PubMed.
- (a) W. Shinoda and M. Mikami, J. Comput. Chem., 2003, 24, 920 CrossRef CAS PubMed; (b) http://simulo.apchem.nagoya-u.ac.jp/personal/wshinoda/index.html .
- J. P. Ryckaert, G. Ciccotti and H. J. C. Berendsen, J. Comput. Phys., 1997, 23, 327 CrossRef.
- (a) M. Tuckerman and B. J. Berne, J. Chem. Phys., 1992, 97, 1990 CrossRef CAS PubMed; (b) G. J. Martyna, M. E. Tuckerman, D. J. Tobias and M. L. Klein, Mol. Phys., 1996, 87, 1117 CrossRef CAS.
- M. P. Allen and D. J. Tildesley, Computer simulation of liquids, Clarendon Press, Oxford, U.K., 1987 Search PubMed.
- G. J. Martyna, M. L. Klein and M. Tuckerman, J. Chem. Phys., 1992, 97, 2635 CrossRef PubMed.
- H. C. Andersen, J. Chem. Phys., 1980, 72, 2384 CrossRef CAS PubMed.
- (a) J.-C. Soetens, C. Millot and B. Maigret, J. Phys. Chem. A, 1998, 102, 1055 CrossRef CAS; (b) M. Takeuchi, Y. Kameda, Y. Umebayashi, S. Ogawa, T. Sonoda, S. Ishiguro, M. Fujita and M. Sano, J. Mol. Liq., 2009, 148, 99 CrossRef CAS PubMed; (c) S. Tsuzuki, W. Shinoda, H. Saito, M. Mikami, H. Tokuda and M. Watanabe, J. Phys. Chem. B, 2009, 113, 10641 CrossRef CAS PubMed; (d) W. L. Jorgensen, D. S. Maxwell and J. Tirado-Rives, J. Am. Chem. Soc., 1996, 118, 11225 CrossRef CAS.
- It is well recognized that the self-diffusion coefficients of ions in ionic liquids obtained by molecular dynamics simulations using commonly used non-polarizable force field are about one order smaller than the experimental values in general. Ref. 13c and molecular dynamics simulations by other groups show that the calculated self-diffusion coefficients well reproduce the qualitative trend of the ion dependence of the self-diffusion coefficients, although the absolute values of the calculated self-diffusion coefficients are smaller than experimental ones.
- S. Tsuzuki, ChemPhysChem, 2012, 13, 1664 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c4cp04718d |
| This journal is © the Owner Societies 2015 |