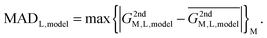Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
How simple is too simple? Computational perspective on importance of second-shell environment for metal-ion selectivity†
Ondrej
Gutten
and
Lubomír
Rulíšek
*
Institute of Organic Chemistry and Biochemistry, Gilead Sciences Research Center & IOCB, Academy of Sciences of the Czech Republic, Flemingovo nám. 2, 166 10 Praha 6, Czech Republic. E-mail: rulisek@uochb.cas.cz; Fax: +420-220-183-578; Tel: +420-220-183-263
First published on 17th February 2015
Abstract
The metal-ion selectivity in biomolecules represents one of the most important phenomena in bioinorganic chemistry. The open question to what extent is the selectivity in the complex bioinorganic structures such as metallopeptides determined by the first-shell ligands of the metal ion is answered herein using six model peptides complexed with the set of divalent metal ions (Mn2+, Fe2+, Co2+, Ni2+, Cu2+, Zn2+, Cd2+, and Hg2+) and their various first-shell representations. By calculating the differences among the free energies of complexation of metal ions in these peptides and their model (truncated) systems it is quantitatively shown that the definition of the first shell is paramount to this discussion and revolves around the chemical nature of the binding site. Despite the vast conceivable diversity of peptidic structures, that suggest certain fluidity of this definition, major contributing factors are identified and assessed based on their importance for capturing metal-ion selectivity. These factors include soft/hard character of ligands and various non-covalent interactions in the vicinity of the binding site. The relative importance of these factors is considered and specific suggestions for effective construction of the models are made. The relationship of first-shell models and their corresponding parent peptides is discussed thoroughly, both with respect to their chemical similarity and potential disparity introduced by generally “non-alignable” conformational flexibility of the two systems. It is concluded that, in special cases, this disparity can be negligible and that heeding the chemical factors contributing to selectivity during construction of the model can successfully result in models that retain the affinity profile for various metal ions with high fidelity.
1. Introduction
Computational modeling represents an indispensable tool in discovering fundamental physico-chemical principles underlying chemical and biochemical processes.1 One of the important biological phenomena is an uptake and binding of metal ions in biomolecules.2 Since various metal ions play various roles in biological machinery, Nature has to fine-tune the selectivity of metal-binding sites present in proteins and RNA/DNA for the specific metal ion.3 Therefore, deciphering the mechanisms and factors behind the metal ion selectivity4–6 is a highly desirable task which may ultimately lead to answering the fundamental question ‘Why Nature selected specific metal ions for performing specific tasks?’7Most of the experimental and computational findings in the area of metal-ion selectivity have been very recently reviewed by Dudev and Lim.6 As highlighted in their review, there are two ‘external’ factors (i.e., independent of the constitution of particular metal-binding site) one always needs to take into account in any considerations of the metal-ion selectivity: (i) average concentrations of metal ions in intracellular and extracellular fluids,8 and (ii) the inherent ‘binding properties’ of metal ions. Concerning the former, it can be reminded that the concentrations of unbound metal ions in cytosol range from millimolar (Na+, K+, Mg2+) through micro- (Mn2+, Fe2+, Ca2+) nano- (Co2+, Ni2+) to femto- (Zn2+) and attomolar (Cu+/Cu2+).9 The latter external factor is mostly exemplified by the Irving–Williams series10 which qualitatively ranks the stabilities of complexes formed by divalent metal ions. This series has its physico-chemical origin in the second ionization enthalpies of the metals11 and predicts the following order:12
| Mg2+ < Mn2+ < Fe2+ < Co2+ < Ni2+ < Cu2+ > Zn2+. |
Thus, copper(II) in general forms the most stable complexes with a ‘generic’ set of ligands, followed by Zn2+/Ni2+ whereas complexes of Mg2+ are expected to have the lowest stability constants (β). In tuning the metal-ion selectivity, one has to consider the Irving–Williams series as a ‘baseline’ with respect to which the modifications in the computed or measured metal-ion stabilities are evaluated.
Last, but not least authors of the title review6 clearly summarize most of the areas where metal-ion selectivity is of key importance, notably in function of sodium/potassium/calcium ion channels13–15 and in structure–function of almost all metalloproteins (both regulatory and enzymatic).16–18
Over the last two decades, many studies were reported that addressed the problem of metal-ion selectivity from a computational and quantum chemical perspective.19–28 These most often involved quantum chemical calculations of the small model complexes, both in vacuo and polarized dielectric continuum (to address the effects of the environment, such as solution or protein). Quite often, the results were qualitatively correlated with the experimentally determined stability constants21 or phenomenological information obtained from the abundance of metal ions in the sites of metalloproteins.29–31 In a recent study,32 an attempt was made to conceive a robust and accurate computational protocol that would yield stability constants (β) of selected metal ions (Mn2+, Fe2+, Co2+, Ni2+, Cu2+, Zn2+, Cd2+, and Hg2+) in small model complexes. The protocol was benchmarked on the series of complexes with the known experimental values of β. It was concluded that current computational approaches are likely to suffer from both metal-dependent and ligand-dependent systematic shifts and the straightforward ‘ab initio’ predictions of the ‘absolute’ values of these thermodynamic properties are likely still beyond their grasp. At the same time, it was demonstrated that a relatively easy procedure can be followed that partially accounts for these systematic shifts and the metal-ion selectivity for a particular model site can be in many cases predicted to 1–2 kcal mol−1 accuracy.32
Thus, under an optimistic assumption that computational issues pertinent to the binding of metal ions in small complexes (e.g. metal-binding sites represented by the first-shell ligands) were at least partially solved, a question emanates to what extent are the second-shell effects (which may also include water mediated binding of certain ions to metal binding sites or ion channels) important for the metal-ion selectivity of the site. Some of these issues were addressed in computational studies of ion channels33,34 where second-shell residues are expected to have stabilizing effect on certain type of coordination geometries which, in turn, favor the binding of specific metal ion (and not of its counterpart). In an analogous way, the computations together with statistical survey in Protein Data Bank were used to correlate structure and composition of the outer coordination sphere of metal sites in metalloproteins with those of the inner sphere.35–37 Despite these achievements, the comprehensive study that may yield the robust computational protocol to treat these effects rigorously and quantitatively, is lacking.
This immediately leads to the central question addressed in this work: “How much of the metal-ion selectivity is captured by the first-shell ligand residues of a particular site in metalloprotein?” In answering such a question, one needs to quantitatively assess the stability constants of metal ions in peptidic scaffolds from the first principles. To accomplish such a computational task involves exploring the limits of contemporary quantum chemistry and computational modeling, notably accurate calculations of solvation energies of charged systems.
While the ultimate (and perhaps still distant) goal of this and related studies is the quantitative prediction of stability constants of metal ions in the peptide structures with an accuracy of 1–2 pK (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β) units, we expect that several important questions can (and will) be raised and answered on the way towards its accomplishment. As mentioned above, these include (i) the suitability of the first-shell-only representation (that is of the model complex [M(Yi)n]c+ where Yi are truncated metal binding amino acids) of the whole metal-binding peptide in calculations of complexation energies and stability constants with special attention paid to their relative values (which, in turn, determine the metal-ion selectivity) and (ii) justifiability of various constraints during the geometry optimization to preserve the original coordination environment in the whole [metal + peptide] complex. The positive answer to the first question would not only provide us with an exciting opportunity to quickly scan various metal sites (both catalytic and functional) for their inherent metal-binding properties and shed further insight into the role of metal ions in biomolecules, but also open new avenues in bottom-up approach for design of novel specific metal-binding sites.
β) units, we expect that several important questions can (and will) be raised and answered on the way towards its accomplishment. As mentioned above, these include (i) the suitability of the first-shell-only representation (that is of the model complex [M(Yi)n]c+ where Yi are truncated metal binding amino acids) of the whole metal-binding peptide in calculations of complexation energies and stability constants with special attention paid to their relative values (which, in turn, determine the metal-ion selectivity) and (ii) justifiability of various constraints during the geometry optimization to preserve the original coordination environment in the whole [metal + peptide] complex. The positive answer to the first question would not only provide us with an exciting opportunity to quickly scan various metal sites (both catalytic and functional) for their inherent metal-binding properties and shed further insight into the role of metal ions in biomolecules, but also open new avenues in bottom-up approach for design of novel specific metal-binding sites.
Six model systems studied in this work, schematically depicted in Fig. 1, and described in more details in Section 2.2., are considered. They were carefully selected to represent the considerable part of the ‘spectrum’ of the experimentally observed binding modes. Two of them represent in silico designed metal-binders that were tested experimentally both in gas-phase and solution.39 Unfortunately, no experimental structural information exists on the nature of the binding of metal ions by these peptides. The other four systems represent the continuous metal-binding amino acid sequences in the cores of selected metalloproteins for which the crystal structure was available (cf., Section 2.2.).
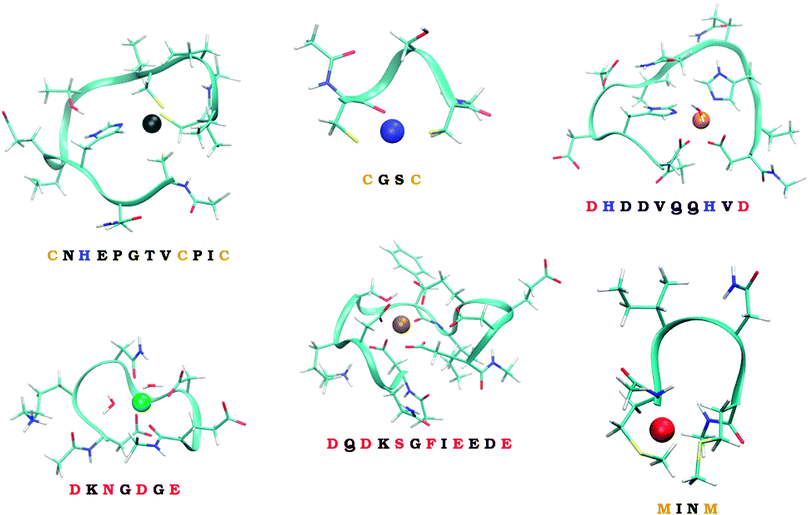 | ||
| Fig. 1 The six studied peptides. The peptides are abbreviated by the amino-acid residues participating in binding of a metal ion. The larger peptides (CHCC, DHHD, DNDO, DDSOEE) are based on structures found in MESPEUS database.38 The smaller two peptides (CC, MM) come from previous research in our laboratory.39 Vid Section 2.2. for details. | ||
The series of metal ions with the potential of metal-binding by the peptides includes Mn2+, Fe2+, Co2+, Ni2+, Cu2+, Zn2+, Cd2+, and Hg2+ ions as they represent the most common divalent ions and coincides with the selection in our previous work.32
2. Computational details and methodological issues
2.1. Quantum chemical methods
All calculations reported in this work were performed using the TURBOMOLE 6.5 program. The quantum chemical calculations were performed using the density functional theory (DFT). The geometry optimizations were carried out at the DFT level, employing the density-fitted (vide infra) BP86 functional (RI-BP86)40,41 in combination with def-TZVP basis set.42,43 In case of peptide systems (vide infra) only the SV basis set44 was used for atoms other than the metal ion (for which def-TZVP was used) in geometry optimizations whereas the single point calculations of peptide systems were also carried out using the def-TZVP basis set on all atoms. The effect of solvent (water) environment was modeled by COSMO method (the atomic radii of 2.0 Å for Mn, Fe, Co, Ni and Zn, 2.2 Å for Cd, 2.4 Å for Hg and the defaults for the rest, and the dielectric constant parameter ε = 80.0). The single-point energies were calculated using the same protocol, with dielectric constant of ε = ∞ (ideal conductor) or ε = 1 (vacuum). All calculations were expedited by expanding the Coulomb integrals in an auxiliary basis set, using the resolution-of-identity (RI) approximation (density fitting).45 Grimme's D3 dispersion has been applied.46All metal-ions (Mn, Fe, Co, Ni, Cu, Zn, Cd, Hg) were considered in their +2 oxidation state. For open-shell metal ions in the series (Mn–Cu), high-spin states were considered, in line with our previous work.26,32 These are assumed to be ground electronic states for all of the studied complexes containing mostly low-field ligands. Stuttgart/Dresden pseudopotentials for Cd and Hg ions were applied.47 We consider it as a plausible approximation to relativistic effects, since non-scalar relativistic effects (such as spin–orbit coupling) are estimated to play negligible role for the reaction energetics. The use of ECPs is also in line with our previous benchmark studies.26,32
Free energies of interaction with solvent of all studied species were calculated using the COSMO-RS method48,49 (conductor-like screening model for realistic solvation) as implemented in the COSMOtherm program,50 using the “BP_TZVP_C30_1201.ctd” parametrization file.
2.2. Studied systems
To quantify how much of the selectivity is lost upon reducing a system to its model we have chosen a number of peptides, ranging in size and coordination shell of the metal ion. Out of the total of 6 peptides, four were inspired by PDB structures, while the remaining two were obtained from previous theoretical studies.The selected PDB structures were required to possess a binding site for a metal ion with all of the binding partners within a relatively short sequence of amino acids. The structures were identified using the information contained in the MESPEUS database.38 The whole metalloprotein (PDB) structure was reduced (truncated) to the minimalistic metal-binding continuous sequence and metal-bound water molecules; terminated with acetyl group at the N-terminus and N-methyl at the C-terminus. Namely, the four peptide sequences considered were CNHEPGTVCPIC (PDB code: 1G71; referred to as CHCC according to the metal-binding residues), DQDKSGFIEEDE (PDB code: 2PAL, referred to as DDSOEE, O standing for backbone carbonyl), DKNGDGE (PDB code: 1IGV; includes 2 water molecules; referred to as DNDO), DHDDVQQHVD (PDB code: 1B9M; includes 1 water molecule; referred to as DHHD).
The remaining two peptides were CGSC (referred to as CC) and MINM (referred to as MM). The binding modes of these two peptides are merely putative. Nevertheless, these two peptides were previously synthesized and binding of ions in the gas phase experimentally determined by mass spectrometry.39 Unfortunately, neither the structural information, nor the solution thermodynamics was obtained for these two systems.
Metal-binding cysteine side chains of CHCC and CC peptides (which were the only Cys residues on both peptides), as well as all aspartate and glutamate side-chains of CHCC, DHHD, DNDO and DDSOEE peptides, were considered in deprotonated form. The studied systems are depicted in Fig. 1. Each system was optimized with each of the eight metal ions, resulting in 6 (peptides) × 8 (metal ions) = 48 structures.
2.3. First-shell models of peptides
A total of four different first-shell models were constructed. In all cases, the truncated fragment was terminated with hydrogen atom(s). The simplest model, referred to as TINY, consists of ligands represented by the smallest possible functional fragment, ranging from (HS−) as a model for deprotonated cysteine side-chain, to imidazole as a model for histidine side-chain. The second model, referred to as SMALL, differs from the TINY by an addition of a methyl residue (along the truncated side chain). The models denoted as ALPHA were then truncated at the Cα atoms of the amino acid (i.e. side chains were capped by the –CαH3 group). Finally, the FULL_AA model contains the full amino acid residue with both of the peptide bonds included (capped by H atoms on both N- and C-‘terminus’). The models are presented in Scheme 1.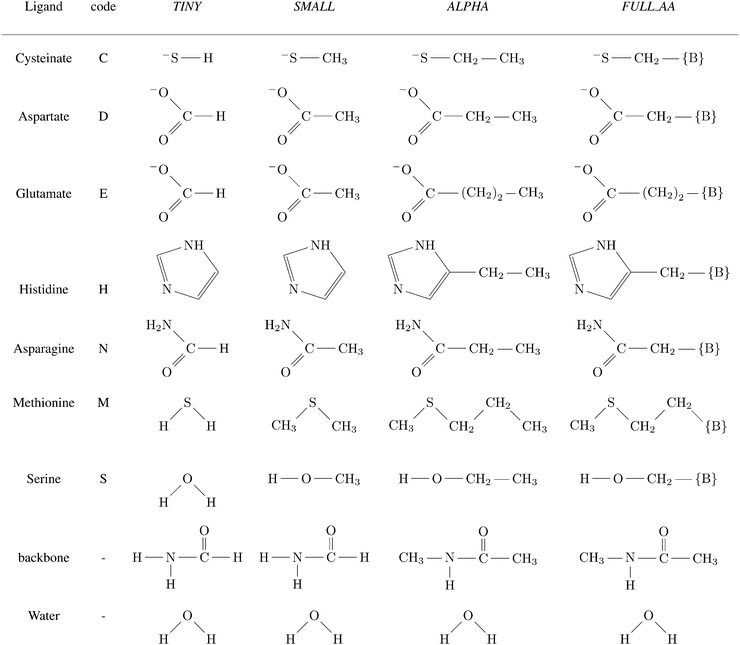 | ||
Scheme 1 Ligands and their representation in individual models. {B} signifies attachment to the peptide backbone, i.e.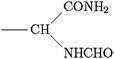 . . | ||
In general, only the substituted hydrogens were optimized in these first-shell models, whereas the remaining atoms were kept frozen in the Cartesian coordinates of their parent system.
The models, by definition, lack the interaction with distant groups and their conformational freedom is unrelated to that of the parent system (see Section 2.4.2). These features are essential for the models to serve their primary purpose – a comprehensive tool for isolating and studying metal-specific interactions of the binding site and the metal ion, and identifying their features and behavior in various settings. The models can be utilized in other ways too, although one has to keep in mind the limitations these features imply.
Firstly, the models can be used in the ‘top-down’ approach, where they can serve as small and cheap models for the selectivity of a specific conformation of the parent system. If more than a single conformation of the binding site is relevant, a single calculation of the parent system for each conformation can be complemented with the model systems for each of the metal ions. This is cheaper than full scale calculation for each metal ion in each conformation.
Alternatively, in the ‘bottom-up’ approach, the models can be used as templates for constructing (e.g. peptidic) scaffolds that can support the binding geometry. Since the model is constructed in a way that it contains almost all selective interactions, the resulting system (e.g. polypeptide chain with the metal-binding site) may retain the selectivity properties identical to those of the model. Rigid scaffolds can also eliminate the need for conformational sampling.
2.4. Studied physico-chemical quantities and the computational setup
| GM,L = Eel + GIS | (1) |
The definition deliberately ignores zero-point vibrational energy and thermal corrections to vibrational, translational and rotational partition function. As discussed thoroughly in previous work,32 these two terms present a non-trivial technical challenge – stemming from finding minima for large (and ideally also solvated) systems, and differences between solvent and gas-phase structures. As these are not expected to be heavily metal-dependent, we preferred to use eqn (1) as the practical (albeit not theoretically pure) approach and plausible approximation to the free energy of the complex. In our previous work, this simple approach somewhat surprisingly yielded better relative stability constants (differences in experimental measure of binding/complexation Gibbs free energies) for a diverse set of model complexes (8 metal ions + 6 sets of ligands) when compared to experimental data.32
In discussing metal-ion selectivity, it is usually advantageous to consider relative values of quantities, rather than their absolute values. These can be brought into spotlight by shifting the quantity equally for all metal ions – an operation that does not change the differences among the values of a quantity. Where applicable, we use quantities shifted in this fashion and indicate the fact by “REL” superscript:
XRELM,L = XM,L − max![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N{XN,L} N{XN,L} | (2) |
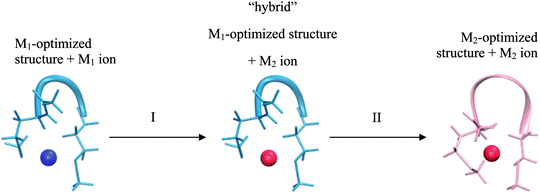
This realization is in no conflict with the intended purpose of the study – quite the contrary, it allows isolating factors which can influence selectivity but are not part of the model. Consider two cases of a peptide binding a different metal-ion in each case. These two systems differ not only in a metal ion bound, but also in geometry of the peptide/ligands. Comparing such two systems can be viewed as a 2-step transition process: (I) changing a metal ion and (II) relaxing a structure (Fig. 2).
The most important difference between a peptide and its model is the presence of the 2nd shell (i.e. the part of a peptide not included in the model) in the former system. Thus, the overall difference in selectivity of a peptide and its model will be determined by the interaction of the 2nd shell with a metal ion (and the 1st shell) during both of the substeps – giving rise to two contributions: a metal-induced selectivity (step I in Fig. 2) and a structure-induced selectivity (step II in Fig. 2). It is instructive to examine these two contributions separately.
Metal-induced selectivity. The interaction of an ion with 2nd shell can be significant. However, minimizing 2nd-shell metal-induced selectivity (step I in Fig. 2) requires merely absence of metal-specific interactions with the 2nd shell, which can be achieved by proper design of a model. This contribution can be studied by examining unrelaxed systems with an exchanged metal-ion (“hybrid” in Fig. 2) and is the main focus of Section 3.2. The intermediate “hybrid” system is not a minimum on a potential energy surface, since the system with an exchanged metal ion is deliberately not optimized. This setting is pivotal for eliminating the structural effects, which allows for in-depth analysis of selectivity relationships. Quantities pertaining to such systems are indicated with “hybrid” superscript.
Structure-induced selectivity. Magnitude of the 2nd-shell structure-induced selectivity (step II in Fig. 2) is more dependent on the actual peptide rather than on the nature of the model, and is strictly zero only for perfectly rigid peptides. Thus, rather than asking what is the impact of different free energies of relaxation on selectivity in case of (arbitrary) conformations of the studied systems, we seek to gain insight into what is the bottom limit of this influence. The issue is discussed in Section 3.3.
Hybrid systems. Each of the 48 structures (see Section 2.2.) was used for construction and calculation of “hybrid” systems. This resulted in 48 × 8 (each ion is substituted by each of the 7 remaining ones) × 5 (representations, i.e. original peptide, TINY, SMALL, ALPHA, and FULL_AA models) = 1920 systems for the discussion of metal-induced selectivity (see Section 3.2.).
3. Results and discussion
3.1. Identifying relevant and descriptive physico-chemical quantities
The Gibbs free energy of a system defined in eqn (1) is the primary thermodynamic quantity obtained from the calculations, however, it is not a convenient one to discuss retention of selectivity properties of the model systems.Rather than using e.g. hexahydrated metal ion as reference and examining the parent system and the model separately i.e. (GM,L,peptide − GM,(H2O)6)REL and (GM,L,model − GM,(H2O)6)REL, it is beneficial to consider the difference of these two, i.e.
| G2ndM,L,model = (GM,L,peptide − GM,L,model)REL | (3) |
Using the parent system as a reference state, this quantity directly describes the interaction of a metal ion with the 2nd shell. In an ideal case, the model would capture all of the selectivity of a peptide, resulting in this quantity being invariantly zero for all metal ions (M) and systems (L).
In reality, this will not be the case, and the variation of this quantity, examined as average absolute deviation and maximum absolute deviation (eqn (4)), will determine the faithfulness of a model. As will turn out later it might be advantageous that the average is taken over all metal ions (M) but not over different systems (L), as the nature of the systems and even specific structural details will prove to be relevant for the discussion.
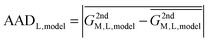 | (4) |
Using quantities defined in eqn (3) and (4) and shown in Table 1, it can now be immediately seen that the model works relatively well for CC, MM and CHCC systems (incidentally, these have the largest range of (GM,L − GM,(H2O)6)REL, i.e. the most selective, cf.Table 1). On the other hand, the average absolute deviation is ∼3 kcal mol−1 (maximum absolute deviation >6 kcal mol−1) for DNDO and DDSOEE systems, which is even more significant in light of their low selectivity (range of (GM,L − GM,(H2O)6)REL ∼ 15 kcal mol−1).
| System | M2+ | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Quantity | Mn2+ | Fe2+ | Co2+ | Ni2+ | Cu2+ | Zn2+ | Cd2+ | Hg2+ |
![[A with combining low line]](https://www.rsc.org/images/entities/b_char_0041_0332.gif) ![[A with combining low line]](https://www.rsc.org/images/entities/b_char_0041_0332.gif) ![[D with combining low line]](https://www.rsc.org/images/entities/b_char_0044_0332.gif) ![[L with combining low line]](https://www.rsc.org/images/entities/b_char_004c_0332.gif) ![[, with combining low line]](https://www.rsc.org/images/entities/b_char_002c_0332.gif) ![[A with combining low line]](https://www.rsc.org/images/entities/b_char_0041_0332.gif) ![[L with combining low line]](https://www.rsc.org/images/entities/b_char_004c_0332.gif) ![[P with combining low line]](https://www.rsc.org/images/entities/b_char_0050_0332.gif) ![[H with combining low line]](https://www.rsc.org/images/entities/b_char_0048_0332.gif) ![[A with combining low line]](https://www.rsc.org/images/entities/b_char_0041_0332.gif) (MADL,ALPHA)b (MADL,ALPHA)b |
|
| a All values are in kcal mol−1. Metal-dependent shifts, ΔGcorr, pertaining to the protocol and reference states used and shown to lead to the best computational estimates to the experimental β in our previous work (ref. 32) were applied. ΔGcorr = 0.2, −0.9, 1.9, −1.1, 2.5, −1.6, 0.4, −1.4 kcal mol−1 for Mn2+, Fe2+, Co2+, Ni2+, Cu2+, Zn2+, Cd2+, and Hg2+, respectively. b Lower values of AADL,ALPHA and MADL,ALPHA indicate high retention of metal-ion selectivity in the model. See eqn (4) for definition. c These large values can be traced to a different position of a 2nd-shell charged group, resulting in significantly different interaction with a metal-ion. | ||||||||||
| CC | (GM,L,peptide − GM,(H2O)6)REL | 0.0 | −4.7 | −4.7 | −5.2 | −25.7 | −11.2 | −20.6 | −57.8 | |
| (GM,L,APLHA − GM,(H2O)6)REL | 0.0 | −5.7 | −4.1 | −3.9 | −23.9 | −11.0 | −18.7 | −54.6 | ||
| G2ndM,L,APLHA | −0.9 | 0.0 | −1.5 | −2.2 | −2.7 | −1.1 | −2.8 | −4.2 |
![[1 with combining low line]](https://www.rsc.org/images/entities/b_char_0031_0332.gif) ![[. with combining low line]](https://www.rsc.org/images/entities/b_char_002e_0332.gif) ![[0 with combining low line]](https://www.rsc.org/images/entities/b_char_0030_0332.gif) (2.2)
(2.2)
|
|
| MM | (GM,L,peptide − GM,(H2O)6)REL | 0.0 | −2.5 | −6.5 | −8.6 | N/A | −10.1 | −21.5 | −59.8 | |
| (GM,L,ALPHA − GM,(H2O)6)REL | 0.0 | −3.3 | −7.5 | −9.6 | −10.8 | −21.4 | −57.8 | |||
| G2ndM,L,APLHA | −1.0 | −0.1 | 0.0 | 0.0 | −1.0 | −0.2 | −1.1 | −2.9 |
![[0 with combining low line]](https://www.rsc.org/images/entities/b_char_0030_0332.gif) ![[. with combining low line]](https://www.rsc.org/images/entities/b_char_002e_0332.gif) ![[7 with combining low line]](https://www.rsc.org/images/entities/b_char_0037_0332.gif) (2.2)
(2.2)
|
|
| DHHD | (GM,L,peptide − GM,(H2O)6)REL | −8.2 | −7.3 | −9.8 | 0.0 | −6.1 | −10.7 | −7.1 | −18.8 | |
| (GM,L,ALPHA − GM,(H2O)6)REL | −11.0 | −11.8 | −14.3 | 0.0 | −10.6 | −14.2 | −6.2 | −18.3 | ||
| G2ndM,L,APLHA | −1.8 | 0.0 | −0.1 | −4.6 | −0.1 | −1.0 | −5.4 | −5.0 |
![[2 with combining low line]](https://www.rsc.org/images/entities/b_char_0032_0332.gif) ![[. with combining low line]](https://www.rsc.org/images/entities/b_char_002e_0332.gif) ![[1 with combining low line]](https://www.rsc.org/images/entities/b_char_0031_0332.gif) (3.2)
(3.2)
|
|
| DNDO | (GM,L,peptide − GM,(H2O)6)REL | −9.1 | −6.1 | −7.1 | −5.7 | 0.0 | −6.9 | −9.6 | −15.1 | |
| (GM,L,ALPHA − GM,(H2O)6)REL | −5.9 | 0.0 | −9.3 | −6.6 | −6.7 | −8.6 | −13.0 | −20.5 | ||
| G2ndM,L,APLHA | −10.0 | −12.8 | −4.5 | −5.9 | 0.0 | −5.1 | −3.4 | −1.4 |
![[3 with combining low line]](https://www.rsc.org/images/entities/b_char_0033_0332.gif) ![[. with combining low line]](https://www.rsc.org/images/entities/b_char_002e_0332.gif) ![[1 with combining low line]](https://www.rsc.org/images/entities/b_char_0031_0332.gif) (7.4)
(7.4)
|
|
| CHCC | (GM,L,peptide − GM,(H2O)6)REL | 0.0 | −10.1 | −12.8 | −7.2 | −22.5 | −9.1 | −11.0 | −40.7 | |
| (GM,L,ALPHA − GM,(H2O)6)REL | 0.0 | −8.7 | −11.2 | −5.0 | −20.4 | −8.9 | −14.2 | −40.5 | ||
| G2ndM,L,APLHA | −3.2 | −4.6 | −4.8 | −5.5 | −5.3 | −3.4 | 0.0 | −3.5 |
![[1 with combining low line]](https://www.rsc.org/images/entities/b_char_0031_0332.gif) ![[. with combining low line]](https://www.rsc.org/images/entities/b_char_002e_0332.gif) ![[3 with combining low line]](https://www.rsc.org/images/entities/b_char_0033_0332.gif) (3.8)
(3.8)
|
|
| DDSOEE | (GM,L,peptide − GM,(H2O)6)REL | −15.3 | −12.4 | 0.0 | −0.7 | −1.8 | −2.9 | −6.1 | −16.6 | |
| (GM,L,ALPHA − GM,(H2O)6)REL | −11.8 | −9.7 | −2.6 | 0.0 | −1.2 | −5.2 | −13.4 | −21.9 | ||
| G2ndM,L,APLHA | −10.9 | −10.1 | −4.8 | −8.1 | −8.0 | −5.1 | 0.0 | −2.0 |
![[3 with combining low line]](https://www.rsc.org/images/entities/b_char_0033_0332.gif) ![[. with combining low line]](https://www.rsc.org/images/entities/b_char_002e_0332.gif) ![[2 with combining low line]](https://www.rsc.org/images/entities/b_char_0032_0332.gif) (6.1)
(6.1)
|
|
G 2ndM,L describes the information about the metal selectivity retained by a model much more clearly than the original quantity, (GM,L − GM,(H2O)6)REL. The set of eight values (one for each metal ion) can be comprehensively reduced to AADL,model and MADL,model, quantities that will be the cornerstone of the ensuing discussion.
3.2. Selectivity factors studied on “hybrid” systems
The results obtained in the previous section are not sufficient to fully comprehend the role of 1st-shell ligands, as the data compare systems with different metal ions and different structures (i.e. include both steps I and II from Fig. 2). The structural changes are not unimportant, but it is impossible to undertake full conformational sampling at the given methodological level. Therefore, we choose to separate the structural contribution to selectivity, which we can study only to limited extent, from the chemical effect of exchanging a metal ion, which we can study in detail in “hybrid” systems (see Section 2.4.2). The following subsections (3.2.1, 3.2.2 and 3.2.3) study the influence of various factors on “hybrid” systems.The values of G2nd,REL,hybridM,L are collected in Tables S1–S24 (ESI†). These values exhibit a strong trend present in virtually all structures and systems, decreasing gradually across the row to reach a minimum (the most negative value; implying the strongest interaction with the 2nd shell) at Ni2+ or Cu2+, while the maximum (the weakest influence) is usually exhibited by Cd2+ systems. Thus, the models skew the relative free energy between e.g. Cu2+ and Cd2+ in favor of the latter. While this trend follows, at least in partial, the Irving–Williams series, its physico-chemical origin remains unknown to us. Bearing this trend in mind, we choose to present only the AADhybridL,model (and MADhybridL,model).
These values for one of the structures (selected as a representative example), of all six peptide systems and for all four representations are presented in Table 2. Despite the diversity of the systems, most of the AADhybridL,model values are below 1 kcal mol−1 even for the SMALL model, which translate into MADhybridL,model values below ∼2 kcal mol−1 (videTable 2). Examining relationship between these values and the nature of the systems provides insight into the importance of the 2nd shell for selectivity and basis for constructing a robust and well-balanced model.
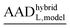 and (MADhybridL,model), for Cd2+-optimized structures, chosen as a representative examplea
and (MADhybridL,model), for Cd2+-optimized structures, chosen as a representative examplea
| Model | System | |||||
|---|---|---|---|---|---|---|
| CC | MM | DHHD | DNDO | CHCC | DDSOEE | |
| a All values in kcal mol−1. | ||||||
| TINY |
![[2 with combining low line]](https://www.rsc.org/images/entities/b_char_0032_0332.gif) ![[. with combining low line]](https://www.rsc.org/images/entities/b_char_002e_0332.gif) ![[2 with combining low line]](https://www.rsc.org/images/entities/b_char_0032_0332.gif) (4.4) (4.4) |
![[1 with combining low line]](https://www.rsc.org/images/entities/b_char_0031_0332.gif) ![[. with combining low line]](https://www.rsc.org/images/entities/b_char_002e_0332.gif) ![[8 with combining low line]](https://www.rsc.org/images/entities/b_char_0038_0332.gif) (2.6) (2.6) |
![[3 with combining low line]](https://www.rsc.org/images/entities/b_char_0033_0332.gif) ![[. with combining low line]](https://www.rsc.org/images/entities/b_char_002e_0332.gif) ![[8 with combining low line]](https://www.rsc.org/images/entities/b_char_0038_0332.gif) (5.6) (5.6) |
![[2 with combining low line]](https://www.rsc.org/images/entities/b_char_0032_0332.gif) ![[. with combining low line]](https://www.rsc.org/images/entities/b_char_002e_0332.gif) ![[5 with combining low line]](https://www.rsc.org/images/entities/b_char_0035_0332.gif) (5.0) (5.0) |
![[0 with combining low line]](https://www.rsc.org/images/entities/b_char_0030_0332.gif) ![[. with combining low line]](https://www.rsc.org/images/entities/b_char_002e_0332.gif) ![[6 with combining low line]](https://www.rsc.org/images/entities/b_char_0036_0332.gif) (1.9) (1.9) |
![[0 with combining low line]](https://www.rsc.org/images/entities/b_char_0030_0332.gif) ![[. with combining low line]](https://www.rsc.org/images/entities/b_char_002e_0332.gif) ![[8 with combining low line]](https://www.rsc.org/images/entities/b_char_0038_0332.gif) (1.1) (1.1) |
| SMALL |
![[0 with combining low line]](https://www.rsc.org/images/entities/b_char_0030_0332.gif) ![[. with combining low line]](https://www.rsc.org/images/entities/b_char_002e_0332.gif) ![[9 with combining low line]](https://www.rsc.org/images/entities/b_char_0039_0332.gif) (1.3) (1.3) |
![[0 with combining low line]](https://www.rsc.org/images/entities/b_char_0030_0332.gif) ![[. with combining low line]](https://www.rsc.org/images/entities/b_char_002e_0332.gif) ![[8 with combining low line]](https://www.rsc.org/images/entities/b_char_0038_0332.gif) (1.7) (1.7) |
![[1 with combining low line]](https://www.rsc.org/images/entities/b_char_0031_0332.gif) ![[. with combining low line]](https://www.rsc.org/images/entities/b_char_002e_0332.gif) ![[5 with combining low line]](https://www.rsc.org/images/entities/b_char_0035_0332.gif) (4.1) (4.1) |
![[0 with combining low line]](https://www.rsc.org/images/entities/b_char_0030_0332.gif) ![[. with combining low line]](https://www.rsc.org/images/entities/b_char_002e_0332.gif) ![[4 with combining low line]](https://www.rsc.org/images/entities/b_char_0034_0332.gif) (1.0) (1.0) |
![[0 with combining low line]](https://www.rsc.org/images/entities/b_char_0030_0332.gif) ![[. with combining low line]](https://www.rsc.org/images/entities/b_char_002e_0332.gif) ![[3 with combining low line]](https://www.rsc.org/images/entities/b_char_0033_0332.gif) (0.7) (0.7) |
![[0 with combining low line]](https://www.rsc.org/images/entities/b_char_0030_0332.gif) ![[. with combining low line]](https://www.rsc.org/images/entities/b_char_002e_0332.gif) ![[5 with combining low line]](https://www.rsc.org/images/entities/b_char_0035_0332.gif) (0.7) (0.7) |
| ALPHA |
![[0 with combining low line]](https://www.rsc.org/images/entities/b_char_0030_0332.gif) ![[. with combining low line]](https://www.rsc.org/images/entities/b_char_002e_0332.gif) ![[4 with combining low line]](https://www.rsc.org/images/entities/b_char_0034_0332.gif) (0.6) (0.6) |
![[0 with combining low line]](https://www.rsc.org/images/entities/b_char_0030_0332.gif) ![[. with combining low line]](https://www.rsc.org/images/entities/b_char_002e_0332.gif) ![[5 with combining low line]](https://www.rsc.org/images/entities/b_char_0035_0332.gif) (1.1) (1.1) |
![[0 with combining low line]](https://www.rsc.org/images/entities/b_char_0030_0332.gif) ![[. with combining low line]](https://www.rsc.org/images/entities/b_char_002e_0332.gif) ![[4 with combining low line]](https://www.rsc.org/images/entities/b_char_0034_0332.gif) (1.0) (1.0) |
![[0 with combining low line]](https://www.rsc.org/images/entities/b_char_0030_0332.gif) ![[. with combining low line]](https://www.rsc.org/images/entities/b_char_002e_0332.gif) ![[1 with combining low line]](https://www.rsc.org/images/entities/b_char_0031_0332.gif) (0.2) (0.2) |
![[0 with combining low line]](https://www.rsc.org/images/entities/b_char_0030_0332.gif) ![[. with combining low line]](https://www.rsc.org/images/entities/b_char_002e_0332.gif) ![[3 with combining low line]](https://www.rsc.org/images/entities/b_char_0033_0332.gif) (0.9) (0.9) |
![[0 with combining low line]](https://www.rsc.org/images/entities/b_char_0030_0332.gif) ![[. with combining low line]](https://www.rsc.org/images/entities/b_char_002e_0332.gif) ![[4 with combining low line]](https://www.rsc.org/images/entities/b_char_0034_0332.gif) (1.4) (1.4) |
| FULL_AA |
![[0 with combining low line]](https://www.rsc.org/images/entities/b_char_0030_0332.gif) ![[. with combining low line]](https://www.rsc.org/images/entities/b_char_002e_0332.gif) ![[2 with combining low line]](https://www.rsc.org/images/entities/b_char_0032_0332.gif) (0.3) (0.3) |
![[0 with combining low line]](https://www.rsc.org/images/entities/b_char_0030_0332.gif) ![[. with combining low line]](https://www.rsc.org/images/entities/b_char_002e_0332.gif) ![[1 with combining low line]](https://www.rsc.org/images/entities/b_char_0031_0332.gif) (0.3) (0.3) |
![[0 with combining low line]](https://www.rsc.org/images/entities/b_char_0030_0332.gif) ![[. with combining low line]](https://www.rsc.org/images/entities/b_char_002e_0332.gif) ![[1 with combining low line]](https://www.rsc.org/images/entities/b_char_0031_0332.gif) (0.2) (0.2) |
![[0 with combining low line]](https://www.rsc.org/images/entities/b_char_0030_0332.gif) ![[. with combining low line]](https://www.rsc.org/images/entities/b_char_002e_0332.gif) ![[1 with combining low line]](https://www.rsc.org/images/entities/b_char_0031_0332.gif) (0.2) (0.2) |
![[0 with combining low line]](https://www.rsc.org/images/entities/b_char_0030_0332.gif) ![[. with combining low line]](https://www.rsc.org/images/entities/b_char_002e_0332.gif) ![[1 with combining low line]](https://www.rsc.org/images/entities/b_char_0031_0332.gif) (0.3) (0.3) |
![[0 with combining low line]](https://www.rsc.org/images/entities/b_char_0030_0332.gif) ![[. with combining low line]](https://www.rsc.org/images/entities/b_char_002e_0332.gif) ![[2 with combining low line]](https://www.rsc.org/images/entities/b_char_0032_0332.gif) (0.3) (0.3) |
In general, the AADhybridL,model values decrease as the size of the model increases (Tables S1–S24, ESI†):
| AADhybridL,FULL_AA < AADhybridL,ALPHA < AADhybridL,SMALL < AADhybridL,TINY |
There are a few remarkable exceptions to this progression, but the magnitude of this discrepancy is diminutive (<few tenths of kcal mol−1) and they are not highlighted in further discussions.
The influence is most visibly exhibited by the TINY model. While systems with predominantly soft residues (CC, MM, CHCC) have AADhybridL,model values of ∼2 kcal mol−1, those of harder ligands are 1 kcal mol−1 or less.
The hardness characteristic can be thought of as the distance at which the ligand can be polarized by its environment. Thus, while all systems converge to the original peptide as we increase the size of the model, the soft ligands will be more sensitive to this change than the hard ligands. Moving from TINY to SMALL model, the AADhybridL,model values drop below 1 kcal mol−1 in all cases, but the decrease continues upon moving further to ALPHA model only for soft ligands; while being almost nonexistent for hard ligands. In general, a similar level of selectivity is achieved by larger model (ALPHA) for sulfur based ligands, while smaller model (SMALL or even TINY) is sufficient for harder ligands.
It should be noted that only hydrogen bonds to atoms directly ligating the central metal ion are considered, as these are the ones that can be expected to chemically (and possibly selectively) influence the binding of a metal ion. Other hydrogen bonds and interactions are unlikely to depend on the identity of the metal ion and can influence the binding only indirectly through structural change (not addressed in the “hybrid” systems studied here).
The following analysis is performed for each relevant peptide (bearing at least some hydrogen bonds to binding atoms) on one of the structures, selected as a representative example. It comes at no surprise (Table S25, ESI†) that there are almost none hydrogen bonds in the smaller representations of the full peptide (up to FULL_AA model). Thus, the effect of a hydrogen bond, if any, is present in the full peptide and FULL_AA model but usually not in the smaller models – which can contribute to different selectivity of a peptide and its model. The “ester” systems, on the other hand, do not possess these hydrogen bonds in either a model or its parent, which results in models being a more faithful representation of its parent system. The FULL_AA model (of a peptide system) usually contains these hydrogen bonds, thus we expect little differences in values of AADhybridL,FULL_AA based on peptides and those based on their “ester” analogue.
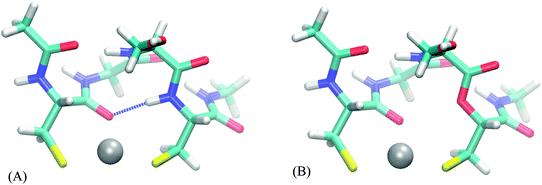
The AADhybridL,model values (Table 3) are almost identical in all but few cases, the differences ranging from −0.2 to 0.5 kcal mol−1. The smallest differences are observed in the DHHD, DNDO and DDSOEE systems all of which include hydrogen bonds to hard ligands (carboxyl groups/water molecule/serine alcohol group). On the other hand, AADhybridL,model differ by 0.2–0.5 kcal mol−1 in case of CC and CHCC systems, where the hydrogen bond acceptor is amide bond carbonyl and cysteine thiolate groups, respectively. This amount constitutes 20–70% of the total AADhybridL,model. Moreover, in CHCC system the hydrogen bonds are far from the ideal orientation and in case of strong hydrogen bond, the influence can be expected to be much higher. We thus conclude that the effect of hydrogen bond is potentially significant for strong hydrogen bonds to softer ligands.
| Model | System | |||||
|---|---|---|---|---|---|---|
| CC | DHHD | DNDO | CHCC | DDSOEE | ||
| a All values in kcal mol−1. | ||||||
| TINY | Peptide | 2.3 | 0.4 | 0.7 | 2.1 | 0.8 |
| Ester | 1.9 | 0.3 | 0.6 | 1.9 | 1.0 | |
| SMALL | Peptide | 1.0 | 0.3 | 0.6 | 0.9 | 0.6 |
| Ester | 0.4 | 0.3 | 0.6 | 0.7 | 0.6 | |
| ALPHA | Peptide | 0.7 | 0.3 | 0.4 | 0.9 | 0.6 |
| Ester | 0.2 | 0.4 | 0.4 | 0.7 | 0.4 | |
| FULL_AA | Peptide | 0.2 | 0.3 | 0.3 | 0.3 | 0.1 |
| Ester | 0.2 | 0.2 | 0.2 | 0.4 | 0.2 | |
A ligand can also act as a hydrogen bond donor, as exemplified by terminal glutamate of DNDO peptide, which can interact with one of the metal-bound water molecules. The validity of attributing the differences in selectivity to the single carboxyl moiety is confirmed by comparing AADhybridL,model values of original systems to a “mutated” peptide (glutamate → norvaline), presented in Table 4. However, a water molecule is the smallest of the studied ligands, which allows for relative proximity of the charged moiety to a metal ion, which is probably the cause of the observed differences, rather than the existence of the hydrogen bond.
| Structure | Glutamate leaning ina | Glutamate leaning outb | ||
|---|---|---|---|---|
| a Fe2+-optimized structure, see ESI for coordinates. b Co2+-optimized structure, see ESI for coordinates. c Distance between a metal-ion and proximal oxygen of the terminal glutamate side-chain carboxyl group in Ångströms. d Values in kcal mol−1. | ||||
| C-terminal residue | Glutamate | Norvaline | Glutamate | Norvaline |
| d(M–OOC)c | 4.22 | — | 5.29 | — |
| AADhybridL,modeld | ||||
|---|---|---|---|---|
| TINY | 1.2 | 0.9 | 0.6 | 0.7 |
| SMALL | 1.1 | 0.8 | 0.6 | 0.5 |
| ALPHA | 0.9 | 0.6 | 0.4 | 0.4 |
| FULL_AA | 0.5 | 0.2 | 0.2 | 0.2 |
As in the previous section, we strive to compare systems that differ significantly in this respect (i.e. in the screening of metal-ion), while being as similar as possible in other respects. The most straightforward procedure is to change the number of water molecules in the systems, as these constitute ligands that are not covalently bound to the rest of the system and, thus, no other changes are necessary. Representative structures of peptides CC and DNDO that demonstrate the range of this influence vividly were chosen for discussion. In case of CC peptide, 2 water molecules were added. In case of DNDO, 2 water molecules were removed. In both cases the structures were subsequently optimized, however, in the latter case both the non-optimized and optimized structures were used for selectivity analysis, i.e. for construction and calculation of “hybrid” systems. The results are presented in Table 5.
| AADhybridL,modeld | ||||||||
|---|---|---|---|---|---|---|---|---|
| TINY | 1.7 | 1.5 | 0.6 | 0.9 | 1.1 | 0.8 | 1.3 | 3.1 |
| SMALL | 0.8 | 0.8 | 0.6 | 0.7 | 0.9 | 0.6 | 1.1 | 2.3 |
| ALPHA | 0.6 | 0.9 | 0.4 | 0.5 | 0.4 | 0.7 | 0.4 | 1.5 |
| FULL_AA | 0.2 | 0.1 | 0.2 | 0.4 | 0.3 | 0.3 | 0.4 | 0.9 |
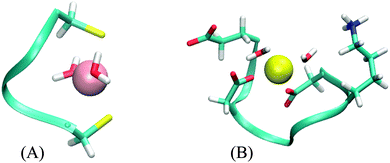
The CC system mode of binding is a distorted plane with the ligands forming a triangle. The two water molecules are added in a line approximately perpendicular to this plane, resulting in a square pyramidal formation (Fig. 4A). There is no part of the peptide being screened by these water molecules. Correspondingly, the values of AADhybridL,model for the two systems are almost identical (see Table 5).
The DNDO system, on the other hand, has an octahedral binding mode with 2 water molecules in cis-positions that “eclipse” two charged groups – a glutamate (already discussed in Section 3.2.2) and a lysine side-chain (Fig. 4B). The removal of the water molecules exposes these charged moieties – which are not part of any of the models – to the metal ion. In all studied cases, this leads to a significant increase in 2nd-shell selectivity. The situation is largely remedied upon optimizing the structures, which distort to almost tetrahedral geometry. The screening is nevertheless deteriorated, compared to the original octahedral structure, and the values of AADhybridL,model are thus higher.
Results for two DNDO structures are shown in Table 5. The original “2-water” systems and even optimized “0-water” systems show similar 2nd-shell selectivity, but there are immense differences in the selectivity of the “0-water” non-optimized structures. The fact that both of these structures were equally submitted to the selectivity analysis (as performed in the previous cases) shows that the difference must pertain to the structure of the peptide. This is alarming, as the two structures are virtually identical. An extensive investigation suggests that the difference is not due to coordination geometry, ligand–metal distances, nor solvent cavity construction. Despite all our efforts, we have not been able to pinpoint the source of this discrepancy. Although the cause of this phenomenon can be artificial, its disappearance in optimized structure does manifest the importance of a properly screened binding site; the absence of which will severely hamper the accuracy regardless of the model used.
A different point of view on the addition/removal of water molecules is to think of it as an exchange of an explicit water molecule for an implicit one or vice versa (it can be reminded that despite advanced treatment of solvation in the COSMO-RS method, the method still belongs to a class of polarized continuum models, PCM). While in the case of the CC system, where the water molecules do not screen a part of the peptide, this seems to leave the selectivity undisturbed, the values of GM,L should still be compared only among systems of identical 1st shell composition.
3.3. Structure-induced selectivity
As discussed in Section 2.4.2, the overall metal-ion selectivity is determined by combined effect of metal-induced and structure-induced selectivity. The overall selectivity has been studied by analyzing fully optimized structures (Table 1). The metal-induced selectivity (thoroughly discussed in Section 3.2.) has been analyzed by examining interactions of a specific structure with a series of metal ions (“hybrid” systems, Fig. 2). We now return to the question of what is the lower limit of structure relaxation on selectivity (step II in Fig. 2).Table 6 compares the selectivity of one of the hybrid systems, a representative example of metal-induced selectivity, with the fully relaxed structures, representative of the overall selectivity.
| Model | System | ||||||
|---|---|---|---|---|---|---|---|
| CC | MM | DHHD | DNDO | CHCC | DDSOEE | ||
| TINY | Hybrid | 2.2 | 3.8 | 0.6 | 0.8 | 2.1 | 1.0 |
| Fully relaxed | 2.3 | 3.7 | 1.1 | 2.7 | 2.6 | 2.6 | |
| SMALL | Hybrid | 0.9 | 1.5 | 0.3 | 0.5 | 0.8 | 0.7 |
| Fully relaxed | 0.9 | 1.0 | 1.8 | 2.9 | 1.4 | 2.8 | |
| ALPHA | Hybrid | 0.4 | 0.4 | 0.3 | 0.4 | 0.7 | 0.7 |
| Fully relaxed | 1.0 | 0.7 | 2.1 | 3.1 | 1.3 | 3.2 | |
| FULL_AA | Hybrid | 0.2 | 0.1 | 0.1 | 0.2 | 0.3 | 0.2 |
| Fully relaxed | 0.4 | 0.3 | 1.7 | 3.2 | 0.7 | 2.1 | |
In some of the studied systems (DHHD, DNDO, DDSOEE), the disparity is destructive for the utility of the models. The most contributing structural changes are flexible charged groups which cause significantly altered interaction with a metal-ion. In the other cases (CC, MM, CHCC), the structure and selectivity of 2nd shell is virtually unchanged, or even lower after full relaxation. This results from interplay of metal-induced and structure-induced selectivity. While these are comprehensible and practical concepts for discussion, they are not independent but tend to partially cancel each other in these scenarios of diminutive changes of 2nd-shell structure.
As no conformational sampling has been performed, this merely shows that there exists a local minimum where the effect of structure-induced selectivity is minimal. A proper sampling is likely to reveal energetically more relevant structures that do not possess this property. However, this does demonstrate that the assumption of low structure-induced selectivity on the overall selectivity is not inherently incorrect, signaling a green light to the start of search for systems with this characteristics.
This section, together with previous discussion, points out that in cases where the 2nd-shell structure is not sensitive to the identity of bound metal ion, the selectivity is to a large extent confined to the 1st shell. The rigidity condition mentioned in Section 2.4.2 has its origins in this discussion.
For these rigid systems, using a single 1st-shell model structure for each metal ion is sufficient for reproducing selectivity of the parent systems with reasonable accuracy. Looking back at Tables 1 and 2, the satisfactory performance of the models in these cases should now be fully comprehensible.
For ‘bottom-up’ design procedures, the structures of 1st-shell models have to be obtained without prior knowledge of the parent structure. This can be aided by constrained optimization reflecting structural support of the 2nd shell and should consider specifics of the system.
The factors relevant for selectivity identified in this study are of ‘chemical’ and structural nature. Their containment into the described models, that we believe has been sufficiently demonstrated herein, renders them largely independent of the nature of the 2nd shell. As long as the structural and conformational aspects are treated properly, the utility of the models can be expanded outside of the peptide context examined here. Thus, systems such as polymeric scaffolds, cluster models, zeolites, etc. can all be expected to be equally well described by these models. From the methodological perspective, both ‘top-down’ and ‘bottom-up’ approaches to studying and designing metal-binding systems can benefit from the models. The protocol and the models could conceivably be used for e.g. predicting differences in redox potentials of bound metal ions. Caution and further testing is advised, however, as the higher oxidation states can significantly affect not only the quality of treatment but also e.g. the required size of the model.
4. Summary
The overall metal-ion selectivity of a system is defined by different ligand(peptide)–metal interactions and by structural response of the system (ligand) to these interactions. A 1st shell model of a system can only retain information about selectivity if this response, i.e. free energy of relaxation upon exchanging a metal ion, is low. Existence of local minima with this property suggests this condition is achievable, yet overall rigidity of a peptide may be inevitable in order to ensure comparable conformational freedom.The metal-induced selectivity of a system is a complex function of multiple factors, that define measure of its localization to a binding site, i.e. the possibility of capturing it using a 1st shell model of the system. It is essential that this model includes all of the ligands bound to a metal-ion. This requirement alone usually ensures that the binding is described reasonably well by the model and that the metal-ion is properly “shielded” from parts of a system further away, bringing the average absolute error to values no higher than few units kcal mol−1. However, some binding geometries can prove to be problematic due to insufficient shielding, e.g. linear or square planar geometry.
Achieving more satisfactory accuracy requires consideration of the nature of ligands. Softer ligands, represented in the realm of metalloproteins by cysteine and methionine residues, require bulkier representation, e.g. the whole side-chain of a residue. Hard ligands, like carboxyl groups, alcohols, amines, can be described at a similar level of accuracy more economically by the functional group plus single methyl group. Imidazole is sufficient to represent histidine side-chain, N-methylmethylamide to represent backbone amide group, and methylamide to represent glutamine and asparagine ligands. This level of description can be expected to result in average absolute deviations below 1 kcal mol−1, which translates to maximum relative error (among studied metal ions) below 3 kcal mol−1. Moreover, most of this relative error derives from bias that appears consistently in the model and can be corrected for heuristically, although this may not be desirable, due to insufficient understanding of this bias.
Non-covalent partners of ligands usually influence retention of selectivity in a negative way. The presence of charged groups can be influential, especially in case of insufficient screening or proximity to metal ion due to small 1st shell ligand, e.g. water molecule. In case of hydrogen bonding the effect is much less significant, influencing average absolute deviation by tenths of kcal mol−1. The strength of the hydrogen bond as well as softness of the acceptor can increase this value.
The overall error in reproducing metal-ion selectivity of a system will stem from inaccuracy of the protocol (∼2 kcal mol−1 in relative free energies32), approximation introduced by the model (<1 kcal mol−1) and assumption of low structure-induced selectivity (the error can be arbitrarily large but, as argued in Section 3.3, conceivably negligible). While some cancellation of errors can be expected, the average errors in the order of units of kcal mol−1 (translating to individual relative errors of roughly up to 5 kcal mol−1) must be expected. As the ranges of free energies of binding are in the order of several tens of kcal mol−1, the protocol holds a promise as a tool for fast estimation of selectivity.
Acknowledgements
The project was supported by the Academy of Sciences of the Czech Republic (RVO 61388963) and Grant Agency of the Czech Republic (14-31419S).References
- A. Warshel, Computer Modeling of Chemical Reactions in Enzymes and Solutions, John Wiley & Sons, Inc., New York, 1997 Search PubMed.
- J. J. R. Fraústo da Silva and R. J. P. Williams, The Biological Chemistry of the Elements, Oxford University Press, Inc., New York, 2nd edn, 2001 Search PubMed.
- Handbook of Metal–Ligand Interactions in Biological Fluids, ed. G. Berthon, Marcel Dekker, New York, 1995, vol. 2 Search PubMed.
- R. K. O. Sigel and H. Sigel, Acc. Chem. Res., 2010, 43, 974–984 CrossRef CAS PubMed.
- T. Dudev and C. Lim, Chem. Rev., 2003, 103, 773–787 CrossRef CAS PubMed.
- T. Dudev and C. Lim, Chem. Rev., 2014, 114, 538–556 CrossRef CAS PubMed.
- R. J. P. Williams, BioMetals, 2007, 20, 107–112 CrossRef CAS PubMed.
- H. F. Lodish, Molecular Cell Biology, Scientific American Books, New York, 1999 Search PubMed.
- The full set of metal ion concentrations with the respective references can be found in Table 2 of ref. 6.
- H. Irving and R. J. P. Williams, Nature, 1948, 162, 746 CrossRef CAS.
- F. A. Cotton and G. Wilkinson, Advanced Inorganic Chemistry, John Wiley & Sons, New York, 1988 Search PubMed.
- R. J. P. Williams, Coord. Chem. Rev., 2001, 216–217, 583 CrossRef CAS.
- B. Hille, Ionic Channels of Excitable Membranes, Sinauer Associates, Sunderland, MA, 3rd edn, 2001 Search PubMed.
- J. Aqvist and V. Luzhkov, Nature, 2000, 404, 881 CrossRef CAS PubMed.
- X. S. Wu, H. D. Edwards and W. A. Sather, J. Biol. Chem., 2000, 275, 31778 CrossRef CAS PubMed.
- R. J. P. Williams, Coord. Chem. Rev., 2001, 216–217, 583 CrossRef CAS.
- K. A. McCall and C. A. Fierke, Biochemistry, 2004, 43, 3979 CrossRef CAS PubMed.
- Y. Li and D. B. Zamble, Chem. Rev., 2009, 109, 4617 CrossRef CAS PubMed.
- L. Rulíšek and Z. Havlas, J. Phys. Chem. A, 1999, 103, 1634–1639 CrossRef.
- L. Rulíšek and Z. Havlas, J. Am. Chem. Soc., 2000, 122, 10428–10439 CrossRef.
- L. Rulíšek and Z. Havlas, J. Phys. Chem. A, 2002, 106, 3855–3866 CrossRef.
- L. Rulíšek and Z. Havlas, Int. J. Quantum Chem., 2003, 91, 504–510 CrossRef.
- L. Rulíšek and Z. Havlas, J. Phys. Chem. B, 2003, 107, 2376–2385 CrossRef.
- T. Dudev and C. Lim, J. Phys. Chem. B, 2001, 105, 10709–10714 CrossRef CAS.
- T. Dudev and C. Lim, Acc. Chem. Res., 2007, 40, 85–93 CrossRef CAS PubMed.
- O. Gutten, I. Beššeová and L. Rulíšek, J. Phys. Chem. A, 2011, 115, 11394–11402 CrossRef CAS PubMed.
- T. Dudev and C. Lim, J. Phys. Chem. B, 2009, 113, 11754 CrossRef CAS PubMed.
- T. Dudev, J. A. Cowan and C. Lim, J. Am. Chem. Soc., 1999, 121, 7665 CrossRef CAS.
- L. Rulíšek and J. Vondrášek, J. Inorg. Biochem., 1998, 71, 115–127 CrossRef.
- J. P. Glusker, Adv. Protein Chem., 1991, 42, 1–76 CrossRef CAS.
- H. Zheng, M. Chruszcz, P. Lasota, L. Lebioda and W. Minor, J. Inorg. Biochem., 2008, 102, 1765–1776 CrossRef CAS PubMed.
- O. Gutten and L. Rulíšek, Inorg. Chem., 2013, 52, 10347–10355 CrossRef CAS PubMed.
- T. Dudev and C. Lim, J. Am. Chem. Soc., 2010, 132, 2321 CrossRef CAS PubMed.
- T. Dudev and C. Lim, Phys. Chem. Chem. Phys., 2012, 14, 12451 RSC.
- T. Dudev, Y. L. Lin, M. Dudev and C. Lim, J. Am. Chem. Soc., 2003, 125, 3168 CrossRef CAS PubMed.
- A. T. Maynard and D. G. Covell, J. Am. Chem. Soc., 2001, 123, 1047 CrossRef CAS PubMed.
- T. Dudev and C. Lim, J. Am. Chem. Soc., 2006, 128, 1553 CrossRef CAS PubMed.
- K. Hsin, Y. Sheng, M. M. Harding, P. Taylor and M. D. Walkinshaw, J. Appl. Crystallogr., 2008, 41, 963–968 CAS.
- M. Kožíšek, A. Svatoš, M. Buděšínský, A. Muck, M. C. Bauer, P. Kotrba, T. Ruml, Z. Havlas, S. Linse and L. Rulíšek, Chem. – Eur. J., 2008, 14, 7836–7846 CrossRef PubMed.
- A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100 CrossRef CAS.
- J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822–8824 CrossRef.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- A. Schäfer, C. Huber and R. Ahlrichs, J. Chem. Phys., 1994, 100, 5829–5835 CrossRef PubMed.
- A. Schäfer, H. Horn and R. Ahlrichs, J. Chem. Phys., 1992, 97, 2571 CrossRef PubMed.
- K. Eichkorn, O. Treutler, H. Öhm, M. Häser and R. Ahlrichs, Chem. Phys. Lett., 1995, 240, 283–290 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- D. Andrae, U. Haeussermann, M. Dolg, H. Stoll and H. Preuss, Theor. Chim. Acta, 1990, 77, 123–141 CrossRef CAS.
- A. Klamt, J. Phys. Chem., 1995, 99, 2224–2235 CrossRef CAS.
- A. Klamt, V. Jonas, T. Buerger and J. C. W. Lohrenz, J. Phys. Chem., 1998, 102, 5074–5085 CrossRef CAS.
- F. Eckert and A. Klamt, COSMOtherm, version C3.0, release 12.01, COSMOlogic GmbH & Co. KG Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: The equilibrium geometries of all the molecules studied and Tables S1–S35. See DOI: 10.1039/c4cp04876h |
| This journal is © the Owner Societies 2015 |