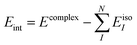Subsystem-DFT potential-energy curves for weakly interacting systems†
Received
28th October 2014
, Accepted 27th November 2014
First published on 23rd December 2014
Abstract
Kohn–Sham density-functional theory (DFT) within the local-density approximation (LDA) or the generalized-gradient approximation (GGA) is known to fail for the correct description of London dispersion interactions. Often, not even bound potential-energy surfaces are obtained for van der Waals complexes, unless special correction schemes are employed. In contrast to that, there has been some evidence for the fact that subsystem-based density functional theory produces interaction energies for weakly bound systems which are superior to Kohn–Sham DFT results without dispersion corrections. This is usually attributed to an error cancellation between the approximate exchange–correlation and non-additive kinetic-energy functionals employed in subsystem DFT. Here, we investigate the accuracy of subsystem DFT for weakly interacting systems in detail, paying special attention to the shape of the potential-energy surfaces (PESs). Our test sets include the extensive S22x5 and S66x8 data sets. Our results indicate that subsystem DFT PESs strongly vary depending on the functional. LDA results are usually quite good, but behave differently from their KS counterparts. GGA results from the popular Perdew–Wang (PW91) set of functionals produce PESs that are often, but not in general overbinding. Results from Becke–Perdew (BP86) GGAs, by contrast, show the typical problems known from the corresponding KS results. We provide some preliminary results for empirical corrections for both PW91 and BP86 in subsystem DFT.
1 Introduction
It has been well established during the past years that Kohn–Sham density functional theory (DFT) within the local-density approximation (LDA) and typical generalized gradient approximations (GGAs), but also DFT employing hybrid exchange–correlation (XC) functionals is problematic for the description of London dispersion forces (for reviews, see e.g., ref. 1–3). Already in 1994, Kristyán and Pulay have noted that “the total exchange–correlation energy of two non-overlapping charge distributions is the sum of the individual contributions for any (semi)local DFT”,4 and consequently, such approximate XC functionals must fail for the long-range behavior of dispersion interactions. But also the so-called medium-range dispersion at distances with weak but non-zero density overlap is usually not well described. Consequently, several correction schemes have been developed within the DFT community. Among the commonly used ones are semilocal and hybrid XC functionals which are highly parametrized to recover medium-range dispersion,5,6 (empirical) pair-wise potentials with the desired −C6/R6 long-range behavior (e.g., the so-called DFT-D methods),7–10 non-local van der Waals (vdW) functionals,11,12 and one-electron potentials.13,14
Subsystem DFT15,16 (abbreviated as sDFT hereafter; for a recent review, see ref. 17) is a density-functional theory variant in which interacting subsystems are described in terms of separate Kohn–Sham-like reference systems. It is related to the frozen-density embedding (FDE) method,18,19 which, for the purposes of this study, can be regarded as a non-selfconsistent variant of sDFT (see ref. 17 for more details). In sDFT, the non-additive part of the kinetic energy needs to be approximated in terms of a density-dependent functional. Since this is seemingly easier for weakly overlapping electron densities than for strong chemical bonds, it is commonly assumed (and confirmed by calculations20–23) that sDFT works well for weakly interacting systems. This is easy to understand for polar molecules, where the intermolecular interactions are dominated by electrostatics: these interactions are treated essentially exactly in sDFT. For non-polar molecules, however, one should actually expect similar failures as in Kohn–Sham- (KS-)DFT. Especially the long-range dispersion should suffer from the same problems. In fact, already Senatore and Subbaswamy observed in 1986 that the proper – (C6/R6) long-range distance dependence for London dispersion interactions cannot be obtained from approximate sDFT as employed in their work.15 A quite natural idea is thus to employ DFT-D corrections also in the context of sDFT, as has been used by one of the present authors.24 This can be further motivated by the fact that sDFT and KS-DFT become equivalent in the limit of exact non-additive kinetic-energy functionals (given the same approximation for the XC functional). Also the concept of non-local van-der-Waals functionals has been successfully transferred to the FDE context.25 The situation for medium-range dispersion in sDFT employing standard GGA-type functionals [most often of Perdew–Wang91 (PW91) type] is more complicated due to the interplay of (attractive) exchange–correlation and (repulsive) non-additive kinetic-energy components. This calls for a more detailed analysis of the behavior at medium range, which directly affects the interaction energies and bond distances of van-der-Waals complexes. In order to use sDFT for geometry optimizations or molecular dynamics simulations, equilibrium distances as well as the shape of the potential energy surfaces and accurate interaction energies are of great importance.20,26
Interestingly, sDFT has been reported to provide better interaction energies for weakly bound systems. In fact, already the Gordon–Kim model, which is a predecessor method of sDFT, produced rather accurate interaction energies for rare-gas dimers.27,28 Extensive early studies of interaction energies from FDE were conducted by Wesołowski and co-workers,23,29–34 which have been reviewed in ref. 35. One particularly interesting set of results was obtained by Wesołowski and Tran in 2003.23 They investigated 25 interacting closed-shell systems and found that sDFT resulted in much better interaction energies than KS-DFT for GGA-type functionals. Also for LDA-type functionals, very good results were obtained in such cases where the density overlap is very small (e.g., rare gas atom dimers). In another study, Wesołowski and co-workers21 have addressed intermolecular complexes from the test sets of Zhao and Truhlar.36–38 Here it was found that sDFT using LDA works very well (in fact often better than KS-DFT) for several classes of weakly interacting systems, with the exception of π-stacking interactions and complexes with strong charge-transfer character. Later, this study was extended by (i) investigating a broader range of kinetic-energy functionals and (ii) including additional transition-metal complex benchmark sets.39 In that study, it could be confirmed that already the LDA often offers good interaction energies, while GGA-functionals usually lead to a significant improvement.
An apparent explanation for this often superior accuracy of sDFT over KS-DFT (using the same XC-approximation) for weakly interacting complexes is a fortunate error cancellation between the non-additive XC and kinetic-energy functional approximations. But even though several studies on (interaction) energies from sDFT have appeared in recent years,24,25,40 there has been no systematic test of potential-energy surfaces for weakly bound systems with this method. For individual complexes like an H2⋯NCH,29 an F–H⋯NCH complex,33 benzene dimer,32 or cytosine dimer21 some sDFT-PESs are available in the literature. In addition, a study addressing equilibrium geometries of the complexes from the HB6/04, DI6/04, and WI9/04 test sets36,37 has been conducted with sDFT in ref. 20. There, it was found that LDA leads to “excellent intermolecular equilibrium distances for hydrogen-bonded complexes”, with a maximum error of 0.13 Å for the ammonium dimer. For rare gas atom dimers, somewhat larger errors of up to 0.32 Å were obtained. GGA-type functionals hardly offered any improvement in those cases. In fact, many structures were found to be worse than with LDA. Another aspect motivating our current work is that there are almost no applications of sDFT to the popular S2241 and S6642 test sets and their extended versions, which include several points along a potential-energy curve; only Pavanello and co-workers have included one specific combination of GGA-type functionals in their study for the S22 test set.25 Also, many previous studies relied on equilibrium structures for weakly interacting complexes obtained from accurate reference methods such as coupled cluster theory.
Here, we fill this gap and conduct a study focussing more on the characteristic features of (entire) potential-energy curves. In particular, bond lengths and interaction energies at consistently obtained equilibrium distances will be investigated. Furthermore, we will analyze the overall shape of the potential-energy curves and indicate possible empirical corrections to further improve them. One additional comment needs to be made here: many previous studies of sDFT use PW91-type43,44 approximations as a typical GGA, while this functional is somewhat unusual in its description of weakly interacting complexes (when compared to other typical GGAs) in the KS-DFT context. This needs to be kept in mind, since many dispersion corrections in DFT address the more common behavior found, e.g., in GGA functionals like BP8645,46 or BLYP.45,47 In order to allow comparisons for these two different types of behavior, we will include both PW91 and BP86 in our tests, in addition to LDA.
This work is organized as follows: in Section 2, we present the methodology employed here, followed by an overview over the computational details in Section 3. Section 4 contains a (re-) investigation of potential-energy curves for rare-gas dimers. In Section 5, we present single-point interaction-energy calculations for a large set of test structures at geometries taken from reference electronic-structure methods. This includes the S22 and S66 test sets. Subsequently, we investigate potential-energy curves of closed-shell dimers in Section 6, where we employ the extended S22x548 and S66x842 test sets. Finally, we outline possible strategies for the improvement of sDFT potential-energy curves, and we conclude from our results in Section 7.
2 Methodology
The main idea of subsystem-DFT is a partitioning of the total electron density ρtot into subsystem densities ρI,| | 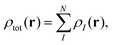 | (1) |
where N is the number of subsystems. Each of these densities will be expressed in terms of an individual Kohn–Sham-like reference system of non-interacting particles, i.e., through a set of orbitals ψIi,| | 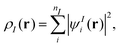 | (2) |
where nI is the number of electrons in subsystem I. This is in contrast to Kohn–Sham-DFT, where the total density is expressed in terms of one single system of non-interacting particles described by orbitals ψtoti,| | 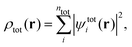 | (3) |
where 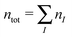 is the total number of electrons in all subsystems. The total energy expression in subsystem DFT can be formulated such that the DFT nature of the approach is emphasized,
is the total number of electrons in all subsystems. The total energy expression in subsystem DFT can be formulated such that the DFT nature of the approach is emphasized,| | 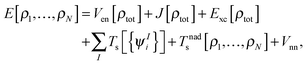 | (4) |
where Vnn is the nucleus–nucleus repulsion energy, and Ven, J, Exc, and Ts are the electron–nucleus interaction, the electron–electron Coulomb, the exchange–correlation, and the single-particle kinetic energy, respectively, as defined in the context of Kohn–Sham DFT. The non-additive kinetic energy functional is defined as,| | 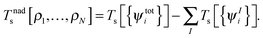 | (5) |
Although the exact form of Tnads is only known in terms of orbitals rather than in terms of densities, a key aspect of most practical sDFT calculations is that Tnads is evaluated using explicit density-dependent approximations. Note that formally also the exchange–correlation energy can be partitioned into subsystem contributions Exc[ρI] and a non-additive part,| | 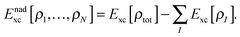 | (6) |
Realizing that all Coulomb-like energy terms naturally consist of intra- and inter-subsystem terms, we can write the total energy in sDFT in a hybrid-energy fashion,| | 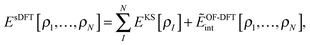 | (7) |
where EKS[ρI] is the Kohn–Sham energy of subsystem I (including the nucleus–nucleus interactions), and ẼOF-DFTint is the interaction energy between the subsystems with densities as obtained in the complex, which is evaluated in an orbital-free- (OF-) DFT manner,| | 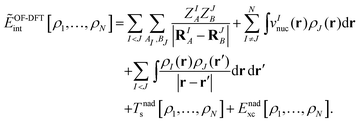 | (8) |
Here, the sums over AI and BJ run over all nuclei A and B in subsystems I and J (with nuclear charges ZIA, ZJB at positions RIA, RJB), respectively, and vInuc(r) is the nuclear potential of the nuclei in subsystem I. Note that the “true” interaction energy differs from this expression, as will be discussed below. Minimization of EsDFT[ρ1,…,ρN] with respect to the electron density of system I (keeping all other subsystem densities fixed) gives rise to the so-called Kohn–Sham equations with constrained electron density (KSCED),19| | 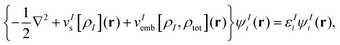 | (9) |
where vIs(r) is the Kohn–Sham effective potential that would appear for the isolated subsystem I. The embedding potential for subsystem I is given as| | 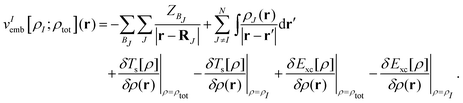 | (10) |
In sDFT, this energy minimization is carried out iteratively for all subsystem densities, until the total energy functional is minimized. In the strict definition of FDE, only the electron density of one single (active) subsystem is optimized in a given, fixed background (environment) electron density of all other subsystems. This means that this density does not even need to be represented in terms of (one or several) sets of Kohn–Sham orbitals as in sDFT. Usually, however, also in FDE the densities of the environment systems are represented in terms of orbitals (e.g., of isolated systems), so that also an approximate total energy can be evaluated. This corresponds to a wider definition of FDE, which coincides with an approximate sDFT (see, e.g., the preface to ref. 49 or ref. 17 for a more detailed discussion of these formal aspects).
The “true” interaction energy Eint in a complex is defined as
which in the case of sDFT means
| | 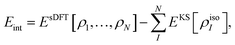 | (11) |
where
Ecomplex (or
EsDFT, respectively) is the total energy of the complex and the total energy of the isolated monomer
I is given by
EKS[
ρisoI], where
ρisoI is the density of the isolated subsystem
I. This will be the definition used in the following sections. It can differ from the expression given in
eqn (8) for two reasons: (i) the electron densities in the complex can be different from the isolated-molecule densities, and (ii) structural relaxation may take place. The latter point will be ignored in this study,
i.e., we only consider fixed monomer structures. For the case of sDFT, a relation between the two definitions of the interaction energy can be established as follows: we rewrite
Eint in terms of
ẼOF-DFTint from
eqn (8) and of an additional term taking the change in the monomer energies into account,
| | 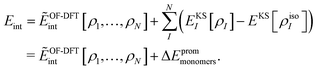 | (12) |
Here,
EKSI[
ρI] is the total energy of the relaxed monomer
I in the complex. If we sum up all promotion energies for all subsystems, we get the total promotion energy Δ
Eprommonomers. This definition of the promotion energy is in line with the definition as given in
ref. 24 (also called “internal strain energy” in
ref. 33). The energy decomposition used here
24 arises naturally from the different energy contributions in sDFT. It shows some similarities (
e.g. in the form of the electrostatic terms) to the energy decomposition analyses (EDAs) developed by Morokuma
50,51 and by Ziegler and Rauk
52 (for a review, see
ref. 53). The promotion energy arises because of mutual relaxation in the monomer densities due to electrostatic and short-range quantum-mechanical effects upon forming the complex. It is, by definition, always positive.
For further analysis of the interaction energy, it is useful to separate ẼOF-DFTint into different contributions,
| | | ẼOF-DFTint[ρ1,…,ρN] = Eelstatint[ρ1,…,ρN] + Tnads[ρ1,…,ρN] + Enadxc[ρ1,…,ρN], | (13) |
where we combined all electrostatic terms [the first three terms in
eqn (8)] into the electrostatic interaction energy
Eelstatint[
ρ1,…,
ρN].
For van-der-Waals (vdW) complexes of non-polar molecules, the electron densities may actually be well approximated by the densities of the isolated molecules. Consequently, an energy evaluation neglecting the mutual relaxation of the densities under the influence of the embedding potential may still give results close to the fully relaxed case, since promotion energies are usually close to zero in those cases.
3 Computational details
We will provide results from three different choices of approximate functionals, where always conjoint approximations54 for exchange and non-additive kinetic energy are employed:
(i) the local density approximation (LDA); this is the simplest possible choice, which is parameter-free and has proven quite successful in previous studies.20–23 The non-additive kinetic energy contributions are evaluated using the Thomas–Fermi (TF) model.55,56 These combinations will be denoted as KS-LDA and sDFT-LDA/TF for supermolecular KS-DFT calculations and sDFT, respectively.
(ii) the PW91-GGA for exchange, correlation, and, in reparametrized form, for the non-additive kinetic energy;29,57 PW91k is one of the most widely used approximations for the non-additive kinetic energy in FDE and subsystem-DFT applications, and was very successfully applied for interaction energies in ref. 23. However, the corresponding XC functional is non-typical for standard KS-DFT calculations on weakly interacting complexes, as it often produces bound potential-energy curves (in contrast to many other GGAs). This leads to the abbreviations KS-PW91 and sDFT-PW91/PW91k, respectively.
(iii) the Becke88 GGA for exchange,45 and the corresponding (reparametrized) functional for the non-additive kinetic energy by Lee, Lee, and Parr,54 which is usually denoted as LLP91. Here, we choose the Perdew8646 functional for the correlation part, which leads to the common XC-GGA known as BP or BP86 with the typical failure for dispersion interactions. The corresponding calculations here will be labeled as KS-BP86 and sDFT-BP86/LLP91, respectively.
All sDFT calculations were carried out with the FDE/subsystem DFT implementation39,58 in the ADF 2014.0159 program package. Usual KS-DFT calculations were also carried out with ADF 2014.01. All calculations were done without explicit use of point-group symmetry. The TZ2P60 basis set was used in all calculations and we used the mono-molecular expansion in the case of sDFT. This expansion is free of the basis set superposition error (BSSE) and gives good results as long as no charge-transfer like interactions are important.21,24 Moreover, we want to assess the reliability of efficient and practically applicable sDFT setups suitable for production calculations, so that no super-molecular basis sets are considered. For a comparison of results from mono-molecular and super-molecular basis sets, we refer the reader to ref. 21 and 24. We have employed the pair fitting61 (together with the standard auxiliary fit functions for the basis set) for the evaluation of Coulomb-potentials and energy terms in all KS and sDFT calculations. KS-DFT interaction energies were corrected for basis set superposition errors using the counterpoise method.62 More detailed information about the calculations is provided in the ESI.†
4 Rare-gas dimers re-investigated
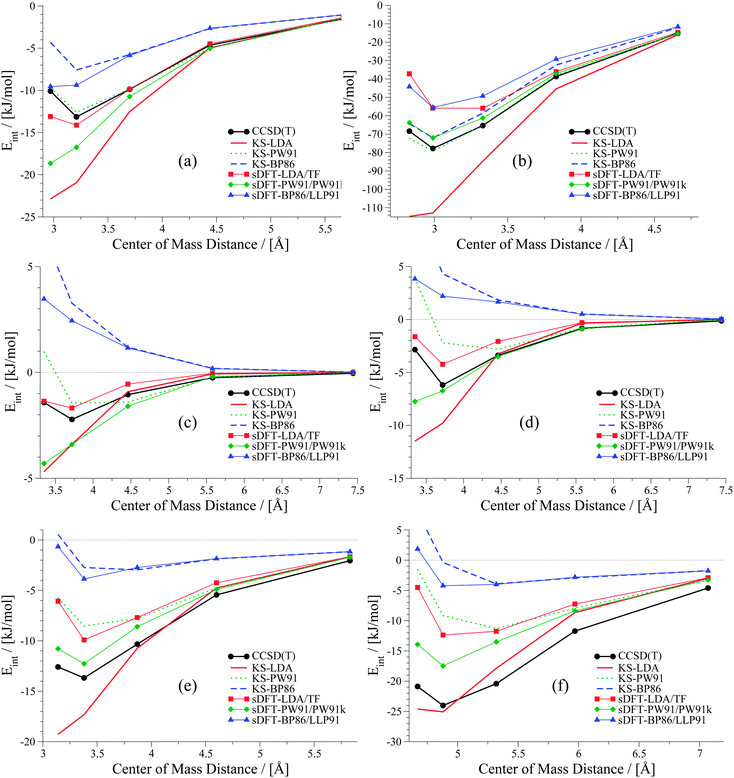
We start our investigation with prototypical and simple test systems for van-der-Waals interactions, namely, rare-gas atom dimers.
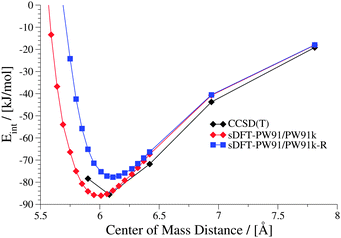
It was shown in ref. 21 that equilibrium distances for He⋯Ne, He⋯Ar, Ne⋯Ne and Ne⋯Ar derived with sDFT-LDA/TF are in good agreement with reference geometries. Also interaction energies for the above systems as well as for Ar⋯Ar from sDFT-LDA/TF were shown to be in good agreement with reference CCSD(T) ones.20,23 So far, there was no detailed comparison of entire rare-gas dimer PESs. A set of rare-gas atom dimer PESs is presented in Fig. 1. Here, we compare energies we derived from BSSE-corrected CCSD(T)/aug-cc-pVQZ (aug-cc-pVQZ-PP for Xenon; for more details see ESI†) and sDFT. For comparison, we also include the corresponding KS-DFT results. The choices for exchange–correlation and non-additive kinetic-energy functionals are motivated in Section 3. Looking first at the KS-DFT results, we observe that KS-LDA curves are too attractive (see also, e.g., ref. 63 and 64 for analyses of KS-DFT for rare-gas dimers): they lead to shorter equilibrium distances and larger interaction energies when compared to the CCSD(T) reference. KS-PW91 leads to a bound curve with varying quality of equilibrium distances in all cases (reasonable for Ne⋯Ne and Kr⋯Kr, but too long for Ar⋯Ar and Xe⋯Xe), while KS-BP86 leads to the well-known65 behavior of purely repulsive potential-energy curves. The sDFT interaction energies follow the overall trends of their KS-DFT counterparts, however, with some differences. The sDFT-LDA/TF potential-energy curves become less attractive and equilibrium distances are improved in most cases when compared to KS-LDA. sDFT-PW91/PW91k potential-energy curves are more attractive than their KS-PW91 counterparts, which also degrades the description of equilibrium distances. The sDFT-BP86/LLP91 curves are purely repulsive so that this combination of functionals cannot be used to describe rare-gas dimers adequately.
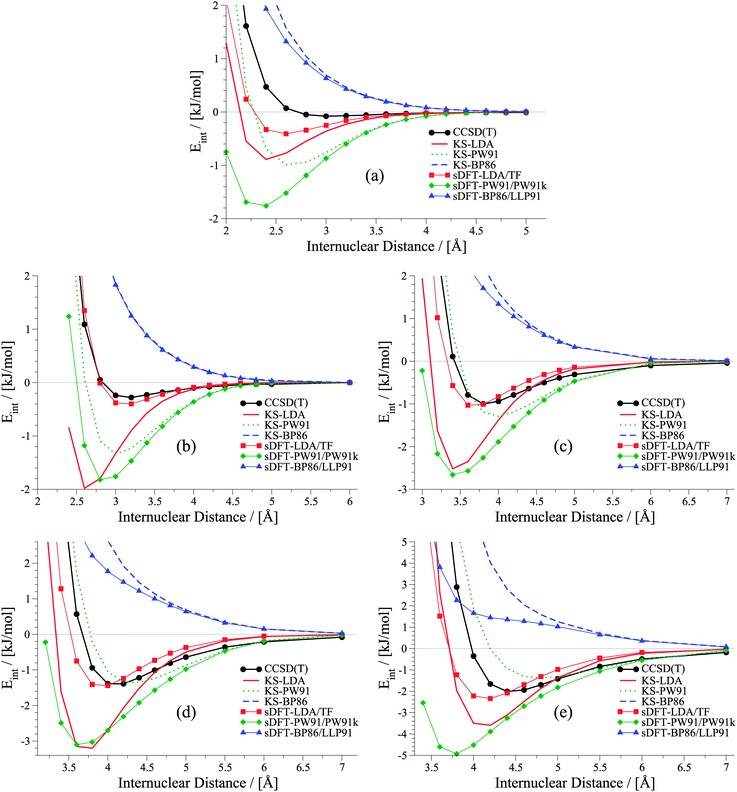 |
| | Fig. 1 Potential energy curves for rare-gas dimers: (a) helium dimer, (b) neon dimer, (c) argon dimer, (d) krypton dimer, (e) xenon dimer. | |
It becomes obvious that the quality of sDFT results for weak interactions strongly depends on the choice of the functionals. In fact, the potential-energy curves of sDFT-BP86/LLP91 are just as poor as KS-BP86. The bound character of the KS-DFT curves for LDA and PW91 is recovered in the sDFT calculations. sDFT-LDA/TF binding energies are lowered, while sDFT-PW91/PW91k binding energies are increased compared to their KS counterparts. This also leads to larger equilibrium distances in sDFT-LDA/TF and smaller ones in sDFT-PW91/PW91k when compared to KS-DFT. At CCSD(T) equilibrium distances, the interaction energies from sDFT-LDA/TF are rather good. But this does not automatically imply the same accuracy for equilibrium distances. The sDFT-LDA/TF curves nicely follow the CCSD(T) ones at medium and larger distances. This observation is in line with the early results by Gordon and Kim,28 who used an approach similar to sDFT-LDA/TF with unrelaxed densities. Although the densities in the present calculations are fully relaxed (and not derived from Hartree–Fock theory) the behavior of the sDFT-LDA/TF interaction energies is very similar to those presented in ref. 28.
5 Single-point interaction energies
As shown above, sDFT-LDA/TF interaction energies for rare-gas dimers are usually quite accurate, while those derived from sDFT-PW91/PW91k are generally too attractive, and sDFT-BP86/LLP91 does not describe bound states. In order to further investigate the behavior for chemically more relevant systems, we re-investigate the test set employed by Wesołowski and Tran.23 Our study is based on a subsystem DFT energy implementation39 in the Slater-basis code ADF,59 while their previous study made use of a Gauss-basis implementation33 in the DEMON code.66,67 These results thus also serve the purpose of additional validation of the ADF implementation and a comparison of the two types of basis sets. We then continue with an application of sDFT to the popular S22-41,68 and S66-42,68 test sets. The structures investigated in the following are fixed structures from the reference articles, which have not been re-optimized in the present work unless noted otherwise.
5.1 The test set by Wesołowski and Tran
Our first test set is the set of 25 intermolecular complexes studied in ref. 23 with interaction energies between −0.3 and −12.0 kJ mol−1. The structures were derived as follows: the monomer structures for complexes 1, 7, 8, 10, 14, 16, 19–25 in Table 1 were taken from references within ref. 23 and their respective supporting information. For all other complexes, the monomers were optimized with MP2/6-31G* in the original references, but coordinates were not reported. In order to get as close to the reference monomer structures as possible, we used the same method to derive optimized monomer structures using the GAUSSIAN 0969 program package. The distances between the monomers were then taken from the respective references within ref. 23. We define the error ΔE of the DFT interaction energy EDFTint with respect to the reference interaction energy Erefint as ΔE = Erefint − EDFTint. Hence, positive values represent a too negative interaction energy, i.e., an overestimation of the interaction. In view of the different types of basis functions used, the results obtained with ADF are in good agreement with data presented in ref. 23. The errors ΔE are graphically presented in Fig. 2. The sDFT values have a maximum absolute deviation of 2.21 (C6H6⋯C6H6) and 1.18 kJ mol−1 (C2H4⋯C2H4) for sDFT-LDA/TF and sDFT-PW91/PW91k, respectively, when compared to the results from ref. 23. The mean absolute deviations (MADs) relative to ref. 23 for sDFT-LDA/TF and sDFT-PW91/PW91k are 0.49 and 0.41 kJ mol−1, respectively and 0.70 and 0.61 kJ mol−1 for KS-LDA and KS-PW91. Maximum absolute deviations are 3.05 and 6.13 kJ mol−1 (both C6H6⋯C6H6) for KS-LDA and KS-PW91, respectively. Because the latter deviation seems quite large, we checked this interaction energy against results from ORCA 3.0.270 with RI-DFT/cc-pVTZ,71 which supports our findings with an interaction energy of 3.26 kJ mol−1 (compared to our value of 3.08 kJ mol−1). The magnitude of the interaction is similar in ref. 23, but the sign is different (−3.05 kJ mol−1). In contrast to ref. 23, we observe that the average absolute error of KS-LDA with respect to the wave-function reference results is smaller than that of sDFT-LDA/TF, which can most likely be attributed to the basis set. For this test set, KS-LDA is always in the regime of chemical accuracy (∼1 kcal mol−1) and usually slightly too attractive. sDFT-LDA/TF, by contrast, yields interaction energies that are almost always less attractive than the reference wave-function data, and always less attractive than their KS-DFT counterparts (see Table 2). This situation is reversed for PW91: while KS-PW91 mostly underestimates interaction energies, sDFT-PW91/PW91k usually overestimates them.
Table 1 Errors between sDFT- and reference [CCSD(T) or MP2] interaction energies taken from ref. 23. Errors are defined as ΔE = Erefint − EDFTint, where EDFTint refers to the interaction energy derived from KS-DFT or sDFT. Errors from KS-DFT have been included for comparison. All values are given in kJ mol−1. MD and MAD stand for mean deviation and mean absolute deviation, respectively
| No. |
Complex |
E
refint (ref. 23) |
ΔE |
| KS-DFT |
sDFT |
| LDA |
PW91 |
BP86 |
LDA/TF |
PW91/PW91k |
BP86/LLP91 |
| 1 |
Ar⋯Ar |
−1.09 |
0.78 |
0.10 |
−3.31 |
−0.08 |
1.17 |
−2.80 |
| 2 |
C2F6⋯C2F6 |
−4.27 |
1.43 |
−2.29 |
−11.41 |
−3.08 |
0.66 |
−10.43 |
| 3 |
C2H2⋯C2H2 |
−7.03 |
2.35 |
−0.96 |
−5.24 |
−0.07 |
1.46 |
−4.20 |
| 4 |
C2H4⋯C2H4 |
−5.56 |
2.33 |
−3.01 |
−8.56 |
−2.17 |
−0.18 |
−7.56 |
| 5 |
C2H4⋯CH4 |
−2.05 |
1.60 |
−0.19 |
−3.63 |
0.51 |
1.47 |
−2.79 |
| 6 |
C2H6⋯CH4 |
−2.97 |
2.85 |
−3.71 |
−8.94 |
−2.66 |
0.15 |
−7.25 |
| 7 |
C3H6⋯Ar |
−3.60 |
1.75 |
−2.10 |
−7.98 |
−1.79 |
0.49 |
−6.95 |
| 8 |
C3H6⋯Ne |
−1.51 |
1.65 |
0.48 |
−4.81 |
−0.53 |
1.60 |
−4.58 |
| 9 |
C3H8⋯C3H8 |
−8.12 |
1.08 |
−6.13 |
−13.64 |
−5.74 |
−2.70 |
−12.62 |
| 10 |
C6H6⋯Ar |
−4.64 |
0.47 |
−3.82 |
−9.50 |
−2.30 |
−0.29 |
−7.59 |
| 11 |
C6H6⋯C2H2 |
−11.84 |
1.55 |
−5.86 |
−11.88 |
−4.78 |
−2.51 |
−10.79 |
| 12 |
C6H6⋯C2H4 |
−8.62 |
1.79 |
−6.91 |
−13.33 |
−5.39 |
−2.15 |
−11.12 |
| 13 |
C6H6⋯C2H6 |
−7.61 |
2.03 |
−7.20 |
−14.05 |
−5.53 |
−1.67 |
−11.30 |
| 14 |
C6H6⋯C6H6 |
−10.29 |
−0.80 |
−13.37 |
−22.11 |
−7.94 |
−3.33 |
−15.76 |
| 15 |
C6H6⋯CH4 |
−6.07 |
1.69 |
−4.30 |
−9.84 |
−3.13 |
−0.87 |
−8.31 |
| 16 |
C6H6⋯Ne |
−1.84 |
0.69 |
−0.21 |
−5.05 |
−1.07 |
0.74 |
−4.89 |
| 17 |
CF4⋯CF4 |
−3.26 |
0.95 |
−1.86 |
−9.52 |
−2.38 |
0.49 |
−8.70 |
| 18 |
CH4⋯CH4 |
−2.09 |
0.93 |
−0.48 |
−4.99 |
−0.53 |
1.08 |
−4.37 |
| 19 |
F2⋯Ar lin. |
−1.46 |
1.34 |
0.75 |
−3.23 |
−0.89 |
0.76 |
−3.79 |
| 20 |
F2⋯Ne lin. |
−0.71 |
1.58 |
1.03 |
−3.19 |
−0.56 |
1.35 |
−3.55 |
| 21 |
F2⋯Ne T |
−0.71 |
1.48 |
0.84 |
−3.44 |
−0.26 |
1.57 |
−3.40 |
| 22 |
N2⋯Ar lin. |
−0.92 |
0.58 |
0.23 |
−2.88 |
−0.01 |
1.15 |
−2.42 |
| 23 |
N2⋯Ar T |
−1.21 |
0.61 |
−0.02 |
−3.68 |
−0.14 |
1.20 |
−3.02 |
| 24 |
N2⋯N2 |
−0.92 |
0.55 |
−0.35 |
−3.89 |
−0.48 |
0.92 |
−3.31 |
| 25 |
Ne⋯Ne |
−0.33 |
0.77 |
0.98 |
−1.85 |
0.08 |
1.30 |
−1.83 |
|
|
|
|
MD |
|
1.28 |
−2.34 |
−7.60 |
−2.04 |
0.15 |
−6.53 |
|
|
MAD |
|
1.35 |
2.69 |
7.60 |
2.09 |
1.25 |
6.53 |
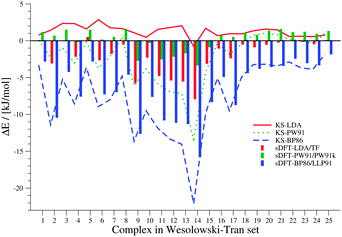 |
| | Fig. 2 Errors between sDFT- and reference interaction energies from ref. 23 for the test set by Wesołowski and Tran. Errors are defined as ΔE = Erefint − EDFTint. Errors from KS-DFT have been included for comparison. All values are given in kJ mol−1. | |
Table 2 Mean deviations (MDs) and mean absolute deviations (MADs) of sDFT interaction-energy errors with respect to their KS-DFT counterparts for the Wesołowski-Tran test set. The error ΔE = EKS-DFTint − EsDFTint is given in kJ mol−1
| sDFT |
MD(ΔE) |
MAD(ΔE) |
| LDA/TF |
−3.32 |
3.32 |
| PW91/PW91k |
2.49 |
2.49 |
| BP86/LLP91 |
1.06 |
1.14 |
For KS-BP86 and sDFT-BP86/LLP91, the interaction energies are very similar: the mean and mean absolute deviations (MD and MAD, respectively) between sDFT-BP86/LLP91 and KS-BP86 interaction energies are 1.06 and 1.14 kJ mol−1, respectively. Hence, sDFT-BP86/LLP91 shows the best agreement with the corresponding KS-DFT results, which also means that it shows the typical problems of KS-BP86 in the description of weak interactions. But this, in turn, implies that empirical dispersion corrections developed for KS-BP86 could easily be transferred to its sDFT counterpart (see Section 6.3).
5.2 The S22 and S66 test sets
We continue our investigation with the S2241,68 and S6642,68 test sets. These test sets have been established as a standard test for the accuracy of electronic-structure methods for weakly interacting systems.25,72–74
In both sets, the complexes are grouped into three subsets in ref. 41 and 42, based on findings from symmetry adapted perturbation theory calculations. We use the same classification scheme here. The S22 and S66 complexes are explicitly listed for the three different categories in Tables 3 and 4. Both sets contain only the equilibrium structures (obtained with CCSD(T) and MP2) of the respective complexes. Because the interaction energies for these reference structures are similar for both sets, they are discussed together here. The results are summarized in Fig. 3 and 4.
Table 3 Complexes in the S22 test set. “2-PY” and “2-PO” are 2-pyridoxine and 2-aminopyridine, respectively. (HB), (S) and (TS) stand for hydrogen bonded, stacked and T-shaped, respectively
| No. |
H-bonded complexes |
No. |
vdW complexes |
No. |
Mixed complexes |
| 1 |
Ammonia dimer |
8 |
Methane dimer |
16 |
Ethene–ethyne |
| 2 |
Water dimer |
9 |
Ethene dimer |
17 |
Benzene–water |
| 3 |
Formic acid dimer |
10 |
Benzene–methane |
18 |
Benzene–ammonia |
| 4 |
Formamide dimer |
11 |
Benzene dimer (S) |
19 |
Benzene–HCN |
| 5 |
Uracil dimer (HB) |
12 |
Pyrazine dimer (S) |
20 |
Benzene dimer (TS) |
| 6 |
2-PY – 2-PO |
13 |
Uracil dimer (S) |
21 |
Indole–benzene (TS) |
| 7 |
Adenine–thymine |
14 |
Indole–benzene (S) |
22 |
Phenole dimer (HB) |
|
|
|
15 |
Adenine–thymine (S) |
|
|
Table 4 Complexes in the S66 test set. The “peptide” is N-methylacetamide. (TS) stands for T-shaped
| No. |
H-bonded complexes |
No. |
vdW complexes |
No. |
Mixed complexes |
| 1 |
Water–water |
24 |
Benzene–benzene |
47 |
Benzene–benzene (TS) |
| 2 |
Water–MeOH |
25 |
Pyridine–pyridine |
48 |
Pyridine–pyridine (TS) |
| 3 |
Water–MeNH2 |
26 |
Uracil–uracil |
49 |
Benzene–pyridine (TS) |
| 4 |
Water–peptide |
27 |
Benzene–pyridine |
50 |
Benzene–ethyne |
| 5 |
MeOH–MeOH |
28 |
Benzene–uracil |
51 |
Ethyne–ethyne (TS) |
| 6 |
MeOH–MeNH2 |
29 |
Pyridine–uracil |
52 |
Benzene–AcOH |
| 7 |
MeOH–peptide |
30 |
Benzene–ethene |
53 |
Benzene–AcNH2 |
| 8 |
MeOH–water |
31 |
Uracil–ethene |
54 |
Benzene–water |
| 9 |
MeNH2–MeOH |
32 |
Uracil–ethyne |
55 |
Benzene–MeOH |
| 10 |
MeNH2–MeNH2 |
33 |
Pyridine–ethene |
56 |
Benzene–MeNH2 |
| 11 |
MeNH2–peptide |
34 |
Pentane–pentane |
57 |
Benzene–peptide |
| 12 |
MeNH2–water |
35 |
Neopentane–pentane |
58 |
Pyridine–pyridine |
| 13 |
Peptide–MeOH |
36 |
Neopentane–neopentane |
59 |
Ethyne–water |
| 14 |
Peptide–MeNH2 |
37 |
Cyclopentane–neopentane |
60 |
Ethyne–AcOH |
| 15 |
Peptide–peptide |
38 |
Cyclopentane–cyclopentane |
61 |
Pentane–AcOH |
| 16 |
Peptide–water |
39 |
Benzene–cyclopentane |
62 |
Pentane–AcNH2 |
| 17 |
Uracil–uracil |
40 |
Benzene–neopentane |
63 |
Benzene–AcOH |
| 18 |
Water–pyridine |
41 |
Uracil–pentane |
64 |
Peptide–ethene |
| 19 |
MeOH–pyridine |
42 |
Uracil–cyclopentane |
65 |
Pyridine–ethyne |
| 20 |
AcOH–AcOH |
43 |
Uracil–neopentane |
66 |
MeNH2–pyridine |
| 21 |
AcNH2–AcNH2 |
44 |
Ethene–pentane |
|
|
| 22 |
AcOH–uracil |
45 |
Ethyne–pentane |
|
|
| 23 |
AcNH2–uracil |
46 |
Peptide–pentane |
|
|
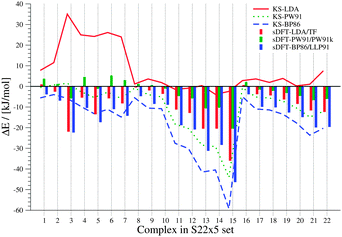 |
| | Fig. 3 Errors between sDFT- and reference CCSD(T)/CBS interaction energies from ref. 68 for the S22 test set. Errors are defined as ΔE = Erefint − EDFTint. Errors from KS-DFT have been included for comparison. All values are given in kJ mol−1. | |
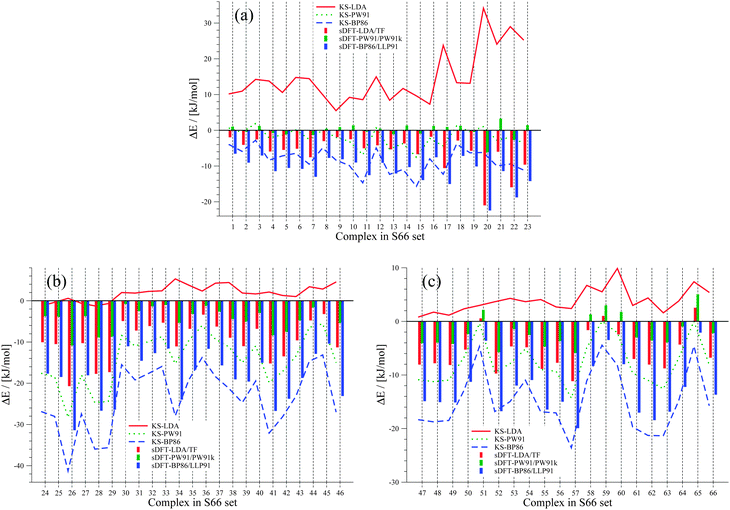 |
| | Fig. 4 Errors between sDFT- and reference CCSD(T)/CBS interaction energies from ref. 68 for the S66 test set. The different pictures describe (a) hydrogen-bonded complexes, (b) vdW complexes and (c) mixed complexes. Errors are defined as ΔE = Erefint − EDFTint. Errors from KS-DFT have been included for comparison. All values are given in kJ mol−1. | |
From these figures, we see that KS-LDA interaction energies are usually too attractive, while this is very rarely the case for sDFT-LDA/TF compared to the reference. Compared to their KS-DFT counterparts, sDFT-LDA/TF interaction energies are commonly less attractive, which is in line with the findings from Section 5.1. The MDs of sDFT-LDA/TF from KS-LDA are quite large (cf.Table 5), but the MADs of both methods compared to the reference are similar (8.65 vs. 9.69 kJ mol−1 with KS-LDA and sDFT-LDA/TF for S22, respectively and 7.07 vs. 7.27 kJ mol−1 respectively for S66). sDFT-LDA/TF interaction energies are quite poor when π-interactions play a role, which is also in agreement with previous results from the literature.20,21,23 However, π–π-stacked interactions are quite well described by KS-LDA (also in line with findings from ref. 75). KS-LDA quite nicely fits to the reference interaction energies of the vdW and mixed bonded complexes.
Table 5 MDs and MADs of sDFT interaction-energy errors with respect to their KS-DFT counterparts for the S22 and S66 test sets. The error ΔEDFT = EKS-DFTint − EsDFTint is given in kJ mol−1
| |
S22 test set |
S66 test set |
| sDFT |
MD(ΔE) |
MAD(ΔE) |
MD(ΔE) |
MAD(ΔE) |
| LDA/TF |
−17.42 |
17.42 |
−14.09 |
14.09 |
| PW91/PW91k |
7.24 |
7.89 |
5.80 |
6.07 |
| BP86/LLP91 |
2.23 |
4.42 |
1.55 |
3.68 |
Interaction energies from KS-BP86 and sDFT-BP86/LLP91 are most often too repulsive compared to the reference for these test sets. The MADs between sDFT and KS-DFT are similar for BP86 and PW91 (cf.Table 5). For both approximations, the sDFT interaction energies are mostly more attractive than the KS-DFT ones for vdW and mixed interactions. For hydrogen-bonded systems, sDFT-BP86/LLP91 is usually less attractive than its KS-BP86 counterpart. None of the sDFT approximations show a general overestimation of dispersion-dominated interaction energies, while simple KS-LDA does in almost all cases. Interaction energies from sDFT-LDA/TF and sDFT-BP86/LLP91 show similar MADs from the reference compared to their KS-DFT counterparts. Interaction energies from KS-PW91 and KS-BP86 are usually not attractive enough when compared to the reference. Since interaction energies from sDFT-PW91/PW91k are quite systematically more attractive than KS-PW91 interaction energies, the MAD of sDFT-PW91/PW91k interaction energies is the best for these test sets (4.72 and 2.90 kJ mol−1 for S22 and S66, respectively).
6 Potential-energy curves from FDE
6.1 S22x5 test set
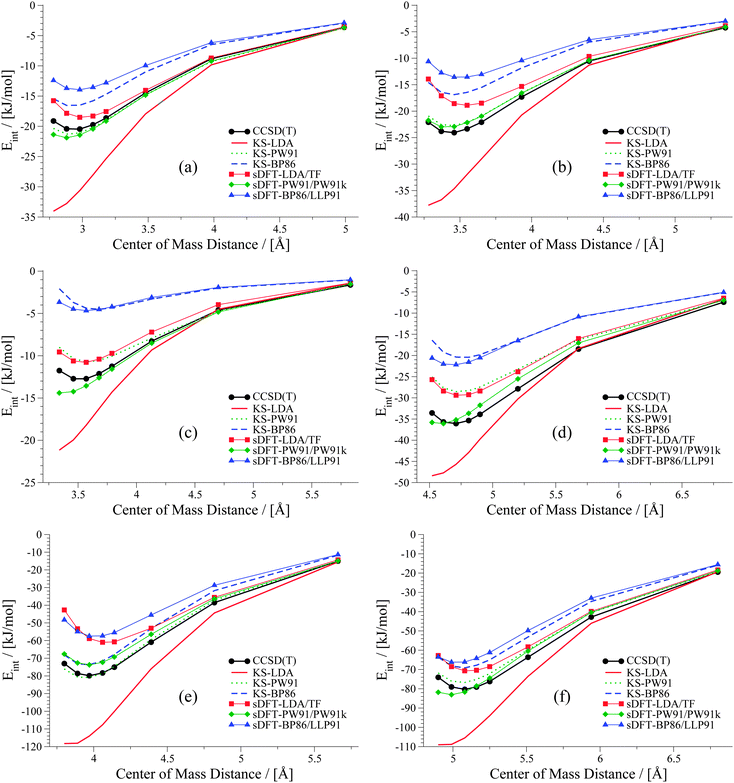
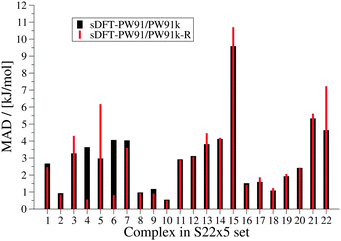
We now discuss systematics in PESs derived from sDFT and start with the S22x5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 48,68 test set, which consists of the complexes listed in Table 3. In addition to the equilibrium structures, this set contains four extra structures displaced from equilibrium for each complex in the set. In the displaced structures, the intermolecular distance is varied, so that the S22x5 set concerns representative parts of the intermolecular potential-energy curves. The MADs for each set of sDFT calculations for the S22x5 test set are presented in Fig. 5 along with their KS-DFT counterparts. Not just for equilibrium structures, but also for PESs, the average MAD of sDFT-PW91/PW91k with a magnitude of 2.92 kJ mol−1 is the smallest among the DFT approximations tested here. Six examples for PESs are presented in Fig. 6. The complete set, together with the values graphically shown in Fig. 5 are provided in the ESI.†
48,68 test set, which consists of the complexes listed in Table 3. In addition to the equilibrium structures, this set contains four extra structures displaced from equilibrium for each complex in the set. In the displaced structures, the intermolecular distance is varied, so that the S22x5 set concerns representative parts of the intermolecular potential-energy curves. The MADs for each set of sDFT calculations for the S22x5 test set are presented in Fig. 5 along with their KS-DFT counterparts. Not just for equilibrium structures, but also for PESs, the average MAD of sDFT-PW91/PW91k with a magnitude of 2.92 kJ mol−1 is the smallest among the DFT approximations tested here. Six examples for PESs are presented in Fig. 6. The complete set, together with the values graphically shown in Fig. 5 are provided in the ESI.†
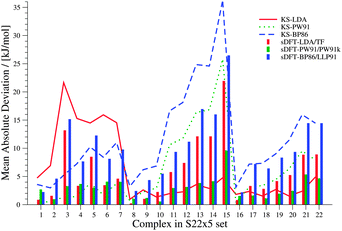 |
| | Fig. 5 MADs per molecule of sDFT interaction energies with respect to reference CCSD(T)/CBS energies taken from ref. 68 for the S22x5 test set. MADs from KS-DFT have been included for comparison. | |
 |
| | Fig. 6 PESs for six examples in the S22x5 test set: (a) ammonia dimer, (b) formic acid dimer, (c) methane dimer, (d) ethene dimer, (e) benzene–water and (f) indole–benzene T-shaped. | |
The weaker the interactions between the complexes are (i.e., at large intermolecular distances), the less pronounced should be the effect of the non-additive contributions to the embedding potential and to the interaction energy. Hence, the results of KS-DFT and sDFT converge for larger distances. This can clearly be seen for all curves in this test set. In order to clarify the origin of binding in sDFT for weakly interacting systems, a decomposition of the sDFT interaction energy contributions according to eqn (12) and (13) for the three different sDFT approximations used here is presented for the ammonia and methane dimer complexes in Fig. 7 and 8, respectively.
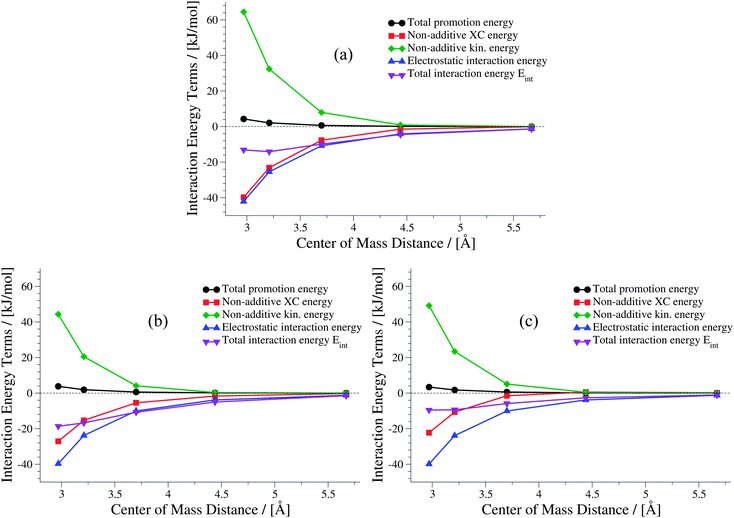 |
| | Fig. 7 Contributions to the sDFT interaction energies [cf.eqn (8)] for the ammonia dimer PES of the S22x5 test set. The different approximations are (a) sDFT-LDA/TF, (b) sDFT-PW91/PW91k, (c) sDFT-BP86/LLP91. | |
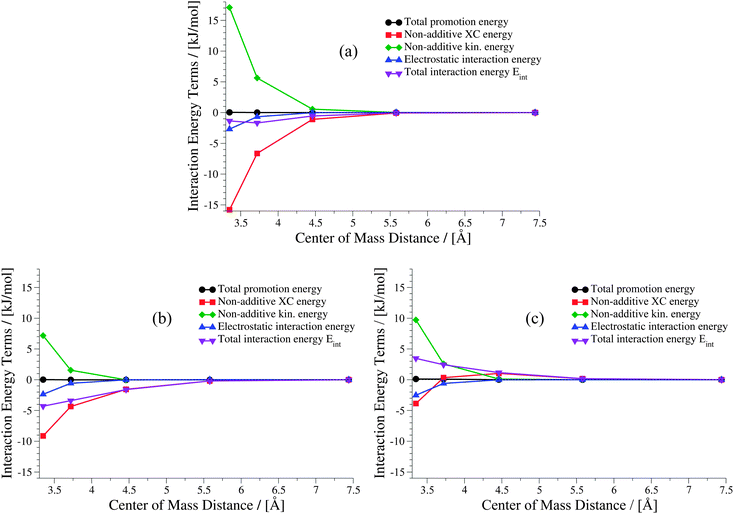 |
| | Fig. 8 Contributions to the sDFT interaction energies [cf.eqn (8)] for the methane dimer PES of the S22x5 test set. The different approximations are (a) sDFT-LDA/TF, (b) sDFT-PW91/PW91k, (c) sDFT-BP86/LLP91. | |
Around a center of mass distance of 3.7 Å and shorter distances for the ammonia dimer, the non-additive exchange–correlation energy Enadxc has values comparable to the total electrostatic interaction in the sDFT-LDA/TF case. The magnitude of the non-additive kinetic energy Tnads is similar to Enadxc for all but the shortest distances. But Tnads is of opposite sign. Therefore, all non-additive contributions play a non-negligible role in the description of the interaction of the two subsystems. The non-additive terms more or less cancel for center-of-mass distances of 3.5 Å and larger. Hence, the total interaction energy appears to be almost identical to the total electrostatic interaction energy. A similar picture is observed for sDFT-PW91/PW91k, while sDFT-BP86/LLP91 shows a smaller (in magnitude) XC contribution, thus leading to a more repulsive total interaction energy curve.
For the methane dimer (Fig. 8) it is clearly demonstrated that binding occurs mainly because of the non-additive exchange–correlation parts in sDFT-LDA/TF and sDFT-PW91/PW91k. The non-additive exchange–correlation energy is even positive for sDFT-BP86/LLP91 for distances larger than 3.75 Å. The magnitude of the non-additive contributions is clearly larger than that of the electrostatic interaction energy, as one could expect for these non-polar molecules. In both examples presented here, the polarization of the subsystems plays a minor role for the interaction energy. Depending on the polarity and polarizability of the monomers in the complex, this is not generally the case for all intermolecular complexes. For the equilibrium structures of the S22x5 test set (which is, in fact, the S22 test set) a maximum monomer polarization energy of Epolmonomer ≈ 50 kJ mol−1 can be observed for the formic acid dimer.‡ Thus, monomer polarization energies can be of significant magnitude. For the S22 and S66 test sets this is typically the case for hydrogen-bonded complexes. All promotion energies for the S22 and S66 test sets can be found in the ESI† (Tables 3 and 4).
The overall average MAD of sDFT-PW91/PW91k is the best for this benchmark set (2.92 kJ mol−1), but taking only the second and third block into account (complexes 8–22), KS-LDA shows, on average, even smaller deviations with respect to the reference. The average MADs of KS-LDA and sDFT-LDA/TF are almost equivalent (5.95 and 5.98 kJ mol−1, respectively) although their descriptions of the PESs differ largely from each other. As explained before, for large distances the KS-DFT and sDFT interaction energies coincide. Hence, the MADs of both methods are very similar, because most of the data points belong to this region. KS-LDA is mostly too attractive for the complexes in this set, so that equilibrium distances are generally too short. For complexes 11–15, which are all π–π stacked complexes, KS-LDA interaction energies across the whole PES are usually very good. This is in line with the findings in ref. 75. For the interaction energies at equilibrium distances (see Section 5) we have seen that sDFT-LDA/TF is usually less attractive than KS-LDA. This picture is reversed for PW91 and BP86, where PESs from sDFT are usually more attractive than their KS-DFT counterparts. This usually remains true for the whole PES (see Fig. 6), except for cases where sDFT and KS-DFT are very similar anyway [cf.Fig. 6(e)]. For hydrogen-bonded complexes, sDFT-BP86/LLP91 is most often less attractive than KS-BP86 for the whole PES. While KS-PW91 usually does not describe vdW complexes sufficiently well, interaction energies of sDFT-PW91/PW91k are better at equilibrium distances of the reference method. But the repulsive part of the PESs at shorter distances is usually poorly described. For the first group of molecules in the S22x5 test set (hydrogen-bonded complexes), sDFT-PW91/PW91k is more attractive than KS-PW91 when the X–H bond (where X can be N or O) is pointing directly towards the donating lone pair of the other monomer. In the second group it can be seen that sDFT-PW91/PW91k interaction energies are not attractive enough to fit the reference, but usually the functional form is qualitatively acceptable. At short distances, however, interaction energies are usually more attractive than the reference. Regarding the last group, consisting mainly of X–H⋯π-interactions, sDFT-PW91/PW91k interaction energies are still more attractive than KS-PW91 and the error with respect to the reference is typically in the range of chemical accuracy for the whole PES.
6.2 S66x8 test set
We extend our investigation on PESs from sDFT with the larger S66x8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 42,68 test set, which consists of equilibrium structures of the complexes described in Table 4 plus 7 displaced structures for each complex in the set. The MADs are visualized in Fig. 9. The complete set of figures for all PESs together with the values corresponding to Fig. 9 are provided in the ESI.† Here, we choose to provide examples for six complexes for each of the three categories (hydrogen bonding, vdW, mixed interactions). The first set is presented in Fig. 10 for hydrogen-bonded complexes.
42,68 test set, which consists of equilibrium structures of the complexes described in Table 4 plus 7 displaced structures for each complex in the set. The MADs are visualized in Fig. 9. The complete set of figures for all PESs together with the values corresponding to Fig. 9 are provided in the ESI.† Here, we choose to provide examples for six complexes for each of the three categories (hydrogen bonding, vdW, mixed interactions). The first set is presented in Fig. 10 for hydrogen-bonded complexes.
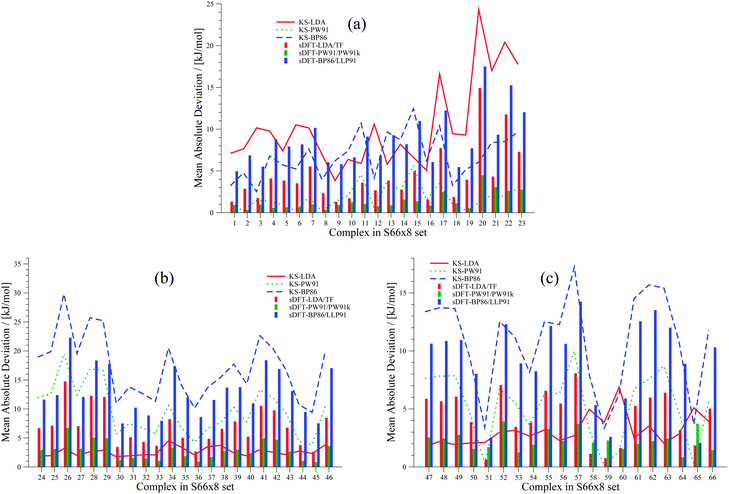 |
| | Fig. 9 MADs per molecule of sDFT interaction energies with respect to reference CCSD(T)/CBS energies taken from ref. 68 for the S66x8 test set. The different pictures describe (a) hydrogen-bonded complexes, (b) vdW complexes and (c) mixed complexes. MADs from KS-DFT have been included for comparison. | |
 |
| | Fig. 10 PESs for six hydrogen-bonded examples from the S66x8 test set: (a) water dimer, (b) MeOH dimer, (c) MeNH2–MeOH, (d) peptide dimer, (e) AcOH dimer (f) AcNH2–uracil. | |
As we have seen before, KS-LDA is too attractive (with respect to the reference) for all hydrogen-bonded complexes. Moreover, interaction energies derived from its sDFT counterpart are in general more repulsive than the reference. Therefore equilibrium distances from sDFT-LDA/TF are usually larger than those from KS-LDA, but also fit better to the reference. KS-PW91 interaction energies are very similar to those from sDFT-PW91/PW91k for systems involving one hydrogen bond between two hydroxy-groups. If an N–H-group is the acceptor of a hydrogen bond from an electron donating group (e.g. AcNH2 dimer), the differences become larger and sDFT-PW91/PW91k is usually more attractive than KS-PW91 (and mostly also the reference) around distances smaller than the reference equilibrium. The same behavior can be recognized for sDFT-BP86/LLP91 and its KS-DFT counterpart. If N–H-groups take part as the accepting partner in a hydrogen bond, sDFT-BP86/LLP91 interaction energies are close to KS-BP86, but at smaller distances they tend to be more attractive. However, BP86 in any formulation is not able to recover reference interaction energies, but equilibrium distances are modeled quite well for hydrogen-bonded complexes in this set.
The second set, containing six examples from vdW-bonded complexes, is shown in Fig. 11. Again KS-LDA describes potential energy surfaces of π–π-stacked complexes quite accurately, while equilibrium distances are often too small compared to the reference. For larger distances KS-LDA is always quite accurate for this group of vdW-dominated interactions (also due to the smaller magnitude of interaction energies). With sDFT-LDA/TF the bonding character of KS-LDA is kept, but interaction energies are more repulsive than the reference. Equilibrium distances, however, are often quite accurate. KS-PW91 gives bounding curves, but they are usually too repulsive around reference equilibrium geometries. Hence, equilibrium distances derived from KS-PW91 are usually too large. Interaction energies derived from sDFT-PW91/PW91k for π–π-stacked interactions are often close to the reference, but the repulsive parts of the PESs are again too attractive. Thus, equilibrium distances are usually too small. KS-BP86 results in repulsive curves without bonding character, except for some rare cases where equilibrium distances are very poor. sDFT-BP86/LLP91 follows the trends of its KS-DFT counterpart, but tends to be more attractive around reference equilibrium geometries.
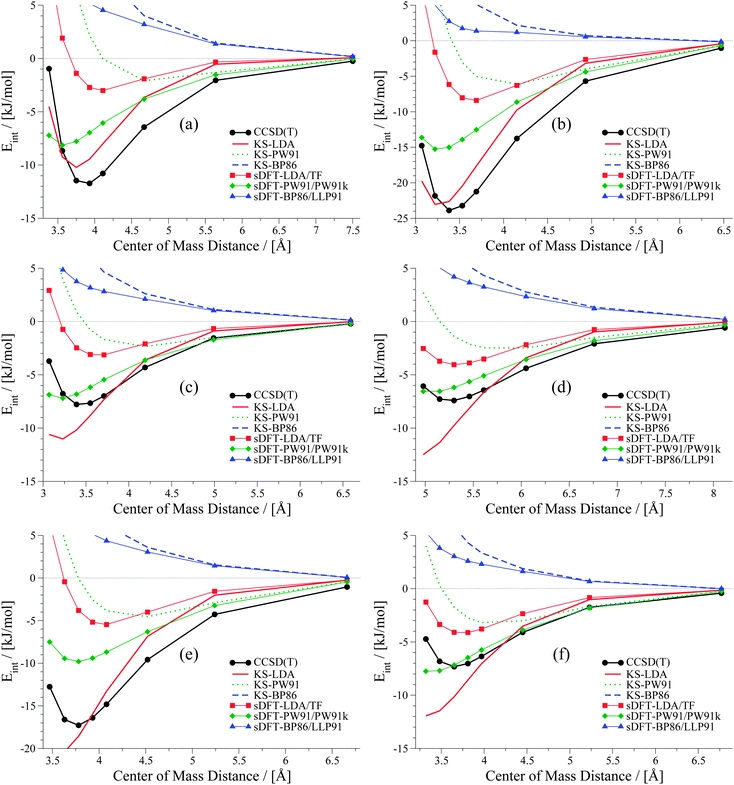 |
| | Fig. 11 PESs for six vdW-bonded examples from the S66x8 test set: (a) benzene dimer, (b) benzene–uracil, (c) pyridine–ethene, (d) neopentane dimer, (e) uracil–cyclopentane and (f) ethyne–pentane. | |
The six examples of the last set consisting of mixed-type interactions are presented in Fig. 12. The trends discussed above for LDA and PW91 also hold for this set of PESs, so that sDFT-LDA/TF often describes reference equilibrium distances better than its KS-DFT counterpart. Interaction energies from sDFT-LDA/TF are again mostly not attractive enough, while KS-LDA is much too attractive at short distances (always compared to the reference). KS-PW91 is in general too repulsive. However, interaction energies as well as equilibrium distances for the ethyne-involving complexes in this group are very often quite accurate. Also for this set, sDFT-PW91/PW91k is systematically more attractive than its KS-DFT counterpart, which leads to equilibrium distances that are usually shorter than the reference. As we have seen in Section 5, interaction energies from sDFT-PW91/PW91k can be quite accurate at reference equilibrium distances. Nonetheless, the qualitative picture is usually not correct, because the repulsive part is not described correctly. KS-BP86 shows bounding curves for complexes where electrostatic interactions are more pronounced. Apart from that, interaction energies from KS-BP86 are usually too repulsive and equilibrium distances are often too large. In those cases where equilibrium distances from KS-BP86 nicely fit the reference, PESs derived from sDFT-BP86/LLP91 are too attractive at shorter distances. This trend for mixed-bonded interactions is similar to the one observed for PW91 when comparing KS-DFT and sDFT. Here this is mostly the case if some kind of hydrogen-bonded interaction without proper orientation of the donating lone-pair towards the accepting X–H-bond is present.
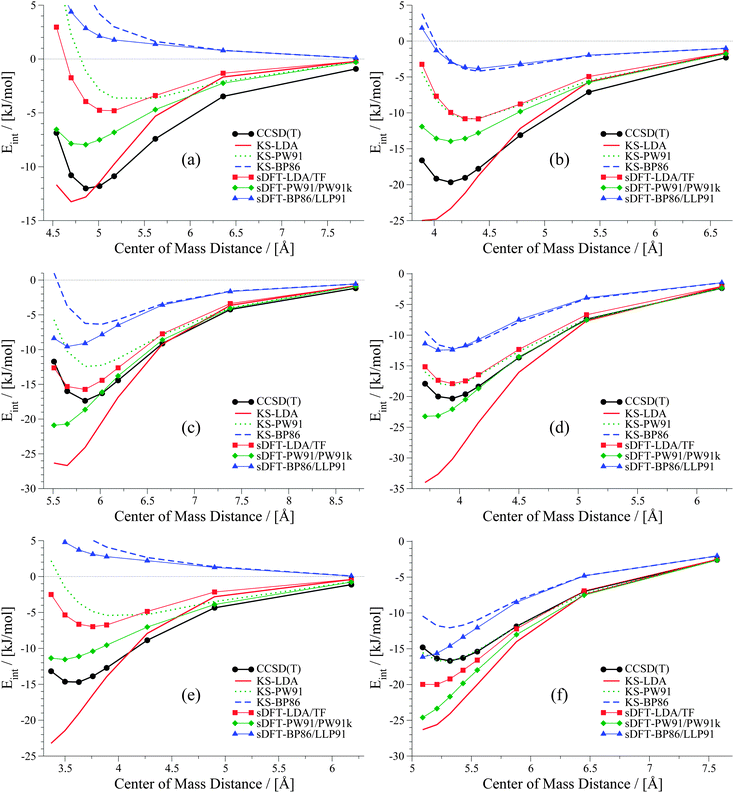 |
| | Fig. 12 PESs for six mixed-bonded examples from the S66x8 test set: (a) benzene dimer T-shaped, (b) benzene–AcOH, (c) pyridine dimer, (d) ethyne–AcOH, (e) pentane–AcNH2 and (f) pyridine–ethyne. | |
6.3 Applying DFT-D3(BJ) to sDFT
Already in previous work, the idea of improving sDFT interaction energies by empirical DFT-D corrections was explored by one of the present authors.24 In that work, the DFT-D2 scheme76 and the sDFT-BLYP/TW0245,47,77 approximations were used, but only reference equilibrium structures were considered. For PESs, we have seen in the previous sections that sDFT-BP86/LLP91 results are often very similar to their KS-DFT counterparts, and thus show the typical weaknesses of non-dispersion corrected KS-DFT approximations. Hence, it can be anticipated that the DFT-D scheme should lead to similar improvements in KS-BP86 and in sDFT-BP86/LLP91. To test this assumption, we apply the latest version of the DFT-D scheme, DFT-D3(BJ),10,78 in its original parametrization for KS-BP86 to sDFT-BP86/LLP91 interaction energies. The DFT-D3(BJ) correction was calculated using the dftd3 program (V3.1 Rev 0).79 As most of the data points in the S22x5 and S66x8 test sets describe large distances, the average MAD with sDFT-BP86/LLP91-D3(BJ) gets systematically lower. The average MAD drops down from 9.68 to 3.84 kJ mol−1 and from 10.32 to 3.10 kJ mol−1 for the S22x5 and S66x8 test sets, respectively. Two examples are shown in Fig. 13 to illustrate the effect of DFT-D3(BJ) for sDFT-BP86/LLP91 for a hydrogen-bonded and a vdW-bonded complex. The complete set of sDFT-BP86/LLP91-D3(BJ) PESs is provided in the ESI.†
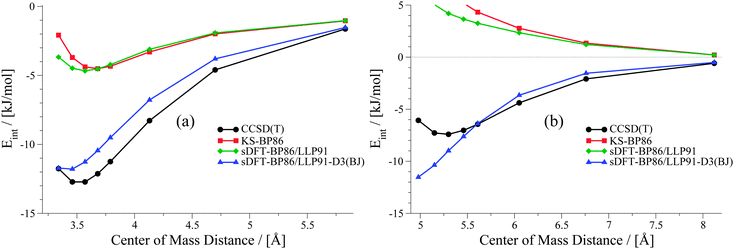 |
| | Fig. 13 PESs from sDFT-D3(BJ) for (a) MeNH2–MeOH and (b) neopentane dimer. | |
Clearly, interaction energies at larger distances are improved significantly. But in cases where the description of the PES with sDFT-BP86/LLP91 at short distances deviates from KS-BP86, the DFT-D3(BJ) correction usually further worsens the result since it adds additional attractive contributions. Therefore, the description of the PESs is qualitatively only improved for large distances. An adaption of the damping function for short distances is thus needed for further improvement of sDFT-BP86/LLP91-D3(BJ) interaction energies.
6.4 Repulsive empirical corrections for sDFT
Contrary to the behavior of sDFT-BP86/LLP91, we have seen that sDFT-PW91/PW91k interaction energies are often very good at reference equilibrium distances. But they are usually more attractive than the reference at shorter distances for the examples in the S22x5 and S66x8 test sets. In those cases, equilibrium distances tend to be too short. Here, we provide a first test for a possible empirical correction of interaction energies (and consequently also equilibrium bond distances) of the widely used sDFT-PW91/PW91k approximation. Inspired by the corresponding expressions for dispersion corrections in the DFT-D methods,2 we model the difference ΔEint = Erefint − EsDFT-PW91/PW91kint between reference (Erefint) and sDFT-PW91/PW91k (EsDFT-PW91/PW91kint) interaction energies [defined according to eqn (12)] with an empirical repulsive energy term. We decide to use a Buckingham-like exponential, which is motivated by the fact that the repulsive correction should be related to the overlap of the subsystem densities. Preliminary studies also revealed that the repulsive 1/R12 component of a Lennard-Jones potential is not suited here. Finally, the atom-pair dependent energy correction Γ is given by| | 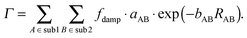 | (14) |
Here, A and B refer to atoms of subsystems 1 and 2, respectively and aIJ and bIJ are empirical atom-pair (IJ) specific parameters. The damping term fdamp makes sure that the correction Γ in eqn (14) vanishes for regions where descriptions of KS-DFT and sDFT should be equivalent. The damping function [eqn (15)] thus differs from the form of a zero damping function as employed in ref. 78 only by the sign of the exponent γ in the denominator.| | 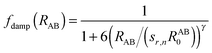 | (15) |
The function has a value of one if the internuclear distance equals zero, and it decays smoothly to zero for larger distances. The parameter RAB0 is a pre-defined cut-off radius for atom pair AB taken from ref. 10. The parameter sr,n is a radius scaling factor (in principle functional dependent) and γ is a parameter that defines the steepness of the function. For fitting our test parameters here, we only used those complexes from the S22x5 test set for which sDFT-PW91/PW91k was clearly overbinding, i.e., where interaction energies at equilibrium distances were lower than the reference (complexes 1, 2, 4, 6–9 and 16, cf.Table 3 and Fig. 3). The model function Γ [eqn (14)] without fdamp was fitted to ΔEint using the locally modified Levenberg–Marquardt algorithm from ref. 80. Afterwards, parameters for the damping function fdamp were obtained by fitting the complete model function Γ to ΔEint while fixing the optimized parameters aIJ and bIJ, resulting in sr,n = 0.51 and γ = 6.00. Optimized parameters with negative sign were discarded in order not to add artificial attractive terms. The corrected version of sDFT-PW91/PW91k interaction energies, will be termed sDFT-PW91/PW91k-R in the following. It is calculated as| | | EsDFT-PW91/PW91k-Rint = EsDFT-PW91/PW91kint + Γ. | (16) |
The final results from the fit are summarized in Table 6. Interaction energies from sDFT-PW91/PW91k-R are by construction more repulsive than those from sDFT-PW91/PW91k. For the chosen training set of 8 complexes (vide supra) the MAD of the interaction energies for the respective PES was significantly improved (see Fig. 14), showing that the form of the correction is adequate for these cases. Also for the other complexes in the S22x5 test set, equilibrium distances as well as the qualitative picture of the PESs are often improved (cf.Fig. 15). Since we only add repulsive corrections, however, interaction energies often get worse. In conclusion, this fit is not a general improvement, although it can improve the description of equilibrium distances and the general shapes of the PESs.
Table 6 Final set of parameters for sDFT-PW91/PW91k-R
| |
a
IJ
parameters |
b
IJ
parameters |
| H |
C |
N |
O |
H |
C |
N |
O |
| H |
6603.16 |
0.00 |
5.65 |
10198.66 |
3.19 |
0.00 |
0.64 |
3.57 |
| C |
— |
5991.67 |
0.00 |
0.00 |
— |
2.59 |
0.00 |
0.00 |
| N |
— |
— |
0.00 |
82.60 |
— |
— |
0.00 |
0.60 |
| O |
— |
— |
— |
0.00 |
— |
— |
— |
0.00 |
 |
| | Fig. 14 MADs of interaction energies per molecule for the empirically repulsion-corrected version sDFT-PW91/PW91k-R in comparison to non-corrected sDFT-PW91/PW91k results for the S22x5 test set. All values given in kJ mol−1. | |
 |
| | Fig. 15 Interaction energies for the sDFT-PW91/PW91k approximation and the empirically repulsion-corrected version sDFT-PW91/PW91k-R in comparison to reference data for the uracil dimer in the S22x5 test set. | |
7 Discussion and conclusions
In this work, we have investigated sDFT interaction energies for three different conjoint approximations54 (sDFT-LDA/TF, sDFT-PW91/PW91k, sDFT-BP86/LLP91) for several test sets including the S22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 41 and S66
41 and S66![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 42 sets. We have confirmed that sDFT interaction energies from sDFT-LDA/TF and sDFT-PW91/PW91k are often better than their KS-DFT counterparts at reference (i.e., high-level wave-function) equilibrium geometries. But they are not generally better in reproducing equilibrium distances or shapes of PESs. We then investigated entire potential-energy curves from sDFT for 5 rare-gas dimer systems as well as for the S22x548 and S66x842 sets. The shapes of the PESs strongly depend on the choice of approximations used for Exc/Enadxc and Tnads. The bonding character of KS-DFT PESs (if existent for the respective complex) is usually reproduced by the sDFT counterpart. We have seen that sDFT-BP86/LLP91 shows the best agreement with the corresponding KS-DFT results. This similarity implies that the sDFT-BP86/LLP91 interaction energies share the weaknesses (especially for vdW-bonded complexes) with their KS-DFT counterpart, but this can easily be remedied by empirical DFT-D corrections. In the recent literature21–23,31,33 sDFT-PW91/PW91k is often mentioned for its good interaction energies at reference equilibrium geometries. This has been confirmed here. But equilibrium geometries from sDFT-PW91/PW91k are not necessarily of the same quality, since potential-energy curves are often not repulsive enough at short distances. Hence, we briefly explored the idea of using an empirical repulsive correction in the spirit of DFT-D. Our simple parametrization here demonstrates that this can improve bond distances and shapes of PESs from sDFT-PW91/PW91k. But since the error in sDFT-PW91/PW91k interaction energies does not show a uniform behaviour for different complexes, the correction in its present form often leads to worse interaction energies. Further work along these lines is clearly needed for high-quality PESs from sDFT.
42 sets. We have confirmed that sDFT interaction energies from sDFT-LDA/TF and sDFT-PW91/PW91k are often better than their KS-DFT counterparts at reference (i.e., high-level wave-function) equilibrium geometries. But they are not generally better in reproducing equilibrium distances or shapes of PESs. We then investigated entire potential-energy curves from sDFT for 5 rare-gas dimer systems as well as for the S22x548 and S66x842 sets. The shapes of the PESs strongly depend on the choice of approximations used for Exc/Enadxc and Tnads. The bonding character of KS-DFT PESs (if existent for the respective complex) is usually reproduced by the sDFT counterpart. We have seen that sDFT-BP86/LLP91 shows the best agreement with the corresponding KS-DFT results. This similarity implies that the sDFT-BP86/LLP91 interaction energies share the weaknesses (especially for vdW-bonded complexes) with their KS-DFT counterpart, but this can easily be remedied by empirical DFT-D corrections. In the recent literature21–23,31,33 sDFT-PW91/PW91k is often mentioned for its good interaction energies at reference equilibrium geometries. This has been confirmed here. But equilibrium geometries from sDFT-PW91/PW91k are not necessarily of the same quality, since potential-energy curves are often not repulsive enough at short distances. Hence, we briefly explored the idea of using an empirical repulsive correction in the spirit of DFT-D. Our simple parametrization here demonstrates that this can improve bond distances and shapes of PESs from sDFT-PW91/PW91k. But since the error in sDFT-PW91/PW91k interaction energies does not show a uniform behaviour for different complexes, the correction in its present form often leads to worse interaction energies. Further work along these lines is clearly needed for high-quality PESs from sDFT.
Finally, it should be pointed out that the results obtained here indicate only a minor dependence of the interaction energy on the embedding potential for vdW-bonded (and mixed-bonded) complexes. This can be seen from the fact that the promotion energy components of the interaction energies are often small (see the examples in Fig. 7 and 8 and the complete list of ΔEprommonomer in the ESI†). The differences in the embedding potentials for different sDFT approximations presented here are usually very small even for polar complexes, when judging from the differences caused in ΔEprommonomer: maximum differences in ΔEprommonomer occur between sDFT-LDA/TF and sDFT-BP86/LLP91 with 4.46 and 5.51 kJ mol−1 for the S22 (formic acid dimer) and S66 (acetic acid dimer) test sets, respectively.
Overall, we conclude that sDFT certainly has the potential to produce accurate PESs, if similar effort as in KS-DFT is spent for optimizing the corresponding energy contributions.
Acknowledgements
Financial support by the SFB 858 funded by the Deutsche Forschungsgemeinschaft is gratefully acknowledged.
References
- E. R. Johnson, I. D. Mackie and G. A. DiLabio, J. Phys. Org. Chem., 2009, 22, 1127 CrossRef CAS.
- S. Grimme, WIREs Comput. Mol. Sci., 2011, 1, 211 CrossRef CAS.
- J. Klimeš and A. Michaelides, J. Chem. Phys., 2012, 137, 120901 CrossRef PubMed.
- S. Kristyán and P. Pulay, Chem. Phys. Lett., 1994, 229, 175 CrossRef.
- Y. Zhao and D. G. Truhlar, J. Chem. Phys., 2006, 125, 194101 CrossRef PubMed.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215 CrossRef CAS.
- S. Grimme, J. Comput. Chem., 2004, 25, 1463 CrossRef CAS PubMed.
- P. Jurečka, J. Černý, P. Hobza and D. R. Salahub, J. Comput. Chem., 2004, 25, 1463 CrossRef PubMed.
- A. Tkatchenko and M. Scheffler, Phys. Rev. Lett., 2009, 102, 073005 CrossRef.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- M. Dion, H. Rydberg, E. Schröder, D. C. Langreth and B. I. Lundqvist, Phys. Rev. Lett., 2004, 92, 246401 CrossRef CAS PubMed.
- K. Lee, E. D. Murray, L. Kong, B. I. Lundqvist and D. C. Langreth, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 081101(R) CrossRef.
- O. A. von Lilienfeld, I. Tavernelli and U. Rothlisberger, Phys. Rev. Lett., 2004, 93, 153004 CrossRef.
- Y. Y. Sun, Y.-H. Kim, K. Lee and S. B. Zhang, J. Chem. Phys., 2008, 129, 154102 CrossRef CAS PubMed.
- G. Senatore and K. R. Subbaswamy, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 34, 5754 CrossRef CAS.
- P. Cortona, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44, 8454 CrossRef.
- C. R. Jacob and J. Neugebauer, WIREs Comput. Mol. Sci., 2014, 4, 325 CrossRef CAS.
- T. A. Wesołowski and A. Warshel, J. Phys. Chem., 1993, 97, 8050 CrossRef.
- T. A. Wesołowski and J. Weber, Chem. Phys. Lett., 1996, 248, 71 CrossRef.
- M. Dułak, J. W. Kamiński and T. A. Wesołowski, J. Chem. Theory Comput., 2007, 3, 735 CrossRef.
- M. Dułak and T. A. Wesołowski, J. Mol. Model., 2007, 13, 631 CrossRef PubMed.
- R. Kevorkyants, M. Dułak and T. A. Wesołowski, J. Chem. Phys., 2006, 124, 024104 CrossRef CAS PubMed.
- T. A. Wesołowski and F. Tran, J. Chem. Phys., 2003, 118, 2072 CrossRef PubMed.
- S. M. Beyhan, A. W. Götz and L. Visscher, J. Chem. Phys., 2013, 138, 094113 CrossRef PubMed.
- R. Kevorkyants, H. Eshuis and M. Pavanello, J. Chem. Phys., 2014, 141, 044127 CrossRef PubMed.
- M. Iannuzzi, B. Kirchner and J. Hutter, Chem. Phys. Lett., 2006, 421, 16 CrossRef CAS PubMed.
- R. G. Gordon and Y. S. Kim, J. Chem. Phys., 1972, 56, 3122 CrossRef CAS PubMed.
- Y. S. Kim and R. G. Gordon, J. Chem. Phys., 1974, 60, 1842 CrossRef CAS PubMed.
- T. A. Wesołowski, H. Chermette and J. Weber, J. Chem. Phys., 1996, 105, 9182 CrossRef PubMed.
- T. A. Wesołowski, J. Chem. Phys., 1997, 106, 8516 CrossRef PubMed.
- T. A. Wesołowski, Y. Ellinger and J. Weber, J. Chem. Phys., 1998, 108, 6078 CrossRef PubMed.
- F. Tran, J. Weber and T. A. Wesołowski, Helv. Chim. Acta, 2001, 84, 1489 CrossRef CAS.
- T. A. Wesołowski, P.-Y. Morgantini and J. Weber, J. Chem. Phys., 2002, 116, 6411 CrossRef PubMed.
- F. Tran, B. Alameddinee, T. A. Jenny and T. A. Wesołowski, J. Phys. Chem. A, 2004, 108, 9155 CrossRef CAS.
-
T. A. Wesołowski, One-electron Equations for Embedded Electron Density: Challenge for Theory and Practical Payoffs in Multi-Level Modeling of Complex Polyatomic Systems, in Computational Chemistry: Reviews of Current Trends, ed. J. Leszczynski, World Scientific, Singapore, 2006, vol. 10, pp. 1–82 Search PubMed.
- Y. Zhao and D. G. Truhlar, J. Phys. Chem. A, 2005, 109, 5656 CrossRef CAS PubMed.
- Y. Zhao and D. G. Truhlar, Phys. Chem. Chem. Phys., 2005, 7, 2701 RSC.
- Y. Zhao and D. G. Truhlar, J. Chem. Theory Comput., 2005, 1, 415 CrossRef CAS.
- A. W. Götz, S. M. Beyhan and L. Visscher, J. Chem. Theory Comput., 2009, 5, 3161 CrossRef.
- S. Laricchia, L. A. Constantin, E. Fabiano and F. D. Sala, J. Chem. Theory Comput., 2014, 10, 164 CrossRef CAS.
- P. Jurečka, J. Sponer, J. Černy and P. Hobza, Phys. Chem. Chem. Phys., 2006, 8, 1985 RSC.
- J. Řezáč, K. E. Riley and P. Hobza, J. Chem. Theory Comput., 2011, 7, 2427 CrossRef PubMed.
- J. P. Perdew,
et al.
, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 6671 CrossRef CAS.
-
J. P. Perdew, in Electronic Structure of Solids, ed. P. Ziesche and H. Eschrig, Akademie Verlag, Berlin, 1991, p. 11 Search PubMed.
- A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098 CrossRef CAS.
- J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822 CrossRef.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785 CrossRef CAS.
- L. Gráfová, M. Pitoňák, J. Řezáč and P. Hobza, J. Chem. Theory Comput., 2010, 6, 2365 CrossRef.
-
Recent Progress in Orbital-Free Density Functional Theory, ed. T. A. Wesołowski and Y. A. Wang, World Scientific, Singapore, 2013 Search PubMed.
- K. Morokuma, J. Chem. Phys., 1971, 55, 1236 CrossRef CAS PubMed.
- K. Kitaura and K. Morokuma, Int. J. Quantum Chem., 1976, 10, 325 CrossRef CAS.
- T. Ziegler and A. Rauk, Theor. Chim. Acta, 1977, 46, 1 CrossRef CAS.
- M. von Hopffgarten and G. Frenking, WIREs Comput. Mol. Sci., 2012, 2, 43 CrossRef CAS.
- H. Lee, C. Lee and R. G. Parr, Phys. Rev. A: At., Mol., Opt. Phys., 1991, 44, 768 CrossRef CAS.
- L. A. Thomas, Proc. Cambridge Philos. Soc., 1927, 23, 542 CrossRef CAS.
- E. Fermi, Z. Phys., 1928, 48, 73 CrossRef CAS.
- A. Lembarki and H. Chermette, Phys. Rev. A: At., Mol., Opt. Phys., 1994, 50, 5328 CrossRef CAS.
- C. R. Jacob, J. Neugebauer and L. Visscher, J. Comput. Chem., 2008, 29, 1011 CrossRef CAS PubMed.
- Amsterdam density functional program, Theoretical Chemistry, Vrije Universiteit, Amsterdam, URL: http://www.scm.com.
- E. van Lenthe and E. J. Baerends, J. Comput. Chem., 2003, 24, 1142 CrossRef CAS PubMed.
- G. te Velde,
et al.
, J. Comput. Chem., 2001, 22, 931 CrossRef CAS.
- S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553 CrossRef CAS.
- T. van Mourik and R. J. Gdanitz, J. Chem. Phys., 2002, 116, 9620 CrossRef CAS PubMed.
- M. J. Allen and D. J. Tozer, J. Chem. Phys., 2002, 117, 11113 CrossRef CAS PubMed.
- J. M. Pérez-Jordá and A. D. Becke, Chem. Phys. Lett., 1995, 233, 134 CrossRef.
-
A. M. Köster, et al., deMon 2003, NRC, Canada, http://www.deMon-software.com, 2003 Search PubMed.
-
D. R. Salahub, A. Goursot, J. Weber and A. M. Köster, Applied density functional theory and the deMon codes 1964–2004, in Theory and Applications of Computational Chemistry: The First Forty Years, ed. C. E. Dykstra, G. Frenking, K. S. Kim and G. E. Scuseria, Elsevier, Amsterdam, 2005, pp. 1079–1097 Search PubMed.
- J. Řezáč,
et al.
, Collect. Czech. Chem. Commun., 2008, 73, 1261 CrossRef , http://www.begdb.com.
-
M. J. Frisch, et al., Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford CT, 2013 Search PubMed.
- F. Neese, WIREs Comput. Mol. Sci., 2012, 2, 73 CrossRef CAS.
- T. H. Dunning Jr., J. Chem. Phys., 1989, 90, 1007 CrossRef PubMed.
- L. Goerigk, H. Kruse and S. Grimme, ChemPhysChem, 2011, 12, 3421 CrossRef CAS PubMed.
- N. Mardirossian and M. Head-Gordon, Phys. Chem. Chem. Phys., 2014, 16, 9904 RSC.
- J. Wellendorff,
et al.
, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 235149 CrossRef.
- M. Swart, T. van der Wijst, C. F. Guerra and F. M. Bickelhaupt, J. Mol. Model., 2007, 13, 1245–1257 CrossRef CAS PubMed.
- S. Grimme and T. Schwabe, Phys. Chem. Chem. Phys., 2006, 8, 4398 RSC.
- F. Tran and T. A. Wesołowski, Int. J. Quantum Chem., 2002, 89, 441 CrossRef CAS.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456 CrossRef CAS PubMed.
-
S. Grimme, http://www.thch.uni-bonn.de/tc/.
-
W. H. Press, S. A. Teukolsky, W. T. Vetterling and B. P. Flannery, Numerical Recipes in Fortran 77, 1992 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c4cp04936e |
| ‡ Note that promotion energies are in principle arbitrary, because the partitioning of the density is in principle arbitrary. However, this is not a problem in practical calculations (for more details, see ref. 24). |
|
| This journal is © the Owner Societies 2015 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article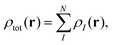
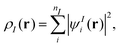
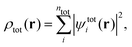
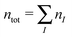 is the total number of electrons in all subsystems. The total energy expression in subsystem DFT can be formulated such that the DFT nature of the approach is emphasized,
is the total number of electrons in all subsystems. The total energy expression in subsystem DFT can be formulated such that the DFT nature of the approach is emphasized,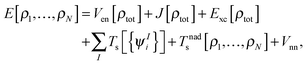
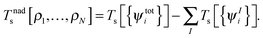
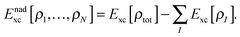
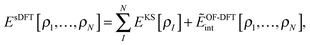
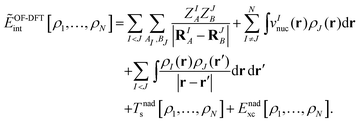
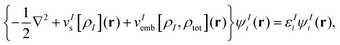
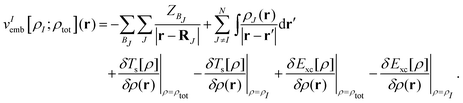
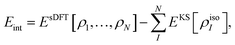
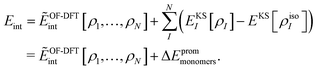




![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 48,68 test set, which consists of the complexes listed in Table 3. In addition to the equilibrium structures, this set contains four extra structures displaced from equilibrium for each complex in the set. In the displaced structures, the intermolecular distance is varied, so that the S22x5 set concerns representative parts of the intermolecular potential-energy curves. The MADs for each set of sDFT calculations for the S22x5 test set are presented in Fig. 5 along with their KS-DFT counterparts. Not just for equilibrium structures, but also for PESs, the average MAD of sDFT-PW91/PW91k with a magnitude of 2.92 kJ mol−1 is the smallest among the DFT approximations tested here. Six examples for PESs are presented in Fig. 6. The complete set, together with the values graphically shown in Fig. 5 are provided in the ESI.†
48,68 test set, which consists of the complexes listed in Table 3. In addition to the equilibrium structures, this set contains four extra structures displaced from equilibrium for each complex in the set. In the displaced structures, the intermolecular distance is varied, so that the S22x5 set concerns representative parts of the intermolecular potential-energy curves. The MADs for each set of sDFT calculations for the S22x5 test set are presented in Fig. 5 along with their KS-DFT counterparts. Not just for equilibrium structures, but also for PESs, the average MAD of sDFT-PW91/PW91k with a magnitude of 2.92 kJ mol−1 is the smallest among the DFT approximations tested here. Six examples for PESs are presented in Fig. 6. The complete set, together with the values graphically shown in Fig. 5 are provided in the ESI.†




![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 42,68 test set, which consists of equilibrium structures of the complexes described in Table 4 plus 7 displaced structures for each complex in the set. The MADs are visualized in Fig. 9. The complete set of figures for all PESs together with the values corresponding to Fig. 9 are provided in the ESI.† Here, we choose to provide examples for six complexes for each of the three categories (hydrogen bonding, vdW, mixed interactions). The first set is presented in Fig. 10 for hydrogen-bonded complexes.
42,68 test set, which consists of equilibrium structures of the complexes described in Table 4 plus 7 displaced structures for each complex in the set. The MADs are visualized in Fig. 9. The complete set of figures for all PESs together with the values corresponding to Fig. 9 are provided in the ESI.† Here, we choose to provide examples for six complexes for each of the three categories (hydrogen bonding, vdW, mixed interactions). The first set is presented in Fig. 10 for hydrogen-bonded complexes.




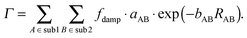
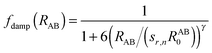
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 41 and S66
41 and S66![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 42 sets. We have confirmed that sDFT interaction energies from sDFT-LDA/TF and sDFT-PW91/PW91k are often better than their KS-DFT counterparts at reference (i.e., high-level wave-function) equilibrium geometries. But they are not generally better in reproducing equilibrium distances or shapes of PESs. We then investigated entire potential-energy curves from sDFT for 5 rare-gas dimer systems as well as for the S22x548 and S66x842 sets. The shapes of the PESs strongly depend on the choice of approximations used for Exc/Enadxc and Tnads. The bonding character of KS-DFT PESs (if existent for the respective complex) is usually reproduced by the sDFT counterpart. We have seen that sDFT-BP86/LLP91 shows the best agreement with the corresponding KS-DFT results. This similarity implies that the sDFT-BP86/LLP91 interaction energies share the weaknesses (especially for vdW-bonded complexes) with their KS-DFT counterpart, but this can easily be remedied by empirical DFT-D corrections. In the recent literature21–23,31,33 sDFT-PW91/PW91k is often mentioned for its good interaction energies at reference equilibrium geometries. This has been confirmed here. But equilibrium geometries from sDFT-PW91/PW91k are not necessarily of the same quality, since potential-energy curves are often not repulsive enough at short distances. Hence, we briefly explored the idea of using an empirical repulsive correction in the spirit of DFT-D. Our simple parametrization here demonstrates that this can improve bond distances and shapes of PESs from sDFT-PW91/PW91k. But since the error in sDFT-PW91/PW91k interaction energies does not show a uniform behaviour for different complexes, the correction in its present form often leads to worse interaction energies. Further work along these lines is clearly needed for high-quality PESs from sDFT.
42 sets. We have confirmed that sDFT interaction energies from sDFT-LDA/TF and sDFT-PW91/PW91k are often better than their KS-DFT counterparts at reference (i.e., high-level wave-function) equilibrium geometries. But they are not generally better in reproducing equilibrium distances or shapes of PESs. We then investigated entire potential-energy curves from sDFT for 5 rare-gas dimer systems as well as for the S22x548 and S66x842 sets. The shapes of the PESs strongly depend on the choice of approximations used for Exc/Enadxc and Tnads. The bonding character of KS-DFT PESs (if existent for the respective complex) is usually reproduced by the sDFT counterpart. We have seen that sDFT-BP86/LLP91 shows the best agreement with the corresponding KS-DFT results. This similarity implies that the sDFT-BP86/LLP91 interaction energies share the weaknesses (especially for vdW-bonded complexes) with their KS-DFT counterpart, but this can easily be remedied by empirical DFT-D corrections. In the recent literature21–23,31,33 sDFT-PW91/PW91k is often mentioned for its good interaction energies at reference equilibrium geometries. This has been confirmed here. But equilibrium geometries from sDFT-PW91/PW91k are not necessarily of the same quality, since potential-energy curves are often not repulsive enough at short distances. Hence, we briefly explored the idea of using an empirical repulsive correction in the spirit of DFT-D. Our simple parametrization here demonstrates that this can improve bond distances and shapes of PESs from sDFT-PW91/PW91k. But since the error in sDFT-PW91/PW91k interaction energies does not show a uniform behaviour for different complexes, the correction in its present form often leads to worse interaction energies. Further work along these lines is clearly needed for high-quality PESs from sDFT.