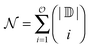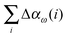Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Incremental evaluation of coupled cluster dipole polarizabilities†
Joachim
Friedrich
*a,
Harley R.
McAlexander
b,
Ashutosh
Kumar
b and
T. Daniel
Crawford
b
aInstitute for Chemistry, Chemnitz University of Technology, Straße der Nationen 62, 09111 Chemnitz, Germany. E-mail: joachim.friedrich@chemie.tu-chemnitz.de
bDepartment of Chemistry, Virginia Tech, Blacksburg, Virginia 24061, USA
First published on 16th December 2014
Abstract
In this work we present the first implementation of the incremental scheme for coupled cluster linear-response frequency-dependent dipole polarizabilities. The implementation is fully automated and makes use of the domain-specific basis set approach. The accuracy of the approach is determined on the basis of a test suite of 47 molecules and small clusters. The local approximation in the coupled cluster singles and doubles polarizability exhibits a mean error of 0.02% and a standard deviation of 0.32% when using a third-order incremental expansion. With the proposed approach, it is possible to compute polarizabilities with larger basis sets compared to the canonical implementation and thus it is possible to obtain higher total accuracy. The incremental scheme yields the smallest errors for weakly-bound and quasi-linear systems, while two- and three-dimensional (cage-like) structures exhibit somewhat larger errors as compared to the full test set.
1 Introduction
Quantum chemical methods such as coupled cluster theory1–4 can provide robust and reliable simulations of both resonant and non-resonant interactions of molecules with electric and magnetic fields.5 The coupled cluster singles and doubles (CCSD) method,6 as well as CCSD augmented with approximate triples [e.g., CCSD(T) or CC3],7,8 have been found to provide very high accuracy in simulations of UV/vis9–14 and circular dichroism spectra15–19 as well as dipole (hyper)polarizabilities, magnetizabilities, or optical rotations.17–25Unfortunately, conventional coupled cluster methods based on canonical molecular orbitals (MOs) are limited to relatively small molecules and clusters (containing ca. 20 non-hydrogen atoms, in the absence of symmetry) both due to their slow convergence with respect to the one-particle basis set26 and their high-degree polynomial scaling—![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (N6) for CCSD and at least
(N6) for CCSD and at least ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (N7) for methods that include triples. The former typically requires basis functions with high levels of angular momentum for precise computations near the complete-basis-set (CBS) limit, though the problem can be reduced somewhat though CBS extrapolations27 or by introducing terms into the wave function that include the electron–electron distance explicitly.28,29
(N7) for methods that include triples. The former typically requires basis functions with high levels of angular momentum for precise computations near the complete-basis-set (CBS) limit, though the problem can be reduced somewhat though CBS extrapolations27 or by introducing terms into the wave function that include the electron–electron distance explicitly.28,29
The polynomial scaling wall was first addressed by the pioneering efforts of Pulay and Saebø in the development of the local correlation framework.30,31 By adopting a more localized representation of the occupied and virtual MO spaces, one can take advantage of the resulting sparsity in the wave function, reducing the number of parameters/amplitudes that must be computed and stored. The Pulay–Saebø approach has been utilized with great success by Werner, Schütz, and co-workers, for example, who have extended the applicability of coupled cluster methods to systems containing more than a hundred atoms.32–38 Alternative local correlation approaches in the same spirit include the orbital-specific virtual idea of Yang et al.39 and the local pair-natural-orbital (LPNO) approach recently reintroduced by Neese and co-workers.40–42 Other methods make use of a fragmentation approach in which a larger system is partitioned into smaller components, such as the fragment-MO approach of Fedorov, Kitaura, Gordon and co-workers,43–47 divide-and-conquer scheme,48–50 the natural linear scaling coupled cluster51–53 or the cluster-in-molecule method (CIM).54–60 (For a recent review of fragmentation methods, see ref. 61.)
While the development of fast coupled cluster methods to compute highly accurate energies of large systems has seen great success in the last few years, the computation of many other properties has advanced more slowly. Within the Pulay–Saebø framework, Werner, Schütz, Korona, and co-workers62–64 have carried out locally correlation coupled cluster computations of dipole moments, static polarizabilities, and excitation energies at the CCSD level, while Schütz and co-workers have reported local second-order CC (CC2) computations of transition properties, excitation energies, and excited-state dipole moments.65–67 Crawford and co-workers have also utilized the Pulay–Saebø approach in the computation of dynamic response functions, including excitation energies,68 frequency-dependent polarizabilities,69 and optical rotations.70–72
In this work we apply the incremental scheme of Stoll73–75 to compute the CCSD frequency-dependent dipole polarizabilities. The incremental scheme is a generalization of the Bethe–Goldstone expansion and was introduced to quantum chemistry by Nesbet.76–78 In this method the system is divided into domains of localized occupied orbitals. The total energy of the system is obtained by computing the correlation energies of single domains, of domain pairs, of domain triples, etc. until the desired accuracy is obtained. This method was successfully applied to compute coupled cluster energies in various applications for periodic systems,79–90 to closed-91–98 and open-shell molecular systems,99,100 and recently also to metals with a multireference wavefunction.101 In the context of properties, Yang and Dolg computed static first- and second-order polarizabilities102 and Friedrich et al. computed dipole and quadrupole moments.103 In this work we implemented the incremental CCSD polarizabilities within the PSI4 program package using the domain-specific basis set approach to reduce the computational effort. The performance of the incremental scheme for CCSD polarizabilities is analyzed for a set of 47 molecules using the cc-pVDZ basis set and for 23 using the aug-cc-pVDZ basis set.
Finally we note that the errors provided in this work are solely those of the local approximations. The small double-ζ basis sets applied in this work introduce a significant error in the dipole-polarizability and therefore it is necessary to use significantly larger basis sets in production calculations.104 When attempting to achieve high accuracy coupled cluster calculations, it is also necessary to include higher excitations in the calculations of the polarizabilities.105
2 Theory
In coupled cluster response theory,5,106 the linear response function associated with dynamic perturbations![[A with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0041_20d1.gif) and
and ![[B with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0042_20d1.gif) is the second derivative of the coupled cluster time-averaged Lagrangian functional (quasi-energy),
is the second derivative of the coupled cluster time-averaged Lagrangian functional (quasi-energy),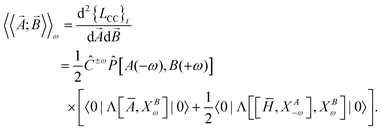 | (1) |
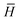 = e−THeT, = e−THeT, | (2) |
![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) , symmetrizes the expression with respect to the perturbations and Ĉ±ω symmetrizes with respect to complex conjugation and sign reversal of the frequency, ω. The first-order perturbed wave functions with respect to perturbation A, XAω, are obtained by solving the systems of linear equations,
, symmetrizes the expression with respect to the perturbations and Ĉ±ω symmetrizes with respect to complex conjugation and sign reversal of the frequency, ω. The first-order perturbed wave functions with respect to perturbation A, XAω, are obtained by solving the systems of linear equations,〈ϕ|(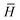 − ω)XAω|0〉 = −〈ϕ| − ω)XAω|0〉 = −〈ϕ|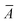 |0〉. |0〉. | (3) |
If the operators ![[A with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0041_20d1.gif) and
and ![[B with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0042_20d1.gif) are both taken to be the electric-dipole operator (which can be cast in either the length or velocity representations),107 the frequency-dependent dipole-polarizability tensor, αω, is the negative of the resulting linear-response function
are both taken to be the electric-dipole operator (which can be cast in either the length or velocity representations),107 the frequency-dependent dipole-polarizability tensor, αω, is the negative of the resulting linear-response function
| αω = −〈〈μ;μ〉〉ω. | (4) |
In conventional calculations of the coupled cluster linear response function, contributions arising from the relaxation of the reference MOs (typically Hartree–Fock orbitals) are neglected in order to preserve the (first-order) pole structure of the response function as the field frequency approaches a resonance. The MO response is typically small for such properties and accounted for in large part by the inclusion of the single-excitation operator in the cluster expansion.108
The incremental scheme is a many-body approach where the total system is partitioned into disjoint sets of localized occupied orbitals, referred to as one-site domains.109–111 In this scheme only the correlation part of the energy is partitioned, and the total energy of the system is computed by:73,109
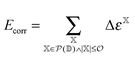 | (5) |
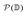 is the power set of the set of the domains
is the power set of the set of the domains ![[Doublestruck D]](https://www.rsc.org/images/entities/char_e167.gif) . The restriction to the cardinality of the sets
. The restriction to the cardinality of the sets 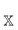 truncates the incremental series at the desired order
truncates the incremental series at the desired order ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) . The general increment is defined as:
. The general increment is defined as: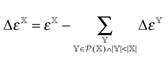 | (6) |
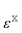 is the correlation energy of the combined subsystems of
is the correlation energy of the combined subsystems of 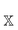 . Properties that may be expressed as (quasi)energy derivatives, such as the frequency-dependent dipole-polarizability, may be calculated in exactly the same manner as the energy:
. Properties that may be expressed as (quasi)energy derivatives, such as the frequency-dependent dipole-polarizability, may be calculated in exactly the same manner as the energy: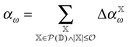 | (7) |
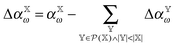 | (8) |
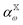 is the polarizability of the combined subsystems of
is the polarizability of the combined subsystems of 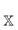 . Furthermore this task is somewhat simplified in the case of response properties, in that orbital relaxation contributions are excluded, as noted above.
. Furthermore this task is somewhat simplified in the case of response properties, in that orbital relaxation contributions are excluded, as noted above.
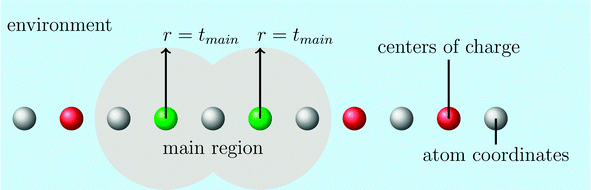
The computation can be further simplified by reducing the virtual space in each partition. This can be accomplished via the domain-specific basis set approximation, within which we classify the atoms into a main region and its environment using the parameter tmain (see Fig. 1). With this procedure we select all atoms close to the occupied orbitals in the domain as important and thus treat them with a large basis set, whereas all atoms in the environment are treated with a small double-ζ basis set without polarization functions. After the construction of the domain-specific basis set we generate orthogonal localized occupied orbitals in this basis set by a Hartree–Fock calculation and a subsequent Boys localization.112
Finally, a distance screening cutoff may be employed to achieve linear scaling in the number of domain calculations with increasing the size of the system. Considering eqn (5) the number of calculations ![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) grows with
grows with
However it is not necessary to compute all increments, since the increments decay with increasing order and with the spatial distance of the underlying domains. We account for this by applying an order-dependent truncation threshold tdist(i) = f/(i − 1)2, where i is the index of the order and f an adjustable parameter (vide infra).110,113
3 Computational details
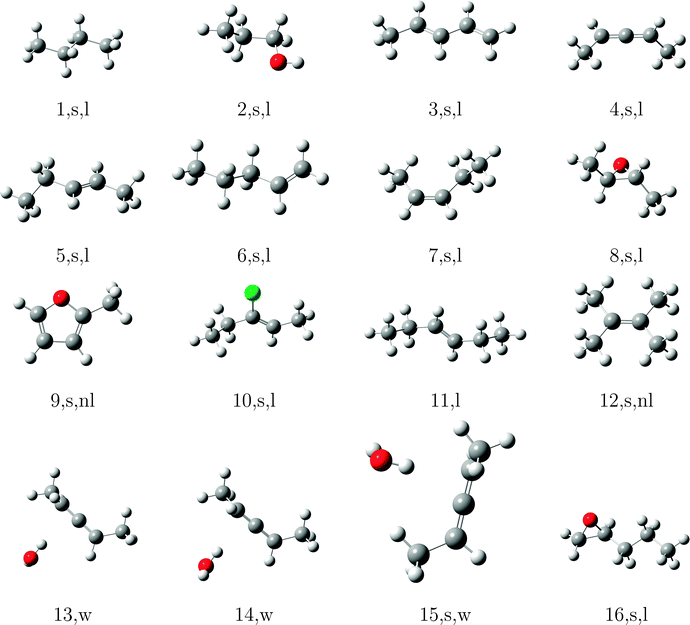
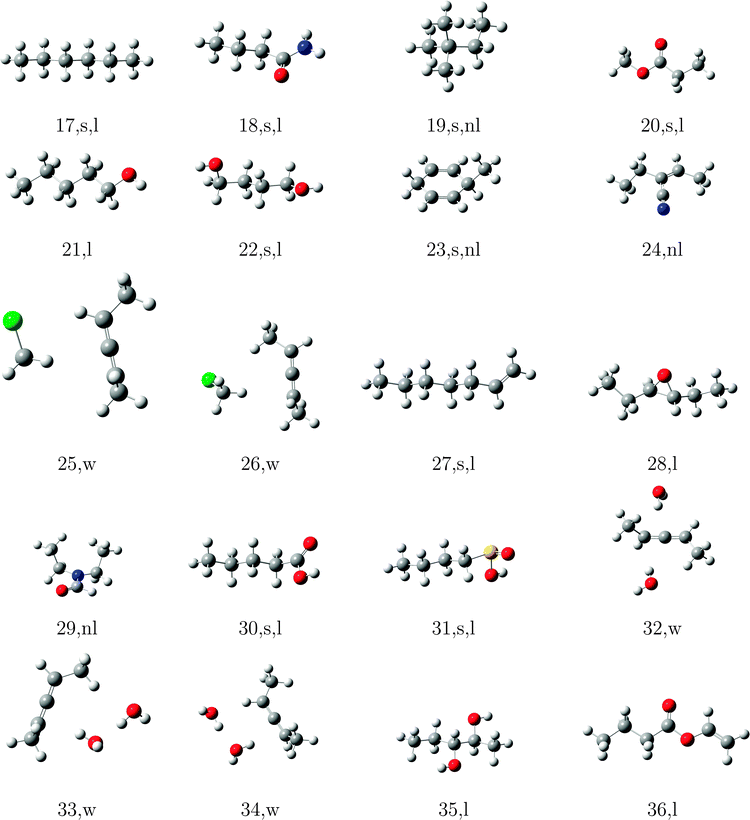
In order to test the incremental scheme's performance for dynamic polarizabilities, a test set of 47 molecules and clusters was selected containing both first row (C, O, N) and second row (S, Cl) elements. The systems are shown in Tables 1–3 and are ordered according to the increasing magnitude of the CCSD correlation energy. The Cartesian coordinates of each structure, the incremental CCSD and MP2 energies, and the corresponding errors are given in the ESI.† Most of the structures were optimized at the BP86/def2-TZVP114–117 level of theory, as reported in ref. 118, and structures 4, 13–15, 25, 26, 32–34, 41–45 were optimized at the B3LYP/aug-cc-pVDZ level of theory.119–124The partitioning of the occupied space was carried with a fully automatic black box scheme,118 in conjunction with coupled cluster calculations performed with a development version of the PSI4 program package.125 The truncation parameters113,118,126 in the incremental series are tmain = 3 Bohr, the dsp = 4 and f = 30. dsp is a measure for the number of occupied orbitals in a domain, i.e. it controls the size of the domain. The main region of each increment was treated with the cc-pVDZ basis set for the large test set and with the aug-cc-pVDZ basis set in smaller subset. In the environment we applied the 6-31G basis set127 in all calculations. The required increment data such as MO-coefficients, overlap and dipole integrals was obtained via an interface to the PSI4 code. Core orbitals (1s for C, N, and O; 1s2s2p for S and Cl) were frozen in all reference and increment computations. Hardware limitations prevented computation of reference CCSD polarizabilities in the aug-cc-pVDZ basis set for some cases, and thus a subset of 23 structure (1–10, 12, 15–20, 22, 23, 27, 30, 31, 40) was used to determine basis set effects. In order to perform an analysis of the errors Δi = Eapproxi − Erefi introduced by local approximations, we employed the following statistical measures:
For a graphical representation of the errors we assume a Gaussian distribution:
4 Results and discussion
4.1 Accuracy of dipole polarizabilities
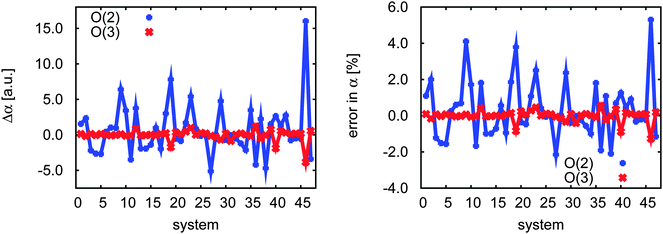
Although we computed the dipole polarizabilities for all 47 test systems across a range of wavelengths from 355 to 633 nm, the errors due to the incremental expansion are very similar. Therefore we will focus the discussion primarily on the results obtained with λ = 589 nm. In the left-hand plot of Fig. 2 we present the absolute and relative errors due to the incremental expansion in the right-hand plot. At second order, the maximum absolute error is 17 a.u. and the mean error is 0.5 a.u. At the third order both maximum absolute error and mean error decrease by nearly an order of magnitude to 3.0 a.u. and 0.06 a.u., respectively. The relative errors are plotted on the right-hand side of Fig. 2 and show the same pattern. The relative maximum absolute errors are around 5% at second order and around 1% at the third order expansion, whereas the mean error decreases from 0.25% at second order to only 0.02% at third order.Based on the work of Hald et al.104 we expect a basis set error of a few %, when going from the double to the triple-ζ level. From this perspective the incremental scheme in combination with the domain-specific basis set becomes very attractive, as it becomes more efficient in larger basis sets. Furthermore one can use the incremental scheme to reduce the total error in the calculation, since a larger basis set may be computationally affordable and the local approximations introduce only small errors (vide infra). Based on the results of Christiansen et al.105 it is evident that also the higher excitations may contribute to the polarizability up to a few %. Since the errors of the local approximations are smaller on average, it is very promising to include higher excitations in the incremental property calculations.
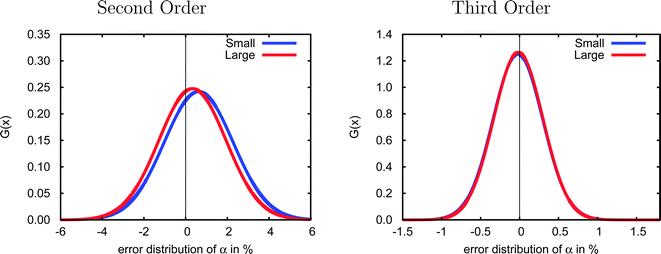
Due to the computational demands of the CCSD method we were not able to obtain polarizabilities for all 47 test cases using the aug-cc-pVDZ basis set, and thus we considered a smaller set of 23 systems (1–10, 12, 15–20, 22, 23, 27, 30, 31, 40) to investigate basis-set effects. As shown in Fig. 3, the error distributions in both second and third order are very similar for the small and large test sets, suggesting that the smaller group of molecules is sufficiently representative of the complete test set that it may be used to investigate basis set effects.
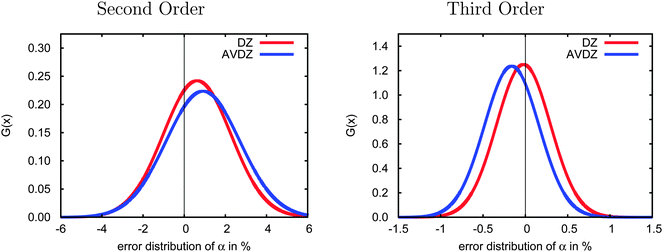
In Fig. 4 we present the errors in the CCSD dipole polarizabilities due to the incremental scheme using the 23-molecule test set obtained with the cc-pVDZ basis set (referred to as DZ and plotted in red) and with the aug-cc-pVDZ basis set (AVDZ, blue curves). In second order, the polarizabilities are slightly overestimated on average, and the addition of diffuse basis functions increases this error by ca. 0.27%. However, at third order, the opposite trend dominates, and a slight underestimation is observed as compared to the full canonical CCSD polarizabilities. Furthermore, diffuse functions increase this error by 0.14%, but the error remains small in both orders.
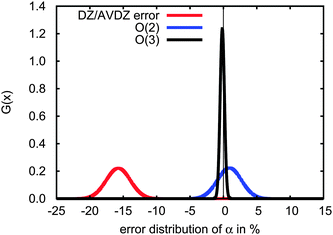
Which approximation introduces the larger errors, the basis set or the order of truncation of the incremental scheme? In Fig. 5, the red Gaussian distribution gives the errors in the dipole polarizabilities obtained with the cc-pVDZ basis set as compared to the aug-cc-pVDZ basis set, while the blue and black distributions represent the errors in the second- and third-order expansions, respectively, obtained with the aug-cc-pVDZ basis set. The basis-set truncation yields a mean error of approximately 16% due to the lack of diffuse functions, while even the second-order expansion produces a mean error of less than 2%. Clearly a second-order expansion is acceptable, but the use of diffuse functions is essential.
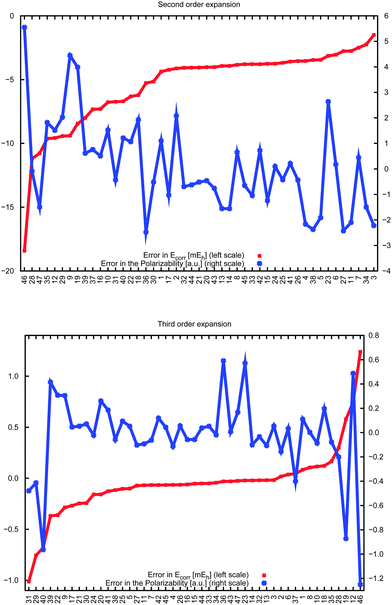
Fig. 6 compares the errors in the correlation energy (red curve) to the errors in the dipole polarizabilities (blue) due to the incremental-scheme truncation at second order (top) and third order (bottom), with the data ordered according to increasing energy errors. In general the variation of the errors in the polarizability is higher than the variation in the energy, which is unsurprising given that energy depends only on the wave function, whereas linear-response properties are related to the derivative of the wave function with respect to an external field. For the third-order expansion, a large error in the energy clearly correlates to a large error in the polarizability, but no obvious systematic trends appear in the second-order expansion. In addition, there are select cases for which the energy is well reproduced by the incremental scheme but relatively large errors appear in the polarizability (vide infra). Therefore the errors in the energies cannot be used to estimate the corresponding accuracy of the polarizability.
4.2 Corrections for basis set errors
As noted above, omission of diffuse functions in the basis set yields CCSD/cc-pVDZ dipole polarizabilities that are roughly 16% too low as compared to the CCSD/aug-cc-pVDZ level. If this mean error (μ) is simply used to shift the polarizabilities, one obtains the distribution plotted in cyan in Fig. 7. However, we may devise an improved basis-set correction using lower orders in the incremental scheme. When using the domain-specific basis set in the incremental scheme, only a few atoms require the large basis set at low order. Furthermore, the computation of the higher-order terms requires by far the most CPU-time. Therefore it is very attractive to carry out the incremental expansion in a small basis set and estimate the basis set effect from low order terms with the large basis set. We may estimate the basis-set error,| Δαω = αω(cc-pVDZ) − αω(aug-cc-pVDZ), | (9) |
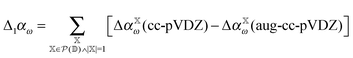 | (10) |
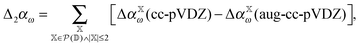 | (11) |
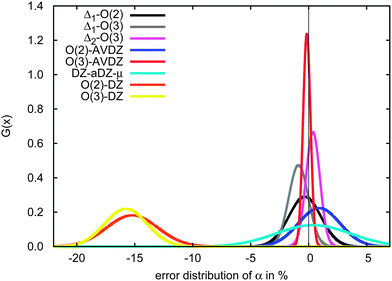 | ||
| Fig. 7 Performance of simple methods to correct CCSD polarizabilities for basis set errors. Cyan: subtraction of the mean CCSD/cc-pVDZ basis set error; black: second-order incremental CCSD/cc-pVDZ expansion with a first-order basis-set correction [eqn (10)]; grey: third-order CCSD/cc-pVDZ expansion and first-order basis-set correction [eqn (10)]; pink: third-order incremental expansion and second-order basis-set correction [eqn (11)]; blue: second-order incremental expansion in the large aug-cc-pVDZ basis set; red: third-order incremental expansion in the large aug-cc-pVDZ basis set. Orange: uncorrected second-order incremental expansion; yellow: uncorrected third-order incremental expansion. | ||
4.3 Accuracy for specific types of systems
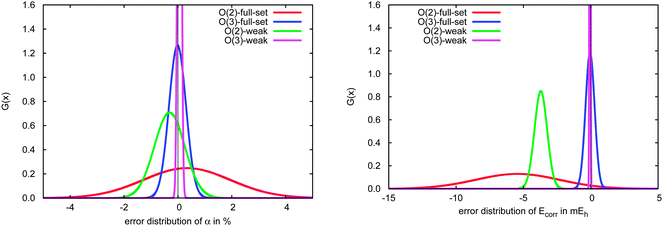
The significant variation in polarizability errors shown in Fig. 6—and the lack of such variations in the correlation energies—motivates one to consider the characteristics of the molecular systems that might lead to larger errors in the incremental scheme for response properties. We thus classify the molecules in our test set using three criteria: (1) weakly bound systems (13–15, 25, 26, 32–34, and 41–45); (2) quasi-linear/chain-like molecules (1–8, 10, 11, 16–18, 20–22, 27, 28, 30, 31, 35–40, and 47); (3) branched/three-dimensional structures (9, 12, 19, 23, 24, 29, and 46). We compare the performance of the incremental scheme for both the dipole polarizability and the correlation energy.Fig. 8 depicts the error distributions in the polarizability (left) and correlation energy (right) for the weakly bound systems, all of which are optimized structures of dimethylallene (2,3-pentadiene) interacting with one or more molecules of water or chloromethane. Comparing the Gaussian distributions, we find the same trend for the polarizabilities and the energies: the second order for the full set has a rather broad distribution, while the third order is significantly more compact. Considering the subset of weakly interacting systems, we find a relatively compact Gaussian at second order and very sharply peaked Gaussian at third order. Furthermore, the distributions for the full set are in any case significantly broader than those of the subset. Clearly the incremental scheme performs well for the weakly interacting systems considered here, which is unsurprising given the local nature of the interactions in such species. This suggests that the incremental scheme may be particularly valuable for describing the properties of solvated molecules, especially additive properties such as energies and polarizabilities.
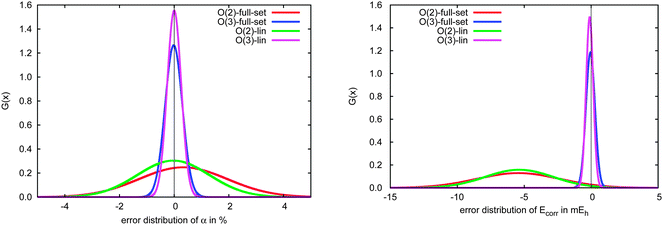
The errors in the incremental scheme for quasi-linear molecules are shown in Fig. 9. Unlike the set of weakly bound systems described above, for this subset we find very similar distributions compared to the full set, though the distributions are somewhat narrower at each order for the linear systems. Furthermore, while the correlation energies from the second-order incremental scheme are too small for most of the systems considered here, thus leading to Gaussian distributions shifted away from zero (relatively large mean error), errors in the dipole polarizability vary more consistently around zero, leading to smaller (relative) mean errors. At third-order, however, the distributions for both polarizabilities and correlation energies shift much closer to zero. The relatively narrow distributions of errors for linear species arises because the number of interactions between domains increases linearly with the size of the system, leading to a relatively slow accumulation of errors within the incremental scheme.
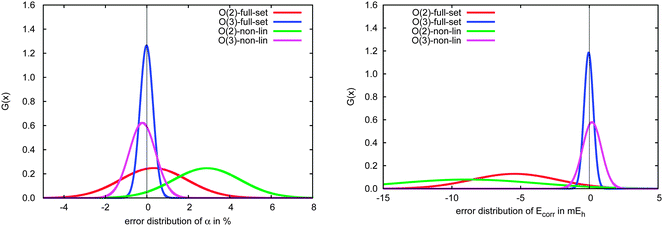
In Fig. 10 we compare the performance of the incremental scheme for the remaining systems, which contain two- and three-dimensional moieties and thus more strongly interacting domains. These structures are clearly the source of the largest errors arising from the incremental expansion in both polarizabilities and correlation energies, as they yield even broader error distributions than the full test set. This observation, which holds for both the second- and third-order expansions in both polarizabilities and correlation energies, can be explained by the fact that a three-dimensional structure naturally includes more domains that are spatially proximate. Thus, approximations to the interactions between and within a domain, such as those introduced by the incremental scheme, necessarily accumulate a larger number of errors in two- and three-dimensional molecules as compared to a quasi-linear compound or weakly bound complex.
4.4 Applicability
As noted earlier, due to the substantial computational effort of the canonical CCSD linear-response method we elected to compute the dipole polarizabilities with the aug-cc-pVDZ basis set for a subset of our 47-molecule test suite, and compound 33—dimethylallene interacting with two water molecules—provides an example of the computational bottleneck. The convergence of the incremental scheme for the wavelength-dependent CCSD dipole polarizability of this structure is given in Table 4 for four wavelengths (λ = 355, 436, 589, and 633 nm).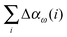 is the sum of all contributions up to order i. “Canonical” refers to the untruncated CCSD linear-response result
is the sum of all contributions up to order i. “Canonical” refers to the untruncated CCSD linear-response result
| cc-pVDZ | aug-cc-pVDZ | |||||
|---|---|---|---|---|---|---|
| Order i | α ω (i) | Error | α ω (i) | |||
| a.u. | a.u. | a.u. | % | a.u. | a.u. | |
| 355 nm | ||||||
| 1 | 199.8 | 199.8 | −26.0 | −11.5 | 255.2 | 255.2 |
| 2 | 23.6 | 223.5 | −2.4 | −1.0 | 26.0 | 281.2 |
| 3 | 2.5 | 226.0 | 0.1 | 0.1 | 1.2 | 282.4 |
| Canonical | 225.9 | |||||
| 436 nm | ||||||
| 1 | 196.0 | 196.0 | −23.2 | −10.6 | 249.5 | 249.5 |
| 2 | 21.5 | 217.5 | −1.7 | −0.8 | 23.3 | 272.8 |
| 3 | 1.9 | 219.4 | 0.2 | 0.1 | 0.4 | 273.3 |
| Canonical | 219.2 | |||||
| 589 nm | ||||||
| 1 | 192.8 | 192.8 | −21.0 | −9.8 | 244.8 | 244.8 |
| 2 | 19.8 | 212.7 | −1.2 | −0.6 | 21.2 | 266.0 |
| 3 | 1.4 | 214.1 | 0.2 | 0.1 | −0.1 | 265.9 |
| Canonical | 213.9 | |||||
| 633 nm | ||||||
| 1 | 192.3 | 192.3 | −20.7 | −9.7 | 244.1 | 244.1 |
| 2 | 19.6 | 211.9 | −1.1 | −0.5 | 20.9 | 265.0 |
| 3 | 1.3 | 213.2 | 0.2 | 0.1 | −0.1 | 264.8 |
| Canonical | 213.0 | |||||
As observed before, the results change significantly when adding diffuse functions, and the cc-pVDZ dipole polarizabilities are about 20% too small for the second- and third-order expansions compared to the aug-cc-pVDZ basis. In addition, we find that the basis set errors are much larger than those arising from local approximations in the incremental scheme. Considering the second-order expansion, for example, we find an maximum error of 1% in the polarizability when using the cc-pVDZ basis set, falling to ca. 0.1% at third-order. We thus may conclude that the incremental scheme can be used to increase the accuracy of the dipole polarizabilities at the CCSD level of theory, since it makes it feasible to employ significantly larger basis.
5 Conclusion
We have presented the first implementation of the incremental scheme for CCSD dipole polarizabilities. The method is fully automatic and makes use of the domain-specific basis set approach. The accuracy of the results has been analyzed using a test suite of 47 molecular systems for which we find that a second-order incremental expansion provides CCSD dipole polarizabilities with a mean error of 0.6% and a standard deviation of 1.7%. At the third-order level the mean error falls to only −0.02% with a corresponding standard deviation of 0.3%. With the proposed approach we are able to compute the CCSD polarizabilities using larger basis sets than is feasible with the canonical approach. Thus, given the strong basis-set dependence of properties such as polarizabilities—particular on diffuse functions—the incremental scheme can be used to increase the total accuracy of the computation of dipole polarizabilities.In addition, we analyzed which type of molecular structures lead to smaller or larger errors within the incremental scheme. Weakly interacting systems, such as those involved in solvation or those dominated by dispersion interactions, as well as quasi-linear structures can be treated with higher accuracy than two- or three-dimensional species. The reason for the differences is associated with the number of strong interactions between and within domains in each type of system, with cage-like compounds yielding the largest errors.
Acknowledgements
JF thanks the German science foundation (FR2898/4-1) and the Fonds der Chemischen Industrie for financial support. Work at Virginia Tech was supported by grants CHE-1058420 and ACI-1147794 from the U.S. National Science Foundation.References
- R. J. Bartlett, Mol. Phys., 2010, 108, 2905–2920 CrossRef CAS.
- R. J. Bartlett and M. Musial, Rev. Mod. Phys., 2007, 79, 291–352 CrossRef CAS.
- R. J. Bartlett, How and why coupled-cluster theory became the pre-eminent method in an ab initio quantum chemistry, in Theory and Applications of Computational Chemistry: The First Forty Years, ed. C. Dykstraet al., Elsevier, New York, 2005, ch. 42, pp. 1191–1221 Search PubMed.
- T. D. Crawford and H. F. Schaefer, An introduction to coupled cluster theory for computational chemists, in Reviews in Computational Chemistry, ed. K. B. Lipkowitz and D. B. Boyd, VCH Publishers, New York, 2000, ch. 2, vol. 14, pp. 33–136 Search PubMed.
- H. Koch and P. Jørgensen, J. Chem. Phys., 1990, 93, 3333–3344 CrossRef CAS PubMed.
- G. D. Purvis and R. J. Bartlett, J. Chem. Phys., 1982, 76, 1910–1918 CrossRef CAS PubMed.
- K. Raghavachari, G. W. Trucks, J. A. Pople and M. Head-Gordon, Chem. Phys. Lett., 1989, 157, 479 CrossRef CAS.
- H. Koch, O. Christiansen, P. Jørgensen, A. M. S. de Merás and T. Helgaker, J. Chem. Phys., 1997, 106, 1808–1818 CrossRef CAS PubMed.
- H. Koch, H. J. Aa Jensen, P. Jørgensen and T. Helgaker, J. Chem. Phys., 1990, 93, 3345–3350 CrossRef CAS PubMed.
- H. Koch, O. Christiansen, P. Jørgensen and J. Olsen, Chem. Phys. Lett., 1995, 244, 75–82 CrossRef CAS.
- H. Sekino and R. J. Bartlett, Int. J. Quantum Chem., Symp., 1984, 18, 255 CrossRef CAS.
- J. F. Stanton and R. J. Bartlett, J. Chem. Phys., 1993, 98, 7029–7039 CrossRef CAS PubMed.
- O. Christiansen, H. Koch, A. Halkier, P. Jørgensen, T. Helgaker and A. S. de Merás, J. Chem. Phys., 1996, 105, 6921–6931 CrossRef CAS PubMed.
- T. B. Pedersen and H. Koch, Chem. Phys. Lett., 1998, 293, 251–260 CrossRef CAS.
- L. D. Barron, Molecular Light Scattering and Optical Activity, Cambridge University Press, Camridge, UK, 2nd edn, 2004 Search PubMed.
- T. B. Pedersen, H. Koch and K. J. Ruud, Chem. Phys., 1999, 110, 2883–2892 CAS.
- M. Pecul and K. Ruud, Adv. Quantum Chem., 2005, 50, 185–212 CrossRef CAS.
- T. D. Crawford, Theor. Chem. Acc., 2006, 115, 227–245 CrossRef CAS PubMed.
- T. D. Crawford, M. C. Tam and M. L. Abrams, J. Phys. Chem. A, 2007, 111, 12057–12068 CrossRef CAS PubMed.
- J. F. Stanton and R. J. Bartlett, J. Chem. Phys., 1993, 99, 5178–5183 CrossRef CAS PubMed.
- P. B. Rozyczko, S. A. Perera, M. Nooijen and R. J. Bartlett, J. Chem. Phys., 1997, 107, 6736–6747 CrossRef CAS PubMed.
- P. Rozyczko and R. J. Bartlett, J. Chem. Phys., 1997, 107, 10823–10826 CrossRef CAS PubMed.
- O. Christiansen, C. Hättig and J. Gauss, J. Chem. Phys., 1998, 109, 4745–4757 CrossRef CAS PubMed.
- J. Gauss, O. Christiansen and J. F. Stanton, Chem. Phys. Lett., 1998, 296, 117–124 CrossRef CAS.
- K. Ruud, T. Helgaker, K. L. Bak, P. Jørgensen and H. J. Jensen, J. Chem. Phys., 1999, 99, 3847–3859 CrossRef PubMed.
- C. Hättig, W. Klopper, A. Köhn and D. P. Tew, Chem. Rev., 2012, 112, 4–74 CrossRef PubMed.
- A. Halkier, T. Helgaker, P. Jørgenson, W. Klopper, H. Koch, J. Olsen and A. K. Wilson, Chem. Phys. Lett., 1998, 286, 243–252 CrossRef CAS.
- W. Klopper, F. R. Manby, S. Ten-no and E. F. Valeev, Int. Rev. Phys. Chem., 2006, 25, 427 CrossRef CAS.
- L. Kong, F. A. Bischoff and E. F. Valeev, Chem. Rev., 2012, 112, 75–107 CrossRef CAS PubMed.
- P. Pulay, Chem. Phys. Lett., 1983, 100, 151–154 CrossRef CAS.
- S. Saebø and P. Pulay, Chem. Phys. Lett., 1985, 113, 13 CrossRef.
- C. Hampel and H.-J. Werner, J. Chem. Phys., 1996, 104, 6286–6297 CrossRef CAS PubMed.
- M. Schütz, G. Hetzer and H. J. Werner, J. Chem. Phys., 1999, 111, 5691–5705 CrossRef PubMed.
- M. Schütz, J. Chem. Phys., 2000, 113, 9986–10001 CrossRef PubMed.
- H.-J. Werner and M. Schütz, J. Chem. Phys., 2011, 135, 144116 CrossRef PubMed.
- H.-J. Werner, J. Chem. Phys., 2008, 129, 101103 CrossRef PubMed.
- T. B. Adler and H.-J. Werner, J. Chem. Phys., 2011, 135, 144117 CrossRef PubMed.
- T. B. Adler and H.-J. Werner, J. Chem. Phys., 2009, 130, 241101 CrossRef PubMed.
- J. Yang, Y. Kurashige, F. R. Manby and G. K. L. Chan, J. Chem. Phys., 2011, 134, 044123 CrossRef PubMed.
- F. Neese, A. Hansen and D. G. Liakos, J. Chem. Phys., 2009, 131, 064103 CrossRef PubMed.
- D. G. Liakos, A. Hansen and F. Neese, J. Chem. Theory Comput., 2011, 7, 76–87 CrossRef CAS.
- C. Riplinger and F. Neese, J. Chem. Phys., 2013, 138, 034106 CrossRef PubMed.
- D. G. Fedorov and K. Kitaura, J. Chem. Phys., 2004, 121, 2483–2490 CrossRef CAS PubMed.
- D. G. Fedorov and K. Kitaura, J. Chem. Phys., 2005, 123, 134103 CrossRef PubMed.
- S. R. Pruitt, M. A. Addicoat, M. A. Collins and M. S. Gordon, Phys. Chem. Chem. Phys., 2012, 14, 7752–7764 RSC.
- D. G. Fedorov, T. Nagata and K. Kitaura, Phys. Chem. Chem. Phys., 2012, 14, 7562–7577 RSC.
- Y. Mochizuki, K. Yamashita, T. Nakano, Y. Okiyama, K. Fukuzawa, N. Taguchi and S. Tanaka, Theor. Chem. Acc., 2011, 130, 515–530 CrossRef CAS PubMed.
- W. Yang, Phys. Rev. Lett., 1991, 66, 1438–1441 CrossRef CAS.
- M. Kobayashi and H. Nakai, J. Chem. Phys., 2009, 131, 114108 CrossRef PubMed.
- M. Kobayashi and H. Nakai, Phys. Chem. Chem. Phys., 2012, 14, 7629–7639 RSC.
- N. Flocke and R. J. Bartlett, J. Chem. Phys., 2004, 121, 10935 CrossRef CAS PubMed.
- T. F. Hughes, N. Flocke and R. J. Bartlett, J. Phys. Chem. A, 2008, 112, 5994–6003 CrossRef CAS PubMed.
- T. F. Hughes and R. J. Bartlett, J. Chem. Phys., 2008, 129, 054105 CrossRef PubMed.
- W. Förner, J. Ladik, P. Otto and J. Cizek, Chem. Phys., 1985, 97, 251 CrossRef.
- S. Li, J. Shen, W. Li and Y. Jiang, J. Chem. Phys., 2006, 125, 074109 CrossRef PubMed.
- W. Li and P. Piecuch, J. Phys. Chem. A, 2010, 114, 6721–6727 CrossRef CAS PubMed.
- W. Li, P. Piecuch, J. R. Gour and S. Li, J. Chem. Phys., 2009, 131, 114109 CrossRef PubMed.
- W. Li, Y. Guo and S. Li, Phys. Chem. Chem. Phys., 2012, 14, 7854–7862 RSC.
- Z. Rolik and M. Kallay, J. Chem. Phys., 2012, 135, 104111 CrossRef PubMed.
- Z. Rolik, L. Szegedy, I. Ladjánszki, B. Ladóczki and M. Kállay, J. Chem. Phys., 2013, 139, 094105 CrossRef PubMed.
- M. S. Gordon, D. G. Fedorov, S. R. Pruitt and L. V. Slipchenko, Chem. Rev., 2012, 112, 632–672 CrossRef CAS PubMed.
- T. Korona and H.-J. Werner, J. Chem. Phys., 2003, 118, 3006–3019 CrossRef CAS PubMed.
- T. Korona, K. Pflüger and H.-J. Werner, Phys. Chem. Chem. Phys., 2004, 6, 2059–2065 RSC.
- T. Korona, D. Kats, M. Schütz, T. B. Adler, Y. Liu and H.-J. Werner, Local Approximations for an Efficient and Accurate Treatment of Electron Correlation and Electron Excitations in Molecules, in Linear-Scaling Techniques in Comptuational Chemistry and Physics, ed. R. Zaleśny, M. G. Papadopoulos, P. G. Mezey and J. Leszczynski, Springer, Netherlands, 2011, vol. 13, pp. 345–407 Search PubMed.
- D. Kats, T. Korona and M. Schütz, J. Chem. Phys., 2006, 125, 104106 CrossRef PubMed.
- D. Kats, T. Korona and M. Schütz, J. Chem. Phys., 2007, 127, 064107 CrossRef PubMed.
- K. Freundorfer, D. Kats, T. Korona and M. Schütz, J. Chem. Phys., 2010, 133, 244110 CrossRef PubMed.
- T. D. Crawford and R. A. King, Chem. Phys. Lett., 2002, 366, 611–622 CrossRef CAS.
- N. J. Russ and T. D. Crawford, Chem. Phys. Lett., 2004, 400, 104–111 CrossRef CAS PubMed.
- N. J. Russ and T. D. Crawford, Phys. Chem. Chem. Phys., 2008, 10, 3345–3352 RSC.
- T. D. Crawford, Reduced-Scaling Coupled-Cluster Theory for Response Properties of Large Molecules, in Recent Progress in Coupled Cluster Methods: Theory and Applications, ed. P. Carsky, J. Pittner and J. Paldus, Springer, Berlin, 2010, ch. 2, vol. 11, pp. 37–55 Search PubMed.
- H. R. McAlexander, T. J. Mach and T. D. Crawford, Phys. Chem. Chem. Phys., 2012, 14, 7830–7836 RSC.
- H. Stoll, Chem. Phys. Lett., 1992, 191, 548–552 CrossRef CAS.
- H. Stoll, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 6700–6704 CrossRef CAS.
- H. Stoll, J. Chem. Phys., 1992, 97, 8449–8454 CrossRef CAS PubMed.
- R. K. Nesbet, Phys. Rev., 1967, 155, 51–55 CrossRef CAS.
- R. K. Nesbet, Phys. Rev., 1968, 175, 2–9 CrossRef CAS.
- R. K. Nesbet, Adv. Chem. Phys., 1969, 14, 1–34 CrossRef CAS.
- K. Doll, M. Dolg, P. Fulde and H. Stoll, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, 4842–4848 CrossRef CAS.
- K. Doll, M. Dolg and H. Stoll, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 13529–13534 CrossRef CAS.
- K. Doll, M. Dolg, P. Fulde and H. Stoll, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 55, 10282–10287 CrossRef CAS.
- S. Kalvoda, M. Dolg, H.-J. Flad and P. Fulde, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 2127–2133 CrossRef CAS.
- K. Rosciszewski, B. Paulus, P. Fulde and H. Stoll, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60, 7905–7910 CrossRef CAS.
- K. Rosciszewski, B. Paulus, P. Fulde and H. Stoll, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 5482–5488 CrossRef CAS.
- H. Stoll, B. Paulus and P. Fulde, J. Chem. Phys., 2005, 123, 144108 CrossRef PubMed.
- C. Müller, B. Herschend, K. Hermansson and B. Paulus, J. Chem. Phys., 2008, 128, 214701 CrossRef PubMed.
- I. Schmitt, K. Fink and V. Staemmler, Phys. Chem. Chem. Phys., 2009, 11, 11196–11206 RSC.
- C. Müller, K. Hermansson and B. Paulus, Chem. Phys., 2009, 362, 91–96 CrossRef PubMed.
- V. Staemmler, J. Phys. Chem. A, 2011, 115, 7153–7160 CrossRef CAS PubMed.
- C. Müller, D. Usvyat and H. Stoll, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 245136 CrossRef.
- S. Kalvoda, B. Paulus, M. Dolg, H. Stoll and H.-J. Werner, Phys. Chem. Chem. Phys., 2001, 3, 514–522 RSC.
- B. Paulus, Int. J. Quantum Chem., 2004, 100, 1026 CrossRef CAS.
- J. Friedrich, E. Perlt, M. Roatsch, C. Spickermann and B. Kirchner, J. Chem. Theory Comput., 2011, 7, 843–851 CrossRef CAS.
- C. Spickermann, E. Perlt, M. Domaros, M. Roatsch, J. Friedrich and B. Kirchner, J. Chem. Theory Comput., 2011, 7, 868–875 CrossRef CAS.
- E. Perlt, J. Friedrich, M. Domaros and B. Kirchner, ChemPhysChem, 2011, 12, 3474–3482 CrossRef CAS PubMed.
- I. Polenz, F. G. Schmidt, J. Friedrich, I. Tchernook and S. Spange, Macromol. Chem. Phys., 2013, 214, 1473–1483 CrossRef CAS.
- J. Zhang and M. Dolg, J. Chem. Theory Comput., 2013, 9, 2992–3003 CrossRef CAS.
- J. Zhang, N. Heinz and M. Dolg, Inorg. Chem., 2014, 53, 7700–7708 CrossRef CAS PubMed.
- M. Modl, M. Dolg, P. Fulde and H. Stoll, J. Chem. Phys., 1997, 106, 1836–1846 CrossRef CAS PubMed.
- J. Friedrich, M. Hanrath and M. Dolg, J. Phys. Chem. A, 2008, 112, 8762–8766 CrossRef CAS PubMed.
- E. N. Voloshina and B. Paulus, J. Chem. Theory Comput., 2014, 10, 1698–1706 CrossRef CAS.
- J. Yang and M. Dolg, J. Chem. Phys., 2007, 127, 084108 CrossRef PubMed.
- J. Friedrich, S. Coriani, T. Helgaker and M. J. Dolg, Chem. Phys., 2009, 131, 154102 Search PubMed.
- K. Hald, F. Pawłowski, P. Jørgenson and C. Hättig, J. Chem. Phys., 2003, 118, 1292 CrossRef CAS PubMed.
- O. Christiansen, J. Gauss and J. F. Stanton, Chem. Phys. Lett., 1998, 292, 437 CrossRef CAS.
- O. Christiansen, P. Jørgensen and C. Hättig, Int. J. Quantum Chem., 1998, 68, 1–52 CrossRef CAS.
- P. Jørgensen and J. Simons, Second Quantization-Based Methods in Quantum Chemistry, Academic Press, New York, 1981 Search PubMed.
- R. Kobayashi, H. Koch and P. Jørgensen, Chem. Phys. Lett., 1994, 219, 30–35 CrossRef CAS.
- J. Friedrich, M. Hanrath and M. Dolg, J. Chem. Phys., 2007, 126, 154110 CrossRef PubMed.
- J. Friedrich, M. Hanrath and M. Dolg, J. Phys. Chem. A, 2007, 111, 9830–9837 CrossRef CAS PubMed.
- J. Friedrich, M. Hanrath and M. Dolg, Chem. Phys., 2007, 338, 33–43 CrossRef CAS PubMed.
- J. M. Foster and S. F. Boys, Rev. Mod. Phys., 1960, 32, 300 CrossRef CAS.
- J. Friedrich, M. Hanrath and M. Dolg, Z. Phys. Chem., 2010, 224, 513–525 CrossRef CAS.
- A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100 CrossRef CAS.
- S. H. Vosko, M. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200 CrossRef CAS PubMed.
- J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822–8824 CrossRef.
- A. Schäfer, H. Horn and R. I. Ahlrichs, J. Chem. Phys., 1992, 97, 2571–2577 CrossRef PubMed.
- J. Friedrich and J. Hänchen, J. Chem. Theory Comput., 2013, 9, 5381–5394 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648 CrossRef CAS PubMed.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS.
- T. H. Dunning Jr., J. Chem. Phys., 1989, 90, 1007–1023 CrossRef PubMed.
- R. A. Kendall, T. H. Dunning Jr. and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796–6806 CrossRef CAS PubMed.
- D. E. Woon and T. H. Dunning, J. Chem. Phys., 1993, 98, 1358 CrossRef CAS PubMed.
- J. M. Turney, et al. , Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 556–565 CrossRef CAS.
- J. Friedrich and K. Walczak, J. Chem. Theory Comput., 2013, 9, 408–417 CrossRef CAS.
- W. J. Hehre, R. Ditchfield and J. A. Pople, J. Chem. Phys., 1972, 56, 2257 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: The supplementary material contains the Cartesian coordinates for all 47 test molecules, as well as incremental CCSD energies, polarizabilities, and corresponding errors. See DOI: 10.1039/c4cp05076b |
| This journal is © the Owner Societies 2015 |