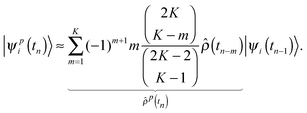“On-the-fly” coupled cluster path-integral molecular dynamics: impact of nuclear quantum effects on the protonated water dimer
Received
10th November 2014
, Accepted 28th January 2015
First published on 30th January 2015
Abstract
We present an accelerated ab initio path-integral molecular dynamics technique, where the interatomic forces are calculated “on-the-fly” by accurate coupled cluster electronic structure calculations. In this way not only dynamic electron correlation, but also the harmonic and anharmonic zero-point energy, as well as tunneling effects are explicitly taken into account. This method thus allows for very precise finite temperature quantum molecular dynamics simulations. The predictive power of this novel approach is illustrated on the example of the protonated water dimer, where the impact of nuclear quantum effects on its structure and the 1H magnetic shielding tensor are discussed in detail.
1 Introduction
In chemical physics there is a vast variety of relevant problems, where nuclear quantum effects (NQE), such as quantum mechanical zero-point energy (ZPE) and tunneling effects, are of crucial importance. Especially, for systems containing light atoms at low temperatures, these effects must be explicitly taken into account to obtain the correct quantitative, and sometimes even qualitative behavior. Ab initio path-integral molecular dynamics (AI-PIMD) pioneered by Marx, Tuckerman and Parrinello,1–5 has been exceedingly successful in explaining and predicting a large variety of physical phenomena.6–23 However, the accuracy and increased predictive power of AI-PIMD simulations, where the interatomic interactions are computed “on-the fly” from first principles by electronic structure calculations, comes at a significant computational cost, which has to be carefully balanced against system size and sampling requirements. For this reason, density functional theory is to date the almost exclusively employed electronic structure method.24,25 But, even the DFT-based AI-PIMD approach is not without problems: the temperature scale is energetically tiny so that an error as small as 0.2 kcal mol−1, which is one order of magnitude smaller than the strength of a typical hydrogen-bond between water molecules,26–28 may cause that simulated water might either freeze or evaporate.29,30
Hence, it would be very desirable to accelerate more accurate wave function-based ab initio calculations that incorporate the relevant physics of electron correlation in a more systematic way,31,32 such that genuine finite-temperature quantum molecular dynamics (MD) simulations including tunneling and NQE can be routinely performed, thus making completely new phenomena accessible to quantum chemical computations. Inspired by the second generation Car–Parrinello approach of Kühne et al.,33–35 an accelerated coupled cluster (CC) theory32,36–38 based AI-PIMD scheme is presented, where in each time step the interatomic forces are calculated by the coupled cluster singles and doubles (CCSD) method.39 To the best of our knowledge, this is the first MD simulation at the CC level of theory and in particular also the first CC-based AI-PIMD ever performed.
The resulting CC-PIMD approach will be employed to investigate the impact of NQE on the structure and the nuclear magnetic shielding tensor of the protonated water dimer, which has been previously studied using conventional semi-classical ab initio MD at the MP2 level of theory.40,41 However, prior to that we briefly outline the basic principles of the PIMD and CC theories that are at the bases of our CC-PIMD scheme.
2 “On-the-fly” coupled cluster path-integral molecular dynamics
In the PIMD formalism, each of the N quantum nuclei is replaced by a classical harmonic P-bead ring-polymer. This modified system is isomorphic to the original quantum system, which allows to calculate exact canonical quantum-mechanical properties of the original system by sampling the extended path-integral phase space.42–44 In the limit of P → ∞, sampling ZP(β) classically is equivalent to the exact canonical quantum partition function Z(β), i.e.| | 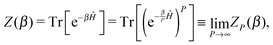 | (1) |
where| | 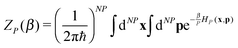 | (2) |
and β = 1/(kBT) is the inverse temperature, while x and p denote the positions and momenta of all N × P particles. The so-called bead-Hamiltonian HP that describes the interactions between them is given by| | 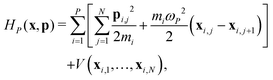 | (3) |
where mi is the particles mass and ωP = P/(βℏ) is the frequency of the harmonic spring potential between adjacent beads. As already alluded to, the interatomic potential V(xi,1,…,xi,N) is throughout evaluated at each time step and for each bead at the CCSD level of theory.39
To ensure size-extensivity, in the CC theory,32,37,38 the exact wave function is given by the exponential ansatz36
| | |Ψexact〉 = e![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) |Φ〉, |Φ〉, | (4) |
where |
Φ〉 is the reference wave function that in the present work is a Slater determinant made up from Hartree–Fock (HF) molecular orbitals (MOs) |
ψi〉. The cluster operator
is composed of a series of connected excitation operators that in second quantization reads as
| | 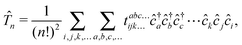 | (6) |
where we have adopted the usual convention that
i,
j,
k,… refer to occupied and
a,
b,
c,… to unoccupied orbitals in |
Φ〉, while
ĉ† and
ĉ are creation and annihilation operators, respectively. The
tabc…ijk… are the yet unknown cluster amplitudes, meaning that the problem of determining
![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif)
reduces to finding the expansion coefficients of its second quantized operators. In this notation, CCSD corresponds to an approximation of the exact wave function by truncating
eqn (5) after the two-body cluster contributions.
The computational cost of the electronic structure calculations can be substantially reduced, by design of a coupled electron–ion dynamics that keeps the electronic degrees of freedom very close to the instantaneous Born–Oppenheimer surface. In the present scheme, however, only the HF orbitals are propagated by adopting the predictor–corrector integrator of Kolafa to the electronic structure problem.33,45 Due to the fact that the dynamics of the single-particle density operator 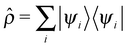 is much smoother than that of the more widely varying MOs, the predicted density operators
is much smoother than that of the more widely varying MOs, the predicted density operators ![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) p(tn) at time tn is expressed in terms of K previous
p(tn) at time tn is expressed in terms of K previous ![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) (tn−m), which is then used as an approximate projector on to the occupied subspace |ψi(tn−1)〉 to obtain the predicted MOs
(tn−m), which is then used as an approximate projector on to the occupied subspace |ψi(tn−1)〉 to obtain the predicted MOs
| | 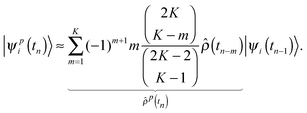 | (7) |
The efficiency of this approach is such that |
ψpi(
tn) 〉 is already very close to the instantaneous electronic ground state. However, contrary to the original second generation Car–Parrinello MD approach of Kühne
et al.,
30,33,34 where in each MD step only a single preconditioned electronic gradient calculation is required as the corrector, here the predicted MOs are only used as an initial guess for the HF self-consistent field cycle.
46 Nevertheless, in the present case still an up to five-fold speed-up with respect to simply utilizing the MOs from the previous time step has been observed, although so far apparently only in the HF part. Since the latter constitutes only a small fraction of the total calculation, at the present level of theory, the overall speed-up is just 10%. Nevertheless, the possibility to extend the present method to additionally propagating the cluster amplitudes has to be emphasized and will be presented elsewhere.
3 Computational details
The following CC-MD and CC-PIMD simulations were conducted using a modified version of i-PI,47 whereas the forces were calculated at the CCSD/cc-pVDZ level of theory48–52 using the CFOUR program package.53,54 They were all performed in the canonical NVT ensemble at 300 K using a discretized timestep of 0.25 fs for 28 ps. We found that the nuclear Schrödinger equation is essentially exactly solved for P = 32 beads that is hence employed throughout. For the purpose to quantify the impact of NQE, an additional CC-MD simulation with classical nuclei (P = 1) has been performed, which altogether amounts to nearly 4 million CCSD/cc-pVDZ calculations. The isotropic nuclear shielding with and without NQE has been calculated as an ensemble average over each time 4000 decorrelated snapshots at the CCSD(T)/cc-pVTZ level of theory.55,56
4 Application to the protonated water dimer
Comparing the results of our CC-MD and CC-PIMD simulations, we found that the inclusion of NQE just leads to a slightly more delocalized quantum proton and entails only a tiny increase of the average intermolecular O–O bond length from 2.417 Å to 2.424 Å. Even though the qualitative trend is identical to previous DFT-based AI-PIMD simulations, the latter yields average bond lengths that are longer by about 0.03 Å.7 Nevertheless, the importance of NQE is much more apparent whenever light atoms such as hydrogen are involved as demonstrated by the dramatic change of the O1H+O2 angle that decreases from 168.99° to 164.29°, which is due to the substantially enhanced anharmonicity of the bending angle. In any case, the difference of the eventual bending angle by 9°–11° from DFT-based AI-PIMD and more accurate, but static CC calculations,7,57–59 respectively, is a striking manifestation of the importance to sample both thermal and quantum fluctuations of many coupled degrees of freedom concurrently.
In what follows we will focus on the nature of the shared quantum proton. On the one hand static calculations at the HF level of theory predict an asymmetric bonding where the proton is covalently bonded to either one of the water molecules (H2O–H+OH2), which suggest that the proton moves within a double-well potential. On the other hand, however, accurate MP2 and CC calculations predict that the proton is shared between the water molecules (H2O⋯H+OH2),57,58,60,61i.e. a single-well potential. As can be seen in Fig. 1, the free-energy distributions of both of our simulations obey a single-well only, although the one of the CC-PIMD calculation is much more delocalized. The latter is to be expected and is in qualitative very good agreement with previous AI-PIMD simulations at the DFT level.7,11 Moreover, the inclusion of NQE reduces the correlation between the proton reaction coordinate ν = rO1H+ − rO2H+ of Tuckerman et al.7 and the intermolecular O–O distance, which is in overall excellent agreement with the work of Limbach et al.62 For the purpose to study the delocalization in more detail, we have decomposed the O–H pair correlation function (PCF) into two separate contributions as shown in Fig. 2. The first peak denotes the covalent intramolecular O–H bond, while the second is due to the hydrogen-bonded O⋯H+. From this it follows, that the proton experiences rather large quantum fluctuations, which results in unexpectedly large excursions between the water molecules. In fact, we found that in our CC-PIMD simulation, the two distributions exhibit a sizeable overlap, which corresponds to the fact that due to NQE the proton is occasionally allowed to approach the O atom even closer than its respective covalently-bonded H atom. By contrast, in the semi-classical CC-MD simulation, the associated overlap is very small, with the result that the proton is essentially never closer to one of the O atoms than the typical covalent O–H bond length. In other words, even though the probability of these transient excursions is rather small, they are emerging much more often than generally appreciated. In addition, the effect of these quantum fluctuations is significant and are not seen in simulations with classical nuclei. In that respect the present effect is similar to the recently observed transient proteolysis events in liquid water.21
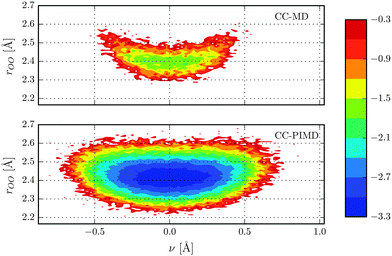 |
| | Fig. 1 Free energy distribution in kcal mol−1 of the shared proton of our CC-MD and CC-PIMD simulations as a function of the intermolecular O–O distance and the proton reaction coordinate ν. | |
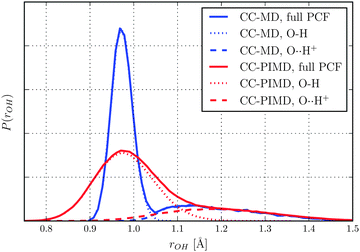 |
| | Fig. 2 Total O–H PCF as obtained by CC-MD and CC-PIMD simulations and its decomposition into covalent (O–H), as well as hydrogen-bonded (O⋯H+) contributions. | |
Nuclear magnetic shielding is one of the most sensitive probes to small changes in molecular electronic structure. It is therefore commonly used to assess the accuracy of theoretical electronic structure methods, and has recently also been employed as a probe for the quantum nature of the proton in hydrogen-bonded systems.63 In order to investigate the impact of NQE on the electronic structure, in Fig. 3 the 1H isotropic nuclear magnetic shielding σ is shown as a function of the proton reaction coordinate ν. We found that the shielding tensor of the proton strongly depends on ν, which immediately suggests that the same may also hold for the recently found asymmetry in liquid water.26–28 Although the correlation is somewhat more pronounced than in the previous static calculations of Limbach et al.,62 the agreement is generally very good. Including NQE, the average isotropic nuclear shielding increases by 3 ppm, which is a direct consequence of the aforementioned transient excursions of the proton.21 In fact, all the principal components of the shielding tensor show small, but significant differences between the simulations with classical and quantum nuclei. Furthermore, using classical nuclei the differences in the isotropic nuclear shielding of the proton between HF and CC is 7.4 ppm, while including nuclear NQE reduces the difference to 1.5 ppm only. The fact that for this quantity, the CC correction and NQE are competing immediately suggests that using PIMD the particular level of theory for the electronic structure calculations is less important. To study the impact of NQE on the vapour-to-liquid chemical shift, we are considering the hydrogen-bonded proton as the liquid-like proton, to mimic the situation of an excess proton solvated in water and the remaining hydrogen atoms as gas-like. The isotropic nuclear magnetic shielding values of the latter as a function of the hydrogen–oxygen distance rOH are shown in Fig. 4. Even though, at the presence of NQE, the shielding is much more delocalized, the mean value differ by less than one ppm, at variance to the proton of Fig. 3. As a consequence, the NQE induced change of our vapor-to-chemical shift estimate is −3.7 ppm, which again is mainly a result of the transient proton excursions and as such another manifestation on the importance of NQE.21 The corresponding value at the HF level of theory is 2.2 ppm, or in other words, NQE and CC correction cooperative, but again the former slightly more important. Fig. 5 for instance, reveals a clearly different spatial dependence for the maximum eigenvalue of σ. Furthermore, the difference between the largest and smallest eigenvalues of the shielding tensor (the span) decreases by 8 ppm in case of the CC-PIMD simulation including NQE. These components of the shielding tensor can be readily probed by solid state NMR64–66 and via the NMR relaxation even in the liquid state,67 which possibly provide an experimental way to measure the geometry and the strength of a hydrogen bond that is more sensitive than the widely used isotropic shielding. It should be noted that we expect NQE to be even more pronounced if the solvation environment of the proton were less symmetric, e.g. by an isotopic exchange. This would provide a means to quantify the contribution of NQE to isotope effects in NMR, with the possibility for comparison with experimental benchmarks.
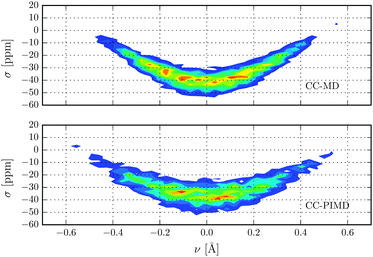 |
| | Fig. 3 Isotropic nuclear magnetic shielding of the proton in units of ppm as a function of the proton reaction coordinate ν. | |
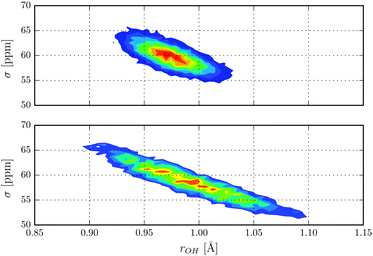 |
| | Fig. 4 Isotropic nuclear magnetic shielding of the four hydrogens in units of ppm as a function of the hydrogen–oxygen distance rOH. | |
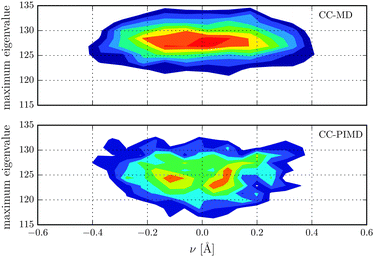 |
| | Fig. 5 Distribution of the maximum eigenvalue of the proton magnetic shielding tensor in units of ppm with respect to the proton reaction coordinate ν. | |
Acknowledgements
Financial support from the Graduate School of Excellence MAINZ and the IDEE project of the Carl Zeiss Foundation is kindly acknowledged.
References
- D. Marx and M. Parrinello, J. Chem. Phys., 1996, 104, 4077 CrossRef CAS PubMed.
- M. E. Tuckerman, D. Marx, M. L. Klein and M. Parrinello, J. Chem. Phys., 1996, 104, 5579–5588 CrossRef CAS PubMed.
- M. Pavese, D. R. Berard and G. A. Both, Chem. Phys. Lett., 1999, 300, 93–98 CrossRef CAS.
- M. Shiga, M. Tachikawa and S. Miura, J. Chem. Phys., 2001, 115, 9149 CrossRef CAS PubMed.
- M. Shiga and A. Nakayama, Chem. Phys. Lett., 2008, 451, 175–181 CrossRef CAS PubMed.
- D. Marx and M. Parrinello, Nature, 1995, 375, 216–218 CrossRef CAS.
- M. E. Tuckerman, D. Marx, M. L. Klein and M. Parrinello, Science, 1997, 275, 817–820 CrossRef CAS.
- R. O. Weht, J. Kohanoff, D. A. Estrin and C. Chakravarty, J. Chem. Phys., 1998, 108, 8848 CrossRef CAS PubMed.
- M. Benoit, D. Marx and M. Parrinello, Nature, 1998, 392, 258–261 CrossRef CAS PubMed.
- H. S. Mei, M. E. Tuckerman, D. E. Sagnella and M. L. Klein, J. Phys. Chem. B, 1998, 102, 10446–10458 CrossRef CAS.
- D. Marx, M. E. Tuckerman, J. Hutter and M. Parrinello, Nature, 1999, 397, 601–604 CrossRef CAS PubMed.
- M. E. Tuckerman, D. Marx and M. Parrinello, Nature, 2002, 417, 925–929 CrossRef CAS PubMed.
- D. Marx, ChemPhysChem, 2006, 7, 1848–1870 CrossRef CAS PubMed.
- J. A. Morrone and R. Car, Phys. Rev. Lett., 2008, 101, 17801 CrossRef.
- A. Kaczmarek, M. Shiga and D. Marx, J. Phys. Chem. A, 2009, 113, 1985–1994 CrossRef CAS PubMed.
- G. A. Luduena, M. Wegner, L. Bjalie and D. Sebastiani, ChemPhysChem, 2010, 11, 2353–2360 CrossRef CAS PubMed.
- M. Shiga, K. Suzuki and M. Tachikawa, J. Chem. Phys., 2010, 132, 114104 CrossRef PubMed.
- X.-Z. Li, B. Walker and A. Michaelides, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 6369–6373 CrossRef CAS.
- V. Srinivasan and D. Sebastiani, J. Phys. Chem. C, 2011, 115, 12631–12635 CAS.
- R. L. Hayes, S. J. Paddison and M. E. Tuckerman, J. Phys. Chem. A, 2011, 115, 6112–6124 CrossRef CAS PubMed.
- M. Ceriotti, J. Cuny, M. Parrinello and D. E. Manolopoulos, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 15591–15596 CrossRef CAS PubMed.
- O. Svoboda, D. Hollas, M. Ončák and P. Slaviček, Phys. Chem. Chem. Phys., 2013, 15, 11531–11542 RSC.
- M. Dracinsky and P. Hodgkinson, Chem. – Eur. J., 2014, 20, 2201–2207 CrossRef CAS PubMed.
- R. O. Jones and O. Gunnarsson, Rev. Mod. Phys., 1989, 61, 689–746 CrossRef CAS.
- W. Kohn, Rev. Mod. Phys., 1999, 71, 1253–1266 CrossRef CAS.
- T. D. Kühne and R. Z. Khaliullin, Nat. Commun., 2013, 4, 1450 CrossRef PubMed.
- R. Z. Khaliullin and T. D. Kühne, Phys. Chem. Chem. Phys., 2013, 15, 15746–15766 RSC.
- T. D. Kühne and R. Z. Khaliullin, J. Am. Chem. Soc., 2014, 136, 3395 CrossRef PubMed.
- M. Parrinello, Solid State
Commun., 1997, 102, 107 CrossRef.
- T. D. Kühne, M. Krack and M. Parrinello, J. Chem. Theory Comput., 2009, 5, 235 CrossRef.
- J. A. Pople, Angew. Chem., Int. Ed., 1999, 38, 1894–1902 CrossRef CAS.
-
T. Helgaker, J. Olsen and P. Jorgensen, Molecular Electronic-Structure Theory, John Wiley & Sons, Chichster, 2000 Search PubMed.
- T. D. Kühne, M. Krack, F. R. Mohamed and M. Parrinello, Phys. Rev. Lett., 2007, 98, 066401 CrossRef PubMed.
- T. D. Kühne, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 391–406 CrossRef.
- K. Karhan, R. Z. Khaliullin and T. D. Kühne, J. Chem. Phys., 2010, 132, 114104 CrossRef PubMed.
- J. Čížek, J. Chem. Phys., 1966, 45, 4256 CrossRef PubMed.
-
J. Gauss, Encyclopedia of Computational Chemistry, Wiley, Chichster, 1998, vol. 1, pp. 615–636 Search PubMed.
- R. J. Bartlett and M. Musia, Rev. Mod. Phys., 2007, 79, 291–352 CrossRef CAS.
- G. D. Purvis and R. J. Bartlett, J. Chem. Phys., 1982, 76, 1910–1918 CrossRef CAS PubMed.
- J. Sauer and J. Döbler, ChemPhysChem, 2005, 6, 1706–1710 CrossRef CAS PubMed.
- S. Lammers and M. Meuwly, J. Phys. Chem. A, 2007, 111, 1638–1647 CrossRef CAS PubMed.
-
R. P. Feynman and A. Hibbs, Quantum Mechanics and Path Integrals, McGraw-Hill, New York, 1965 Search PubMed.
- D. Chandler, J. Chem. Phys., 1981, 74, 4078 CrossRef CAS PubMed.
- M. Parrinello and A. Rahman, J. Chem. Phys., 1984, 80, 860 CrossRef CAS PubMed.
- J. Kolafa, J. Comput. Chem., 2004, 25, 335–342 CrossRef CAS PubMed.
- D. Richters and T. D. Kühne, J. Chem. Phys., 2014, 15, 134109 CrossRef PubMed.
- M. Ceriotti, J. More and D. E. Manolopoulos, Comput. Phys. Commun., 2014, 185, 1019–1026 CrossRef CAS PubMed.
- A. C. Scheiner, G. E. Scuseria, J. E. Rice, T. J. Lee and H. F. Schaefer, J. Chem. Phys., 1987, 87, 5361 CrossRef CAS PubMed.
- J. F. Stanton, J. Gauss, J. D. Watts and R. J. Bartlett, J. Chem. Phys., 1991, 94, 4334 CrossRef CAS PubMed.
- J. Gauss, J. F. Stanton and R. J. Bartlett, J. Chem. Phys., 1991, 95, 2623 CrossRef CAS PubMed.
- J. Gauss, W. J. Lauderdale, J. F. Stanton, J. D. Watts and R. J. Bartlett, Chem. Phys. Lett., 1991, 182, 207–215 CrossRef CAS.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007 CrossRef CAS PubMed.
- M. E. Harding, T. Metzroth, J. Gauss and A. A. Auer, J. Chem. Theory Comput., 2008, 4, 64–74 CrossRef CAS.
-
J. F. Stanton, J. Gauss, M. Harding, P. Szalay, A. Auer, R. J. Bartlett, U. Benedikt, C. Berger, D. Bernholdt, Y. Bombleet al., for the current version, see http://www.cfour.de, 2011.
- J. Gauss and J. F. Stanton, J. Chem. Phys., 1996, 104, 2574 CrossRef CAS PubMed.
-
J. Gauss and J. F. Stanton, Calculation of NMR and EPR Parameters: Theory and Applications, Wiley-VCH, Weinheim, 2004, p. 123 Search PubMed.
- E. F. Valeev and H. F. Schaefer III, J. Chem. Phys., 1998, 108, 7197–7201 CrossRef CAS PubMed.
- A. A. Auer, T. Helgaker and W. Klopper, Phys. Chem. Chem. Phys., 2000, 2, 2235–2238 RSC.
- M. Dagrada, M. Casula, A. M. Saitta, S. Sorella and F. Mauri, J. Chem. Theory Comput., 2014, 10, 1980–1993 CrossRef CAS.
- J. E. Del Berne, S. A. Perera and R. J. Bartlett, J. Phys. Chem. A, 1999, 103, 8121–8124 CrossRef.
- A. L. Sobolewski and W. Domcke, J. Phys. Chem. A, 2002, 106, 4158–4167 CrossRef CAS.
- H. H. Limbach, P. M. Tolstoy, N. Perez-Hernandez, J. Guo, I. G. Shenderovich and G. S. Denisov, Isr. J. Chem., 2009, 49, 199–216 CrossRef CAS.
- A. A. Hassanali, J. Cuny, M. Ceriotti, C. J. Pickard and M. Parrinello, J. Am. Chem. Soc., 2012, 134, 8557–8569 CrossRef CAS PubMed.
- J. S. Waugh, L. M. Huber and U. Haeberlen, Phys. Rev. Lett., 1968, 20, 180–182 CrossRef CAS.
- S. G. Kukolich, J. Am. Chem. Soc., 1975, 97, 5704–5707 CrossRef CAS.
- F. Schönborn, H. Schmitt, H. Zimmermann, U. Haeberlen, C. Corminboeuf, G. Gromann and T. Heine, J. Magn. Reson., 2005, 175, 52–64 CrossRef PubMed.
- K. Modig and B. Halle, J. Am. Chem. Soc., 2002, 124, 12031–12041 CrossRef CAS PubMed.
|
| This journal is © the Owner Societies 2015 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article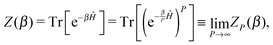
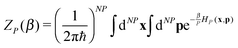
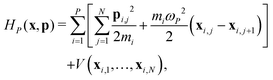
![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) |Φ〉,
|Φ〉,![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) =
= ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) 1 +
1 + ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) 2 +
2 + ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) 3 +⋯,
3 +⋯,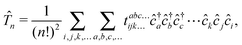
![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) reduces to finding the expansion coefficients of its second quantized operators. In this notation, CCSD corresponds to an approximation of the exact wave function by truncating eqn (5) after the two-body cluster contributions.
reduces to finding the expansion coefficients of its second quantized operators. In this notation, CCSD corresponds to an approximation of the exact wave function by truncating eqn (5) after the two-body cluster contributions.
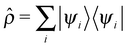 is much smoother than that of the more widely varying MOs, the predicted density operators
is much smoother than that of the more widely varying MOs, the predicted density operators ![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) p(tn) at time tn is expressed in terms of K previous
p(tn) at time tn is expressed in terms of K previous ![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) (tn−m), which is then used as an approximate projector on to the occupied subspace |ψi(tn−1)〉 to obtain the predicted MOs
(tn−m), which is then used as an approximate projector on to the occupied subspace |ψi(tn−1)〉 to obtain the predicted MOs