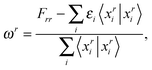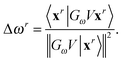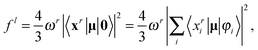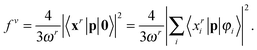Numerically accurate linear response-properties in the configuration-interaction singles (CIS) approximation
Received
19th January 2015
, Accepted 8th April 2015
First published on 27th April 2015
Abstract
In the present work, we report an efficient implementation of configuration interaction singles (CIS) excitation energies and oscillator strengths using the multi-resolution analysis (MRA) framework to address the basis-set convergence of excited state computations. In MRA (ground-state) orbitals, excited states are constructed adaptively guaranteeing an overall precision. Thus not only valence but also, in particular, low-lying Rydberg states can be computed with consistent quality at the basis set limit a priori, or without special treatments, which is demonstrated using a small test set of organic molecules, basis sets, and states. We find that the new implementation of MRA-CIS excitation energy calculations is competitive with conventional LCAO calculations when the basis-set limit of medium-sized molecules is sought, which requires large, diffuse basis sets. This becomes particularly important if accurate calculations of molecular electronic absorption spectra with respect to basis-set incompleteness are required, in which both valence as well as Rydberg excitations can contribute to the molecule's UV/VIS fingerprint.
I. Introduction
Electronically excited states of molecules play an essential role in e.g. photochemistry and photophysics, which have attracted much attention due to their key role in natural and artificial photosynthesis. The toolbox of quantum chemistry provides a number of methods to compute excited states, such as time-dependent DFT (TDDFT), time-dependent Hartree–Fock (TDHF), and linear-response (LR) coupled cluster (CC).1–3 TDDFT is an efficient formulation and yields accurate results for valence excited states and properties, but can severely fail for charge-transfer states and Rydberg states. Coupled-cluster models provide a way to systematically decrease the method error leading to the exact solution of the Schrödinger equation, but the reduction of the method error leads inescapably to an increase in scaling with respect to the system size and thus significantly longer computation times.
In this article we use the formalism of multi-resolution analysis (MRA) to compute the excited states of small- and medium-sized molecules. Unlike standard quantum chemistry, MRA needs to be formulated in the so-called first quantization, i.e. in the real-space representation of operators and states. In the original formulation by Schrödinger, observables are represented by operators and states by functions.4 Since from all mathematical solutions of the Schrödinger equation only particular ones are suited as physical solutions due to certain constraints such as norm and differentiability, this formulation was denoted as first quantization. The name second quantization was chosen based on distinct physical observations, for instance the creation or annihilation of photons requiring also a quantization of the electromagnetic field,5 but for most quantum-chemical applications and for the present work, second quantization denotes pragmatically the introduction of a basis, whose basis functions are combined and rotated to form (occupied and unoccupied) molecular orbitals used to construct approximate solutions of e.g. the Schrödinger equation.6
The fundamental ansatz of virtually all basis set-based methods is the pre-definition of the shape and the number of basis functions, leaving the task to find an approximate solution for an actual problem with a number of adjustable (linear) parameters as small as possible. In quantum chemistry, a lot of effort has been invested in finding optimal basis sets. The big advantage of such pre-parameterized basis sets is at the same time the biggest drawback: experience is not only helpful, it is rather indispensably needed, and many basis sets have been developed which are not used anymore because of imbalance leading to high accuracy in some cases and large errors in other cases. New basis sets are reported in the literature on a regular basis, each optimized for a particular task, for instance explicit correlation,7 (new) relativistic Hamiltonians,8 or the need to investigate advanced properties such as polarizabilities.9 For excited-state calculations, the accuracy of the model is often less important than the quality of the basis, because standard basis sets have been optimized for ground-state energies,10,11 and are often too compact for excited states. The arbitrariness that comes with the use of ground-state basis sets for excited states makes it hard to compute reliable, reproducible data when (excited-state) calculations are limited to a certain basis-set size.
Many problems of pre-defined basis sets are avoided by using multi-resolution analysis (MRA).12–15 MRA functions are represented on an adaptive grid, which is constructed during the solution of the equations. In principle this technique can be used for all methods and molecules, while guaranteeing that the results are accurate up to a requested threshold. This technique has been used before for similar purposes, such as for computing ground state energies,12,14 polarizabilities,16,17 for solving the time-dependent Schrödinger equation,18,19 or computing TDHF/TDDFT excitation energies.13 The increase in accuracy and reliability is paid for by a larger prefactor in computational efficiency compared to traditional LCAO approaches. However, the computational scaling is significantly lower for MRA than for LCAO, so that for large molecules MRA can become more efficient.
In the present work, we address the basis-set convergence for selected linear-response properties using the configuration-interaction singles (CIS) method. In Section II, we review the basic equations for first and second quantization-based CIS response properties. In Section IV, we report our findings concerning the basis-set incompleteness error for a selection of molecules and basis sets. The article closes with summary and conclusions.
II. Methodology
In this section we repeat the linear response formalism for completeness, although it has been given before. The aim is to have a side-by-side comparison of the CIS working equations in first and second quantization. In contrast to the conventional CIS derivation the transition to density functional methods is straightforward within the linear response framework.
A. Linear response
The response of the molecular system with respect to an external, time-dependent perturbation f(t) = feiωt + f†e−iωt can be expressed as a Taylor series,| |  | (1) |
where ρ(t) is the time-dependent density and ρ(0) is the unperturbed ground state density. The perturbed Fock operator F(t) depends on the perturbed density, and can also be expressed in a Taylor series,| | 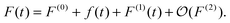 | (2) |
The linear response of the density is computed as the functional derivative of the corresponding zeroth-order equation, e.g. Hartree–Fock or Kohn–Sham equations, with respect to the density:| | 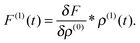 | (3) |
Inserting the expressions into the time-dependent Schrödinger equations and keeping terms up to first order yields| | 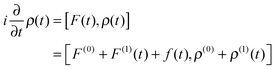 | (4) |
Since the external perturbation oscillates with frequency ω, the perturbed density ρ and the perturbed Fock operator F adopt the same time dependence:| | ρ(1)(t) = ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) eiωt + eiωt + ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) †e−iωt. †e−iωt. | (5) |
Factoring out the explicit time dependence eiωt from the perturbed density, and letting the perturbation go to zero leads to| | 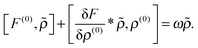 | (6) |
This general equation defines the perturbed density ρ(1) and thus the linear response of the system. Depending on a formulation in first or second quantization, different working equations are obtained as discussed below.
B. CIS excitation energies in second quantization
In second quantization the perturbed densities are expressed as rotations from the occupied to the virtual space:20| | | ρ(1)pq = dpqeiωt + d†qpe−iωt | (7) |
| | ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) pq = dpq pq = dpq | (8) |
with only the occupied/virtual and virtual/occupied blocks of dpq having non-zero entries, which are denoted as x and y (“excitation” and “deexcitation”) vectors The general SCF response equation (eqn (6)) becomes| |  | (10) |
In the Tamm–Dancoff approximation the de-excitation coefficients y are neglected. Using the diagonal nature of the Fock and density matrices the following set of linear equations are obtained:| | 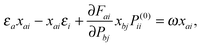 | (11) |
where i, j denote (active) occupied and a, b (active) virtual orbitals, and ε denote Hartree–Fock orbital energies. These can be cast into a matrix eigenvalue problem withwhere we have introduced an additional index r indicating the r-th excitation corresponding to the r-th eigenpair of the matrix A. The closed-shell expression matrix reads for singlet excitations:21| | | Asia,jb = δijδab(εi + εj − εa − εb) + 2(ia|r12−1|jb) − (ij|r12−1|ab), | (13) |
and for triplet excitations:| | | Atia,jb = δijδab(εi + εj − εa − εb) − (ij|r12−1|ab). | (14) |
C. CIS excitation energies in first quantization
In first quantization the perturbed densities ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) and
and ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) † are also expressed as projections from the occupied to the virtual space and vice versa:
† are also expressed as projections from the occupied to the virtual space and vice versa:| |  | (15) |
| | 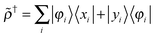 | (16) |
The first-order responses |xi〉 have the same orthogonality properties as the vector x in second quantization:13,16| |  | (17) |
| |  | (18) |
where the superscript r (p) again indicates the r-th (p-th) root of the response equation, i.e. the r-th (p-th) excitation energy, and ρ(0) denotes the ground-state density. While in second quantization the orthogonality comes with the hermiticity of the matrix A in the case of CIS (but not for other models), in first quantization the orthogonality must be explicitly enforced even for CIS.
Starting from eqn (6), by left-projecting on 1 − ρ(0), right-projecting on ρ(0), using the orthogonality relationships, and dropping the |yi〉 for the CIS approximation, the three terms in eqn (6) become
| | 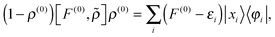 | (19) |
| |  | (20) |
| |  | (21) |
Recombination of these terms and dropping the trailing 〈
φi| yields
| | 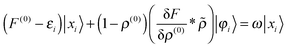 | (22) |
which is reminiscent of the second-quantized formulation of
eqn (12). This can be rearranged to
| | 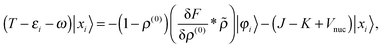 | (23) |
| | 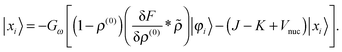 | (24) |
These equations need to be solved iteratively since the solution |
xi〉 is part of the right-hand side through
![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif)
, see
eqn (15). Green's operator
G is the inverse of the Helmholtz operator
22 Given the perturbed density
![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif)
in real space,
| | 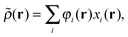 | (26) |
the variation of the Fock operator
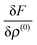
can be computed as follows:
| |  | (27) |
| | 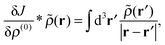 | (28) |
| |  | (29) |
D. Calculation of MRA excitation energies
1. Initial guess for the excitation vectors.
Let ![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) be an excitation operator which generates approximately the excitation orbitals |xi〉 when acting on ground state orbitals |φi〉,
be an excitation operator which generates approximately the excitation orbitals |xi〉 when acting on ground state orbitals |φi〉,| | |xi〉 ≈ ![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) |φi〉. |φi〉. | (30) |
This operator is expanded into polynomials up to n-th order,| |  | (31) |
For symmetric molecules the polynomials are grouped into irreducible representations according to their transformational behavior. In the case of low-order symmetry groups or molecules without symmetry, expansion coefficients in eqn (31) for the initial trial vectors can be obtained from either an approximate higher order symmetry group, or a guess based on intuition, experimental or calculated data such as multipole transition moments.
2. Iterative procedure and orthogonalization.
Eqn (23) has to be solved for each target excitation vector |xr〉 while the individual vectors are orthonormalized in each iteration. A simple Gram–Schmidt orthogonalization fails to converge quickly when trial vectors are containing contributions to several excited states. A way to disentangle these excitations is to compute the Fock matrix elements of the excitation vectors Fpr by projecting the working equations from the left on the excitations 〈xp|,| |  | (32) |
The amplitudes are finally determined by solving the generalized eigenvalue problem of the Fock matrix:| |  | (33) |
where U are the eigenvectors of the perturbed Fock matrix.
The excitation energies ωr of the r-th root can be extracted from the diagonal matrix elements through
| | 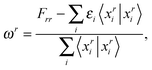 | (34) |
or through an updating scheme,
12| | 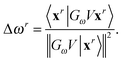 | (35) |
Here
GωV|
x〉 is a short-hand notation for the right-hand side of
eqn (24). The updating procedure is correct to second order with respect to the error in the excitation functions |
xr〉 and thus provides accurate excitation energies. Furthermore, this scheme tends to be more accurate numerically because no derivative operator is involved. In contrast, the perturbed Fock matrix scheme is more stable if the current excitation vectors and energies are far from convergence.
The complete iterative procedure for obtaining MRA excitation vectors at the CIS level of theory reads:
(1) Guess initial trial vectors according to Section II D 1.
(2) Iterate eqn (23) once for all vectors |xr〉.
(3) Orthogonalize the excitations and compute the excitation energies ωr for each vector |xr〉 either by the updating scheme in eqn (35) or through eqn (34).
(4) If not converged, return to 2.
(5) Calculate oscillator strengths.
In CIS, oscillator strengths are obtained as contractions of the ground-state and excitation vectors with an appropriate operator. Explicit expressions for the oscillator strengths read for the length gauge (superscript l) and the velocity gauge (superscript v):23
| | 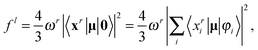 | (36) |
| | 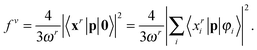 | (37) |
The MRA formalism grants gauge invariance with respect to basis set incompleteness, but the gauge dependence inherent in the CIS model still persists.
III. Computational details
All LCAO-based calculations were performed with the ricc2 (CCS and CCSD) and escf (CIS) modules of the Turbomole program package version 6.5.24 Standard basis sets were taken from the Turbomole basis set library.25–27 The Rydberg basis used was “CM2” taken from ref. 28, consisting of 2s2p2d with exponents 0.01 and 0.0033, respectively, which are placed in the center of mass of the molecules.29
The MRA treatment has been implemented in a local version of the MADNESS library.30 The precision threshold of all functions (orbitals and excitation vectors) was set to 10−5 in the response equation and 10−6 in the ground state calculation. The polynomial order was chosen to be k = 8. Calculations were considered converged when the norm of the excitation vectors would not change more than 10−3.
IV. Results and discussion
This section is organized as follows. We first analyze the use of different initial trial vectors and convergence behavior for MRA CIS excitation energies. Using the new MRA implementation, we review basis-set based results using different basis sets and augmentation strategies in terms of basis-set incompleteness error and convergence to the basis-set limit. Excitation energies are treated for singlet and triplet excitations, while oscillator strengths are only discussed for singlet excited states because triplet excitations are spin-forbidden in non-relativistic treatments thus lacking a physical meaning. Finally, we discuss the performance of the new implementation of MRA CIS excitation energies.
A. Initial trial vectors and convergence in MRA CIS
Similar to LCAO calculations the quality of the initial trial vectors is crucial for recovering the lowest excited states if not all roots are to be determined. In LCAO methods this problem arises mainly in symmetric systems such as benzene and is not dominant in asymmetric molecules. However, in MRA the configuration space is much larger and thus the problem is present in virtually all calculations. While in LCAO methods the guess is based on orbital energy differences, such an approach is not available in MRA methods, because no virtual orbitals exist and therefore no orbital energies as well.
Physically motivated initial trial vectors are obtained by multiplying the ground-state orbitals with a dipole operator, leading to a fast convergence for bright states, i.e. states with large oscillator strengths, but typically misses dark states, i.e. states with small oscillator strengths. Initial trial vectors for molecules with high symmetry can be obtained from symmetry-adapted guess functions, which converge quickly in all cases to the corresponding excited states. While the actual MRA calculations are carried out without applying point-group symmetry, the initial trial vectors may exhibit a particular symmetry. Trial vectors can also be based on a LCAO calculation in a small basis, mapping the ground-state orbitals using a Procrustes rotation.
In Fig. 1 the convergence of the MRA-CIS excitation energies of the helium atom is shown. The guess excitation vectors |x〉 are excitations to the hybrid sp3 orbitals. Whether these excitations can be quickly disentangled (perturbed Fock matrix diagonalization) or not (Gram–Schmidt orthogonalization) depends on the orthonormalization procedure. In addition, we used a Krylov subspace method31 to accelerate the convergence of the excitation vectors.
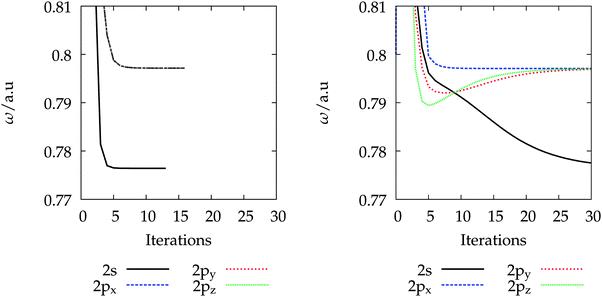 |
| | Fig. 1 Convergence behavior for s- and p-type excited states of the helium atom with different orthonormalization procedures: perturbed Fock matrix orthogonalization (left) and Gram–Schmidt orthogonalization (right). For the perturbed Fock matrix orthogonalization (left) all components converge smoothly within less than 10 iterations, while in the Gram–Schmidt orthogonalization (right) no convergence is achieved after 20 iterations. | |
B. CIS model error and basis set incompleteness
In Table 1, two low-lying excitation energies of the ethylene molecule are listed, with 11B3u being a valence excitation, and 21B3u a Rydberg excitation. The reference MRA values were obtained with our new implementation. The basis set convergence for the valence excitation (11B3u) is quite rapid, and already the smallest basis set, aug-cc-pVDZ, exhibits a basis-set incompleteness error of only about 25 meV, while the standard deviation concerning the method error of CCS can be assumed to be about 1.2 eV.32 The Rydberg excitation (21B3u), on the other hand, shows no rapid convergence with respect to the basis set, and the smallest basis set, aug-cc-pVDZ, shows a basis-set incompleteness error of about 1.5 eV, which is about the same order of magnitude as the method error. Increasing the basis set with respect to the cardinal number, as done for ground-state energy calculations, decreases the error only slowly and leads to errors of about 1.1 eV and 0.8 eV for aug-cc-pVTZ and aug-cc-pVQZ, respectively, indicating that no higher l-quantum numbers are missing in the basis set. A severe problem is that such a behavior can easily be misinterpreted as “proper” convergence if only ground-state basis sets are employed, although it is only a pseudo-convergence because the missing (diffuse) functions are not taken into account. A fairly rapid convergence with respect to the basis set is obtained if additional diffuse functions are added, which are less important in ground-state calculations. This illustrates how computing certain properties can change the basis-set requirements drastically, which requires “experience-based” development and application of basis sets.
Table 1
1B3u excitation energies of C2H4 in eV calculated using different basis sets and coupled cluster methods. Excitation energies of configuration-interaction singles (CIS) and coupled cluster singles (CCS) yield identical results. (RCC = 2.5187 bohr, RCH = 2.0422 bohr, and ΘHCH = 121.35°)
|
|
11B3u (valence) |
21B3u (Rydberg) |
| CCS |
CCSD |
CCS |
CCSD |
|
Calculations did not converge.
|
| aug-cc-pVDZ |
7.745 |
8.042 |
10.620 |
10.430 |
| aug-cc-pVTZ |
7.730 |
8.027 |
10.135 |
10.372 |
| aug-cc-pVQZ |
7.726 |
8.030 |
9.834 |
10.183 |
|
|
| d-aug-cc-pVDZ |
7.725 |
8.014 |
9.043 |
9.349 |
| d-aug-cc-pVTZ |
7.718 |
8.016 |
9.046 |
9.449 |
| d-aug-cc-pVQZ |
7.719 |
n.c.a |
9.045 |
n.c.a |
|
|
| MRA |
7.718 |
— |
9.033 |
— |
In the present example the computation of excitation energies with balanced quality is only possible if the basis-set incompleteness error can be controlled. However, even with quite large basis sets there is no guarantee to achieve basis-set convergence, and, in addition very large basis sets often lead to linear dependencies, convergence problems, and decreased computational efficiency (vide infra).
C. Basis-set convergence
We computed singlet and triplet CIS excitation energies of a small test set of molecules with different basis sets and compared them to the basis-set limit calculations from MRA, as obtained with our new implementation. The test set consists of the six lowest singlet and six lowest triplet excitations of water, ammonia, ethylene, benzene, norbornane, cyclopropane, and formaldehyde, totaling 84 states. The basis sets were selected to represent different cardinal numbers (X = D, T, Q) of commonly used basis set families, as well as a benchmarking basis set (d-aug-cc-pVQZ). The aim of this section is not to provide an extensive assessment of basis sets, but to put the MRA results into context.
In Table 2 we compare MRA CIS to widely-used basis set families, namely the Dunning-type and Karlsruhe-type. The correlation-consistent basis sets pioneered by Dunning,11 abbreviated as cc-pVXZ, are primarily constructed to provide accurate ground-state energies for correlated methods. Additional diffuse functions are provided through augmentation functions, leading to aug-cc-pVXZ basis sets. Furche and Rappoport9 constructed optimized basis sets for response properties for density-functional theory (DFT) applications based on static polarizability calculations. These basis sets have at most one additional spd set of diffuse basis functions and thus correspond approximately to the aug-cc-pVXZ basis sets, while being more compact and consisting of a reduced number of basis functions. Consequently all of these sets are sufficient for describing valence excited states, but fail to describe Rydberg states accurately.
Table 2 The first 7 singlet and triplet CIS excitation energies of the ethylene molecule in eV, as well as excitation 21B3u
| State |
Γ |
def2-SVPD |
SVPD+d |
def2-TZVPD |
def2-TZVPD+CM2 |
aug-cc-pVQZ |
d-aug-cc-pVQZ |
MRA |
| T1 |
3B3u |
3.621 |
3.614 |
3.619 |
3.617 |
3.617 |
3.617 |
3.616 |
| T2 |
3B1u |
7.580 |
7.009 |
7.194 |
6.942 |
6.927 |
6.922 |
6.922 |
| T3 |
3B3g |
8.565 |
7.700 |
8.452 |
7.759 |
7.652 |
7.638 |
7.639 |
| T4 |
3Ag |
10.930 |
7.838 |
10.114 |
7.974 |
7.912 |
7.771 |
7.770 |
| T5 |
3B2g |
8.599 |
7.860 |
8.128 |
7.792 |
7.788 |
7.771 |
7.772 |
| T6 |
23B3g |
9.157 |
8.536 |
8.565 |
8.505 |
8.496 |
8.495 |
8.495 |
| T7 |
23B1u |
9.912 |
8.612 |
9.285 |
8.611 |
8.824 |
8.506 |
8.478 |
|
|
| S1 |
1B1u |
7.904 |
7.218 |
7.489 |
7.156 |
7.149 |
7.140 |
7.141 |
| S2 |
1B3u |
8.064 |
7.781 |
7.896 |
7.818 |
7.726 |
7.719 |
7.718 |
| S3 |
1B3g |
9.238 |
7.782 |
8.666 |
7.836 |
7.742 |
7.724 |
7.723 |
| S4 |
1B2g |
8.823 |
7.955 |
8.310 |
7.897 |
7.901 |
7.878 |
7.877 |
| S5 |
1Ag |
11.890 |
8.156 |
11.105 |
8.192 |
8.403 |
8.101 |
8.101 |
| S6 |
21B1u |
10.536 |
8.666 |
9.881 |
8.679 |
8.903 |
8.587 |
8.570 |
| S7 |
1Au |
11.347 |
8.846 |
10.328 |
8.824 |
8.894 |
8.788 |
8.742 |
| ⋯ |
⋯ |
⋯ |
⋯ |
⋯ |
⋯ |
⋯ |
⋯ |
⋯ |
| S12 |
21B3u |
13.116 |
9.111 |
12.248 |
9.021 |
9.834 |
9.045 |
9.033 |
Up to doubly augmented triple zeta basis sets are needed to converge excitation energies (or excited-state properties) to the basis set limit. Alternatively, the atom-centered basis sets are supplemented with diffuse center-of-mass (CM) basis sets to describe the Rydberg states. This procedure works very well, but still the ordering of the states might be incorrect, e.g. the 3B2g and the 3Ag states of ethylene in the case of the basis def2-TZVPD+CM2, see Table 2. Furthermore, the excitation energies might still exhibit large errors if the CM basis functions are combined with the small valence basis set.
Some statistical measurements of the lowest excitations of the test set molecules are given in Fig. 2, all with respect to MRA calculations which have been considered as the basis set limit. No standard deviation or variance is given because the distributions are not Gaussian shaped. It can be seen that the doubly augmented d-aug-cc-pVQZ basis set exhibits only small errors and are in good agreement with the MRA calculations. However, this basis is very large and contains diffuse functions, which leads to a low computational efficiency. The singly augmented aug-cc-pVQZ can yield significant deviations >0.5 eV for 15 of the 84 states, but can be considered to be in reasonable agreement with the basis-set limit. In contrast, the CM-augmented def2-TZVPD basis set seems more balanced, since only few states exhibit large deviations. For medium-sized basis sets such as def2-TZVPD little can be said about the quality of the individual states due to the almost equal distribution of errors, although the basis set has already been optimized for response properties.
 |
| | Fig. 2 Graphical representation of errors obtained using different basis sets compared to the MRA limit. Included are singlet and triplet states of the test set of 7 molecules. The total number of states is 84. Conventional basis sets are not able to account for Rydberg states and additional diffuse functions have to be used. MRA, on the other hand, is able to achieve accurate results for all states without special considerations. | |
An alternative ad hoc correction of the singly augmented basis sets can be the addition of a second set of diffuse functions, taken from the Dunning family, resulting in “doubly augmented” basis sets and in significantly improved behavior, e.g. “def2-SVPD+d”, which are obtained by adding the second set of diffuse functions from d-aug-cc-pVDZ and d-aug-cc-pVTZ, respectively. This additional set of diffuse functions are essential for the description of Rydberg states, for both the Karlsruhe-type or the Dunning-type. In addition it is quite problematic that neglecting the second set of diffuse basis functions might lead to pseudo-convergence.
Assuming that CIS exhibits a standard deviation of about 1.2 eV and maximum errors as large as 2.4 eV,32 the number of states inside an error bar of 1.0 eV counts as follows: 47 for SVPD (56%), 81 for SVPD+d (96%), 69 for TZVPD (82%), 83 for TZVPD+CM2 (99%), and 81 for aug-cc-pVQZ (96%) and d-aug-cc-pVQZ (100%). This means, for instance, that for the smallest basis set, def2-SVPD, 37 states (about 50%) exhibit errors larger than the method error. However, when for this basis set additional diffuse functions are included, leading to the basis set denoted as SVPD+d here, 35 (out of 37) states drop below 1.0 eV error and only two states remain beyond 1.0 eV error. We thus estimate that 35 states have a significant Rydberg character, while the accuracy of the two remaining states can be increased by using TZVPD, indicating a significant valence character. Leaving out Rydberg-type excitations, it means that the SVPD basis set is able to obtain 47 out of 49 valence excitations below 1.2 eV accuracy, i.e. the estimated method error.
Within the limited test set the SVPD basis thus seems to yield an acceptable accuracy for the lowest excitations in the CIS approximation. For more accurate methods such as CCSD this is not true any more, since the method error is significantly lowered. In the TDDFT framework the situation is inversed, since the small basis set is not able to describe Rydberg or charge-transfer states, but neither is TDDFT, so that the errors might be balanced again, albeit at a low level.
The oscillator strengths show a similar behavior compared to the excitation energies. Exemplary results are presented for the water molecule in Table 3. All oscillator strengths as obtained with the best basis set, d-aug-cc-pVQZ, yield only small differences compared to the reference MRA results. One exception is the oscillator strength in the velocity representation belonging to the 31B2 excitation with an excitation energy of 11.921 eV, which has an error of one order of magnitude. The error is again found in the LCAO calculations, where the oscillator strengths converge slower than the corresponding excitation energy. For properties of the excited states an accurate description of the excited wave functions is even more important than for the excitation energies by themselves.
Table 3 CIS excitation energies in eV and oscillator strengths for selected excitations of the water molecule
| Γ |
|
def2-TZVPD |
TZVPD+CM |
d-aug-cc-pVQZ |
MRA (k = 8, ε = 1 × 10−4) |
| 11B2 |
Excitation energy |
8.908 |
8.806 |
8.778 |
8.778 |
| Length |
5.0 × 10−2 |
4.9 × 10−2 |
4.8 × 10−2 |
4.8 × 10−2 |
| Velocity |
7.2 × 10−2 |
7.0 × 10−2 |
7.1 × 10−2 |
7.1 × 10−2 |
|
|
| 11A2 |
Excitation energy |
10.627 |
10.503 |
10.443 |
10.443 |
| Length |
0 |
0 |
0 |
0 |
| Velocity |
0 |
0 |
0 |
0 |
|
|
| 11A1 |
Excitation energy |
11.165 |
11.010 |
10.966 |
10.967 |
| Length |
1.0 × 10−1 |
8.1 × 10−2 |
7.1 × 10−2 |
7.0 × 10−2 |
| Velocity |
8.7 × 10−2 |
7.6 × 10−2 |
6.5 × 10−2 |
6.4 × 10−2 |
|
|
| 21B2 |
Excitation energy |
11.791 |
11.274 |
11.190 |
11.187 |
| Length |
1.3 × 10−2 |
8.2 × 10−3 |
1.1 × 10−2 |
1.1 × 10−2 |
| Velocity |
1.6 × 10−2 |
7.4 × 10−3 |
1.0 × 10−2 |
1.0 × 10−2 |
|
|
| 21A1 |
Excitation energy |
12.182 |
11.577 |
11.505 |
11.495 |
| Length |
1.6 × 10−2 |
2.4 × 10−2 |
3.4 × 10−2 |
3.6 × 10−2 |
| Velocity |
9.3 × 10−3 |
1.6 × 10−2 |
2.4 × 10−2 |
2.6 × 10−2 |
|
|
| 31B2 |
Excitation energy |
13.742 |
11.954 |
11.937 |
11.922 |
| Length |
2.4 × 10−3 |
4.2 × 10−4 |
1.3 × 10−4 |
2.0 × 10−5 |
| Velocity |
3.0 × 10−3 |
2.5 × 10−3 |
1.7 × 10−3 |
1.3 × 10−3 |
D. Spatial extent of excited states
In Fig. 3, we have plotted the MRA solution vectors |xHOMO〉 corresponding to the highest occupied molecular orbital (HOMO) of the ethylene molecule for excitations S1 and S12 from Table 2, where excitation S1 corresponds to a valence state and S12 to a Rydberg state. It can be clearly seen that the Rydberg state extends significantly beyond the ethylene molecule, which illustrates why basis sets suited for ground-state calculations are not suited in general for describing such a state. The shape of the solution vectors |x〉 reveals that no simple mapping to the molecular geometry is observed, which supports the qualitative observation that center-of-mass (CM) basis sets lead to significantly improved accuracy for Rydberg states, while increasing the cardinal number of a given basis set often hardly yields improvements (vide supra).
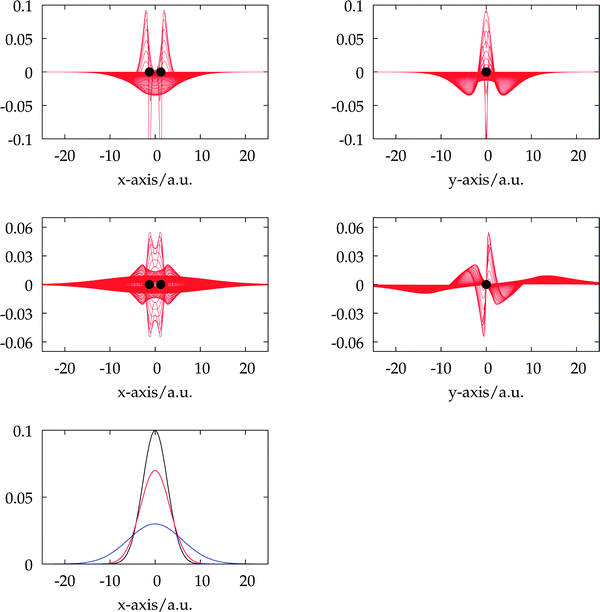 |
| | Fig. 3 Excited-state solution vectors corresponding to the HOMO for 1B1u (top) and 21B3u (bottom) of the ethylene singlet excitations of Table 2 (left: view along the y axis, right: view along the x axis), respectively. The ethylene molecule is oriented along the x axis and the hydrogens are located in the xy plane. The graphical representation illustrates that the spatial extension of the valence excitation is significantly smaller compared to the Rydberg excitation. In the bottom plot the most diffuse s-functions from different basis sets are plotted. The exponents of the Gaussians are 0.067 (def2-SVPD, black), 0.047 (aug-cc-pVDZ, red) and 0.014 (d-aug-cc-pVDZ, blue). | |
E. Computation times
In MRA-CIS the most time consuming step for each iteration step is the calculation of the exchange operator applied on the response vector |x〉, scaling quadratically with the number of occupied orbitals Nocc and linearly with the number of excitations. CPU times for one iteration of one excitation vector |x〉 are plotted for 6 different organic molecules in Fig. 4. The computational time grows approximately quadratically with the number of occupied orbitals. Conventional CIS calculations scale with N2 to N4, where the actual measured scaling depends on applied approximations and the size of the calculation leading to “in-core” or “out-of-core” algorithms.1 A quadratic scaling is reached only in calculations with small basis sets, while it usually cannot be achieved for diffuse basis sets.
 |
| | Fig. 4 Averaged CPU times for one iteration of one excitation vector in seconds, revealing a quadratic scaling of the MRA method as implemented. The molecules employed are water (10 electrons), formaldehyde (16 electrons), cyclopropane (24 electrons), acetone (32 electrons), benzene (42 electrons), norbornane (54 electrons), thymine (66 electrons), camphor (84 electrons) and phenantrene (94 electrons). | |
While LCAO calculations have a fast initial convergence and take only seconds for small molecules and basis sets, MRA calculations have relatively large overhead due to the increased accuracy. This is shown in Fig. 5, where total CPU times for the calculation of the lowest 10 excitation energies of toluene are given.
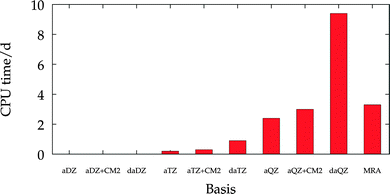 |
| | Fig. 5 Total CPU times in days for the calculation of the 10 lowest CIS singlet excitation energies of toluene (50 electrons) in C1 symmetry with basis sets aug-cc-pVXZ (abbreviated as aXZ) and d-aug-cc-pVXZ (abbreviated as daXZ), as well as MRA. | |
V. Conclusions
In the present work, we report an efficient implementation of CIS excitation energies using multi-resolution analysis (MRA). This method allows for an unbiased calculation of excitation energies guaranteeing the same accuracy for valence as well as Rydberg excited states a priori, i.e. without special treatment. While Gaussian basis sets are hard to beat for lower accuracy, MRA enables the systematic exploration of the basis set limit.
The new MRA implementation was used to investigate the accuracy of excitation energies of selected compounds and basis sets. The analysis revealed a rather moderate performance for conventional basis sets when molecular absorption spectra are to be studied, because they are not able to yield accurate excitation energies for Rydberg states, which also occur among the lowest excitations. We found that only a very large and diffuse basis set, d-aug-cc-pVQZ, can yield reliable excitation energies for both valence and Rydberg excitations. However, the (almost saturated) augmentation of larger basis sets does not seem desirable due to linear dependencies and resulting numerical instabilities. For instance, even for the simple ethylene molecule the CCSD calculations did not converge. This leads to the severe problem of pseudo-convergence when, based on numerical issues, additional diffuse functions have to be excluded from further considerations in excited-state calculations of extended systems.
Based on the current implementation, the calculation of CIS excitation energies using MRA is comparably cheap and guarantees a numerically accurate treatment of excited states. The approach can be used as a benchmark for constructing or analyzing new basis sets. Due to the favorable scaling MRA CIS calculations can also be used directly to compute the UV/VIS spectra of small- and medium-sized molecules without basis set artifacts.
The future prospects are twofold: first, the current implementation is massively parallel and can be used to compute the CIS excitation energies of large molecules, taking advantage of the quadratic scaling algorithm. Second, correlated wave-function models beyond CIS, such as CC2 or CCSD, will be developed for MRA to balance the error in the model. For these, the main obstacle is the higher dimensionality of the wave function, i.e. six dimensional (6D) for CC2 and CCSD instead of three dimensional (3D) in the case of CIS, which needs to be overcome.14 Work along these lines is in progress.
Acknowledgements
F.A.B. gratefully acknowledges financial support from the Deutsche Forschungsgemeinschaft DFG (BI-1432/2-1) and the Fonds der Chemischen Industrie (FCI). S. H. would like to thank Fonds der Chemischen Industrie for financial support.
References
-
F. Furche and D. Rappoport, Density functional methods for excited states: equilibrium structure and electronic spectra, in Computational Photochemistry, ed. M. Olivucci, Elsevier, Amsterdam, 2005, pp. 93–128 Search PubMed.
- A. Dreuw and M. Head-Gordon, Chem. Rev., 2005, 105, 4009 CrossRef CAS PubMed.
- O. Christiansen, P. Jørgensen and C. Hättig, Int. J. Quantum Chem., 1998, 68, 1 CrossRef CAS.
- E. Schrödinger, Ann. Phys., 1926, 384, 361 CrossRef PubMed.
- P. A. Dirac, Proc. R. Soc. A, 1927, 114, 243 CrossRef CAS.
- E. Schrödinger, Ann. Phys., 1926, 384, 734 CrossRef PubMed.
- K. A. Peterson, T. B. Adler and H.-J. Werner, J. Chem. Phys., 2008, 128, 084102 CrossRef PubMed.
- K. A. Peterson and K. E. Yousaf, J. Chem. Phys., 2010, 133, 174116 CrossRef PubMed.
- D. Rappoport and F. Furche, J. Chem. Phys., 2010, 133, 134105 CrossRef PubMed.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297 RSC.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007 CrossRef CAS PubMed.
- R. J. Harrison, G. I. Fann, T. Yanai, Z. Gan and G. Beylkin, J. Chem. Phys., 2004, 121, 11587 CrossRef CAS PubMed.
- T. Yanai, R. J. Harrison and N. Handy, Mol. Phys., 2005, 103, 413 CrossRef CAS PubMed.
- F. A. Bischoff and E. F. Valeev, J. Chem. Phys., 2013, 139, 114106 CrossRef PubMed.
- L. Frediani, E. Fossgaard, T. Flå and K. Ruud, Mol. Phys., 2013, 111, 1143 CrossRef CAS PubMed.
- H. Sekino, Y. Maeda, T. Yanai and R. J. Harrison, J. Chem. Phys., 2008, 129, 034111 CrossRef PubMed.
- T. Kato, Y. Yokoi and H. Sekino, Int. J. Quantum Chem., 2012, 113, 286 CrossRef PubMed.
- S. Hamada and H. Sekino, Int. J. Quantum Chem., 2011, 111, 1480 CrossRef CAS PubMed.
- N. Vence, R. Harrison and P. Krstić, Phys. Rev. A: At., Mol., Opt. Phys., 2012, 85, 033403 CrossRef.
- S. Hirata and M. Head-Gordon, Chem. Phys. Lett., 1999, 314, 291 CrossRef CAS.
- R. Bauernschmitt and R. Ahlrichs, Chem. Phys. Lett., 1996, 256, 454 CrossRef CAS.
- G. Beylkin and M. J. Mohlenkamp, SIAM J. Sci. Comput., 2005, 26, 2133 CrossRef.
- T. B. Pedersen and H. Koch, Chem. Phys. Lett., 1998, 293, 251 CrossRef CAS.
- TURBOMOLE V6.5 2013, a development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989–2007, TURBOMOLE GmbH, since 2007; available from http://www.turbomole.com.
- T. H. Dunning Jr., J. Chem. Phys., 1989, 90, 1007 CrossRef PubMed.
- R. A. Kendall, T. H. Dunning Jr. and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796 CrossRef CAS PubMed.
- D. E. Woon and T. H. Dunning, J. Chem. Phys., 1994, 100, 2975 CrossRef CAS PubMed.
- O. Christiansen,
et al.
, J. Chem. Phys., 1996, 105, 6921 CrossRef CAS PubMed.
- K. Kaufmann, W. Baumeister and M. Jungen, J. Phys. B: At., Mol. Opt. Phys., 1999, 22, 2223 CrossRef.
- MADNESS, Multiresolution Adaptive Numerical Environment for Scientific Simulation, http://code.google.com/p/m-a-d-n-e-s-s.
- R. J. Harrison, J. Comput. Chem., 2002, 25, 328 CrossRef PubMed.
- H. Larsen, K. Hald, J. Olsen and P. Jørgensen, J. Chem. Phys., 2001, 115, 3015 CrossRef CAS PubMed.
|
| This journal is © the Owner Societies 2015 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article
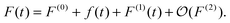
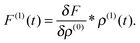
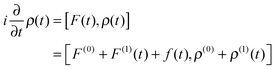
![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) eiωt +
eiωt + ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) †e−iωt.
†e−iωt.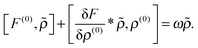
![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) pq = dpq
pq = dpq
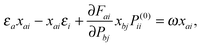
![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) and
and ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) † are also expressed as projections from the occupied to the virtual space and vice versa:
† are also expressed as projections from the occupied to the virtual space and vice versa:
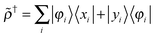


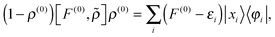


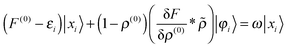
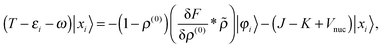
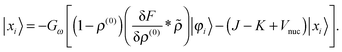
![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) , see eqn (15). Green's operator G is the inverse of the Helmholtz operator22
, see eqn (15). Green's operator G is the inverse of the Helmholtz operator22![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) in real space,
in real space,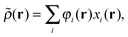
 can be computed as follows:
can be computed as follows:
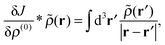

![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) be an excitation operator which generates approximately the excitation orbitals |xi〉 when acting on ground state orbitals |φi〉,
be an excitation operator which generates approximately the excitation orbitals |xi〉 when acting on ground state orbitals |φi〉,![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) |φi〉.
|φi〉.