Open Access Article
Open Access ArticleEvidence for the existence of Li2S2 clusters in lithium–sulfur batteries: ab initio Raman spectroscopy simulation
Pouya
Partovi-Azar
a,
Thomas D.
Kühne
b and
Payam
Kaghazchi
*c
aDepartment of Chemistry, University of Paderborn, Warburger Str. 100, D-33098 Paderborn, Germany
bDepartment of Chemistry and Institute for Lightweight Design with Hybrid Systems, University of Paderborn, Warburger Str. 100, D-33098 Paderborn, Germany
cPhysical and Theoretical Chemistry, Freie Universität Berlin, Takustr. 3, 14195 Berlin, Germany. E-mail: payamk@zedat.fu-berlin.de
First published on 24th July 2015
Abstract
Using density functional theory calculations and ab initio molecular dynamics simulations we have studied the structures and the Raman spectra of Li2S4 clusters, which are believed to be the last polysulfide intermediates before the formation of Li2S2/Li2S during the discharge process in Li–S batteries. Raman spectra have been obtained using a new technique to estimate polarizabilities using Wannier functions. We have observed clear evidence of Li2S4 → Li2S2 transition by studying systematic changes in the simulated Raman spectra of (Li2S4)n, n = 1, 4, and 8 towards that of (Li2S2)8. Furthermore, we have shown that the dominant Raman peak of the Li2S2 cluster at ∼440 cm−1 arises from sulfur–sulfur stretching mode. This peak has been experimentally observed in the discharged state of Li–S batteries and has also been attributed to the formation of Li2S2. We have also demonstrated that the transition is mainly due to the strong electrostatic interactions between Li2S4 monomers, which results in energy lowering by arranging the local Li+δ–S−δ dipole moments in an anti-parallel fashion.
1 Introduction
Lithium–sulfur (Li–S) batteries are promising energy storage systems with a high theoretical energy density of 2500 W h kg−1 (or 2800 W h L−1).1 During the discharge process in Li–S batteries, lithium ions react with sulfur on the cathode, leading to the formation of soluble Li–polysulfides, for example Li2S8, Li2S6, and Li2S4 clusters, followed by the formation of insoluble Li2S2, and eventually Li2S crystals.2,3 There have been many experimental studies, such as in situ Raman,4–8 X-ray diffraction,4,6,9 scanning electron,4,6 transmission electron,6,9 electron paramagnetic resonance,10 and ultraviolet-visible spectroscopies,11 all aimed at understanding the processes occurring during discharge/charge cycles, and investigating the cathode structure. Li2S4 clusters are expected to be the last intermediates in the S8 → Li2S transition.10,12,13 Nevertheless, it is not fully understood yet whether any other product, for example Li2S2, exists besides Li2S crystals in the discharged state.14–18 Li2S2, however, has not been clearly identified in experimental measurements on Li–S batteries during discharge.19,20 It is partially due to the fact that it is experimentally difficult to isolate intermediate Li–polysulfide clusters and perform the measurements on them separately. However, theoretical simulations on structures, energetics, and vibrational properties enable one to study the structural transitions during the discharge process with molecular resolution, and can provide a complementary picture to experimental results. There are important studies based on density functional theory (DFT) calculations as well as many-body techniques aiming at understanding the structures of the Li–polysulfides and the mechanism of their transition to Li2S2/Li2S (for the most recent studies, see ref. 17, 18 and 21–23). There have also been promising advances in simulation of the vibrational spectra of systems with general symmetries.24–32 In particular, ab initio simulation of the Raman spectra of candidate structures combined with experimental Raman data can unambiguously identify the most probable atomic configurations. It has been shown recently that the electronic properties of a system introduce distinct features in the vibrational spectra.29,32 Therefore, the electronic properties of the system need to be explicitly taken into account, and as such, classical simulations, usually based on interatomic parametric potentials, may not be the most suitable choice. Moreover, in order to have a realistic simulation, directly comparable to experimental measurements, finite-temperature effects need to be taken into account as well, a feature which is absent in perturbative methods at zero temperature.33,34 All these requirements can be met by ab initio molecular dynamics (AIMD) simulations, in which forces are calculated “on-the-fly” using DFT.26,35 To the best of our knowledge, ab initio simulation of Raman spectroscopy on individual Li–polysulfide clusters has not been performed so far.In this article, using DFT calculations and AIMD simulations we first determine the atomic structures of (Li2S4)1, (Li2S4)4, and (Li2S4)8 polysulfides. Furthermore, using a new method based on the Wannier function technique along with the second-generation Car–Parrinello method of Kühne et al.,36,37 we obtain the polarizabilities of the structures as a function of time and thereby the Raman spectra of the clusters. We observe a clear tendency to form the Li2S2 structure as the size of the cluster grows. The crystallization is found to be due to the strong electrostatic interaction between Li2S4 monomers, which results in anti-parallel arrangement of the local Li+δ–S−δ dipole moments.
2 Computational details
The minimum-energy structures of (Li2S4)n clusters have been obtained at the DFT level of theory using the mixed Gaussian and plane-wave code CP2K/QUICKSTEP38,39 in conjunction with a very accurate TZV2PX Gaussian basis set,40 Goedecker–Teter–Hutter pseudo potentials41 and the Perdew–Burke–Ernzerhof (PBE) exchange–correlation functional,42,43 plus semi-empirical correction for the long-range dispersion interactions (DFT-D3).44 A real-space grid was represented by a plane-wave energy cutoff of 270 Ry, and the convergence criterion for the self-consistent field was set to 10−6. The clusters were modeled using supercells with unit cells of 16 × 16 × 16 Å3, 21 × 21 × 21 Å3, and 37 × 37 × 37 Å3 for (Li2S4)1, (Li2S4)4, and (Li2S4)4, respectively, and therefore, the Brillouin zone was sampled only using the Γ-point. The minimum-energy structures were obtained using a BFGS optimizer.45–49 Convergence criteria for the maximum geometry change, and the maximum force component were set to 1.6 × 10−3 Å, and 0.02 eV Å−1, respectively. Vibrational normal mode analysis50 was carried out with an atomic displacement of 5 × 10−3 Å.The intensity of the isotropic Raman scattering, σ, as a function of the frequency of the incident beam, ν, is related to the mean polarizability, Ā = 1/3Tr[Â] through31,51
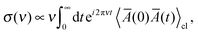 | (1) |
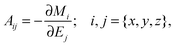 | (2) |
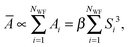 | (3) |
All Raman spectra in this work were obtained by performing 20 ps AIMD simulations in the canonical ensemble to achieve equilibration, followed by 10 ps AIMD in the micro-canonical ensemble to remove thermostat effects and to sample polarizabilities. A time-step of 1 fs was used in all the simulations and the polarizabilities were sampled for every 5 fs. All AIMD simulations were also carried out using the CP2K/QUICKSTEP software package with the same simulation setup as mentioned before.
3 Results and discussion
We first start by calculating the isotropic Raman spectrum of the S8 molecule in the gas phase. The spectrum is shown in Fig. 1. The S8 molecule is known to have eleven fundamental vibrational modes, among which six peaks at 86, 152, 218, 248, 437, and 475 cm−1 are Raman active. The two dominant peaks are observed at 218 and 475 cm−1.62 Our simulated spectrum shows six peaks at around 63, 145, 218, 232, 427, and 470 cm−1, two of which, namely 218 cm−1 and 470 cm−1 being the dominant ones. The Raman spectrum presented here using the WP method is in agreement with previous experimental63–65 and theoretical17 studies, showing a mean absolute error of ∼10 cm−1 with respect to the experimental data reported in ref. 62. It is worth mentioning here that the choice of basis set is crucial, especially for the case of low-frequency modes below 150 cm−1. These frequencies are absent when the DZVP basis set is employed, while they emerge when more diffuse basis functions, such as TZV2PX, are used. Vibrational normal mode analysis at zero temperature reveals that the most dominant peak is due to doubly degenerate asymmetric bending mode of the three consecutive sulfur atoms in the S8 molecule. However, the stretching modes occur in the frequency range of 350 to 470 cm−1 with much lower intensity. Similar findings have also been reported experimentally.63–66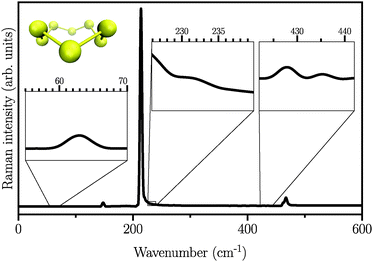 | ||
| Fig. 1 Atomic structure and isotropic Raman spectrum of S8 molecules in the gas phase. Insets are zoomed views of weak Raman activities. | ||
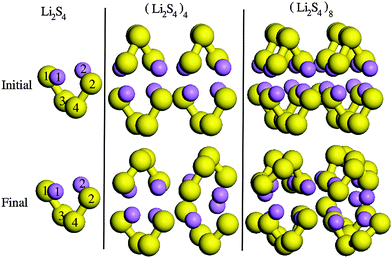
In order to find the structural transition of Li2S4 to Li2S2/Li2S, we have examined a variety of possible arrangements of Li2S4 clusters with four and eight monomers at the DFT level. The charge population analysis on Li and S atoms of (Li2S4)n structures using Mulliken population analysis (MPA)67 reveals that the minimum-energy structures are those with an anti-parallel arrangement of local dipole moments of Li+δ–S−δ in Li2S4 molecules. The electrons are partially transferred from Li to S atoms, leaving the −δ charge on S and the +δ charge on Li, leading to the lowest electrostatic repulsion and highest electrostatic attraction between Li2S4 monomers (see Fig. 2). For a single Li2S4 molecule, the electron charges are transferred from Li1 and Li2 atoms to all S atoms (see Fig. 2). However, the major part (∼85%) of electron charges is transferred to the nearest S1 and S2 atoms and only small part to the next nearest atoms, namely S3 and S4. The averaged electron transfer (using MPA) is calculated to be 0.49 |e|. The calculated dipole moment for the isolated Li2S4 molecule is 2.63 Debye, which is comparable to that of a water molecule in bulk liquid water.68 However, the residual total dipole moments of 0.11 Debye and 0.31 Debye for (Li2S4)4 and (Li2S4)8 clusters, respectively, show a large cancellation of dipole moments which would lead to a zero net polarization for (Li2S4)n as n → ∞. These results are also in line with the energy gain of the clusters as a function of the number of Li2S4 monomers. The formation energy of (Li2S4)n as a function of the cluster size n can be written as
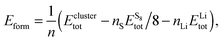 | (4) |
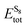 , and ELitot are the total energy of (Li2S4)n clusters, a single S8 molecule, and a Li atom, respectively. nS and nLi are the number of S and Li atoms in (Li2S4)n clusters, respectively. As shown in Fig. 3, we find that the formation energy increases with n. The energy gain with increasing size of (Li2S4)n clusters is comparable to the Coulomb interaction energy between Li+δ and S−δ point charges of interacting Li2S4 molecules, namely
, and ELitot are the total energy of (Li2S4)n clusters, a single S8 molecule, and a Li atom, respectively. nS and nLi are the number of S and Li atoms in (Li2S4)n clusters, respectively. As shown in Fig. 3, we find that the formation energy increases with n. The energy gain with increasing size of (Li2S4)n clusters is comparable to the Coulomb interaction energy between Li+δ and S−δ point charges of interacting Li2S4 molecules, namely 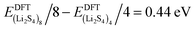 , while
, while 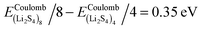 . As can be seen in Fig. 3, the formation energy may still increase with the size of clusters, which is due to the fact that the number of dangling bonds around the (Li2S4)8 cluster is still large compared to the saturated S bonds. We therefore expect that the formation energy of (Li2S4)n, n → ∞ is even lower than that for (Li2S4)8. This clearly indicates a tendency towards forming an iconic crystal.
. As can be seen in Fig. 3, the formation energy may still increase with the size of clusters, which is due to the fact that the number of dangling bonds around the (Li2S4)8 cluster is still large compared to the saturated S bonds. We therefore expect that the formation energy of (Li2S4)n, n → ∞ is even lower than that for (Li2S4)8. This clearly indicates a tendency towards forming an iconic crystal.
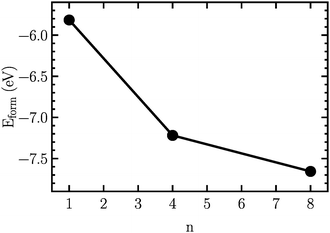 | ||
| Fig. 3 Formation energy as a function of the cluster size, n. The structures are illustrated in Fig. 2. | ||
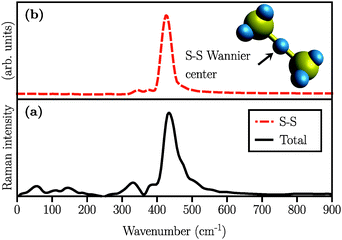
The simulated Raman spectra are presented in Fig. 4. In comparison with the Raman spectrum of the S8 molecule (Fig. 1), we find three new large peaks at around 330, 380, and 450 cm−1, for the Li2S4 monomer (Fig. 4(a)). As the size of the (Li2S4)n increases from n = 1 (Fig. 4(a)) to n = 8 (Fig. 4(c)), the peak at ∼200 cm−1 loses its relative intensity with respect to the new peaks at 330, 380, and 450 cm−1. As stated before, a S8 molecule has a dominant vibrational mode at ∼200 cm−1 which comes from the asymmetric bending of the three consecutive sulfur atoms in the ring. Therefore, the peak at around 200 cm−1 in Fig. 4 should also arise from the collective vibrations of sulfur atoms in Li2Sx clusters with x ≥ 3. Note that the stretching vibrations of the S8 ring have frequencies above 350 cm−1 with rather weak intensities. Moreover, in the case of (Li2S4)2 (Fig. 4(b)), the peak at 330 cm−1 becomes less notable, while the peaks at 380 and 450 cm−1 turn more significant. When the (Li2S4)8 cluster forms, we find a dominant peak at ∼440 cm−1 and a smaller peak at ∼380 cm−1 (Fig. 4(c)). Recently, these two peaks have been experimentally attributed to the formation of crystalline Li2S2/Li2S structures: it has been shown by Raman spectroscopy studies that during the discharge process, when a Li–S battery is discharged to 1.7 V, two dominant peaks emerge for the cathode at ∼380 cm−1 and ∼440 cm−1.5,16 The former peak is very close to the experimentally observed characteristic peak of the Li2S crystal at 375 cm−1.69 Using normal mode analysis for a Li2S4 monomer at zero temperature we also observe Raman-active modes mainly in the frequency range of 350–500 cm−1. This shows that the Raman activity between 350 and 500 cm−1 in Fig. 4 mostly arises from lithium–sulfur interactions. Additionally, the decline in the relative intensity of the ∼200 cm−1 peak with respect to the ones at 380 and 440 cm−1 indicates a clear transition from Li2Sx clusters with x ≥ 3 to structures with x < 3. The possible structures would be Li2S2 or Li2S. We find that the peak at 440 cm−1 is due to sulfur–sulfur stretching vibration (see insets in Fig. 4(a)–(c)). This can be directly seen by replacing Ā in eqn (1) with Ai, where i is the index of a Wannier function centered along a typical S–S bond in (Li2S4)n structures. Here we have set i to be the index of the Wannier function along the S1–S3 (or S2–S4) bond shown in Fig. 2.
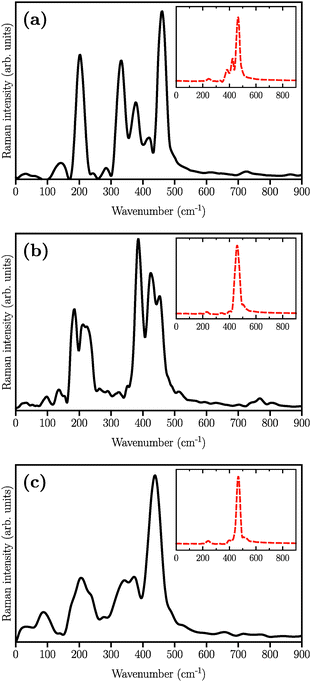 | ||
| Fig. 4 Simulated Raman spectra of (a) (Li2S4)1, (b) (Li2S4)4, and (c) (Li2S4)8. The structures are illustrated in Fig. 2. The insets show the contribution of S–S stretching vibration to the total Raman spectra. | ||
We also simulated the Raman spectrum of the (Li2S2)8 cluster which was in this case obtained after 60 ps of AIMD simulation in the canonical ensemble at 300 K, followed by a 20 ps production run in the micro-canonical ensemble. The Raman spectrum is shown in Fig. 5(a). The peak at ∼440 cm−1 is also present in the (Li2S2)8 cluster which, in turn, implies the existence of the S–S covalent bond. This peak has been experimentally attributed to Li2S2.5,16Fig. 5(b) shows the S–S stretching contribution to the total spectrum along with the corresponding Wannier function used to calculate the spectrum. Additionally, by studying the S–S bond length during our long AIMD simulation (60 ps), we do not observe any S–S bond breaking which shows that (Li2S2)8 is stable. Furthermore, there is no Raman activity observed at around 200 cm−1 in Fig. 5(a), which is in line with our previous assignment of this vibration to more than two covalently bonded sulfur atoms. However, in all the insets of Fig. 4 there is a weak activity slightly above 200 cm−1 which can be due to the coupling of collective sulfur vibrations with S–S stretching. Based on these observations, we therefore ascribe the peak at ∼440 cm−1 in Fig. 4(b) and (c) to the formation of the Li2S2 structure in (Li2S4)4 and (Li2S4)8 clusters.
4 Conclusions
In summary, we have performed DFT calculations and AIMD simulations to investigate the structure of Li2S4 and Li2S2 clusters. We have also simulated the Raman spectra of the most favorable structures, based on the Wannier function technique to study Li2S4 → Li2S2 structural transition in Li–S batteries during the discharge process. Our findings show that Li2S4 monomers bind strongly to each other due to the electrostatic interactions between Li+δ–S−δ dipoles of the interacting monomers and form larger clusters. In particular, we observe a dominant Raman peak at ∼440 cm−1 in (Li2S4)n clusters which we then assign to S–S stretching mode. The other peak at ∼200 cm−1, which corresponds to the vibration of more than two covalently bonded sulfur atoms, loses its intensity as the cluster size grows. Simultaneously, the peak at 440 cm−1 becomes more notable with the cluster size. Particularly, in the case of the (Li2S2)8 cluster, we find a dominant peak at ∼440 cm−1 with nearly no Raman activity at around 200 cm−1. Therefore, we have been able to identify the structural transition to Li2S2 by following the trend in the Raman spectra. Moreover, we unambiguously ascribe the experimentally observed peak at around 440 cm−1 to the existence of the Li2S2 structure. This work has implications in understanding the structure of the sulfur cathode in Li–S batteries. The simulation method presented in this work also enables one to routinely simulate the Raman spectrum “on-the-fly” based on ab initio molecular dynamics simulations, with minimal extra computational cost. Therefore, the method can be used as an efficient approach to study the structure of complex systems relevant to energy storage.Acknowledgements
P. K. acknowledges support from the “Bundesministerium für Bildung und Forschung” (BMBF).References
- Y. Yang, G. Zheng and Y. Cui, Chem. Soc. Rev., 2013, 42, 3018–3032 RSC.
- L.-X. Miao, W.-K. Wang, A.-B. Wang, K.-G. Yuan and Y.-S. Yang, J. Mater. Chem. A, 2013, 1, 11659–11664 CAS.
- G. Zhou, D.-W. Wang, F. Li, P.-X. Hou, L. Yin, C. Liu, G. Q. M. Lu, I. R. Gentle and H.-M. Cheng, Energy Environ. Sci., 2012, 5, 8901–8906 CAS.
- Z. W. Seh, H. Wang, P.-C. Hsu, Q. Zhang, W. Li, G. Zheng, H. Yao and Y. Cui, Energy Environ. Sci., 2014, 7, 672–676 CAS.
- H. Yao, K. Yan, W. Li, G. Zheng, D. Kong, Z. W. Seh, V. K. Narasimhan, Z. Liang and Y. Cui, Energy Environ. Sci., 2014, 7, 3381–3390 CAS.
- Z. W. Seh, J. H. Yu, W. Li, P.-C. Hsu, H. Wang, Y. Sun, H. Yao, Q. Zhang and Y. Cui, Nat. Commun., 2014, 5, 1–8 Search PubMed.
- M. A. Lowe, J. Gao and H. D. Abruña, RSC Adv., 2014, 4, 18347–18353 RSC.
- K. H. Wujcik, J. Velasco-Velez, C. H. Wu, T. Pascal, A. A. Teran, M. A. Marcus, J. Cabana, J. Guo, D. Prendergast and M. Salmeron, et al. , J. Electrochem. Soc., 2014, 161, A1100–A1106 CrossRef CAS PubMed.
- Y. Yang, M. T. McDowell, A. Jackson, J. J. Cha, S. S. Hong and Y. Cui, Nano Lett., 2010, 10, 1486–1491 CrossRef CAS PubMed.
- Q. Wang, J. Zheng, E. Walter, H. Pan, D. Lv, P. Zuo, H. Chen, Z. D. Deng, B. Y. Liaw and X. Yu, et al. , J. Electrochem. Soc., 2015, 162, A474–A478 CrossRef CAS PubMed.
- C. Barchasz, F. Molton, C. Duboc, J.-C. Leprêtre, S. Patoux and F. Alloin, Anal. Chem., 2012, 84, 3973–3980 CrossRef CAS PubMed.
- M. Cuisinier, P.-E. Cabelguen, S. Evers, G. He, M. Kolbeck, A. Garsuch, T. Bolin, M. Balasubramanian and L. F. Nazar, J. Phys. Chem. Lett., 2013, 4, 3227–3232 CrossRef CAS.
- J. Song, S. J. Lee, Y. Kim, S.-S. Kim, K. T. Lee and N.-S. Choi, ECS Electrochem. Lett., 2014, 3, A26–A29 CrossRef CAS PubMed.
- X. Ji and L. F. Nazar, J. Mater. Chem., 2010, 20, 9821–9826 RSC.
- A. Manthiram, Y. Fu and Y.-S. Su, Acc. Chem. Res., 2012, 46, 1125–1134 CrossRef PubMed.
- J.-T. Yeon, J.-Y. Jang, J.-G. Han, J. Cho, K. T. Lee and N.-S. Choi, J. Electrochem. Soc., 2012, 159, A1308–A1314 CrossRef CAS PubMed.
- L. Wang, T. Zhang, S. Yang, F. Cheng, J. Liang and J. Chen, J. Energy Chem., 2013, 22, 72–77 CrossRef CAS.
- G. Yang, S. Shi, J. Yang and Y. Ma, J. Mater. Chem. A, 2015, 3, 8865–8869 CAS.
- J. Nelson, S. Misra, Y. Yang, A. Jackson, Y. Liu, H. Wang, H. Dai, J. C. Andrews, Y. Cui and M. F. Toney, J. Am. Chem. Soc., 2012, 134, 6337–6343 CrossRef CAS PubMed.
- S. Waluś, C. Barchasz, J.-F. Colin, J.-F. Martin, E. Elkam, J.-C. Leprêtre and F. Alloin, Chem. Commun., 2013, 49, 7899–7901 RSC.
- H. Park, H. S. Koh and D. J. Siegel, J. Phys. Chem. C, 2015, 119, 4675–4683 CAS.
- B. Wang, S. M. Alhassan and S. T. Pantelides, Phys. Rev. Appl., 2014, 2, 034004 CrossRef.
- R. S. Assary, L. A. Curtiss and J. S. Moore, J. Phys. Chem. C, 2014, 118, 11545–11558 CAS.
- R. Ramírez, P. Kumar and D. Marx, J. Chem. Phys., 2004, 121, 3973 CrossRef PubMed.
- R. Iftimie and M. E. Tuckerman, J. Chem. Phys., 2005, 122, 214508 CrossRef PubMed.
- R. Iftimie, P. Minary and M. E. Tuckerman, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 6654–6659 CrossRef CAS PubMed.
- G. Cicero, J. C. Grossman, E. Schwegler, F. Gygi and G. Galli, J. Am. Chem. Soc., 2008, 130, 1871–1878 CrossRef CAS PubMed.
- A. Morita and T. Ishiyama, Phys. Chem. Chem. Phys., 2008, 10, 5801–5816 RSC.
- D. Donadio, G. Cicero, E. Schwegler, M. Sharma and G. Galli, J. Phys. Chem. B, 2009, 113, 4170–4175 CrossRef CAS PubMed.
- C. Zhang, D. Donadio and G. Galli, J. Phys. Chem. Lett., 2010, 1, 1398–1402 CrossRef CAS.
- T. Ishiyama, V. V. Sokolov and A. Morita, J. Chem. Phys., 2011, 134, 024510 CrossRef PubMed.
- Q. Wan, L. Spanu, G. A. Galli and F. Gygi, J. Chem. Theory Comput., 2013, 9, 4124–4130 CrossRef CAS.
- P. Giannozzi and S. Baroni, J. Chem. Phys., 1994, 100, 8537–8539 CrossRef CAS PubMed.
- S. Baroni, S. De Gironcoli, A. Dal Corso and P. Giannozzi, Rev. Mod. Phys., 2001, 73, 515 CrossRef CAS.
- D. Marx and J. Hutter, Ab initio molecular dynamics: basic theory and advanced methods, Cambridge University Press, 2009 Search PubMed.
- T. D. Kühne, M. Krack, F. R. Mohamed and M. Parrinello, Phys. Rev. Lett., 2007, 98, 066401 CrossRef PubMed.
- T. D. Kühne, WIREs Comput. Mol. Sci., 2014, 4, 391 CrossRef PubMed.
- G. Lippert, J. Hutter and M. Parrinello, Mol. Phys., 1997, 92, 477–488 CrossRef CAS PubMed.
- J. VandeVondele, M. Krack, F. Mohamed, M. Parrinello, T. Chassaing and J. Hutter, Comput. Phys. Commun., 2005, 167, 103–128 CrossRef CAS PubMed.
- J. VandeVondele and J. Hutter, J. Chem. Phys., 2007, 127, 114105 CrossRef PubMed.
- S. Goedecker, M. Teter and J. Hutter, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 1703 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS.
- M. Krack, Theor. Chem. Acc., 2005, 114, 145–152 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- C. G. Broyden, IMA J. Appl. Math., 1970, 6, 76–90 CrossRef PubMed.
- C. G. Broyden, IMA J. Appl. Math., 1970, 6, 222–231 CrossRef.
- R. Fletcher, Comput. J., 1970, 13, 317–322 CrossRef.
- D. Goldfarb, Math. Comput., 1970, 24, 23–26 CrossRef.
- D. F. Shanno, Math. Comput., 1970, 24, 647–656 CrossRef.
- R. M. Martin, Electronic structure: basic theory and practical methods, Cambridge University Press, 2004 Search PubMed.
- P. Atkins and J. De Paula, Atkins' physical chemistry, Oxford University Press, 2010 Search PubMed.
- I. Souza, J. Íñiguez and D. Vanderbilt, Phys. Rev. Lett., 2002, 89, 117602 CrossRef.
- P. Umari and A. Pasquarello, Phys. Rev. Lett., 2002, 89, 157602 CrossRef CAS.
- N. Marzari, A. A. Mostofi, J. R. Yates, I. Souza and D. Vanderbilt, Rev. Mod. Phys., 2012, 84, 1419 CrossRef CAS.
- R. Resta, Phys. Rev. Lett., 1998, 80, 1800 CrossRef CAS.
- P. L. Silvestrelli, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 9703–9706 CrossRef CAS.
- G. Berghold, C. J. Mundy, A. H. Romero, J. Hutter and M. Parrinello, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 61, 10040 CrossRef CAS.
- I. Vasiliev, S. Öğüt and J. R. Chelikowsky, Phys. Rev. Lett., 1997, 78, 4805 CrossRef CAS.
- A. Putrino and M. Parrinello, Phys. Rev. Lett., 2002, 88, 176401 CrossRef.
- J. S. Murray, P. Lane, T. Brinck, K. Paulsen, M. E. Grice and P. Politzer, J. Phys. Chem., 1993, 97, 9369–9373 CrossRef CAS.
- P. Partovi-Azar, T. D. Kühne, 2015, arXiv preprint arXiv:1504.03639.
- B. Meyer, Chem. Rev., 1976, 76, 367–388 CrossRef CAS.
- R. Steudel and H.-J. Mäusle, Angew. Chem., Int. Ed. Engl., 1977, 16, 112–113 CrossRef PubMed.
- A. Talyzin, L.-E. Tergenius and U. Jansson, J. Cryst. Growth, 2000, 213, 63–69 CrossRef CAS.
- S. N. White, Chem. Geol., 2009, 259, 240–252 CrossRef CAS PubMed.
- P. D. Harvey and I. S. Butler, J. Raman Spectrosc., 1986, 17, 329–334 CrossRef CAS PubMed.
- R. S. Mulliken, J. Chem. Phys., 1955, 23, 1833–1840 CrossRef CAS PubMed.
- T. D. Kühne, M. Krack and M. Parrinello, J. Chem. Theory Comput., 2009, 5, 235–241 CrossRef.
- Z. Lin, Z. Liu, N. J. Dudney and C. Liang, ACS Nano, 2013, 7, 2829–2833 CrossRef CAS PubMed.
| This journal is © the Owner Societies 2015 |