Uranyl extraction by N,N-dialkylamide ligands studied using static and dynamic DFT simulations

Abstract

We report DFT static and dynamic studies on uranyl complexes [UO₂(NO₃)_x(H₂O)_yL_z]^2−x involved in the uranyl extraction from water to an “oil” phase (hexane) by an amide ligand L (N,N-dimethylacetamide). Static DFT results “in solution” (continuum SMD models for water and hexane) predict that the stepwise formation of [UO₂(NO₃)₂L₂] from the UO₂(H₂O)₅²⁺ species is energetically favourable, and allow us to compare cis/trans isomers of penta- and hexa-coordinated complexes and key intermediates in the two solvents. DFT-MD simulations of [UO₂(NO₃)₂L₂], [UO₂(NO₃)₂(H₂O)L₂], and [UO₂(NO₃)(H₂O)L₂]⁺ species in explicit solvent environments (water, hexane, or the water/hexane interface) represented at the MM or full-DFT level reveal a versatile solvent dependent binding mode of nitrates, also evidenced by metadynamics simulations. In water and at the interface, the latter exchange from bi- to monodentate, via in plane rotational motions in some cases. Remarkably, structures of complexes at the interface are more “water-like” than gas phase- or hexane-like. Thus, the order of U–O_NO3/U–O_L bond distances observed in the gas phase (U–O_nit < U–O_L) is inverted at the interface and in water. Overall, the results are consistent with the experimental observation of uranyl extraction from nitric acid solutions by amide analogues (bearing “fatty” substituents), and allow us to propose possible extraction mechanisms, involving complexation of L “right at the interface”. They also point to the importance of the solvent environment and the dynamics on the structure and stability of the complexes.

---

1. Introduction

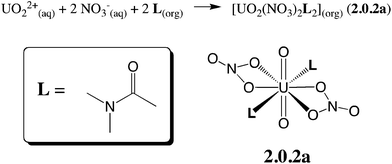
Oil-soluble N,N-dialkylamide ligands bearing hydrophobic alkyl chains represent an interesting alternative to tri-n-butylphosphate (TBP) for the reprocessing of nuclear waste solutions by liquid–liquid extraction. Like TBP, they selectively extract UO₂²⁺ from concentrated nitric acid solutions, and share most of its assets (e.g. stability towards radiolysis, etc.).¹ In solution, they also form a neutral complex of 1 : 2 stoichiometry,² namely UO₂(NO₃)₂(L)₂, where U is hexacoordinated in the equatorial plane by two trans ligands L and two bidentate nitrates (see Scheme 1), as in X-ray structure analogues.³ Additionally, being free of phosphorus atoms they are fully incinerable and are thus “greener” than TBP. In the source phase (water) UO₂²⁺ is solubilized as (nitrato)aquo complexes [UO₂(NO₃)_x(H₂O)_y]^2−x. Transfer to the organic phase therefore requires displacement of the coordinated water by lipophilic ligands while co-extracting nitrates to keep the complex neutral. The intimate complexation and extraction mechanism is unknown and intriguing since L partitions to the organic phase, immiscible with the aqueous source phase, while the uncomplexed cation is insoluble in the oil phase. Understanding where and how uranyl complexation takes place in biphasic solutions is crucial from a fundamental and an industrial point of view. In practice, ion extraction is not a simple process, since the two phases are agitated and involve heterogeneous mixtures (like salts and concentrated acids in the source phase and aggregates, micelles or microemulsions in the oil phase).^1c,4 Early kinetic studies on uranyl extraction pointed to the importance of interfacial complexation reactions,⁵ without affording microscopic characterization of the interface, though. Microscopic views stem from classical molecular dynamics “MD” simulations on explicitly represented nanosized oil/water solutions of ions,⁶ extractants and their complexes.⁷ The interface is generally found to be quite sharp and abrupt, a few nanometers wide, and to fluctuate with time, without local intersolvent mixing. Extractants like TBP^7c,8 or fatty amides⁹ are amphiphilic and adsorb at the aqueous interface, as suggested by surface tension,¹⁰ kinetic or surface spectroscopy¹¹ studies, hinting at a complexation mechanism occurring “at the interface”, without defining its characteristics (size, composition, inter-solvent miscibility, electrostatic properties) though.

Scheme 1 Uranyl nitrate extraction by N,N-dialkylamides. N,N-Dimethylacetamide (L) has been considered herein, as a simplified model for more lipophilic amides featuring longer alkyl chains employed in extraction experiments. “aq” and “org” stand for the aqueous and the organic phases, respectively.

Regarding the accurate description of the evolution of ion coordination features with time and solvent environment, classical MD results are limited, however, by the empirical energy representation. In principle, quantum mechanical QM approaches with an explicit account of solvation effects are more suitable. Two QM approaches are used here, focusing on the uranyl speciation at different key stages of the extraction reaction. First, ab initio Molecular Dynamics (AIMD) simulations have been undertaken in explicitly represented solvent(s) to gain insights into the uranyl speciation and complexation features, and to obtain relevant structural, thermodynamics and kinetics data on chemically relevant model systems in the source phase (water), the receiving phase (hexane), and at their interface. The simulated times (30–40 ps) are long enough to relax and solvate a given structure in its environment and to test its (in)stability, but are far too short to observe spontaneous complexation/decomplexation processes of the ligands. In the second approach, the solute is described at the DFT level, while the solvent is treated by a simple continuum, allowing us to energetically compare different species “in bulk solutions”, namely the water and oil phases. Our DFT and AIMD studies aim at better understanding the nature of [UO₂(NO₃)_x(H₂O)_y(L)_z]^2−x species, and the gradual formation of UO₂(NO₃)₂(L)₂ complexes. To investigate whether the structure of these species at the interface is rather “water-like” or “oil-like”, they will be simulated in the three environments using our recently developed DFT/MM protocol¹² combining a DFT representation of the solute and, at a lower level, a molecular mechanics model for the solvent. These results will allow us to better understand “what happens at the interface”¹³ during uranyl extraction.

2. Methods

2.1. Static DFT calculations

2.1.1. Geometries and thermodynamic corrections. Geometries of all complexes were fully optimized at the BLYP-D3/SDD level, i.e. employing the exchange and correlation functionals of Becke¹⁴ and Lee, Yang, and Parr,¹⁵ respectively, in conjunction with the “SDD” basis, denoting the small-core Stuttgart–Dresden relativistic effective core potential (ECP) on U together with its valence basis set¹⁶ (from which the most diffuse s-, p-, d-, and f-functions were omitted, affording a [7s6p5d3f] contraction), and the standard 6-31G(d,p) basis for all other elements and suitable auxiliary basis sets for the fitting of the Coulomb potential.¹⁷ A fine integration grid was employed (“Ultrafinegrid” keyword). Harmonic frequencies were computed analytically and were used without scaling to obtain enthalpic and entropic corrections at 25 °C. The corresponding correction terms δE_G were estimated at the BLYP-D3/SDD level and have been obtained as the difference of the reaction energy of a given step (ΔE_BLYP-D3/SDD) and the corresponding free energy (ΔG_BLYP-D3/SDD):

δE_G = ΔG_BLYP-D3/SDD − ΔE_BLYP-D3/SDD (1)

The entropic contributions have been evaluated at a pressure of 1354 atm in order to model the changes in entropy for a condensed phase.¹⁸

2.1.2. Refined energies. Refined energies were obtained from single-point calculations on BLYP-D3/SDD geometries (unless otherwise specified). A larger basis set (denoted SDD+) has been employed, consisting of the same ECP and valence basis on U (augmented with a g-function with exponent 0.5), and the aug-cc-pVTZ basis¹⁹ elsewhere, in conjunction with a variety of DFT and ab initio methods, namely, BLYP, BLYP-D3, B3LYP,^15,20 PBE0-D3,²¹ M06,²² M06-2X,²² and CCSD(T). Reaction energies computed at these levels are denoted ΔE_gas.

Energies have been corrected for the basis set superposition error (BSSE) using the counterpoise method.²³ The BSSE energy corrections are denoted δE_BSSE in the rest of the paper.

Estimates of the solvation effects were computed using the SMD model²⁴ where the solute is immersed in a shape adapted isotropic polarizable continuum, with a dielectric constant ε = 78.3553 for water and ε = 1.8819 for hexane. The corresponding media will be denoted hereafter SMD-water and SMD-hexane, respectively. The δE_solv energy correction is defined as the difference between the reaction energy in the continuum (denoted ΔE_SMD) and in the gas phase (ΔE_gas), at the M06-2X/SDD+ level:

δE_solv = ΔE_SMD(M06-2X) − ΔE_gas(M06-2X) (2)

2.1.3. Free energies of reactions in solution. The final ΔG values are calculated as a sum of all energy correction terms, added to the raw gas phase reaction energies (ΔE_gas):

ΔG = ΔE_gas + δE_solv + δE_BSSE + δE_G. (3)

where ΔE_gas is computed with three different density functionals (namely, BLYP-D3, PBE0-D3 and M06-2X) with the SDD+ basis set, whereas δE_solv and δE_G are systematically computed at the M06-2X/SDD+ and BLYP-D3/SDD levels, respectively.

All DFT calculations have been performed with the Gaussian09 software (rev. D.01),²⁵ and CCSD(T) single points were obtained with NWChem (version 6.1.1).²⁶

2.2. Molecular dynamics simulations

2.2.1. Classical MD. Classical “MM” molecular dynamics (MD) simulations were performed with the AMBER force field,²⁷ where the potential energy is described by a sum of bond, angle, and dihedral deformation energies, and pairwise additive 1–6–12 (electrostatic + van der Waals) interactions between non-bonded atoms. Force field parameters on hexane stem from the set of Optimized Potentials for Liquid Simulations (OPLS) developed by Jorgensen,²⁸ where methyl and –CH₂– groups are represented in the united atom approximation with neutral atomic charges. Water is described using the TIP3P model.²⁹ Force-field parameters on UO₂²⁺ and NO₃⁻ were taken from ref. 30. Atomic charges on L were derived from the electrostatic potential obtained from static DFT calculations (B3LYP/6-31G** level). These ESP charges were fitted by the RESP procedure using a hyperbolic restraint of 0.001 a.u. and are provided in Table S1.† van der Waals parameters on L are taken from the AMBER/PARM94 force-field.³¹ Cross-terms in van der Waals interactions were constructed using Lorentz–Berthelot mixing rules. The MD simulations were performed under 3D periodic boundary conditions. Non-bonded interactions were calculated using a 12 Å atom-based cutoff, correcting for the long-range electrostatics using the Ewald summation method.³² Small boxes (for subsequent DFT-MD simulations) contained one complex and 89 H₂O molecules in cubic boxes of cell length 15 Å. Large boxes (for subsequent DFT/MM-MD simulations) contained 3000 hexane molecules and/or 9000 water molecules plus a single uranyl complex, yielding boxes of ca. 45 × 45 × 45 ų for monophasic systems. Biphasic systems were constructed from two adjacent boxes of bulk phases, with the complex initially at the interface, therefore yielding parallelepipedic boxes of ca. 45 × 45 × 90 ų. After 1000 steps of energy minimization, the systems are pre-equilibrated by 50 ps of MD in the NVT ensemble (T = 300 K) followed by 200 ps of MD in the NPT ensemble (T = 300 K, P = 1 atm) to ensure that near-experimental liquid densities are afforded. The MD was then continued for 100 ps in the NVT ensemble. The temperature was controlled by coupling to a thermal bath with a relaxation time of 0.2 ps, using the Berendsen algorithm. Uranyl complexes were simulated as preformed entities, with weak harmonic constraints on all metal–ligand distances (equilibrium distances are set to the corresponding DFT-optimized distances). All C–H, O–H and N–H bonds were constrained with SHAKE, and the Verlet leapfrog algorithm with a time step of 2 fs was used to integrate the equations of motion. These simulations were performed with the AMBER10 software.³³

2.2.2. Ab initio molecular dynamics (DFT-MD). Ab initio MD simulations were performed using the QuickStep module³⁴ of CP2K,³⁵ which performs DFT-MD using a dual basis set method. Here, the wavefunctions are described by a Gaussian basis set while the electron density is described by an auxiliary plane wave basis set. A triple-ζ Gaussian basis set augmented with two sets of d-type and p-type polarization functions (TZV2P) was used on N, O, C and H.³⁶ Plane waves were expanded up to a density cutoff of 400 Ry and used in conjunction with the GTH pseudopotentials³⁷ to describe the core electrons. The pseudopotential and basis set on U have been taken from Rabone and Krack,³⁸ and have been successfully employed to describe uranyl solutions.³⁹ These calculations were performed using the BLYP-D3 functional with NN50 smoothing and without the so-called “three-body terms”. These simulation parameters were chosen because they allow for a satisfying description of liquid water under ambient conditions,⁴⁰ and should therefore provide a proper description of aqueous solutions in general. For every time step of 0.5 fs, the electronic structure was explicitly quenched to a tolerance of 10⁻⁷ Hartree. To maintain the time step and reduce the importance of quantum nuclear effects, hydrogen was substituted with deuterium. All simulations were run in the NVT ensemble, using a single Nosé–Hoover thermostat⁴¹ (T = 320 K, frequency 1800 cm⁻¹), and were started from a “classically” pre-equilibrated box (as described in section 2.2.1. above) from coordinates.

2.2.3. DFT/MM molecular dynamics simulations (DFT/MM-MD). The energies of the DFT and MM regions were computed using the QuickStep and FIST modules of CP2K, respectively. The DFT region is described using the same parameters as in full DFT-MD simulations (TZV2P basis set, 400 Ry cutoff, GTH pseudopotentials, 0.5 fs time step; see above). The interaction between DFT and MM regions was calculated using the procedure developed by Laino et al.⁴² Ten Gaussian functions were used for the Gaussian Expansion of the Electrostatic Potential (GEEP). The DFT box was cubic with a cell length of 16.5 Å. The periodicity was only applied to the MM box and the DFT images were decoupled using the wavelet scheme⁴³ implemented in CP2K. Covalent radii r_c,a of water H and O were set to 0.44 Å and 0.78 Å, respectively. The starting coordinates of the systems were taken after classical MD by following the pre-equilibration procedure described in section 2.2.1. DFT/MM-MD simulations were started after an additional 250 ps of classical MD using the FIST module of CP2K to thermalize the systems (with the same metal–ligand constraints to keep the complex formed).

3. Results and discussion

The paper is organized as follows: we first present a benchmark of density functionals to validate our models in the gas phase. Then, we tackle the question of the speciation of mixed UO₂²⁺/NO₃⁻/H₂O/L complexes in SMD-water. Finally, we investigate the structure and the dynamics of selected complexes by DFT/MM-MD and DFT-MD simulations in explicit hexane, water and at the hexane/water interface. Based on these results, we propose two reaction pathways for the extraction process of UO₂²⁺ by L in hexane/water binary systems.

3.1. Influence of the density functional and validation of the computational protocol in the gas phase

We first screened selected density functionals to account for the relative stability of three isomers of the [UO₂(NO₃)(H₂O)₄]⁺ complex (see Scheme 2). The latter have been studied in detail previously (see ref. 44) by static calculations in the gas phase (BLYP level) and represent a good test case to investigate the relative stability of hexa- vs. penta-coordinated complexes and H₂O dissociation vs. partial decoordination of NO₃⁻, which are relevant to the speciation study undertaken herein. We first computed the relative energies of the three isomers at the CCSD(T) level (the “gold standard” in quantum chemistry) and then considered different density functionals (see relative energies in Table 1).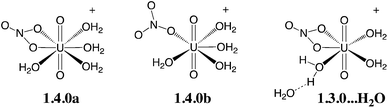

Scheme 2 Isomers of the [UO₂(NO₃)(H₂O)₄]⁺ complex considered for the benchmark of density functionals (see Table 1 for relative energies at various computational levels).

Table 1 Benchmark of density functionals against CCSD(T). Gas phase energies in kcal mol^−1 a

	1.4.0a → 1.4.0b		1.4.0a → 1.3.0…H2O
	ΔEgas	ΔEgas^c (cor.)	ΔEgas	ΔEgas^c (cor.)
a The basis set is aug-cc-pVTZ everywhere. b Car–Parrinello optimizations from ref. 44. c Gas phase energies including a correction for the BSSE (counterpoise method).
Single point energies on BLYP optimized geometries^b
CCSD(T)/SDD+	6.2	[5.5]	−2.4	[−3.8]
BLYP (CP-opt)^b	1.6		−8.7
BLYP/SDD+	2.0	[1.9]	−6.7	[−6.8]
BLYP-D3/SDD+	2.5	[2.5]	−4.0	[−4.1]
BLYP-D3 (CP2K)	3.3		−2.3
PBE0-D3/SDD+	4.6	[4.5]	−4.1	[−4.3]
M06/SDD+	6.1	[6.1]	−1.3	[−1.5]
M06-2X/SDD+	6.6	[6.6]	−0.7	[−0.8]
B3LYP/SDD+	3.4	[3.3]	−5.8	[−5.9]
MP2/SDD+	11.8	[11.9]	0.0	[−0.3]
Single point energies on BLYP-D3/SDD optimized geometries
BLYP-D3/SDD+	2.8	[2.7]	−3.5	[−3.6]
PBE0-D3/SDD+	5.6	[5.6]	−3.1	[−3.2]
M06-2X/SDD+	7.7	[7.7]	0.0	[−0.1]

---

In ref. 44, BLYP calculations showed that the penta-coordinated isomer “1.3.0…H₂O” is the most stable (by 8.7 kcal mol⁻¹), while 1.4.0a and 1.4.0b are very close in energy, the latter being slightly more stable than the former (by 1.6 kcal mol⁻¹). Repeating these calculations at the BLYP/SDD+ level, we obtain similar values (6.8 kcal mol⁻¹ and 1.9 kcal mol⁻¹, respectively). Comparing these results with our CCSD(T)/SDD+ reference,⁴⁵ it is found that BLYP predicts the correct sequence of stability among the series but underestimates both the binding of the sixth aquo ligand and the bidentate coordination mode of the nitrate, making the hexacoordinated complex 1.4.0a artificially too unstable. This feature is (at least partially) due to the lack of an explicit description of van der Waals interactions, and more accurate values can be obtained after addition of the “–D3” correction, i.e. at the BLYP-D3 level. At this level, the relative stability of “1.3.0…H₂O” vs. 1.4.0a is well described, but 1.4.0a is not stabilized enough compared to 1.4.0b (by ca. 3 instead of 5.5 kcal mol⁻¹). PBE0-D3 appears to give more satisfactory results, since it allows for a good description of the H₂O binding in 1.4.0a and better describe the relative stability of 1.4.0avs. 1.4.0b. Interestingly, M06 and M06-2X, which have been recommended for actinide complexes elsewhere,⁴⁶ slightly overestimate the stability of 1.4.0avs. 1.4.0b and significantly underestimate the H₂O binding in 1.4.0a. The popular B3LYP functional, which we employed in previous studies,⁴⁷ gives more balanced results but still underestimates the stability of the hexacoordinated species 1.4.0a compared to the two pentacoordinated species. We also considered the MP2 level that has been widely employed in the literature to study uranyl compounds⁴⁸ and we found significant deviations compared to the CCSD(T) reference (see Table 1). The hybrid functionals considered herein (M06, M06-2X and PBE0-D3) provide more satisfying results.

Given the good performance of PBE0-D3 compared to CCSD(T), we therefore calculated ΔE_gas at this level in the rest of the paper. Results with BLYP-D3 and M06-2X are also provided in the ESI (see Table S2†). For consistency with AIMD simulations (vide infra), the geometries of all complexes have been optimized at the BLYP-D3/SDD level. We note that our conclusions on the relative performances of BLYP-D3, PBE0-D3 and M06-2X single point calculations remain the same on these BLYP-D3/SDD optimized geometries (see Table 1), so that PBE0-D3/SDD+ still appears as the most satisfying model among those tested herein.

3.2. Speciation of [UO₂(NO₃)_x(H₂O)_yL_z]^2−x complexes (x = 0,…, 2, y = 0,…, 5 and z = 0,…, 2) from “static” DFT calculations in SMD-water

We investigated the relative stabilities of [UO₂(NO₃)_x(H₂O)_yL_z]^2−x complexes (x = 0,…, 2, y = 0,…, 5 and z = 0,…, 2) in water relative to the dicationic uranyl pentahydrate [UO₂(H₂O)₅]²⁺ (0.5.0) and free nitrates and L ligands, i.e. according to eqn (4):

[UO₂(H₂O)₅]²⁺_(aq) + xNO₃⁻_(aq) + zL_(aq) → [UO₂(NO₃)_x(H₂O)_yL_z]^2−x_(aq) + (5 − y)H₂O_(aq) (4)

Given the large number of possible stereoisomers, we first focused on a consistent series of complexes where nitrates and/or L are in trans position, as in 2.0.2a and found in the solid state structures³ (see Scheme 3). Selected “isomers” (including some with ligands in cis position) have also been considered (see Scheme 4), as the latter should be more polar and possibly more stable in polar or asymmetrical environments such as bulk water or the interface. Reaction free energies in SMD-water are gathered in Table 2.

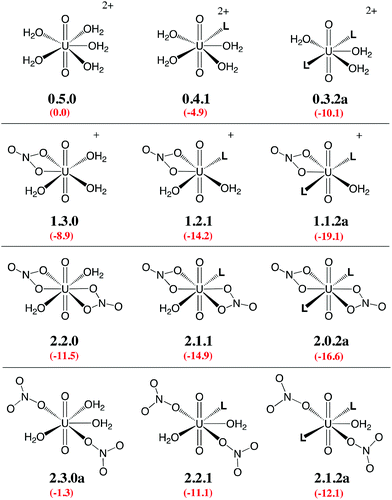Scheme 3 Investigated complexes labelled according to the number of nitrate (first digit), aquo (second digit), and L ligands (third digit). The “a” label corresponds to trans isomers (other isomers are shown in Scheme 4). Reaction free energies in SMD-water according to eqn (4) are given in red (see Table 2 for details).

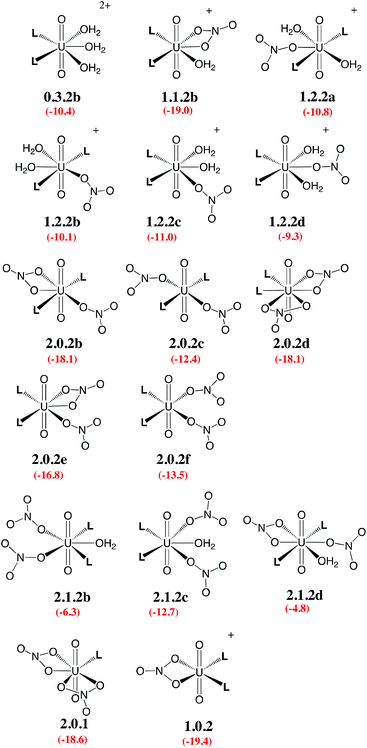Scheme 4 Investigated isomers. See Scheme 3 for the legend.

Table 2 Reaction energies (ΔE_gas), correction terms for BSSE (δE_BSSE), solvation (δE_Solv), and thermochemistry (δE_G), and the resulting reaction free energies (ΔG) in kcal mol⁻¹ in SMD-water^a

	ΔEgas	δEBSSE	δEsolv	δEG	ΔG
a ΔG = ΔEgas + δEBSSE + δESolv + δEG where ΔEgas and δEBSSE are computed at the PBE0-D3/SDD+ level, δESolv is computed at the M06-2X/SDD+ level with water as the solvent, and δEG is computed at the BLYP-D3/SDD level. BSSE corrections are 0.3, 0.5 and 0.5 kcal mol^−1 for the dissociation of H2O, NO3^− and L, respectively.
0.5.0 + L → 0.4.1 + H2O	−35.2	0.2	27.3	2.8	−4.9
0.5.0 + 2L → 0.3.2a + 2H2O	−63.8	0.4	49.1	4.2	−10.1
0.5.0 + 2L → 0.3.2b + 2H2O	−62.1	0.4	46.8	4.6	−10.4
0.5.0 + NO3^− → 1.4.0a + H2O	−191.9	0.2	186.0	4.6	−1.1
0.5.0 + NO3^− → 1.4.0b + H2O	−186.3	0.2	181.6	2.6	−1.9
0.5.0 + NO3^− → 1.3.0…H2O + H2O	−195.0	0.2	184.1	3.1	−7.6
0.5.0 + NO3^− → 1.3.0 + 2H2O	−177.4	−0.1	173.1	−4.5	−8.9
0.5.0 + L + NO3^− → 1.2.1 + 3H2O	−200.8	0.1	189.3	−2.8	−14.2
0.5.0 + 2L + NO3^− → 1.1.2a + 4H2O	−219.6	0.3	201.3	−1.1	−19.1
0.5.0 + 2L + NO3^− → 1.1.2b + 4H2O	−219.1	0.3	199.4	0.5	−19.0
0.5.0 + 2L + NO3^− → 1.2.2a + 3H2O	−229.3	0.6	208.1	9.8	−10.8
0.5.0 + 2L + NO3^− → 1.2.2b + 3H2O	−226.6	0.6	207.6	8.3	−10.1
0.5.0 + 2L + NO3^− → 1.2.2c + 3H2O	−228.8	0.6	207.6	9.6	−11.0
0.5.0 + 2L + NO3^− → 1.2.2d + 3H2O	−225.8	0.6	205.8	10.1	−9.3
0.5.0 + 2NO3^− → 2.2.0 + 3H2O	−301.7	0.1	291.6	−1.5	−11.5
0.5.0 + L + 2NO3^− → 2.1.1 + 4H2O	−311.0	0.3	294.9	1.0	−14.9
0.5.0 + 2L + 2NO3^− → 2.0.2a + 5H2O	−316.0	0.5	296.7	2.3	−16.6
0.5.0 + 2L + 2NO3^− → 2.0.2b + 5H2O	−316.6	0.5	294.4	3.7	−18.1
0.5.0 + 2L + 2NO3^− → 2.0.2c + 5H2O	−307.3	0.5	290.4	4.0	−12.4
0.5.0 + 2L + 2NO3^− → 2.0.2d + 5H2O	−315.0	0.5	294.5	1.8	−18.1
0.5.0 + 2L + 2NO3^− → 2.0.2e + 5H2O	−308.6	0.5	290.1	1.3	−16.8
0.5.0 + 2L + 2NO3^− → 2.0.2f + 5H2O	−302.9	0.5	287.6	1.3	−13.5
0.5.0 + 2L + 2NO3^− → TS2.0.2a–2.0.2b + 5H2O	−313.0	0.5	293.4	4.2	−15.0
0.5.0 + 2L + 2NO3^− → TS2.0.2b–2.0.2c + 5H2O	−306.2	0.5	288.6	3.2	−13.9
0.5.0 + L + 2NO3^− → 2.0.1 + 5H2O	−295.4	0.0	284.0	−7.2	−18.6
0.5.0 + 2L + 2NO3^− → 2.1.2a + 4H2O	−320.6	0.8	297.5	10.2	−12.1
0.5.0 + 2L + 2NO3^− → 2.1.2b + 4H2O	−311.3	0.8	292.7	11.6	−6.3
0.5.0 + 2L + 2NO3^− → 2.1.2c + 4H2O	−322.8	0.8	296.5	12.8	−12.7
0.5.0 + 2L + 2NO3^− → 2.1.2d + 4H2O	−317.4	0.8	298.4	13.3	−4.8
0.5.0 + 2L + 2NO3^− → 1.1.2a…NO3^− + 4H2O	−321.9	0.8	297.1	15.0	−8.9
0.5.0 + 2L + NO3^− → 2.0.2b…H2O + 4H2O	−323.1	0.8	299.2	11.4	−11.7
0.5.0 + 2NO3^− → 2.3.0a + 2H2O	−303.5	0.4	293.8	8.0	−1.3
0.5.0 + L + 2NO3^− → 2.2.1 + 3H2O	−315.5	0.9	297.7	5.7	−11.1
0.5.0 + L + 2NO3^− → 2.0.1 + 5H2O	−295.4	0.0	284.0	−7.2	−18.6
0.5.0 + 2L + NO3^− → 1.0.2 + 5H2O	−197.5	0.0	186.7	−8.6	−19.4

---

Interestingly, in water, both nitrates and L displace water from 0.5.0. The driving force for complexation of a first nitrate is relatively weak when only one water is displaced from 0.5.0, leading either to 1.4.0a (−1.1 kcal mol⁻¹) or 1.4.0b (−1.9 kcal mol⁻¹, see Table 2). However, the displacement of two aquo ligands by a nitrate is more favourable and affords 1.3.0 with a significant free energy gain of 8.9 kcal mol⁻¹. A similar value is obtained when considering the formation of the microsolvated complex “1.3.0…H₂O” (−7.6 kcal mol⁻¹; see Scheme 2). These results therefore suggest that, in bulk water, the mono-nitrate complex should preferably exist as a penta-coordinated species possessing three aquo ligands. The complexation of a second nitrate is also thermodynamically favourable but to a lesser extent, especially when the hexa-coordinated 2.2.0a complex is afforded (ΔG = −11.5 kcal mol⁻¹). Similarly, the displacement of water by amides is thermodynamically favourable in water, regardless of the number of coordinated nitrates. In the dicationic series (0.5.0, 0.4.1 and 0.3.2a/b), every H₂O/L exchange releases ca. 5 kcal mol⁻¹, yielding a highly negative free energy of formation of 0.3.2a (−10.1 kcal mol⁻¹). This feature is observed regardless of the isomer that is considered since the cis isomer (0.3.2b) is found to be isoenergetic with the trans one (0.3.2a). A similar behaviour is observed in the monocationic series (1.3.0, 1.2.1 and 1.1.2a), where the free energy of formation of 1.1.2a amounts to −19.1 kcal mol⁻¹, making this complex one of the most stable among those considered in this study. Monocationic complexes featuring a monodentate nitrate and two aquo ligands (affording a penta-coordination) are higher in free energy by ca. 9 kcal mol⁻¹ (see 1.2.2a–d in Table 2).

When neutral complexes are considered, H₂O → L exchanges are still favourable: complexes with two L ligands (2.0.2a and 2.1.2a) are more stable than those with one or zero. As a result, the formation of 2.0.2a is exergonic in water, by −16.6 kcal mol⁻¹. Neutral complexes possessing two monodentate nitrates and an additional aquo ligand to afford a penta-coordinated uranyl are less stable regardless of the isomer considered (2.1.2a–c, see Schemes 3 and 4): water should thus decoordinate from 2.1.2a to afford 2.0.2a/b. Similarly, a spontaneous release of water from 2.1.2c to afford 2.0.2d/e is predicted.

3.3. Structure, dynamics and solvation patterns of [UO₂(NO₃)₂L₂] (2.0.2) in hexane, water and at the hexane/water interface

We investigated six “isomers” of the [UO₂(NO₃)₂L₂] complex (2.0.2a–f; see Schemes 3 and 4) in the three different environments relevant for the extraction process: bulk hexane, bulk water and the hexane/water interface.

3.3.1. Energy comparison of different “isomers”, investigated by static DFT calculations in the bulk phases. First, we performed static DFT calculations in SMD-hexane and SMD-water. The results gathered in Table 3 show that the relative stabilities of the different isomers markedly depend on the nature of the solvent polarity. In SMD-hexane, 2.0.2a is the most stable isomer. The partial decoordination of a nitrate to afford a η¹ binding mode (in 2.0.2b) costs 1.9 kcal mol⁻¹. The cis isomer 2.0.2d with two bidentate nitrates is almost isoenergetic with 2.0.2a, and the bi- to mono-dentate coordination exchange of a nitrate to afford 2.0.2e is more demanding (5.7 kcal mol⁻¹). The η² to η¹ change of coordination mode of the two nitrates to afford a tetra-coordinated uranyl complex is highly unfavourable, by ca. 11 kcal mol⁻¹, regardless of the cis/trans isomer considered (2.0.2c and 2.0.2f). Also, the full dissociation of one amide ligand from 2.0.2a is thermodynamically uphill, by 9.1 kcal mol⁻¹. The full dissociation of NO₃⁻ is prohibitive, as expected, because it is poorly solvated by hexane. In SMD-water, 2.0.2a is not the most stable of the series anymore and the η²- to η¹ flipping of a nitrate is favoured by −1.5 kcal mol⁻¹. Moreover, the cis isomer (2.0.2d) becomes more stable than 2.0.2a, by −1.6 kcal mol⁻¹. The partial decoordination of the two nitrates is also unfavourable, but to a lesser extent than in hexane (see 2.0.2c and 2.0.2f). In SMD-water, however, the full dissociation of one L or NO₃⁻ ligand becomes possible, since 2.0.1 and 1.0.2 are more stable than 2.0.2a by −2.0 and −2.9 kcal mol⁻¹, respectively, according to this implicit solvation model. As seen above, in the gas phase or in an apolar solvent, such a ligand dissociation is highly endergonic, showing the importance of polar solvation.

Table 3 Relative free energies (kcal mol⁻¹) of isomers of [UO₂(NO₃)₂L₂] and of [UO₂(NO₃)₂(H₂O)L₂] complexes in the gas phase, hexane and water^a

	Gas^b	Hexane^c	Water^d
a Values reported in the table are calculated as: ΔG = ΔEgas + δEBSSE + δESolv + δEG, where ΔEgas and δEBSSE are computed at the PBE0-D3/SDD+ level. b δEsolv = 0. c δEsolv evaluated using parameters of hexane (SMD model). d δEsolv evaluated using parameters of water (SMD model).
[UO2(NO3)2L2] complexes
2.0.2a	0.0	0.0	0.0
2.0.2b	0.8	1.9	−1.5
2.0.2c	10.4	11.1	4.2
2.0.2d	0.6	0.8	−1.6
2.0.2e	6.4	5.7	−0.2
2.0.2f	12.2	12.2	3.1
TS2.0.2a–2.0.2b	4.9	5.1	1.6
TS2.0.2b–2.0.2c	10.7	11.2	2.6
2.0.1 + L	10.7	9.1	−2.0
1.0.2 + NO3^−	107.1	63.5	−2.9
[UO2(NO3)2(H2O)L2] complexes
2.1.2a	−0.3	0.2	0.7
2.1.2b	10.3	10.6	6.5
2.1.2c	0.0	0.0	0.0
2.1.2d	6.0	7.0	7.9
1.1.2a + NO3^−	89.3	47.0	−5.8

---

3.3.2. Dynamics of the [UO₂(NO₃)₂L₂] complex (2.0.2) in the bulk phases and at the interface. To further analyze the structure and stability of the [UO₂(NO₃)₂L₂] complex in the different environments (hexane, water and at the interface), we performed MD simulations in these explicitly represented solvents at the MM level (DFT/MM-MD simulations) or at the full DFT level in water for comparison (DFT-MD simulations) starting from 2.0.2a. The simulated time (32 ps) is too short to observe ligand exchanges but reveals interesting solvent-dependent fluxional behaviour of nitrates, as seen from the time evolution of the U–O_nit distances and the total equatorial coordination number⁴⁹ (Fig. 1).

Fig. 1 Fluxional behaviour of 2.0.2a/b: time evolution (X-axis, in ps) of uranium–O(nitrate) distances (Y-axis, in Å) and of the total equatorial coordination number around uranyl (i.e. including oxygen atoms of nitrates and amides) in water, in hexane and at the hexane/water interface. “DFT-MD” stands for full DFT simulations on a smaller system containing 89 water molecules (see the Methods section).

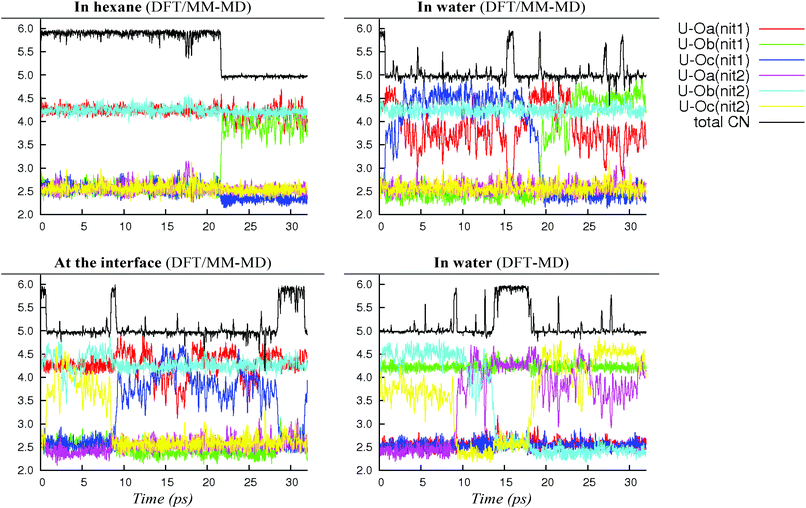
In bulk hexane, the complex retains its hexa-coordination for ca. 22 ps of MD, and then one nitrate becomes monodentate to afford 2.0.2b for the remaining 10 ps of MD. In bulk water, the nitrates exhibit a fluxional behaviour, where one quickly moves from a bidentate to a monodentate coordination mode to afford 2.0.2b, with transient recoordinations to afford 2.0.2a. Interestingly, the identity of the bound O_nit atom can change in the process, namely: “nitrate-1” is bound via O_b during the first 20 ps of MD and via O_c for the remaining 12 ps (see the crossing of the blue and green curves on Fig. 1 at t = 20 ps). The exchange occurs with an associative process, via2.0.2a. A similar behaviour is observed by full DFT-MD simulations, where “nitrate-1” remains bidentate for the whole 32 ps of MD, whereas “nitrate-2” is monodentate (as in 2.0.2b) most of the time, but exhibits a rotational motion: during the first 9 ps, it is originally bound by its O_a atom, then a transient bidentate coordination mode is achieved (for 0.5 ps) and O_a decoordinates (i.e. the anion remains bound by its O_b atom). After 4.5 ps of MD, another rotation is observed, where O_c coordinates to UO₂²⁺ while O_b decoordinates (see Scheme 5). Such a dynamics points to a rather weakened binding of the nitrate to the complex in water, in accord with the result of static calculations shown in Table 3 and with the systematic increase of average U–O_nit distances when moving from hexane (or gas phase) to water (see Table 4).

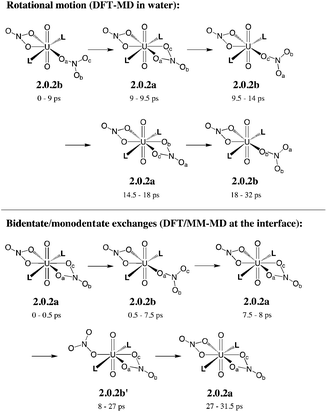Scheme 5 Fluxional coordination of nitrate in 2.0.2a/b: rotational motion and bidentate/monodentate exchanges, as observed from DFT-MD in explicit water and DFT/MM-MD at the interface (over 32 ps). See the time evolution of U–O_nit distances in Fig. 1.

Table 4 Interatomic distances (in Å) as obtained from optimisations in the gas phase and from MD simulations in hexane, at the interface and in water, at the DFT/MM-MD and DFT-MD levels^a

	OPT		MD
	G09	CP2K	DFT/MM-MD			DFT-MD
	Gas^b	Gas	Hexane	Interface	Water	Water
a The BLYP-D3 functional has been employed throughout. b SDD basis set. c Not reported because the lifetime of the hexacoordinated complex (with two bidentate nitrates) is too short; see Fig. 1. d No DFT/MM-MD simulations have been performed on this species.
2.0.2a
d(U=O)	1.81	1.81	1.81(5)			1.82(4)
d(U–Onit)	2.54	2.55	2.57(13)			2.59(10)
d(U–OL)	2.44	2.43	2.46(10)			2.37(9)
2.0.2b
d(U=O)	1.81	1.81	1.81(4)	1.81(5)	1.81(7)	1.82(3)
d(U–Onit)	2.50	2.50	2.52(7)	2.57(14)	2.57(15)	2.56(8)
d(U–O^′nit)	2.37	2.38	2.35(7)	2.40(11)	2.45(14)	2.41(9)
d(U–OL)	2.38	2.37	2.40(8)	2.36(10)	2.33(12)	2.33(7)
2.1.2c
d(U=O)	1.81	1.81	1.81(4)	1.81(8)	1.81(5)	1.82(3)
d(U–Onit)	2.37	2.38	2.40(10)	2.49(15)	2.48(14)	2.51(12)
d(U–OL)	2.47	2.46	2.45(10)	2.39(12)	2.38(10)	2.36(7)
d(U–Owat)	2.50	2.52	2.55(10)	2.54(15)	2.56(12)	2.47(9)
1.1.2a…NO3^−
d(U=O)	1.81	1.81				1.82(3)
d(U–Onit)	2.50	2.50				2.57(10)
d(U–OL)	2.37	2.36				2.33(7)
d(U–Owat)	2.39	2.42				2.45(9)
d(U–Nnit)	4.69	4.81				5.22(53)

---

We note that such an elongation of U–O_nit distances when going from the gas phase to water has already been observed in the cases of 2.2.0⁵⁰ and 1.4.0a/b.⁴⁴ However, no spontaneous nitrate dissociation is observed in the course of our DFT/MM-MD and DFT-MD simulations (over 32 ps). Regarding the L ligand, its strengthened coordination to uranyl in a water environment is a particularly noteworthy and important feature for the extraction mechanism.

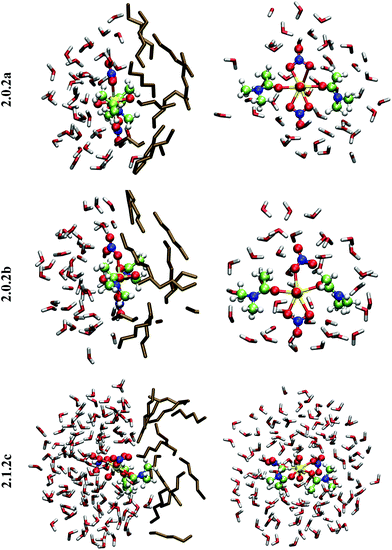
When simulated at the hexane/water interface, the complex does not diffuse toward any of the bulk phase, but remains located in the interfacial domain over the 32 ps of DFT/MM-MD. On average, its O–U–O axis sits perpendicular to the interfacial plane, with the amide and nitrate ligands being co-planar to the interface (see Fig. 2). Interestingly, the complex behaves similarly as in water, since 2.0.2b is afforded most of the time with transient formation of 2.0.2a. However, no rotational motion of NO₃⁻ is observed at the interface. Instead, a dynamical exchange occurs between two “isomers” of 2.0.2b: during the first 8 ps of MD, “nitrate-1” is monodentate and “nitrate-2” is bidentate, then an exchange occurs (via2.0.2a) to obtain the reverse situation where “nitrate-1” is bidentate and “nitrate-2” monodentate (see 2.0.2bvs. 2.0.2b′ in Scheme 5).

Fig. 2 Typical snapshots of 2.0.2a, 2.0.2b and 2.1.2c at the hexane/water interface, as obtained after 32 ps of DFT/MM-MD. Left column: side view with the water phase on the left hand side and the hexane phase on the right hand side. Right column: top view seen from the hexane phase (hexane molecules are hidden for clarity).

3.3.3. Free energy landscape for nitrate rearrangement in the [UO₂(NO₃)₂L₂] complex studied by metadynamics in the bulk phases and at the interface. To gain deeper insights into the environment-dependent dynamics of nitrates and related uranyl coordination features, we performed DFT/MM metadynamics⁵¹ simulations of 2.0.2a in hexane, water and at the interface. Two collective variables (CVs) have been considered: the first is the total equatorial coordination number around uranyl (including nitrates and L oxygens, denoted CN(U,O)),⁴⁹ the second is the difference between the two U–N_nitrate distances. Metadynamics simulations were run for 40 ps (1000 hills), with the same parameters in the three environments (hills added every 40 fs, height: 0.5 kcal mol⁻¹, widths: 0.05 and 0.02 Å for the first and second CV, respectively). The reconstructions of the free energy surfaces are given in Fig. 2.⁵² As a result, 2.0.2a, 2.0.2b and 2.0.2c are afforded during the metadynamics simulations, and the relative stability and heights of the activation barriers are found to depend on the nature of the environment: in hexane, 2.0.2a is more stable than 2.0.2b by ca. 2 kcal mol⁻¹ and an activation barrier of ca. 8 kcal mol⁻¹ has to be overcome for passing from one isomer to the other. The stability of 2.0.2b can be understood by looking at the U–O_nit distances in the two isomers (see Table 4): all are longer in 2.0.2a than in 2.0.2b, pointing to some steric hindrance in the first coordination sphere of 2.0.2a that is released when one nitrate turns from bi- to monodentate (in 2.0.2b).⁵³ This feature is beneficial and balances the cost for U–O_nit bond dissociation. The tetra-coordinated isomer 2.0.2c is also less stable than 2.0.2a by ca. 2 kcal mol⁻¹, and the activation barrier for 2.0.2b → 2.0.2c is also 8–10 kcal mol⁻¹. In water, the free energy surface is somewhat more “flat”, and all three “isomers” 2.0.2a, 2.0.2b and 2.0.2c are within 2 kcal mol⁻¹.⁵⁴ The activation barrier for moving from one structure to another is almost two times smaller than in hexane (i.e. ca. 4 kcal mol⁻¹). The difference can be rationalized by solvation effects, because water solvates the unbound oxygen atoms of nitrates and stabilizes low coordinated complexes featuring monodentate nitrates (over 2.0.2a). These results are in qualitative agreement with static calculations calculated at the higher DFT level in SMD solvents from which the free energies of activation for the two dissociation processes are significantly smaller in water than in hexane (see TS_{2.0.2a–2.0.2b} and TS_{2.0.2b–2.0.2c} in Table 3). They also correlate well with previous results on 2.2.0vs. [UO₂(η¹-NO₃)(η²-NO₃)(H₂O)₂], where both the relative free energies and the kinetic barriers for the η²-to-η¹ transition are halved when going from the gas phase to water.⁵⁰ At the interface, the free energy surface is reminiscent of the one obtained in water (see Fig. 2), featuring three minima that are close in free energy (within 2 kcal mol⁻¹) and connected by rather low free energy barriers (of ca. 4 kcal mol⁻¹).

As discussed above, we should emphasise that the bidentate binding mode of the nitrates may be underestimated by the BLYP-D3 functional that is employed in the DFT/MM-MD simulations (compare CCSD(T)/SDD+ and BLYP-D3(CP2K) in Table 1, where the η²-coordination of NO₃⁻ in 1.4.0avs. η¹-1.4.0b is underestimated by 2.2 kcal mol⁻¹). We therefore expect a larger difference in stabilities between 2.0.2a, 2.0.2b and 2.0.2c, making the tetra-coordinated complex 2.0.2c in reality less stable. Also, the free energy surfaces could be refined by performing longer metadynamics simulations with smaller hills (see Fig. S2†). However, taken together, these metadynamics results point to the solvent-dependent versatility of binding mode of the nitrate that is beneficial for changes in coordination number and for ligand exchange processes occurring along the extraction process.

3.4. Structure, dynamics and solvation patterns of [UO₂(NO₃)₂(H₂O)L₂] (2.1.2c) in hexane, water and at the hexane/water interface

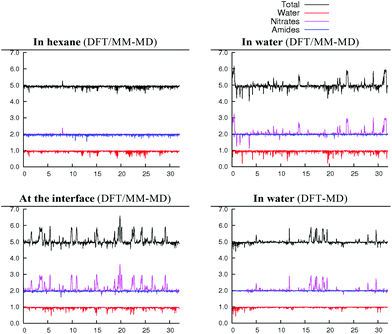
We now consider the hydrated [UO₂(NO₃)₂(H₂O)L₂] complex as a possible precursor of the extracted [UO₂(NO₃)₂L₂] species, by losing its aquo ligand. We decided to start with the cis isomer (2.1.2c) that might be afforded at the interface upon complexation by L via a least motion pathway. This cis isomer being almost isoenergetic with the trans one (2.1.2a) in hexane or in water (see Table 3), the two complexes are expected to be in equilibrium at the interface. Again, DFT/MM-MD simulations have been performed in hexane, water and at the interface for 32 ps along with a full DFT-MD simulation in water. Time evolution of (U,O) coordination numbers around uranyl shows that the complex retains its five ligands for the whole 32 ps of MD, in the three environments (see Fig. 4). Again, nitrates essentially remain monodentate but sometimes display transient bidentate coordinations. Rotational motions are also observed, as depicted in Scheme 5 in the case of 2.0.2b. Average interatomic distances reported in Table 4 show that, intrinsically (i.e., in the gas phase), the three metal–ligand distances follow the order: d(U–O_nit) < d(U–O_L) < d(U–O_wat). NO₃⁻ is the most strongly bound because of its negative charge, while L is intrinsically a better ligand than H₂O (vide supra). In hexane, average metal–ligand distances are almost identical to those found in the gas phase, and thus follow the same order. In water, U–O_nit is elongated by ca. 0.13 Å whereas U–O_L distances are shortened by ca. 0.10 Å, yielding a reverse sequence: d(U–O_L) < d(U–O_wat) < d(U–O_nit). This result points to a weaker binding of monodentate nitrates in water that should stem from their attraction by water, as in the case of 2.0.2a/b discussed below. We note that the weak binding of nitrates in water evidenced by these MD simulations is consistent with the static calculations in the continuum (see Table 3), where the full dissociation of NO₃⁻ from 2.1.2a is found to be favoured by 7 kcal mol⁻¹. However, the process should be associated with a significant kinetic barrier, as no spontaneous nitrate dissociation is observed in the course of DFT-MD and DFT/MM-MD simulations in water. Conversely, the shortening of the U–O_L distances suggests that amides are more strongly bound to the metal in water than in hexane. Interestingly, the U–O_wat distance remains similar in the two environments but a closer look at the average structures in the two media reveals a marked difference: in hexane, the water ligand forms intramolecular hydrogen bonds with the two neighbouring nitrates (as in the gas phase), whereas, in water, it mainly forms intermolecular hydrogen bonds with the solvent. A similar competition between intramolecular and intermolecular hydrogen bonds has been observed in the cases of [UO₂(NO₃)₂(H₂O)₂]⁵⁰ and LaCl_x complexes (x = 1,…, 3).⁵⁵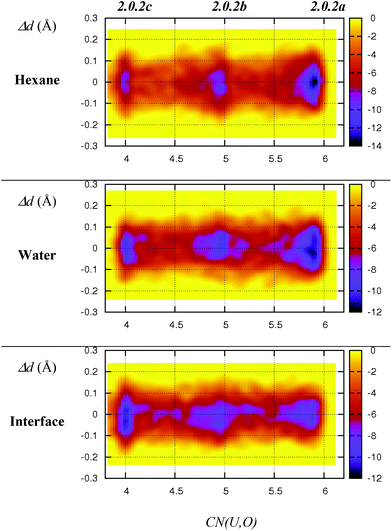

Fig. 3 Free energy surfaces (colour coded in kcal mol⁻¹) of 2.0.2a–c as obtained from DFT/MM metadynamics simulations in hexane, water and at the interface. X-axis: equatorial coordination number around uranyl. Y-axis: differences between the two U–N_nit distances (in Å). The time evolution of the collective variables is given in Fig. S1 in ESI.†

Fig. 4 Time evolution (X-axis, in ps) of equatorial U,O coordination numbers around uranyl in 2.1.2c (Y-axis) in three different environments (water, hexane and at the hexane/water interface). Total equatorial coordination number (black) and separate contributions of water (red), nitrates (purple) and amides (blue).

When simulated in the hexane/water biphasic system, 2.1.2c remains adsorbed at the interface for the whole 32 ps of MD. The snapshot of the complex at the interface presented in Fig. 2 shows that its orientation clearly differs from that of 2.0.2a/b, as the O–U–O axis of 2.1.2c does not sit perpendicular to the interface anymore but is rather tilted, and the equatorial plane of the complex is no longer co-planar with the interface. It tends to adopt an amphiphilic orientation with the two L ligands on the hexane side of the interface and the nitrates and aquo ligands on the water side. Interestingly, metal–ligand distances follow the same sequence as in water (see Table 4). Visual inspection of the trajectories shows that intermolecular hydrogen bonds with (interfacial) water molecules are also predominant over intramolecular hydrogen bonds, in keeping with the fact that the polar [UO₂(NO₃)₂(H₂O)] moiety of the complex is essentially solubilized on the water side of the interface. As a result, the uranyl–nitrate bond appears to be significantly weakened at the interface to a similar extent as in bulk water. Concomitantly, the uranyl–L bond is strengthened at the interface.

3.5. Structure and dynamics of the [UO₂(NO₃)(H₂O)L₂]⁺ complex (1.1.2) in water

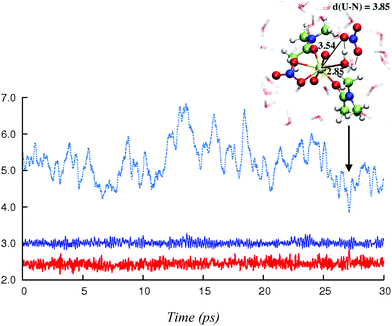
In this section, we explore by MD simulations the stability and structure of another potential precursor of the extracted complex, namely the cationic [UO₂(NO₃)(H₂O)L₂]⁺ species for which a H₂O/NO₃⁻ exchange leads to 2.0.2. As seen above, the 1.1.2a complex, a possible intermediate between the +2 charged 0.5.0 and neutral 2.0.2 species, is also one of the most stable in the studied series in SMD-water. We thus decided to study by DFT-MD its dynamics in the presence of a second shell nitrate ligand. Because the “free” nitrate salt is insoluble in the oil phase, water was chosen as the explicit solvent environment, as a first approach. The complex more likely forms at the interface, but its structure should be similar in the two environments, as seen above. The DFT-MD on the “1.1.2a…NO₃⁻” complex was thus started with the second sphere nitrate constrained to be hydrogen-bonded to the H₂O ligand, for 2.5 ps (by fixing the U–N_nit at 5.5 Å). We then released the constraint for an extra 30 ps of MD. Time evolution of the uranium–nitrogen distance (denoted d(U–N_nit)) shown in Fig. 5 reveals that the free nitrate is quite mobile, with d(U–N_nit) oscillating from 3.85 Å to 6.80 Å. At longer distances, the hydrogen bond with 1.1.2a is disrupted and nitrate is fully surrounded by solvent water molecules. The free anion does not diffuse further into the “bulk” water phase, but essentially remains in the second shell, forming a contact ion pair, on average. This feature is favourable for its further complexation to afford the extracted species 2.0.2a/b. However, neither spontaneous coordination of NO₃⁻ nor full dissociation of H₂O is observed in the course of the DFT-MD (over 30 ps). Interestingly, at some stage of the dynamics (ca. 27 ps), NO₃⁻ approaches the metal and this process is accompanied by an elongation of U–O_wat (see the structure extracted from the DFT-MD in Fig. 3) to reach 2.85 Å. This value is larger than the typical U–O_wat distance in mixed UO₂²⁺/NO₃⁻/H₂O/L complexes (see e.g.2.1.2c in Table 4, where U–O_wat = 2.48(9) Å) and likely corresponds to a structure close to the transition state for a concerted H₂O/NO₃⁻ ligand exchange. However, it is apparent from the structure that the nitrate does not point any of its oxygen toward the metal but remains hydrogen bonded to the solvent and to the coordinated H₂O. As a result, the closest U–O_nit distance remains quite long (namely 3.54 Å), suggesting that the structure afforded during the DFT-MD is still far from the transition structure and that the associated kinetic barrier should be rather high. In order to estimate this barrier, we performed a transition state search by static calculations (PBE0-D3 energies in SMD-water on the gas phase BLYP-D3/SDD geometries, optimized with a single imaginary frequency) using the structure extracted from the DFT-MD as the starting structure (after removing all solvent molecules). Interestingly, no transition state could be located directly from that structure, but we needed to slightly rotate the free nitrate to approach its closest oxygen atom slightly closer to the metal. The search led, in fact, to a (late) transition state for an associative process, where the nitrate coordinates while the U–O_wat bond is retained, i.e. to afford 2.1.2d. The activation barrier from “1.1.2a…NO₃⁻” (as depicted in Fig. 6) is found to be small (+3.7 kcal mol⁻¹) and therefore potentially accessible. Searching for the full pathway connecting the “1.1.2a…NO₃⁻” complex to “2.0.2b…H₂O” in solution is beyond the scope of this study. However, taken together, these DFT-MD results in water and the small difference in their free energies of formation in SMD-water (−8.9 and −11.7 kcal mol⁻¹, respectively, see Table 2) suggest that 1.1.2a can be a potential intermediate along the 0.5.0 to 2.0.2 transformation.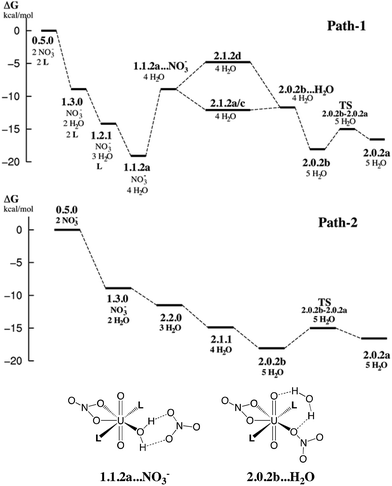

Fig. 5 Time evolution (X-axis, in ps) of the U–O_wat distance (solid red) and of the first shell (solid dark blue) and the second shell (dotted light blue) U–N_nit distances (Y-axis, in Å) in “1.1.2a…NO₃⁻”, as obtained from (unconstrained) DFT-MD in explicit water over 30 ps. The first 2.5 ps of MD with constrained nitrate are not shown (see the text).

Fig. 6 Possible free energy profiles path-1 and path-2 (kcal mol⁻¹) for the stepwise complexation of NO₃⁻ and L by 0.5.0 to afford the extracted complex 2.0.2. Energies estimated from static calculations in SMD-water (top). Bottom: schematic representation of selected intermediates. Other intermediates are depicted in Schemes 3 and 4.

3.6. Proposed extraction mechanism

The results on the relative stabilities of [UO₂(NO₃)_x(H₂O)_yL_z]^2−x complexes and mechanistic considerations allow us to propose reasonable sequences of reactions involved in the uranyl extraction by the amide ligand, starting from 0.5.0 solubilized in water and ending up with 2.0.2a in hexane (see Scheme 1). Two possible routes are schematized in Fig. 6, with relative free energies calculated “in SMD-water”. These are only indicative because of the limitations of the continuum SMD solvation model (lack of explicit H-bond interactions with the solute, for instance). The changes in solvation energies cannot pretend to be accurate, especially for the complexation of charged species in a given medium. See for instance the recently reported case of actinide and lanthanide ion extraction.⁵⁶ When compared to experimental conditions where uranyl is extracted by amide ligands,^1e,57 two important features must be noted. First, the N,N-dimethylacetamide ligand L used here for convenience is soluble in water and thus does not extract uranyl. Its coordination features to uranyl should be similar, however, to those of more hydrophobic oil-soluble amide ligands.⁵⁸ The latter are more bulky and polarizable than L, and thus form stronger bonds with uranyl.⁵⁹ A second important simplification concerns the pH conditions. Experimentally, uranyl extraction occurs from highly acidic media (≈3 M nitric acid solutions where irradiated nuclear fuel is usually dissolved), and increases with the acid concentration.^1e,57 Without acid, uranyl is not extracted. Experimentally, some nitric acid in its HNO₃ form and some water are also co-extracted with the extracted 2.0.2 complex, presumably forming hydrogen bonds with its external nitrate oxygens.

The two proposed routes start by the coordination of one nitrate (path-1) or two nitrates (path-2), respectively, in “bulk water”. The corresponding calculated free energies are overestimated, if one refers to the low stability of the UO₂(NO₃)(H₂O)_x⁺¹ cation in water,⁶⁰ but are consistent with the experimental⁶¹ and computational⁶² evidence of increased nitrate coordination to uranyl when nitric acid is added to the solution. Coordination of nitrate(s) (by exchange with two aquo ligands from 0.5.0 affords 1.3.0 (one nitrate) or 2.2.0 (two nitrates)). Both 1.3.0 and 2.2.0 species are less hydrophilic than the dicationic 0.5.0 species and are thus expected to approach the interface,⁶³ close enough to interact with the carbonyl group of L that displaces H₂O from the complex, affording 1.1.2a in path-1. This complex should sit “right at the interface” in an amphiphilic manner, i.e. with the alkyl groups of the amide on the oil side and the water and nitrate ligands on the water side. As surface active species, such positively charged complexes concentrate at the interface and thus attract free nitrate counterions to afford contact ion pairs as in “1.1.2a…NO₃⁻” via electrostatic interactions. Then, H₂O/NO₃⁻ ligand exchange occurs at the interface to afford the neutral 2.1.2d species, from which water decoordinates, yielding the more hydrophobic 2.0.2b and 2.0.2a complexes. These finally diffuse from the interface to bulk hexane.

In path-2, the first neutral species formed is 2.2.0. From there, displacement of H₂O ligands by L at the interface successively yields the more hydrophobic 2.1.1 and 2.0.2b or 2.0.2a complexes. Interestingly, comparing these two structures, we note that 2.0.2b with a monodentate nitrate is calculated to be slightly more stable in SMD-water, while 2.0.2a with two bidentate nitrates is preferred in SMD-hexane. 2.0.2a should also interact less than 2.0.2b with water at the interface. Thus, the migration of 2.0.2 from the interface to the oil phase is likely correlated with a switch in the η¹ to η² nitrate coordination mode. The free energy profiles provided in Fig. 6 show that both path-1 and path-2 processes are favourable in SMD-water, and are also likely to be so at the interface where interfacial charged species mostly interact with water (see for instance an energy component analysis in recent classical MD simulations).⁹ Interestingly, path-2 that requires more acidic conditions than path-1 mainly corresponds to a regular downhill process, while path-1 involves higher energy intermediates and might thus be kinetically less favourable. In path-1, we located a transition state involved in the key H₂O/NO₃⁻ exchange process and found that the height of the kinetic barrier is rather small, indicating that associative ligand exchange should be entirely plausible, though. It should be noted that in reality, the extraction kinetics not only depends on barriers for ligand coordination/decoordination, but is also generally limited by the diffusion rates, hardly accessible from calculations.

4. Discussion and conclusions

We report DFT studies on selected uranyl complexes involved in the uranyl extraction from water to an “oil” phase (hexane) by an amide ligand L, using two complementary approaches: static DFT results “in SMD-solution” and MD studies in explicit solvent environments (water, hexane, or the water/hexane interface) represented at the MM or full-DFT level. In the following, we summarize the related strengths and weaknesses, as well as the most important results regarding the studied uranyl complexation and extraction processes.

On the methodological side, our “static” results were obtained from high-level DFT calculations, involving a small-core ECP on U and large basis sets including many polarisation and diffuse functions. The PBE0-D3 functional has been employed to compute refined energies, after validation against CCSD(T) calculations. This functional includes a correction for dispersion interactions that are generally lacking in GGA and hybrid functionals. The latter have been recognized to be important to properly describe metal–ligand interactions in several organometallic,⁶⁴ and actinide⁶⁵ complexes, and turn out to be also important to model mono- vs. bidentate coordination or H₂O dissociation in uranyl nitrate complexes herein (see Table 1). As a result, gas phase reaction energies (ΔE_gas) should be quite well predicted. The estimation of changes in solvation free energies remains the most difficult task for present-day DFT modelling, and we tackled this issue by two different approaches of increasing accuracy. First, we employed the recently developed SMD model that is recognized to perform particularly well to compute absolute free energy of solvation and free energies of transfer from water to an organic phase, especially when neutral solutes are considered.²⁴ Solvation of ions still remains a challenging task,²⁴ especially when “strong” explicit interactions with the solvent are involved (namely, hydrogen bonding with water). As a result, the solvation of the nitrates is a difficult case for the SMD model and the latter uncomplexed appears to be not enough solvated, making their complexation in water somewhat too favourable.⁶⁶ However, free energies for exchange of neutral ligands are expected to be better accounted for. In particular, the clear-cut preference for L over H₂O binding in SMD-water and SMD-hexane should be realistic, and is a key feature for the extraction process: L displaces water from uranyl, whatever be the number of coordinated nitrates. In our second approach, the solvent molecules are represented explicitly, and their motions and interactions with the uranyl complexes have been described by performing ab initio MD simulations. Our mixed DFT/MM-MD protocol¹² allowed us to consider systems containing one complex and few thousands of solvent molecules, at a similar computational expense as in fully DFT-MD simulations on small boxes (containing one complex and 89 water molecules only). With the DFT/MM-MD protocol, one can thus simulate “DFT solutes” in quite large solvent boxes, as involved in biphasic systems and their interfaces. Despite a lower accuracy compared to fully DFT-MD (e.g. the lack of back polarization of the first solvation shell by the solute), our DFT/MM model captures most of the solvation effects. For instance, the polarisation of the solute by the solvent¹² and the influence of aqueous solvation on the structure of a uranyl peroxo complex⁶⁷ have been qualitatively well described elsewhere. Herein, for instance, the shortening/elongation of metal-distances in water vs. gas phase (see Table 4) and the fluxional coordination of the nitrates (see Scheme 5) are described satisfactorily when compared to full DFT-MD at the same DFT level. Our simulations of uranyl complexes at the hexane/water interface reveal that their structure in this peculiar nano-domain is more “water-like” than “oil-like”. The binding of L is thus reinforced compared to the gas phase, a feature particularly important in the context of a complexation process occurring “right at the interface”. Another important feature concerns the cis/trans forms of the complexes. DFT/MM-MD simulations, supported by static DFT calculations, reveal that the formation of cis isomers is competitive to that of trans isomers, in the bulk solvents as well as at the interface. Interestingly, the former can be afforded via a least motion pathway upon complexation with interfacial L ligands (oriented in an amphiphilic manner),^9a and then rearrange to less amphiphilic and less surface active trans isomers when diffusing to the organic phase. Taken together, our results allowed us to propose possible paths for the overall extraction process of UO₂²⁺ by N,N-dialkylamide ligands, and shed new light on the key role of the interface in the process. Similar features are expected by other ligands like TBP.⁹ To the best of our knowledge, our study reports the first DFT/MM-MD simulations of a uranyl liquid–liquid extraction system. Further work will focus on improving our hybrid DFT/MM model by considering the actual oil-soluble amide ligand (with long alkyl chains on L, e.g. described at an MM level), and by taking into account the high concentration of L in the organic phase, the ionic strength and the acidic pH of the aqueous phase, thus approaching the complexity of “real” extraction systems. Beyond the case of uranyl extraction, the results have a bearing on biphasic processes in chemistry and biology, involving ion separation or transport or phase transfer catalysis processes.⁶⁸

Acknowledgements

N. S. thanks Univ. Grenoble Alpes, CNRS and ICMG FR 2607 for financial support. MD simulations were performed using the Cecic and Froggy platforms of the CIMENT infrastructure, which is supported by the Rhône-Alpes region (grant CPER07_13 CIRA) and the Equip@Meso project (reference ANR-10-EQPX-29-01) of the programme Investissements d'Avenir supervised by the Agence Nationale pour la Recherche (project “liqsim”). NWChem calculations made use of the facilities of HECToR, the U.K. national high-performance computing service, which is provided by UoE HPCx Ltd at the University of Edinburgh, Cray Inc., and NAG Ltd and funded by the Office of Science and Technology through EPSRC's High End Computing Programme. Support from the ANR ILLA is also acknowledged (G. W.). The authors also thank all the participants of the “Dalton Discussion 14: Advancing the Chemistry of the f-elements” meeting for fruitful discussions.

Notes and references

1. (a) T. H. I. Siddal, J. Phys. Chem., 1960, 64, 1863; (b) G. M. Gasparini and G. Grossi, Sep. Sci. Technol., 1980, 15, 825; (c) C. Musikas and W. W. Schulz, in Principles and Practices of Solvent Extraction, ed. J. Rydberg, C. Musikas and G. R. Choppin, M. Dekker, Inc., New York, 1992, ch. 11, p. 413; (d) C. Musikas, N. Condamines and C. Cuillerdier, Anal. Sci., 1991, 7(Suppl.), 11; (e) P. N. Pathak, D. R. Prabhu, P. B. Ruikar and V. K. Mancha, Solvent Extr. Ion Exch., 2002, 20, 293; (f) M. Miguirditchian, C. Sorel, B. Cames, I. Bisel and P. Baron, in Global 2009, Paris, France, 2009, p. 1032.
2. F. Rodrigues, G. Ferru, L. Berthon, N. Boubals, P. Guilbaud, C. Sorel, O. Diat, P. Bauduin, J. P. Simonin, J. P. Morel, N. Morel-Desrosiers and M. C. Charbonnel, Mol. Phys., 2014, 112, 1362.
3. For X-ray structures of UO₂(NO₃)₂(RCONR^′₂)₂ complexes, see for instance Refcodes DOGZOO (R = C₁₁H₂₃, R′ = C₄H₉) and NOGTAF (R = iPrCH₂, R′ = iPr) in the Cambridge Crystallographic Database. DOGZOO: P. Charpin, M. Lance, M. Nierlich, D. Vigner, N. Descouls and C. Musikas, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1986, 42, 560 NOGTAF: S. Kannan, S. B. Deb, J. S. Gamare and M. G. B. Drew, Polyhedron, 2008, 27, 2557.
4. Y. Meridiano, L. Berthon, X. Crozes, C. Sorel, P. Dannus, M. R. Antonio, R. Chiarizia and T. Zemb, Solvent Extr. Ion Exch., 2009, 27, 607.
5. (a) J. B. Lewis, Nature, 1956, 178, 274; (b) H. T. Hahn, J. Am. Chem. Soc., 1957, 79, 4625; (c) F. Baumgärtner and L. Finsterwalder, J. Phys. Chem., 1970, 74, 108; (d) W. Nitsch, Faraday Discuss. Chem. Soc., 1984, 77, 85.
6. (a) P. Jungwirth and B. Winter, Annu. Rev. Phys. Chem., 2008, 59, 343; (b) F. Berny, R. Schurhammer and G. Wipff, Inorg. Chim. Acta, 2000, 300–302, 384; (c) I. Benjamin, Chem. Rev., 1996, 96, 1449; (d) T.-M. Chang and L. X. Dang, Chem. Rev., 2005, 106, 1305.
7. (a) G. Wipff, E. Engler, P. Guilbaud, M. Lauterbach, L. Troxler and A. Varnek, New J. Chem., 1996, 20, 403; (b) F. Berny, N. Muzet, R. Schurhammer, L. Troxler and G. Wipff, in Current Challenges in Supramolecular Assemblies, NATO ARW Athens, ed. G. Tsoucaris, Kluwer Acad. Pub., Dordrecht, 1998, p. 221; (c) M. Baaden, R. Schurhammer and G. Wipff, J. Phys. Chem. B, 2002, 106, 434.
8. (a) M. Baaden, M. Burgard and G. Wipff, J. Phys. Chem. B, 2001, 105, 11131; (b) M. Jayasinghe and T. L. Beck, J. Phys. Chem. B, 2009, 113, 11662.
9. (a) G. Benay and G. Wipff, J. Phys. Chem. B, 2013, 117, 7399; (b) G. Benay and G. Wipff, J. Phys. Chem. B, 2014, 118, 3133–3149.
10. N. H. Sagert and M. J. Quinn, J. Colloid Interface Sci., 1987, 115, 283.
11. G. Martin-Gassin, P. M. Gassin, L. Couston, O. Diat, E. Benichou and P. F. Brevet, Phys. Chem. Chem. Phys., 2011, 13, 19580.
12. N. Sieffert, M. Bühl, M.-P. Gaigeot and C. A. Morrison, J. Chem. Theory Comput., 2013, 9, 106.
13. H. Watarai, Trends Anal. Chem., 1993, 12, 313.
14. A. D. Becke, Phys. Rev. A, 1988, 38, 3098.
15. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter, 1988, 37, 785.
16. W. Küchle, M. Dolg, H. Stoll and H. Preuss, J. Chem. Phys., 1994, 100, 7535.
17. Generated automatically according to the procedure implemented in Gaussian 09.
18. Following the argument in R. L. Martin, P. J. Hay and L. R. Pratt, J. Phys. Chem. A, 1998, 102, 3565–3573 , where this simple procedure has been proposed as adjustment for the concentration of water molecules in the liquid, and where the necessary value for the pressure has been derived from the experimental density of liquid water. Such an elevated pressure is designed to model the change in entropy existing in the condensed phase when the number of particles varies during a given reaction.
19. (a) T. H. Dunning, J. Chem. Phys., 1989, 90, 1007; (b) R. A. Kendall, T. H. Dunning and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796.
20. A. D. Becke, J. Chem. Phys., 1993, 98, 5648.
21. (a) For the PBE0 functional see: C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158; (b) For the “–D3” correction see: S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
22. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215.
23. S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553.
24. A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378.
25. J. A. Pople, et al.Gaussian 09, Revision D.01, Gaussian, Inc., Pittsburgh, PA, 2009 (the full reference is given in ESI†).
26. M. Valiev, E. J. Bylaska, N. Govind, K. Kowalski, T. P. Straatsma, H. J. J. Van Dam, D. Wang, J. Nieplocha, E. Apra, T. L. Windus and W. A. de Jong, Comput. Phys. Commun., 2010, 181, 1477.
27. D. A. Pearlman, D. A. Case, J. W. Caldwell, W. S. Ross, T. E. Cheatham Iii, S. DeBolt, D. Ferguson, G. Seibel and P. Kollman, Comput. Phys. Commun., 1995, 91, 1.
28. W. L. Jorgensen and J. Tirado-Rives, J. Am. Chem. Soc., 1988, 110, 1657.
29. W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926.
30. P. Guilbaud and G. Wipff, J. Mol. Struct. (THEOCHEM), 1996, 366, 55.
31. W. D. Cornell, P. Cieplak, C. I. Bayly, I. R. Gould, K. M. Merz, D. M. Ferguson, D. C. Spellmeyer, T. Fox, J. W. Caldwell and P. A. Kollman, J. Am. Chem. Soc., 1995, 117, 5179.
32. (a) T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089; (b) U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577; (c) P. P. Ewald, Annalen der Physik, 1921, 369, 253; (d) T. Laino and J. Hutter, J. Chem. Phys., 2008, 129, 074102; (e) A. Y. Toukmaji and J. A. Board, Comput. Phys. Commun., 1996, 95, 73.
33. D. A. Case, T. A. Darden, T. E. Cheatham III, C. L. Simmerling, J. Wang, R. E. Duke, R. Luo, M. Crowley, R. C. Walker, W. Zhang, K. M. Merz, B. Wang, S. Hayik, A. Roitberg, G. Seabra, I. Kolossváry, K. F. Wong, F. Paesani, J. Vanicek, X. Wu, S. R. Brozell, T. Steinbrecher, H. Gohlke, L. Yang, C. Tan, J. Mongan, V. Hornak, G. Cui, D. H. Mathews, M. G. Seetin, C. Sagui, V. Babin and P. A. Kollman, AMBER 10, University of California, San Francisco, 2008.
34. J. VandeVondele, M. Krack, F. Mohamed, M. Parrinello, T. Chassaing and J. Hutter, Comput. Phys. Commun., 2005, 167, 103.
35. For more information on CP2K, see: http://www.cp2k.org (last accessed: November 2014).
36. A. Schafer, C. Huber and R. Ahlrichs, J. Chem. Phys., 1994, 100, 5829.
37. (a) S. Goedecker, M. Teter and J. Hutter, Phys. Rev. B: Condens. Matter, 1996, 54, 1703; (b) C. Hartwigsen, S. Goedecker and J. Hutter, Phys. Rev. B: Condens. Matter, 1998, 58, 3641; (c) M. Krack, Theor. Chem. Acc., 2005, 114, 145.
38. J. Rabone and M. Krack, Comput. Mater. Sci., 2013, 71, 157.
39. O. Hollóczki, Inorg. Chem., 2014, 53, 835.
40. R. Jonchiere, A. P. Seitsonen, G. Ferlat, A. M. Saitta and R. Vuilleumier, J. Chem. Phys., 2011, 135, 154503.
41. (a) S. Nosé, J. Chem. Phys., 1984, 81, 511; (b) G. J. Martyna, M. L. Klein and M. Tuckerman, J. Chem. Phys., 1992, 97, 2635; (c) W. G. Hoover, Phys. Rev. A, 1985, 31, 1695.
42. (a) T. Laino, F. Mohamed, A. Laio and M. Parrinello, J. Chem. Theory Comput., 2005, 1, 1176; (b) T. Laino, F. Mohamed, A. Laio and M. Parrinello, J. Chem. Theory Comput., 2006, 2, 1370.
43. (a) L. Genovese, T. Deutsch, A. Neelov, S. Goedecker and G. Beylkin, J. Chem. Phys., 2006, 125, 074105; (b) L. Genovese, T. Deutsch and S. Goedecker, J. Chem. Phys., 2007, 127, 054704.
44. M. Bühl, R. Diss and G. Wipff, Inorg. Chem., 2007, 46, 5196.
45. Due to program limitations, the so-called T₁-diagnostic (J. T. Lee and P. R. Taylor, Int. J. Quantum Chem. Symp., 1989, 23, 199–207) could not be printed after the CCSD calculations with NWChem. This property is an indication of possible shortcomings of the Hartree–Fock single-reference wavefunction. With a smaller basis set (no g-functions on U, aug-cc-pVDZ on O, C and N, cc-pVDZ on H), this diagnostic could be computed with Gaussian 09, where it amounted to 0.025 for 1a, 1b and 1c. This number is somewhat above the commonly used threshold for the need for a multi-determinantal ansatz (0.02), but similar to those computed for uranyl hydrate (ref. 48), for cis- and trans-uranyl complexes involved in the yl-exchange (ref. 65c) or uranyl peroxo complexes (ref. 67). Note that transition-metal complexes with T₁-values up to 0.05 have been classified as single-reference cases (W. Jiang, N. J. DeYonker and A. K. Wilson, J. Chem. Theor. Comput., 2012, 8, 460–468).
46. J. P. Austin, N. A. Burton, I. H. Hillier, M. Sundararajan and M. A. Vincent, Phys. Chem. Chem. Phys., 2009, 11, 1143.
47. (a) M. Buhl, N. Sieffert, V. Golubnychiy and G. Wipff, J. Phys. Chem. A, 2008, 112, 2428; (b) M. Bühl, N. Sieffert and G. Wipff, Chem. Phys. Lett., 2009, 467, 287; (c) M. Bühl, N. Sieffert, A. Chaumont and G. Wipff, Inorg. Chem., 2011, 50, 299; (d) M. Bühl, N. Sieffert, A. Chaumont and G. Wipff, Inorg. Chem., 2012, 51, 1943.
48. P. Wahlin, C. Danilo, V. Vallet, F. Réal, J.-P. Flament and U. Wahlgren, J. Chem. Theory Comput., 2008, 4, 569.
49. The total equatorial coordination number is defined here as a continuous function of metal–ligand distances: CN = ∑_Nwat(1 − (d^N_watU–O_wat/2.80)²⁵)/(1 − (d^N_watU–O_wat/2.80)⁵⁰) + ∑_Nnit(1 − (d^N_nitU–O_nit/3.10)²⁵)/(1 − (d^N_nitU–O_nit/3.10)⁵⁰) + ∑_NL(1 − (d^N_LU–O_L/2.90)²⁵)/(1 − (d^N_LU–O_L/2.90)⁵⁰) where N_wat, N_nit and N_L are the numbers of water, nitrate, and amide oxygens, respectively. N_wat = 0 (in 2.0.2a/b) or 1 (in 2.1.2c), N_nit = 6 and N_L = 2. Similarly, d^N_watU–O_wat, d^N_nitU–O_nit and d^N_LU–O_L are the N^th metal–water, metal–nitrate and metal–amide U–O distances, respectively (in angstrom).
50. M. Bühl, H. Kabrede, R. Diss and G. Wipff, J. Am. Chem. Soc., 2006, 128, 6357.
51. A. Laio and M. Parrinello, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 12562.
52. Time evolution of the collective variables and results of additional metadynamics simulations are provided in ESI (see Fig. S1 and S2†).
53. Experimental EXAFS data on 2.0.2a are available in the literature: in the case of more hydrophobic amide ligands, U–O_nit is 2.52 Å (see: T. Yaita, S. Suzuki, H. Narita, S. Tachimori, K. Takai, H. Motohashi and K. Kobayashi, Proccedings of the Workshop on Speciation, Techniques and Facilities for Radioactive Materials at Synchrotron Light Sources. 4–6 October 1998, Grenoble, France. pp. 325–330). EXAFS data are also available for a series of 2.0.2a analogues with several phosphate ligands (instead of amides) where U–O_nit distances range from 2.51 to 2.54 Å, depending on the ligand that is considered (see: C. Den Auwer, C. Lecouteux, M. C. Charbonnel, C. Madic and R. Guillaumont, Polyhedron, 1997, 16, 2233 and C. D. Auwer, M. C. Charbonnel, M. T. Presson, C. Madic and R. Guillaumont, Polyhedron, 1998, 17, 4507). These values are in good accord with the average calculated for 2.0.2a in bulk hexane (U–O_nit = 2.57(13) Å, see Table 4).
54. We note that the free energy difference of ca. 2 kcal mol⁻¹ between 2.0.2a and 2.0.2b obtained from metadynamics correlates well with the results of the unconstrained MDs presented in Fig. 1, from which the relative free energy between the two structures can be calculated from their relative populations (denoted P_2.0.2a/P_2.0.2b). We used the coordination number (CN) to discriminate between 2.0.2a and 2.0.2b, considering that 2.0.2a is populated when CN > 5.5 and 2.0.2b when CN ≤ 5.5. The relative free energy is computed as ΔG_{2.0.2a→2.0.2b} = −RT Ln(P_2.0.2b/P_2.0.2a) at T = 320 K. We found −1.7 kcal mol⁻¹ in DFT/MM-MD water, −1.1 kcal mol⁻¹ in DFT-MD water and −1.2 kcal mol⁻¹ at the interface.
55. M. Bühl, N. Sieffert, A. Partouche, A. Chaumont and G. Wipff, Inorg. Chem., 2012, 51, 13396.
56. V. Vallet and I. Grenthe, Solvent Extr. Ion Exch., 2013, 31, 358.
57. P. N. Pathak, L. B. Kumbhare and V. K. Manchanda, Solvent. Extr. Ion Exch., 2001, 19, 105.
58. Previous simulations of 2.0.2 complexes including the more hydrophobic “DEHiBA” ligands showed that the complexes are afforded at the interface and tend to spontaneously transfer to the bulk hexane phase. When at the interface, the solvation pattern of the 2.0.2 complexes with DEHiBA and with L are very similar: the amide groups sit “flat” on the water surface and the long alkyl chains are solubilized at the hexane side of the interface (see ref. 9a). As a result, our conclusions obtained with the simplified L ligand are expected to be transferable to real systems.
59. A. Prestianni, L. Joubert, A. Chagnes, G. Cote and C. Adamo, Phys. Chem. Chem. Phys., 2011, 13, 19371.
60. A value of log₁₀ β⁰₁ = 0.30 ± 0.15 has been estimated for the equilibrium constant in the aqueous system UO₂²⁺ + NO₃⁻ → UO₂NO₃⁺, see (a) I. Grenthe, J. Fuger, R. J. M. Konings, R. J. Lemire, A. B. Muller, C. Nguyen-trung and H. Wanner, in Chemical Thermodynamics Vol. 1: Chemical Thermodynamics of Uranium, ed. H. Wanner and I. Forest, Elsevier, Amsterdam, 1992. Formation constants for uranyl dinitrate complexes are shown to be smaller than those for the mononitrate by roughly one order of magnitude; for results from an extraction-based method see: (b) H. Lahr and W. Knoch, Radiochim. Acta, 1970, 13, 1; for results from a ¹H NMR spectroscopic study in water–acetone mixtures see: (c) A. Fratiello, V. Kubo, R. E. Lee and R. E. Schuster, J. Phys. Chem., 1970, 74, 3726.
61. S. de Houwer and C. Gorller-Walrand, J. Alloys Compd., 2001, 323, 683.
62. X. Ye, R. B. Smith, S. Cui, V. deAlmeida and B. Khomami, Solvent Extr. Ion Exch., 2010, 28, 1.
63. Recent classical MD simulations indeed indicate a driving force for the approach of 2.2.0 to the hexane/water interface in the presence of TBP (see Fig. 10 in ref. 9b).
64. See e.g.: (a) Y. Zhao and D. G. Truhlar, Org. Lett., 2007, 9, 1967; (b) Y. Zhao and D. G. Truhlar, J. Chem. Theory Comput., 2009, 5, 324; (c) N. Sieffert and M. Bühl, Inorg. Chem., 2009, 48, 4622; (d) Y. Minenkov, G. Occhipinti and V. R. Jensen, J. Phys. Chem. A, 2009, 113, 11833.
65. For comparisons of density functionals to model actinyl complexes, see e.g. (a) J. P. Austin, N. A. Burton, I. H. Hillier, M. Sundararajan and M. A. Vincent, Phys. Chem. Chem. Phys., 2009, 11, 1143; (b) F. P. Rotzinger, Chem. – Eur. J., 2007, 13, 800; (c) M. Bühl and G. Schreckenbach, Inorg. Chem., 2010, 49, 3821; (d) See also ref. 67.
66. The free energy of hydration of NO₃⁻ “in SMD-water” can be estimated as: ΔG°hyd(NO₃⁻) = E_SMD-water − E_gas = −61.3 kcal mol⁻¹ at the M06-2X/SDD+ level. This should be compared with the experimental value of −73.2 kcal mol⁻¹ reported in: Y. Marcus, Ion Solvation, Wiley-Interscience, Chichester, U.K., 1985. This result correlates with a tendency of the SMD model to undersolvate anions (see ref. 24), a feature that can lead to overestimated equilibrium constants compared to the experiment. For instance, the calculated free energy of reaction for 0.5.0 + 2NO₃⁻ → 2.2.0 + 3H₂O appears unreasonably large (−11.5 kcal mol⁻¹), presumably because the two nitrates are undersolvated in our SMD model. However, under extraction conditions, the aqueous phase contains a large amount of nitric acid (at ca. 3 M) in such a way that 2.2.0 should still be significantly populated. As a result, the path-2 depicted in Fig. 6 should be realistic. We also note that modelling the free energy of hydration of uranyl–hydrate complexes (such as 0.5.0) by implicit solvation models is also particularly challenging, as shown e.g. in: K. E. Gutowski and D. A. Dixon, J. Phys. Chem. A, 2006, 110, 8840 , and ideally requires the addition of several second-shell water molecules. All these issues justify the use of more elaborate approaches, such as the DFT/MM-MD and DFT-MD simulations undertaken herein, in which the presence of the solvent and the dynamics of the systems are explicitly accounted for.
67. M. Bühl, N. Sieffert and G. Wipff, Dalton Trans., 2014, 43, 11129.
68. (a) I. Benjamin, J. Phys. Chem. B, 2013, 117, 4325; (b) A. G. Volkov, D. W. Deamer, D. L. Tanelian and V. S. Markin, Liquid Interfaces in Chemistry and Biology, John Wiley & Sons, Inc., New York, 1998.

---

Footnote

† Electronic supplementary information (ESI) available: Atomic charges on L (Table S1), reaction free energies at the BLYP-D3/SDD+ and M06-2X/SDD+ levels (Table S2), time of evolution of the collective variable in metadynamics simulations (Fig. S1), additional free energy surfaces obtained from longer metadynamics simulations (Fig. S2 and S3) and Cartesian coordinates of all complexes optimized at the BLYP-D3/SDD level. See DOI: 10.1039/c4dt02443e

---