Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A computational analysis of the apparent nido vs. hypho conflict: are we dealing with six- or eight-vertex open-face diheteroboranes?†‡
João Pedro F.
Nunes
a,
Josef
Holub
b,
David W. H.
Rankin
c,
Derek A.
Wann
*a and
Drahomír
Hnyk
*b
aDepartment of Chemistry, University of York, Heslington, York YO10 5DD, UK. E-mail: derek.wann@york.ac.uk
bInstitute of Inorganic Chemistry of the Academy of Sciences of the Czech Republic, v.v.i., 250 68 Husinec-Řež, Czech Republic. E-mail: hnyk@iic.cas.cz
cSchool of Chemistry, University of Edinburgh, Joseph Black Building, David Brewster Road, Edinburgh, EH9 3FJ, UK
First published on 8th June 2015
Abstract
A series of computational studies have been undertaken to investigate the electronic structures and bonding schemes for six hetero-substituted borane cages, all of which have been presented in the literature as potential hypho structures. The six species are hypho-7,8-[C2B6H13]− (1a), hypho-7,8-[CSB6H11]− (1b), hypho-7,8-[S2B6H9]− (1c), hypho-7,8-[NSB6H11] (1d), exo-7-Me-hypho-7,8-[NCB6H12] (1e), and endo-7-Me-hypho-7,8-[NCB6H12] (1f) and the so-called mno rule has been applied to each of them. As no structural data are known for the carbathia-, azathia-, and dithiahexaboranes, we have also applied the ab initio/GIAO/NMR structural tool for 1b–1d, with 1c having been prepared for this purpose. We conclude that an mno count of 10 means that 1a, 1b, 1d, 1e, and 1f should be termed pseudo-nido or pseudo-hypho. Only 1c can be considered to be correctly termed hypho-7,8-[S2B6H9]−.
Introduction
Polyhedral boranes and heteroboranes have long provided interest covering a range of chemical research,1 where their unexpected structures, innovative bonding schemes, and unusual chemical properties have resulted in them being considered promising candidates for use in medicinal and materials applications. For decades now an understanding of the molecular architectures of these species has led directly and indirectly to practical uses for boranes and future structural studies will undoubtedly lead to potential further uses being identified.The variety of bonding schemes exhibited by polyhedral boranes and heteroboranes was initially noted by Lipscomb,2 with Williams3 and Wade4 also making significant contributions. Williams reported a major breakthrough by recognising that the experimentally isolated nido, arachno, and hypho boranes could be derived from the nearest closo structures by the removal of one, two, and three {BH}2− vertices, respectively. This led to the derivation of Wade's n + 1 electron-pair rule for a closo-type cluster, where n is the number of vertices.4,5 Subsequently, the number of skeletal electron pairs required for stable nido, arachno, and hypho skeletons was determined to be n + 1 + p, where p is the number of missing vertices; it follows that closo-[BnHn]2− requires such a formal charge to comply with Wade's rule. It should be noted that closo systems are known experimentally for n = 5–12, where the icosahedral cluster with Ih point-group symmetry (n = 12) is the most stable of the closo series.
The unusually high stability of closo-[B12H12]2−, as well as the existence of condensed B12 units [for example, in the so-called macropolyhedral boron clusters B20H16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6 and B21H18− (ref. 7)], meant that a generalisation of the electron-counting rules was required since such structures are beyond the scope of the Williams–Wade formalism. A generally applicable electron-counting rule – the so-called mno rule – was derived by Jemmis;8 based on Hückel's rule it allows the structures of macropolyhedral boranes and metallaboranes to be characterised alongside simple boranes. According to the mno rule, m + n + o electron pairs are necessary for a macropolyhedral system to be stable, where m is the number of individual polyhedral subclusters from which a macropolyhedral cluster is composed, n is the number of vertices, and o is the number of single-vertex-sharing condensations. For nido, arachno, and hypho arrangements, one, two, and three additional pairs of electrons are required. Wade's n + 1 rule can be considered as a special case of the mno rule, where m = 1 and o = 0.
6 and B21H18− (ref. 7)], meant that a generalisation of the electron-counting rules was required since such structures are beyond the scope of the Williams–Wade formalism. A generally applicable electron-counting rule – the so-called mno rule – was derived by Jemmis;8 based on Hückel's rule it allows the structures of macropolyhedral boranes and metallaboranes to be characterised alongside simple boranes. According to the mno rule, m + n + o electron pairs are necessary for a macropolyhedral system to be stable, where m is the number of individual polyhedral subclusters from which a macropolyhedral cluster is composed, n is the number of vertices, and o is the number of single-vertex-sharing condensations. For nido, arachno, and hypho arrangements, one, two, and three additional pairs of electrons are required. Wade's n + 1 rule can be considered as a special case of the mno rule, where m = 1 and o = 0.
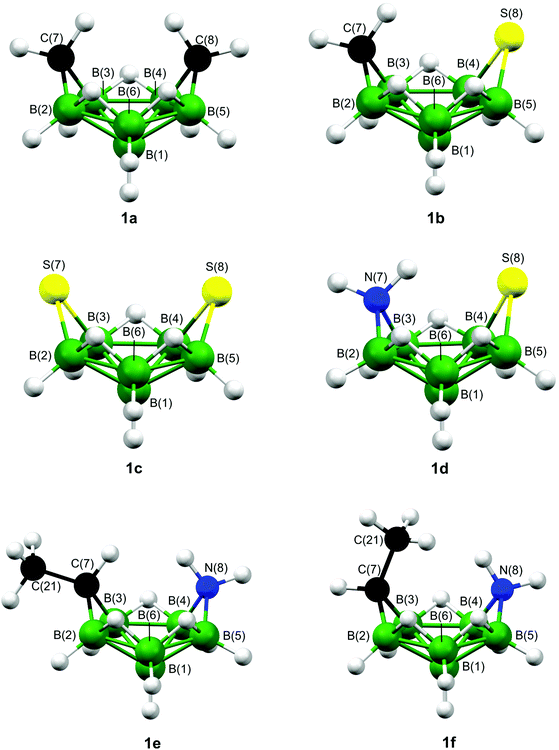
Some hypho and nido complexes have very similar structures and electronic structure investigation would seem sensible to ensure clusters are not wrongly classified. In this work we have performed ab initio and DFT analyses of the bonding schemes for six potential hypho structures {hypho-7,8-[C2B6H13]− (1a), hypho-7,8-[CSB6H11]− (1b), hypho-7,8-[S2B6H9]− (1c), hypho-7,8-[NSB6H11] (1d), exo-7-Me-hypho-7,8-[NCB6H12] (1e), and endo-7-Me-hypho-7,8-[NCB6H12] (1f)}, also employing the mno rule to see what results it yields. All six structures are shown in Fig. 1, while Fig. S1‡ also gives the hydrogen-atom numbering. As no structural data are currently available for the carbathia-, azathia-, and dithiahexaboranes, we have also applied the ab initio/GIAO/NMR structural method to 1b–1d.
Experimental section
NMR
Experimental 11B NMR chemical shifts for 1b and 1d were taken from ref. 9 and 10, respectively; 1c was prepared according to ref. 11.Quantum chemical calculations
The geometries of closo-[B11H11]2− (cB11), nido-[B10H10]4− (nB10) and arachno-[B9H9]6−(aB9) were fully optimised using Gaussian09.12 Each of these structures, as well as that of the related hypho species (hB8), is depicted in Scheme 1. (The scheme is reproduced in Fig. S2,‡ where the atom numbering is given.) The geometry optimisations for each of cB11, nB10, and aB9 were performed at the B2PLYP,13 MP2,14–18 B98,19 B97d,20 PBE,21,22 PW91,23–27 and HFS28–30 levels of theory using the 6-311+G(d,p)31,32 basis set on all atoms; the nature of any stationary points on the potential-energy surfaces were investigated using frequency calculations. The initial geometries for nB10 and aB9 were optimised from geometries obtained by removing one and two vertices from cB11, respectively, using GaussView 5.0.33 The bonding orbitals for cB11, nB10, and aB9 were investigated using natural bond orbital (NBO) analyses to look for three-centre bonds and resonance structures.The geometries of the heteroboranes 1a–1f were also fully optimised using Gaussian09 and the method and basis set combinations described above, with the character of each stationary point verified by frequency calculations. Magnetic shieldings were calculated for 1b–1d by running GIAO34 jobs with TZP basis set II by Huzinaga,35 which is well suited for this purpose. In order to investigate the relationships between 1a–1f and their true borane analogues, the heteroatoms for each borane cage were replaced by hydrogen atoms using GaussView 5.0. The geometries of the species formed by the inclusion of hydrogen atoms in place of heteroatoms were optimised using the same levels of theory and basis sets previously employed, and frequency calculations were performed to verify the nature of any stationary points; the distances between the substituted hydrogen atoms and the boron-cage atoms were fixed at values optimised for the B–C/N/S distances. NBO analyses were also performed for all of the H-substituted structures.
Calculating mno values
The mno rule is used to determine the number of pairs of electrons required for a species to be considered stable by calculating m + n + o (for the meanings of m, n, and o, see above). As an illustration the mno rule is applied to an icosahedral borane by taking the values m = 1, n = 12, and o = 0, yielding m + n + o = 13 electron pairs, the same result as the n + 1 electron-pair rule. Each vertex with one terminal atom contributes all-but-one of its electrons to cluster bonding, with the remaining electron involved in the exo covalent bond. However, in the three isomeric icosahedral carbaboranes closo-C2B10H12, the BH groups each donate one pair of electrons and each CH moiety contributes three electrons (1.5 electron pairs) to the polyhedral bonding, thus satisfying the mno rule [i.e. 10 + (2 × 1.5) = 13 for these neutral carbaboranes].36 Similarly, in the icosahedral azaborane closo-NB11H12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 37 there are eleven BH groups that contribute eleven electron pairs as well as an NH group that donates two electron pairs to the skeletal bonding. Considering molecules containing third-row elements, the neutral icosahedral closo-SB11H11 thiaborane is known,38 in which BH groups provide eleven electron pairs; sulfur has a tendency to retain one of its lone pairs, contributing four electrons (two electron pairs) to the cluster.
37 there are eleven BH groups that contribute eleven electron pairs as well as an NH group that donates two electron pairs to the skeletal bonding. Considering molecules containing third-row elements, the neutral icosahedral closo-SB11H11 thiaborane is known,38 in which BH groups provide eleven electron pairs; sulfur has a tendency to retain one of its lone pairs, contributing four electrons (two electron pairs) to the cluster.
The following closo dianions, presented in order of stability, B12H122−, B11H112−, and B5H52−, can be used to derive nido, arachno, and hypho heteroboranes via the removal and substitution of vertices.39 However, according to the Williams–Wade concept, heteroboranes cannot exist with two, three, or four BH moieties. Closo-[B5H5]2− is, therefore, not a suitable “parent” species for any of the nido, arachno, or hypho heteroborane structures.
There are heteroboranes with molecular shapes based on nido-[B10H10]4− (nB10)40 and arachno-[B9H9]6− (aB9),41 which are derived from the C2v-symmetric closo-[B11H11]2− (cB11), as shown in Scheme 1. As well as closo, nido, and arachno clusters, Scheme 1 depicts the hypothetical hypho-[B8H8]8− (hB8). In contrast, our so-called hypho eight-vertex-type heteroboranes resemble the six-vertex arrangement adopted by nido-[B6H11]+ (nB6),42 shown in Fig. 2. (Fig. S3‡ depicts the same structure but also includes hydrogen-atom numbering.)
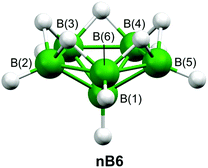 | ||
| Fig. 2 The molecular structure of nido-[B6H11]+, whose structure resembles a hypho eight-vertex heteroborane. For clarity hydrogen-atom numbering has been omitted. | ||
The molecule hypho-7,8-[C2B6H13]− (1a) has previously been structurally characterised by applying the ab initio/GIAO/NMR structural tool,43 which confirmed its Cs-symmetric “helmet-like” structure (Fig. 1). Three other proposed hypho species (also shown in Fig. 1) have been calculated to have the same structural motif as 1a; these are hypho-7,8-[CSB6H11]− (1b),9hypho-7,8-[S2B6H9]− (1c),11 and hypho-7,8-[NSB6H11] (1d).10 The last of these examples (1d) illustrates how nitrogen can be accommodated in an eight-vertex hypho arrangement, with the same arrangement found in exo- and endo-7-Me-hypho-7,8-[NCB6H12] (1e and 1f, respectively). Again, GIAO calculations of the shielding tensors have been used for structural characterisation.44
Results and discussion
Calculations were initially performed to investigate the bonding patterns of the parent cB11, nB10, aB9, and hB8 systems, as shown in Scheme 1. Apart from the standard HF calculations perturbed with the MP2 model chemistry, we employed six density functional theory (DFT) approaches to span all the possibilities afforded by DFT, i.e. B98 (stand-alone hybrid functional), B97D (stand-alone pure functional), HFS (exchange-only functional), PW91 (correlation functional), PBE (exchange-combined functional), and B2PLYP (double-hybrid functional), the latter utilising HF exchange and an MP2-like correlation. All seven model chemistries used the 6-31G(d) basis set for the initial geometry optimisations. However, all attempts to identify a minimum on the potential-energy hypersurface of hB8 failed because of the formation of either a series of flattened triangular borane architectures or a random assembly of eight boron atoms. The final basis set used for optimising cB11, nB10, and aB9 was 6-311G(d,p). Cartesian coordinates for these structures are given in Tables S1–S3.‡ Attempts to use extra diffuse functions on these basis sets caused the optimisations to diverge. Second-derivative analyses of these systems showed that they represented minima on the respective potential-energy hypersurfaces. The seven model chemistries were also used to calculate Hartree–Fock and Kohn–Sham natural orbitals and no two-centre two-electron (2c–2e) bonds were predicted for the cage motifs, only for the terminal B–H bonds.In order to get a deeper insight into the bonding patterns of 1a–1f, we performed entirely the same computational procedures as for cB11, nB10, aB9, and hB8. All of these diheterohexaboranes structures were identified as potential minima at ab initio and all DFT levels. Cartesian coordinates relating to the MP2/6-311+G(d,p) calculations are given in Tables S4–S9.‡ The strong resemblance of each of the 1a–1f molecular geometries to that of nido-[B6H11]+ prompted us to replace each heteroatom with a hydrogen atom (Hr), with the B–Hr distances fixed at the values optimised for the B–C/N/S bond lengths. Any substituents originally bonded to C or N were omitted. The new structures generated were termed 1a/H-1e/H (no calculations were required for 1f/H which is identical to 1e/H). The structure of nido-[B6H11]+ (Fig. 2) was calculated as a comparison as it has the same arrangement of H-bridges; Cartesian coordinates relating to its geometry at the MP2/6-311+G(d,p) level are given in Table S10.‡ As might be expected, frequency calculations performed for each of 1a/H-1e/H showed imaginary frequencies relating to the Hr atoms.
Performing NBO analyses for each of 1a/H-1e/H revealed that three-centre two-electron (3c–2e) bonding is present throughout each of the clusters, i.e. also in B–Hr–B bridges. When these structures were allowed to relax further by optimising the B–Hr distances, 3c–2e bonding persisted for all five species 1a/H-1e/H. The geometry optimisations performed using the 6-311+G** basis sets demonstrate that 3c–2e bonding exists regardless of the lengths of the B–H bridging distances; this was true for all seven methods employed. Similar analyses for 1a–1f (where the heteroatoms are present) showed a different picture, where all B–C/N/S distances were classified as 2c–2e bonds. If the NBO analyses had revealed 2c–2e bonds for B–Hr–B bridges in 1a/H-1e/H, we could have stated that the heteroatoms present in 1a–1f were not part of multicentre bonding. However, as this was not the case, we therefore had to follow another way of finding the nature of bonding in 1a–1f.
Table 1 shows the hybridisation of the heteroatoms in 1a–1f when transforming canonical orbitals to natural ones using NBO analysis. (Such calculations were performed for all levels of theory specified in the Experimental section and then averaged. The range of values is also shown. The characters and hybridisations of the B–C/N/S bonds for each of 1a–1f at all levels of theory are given in Tables S11–S13.‡) Table 1 shows that the heteroatoms in each species are more or less sp3-hybridised, as is the case for textbook examples such as CH4, NH3, and H2S. This means that, as well as 2c–2e bonds to boron atoms, all of the heteroatoms are covalently bonded to hydrogen atoms and any carbon atoms that are external to the cage motif. In addition, NBO analyses showed that heteroatoms in 1a–1f are negatively charged. The average calculated charges are presented in Table 2 (with the corresponding values for each level of theory in Table S14‡) and are in line with those values for classical covalent species such as CH4, NH3, and H2S. However, such an observation is in contrast to the electron distribution experimentally determined for the icosahedral species, in which the midpoint of CC vector and sulfur atom were found to be positively charged as revealed by vector algebra of experimental dipole moments measured for the exo-substituted icosahedra.36d,38b
| Bond | s character/% | p character/% | Hybridisationb | |
|---|---|---|---|---|
| a The characters and hybridisations from each of the individual calculations are given in Tables S11–S13. b The errors quoted are the standard deviation of the values calculated for the different model chemistries. | ||||
| 1a | B(2)–C(7) | 28.45 | 71.53 | 2.51 ± 0.01 |
| B(3)–C(7) | 26.84 | 73.14 | 2.73 ± 0.06 | |
| B(4)–C(8) | 26.84 | 73.14 | 2.73 ± 0.06 | |
| B(5)–C(8) | 28.45 | 71.53 | 2.51 ± 0.01 | |
| 1b | B(2)–C(7) | 28.62 | 71.34 | 2.49 ± 0.01 |
| B(3)–C(7) | 26.08 | 73.89 | 2.83 ± 0.07 | |
| B(4)–S(8) | 16.96 | 82.87 | 4.91 ± 0.37 | |
| B(5)–S(8) | 18.49 | 81.22 | 4.40 ± 0.24 | |
| 1c | B(2)–S(7) | 18.50 | 81.31 | 4.40 ± 0.23 |
| B(3)–S(7) | 16.72 | 83.10 | 4.99 ± 0.36 | |
| B(4)–S(8) | 16.72 | 83.10 | 4.99 ± 0.36 | |
| B(5)–S(8) | 18.50 | 81.31 | 4.40 ± 0.23 | |
| 1d | B(2)–N(7) | 29.38 | 70.61 | 2.40 ± 0.02 |
| B(3)–N(7) | 27.46 | 72.53 | 2.64 ± 0.06 | |
| B(4)–S(8) | 16.61 | 83.20 | 5.02 ± 0.32 | |
| B(5)–S(8) | 17.08 | 82.71 | 4.86 ± 0.32 | |
| 1e | B(2)–C(8) | 26.28 | 73.70 | 2.80 ± 0.03 |
| B(3)–C(8) | 25.80 | 74.19 | 2.88 ± 0.05 | |
| B(4)–N(7) | 28.69 | 71.31 | 2.49 ± 0.05 | |
| B(5)–N(7) | 29.48 | 70.52 | 2.39 ± 0.02 | |
| 1f | B(2)–C(8) | 26.12 | 73.85 | 2.83 ± 0.03 |
| B(3)–C(8) | 26.00 | 73.98 | 2.85 ± 0.05 | |
| B(4)–N(7) | 28.49 | 71.50 | 2.51 ± 0.05 | |
| B(5)–N(7) | 29.41 | 70.59 | 2.40 ± 0.02 | |
| Atom | Chargeb | |
|---|---|---|
| a The charges from each of the individual calculations are given in Table S14. b The errors quoted are the standard deviation of the values calculated for the different model chemistries. | ||
| 1a | C(7) | –0.92 ± 0.02 |
| C(8) | –0.92 ± 0.02 | |
| 1b | C(7) | –0.91 ± 0.02 |
| S(8) | –0.27 ± 0.03 | |
| 1c | S(7) | –0.22 ± 0.03 |
| S(9) | –0.22 ± 0.03 | |
| 1d | N(7) | –0.95 ± 0.02 |
| S(8) | –0.18 ± 0.04 | |
| 1e | N(7) | –0.93 ± 0.02 |
| C(8) | –0.73 ± 0.02 | |
| 1f | N(7) | –0.94 ± 0.02 |
| C(8) | –0.74 ± 0.02 | |
Armed with these results, we applied the mno rule to nido-[B6H11]+ as well as to 1a–1f. For nido-[B6H11]+m = 1, n = 6, o = 0, and p = 1, meaning that eight electron pairs are required to stabilise this system. There are six B–H fragments, each of which contributes one electron pair. The remaining two electron pairs are available from the five bridging hydrogen atoms with one spare electron present; the total number of electron pairs is 6 + 2.5 = 8.5. As there is one excess electron the hypothetical nido-[B6H11]+ is obviously a cation. (For nido-B6H10 we have eight electron pairs and, consequently, the molecule is neutral.)
To apply the mno rule to 1a–1f we need to determine whether they adopt a hypho or a nido electron count. Let's start by supposing that they are considered to be hypho, giving m = 1, n = 8, o = 0, p = 3, meaning that 12 electron pairs are required. In order to comply with a hypho electron count the heteroatoms must contribute the following number of electron pairs: sulfur 2, carbon 2, and nitrogen 2.5 for the charges to be “hypho” correct.
Therefore, for 1a we have 7.5 + 4 = 11.5 electron pairs, thus requiring one extra electron to stabilise the system. This Cs skeleton is therefore characterised with a single negative charge. The same applies to the other non-nitrogen-containing compounds (1b and 1c), where sulfur and/or carbon contributes 4 electron pairs, resulting in an overall single negative charge for these species. However, such electron pair contributions from the heteroatoms are in conflict with the NBO results shown in Table 1, where C, N, and S are more or less sp3-hybridised and are connected to the boron atoms by conventional 2c–2e bonds. Moreover, the carbon and nitrogen atoms are not naked, but rather are bonded also to two exo atoms or groups, i.e. the corresponding one electron pair from each of these heteroatoms cannot contribute to the skeletal moieties.
Secondly, we may formally consider 1a–1f to be nido clusters, where values of n = 6, m = 1, o = 0, and p = 1 yields an mno value of eight and, consequently, eight electron pairs are required to stabilise these molecules, as was the case for nido-[B6H11]+. In the latter, six B–H bonds contribute six electron pairs, and five hydrogen bridges contribute 2.5 electron pairs, i.e. this system must have a single positive charge (6 + 2.5 = 8.5 and so one electron must be removed to get 8). There is also another hypothetical system, nido-[B6H9]−, which has three H-bridges and complies with the mno rule (mno = 8; 6 + 1.5 = 7.5, so the formal charge is −1). On that basis, there is no scope for the two additional bridging bonds that would be required for this to be a nido system with a single negative charge. Such a charge is, however, unambiguously observed for 1a, 1b, and 1c, in which there are five bridges (three B–H–B bridges and two B–C/S–B bridges). The same argument can be applied to relate the neutral molecules 1d, 1e, and 1f to nido-B6H10 (6 + 4/2 = 8; there is no scope for further bridge-type bonding to comply simultaneously with the nido electron count requirement and to keep the system neutral).
Only 1c can truly be considered to be correctly classified as hypho-7,8-[S2B6H9]−, since 1c can afford to accept four electron pairs from the sulfur atoms into cluster bonding leaving one lone pair of electrons on each sulfur atom.
We must therefore conclude that 1a, 1b, 1d, 1e, and 1f are, in reality, neither formally hypho skeletons nor nido structures. To be formally hypho, an mno value of 12 should be satisfied for 1a, 1b, 1d, 1e, and 1f. Moreover, we would actually need to have an mno value of 10 to “accommodate” two extra B–C/N/S–B bridges and to comply with nido requirement. Since each of 1a, 1b, 1d, 1e and 1f is analysed in terms of having a mno value of 12 or 8 (and not 10), we might call these systems pseudo-nido or pseudo-hypho. As stated above, 1c can be correctly classified as hypho-7,8-[S2B6H9]−.
Small clusters are known to be very sensitive to the inclusion of electron dynamic correlation when shielding tensors are being calculated.45 The GIAO-MP2 calculations predict 11B chemical shifts that compare well with experimental values. Table 3 compares computed and experimental 11B chemical shifts for 1b–1d.
| Vertex | ||||||
|---|---|---|---|---|---|---|
| B(1) | B(3) | B(6) | B(4) | B(2) | B(5) | |
| a GIAO-MP2/II//6-311+G**. b Measured in CDCl3. c Ref. 9. d This work. e Ref. 10. | ||||||
| 1b GIAOa | −56.5 | −36.3 | −33.5 | −25.1 | −4.6 | 3.1 |
| Exp.b,c | −54.8 | −33.2 | −29.4 | −23.9 | −3.1 | 2.0 |
| 1c GIAOa | −55.8 | 5.3 | −26.1 | −31.4 | −26.1 | 5.3 |
| Exp.b,d | −52.2 | 6.8 | −22.4 | −25.0 | −22.4 | 6.8 |
| 1d GIAOa | −56.3 | −26.4 | −24.9 | −21.7 | −2.0 | 2.2 |
| Exp.b,e | −55.1 | −25.6 | −22.4 | −20.8 | −1.6 | 1.8 |
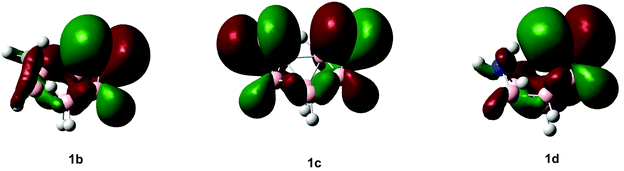
While the computed and experimental 11B NMR chemical shifts generally compare well, the presence of sulfur in 1b–1d makes these fits for some atoms slightly worse than for clusters reported in the literature that do not contain a third-row element. Such discrepancies can be attributed to the inadequacy of using a triple-zeta Huzinaga type-II basis set on sulfur.46 The most striking features of the individual spectra are shifts to low frequencies for the “bottom” boron atom, B(1). When comparing these values we clearly see the difference between the nature of the 11B chemical shifts for B(2) and B(3) in 1b and 1d and those of 1c. Inspecting the highest occupied molecular orbitals (HOMOs; see Fig. 3) for 1b–1d offers an explanation in terms of the entirely different shieldings of B(2) and B(3) when comparing 1b and 1d with Cs-symmetric 1c.
The decent agreement between theory and experiment suggests that MP2/6-311+G(d,p) geometries serve as valid representations of the molecular geometries in solution, which are characterised by very long B–B distances (values are between 1.94 and 1.98 Å) bridged by heteroatoms.
Conclusions
According to these computational efforts, we have concluded that hypho-7,8-[S2B6H9]− (1c) is correctly classified as a formal hypho structure. However, the other compounds studied here should be considered as pseudo-hypho or pseudo-nido, i.e. there is a nido vs. hypho conflict, and also a disagreement with the literature. Conceivably, according to the mno rule all valence electrons of carbon and nitrogen are accounted for in skeletal bonding when assuming hypho electron count. On the contrary, we would need to have 10 electron pairs instead of eight to comply with the formal nido electron count while also having sufficient electrons to allow for the bonding of carbon and nitrogen cage atoms to exo carbon and hydrogens atoms. The fact that hypho-[B8H8]8− has been shown not to exist complements such a conclusion.Acknowledgements
D.A.W. thanks the EPSRC for funding a Career Acceleration Fellowship (EP/I004122), and for partially funding, along with the Department of Chemistry, University of York, a studentship for J.P.F.N. We acknowledge the use of the EPSRC National Service for Computational Chemistry Software hosted at Imperial College in carrying out this work, which also made use of the York Advanced Research Computing Cluster (YARCC) provided by the University of York. We acknowledge the Czech Science Foundation (project number P207/11/07505) for financial support. All data supporting this study are provided either in the results section of this paper or as supplementary information accompanying this paper.References
- See, for example,
(a) K. Wade, Polymer, 1997, 38, 4539 CrossRef
; (b) J. M. Oliva, D. J. Klein, P. v. R. Schleyer and L. Serano-Andres, Pure Appl. Chem., 2009, 81, 719 CrossRef CAS
; and many other references emerging these days.
- W. N. Lipscomb, Adv. Inorg. Chem. Radiochem., 1950, 1, 117 Search PubMed
.
- R. E. Williams, Adv. Inorg. Chem. Radiochem., 1976, 18, 67 CAS
.
-
(a) K. Wade, J. Chem. Soc. D, 1971, 792 RSC
; (b) K. Wade, Adv. Inorg. Chem. Radiochem., 1976, 18, 1 CAS
.
- K. Wade, Inorg. Nucl. Chem. Lett., 1972, 8, 563 CrossRef CAS
.
- D. Hnyk, J. Holub, T. Jelínek, J. Macháček and M. G. S. Londesborough, Collect. Czech. Chem. Commun., 2010, 75, 1115 CrossRef CAS
, and references therein.
- E. Bernhardt, D. J. Brauer, M. Finze and H. Willner, Angew. Chem., Int. Ed., 2007, 46, 2927 CrossRef CAS PubMed
.
- See, for example,
(a) M. M. Balakrishnarajan and E. D. Jemmis, J. Am. Chem. Soc., 2000, 122, 4516 CrossRef CAS
; (b) E. D. Jemmis, M. M. Balakrishnarajan and P. D. Pancharatna, J. Am. Chem. Soc., 2001, 123, 4313 CrossRef CAS PubMed
.
- J. Holub, J. D. Kennedy, T. Jelínek and B. Štíbr, J. Chem. Soc., Dalton Trans., 1994, 1317 RSC
.
- T. Jelínek, J. D. Kennedy and B. Štíbr, J. Chem. Soc., Chem. Commun., 1993, 1628 RSC
.
- S. O. Kang and L. G. Sneddon, J. Am. Chem. Soc., 1989, 111, 3281 CrossRef CAS
.
-
M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford, CT, 2013 Search PubMed
.
- S. Grimme, J. Chem. Phys., 2006, 124, 034108 CrossRef PubMed
.
- M. Head-Gordon, J. A. Pople and M. J. Frisch, Chem. Phys. Lett., 1988, 153, 503 CrossRef CAS
.
- S. Saebø and J. Almlöf, Chem. Phys. Lett., 1989, 154, 83 CrossRef
.
- M. J. Frisch, M. Head-Gordon and J. A. Pople, Chem. Phys. Lett., 1990, 166, 275 CrossRef CAS
.
- M. J. Frisch, M. Head-Gordon and J. A. Pople, Chem. Phys. Lett., 1990, 166, 281 CrossRef CAS
.
- M. Head-Gordon and T. Head-Gordon, Chem. Phys. Lett., 1994, 220, 122 CrossRef CAS
.
- H. L. Schmider and A. D. Becke, J. Chem. Phys., 1998, 108, 9624 CrossRef CAS PubMed
.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787 CrossRef CAS PubMed
.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS
.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396 CrossRef CAS
.
-
J. P. Perdew, in Electronic Structure of Solids ‘91, ed. P. Ziesche and H. Eschrig, Akademie Verlag, Berlin, 1991, p. 11 Search PubMed
.
- J. P. Perdew, J. A. Chevary, S. H. Vosko, K. A. Jackson, M. R. Pederson, D. J. Singh and C. Fiolhais, Phys. Rev. B: Condens. Matter, 1992, 46, 6671 CrossRef CAS
.
- J. P. Perdew, J. A. Chevary, S. H. Vosko, K. A. Jackson, M. R. Pederson, D. J. Singh and C. Fiolhais, Phys. Rev. B: Condens. Matter, 1993, 48, 4978 CrossRef CAS
.
- J. P. Perdew, K. Burke and Y. Wang, Phys. Rev. B: Condens. Matter, 1996, 54, 16533 CrossRef CAS
.
-
K. Burke, J. P. Perdew and Y. Wang, in Electronic Density Functional Theory: Recent Progress and New Directions, ed. J. F. Dobson, G. Vignale and M. P. Das, Plenum, 1998 Search PubMed
.
- P. Hohenberg and W. Kohn, Phys. Rev. B, 1964, 136, 864 CrossRef
.
- W. Kohn and L. J. Sham, Phys. Rev. A, 1965, 140, 1133 CrossRef
.
-
J. C. Slater, The Self-Consistent Field for Molecular and Solids, Quantum Theory of Molecular and Solids, McGraw-Hill, New York, 1974, vol. 4 Search PubMed
.
- R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650 CrossRef CAS PubMed
.
- T. Clark, J. Chandrasekhar and P. v. R. Schleyer, J. Comput. Chem., 1983, 4, 294 CrossRef CAS PubMed
.
- http://www.gaussian.com/g_tech/gv5ref/gv5ref_toc.htm .
-
(a) R. Ditchfield, Mol. Phys., 1974, 27, 789 CrossRef CAS PubMed
; (b) K. Wolinski, J. F. Hinton and P. Pulay, J. Am. Chem. Soc., 1990, 112, 8251 CrossRef CAS
; (c) J. Gauss, J. Chem. Phys., 1993, 99, 3629 CrossRef CAS PubMed
.
-
W. Kutzelnigg, U. Fleischer and M. Schindler, NMR Principles and Progress, Springer, Berlin, 1990 Search PubMed
.
- Structural data accumulated on the three dicarbadodecaboranes 1,2-, 1,7-, and 1,12-C2B10H12 are exemplified in the following publications:
(a) A. R. Turner, H. E. Robertson, K. B. Borisenko, D. W. H. Rankin and M. A. Fox, Dalton Trans., 2005, 1310 RSC
; (b) S. Samdal, H. Møllendal, D. Hnyk and J. Holub, J. Phys. Chem. A, 2011, 115, 3380 CrossRef CAS PubMed
; (c) A. R. Campanelli, A. Domenicano and D. Hnyk, J. Phys. Chem. A, 2015, 119, 205 CrossRef CAS PubMed
; (d) For the charge distribution in the 1,2-isomer see: D. Hnyk, V. Všetečka, L. Drož and O. Exner, Collect. Czech. Chem. Commun., 2001, 66, 1375 CrossRef CAS
.
- D. Hnyk, M. Bühl, P. v. R. Schleyer, H. V. Volden, S. Gundersen, J. Müller and P. Paetzold, Inorg. Chem., 1993, 32, 2442 CrossRef CAS
.
-
(a) D. Hnyk, E. Vajda, M. Bühl and P. v. R. Schleyer, Inorg. Chem., 1992, 31, 2464 CrossRef CAS
; (b) J. Macháček, J. Plešek, J. Holub, D. Hnyk, V. Všetečka, I. Císařová, M. Kaupp and B. Štíbr, Dalton Trans., 2006, 1024 RSC
.
- P. v. R. Schleyer, K. Najafian and A. M. Mebel, Inorg. Chem., 1998, 37, 6765 CrossRef CAS PubMed
.
- Decaborane(14), B10H14, is one of the building blocks of boron cluster chemistry.
- D. A. Wann, P. D. Lane, H. E. Robertson, J. Holub and D. Hnyk, Inorg. Chem., 2013, 52, 4502 CrossRef CAS PubMed
, and references therein.
- In essence, there exists neutral nido-B6H10 structurally characterised in the solid state, see: F. L. Hirshfeld, K. Eriks, R. E. Dickerson, E. L. Lippert Jr. and W. L. Lipscomb, J. Chem. Phys., 1958, 28, 56 CrossRef CAS PubMed
.
- M. G. S. Londesborough, Z. Janoušek, B. Štíbr, D. Hnyk, J. Plešek and I. Císařová, Dalton Trans., 2007, 1221 RSC
.
- T. Jelínek, B. Štíbr, J. D. Kennedy, D. Hnyk, M. Bühl and M. Hofmann, Dalton Trans., 2003, 1326 RSC
.
- D. Hnyk and E. G. Jayasree, J. Comput. Chem., 2013, 34, 656 CrossRef CAS PubMed
, and references therein.
- In closo-1-SB11H11 (see ref. 38b) and closo-1-SB9H9, see D. Hnyk, D. A. Wann, J. Holub, S. Samdal and D. W. H. Rankin, Dalton Trans., 2011, 40, 5734 Search PubMed, the difference between the computed and experimental δ(11B) values of B(12) and B(10) atoms, respectively, atoms that are antipodally coupled with S, using almost the same model chemistries and solvent as for 1d is also ca. 5 ppm; when using C6D6 for the second system such a difference even increases.
Footnotes |
| † Dedicated to the memory of Professor Ken Wade. |
| ‡ Electronic supplementary information (ESI) available: Cartesian coordinates for the structures of cB11, nB10, and aB9 (Tables S1–S3), 1a–1f (Tables S4–S9), and nido-[B6H11]+ (Table S10), the s character, p character, and resultant hybridisation of 1a–1f for all levels of theory (Tables S11–S13), and charges on the heteroatoms of 1a–1f (Table S14). The molecular structures of 1a–1f with full atom numbering (Fig. S1), the equivalent for the closo–nido–arachno–hypho relationship for n = 11 with full atom numbering (Fig. S2), and the molecular structure of nido-[B6H11]+ with full atom numbering (Fig. S3). See DOI: 10.1039/c5dt01460c |
| This journal is © The Royal Society of Chemistry 2015 |