Mathematical modeling of microbial extracellular electron transfer by electrically active microorganisms
Yiwen
Liu
a,
Lai
Peng
a,
Shu-Hong
Gao
a,
Xiaohu
Dai
b and
Bing-Jie
Ni
*a
aAdvanced Water Management Centre, The University of Queensland, St. Lucia, Brisbane, QLD 4072, Australia. E-mail: b.ni@uq.edu.au; Fax: +61 7 3365 4726; Tel: +61 7 3346 3230
bState Key Laboratory of Pollution Control and Resources Reuse, National Engineering Research Center for Urban Pollution Control, College of Environmental Science and Engineering, Tongji University, Shanghai 200092, PR China
First published on 23rd July 2015
Abstract
Extracellular electron transfer by electrically active microorganisms enables the conduction of electrons over long spatial distances in marine sediment, which plays an important role in global biogeochemical cycles through the generated electric currents. In this study, a mathematical model is developed to describe the extracellular electron transfer process by electrically active microorganisms through decoupling the oxidation and reduction processes, taking sulfide-oxidizing bacteria as examples. In this model, extracellular electron carriers are introduced as new components to link the oxidation and reduction reactions and to achieve the long-range indirect electron transport using decoupled Monod kinetics, allowing for the description of distinct separation of contrasting electrochemical regions. The developed model has been successfully applied to reproduce experimental data for sulfide oxidation and electron acceptor reduction via extracellular electron transfer from two independent study reports with different experimental conditions (oxygen or nitrate as electron acceptors) and transfer mechanisms (possibly different extracellular electron carriers) through calibration of three key parameters (koxi, kred and Kmed) that govern the long-range indirect electron transport. The model satisfactorily describes the experimental data from both systems, suggesting the validity and applicability of the model. Modeling results clearly showed two distinct zones with sulfide consumption (sediment floor) and oxygen (or nitrate) reduction (top surface) enabled by electron conduction via electron carriers. The model of this work would enhance our understanding of biogeochemical interactions with natural electric currents allowing oxidation and reduction processes to be spatially separated yet instantly and intimately coupled, while also potentially being applicable to a wide range of electrically active microorganisms.
Water impactExtracellular electron transfer by electrically active microorganisms enables the conduction of electrons over long spatial distances in water systems such as marine sediment, which plays an important role in global biogeochemical cycles. This work proposed a new mathematical model to describe the extracellular electron transfer process by electrically active microorganisms through decoupling the oxidation and reduction processes, with solid validation against experimental data from different water systems. The model supported the existence of two distinct zones for sulfide oxidation and oxygen or nitrate reduction, which would serve as a resourceful tool for better understanding of many different microbial electron transfer reactions occurring in water systems. |
1. Introduction
Electron transfer is fundamental to microbial metabolism, which essentially generates energy for microbial growth.1 Generally, it is dominated by reduction–oxidation reactions, with the electrons transferred from electron donors to electron acceptors through electron transport chains inside the living cells. This also couples with the transfer of protons across a cell membrane,2 and thus establishes an electrochemical proton gradient that drives adenosine triphosphate (ATP) synthesis. Therefore, most previous studies of electron transport metabolism have focused on intracellular electron transfer.In fact, recent studies have demonstrated the existence of extracellular electron transfer in natural systems, thereby allowing some bacteria to be capable of using electron acceptors or donors without direct cell contact.3 Extracellular electron transfer is likely to occur in a system where a terminal oxidant is not easily accessible due to diffusion limitation, such as in sediments.1 For example, aquatic sediments are known to be capable of generating electric current when electrodes mounted in the sediment and the overlying water phase are connected.4 Nielsen et al.3 provided direct evidence that electric currents running through the sediment couple oxygen consumption at the sediment surface to oxidation of sulfide in the deep layer of the sediment. Altering the oxygen concentrations in the bulk liquid led to changes of the sulfide concentrations in the deep sediment more than 12 mm below the oxic zone, a change explicable by transmission of electrons rather than substrate diffusion.
Extracellular electron transfer could be a general microbial mechanism for electrically active microorganisms generating energy for cell growth and/or maintenance by coupling of redox half-reactions through long-range indirect electron transport. To date, several possible mechanisms involved have been proposed. Specifically, some studies reported that bacteria might be able to use redox-active organic small molecules to shuttle electrons between reduced and oxidized compounds.1 In contrast, other studies suggested that electric current might be conducted by bacterial nanowires combined with pyrite, soluble electron shuttles and outer-membrane cytochromes.3 In addition, filamentous bacteria might also play an important role in conduction of electrons over centimeter-long distances, thereby coupling oxygen or nitrate reduction at the surface of marine sediment to sulfide oxidation in deeper layers.5 Furthermore, Roden et al.6 found that iron(III) oxide-reducing bacteria might use solid-phase humic substances in sediments as electron shuttles to transfer the electrons to the oxide surface, thus accelerating iron(III) oxide reduction. Essentially, these mechanisms would involve extracellular electron carriers (i.e., organic substances, nanowires or filamentous bacteria) for electron transport by electrically active microorganisms.
Mathematical modeling of extracellular electron transfer is of great importance toward a full understanding of such a system and optimization of its practical application. Renslow et al.7 built a model incorporating long-range extracellular electron transfer in a microbial fuel cell (MFC) with electrochemically active biofilms. Pan et al.8 developed a model that takes into account the extracellular electron competition among different steps of denitrification and can be used as a practical tool for predicting N2O accumulation during wastewater treatment. Later, Fischer et al.9 developed a model to describe extracellular electron transfer using mechanisms which include Nernst–Planck diffusion and migration of ions coupled with Ohm's law for conduction along filaments.
This study aims to develop a mathematical model to describe the extracellular electron transfer process by electrically active microorganisms through integrating extracellular electron carriers as new model components. By taking sulfide-oxidizing bacteria as examples, the validity and applicability of the developed model is tested by comparing model predictions with experimental data for sulfide oxidation in marine sediment coupled to long-distance oxygen or nitrate reduction from two independent study reports. The model of this work would enhance our understanding of biogeochemical interactions with natural electric currents.
2. Materials and methods
2.1. Model development
The model developed in this work decouples the oxidation (e.g., H2S → SO42−) and reduction processes (e.g., O2 → H2O or NO3− → N2) of electrically active microorganisms (e.g., sulfide-oxidizing bacteria). Extracellular electron carriers are introduced as new components in the model to link the oxidation and reduction processes and achieve extracellular electron transport. In particular, Mred and Mox, defined as the reduced and oxidized forms of extracellular electron carriers, respectively, are included in the model as two new state variables. Since the electron carrier pool is relatively small compared with its turnover rate, the continued availability of Mox for oxidation and Mred for reduction relies on their concomitant regeneration.10 In this modeling work, this recirculation loop is modeled by an increase in Mred being balanced by a decrease in Mox and vice versa (Mred ⇌ Mox + e−), with the total level of electron carriers (Ctot) being held constant (SMred + SMox = Ctot).8,11 The value for Ctot chosen was 0.005 mmol L−1 constantly (Table 1), with SMred and SMox equal at 0.0025 mmol L−1 initially. It should be noted that Mred and Mox are two lumped parameters used in the model. In reality, many other electron carriers are also subsequently involved in extracellular electron transfer. The use of such lumped parameters reduces the complexity of the model, making the implementation and application of the model easier.| Parameter | Value | Unit | Source |
|---|---|---|---|
| K H2S | 0.01 | mmol L−1 | Fischer et al.9 |
| Aerobic sulfide oxidation (Case I) | |||
| k oxi | 5 | mmol gVSS−1 h−1 | Calibrated in this study |
| k red | 1 | mmol gVSS−1 h−1 | Calibrated in this study |
| K O2 | 0.01 | mmol L−1 | Fischer et al.9 |
| K med | 0.001 | mmol L−1 | Calibrated in this study |
| C tot | 0.005 | mmol L−1 | Pan et al.8 |
| Anoxic sulfide oxidation (Case II) | |||
| k oxi | 3 | mmol gVSS−1 h−1 | Calibrated in this study |
| k red | 1 | mmol gVSS−1 h−1 | Calibrated in this study |
| K NO3 | 0.01 | mmol L−1 | Wang et al.15 |
| K med | 0.005 | mmol L−1 | Calibrated in this study |
| C tot | 0.005 | mmol L−1 | Pan et al.8 |
For the sulfide oxidization process in marine sediment, Mox would receive electrons produced by sulfide oxidation in the deep layer of marine sediment and be reduced to Mred (eqn (1)), while Mred would then transport and donate the received electrons to electron acceptors such as oxygen (eqn (2)) or nitrate (eqn (3)) near the sediment surface and is oxidized to Mox.
| H2S + 4H2O + 8Mox → SO42− + 2H+ + 8Mred | (1) |
| 2O2 + 8Mred → 4H2O + 8Mox | (2) |
| 2NO3− + 10Mred + 2H+ → N2 + 6H2O + 10Mox | (3) |
Kinetic control of all these biological reaction rates can be described by the Monod equation.12 The rate of each reaction (roxidation, rreduction,O2 and rreduction,NO3) is modelled by an explicit function of the concentrations of all substrates involved in the reaction, as described in eqn (4)–(6).
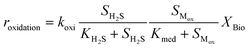 | (4) |
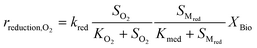 | (5) |
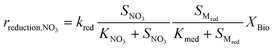 | (6) |
In this work, a one-dimensional sediment model, which has been implemented in AQUASIM,13 is combined with the proposed biological electron transfer model to formulate a new model to describe the spatially decoupled oxidation and reduction reactions. The whole sediment is modelled with 50 layers. Transport of dissolved components in the liquid phase of the sediment is described by Fick's first law as a diffusive flux in the sediment model. The diffusion coefficient values for oxygen, nitrate and sulfide were adopted from the literature. A much higher diffusion coefficient of electron carriers was applied to describe the much faster long-range electron transport process driven by the unique extracellular electron transfer capabilities of electrically active microorganisms. To gain insights into the extracellular electron transfer, modeling results under pseudo-steady-state conditions were acquired and compared to experimental data.
2.2. Experimental data for model evaluation
2.3. Model calibration and validation
The developed model includes several new kinetic parameters as summarized in Table 1. Two of these model parameter values are well established in previous studies. Thus, literature values were directly adopted for these parameters.8,9,15 The remaining three parameters (koxi, kred and Kmed), which are unique to this model and are the key parameters governing the extracellular electron transfer processes, are then calibrated using experimental data in both oxic and anoxic cases.Parameter values were estimated by minimizing the sum of squares of the deviations between the measured data and the model predictions. For each case, the model was first calibrated with one set of experimental data, and then validated through simulation of sulfide oxidation for other sets of experimental data (under different experimental conditions, not used for model calibration) with the obtained best-fit parameter values.
3. Results
3.1. Evaluation of sulfide oxidation coupled to oxygen reduction
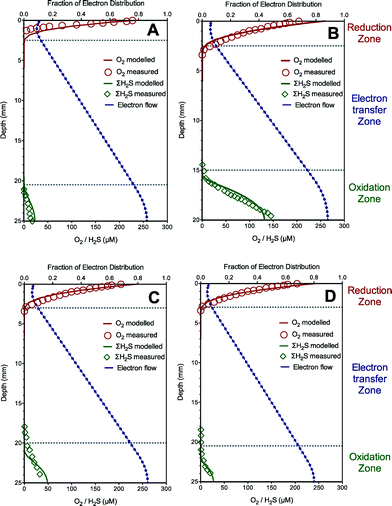
The model is first calibrated to describe the experimental data from the sediment with sulfide oxidation coupled to oxygen reduction via extracellular electron transfer in Case I. The predicted oxygen, total sulfide and electron flow (fraction of electron distribution, i.e., SMred/Ctot) profiles using the established model are illustrated in Fig. 1A, along with the experimental results. The oxygen was rapidly and completely consumed near the sediment surface (ca. 2 mm) due to extracellular electron transfer from sulfide oxidation in the deep layer (ca. 21–25 mm). The model simulation shows that the electrons accumulated in the sulfide oxidation zone, and then diffused into the oxygen reduction zone through a concentration gradient, thus leading to the existence of an electron transfer zone (ca. 19 mm deep) devoid of both oxygen and sulfide. Our model captured all these trends reasonably well. The good agreement between these simulated and measured data supported the fact that the developed model properly captures the trend of sulfide oxidation coupled to distant oxygen reduction via extracellular electron transfer in Case I. The calibrated parameter values giving the optimum model fittings with the experimental data are listed in Table 1.The developed model and calibrated parameter set (Table 1) were then further validated for their ability to predict experimental data of sulfide oxidation coupled to distant oxygen reduction via extracellular electron transfer in the other three tests with different sulfide concentrations in Case I. The model predictions and the experimental results are shown in Fig. 1B–D. The validation results showed that the model predictions matched well with the measured data for oxygen and total sulfide in all three validation experiments, which support the validity of the developed model and confirm that electric currents running through the sediment can couple oxygen consumption at the sediment surface to H2S oxidation in deep layers within the sediment. It is worth mentioning that the electric current was proposed to be conducted by bacterial nanowires combined with pyrite, soluble electron shuttles and outer-membrane cytochromes as extracellular electron carriers in this case study.3 The modelling results suggest that the model is capable of describing extracellular transfer via bacterial nanowires or soluble electron shuttles.
3.2. Evaluation of sulfide oxidation coupled to nitrate reduction
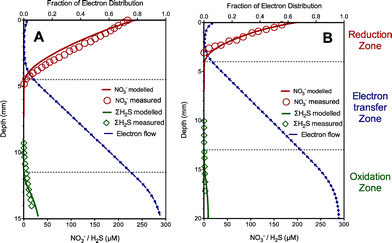
The experimental results obtained from Case II with nitrate as electron acceptors were also used to evaluate the developed model in terms of nitrate, total sulfide and electron flow dynamics. Similarly, in this case, one set of experimental data (Fig. 2A) were used to obtain key kinetic parameter values related to extracellular electron transfer (kox, kred and Kmed) and the resulting parameter values were used to simulate profiles for comparison with another data set (with low sulfide concentrations in the sediment) as validation (Fig. 2B). The values of the estimated parameters in this case are listed in Table 1. As shown in Fig. 2, nitrate, total sulfide and electron flow dynamics were similar to those in Case I with oxygen as electron acceptors, except with deeper penetration of electron acceptors and a shorter distance of the electron transfer zone (ca. 4–6 mm). The model captured these trends reasonably well. Again, the modeling results clearly showed two distinct zones with sulfide consumption (sediment floor) and nitrate reduction (top surface) enabled by extracellular electron conduction. The results indicated that the nitrate reduction rate reached its maximum level at the middle of the reduction zone, where the highest consumption of the electrons occurred because of the availability of both nitrate and electrons. The fraction of electron distribution slightly increased at the top of the reduction zone likely due to the decrease of the nitrate reduction rate leading to less electron utilization. In addition, filamentous bacteria were proposed to play an important role in conduction of electron transport as extracellular electron carriers in this case,5 suggesting that the model is also capable of describing extracellular transfer via filamentous bacteria in marine sediment.4. Discussion
Recently, the previously overlooked extracellular electron transfer process has attracted more attention due to its important role in global biogeochemical cycles.16–22 Increasing evidence has shown that electrically active microorganisms drive the electrochemical half-reactions and the establishment of electron-conducting structures, which significantly contributes to microbial growth in the surface sediment.3,5,12In this work, a new mathematical model is developed to describe the extracellular electron transfer process, which is of significance for understanding and predicting the speed and extent of biochemical reactions over long spatial distances in natural systems.1 The key feature of this model is that the proposed model decoupled the biological oxidation and reduction processes through a pool of extracellular electron carriers, while the most previous microbial models directly coupled the two processes by assuming direct cell contact and thus failed to describe spatially separated biogeochemical processes13 or even considering a decoupled concept but only focuses on modeling in bioelectrochemical systems rather than natural environments.23,24
Substantially, the electron carriers as new model components in the model are lumped from many possible physical electron carriers, including but not limited to soluble or insoluble electron shuttles, nanowires, filamentous bacteria and cytochromes. This novel approach enabled the decoupling of oxidation and reduction processes spatially separated, and subsequently enabled the modeling of distinct separation of contrasting electrochemical regions. More importantly, while underpinned by the current scientific knowledge of electron transfer processes, the model does not replicate all the known biochemical reactions involved to avoid over-parameterization.
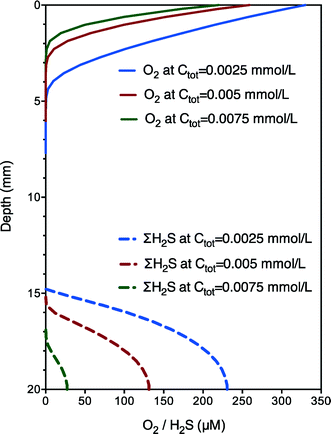
The validity of this developed model was confirmed by independent case studies. The set of best-fit parameter (koxi, kred and Kmed) values are shown in Table 1 and vary within a relatively narrow range. The major difference between the two case studies was the koxi value (5 vs. 3 mmol gVSS−1 h−1), which was coincident with the difference between aerobic and anoxic respiration rates (i.e., 5/3). The parameter values obtained were robust for the prediction of electron transfer dynamics under different experimental conditions (oxygen or nitrate as electron acceptors) with different transfer mechanisms (possibly different extracellular electron carriers), indicating the potential and wide applicability of the developed model for different electrically active microorganisms.3,5 With validated parameter (koxi, kred and Kmed) values, further model simulation runs under aerobic conditions show that both the speed and extent of biochemical rates and the length of the electron transfer zone increased with increasing electron carriers (Ctot) from 0.0025 to 0.0075 mmol L−1 (Fig. 3), confirming the important role of electron carriers. Nevertheless, further model validations using incubations with altered exogenous mediator concentrations are still needed for the model to be developed into a useful tool for practical applications. In addition, the obtained diffusion coefficient of electron carriers was significantly higher than those of sulfide or oxygen, which is though reasonable as the transport or diffusion mechanism of electron carriers should be much different from that of the general substrate. The long-range electron transport is driven not only by concentration gradients but also (more importantly) by the unique extracellular electron transfer capabilities of electrically active microorganisms involving superexchange of electrons (with sufficient potentials and conductivity along the sediment). Thus, the much higher diffusion coefficient of the electron carriers confirmed the high extracellular electron transfer capabilities of the microorganisms. Sensitivity analysis shows that if Ctot is increased by 100%, the estimated values of Kmed would also increase by around 100%. In other words, the ratios of these parameters to Ctot do not change. Examination of the kinetic expressions indicates that relative ratios between Ctot and Kmed rather than their absolute values are important for the reaction rate. Also, the model fit with experimental data is almost not affected. Therefore, an assumed rather than experimentally determined Ctot is adequate for the calibration of the proposed model. The model of this work would enhance our understanding of biogeochemical interactions with natural electric currents allowing oxidation and reduction processes of electrically active microorganisms to be spatially separated yet instantly and intimately coupled.
Modeling biological electron transfer processes is an important step towards understanding the spatially decoupled oxidation and reduction reactions. In our model, electron shuttles such as nanowires and/or filamentous bacteria were considered to describe the movement of electrons from the oxidizing zone to the reducing zone. However, other mediators such as humic acids, cytochromes, activated carbon, etc. remain the potential electron carriers for long-range electron transport. In addition, it has been demonstrated that soluble electron mediators might not be able to account for the entire electron flow through these systems, and ongoing investigations may reveal conditions where these alternative mediators is more important than hitherto assumed. As a result, the model may not be able to describe the percentage of total flux distributed to different mediators and the contribution of each individual mediator. However, these simplifications can be relaxed in the future through integrating another electron mediator component into the model with similar kinetics (eqn (4)–(6)) as more information about electron transfer mechanisms becomes available. While this model may not yet serve as a precise and quantitative predictor of electron flux in various systems (due to the lack of information), it can nevertheless serve as a tool to explore the effect of the availability of total electron carriers on spatially decoupled oxidation and reduction rates.
5. Conclusions
In this work, a new mathematical model is proposed to describe extracellular electron transfer by electrically active microorganisms such as sulfide-oxidizing bacteria in marine sediment. The developed model was successfully applied to reproduce experimental data obtained from two independent case studies with different experimental conditions and clearly showed two distinct zones with sulfide consumption (sediment floor) and oxygen or nitrate reduction (top surface) enabled by extracellular electron transport.Acknowledgements
This study was supported by the Australian Research Council (ARC) through the project DP130103147. Bing-Jie Ni acknowledges the support of ARC Discovery Early Career Researcher Award (DE130100451).References
- M. E. Hernandez and D. K. Newman, Cell. Mol. Life Sci., 2001, 58, 1562–1571 CrossRef CAS.
- P. Mitchell, Nature, 1961, 191, 144–148 CrossRef CAS PubMed.
- L. P. Nielsen, N. Risgaard-Petersen, H. Fossing, P. B. Christensen and M. Sayama, Nature, 2010, 463, 1071–1074 CrossRef CAS PubMed.
- C. E. Reimers, L. M. Tender, S. Fertig and W. Wang, Environ. Sci. Technol., 2001, 35, 192–195 CrossRef CAS.
- U. Marzocchi, D. Trojan, S. Larsen, R. L. Meyer, N. P. Revsbech, A. Schramm, L. P. Nielsen and N. Risgaard-Petersen, ISME J., 2014, 8, 1682–1690 CrossRef CAS PubMed.
- E. E. Roden, A. Kappler, I. Bauer, J. Jiang, A. Paul, R. Stoesser, H. Konishi and H. Xu, Nat. Geosci., 2010, 3, 417–421 CrossRef CAS PubMed.
- R. Renslow, J. Babauta, A. Kuprat, J. Schenk, C. Ivory, J. Fredrickson and H. Beyenal, Phys. Chem. Chem. Phys., 2013, 15, 19262–19283 RSC.
- Y. Pan, B.-J. Ni and Z. Yuan, Environ. Sci. Technol., 2013, 47, 11083–11091 CrossRef CAS PubMed.
- K. M. Fischer, D. J. Batstone, M. C. M. van Loosdrecht and C. Picioreanu, Bioelectrochemistry, 2015, 102, 10–20 CrossRef CAS PubMed.
- S. Gyan, Y. Shiohira, I. Sato, M. Takeuchi and T. Sato, J. Bacteriol., 2006, 188, 7062–7071 CrossRef CAS PubMed.
- E. M. Sipkema, W. de Koning, K. J. Ganzeveld, D. B. Janssen and A. A. C. M. Beenackers, Biotechnol. Prog., 2000, 16, 176–188 CrossRef CAS PubMed.
- C. Pfeffer, S. Larsen, J. Song, M. Dong, F. Besenbacher, R. L. Meyer, K. U. Kjeldsen, L. Schreiber, Y. A. Gorby and M. Y. El-Naggar, Nature, 2012, 491, 218–221 CrossRef CAS PubMed.
- Y. Liu, B.-J. Ni, R. Ganigué, U. Werner, K. R. Sharma and Z. Yuan, Water Res., 2015, 70, 350–359 CrossRef CAS PubMed.
- N. R. Petersen, S. Rysgaard, L. P. Nielsen and N. P. Revsbech, Limnol. Oceanogr., 1994, 39, 573–579 CrossRef.
- A. Wang, C. Liu, N. Ren, H. Han and D. Lee, J. Hazard. Mater., 2010, 178, 35–41 CrossRef CAS PubMed.
- K. Rabaey, J. Rodriguez, L. L. Blackall, J. Keller, P. Gross, D. Batstone, W. Verstraete and K. H. Nealson, ISME J., 2007, 1, 9–18 CrossRef CAS PubMed.
- R. Schauer, N. Risgaard-Petersen, K. U. Kjeldsen, J. J. T. Bjerg, B. B. Jørgensen, A. Schramm and L. P. Nielsen, ISME J., 2014, 8, 1314–1322 CrossRef CAS PubMed.
- N. Risgaard-Petersen, A. Revil, P. Meister and L. P. Nielsen, Geochim. Cosmochim. Acta, 2012, 92, 1–13 CrossRef CAS PubMed.
- Y. Liu, Y. Zhang, X. Quan, J. Zhang, H. Zhao and S. Chen, Bioresour. Technol., 2011, 102, 2578–2584 CrossRef CAS PubMed.
- M. Villano, F. Aulenta, C. Ciucci, T. Ferri, A. Giuliano and M. Majone, Bioresour. Technol., 2010, 101, 3085–3090 CrossRef CAS PubMed.
- A. Okamoto, K. Saito, K. Inoue, K. H. Nealson, K. Hashimoto and R. Nakamura, Energy Environ. Sci., 2014, 7, 1357–1361 CAS.
- R. Nakamura, F. Kai, A. Okamoto and K. Hashimoto, J. Mater. Chem. A, 2013, 1, 5148–5157 CAS.
- S. M. Strycharz, A. P. Malanoski, R. M. Snider, H. Yi, D. R. Lovley and L. M. Tender, Energy Environ. Sci., 2011, 4, 896–913 CAS.
- S. M. Strycharz-Glaven, R. M. Snider, A. Guiseppi-Elie and L. M. Tender, Energy Environ. Sci., 2011, 4, 4366–4379 CAS.
| This journal is © The Royal Society of Chemistry 2015 |