Evaluating the precision of Pb isotope measurement by mass spectrometry

Abstract

Analytical precision for Pb isotope measurement by thermal and plasma source mass spectrometry has improved by an order of magnitude in the last 20 years. Much of this improvement relates to a shift away from the external method of correcting instrumental mass fractionation – where samples are assumed to fractionate to the same extent as an average value of a working measurement standard. Implementation of a variety of techniques, including thallium spiking, sample–standard bracketing and double/triple spiking has provided more robust methods of fractionation correction. Isotope laboratories use one or more of these procedures, but an assessment of the measurement precision and relative merits of each system is needed to determine which is the most appropriate for the purpose. This study reviews each of these methods and provides a comparison based on an extensive analytical record covering 18 years, and using a variety of mass spectrometers. As two or three of the methods have been applied to most measurements, direct and robust comparisons can be made between correction protocols. In particular the effects of sample purity and variable sample matrices on measurement precision and accuracy have been examined. Data acquired from the measurement of rock, soil and metal are used to provide a statistical comparison of the analytical uncertainty of each technique, guiding the choice of the most appropriate method. Isotope standard data acquired over this period is also compared with other high-precision laboratories to generate a set of concordant working ratios for the NIST SRM 981 Pb standard: ²⁰⁶Pb/²⁰⁴Pb = 16.9412; ²⁰⁷Pb/²⁰⁴Pb = 15.4988; ²⁰⁸Pb/²⁰⁴Pb = 36.7233.

---

1. Introduction

Three radioactive decay chains stemming from ²³⁸U, ²³⁵U and ²³²Th generate the radiogenic isotopes of lead: ²⁰⁶Pb, ²⁰⁷Pb and ²⁰⁸Pb respectively. When combined with the non-radiogenic ²⁰⁴Pb, these systems provide a suite of isotope ratios that describe the time-integrated record of U/Pb and Th/Pb in a sample. Because U, Th and Pb are partitioned into natural materials in different ways each lead isotope ratio can independently vary according to when the segregation occurred. For example continental crust generally has a higher ²⁰⁷Pb/²⁰⁴Pb compared to ocean crust because continental material has had a higher U/Pb ratio for a long period of Earth history. However, ocean crust exposed to seawater and hydrothermal alteration commonly acquires high uranium content relative to lead. A product of this high U/Pb is a characteristically radiogenic ²⁰⁶Pb/²⁰⁴Pb relative to unaltered ocean crust.

Superimposed on this geological diversity the effective isotopic composition can vary according to the precision and accuracy of the lead isotope measurement. A number of potential sources can affect the quality of a Pb isotope analysis including: (i) contamination with lead derived from environmental sources during sample collection, sample preparation, chemical refining and sample introduction to the mass spectrometer; (ii) bias caused by differences between the sample matrix relative to the lead isotope standard: i.e. non-spectroscopic matrix effects; (iii) bias and interference generated by mass spectrometry. Of these issues, contamination can be effectively negated by suitable collection, handling and preparation protocols. This involves the removal of metals and silicates in sample processing, and the exclusion of atmospheric and procedural contamination by way of a clean preparation and measurement laboratories and sub-boiled/ultra-purified reagents. Equalising samples and standards can be achieved by isolation of Pb from the sample matrix. Commonly this is done by multiple passes of the sample in an HBr solution through anion exchange chromatography which can provide suitable purification.

As the contamination and sample refining aspects of analysis can be controlled, it is mass spectrometry that has provided the greater challenge and presents opportunities to improve the precision and accuracy of Pb isotope data. Combining multiple Faraday cup detectors with sector field mass dispersion has been the foundation for high-precision isotope measurement since the early 1980's. Indeed, using this detection arrangement, the precision of isotope systems such as ⁸⁷Sr/⁸⁶Sr and ¹⁴³Nd/¹⁴⁴Nd (∼±0.002%) has not dramatically improved since this time. Ratios such as ²⁰⁸Pb/²⁰⁶Pb can theoretically be measured to the same level of precision as Sr and Nd. However, the lack of a non-radiogenic Pb isotope pair means that instrumental mass fractionation cannot be directly constrained during a measurement. Consequently, the precision of Pb by thermal ionization mass spectrometry (TIMS) was conventionally limited to estimations of how mass fractionation changed during measurement and by assuming samples were fractionated by the same factor as standards. Laboratories based their measurement uncertainty on the reproducibility of standards which generally provided an optimistic view of precision (e.g.²⁰⁶Pb/²⁰⁴Pb ±0.052%;¹ ±0.04%²).

A step change in the precision of Pb isotope measurement occurred with the re-invention of double spiking and the development of multi-collector inductively coupled mass spectrometry (MC-ICP-MS). Double spiking was first devised in the 1960’s–70's as a solution to the problem of how to measure the mass fractionation of Pb isotopes.^3,4 But due to problems including differential blanks between the two required measurements, the technique was not widely utilised. However, in the late 1990's^5,6 the technique was promoted as improving precision by greater than five times relative to conventional TIMS Pb analysis. At the same time MC-ICP-MS brought relative stability to within-run mass fractionation and allowed fractionation to be equated between different elements. Like double spiking, this promised a similar level of improvement in precision but with the advantages of measurement via solution and more rapid analysis.

With these advances in instrumentation and techniques, it is good to appreciate how the resulting high-precision data can be used and what limits realistic estimates of repeatability could impose on interpretations. Tabulated numerical data are obligatory, but what is the most appropriate way to visualise high-precision data? What types of trend are produced by correlated measurement uncertainties in high precision data?

An example dataset of basaltic lavas from the Reykjanes Ridge is shown in Fig. 1. These samples were initially analysed using rigorous clean laboratory and TIMS analytical protocols, but externally corrected for mass fractionation assuming all samples are offset by the same amount (f = c: see Section 2.1), which was equivalent to the average quantity for the reference standard.^7,8 The same sample set was then re-measured on the same instrument using the double spike correction procedure.⁹ The f = c corrected data are coincident with the double spike data, suggesting that at least their measurement trueness is similar. However, the precision of f = c is lamentable as the samples are dispersed in a fairly random cloud. In contrast, the equivalent double spike data define a clear linear trend. Furthermore, dividing the double spike data according to geographical distribution reveals that the northern and southern regions form discrete sub-trends.

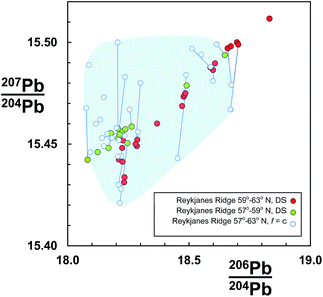Fig. 1 ²⁰⁶Pb/²⁰⁴Pb vs.²⁰⁷Pb/²⁰⁴Pb for Reykjanes Ridge basalts. Data measured by TIMS and corrected for mass fractionation by constant-f (f = c) from ref. 7 and 8, are shown as open symbols. The same sample suite was re-measured by double spike (DS) by Thirlwall et al.,⁹ and here is divided into two groups according to latitude. Individual samples measured by both techniques are connected by a tie-line. Shaded region highlights the f = c determinations.

In this study we evaluate comprehensive datasets of NIST SRM 981 Pb isotope standard together with sample measurements acquired on TIMS and MC-ICP-MS. These data have been generated by a range of users of the isotope facilities in Ocean and Earth Science at the University of Southampton over a period of 18 years. We also present double spike Pb isotope data for the NIST SRM 981 standard measured at the Geological Survey of Japan using the same double spike. Comparisons are made between the overall precision of the main mass fractionation correction techniques: f = c, double spike, Tl-spiking and sample–standard bracketing. Using these data we also explore the potential for recognising the form of uncertainty-generated arrays in sample datasets and examine the potential to increase precision further by sample grouping and repetition.

2. Correction of instrumental mass fractionation

Many isotope systems used in geochronometry, such as Sr, Nd and Hf, have at least one pair of non-radiogenic isotopes. These pairs provide the opportunity to measure a ratio with an assumed constant value, or at least with a limited and constrained mass-related discrimination. Comparing the measured and assumed values of this ratio enables a precise calculation of instrumental mass fractionation (also termed mass discrimination or bias). In most cases this bias is a function of the difference in mass of the isotope pair. For example in the neodymium system the instrumental mass fractionation is typically calculated by measuring ¹⁴⁶Nd/¹⁴⁴Nd (with a two mass unit difference) and relating this to the conventional value of the ratio, 0.7219. This calculated factor can then be proportioned for a mass difference of one for the radiogenic isotope ratio of interest: ¹⁴³Nd/¹⁴⁴Nd. The key limiting factor in measuring lead isotope ratios by mass spectrometry is the lack of two non-radiogenic isotope ratios: only ²⁰⁴Pb is unradiogenic. Consequently, other methods of mass fractionation correction are used to produce accurate Pb isotope ratios, and are outlined below.

2.1 Constant f correction

The lack of two non-radiogenic lead isotopes requires an alternative method of estimating the instrumental mass fractionation. One simple technique is to measure the ratios for an isotope standard, compare them to the accepted values and calculate a typical bias factor for the instrument. This bias, or mass fractionation factor (f) can then be applied to separate determinations of unknown, sample isotope ratios. In the case of Pb, this is proportioned to correct any of the isotope ratios according to their mass difference. Essentially this technique assumes the mass fractionation or mass fractionation for an instrument induces a constant offset from the true value. This constant f correction (f = c) has been used extensively by Pb isotope laboratories prior to 2000 (e.g.ref. 2 and 10) and is also used for U isotopes where anthropogenic changes may have disturbed the natural ratio (e.g.ref. 11 and 12). Although superseded by other techniques (see below), it is still used in a number of studies (e.g.ref. 13 and 14).

A number of assumptions are inherent to the f = c technique; the foremost being that the value of f is the same for samples and the pure Pb isotope standard. This may not be the case as the sample purity is dependent on how well Pb has been isolated from the matrix elements during laboratory processing, usually by ion exchange chromatography. With TIMS analysis the presence of pernicious elements such as Zn in the analyte may suppress ionization of Pb.¹⁵ Typically a TIMS measurement during the initial stages of ionization produces an isotope ratio that has a light bias relative to the true value. Progressive measurement takes the level of mass fractionation closer to, and eventually heavier than, the true value.¹⁶ Standards, with high purity and frequently a higher concentration of Pb, produce strong ion beams at relatively low temperatures (<1080 °C). Consequently, measurements are acquired during the early phase of ionization and have lighter isotope ratios (e.g. a low measured ²⁰⁶Pb/²⁰⁴Pb) compared to samples with more complex matrices. If a high level of suppression occurs during ionization of a sample, then the energy required to ionize lead is increased. As a similar level of ion current is required to make an accurate determination on a sample as for a standard, the consequential high temperatures result in the measured isotope ratios rapidly approaching greater levels of mass fractionation – i.e. effectively heavier isotope ratios. As such, an f = c correction to a typical Pb isotope standard value could result in an over correction of the sample measurement. Potentially this is a source of a bias in the Pb isotope data where the sample could have heavier isotope ratios than their accurate values.

Some evidence for this can be seen in Fig. 1 where f = c data for samples also measured by the double spike are linked by tie-lines. If the double spike analyses are taken as accurate, the f = c data predominantly lie to higher ²⁰⁷Pb/²⁰⁴Pb and slightly higher ²⁰⁶Pb/²⁰⁴Pb; the linked analyses effectively extending along a fractionation vector.

Aside from the potential inaccuracy due to matrix differences between samples and standards, the f = c technique has an inherent imprecision caused by the single correction factor. Laboratories that used the f = c typically adjust measured values to heavier isotope ratios using factors (or c value) between 0.08% and 0.15% amu⁻¹. The particular factor chosen is calculated as an average fractionation level for a number of measurements of the NIST SRM 981 Pb isotope standard. Estimation of the precision of any Pb isotope measurement is consequently based on the standard deviation (usually at the 95% confidence level) of the NIST SRM 981 determinations that make up this average. However, as an estimate of reproducibility this deviation does not include the likelihood that real sample measurements may include a much wider range of fractionation behavior.¹⁶ Consequently, many of the quoted precision values for a series of unknowns from a particular laboratory may significantly underestimate the true reproducibility.

2.2 Double spiking, triple spiking and 2× double spiking

A technique to accurately measure the instrumental mass fractionation of Pb isotopes was initially developed in the late 1960's as a mathematical procedure. This involved a pair of artificially enhanced or spiked isotopes added to part of the sample and measured separately from the pure sample – the “double spike” procedure e.g.ref. 3 and 17etc. Combining the data from the spiked and unspiked analyses allows the amount of fractionation in the unspiked fraction to be deconvolved. However, the technique did not develop into a routine analytical tool as the results were commonly hampered by significant interferences from laboratory and procedural blank contributions^18,19 which outweighed the advantages of the double spike correction. Consequently, the technique stagnated and was not used by most Pb isotope laboratories. However, Woodhead et al.⁵ presented a re-assessment of the double spike technique based on the use of a ²⁰⁷Pb–²⁰⁴Pb spike and demonstrated that ²⁰⁶Pb/²⁰⁴Pb could be reproduced to better than 0.02% (2RSD) using a TIMS. Subsequently, Galer²⁰ evaluated the ideal spike–sample mixture levels using a ²⁰⁷Pb–²⁰⁶Pb–²⁰⁴Pb triple spike and Thirlwall¹⁶ used a ²⁰⁷Pb–²⁰⁴Pb double spike to provide a comprehensive breakdown of the optimal analytical procedures by TIMS. Both Galer and Thirlwall reported Pb isotope ratios for the NIST SRM 981 standard using their multi-isotope spikes (poly-spikes).

Towards the end of the last century high precision isotope ratio mass spectrometry was advanced by the joining of an inductively coupled plasma (ICP) ion source with a multi-collector measurement array. For many elements, such as Hf, Nd, U and Pu (e.g.ref. 21–27), this provided an order of magnitude improvement in ionization efficiency relative to TIMS and consequently enabled the precise determination of isotope ratios on much smaller sample sizes (<30 ng).

More recently, the double spike method has been used in conjunction with MC-ICP-MS.^28–32 These studies demonstrate that the double spike is just as effective at correcting for the isotopically heavy, and ∼8 times greater, mass fractionation of the plasma ion source as a TIMS ion source. There are however, a set of disadvantages to ICP-based determination of Pb isotopes. Interference from background, sample memory and isobaric ²⁰⁴Hg are part of the scenery and can be reduced, but not eliminated, by rigorous cleaning, effective correction procedures and using large Pb ion beams (e.g. 1 × 10⁻¹⁰ A ²⁰⁸Pb). Efficiency, or ion yield, is currently an advantage of TIMS over MC-ICP-MS. Typically, plasma instruments in conjunction with desolvating nebulisers can achieve a Pb yield around 0.5–1.5% (100× ions Pb counted per atoms Pb used), whereas TIMS can achieve 2–10%.^33,34 However the difference in efficiency is narrowing with further advances in aspiration, desolvation, expansion chamber pumping and skimmer/sample cone design. Sensitivity of the Thermo Neptune MC-ICP-MS with jet cone is currently up to 2800 V μg ml⁻¹ΣPb, which equates to ∼3.5% efficiency, but this can be effectively improved by lowering the noise on signals produced by the ion detection system by using pre-amplifier with a highly-resistive register of 10¹² Ω (e.g.ref. 35). Further improvements in the measurement of small ion beams – ²⁰⁴Pb in the lead system – are impending with the development of 10¹³ Ω resistors.³⁶

Achieving higher ion yields, reducing backgrounds and improving detector response is of particular importance where only limited quantities of Pb (<5 ng) are available, but high precision analysis is required. Double or triple spiking using ^206/207Pb–²⁰⁴Pb requires that two separate runs are made on TIMS or MC-ICP-MS. As a matter of course, this increases the amount of sample required to attain suitable signal levels for the unspiked and spiked runs by ∼20%. However, if a ²⁰²Pb–²⁰⁵Pb spike is used the mass fractionation of the inherent sample Pb can be calculated within the single measurement.^37,34 The key weakness of both ²⁰²Pb–²⁰⁵Pb and ^206/207Pb–²⁰⁴Pb spiking protocols is the low-abundance of ²⁰⁴Pb. Even with improvements in amplifier technology, the statistical counting limit of ²⁰⁴Pb is the controlling factor when analysing small quantities of Pb. ^206/207Pb–²⁰⁴Pb poly-spikes improve the abundance of ²⁰⁴Pb in the spiked run, but it remains in its natural abundance (∼1.4%) in the unspiked run. This issue was tackled by designing a spiking system using two double spikes, ²⁰⁵Pb–²⁰⁴Pb and ²⁰⁷Pb–²⁰⁴Pb, and developing a deconvolution of the mass fractionation from two spiked runs.³⁶ As ²⁰⁴Pb signals are boosted by a factor of ∼10 in both measurements, the uncertainties introduced as a result of low abundance are significantly reduced. Kuritani and Nakamura³⁶ report equivalent precision for 1 ng Pb sample size to their typical >10 ng TIMS loading.

2.3 ²⁰³Tl–²⁰⁵Tl spiking

An additional benefit of MC-ICP-MS is that it produces comparable mass fractionation values for elements of similar mass. This has the advantage of enabling the mass fractionation calculated for one element to be used to simultaneously correct the fractionation in another element. Thallium, with non-radiogenic isotopes ²⁰³Tl and ²⁰⁵Tl, provides an opportunity to correct the mass fractionation of Pb within the same multi-collector acquisition.^38–40 The same type of correction procedure also works in reverse, in that if Pb of known isotope composition is added to the Tl isolated from a sample, then any natural variation in ²⁰⁵Tl/²⁰³Tl can be quantified.^41,42

An advantage of thallium spiking over double spiking is that as Tl and Pb isotopes are non-isobaric; only one mass spectrometric run is required. Analytical time and also the amount of Pb consumed in the measurement are reduced as a consequence. However, a number of studies have concluded that Pb isotope determinations using Tl-spiking may have significant limitations. There is the potential for non-spectral matrix element interferences to influence the mass fractionation relationship between Tl and Pb.^43–45 In addition, it is recognized that Tl and Pb may be differentially affected by redox conditions when combined in solution, inducing a reversible Tl isotopic fractionation.⁴⁵ Such complexity in the Tl–Pb relationship is a potential limiting factor and consequently some studies have determined that the precision of the Tl-spiking method is considerably worse than expected given the signal levels.^28,30 However, other studies use more complex fractionation relationships⁴⁶ or solution optimization⁴¹ in an attempt to achieve higher precision data.

2.4 Sample–standard bracketing

In systems where the number of available isotopes is limited and double spiking is not possible (e.g. Cu, Zn), the stability of mass fractionation that is characteristic of MC-ICP-MS instruments can be used to externally correct fractionation bias. Periodically measuring an isotopic reference material and interpolating the bias to intervening samples can avoid the complications incurred by extrapolation to another element, like from Tl to Pb. However, it can potentially be applied where the sample and standard matrices are identical⁴⁷ but may require pre-screening of samples to verify that the chemical purification has been effective. Bracketing can be used in tandem with other methods of correction such as Tl-spiking.⁴⁸ As with Tl-spiking, only a single sample run is required and consequently the quantity of Pb is lower relative to double spiking. However, mass spectrometer usage time can be increased depending on the number of intercalated standards. This, in turn, may depend upon the stability of the mass fractionation during the course of the analytical period.

3. Experimental

3.1 Sample preparation and chemical isolation

A variety of sample types are measured for lead isotopes in the University of Southampton isotope laboratories including soil, metals, hydrothermal fluids and archaeological artifacts. However, the dominant material is rock. Preparation for analysis of water-cleaned solid samples is initiated by crushing using a fly-press. Material is contained within thick polyethylene bags to ensure the impact plates of the press do not make contact with the sample. The crushed fraction is then graded using a Teflon sieve set to isolate chips between 0.5–1.0 mm. This size fraction is then rinsed repeatedly with 18 MΩ water, before ultrasonic agitation in water for 10 min. Samples are dried in an oven overnight at 80 °C. Clean chips are then picked under a binocular microscope to remove altered or extraneous material.

Chemical purification of Pb is completed in class 100 clean laboratories using reagents that have been screened to ensure negligible Pb content. Silicate samples are dissolved for >24 hours in ∼4 ml of an HF–HNO₃ 4 : 1 mixture. Isolation of Pb from the matrix is achieved by taking-up the dissolved residue in 1 M HBr and passing through AG1-X8 200–400 mesh anion exchange resin (Eichrom). One or two stages of this chromatography are employed, depending on the measurement protocol to be used. Final recovery of Pb from the column is via 6 M HCl. Procedural blanks are generally <75 pg Pb assuming two column passes.

3.2 Thermal ionization mass spectrometry (TIMS)

In the period 1996–2009 lead isotope measurements in the University of Southampton were conducted on a VG Sector 54 TIMS, equipped with seven faraday detectors. Prior to 1998 samples were loaded onto zone-refined Re filaments with 0.5 M H₃PO₄ and silica gel. Following evaporation, the filament temperature was raised to a dull-red glow in air to oxidise the sample load. Data were acquired as integrations of 100 × 5 s with an ion current of 5–10 × 10⁻¹² A Pb (equivalent to ∼0.6 V of ²⁰⁸Pb measured across a 10¹² Ω resistor) in static multi-collection mode. Data acquisition was restricted to rhenium filament temperatures between 1050 °C and 1180 °C. Measurements were adjusted for mass fractionation using a linear-law (f = c) correction with a value of 0.12% amu⁻¹, based on the average value obtained for NIST SRM 981.

Later Pb isotope measurements (2001–2009) on this TIMS were corrected for mass fractionation using the Southampton–Brest lead ²⁰⁷Pb–²⁰⁴Pb double spike (SBL74). This spike was formulated in to provide minimized uncertainty propagation with sample isotope compositions in the range ²⁰⁶Pb/²⁰⁴Pb = 14 to 30. SBL74 is calibrated relative to a conventional reference value ²⁰⁸Pb/²⁰⁶Pb = 1.00016 for NIST SRM 982 (ref. 49) and has a composition of ²⁰⁴Pb/²⁰⁶Pb = 9.2317, ²⁰⁷Pb/²⁰⁶Pb = 36.6450 and ²⁰⁸Pb/²⁰⁶Pb = 1.8586. SBL74 is currently used for Pb isotopic determinations by more than 10 laboratories around the world.

TIMS analysis acquired ^20xPb/²⁰⁶Pb ratios on two filament loads: a “natural” run with sample only and a sample–spike mixture run. Samples were loaded as for the earlier measurements, but using the silicic acid–phosphoric acid emitter defined by Gerstenberger and Haase.⁵⁰ The optimum mixture of sample and spike was calculated as ²⁰⁴Pb_Sample/²⁰⁴Pb_Spike (q) = 0.09, with a tolerance range of 0.03–0.65; within which negligible uncertainty magnification was observed. Ratios on both the sample and mixture runs were measured using a multi-dynamic routine similar to Thirlwall.¹⁶ In the Southampton protocol both the natural and mixture runs included an initial measurement block of 20 ratios with >0.9 × 10⁻¹¹ A ²⁰⁸Pb to provide a ²⁰⁸Pb/²⁰⁶Pb value to which dynamic results of each run could be normalized. Final ^20xPb/²⁰⁶Pb ratios for both the natural and mixture runs were integrated from 3 blocks of 20 × 5 s integrations with Pb ion currents of ∼4 × 10⁻¹¹ A Pb, which is around five times more signal than the pre-1998 measurements. As with the earlier non-double spike measurements, rhenium filament temperatures were kept between 1050 °C and 1180 °C. Mass fractionation was calculated via the double spike using a power law correction following the routine of Johnson and Beard.⁵¹ Results for the natural (unspiked) run were also corrected for mass fractionation using f = c (0.14% amu⁻¹), to allow a direct comparison to be made with the double spike corrected values. As the latter can be assumed to equate to the “true” isotope ratios of unknown samples they can be used to rigorously examine the actual spread of f = c corrected data.

For comparison with another laboratory, Pb isotope data for the NIST 981 standard are presented from a VG Sector 54 instrument at the Geological Survey of Japan. These data were acquired using the same SBL74 double spike, chemical separation and loading protocols as post-2000 Southampton. Measurements were made in static mode as an integration of 100 ratios.

3.3 Multi-collector inductively coupled plasma mass spectrometry (MC-ICP-MS)

In addition to the TIMS, between 2000–2004 Pb isotope measurements were also made using a Micromass IsoProbe MC-ICP-MS instrument equipped with 12 Faraday and 5 ion-counting detectors. Immediately prior to measurement, sample solutions were split into a natural fraction, spiked with Tl (NIST 997) to give ∼0.4 × 10⁻¹¹ A ²⁰⁵Tl, and an aliquot spiked with the SBL74 double spike. Samples were run as natural/Tl and DS spiked batches, with a full cleaning of the sample introduction system between. This significantly reduced the possibility of double spike contamination of the non-double spiked run. Both spiked and natural/Tl fractions were introduced to the instrument in 0.4 M HNO₃via a Cetac MCN6000 desolvating nebuliser in conjunction with a 100 μl min⁻¹ nebuliser. Data were acquired statically in the Faraday detectors as 3 blocks of 20 integrations of 5 s from total Pb ion currents of 0.5 × 10⁻¹⁰ A (>3 V ²⁰⁸Pb across 10¹² Ω). Measurements were corrected using the power law deconvolution of Johnson and Beard.⁵¹ Other methodology and standards data for the IsoProbe measurements are provided in Ishizuka et al.²⁹

Pb isotope measurement by MC-ICP-MS was switched to a Thermo Neptune instrument from 2008 onwards. Sample solutions were aspirated using an Aridus II desolvating nebulizer with an uptake of 100 μl min⁻¹. As with the IsoProbe protocol above, a natural fraction and double spiked fraction were run in discrete batches, with rigorous cleaning of the Aridus II between. All samples and standards were preceded by a 5 min wash, with an additional 0.6 M HNO₃ blank measured using the same 8 min acquisition procedure used for the samples. The natural run was routinely spiked with Tl (NIST 997) to give ∼0.5 V ²⁰⁵Tl, and hence enabling a Tl mass fractionation correction to be acquired simultaneously with the double spike corrected data. Isotope ratios on the Neptune were measured in static multi-collector mode with 40–60 × 4.2 s integrations, using total Pb ion currents of >2 × 10⁻¹⁰ A (>12 V ²⁰⁸Pb across 10¹¹ Ω). Overall ion yields are typically 1.4% (an effective sensitivity of ∼1100 V μg ml⁻¹ ΣPb). Mass fractionation was calculated via the double spike using an iterative exponential law correction modified after the power law method of Woodhead et al.⁵

4. Results and discussion

4.1 Assessment of Pb isotope results

A summary of the Pb isotope data and associated measurement precision from TIMS and MC-ICP-MS are presented in Table 1. These include data for the four different mass fractionation correction techniques: f = c, Tl-spike, double spike and sample–standard bracketing. For comparison, the f = c and sample–standard data are corrected to the same NIST SRM 981 poly-spike average values ²⁰⁶Pb/²⁰⁴Pb = 16.9412, ²⁰⁷Pb/²⁰⁴Pb = 15.4988, ²⁰⁸Pb/²⁰⁴Pb = 36.7233 (see below), and Tl-spike is corrected relative to ²⁰⁵Tl/²⁰³Tl = 2.3885 for the NIST SRM 997. This value is higher than the certified ratio of ²⁰⁵Tl/²⁰³Tl = 2.3871 ± 10 (ref. 52) and is estimated as the Tl ratio which best reproduces the poly-spike average value of NIST SRM 981 from n = 50 measurements using an exponential law function to correct for mass discrimination.

Table 1 Compiled data for NIST SRM 981 Pb isotope standard. Upper 4 rows are non-double spike determinations from Southampton. Correction by f = c is expressed as the measured standard values (first row) and for the 2sd of sample ratios expressed relative to the 981 standard. Central rows are the poly-spike laboratories used in the compilation including this study,^{6,28,30,33,34,36,62} and the average value from the Mainz laboratory which is compiled from.^32,63–70 The lower section of the table reproduces the earlier 981 determinations and provides translation factors for each isotope ratio to translate existing data to the poly-spike value^a

			^206Pb/^204Pb	±2sd	^207Pb/^204Pb	±2sd	^208Pb/^204Pb	±2sd	^207Pb/^206Pb	±2sd	^208Pb/^206Pb	±2sd
a * -recalculated to 982 ^208Pb/^206Pb = 1.00016, ** = 1–5 ng average, italic numbers are 2se. Methods DS = double spike; TS = triple spike. Spike ID: ^1 = SBL74 (Southampton) spike; ^2 Mainz spike; ^3 = Royal Holloway spike; ^4 = PML, Japan; ^5 = Geological Survey of Canada.
This study: non-double spike determinations	TIMS f = c, 981 standards		16.9403	0.0248	15.4979	0.0324	36.7213	0.1013	0.91486	0.00061	2.16769	0.00291
	TIMS f = c, samples normalised to 981		16.9403	0.0469	15.4979	0.0642	36.7213	0.2020	0.91486	0.00061	2.16769	0.00291
	MC-ICP-MS Neptune thallium spike		16.9395	0.0069	15.4964	0.0081	36.7154	0.0255	0.91481	0.00018	2.16744	0.00077
	MC-ICP-MS Neptune sample–std		16.9415	0.0066	15.4985	0.0084	36.7212	0.0276	0.91483	0.00015	2.16754	0.00075
Poly-spike study	Method	Instrument
This study Southampton Sector 54	DS (204-207)^1	TIMS	16.9402	0.0027	15.4981	0.0027	36.7222	0.0075	0.91487	0.00008	2.16775	0.00017
This study GSJ Sector 54	DS (204-207)^1	TIMS	16.9403	0.0029	15.5000	0.0038	36.7224	0.0090	0.91497	0.00008	2.16775	0.00011
This study Neptune	DS (204-207)^1	MC-ICP-MS	16.9415	0.0022	15.4985	0.0021	36.7212	0.0063	0.91483	0.00006	2.16754	0.00017
Galer and Abouchami, 1998	TS (204-206-207)^2	TIMS	16.9405	0.0015	15.4963	0.0016	36.7219	0.0044	0.91475	0.00004	2.16771	0.00010
Thirlwall, 2002	DS (204-207)^3	TIMS	16.9408	0.0021	15.4980	0.0025	36.7220	0.0080	0.91483	0.00007	2.16767	0.00041
Thirlwall, 2002	DS (204-207)^3	MC-ICP-MS	16.9417	0.0029	15.4996	0.0031	36.7240	0.0080	0.91488	0.00008	2.16770	0.00024
Kuritani and Nakamura, 2003	DSx2 (204-5/204-7)	TIMS	16.9414	0.0028	15.4992	0.0029	36.7230	0.0075	0.91487	0.00005	2.16765	0.00018
Baker et al., 2004	DS (204-207)^1	MC-ICP-MS	16.9416	0.0013	15.5000	0.0015	36.7262	0.0031	0.91491	0.00004	2.16781	0.00012
Amelin and Davis, 2006*	DS (202-205)^5	TIMS	16.9408	0.0012	15.4987	0.0011	36.7278	0.0029	0.91487	0.00001	2.16800	0.00005
Makishima et al. 2007	DS (204-207)^4	MC-ICP-MS	16.9417	0.0024	15.4988	0.0025	36.7196	0.0066	0.91483	0.00005	2.16741	0.00016
Mainz average 2000–2008	TS (204-206-207)^2	TIMS	16.9415	0.0007	15.4984	0.0021	36.7264	0.0060	0.91482	0.00004	2.16784	0.00014
Hoernle et al., 2011	DS (204-207)^1	TIMS	16.9416	0.0024	15.4998	0.0024	36.7231	0.0063	0.91490	0.00005	2.16763	0.00013
Makishima and Nakamura, 2010**	DS (204-207)^4	MC-ICP-MS	16.9415	0.0030	15.4991	0.0034	36.7233	0.0077	0.91486	0.00005	2.16766	0.00019
NIST SRM 981 poly-spike average			16.9412	0.0003	15.4988	0.0006	36.7233	0.0013	0.914861	0.00003	2.16770	0.00008
Todt et al.,1996	DS (202-205)	TIMS	16.9356		15.4891		36.7006		0.91459		2.16707
Todt et al.,1984		TIMS	16.9374		15.4926		36.7067		0.91470		2.16720
Catanzaro et al., 1968		TIMS	16.9371		15.4913		36.7213		0.91464		2.16810
Todt et al.,1996 to poly-spike conversion factors			1.00033		1.00063		1.00062		1.00030		1.00029
Todt et al.,1984 to poly-spike conversion factors			1.00022		1.00040		1.00045		1.00018		1.00023
Catanzaro et al., 1968 to poly-spike conversion factors			1.00024		1.00048		1.00005		1.00024		0.99982

---

It should be noted that the f = c and Tl-spike ratio data for NIST SRM 981 are generated by calibrating to the poly-spike average values for NIST SRM 981. As such, the Pb isotope ratios presented in Table 1 for these measurement techniques do not provide an assessment of the measurement accuracy or an estimate of the measurement trueness of these methods. However, the measurement precision for isotope ratios produced by the f = c and Tl-spike techniques does reflect the closeness of values produced by replication.

Uncertainty data in Table 1 are quoted as twice the standard deviation (2sd) on each ratio. Where the isotope ratios are an average compiled from a series of datasets, each of which is itself an average of a number of measurements, the uncertainty is expressed as 2sd/√n.

Additional information on the average 2sd per mass unit difference and expressed as parts per million (2sd amu⁻¹ ppm) is provided in the ESI in Table S1.†

Fig. 2 shows the co-variation between Pb isotope ratios for NIST SRM 981, corrected for mass fractionation by three separate techniques on two instruments. As the TIMS f = c analyses have large variance relative to the other techniques shown in Fig. 2, the scale for the TIMS double spike, MC-ICP-MS double spike and MC-ICP-MS Tl-spike (lower three rows of plots) is considerably magnified. The box shown on each of the TIMS f = c plots demarcates the length of the axes of the magnified scale. Trends are also defined that extend from the average NIST SRM 981 value along mass fractionation vectors and, where appropriate, reflect variation in the isotope ratio caused by imprecision in the measurement of the minor ²⁰⁴Pb isotope. An uncertainty ellipse at the 95% confidence level is calculated from each co-variation and plotted parametrically with the standard data. These ellipses should be considered as reflecting a minimum estimate of the true distribution. As two processes, ²⁰⁴Pb uncertainty and mass fractionation,⁵³ can affect isotope ratio pairs, it should be noted that the calculation of covariance and regression values for these ellipses may not equate a simple relationship between two correlated normal distributions.

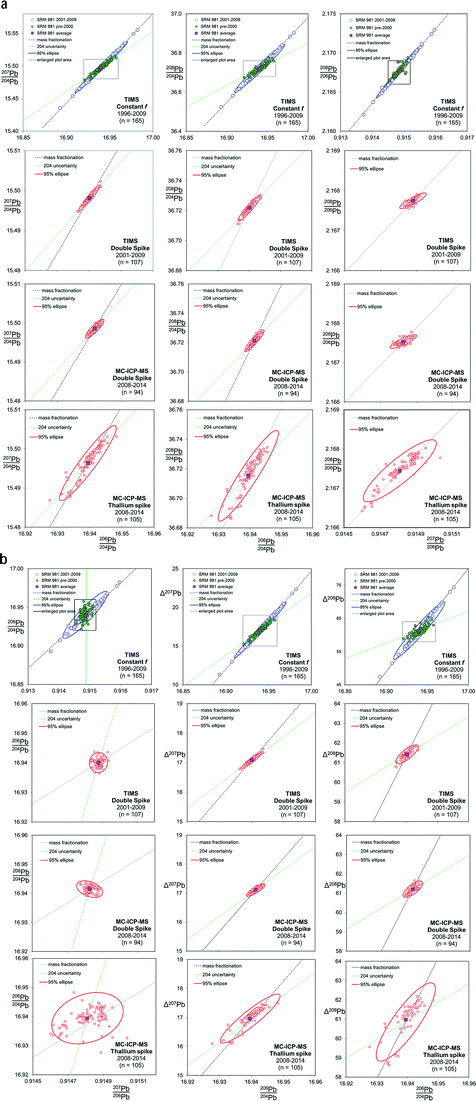Fig. 2 Six Pb ratio–ratio co-variation plots, each shown for four mass fractionation/mass spectrometer correction methods: TIMS f = c; TIMS double spike; MC-ICP-MS double spike; MC-ICP-MS Tl-spike. Mass fractionation vectors and, where appropriate, ²⁰⁴Pb uncertainty vectors are shown. The Δ²⁰⁷Pb and Δ²⁰⁸Pb parameters are from ref. 55 and discussed further in the text. Uncertainty ellipses are generated from covariation regression analysis with axes lengths scaled to 95% confidence.

4.2 TIMS f = c corrected data

TIMS f = c analyses of NIST SRM 981 are separated into two analytical periods as shown in the upper most plots in Fig. 2: pre-2000 and 2001–2009. Pre-2000 data were measured as unspiked analyses only, while the later data are the unspiked runs of the double spike analytical pairs. Average Pb ratios of all the measured data for the standard have then been used to calculate the f-value per amu relative to the poly-spike average (see below and Table 1). This fractionation constant has then been applied to each measurement to effectively centre the dataset on the poly-spike average while retaining the relative distribution of each analysis. An observation that can be made from the f = c plots in Fig. 2 is that pre-2000 data (green filled symbols) has a more limited variance relative to 2001–2009 (blue symbols). It also appears that the scatter in this early data is aligned with the ²⁰⁴Pb uncertainty vector, which is particularly apparent in Δ²⁰⁸Pb–²⁰⁶Pb/²⁰⁴Pb and ²⁰⁶Pb/²⁰⁴Pb–²⁰⁷Pb/²⁰⁶Pb space. 2001–2009 dataset has a greater spread and is clearly distributed parallel to the mass fractionation vector. Table 1 defines the scatter of this data as around 700 ppm amu⁻¹, which equates to an uncertainty of ±0.025 (±0.15%) on ²⁰⁶Pb/²⁰⁴Pb.

The change in the data distribution between the two periods is likely to stem from the differing analytical protocols used. The early period typically acquired data from ∼16 mV ²⁰⁴Pb ion beams (0.6 V ²⁰⁸Pb), while the unspiked runs of the double spike protocol demanded ∼80 mV ²⁰⁴Pb ion beams (3 V ²⁰⁸Pb). The smaller ion beams resulting in more scatter from ²⁰⁴Pb uncertainty, while the larger beams of the later period suppressed this facet. However, the increased energy required to generate the large beams may have resulted in a greater range of fractionation.

Prior to 2000, the majority of studies publishing lead isotope ratios used the f = c correction, with the reproducibility of NIST SRM 981 used to provide an estimate of the measurement precision of samples. However, for reasons outlined above, and by Thirlwall,¹⁶ real sample measurements have the potential to exhibit a greater range of fractionation than the ideal solution isotope standard. This can be effectively quantified by examining the range of mass fractionation observed in actual samples, which can be calculated for the unspiked runs of the double spike analytical pair. As the uncertainty of double spike fractionation factors are more than an order of magnitude smaller than f = c, expansion of the uncertainties through to each sample is calculated to be negligible. In the 2000–2009 period, 834 samples were analysed by TIMS using double spike, and the calculated mass fractionation for these are shown as a histogram is in Fig. 3. These data are also compared with the mass fractionation distribution of the standard data covering this period and pre-2000. The sample distribution is slightly skewed to higher mass, and has a much wider variance than the standards (2sd of 0.00137 vs. 0.00075 f amu⁻¹). Standard data are also skewed, but the average, median and mode are significantly higher than the sample data.

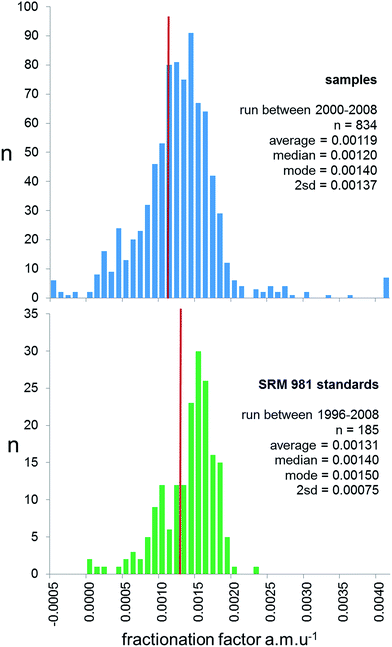Fig. 3 Frequency distribution of fractionation factor (f) for rock samples (upper panel) and SRM 981 Pb standard (lower panel) measured on TIMS. For rock samples f is calculated for the natural run of the double spike correction procedure. For standards f is expressed relative to the poly-spike average in Table 1. Both are calculated as a linear correction per mass unit difference, f = (t/a) − 1)/Δm; where t is the true ratio, a is the measured ratio and Δm is the mass difference of the ratio (e.g.²⁰⁶Pb/²⁰⁴Pb = 2). The red line on both panels represents the average fractionation factor.

There are two aspects of the distributions in Fig. 3 which have consequences for sample data corrected by f = c. Firstly, samples typically are fractionated ∼0.012% amu⁻¹ less than the standards used to calculate f. Following correction by this f-factor, this offset translates into a typical inaccuracy of sample isotope ratios of 270 ppm for ²⁰⁶Pb/²⁰⁴Pb and 540 ppm for ²⁰⁸Pb/²⁰⁴Pb, i.e. an offset to lighter ratios by ∼0.005 and ∼0.020 respectively. Secondly, any estimates of reproducibility based solely on the frequency distribution of standard measurements are likely to underestimate the variance of the sample distribution by a factor of ∼2. This means, for example, the true reproducibility of ²⁰⁶Pb/²⁰⁴Pb would be ±0.047 and ²⁰⁸Pb/²⁰⁴Pb ±0.20 at 95% confidence. As an example, the “TIMS constant f samples” row in Table 1 shows how these uncertainties relate to NIST SRM 981 ratios.

4.3 TIMS and MC-ICP-MS double spike data

For any given parameter in Table 1, the precision of the double spike determination of standards using the Sector 54 TIMS instruments in Southampton and Tokyo are around 10× smaller than those from TIMS f = c (e.g. 64–76 ppm amu⁻¹vs. 706 ppm amu⁻¹ respectively). If the f = c uncertainty is estimated from real samples, this factor rises to ∼20×. In turn, MC-ICP-MS double spike measurements from the Neptune are marginally better again (51 ppm amu⁻¹) than TIMS double spike.

What is notable about the data for both TIMS and MC-ICP-MS double spike methods is that the covariance between the isotope ratio parameters appears to lie along a ²⁰⁴Pb uncertainty vector, rather than a mass fractionation vector. This MC-ICP-MS double spike dataset is examined in more detail in the enlarged plot shown in Fig. 4. Here selected analytical time-periods have been highlighted in ²⁰⁶Pb/²⁰⁴Pb–²⁰⁸Pb/²⁰⁴Pb space. From the whole dataset, the long-axis of the calculated uncertainty ellipse is almost coincident with the ²⁰⁴Pb uncertainty line. When individual time-periods are considered, the data in each forms a tight linear trend which is parallel to the ²⁰⁴Pb line. Each of these trends intercepts the mass fractionation uncertainty line close to the centre of the ellipse, and roughly at its average value.

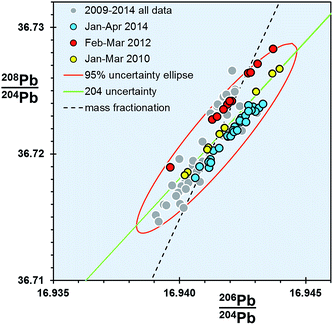Fig. 4 ²⁰⁶Pb/²⁰⁴Pb vs.²⁰⁸Pb/²⁰⁴Pb for NBS SRM 981 measured on Neptune MC-ICP-MS double spike. Three analytical time periods within the dataset are highlighted.

These data suggest that within any given period, the double spike correction has effectively removed any significant variation caused by mass fractionation. Presumably the residual uncertainties are restricted to factors that particularly affect the minor isotope ²⁰⁴Pb, such as signal-to-noise ratio, baselines and peak tailing. More efficient and less noisy Faraday collector and amplifier pairs in the MC-ICP-MS relative to the older-design TIMS can explain the subtle differences in the extent of data scatter along the ²⁰⁴Pb vector.

On this basis future measurement protocols could produce a significant improvement in the resolution of Pb double spike data if, (i) standards from a particular time period are averaged, and a normalising factor generated which adjusts this value to a common standard value (i.e. the poly-spike average). Differences between time periods are unexplained, but could be generated by changes in Faraday cup efficiencies; (ii) improved low-noise, high-impedance 10¹² to 10¹³ amplifiers are deployed to reduce ²⁰⁴Pb uncertainty. The first point would ensure accuracy and coincident plotting of samples measured in different time periods, the second would tighten the scatter and constrain the length of the uncertainty ellipse.

4.4 Tl-spike correction

MC-ICP-MS thallium corrected data are presented in the final row of Fig. 2. As these data are generated from Tl-spike added to the natural run of MC-ICP-MS double spike analytical pair, the two measurements should provide an ideal comparison between the techniques. As such, it is notable that the Tl-corrected ratios have precision around 188 ppm amu⁻¹ (Table 1), which is ∼3× times greater than that of double spike. Distribution of the Tl-corrected data does not appear to visually correlate definitively with either the ²⁰⁴Pb or the mass fractionation vectors. However, on the basis of the ²⁰⁷Pb/²⁰⁶Pb–²⁰⁶Pb/²⁰⁴Pb and ²⁰⁶Pb/²⁰⁴Pb–Δ²⁰⁸Pb plots, mass fractionation is the dominant control on the distribution of measurement values. Theoretically, the ²⁰⁴Pb vector observed in the MC-ICP-MS double spike data (Fig. 4) will be present in the same proportion in the Tl-spiked data. This will then be compiled with the uncertainty produced by any defects in the mass fractionation relationship between Tl and Pb, either on a long-term or within-run basis. Overall, the result of the interaction between the two resulting frequency distributions is the more steeply-aligned and oblate ellipse observed in the Tl-corrected data relative to the shallower and prolate uncertainty ellipse generated by double spiking.

Differences in the magnitude and distribution of Tl-spiked and double-spiked data are examined further in Fig. 5. These plots show the Pb isotopes of six samples of bronze taken from the Belgammel Ram; a Hellenistic-Roman Proembolion found off the Coast of Libya.⁵⁴ Bronze samples were processed via anion exchange to isolate Pb, before the isotopic composition of each was measured by double spiking, with the natural run of the double spike pair also spiked with Tl. As such, both techniques were deployed from single mass spectrometer runs. Two methods were used to correct the Tl-spike data. Firstly, all Pb isotope ratios were corrected by a single mass fractionation (β) factor derived from a specific value of ²⁰⁵Tl/²⁰³Tl (Fig. 5(a)). Secondly, using the correction method devised by Woodhead,⁴⁶ in which corrected ratios are calculated by defining individual β-factors for each ^20xPb/²⁰⁴Pb ratio with ²⁰⁵Tl/²⁰³Tl (Fig. 5(b)). These two methods are compared with the double spike corrected data shown in Fig. 5(c).

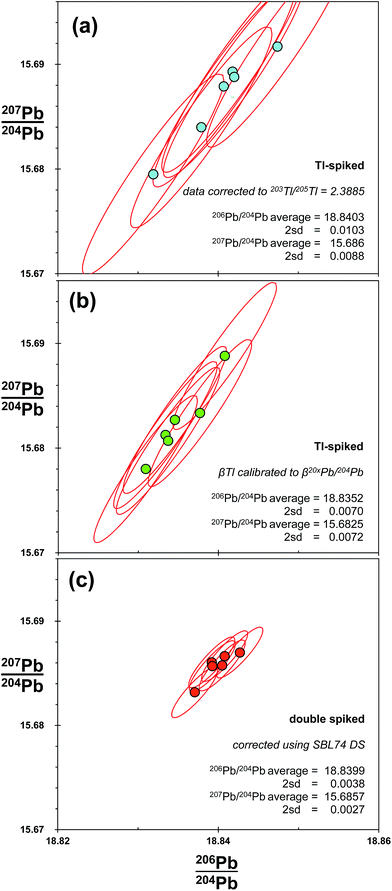Fig. 5 Pb isotope analysis of six samples taken from the Belgammel Ram: a Hellenistic-Roman Bronze Proembolion.⁵⁴ Isotope ratios of each sample are measured during a single run, but corrected for mass fractionation using three methods. (a) Spiking with Tl and an exponential correction of all ^20xPb/²⁰⁴Pb ratios relative to ²⁰³Tl/²⁰⁵Tl = 2.3885; (b) spiking with Tl and an exponential correction where each ^20xPb/²⁰⁴Pb ratio is calibrated against ²⁰³Tl/²⁰⁵Tl for standards with a range of mass fractionation (β) factors.⁴⁶ (c) Double spiked with SBL74; a second aliquot of each sample was measured to calculate mass fractionation of the unspiked sample via an iterative exponential-law deconvolution. Average and 2sd for the six samples are shown for each of the correction techniques. For comparison, uncertainty ellipses for individual samples are the 2sd reproducibility of SRM 981 for the particular correction technique employed (Table 1).

Like the NIST SRM 981 Tl-spiked data, the precision of the single β-Tl data (Fig. 5(a)) is ∼3 times worse than double spike. Using the individual β-Tl correction, the precision is better, but still ∼2 times larger than double spike. As with the Tl-spiked standard data in Fig. 2, the spread of Tl-spiked data for the bronze roughly defines the extent and orientation of the Tl-uncertainty ellipse: i.e. aligned with a mass fractionation vector. In the same way, the double spike Pb from the ram matches the disposition of the DS standard data along a ²⁰⁴Pb vector.

4.5 Sample–standard bracketing correction

Correction via bracketing techniques has the potential to be affected by matrix differences between samples and standard as no internal monitor of mass fractionation is present. If chemical isolation of Pb is comprehensive, then matrix effects should be minimal. However, without screening and testing for a range of contaminants an ideal sample solution cannot be guaranteed. A test of sample–standard bracketing over a range of sample types and analytical conditions can be made by using the mass fractionation calculated from double spiked samples to correct intervening samples. Bracket-corrected samples can then be compared to the data from their own double spike correction. However, as each sample has an independent uncertainty on its double spike mass fractionation determination, the effect of uncertainties propagating from both bracketing analyses needs to be considered.

Fig. 6 summarises the results of mass fractionation variation (for simplicity shown as the linear factor f amu⁻¹) within two sessions: (a) April 2012 and (b) July 2014. Each session is made up of the natural runs from the double spike analytical pair. All samples, and intervening NIST SRM 981 standards, were spiked with Tl. The first run was of peat samples, which had been acid-leached and purified via a single-pass anion exchange procedure. The later run consisted of HF–HNO₃ digested basalt and andesite volcanics, refined through two-pass anion exchange. In both cases sample solutions were diluted and spiked immediately prior to analysis on the MC-ICP-MS.

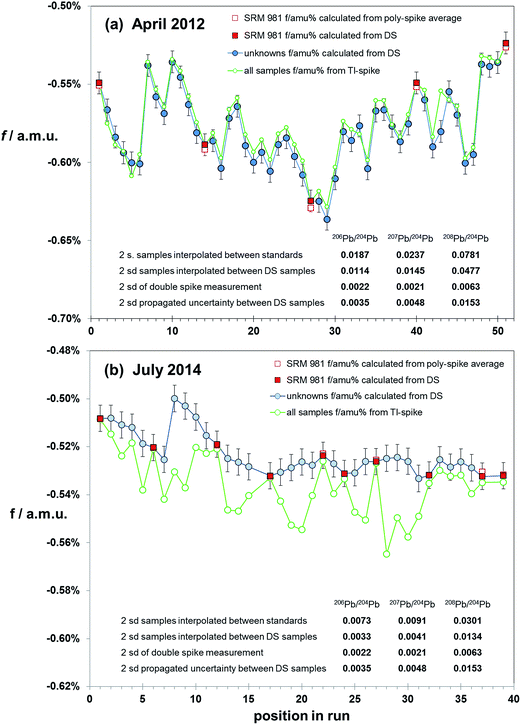Fig. 6 Variation in fractionation (f/amu) in samples during the course of two runs: (a) from April 2012, (b) from July 2014. For simplicity, the fractionation is expressed as linear factor (f). Fractionation of unknown samples (blue filled circles) is calculated by double spike (DS). SRM 981 Pb standards are interspersed with the unknowns, and fractionation for these are calculated by double spike (filled red squares) and relative to the poly-spike average values from Table 1 (open red squares). Error bars represent the ±2sd of f calculated via double spike (±0.006%). Samples were acquired for 100 integrations of 4 seconds, separated by with a 12 min wash, of which the final 7 min is acquired in the same mode as a sample measurement. Initiation of each sample or standard is ∼21 min apart. Inset tables estimate uncertainty as 2sd on ^20xPb/²⁰⁴Pb calculated from (i) interpolation of fractionation between SRM 981 standards, (ii) interpolation of fractionation between bracketing samples (calculated by DS), (iii) estimated double spike reproducibility, (iv) propagated uncertainty for mass fractionation of samples calculated from the interpolation of two adjacent mass fractionations calculated from double spike measurement.

April 2012 analyses reflect more unstable analytical conditions through the course of the 18 hour run with mass fractionation ranging fairly erratically between −0.64% and −0.52% amu⁻¹. Given this variation, it is not surprising that the precision of ratios calculated via interpolation between the standards (spaced at ∼10 samples) are 10 times the double spike uncertainty (see table within Fig. 6(a)). However, if each sample is corrected using the double spike-calculated mass fractionation of its adjacent samples, the uncertainty is reduced to ∼6 times that of the double spike. This is still ∼3 times higher than propagated from the interpolation between two double spike mass fractionation determinations.

July 2014 data have considerably more stable mass fractionation: only changing by 0.03% amu⁻¹ during the 14 hours of measurement, and in a more systematic fashion. Interpolation between standards (spaced at ∼5 samples) produces an uncertainty ∼3 times that of double spiking. Using alternate samples to correct intervening samples produces uncertainties equivalent to, or less than, the propagated double spike interpolation.

Results for the earlier run show that mass fractionation calculated via the Tl-spike produces a broadly similar pattern of variation relative to the double spike determinations. However, it is notable that the Tl-spike mass fractionation for the standards is equivalent to the double spike mass fractionation, while 90% of the samples have lower (less negative) f-factors via Tl-spike. July 2014 data, though produced in more analytical stable conditions and with more rigorous Pb isolation, have notably more scattered Tl-spike mass fractionation compared to the standard and double spike pattern. Furthermore, the Tl-spike mass fractionation for all samples can be seen to have a greater (more negative) and variable f relative to the double spike. At the same time, the Tl-spike fractionation for the standards is equivalent to the double spike and true value determinations.

Both the early and later runs suggest that regardless of chemical refinement, solution preparation and instrumental stability, Tl-spike mass fractionation can be compromised by residual matrix in sample aliquots. Monitoring standard data provides an erroneous overestimate of the quality of sample data in terms of accuracy and resolution. Sample–standard bracketing, with alternate standards, provides a more robust correction than Tl-spiking, approaching that of double spiking where drift in instrumental mass fractionation is limited.

4.6 Towards ultra-high resolution Pb isotopes

Evidence from the double spike corrected data above indicates that further improvement in data quality may be gained from reducing the uncertainty associated with measurement of the minor isotope – ²⁰⁴Pb. This may be achieved by the introduction of a suitably-assigned high-impedance resistor in the Faraday array. In the case of 10¹³ Ω resistors, this could increase the relative signal to noise by a factor of 100 relative to 10¹¹ Ω, and effectively equate ²⁰⁴Pb to the level of ²⁰⁸Pb. An alternative is the 2× double spike approach of Kuritani and Nakamura,³⁶ where the ²⁰⁴Pb is boosted in each of two spiked runs. This is designed for low-level samples, but may well enhance precision of larger sample sizes (>5 ng Pb).

As discussed in 4.3 above, double spike data can potentially be resolved to remove any significant mass fractionation, to leave a Gaussian scatter along the ²⁰⁴Pb vector. This scatter could be reduced by multiple measurements of samples and taking an average. Effectively, the measurement uncertainty, represented as 2sd, switches to the precision of the mean which is denoted by 2se: equating to dividing 2sd by √n. An example of double spike averaging applied to real samples is shown in Fig. 7. These plots use ²⁰⁶Pb/²⁰⁴Pb–²⁰⁷Pb/²⁰⁴Pb together with an alternative perspective by deploying the delta ²⁰⁷Pb/²⁰⁴Pb (Δ²⁰⁷Pb) parameter⁵⁵ as the ordinate. This can be used to effectively “stretch” lead isotope ratio plots to help visualise variations within typically co-linear Pb isotope datasets. These plots show the Pb isotopes of basalt lava samples recovered from discrete locations around Izu-Oshima volcano, Japan. When grouped, samples from each location define an array of roughly equivalent size and shape to the double spike uncertainty ellipse (Fig. 7(a and b)), indicating that each location approximates to a homogeneous composition. What is particularly remarkable in the Δ²⁰⁷Pb plot (a) is that all of these 27 individually-processed samples lie within ±0.18 Δ²⁰⁷Pb units, which is within the precision defined by the Pb standard on the same instrument (±0.20 Δ²⁰⁷Pb; Table 1).

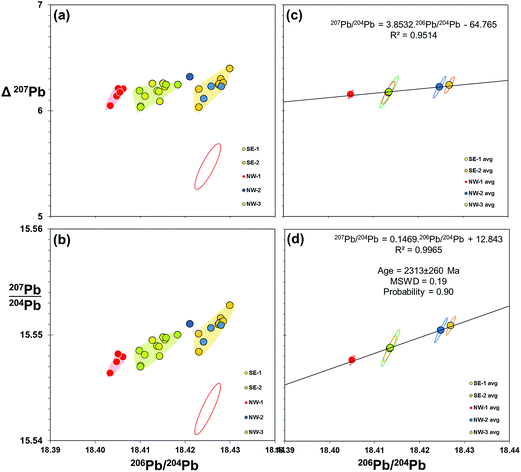Fig. 7 ²⁰⁶Pb/²⁰⁴Pb vs.²⁰⁷Pb/²⁰⁴Pb and Δ²⁰⁷Pb for submarine volcanic rocks from offshore Izu-Oshima, Japan. 4 to 6 samples collected from five spatially-discrete eruptions from the NW and SE of the island are measured for Pb isotopes by double spike on Neptune MC-ICP-MS. Individual sample data with 95% confidence uncertainty ellipse for double spike measurement is shown in (a and b). Average data for each location group are plotted in (c and d) with standard uncertainty ellipses for each mean. Isochron age calculated from slope of regression line given in (d), mean squared weighted deviation (MSWD) and probability of fit calculated from.⁵⁹ Pb isotope data used in these plots is available as a ESI Table.†

Equivalent plots showing the averages and standard uncertainty ellipses for each location group are shown in Fig. 7(c and d). Regressions through the isotope data appear robust (R² = 0.95 and 0.99), passing through the centre of the average data points. Fig. 7(d) is a ²⁰⁶Pb/²⁰⁴Pb–²⁰⁷Pb/²⁰⁴Pb “isochron” plot which the slope of the regression line can be computed as an age. Because these lavas are <0.5 Ma – essentially “zero-age” in geological terms – there is not likely to be any significance to the isochron, however, regression analysis equates to 2313 ± 260 Ma. This age uncertainty (∼10%) is poor by isochron standards, but given the range of isotope ratios involved (²⁰⁶Pb/²⁰⁴Pb maximum–minimum = 0.022), it emphasises the potential applications for increased resolution. This could be in the form of geological age dating, or equally in constraining mixing lines between two or more components that define a sample suite.

4.7 Precision of Pb isotopes with respect to the range of isotopic compositions

Radiogenic isotope systems including Pb, Sr, Nd, and Hf are commonly used to identify processes, components or timescales within geological or oceanographic systems. Additionally, these isotopes can be used to discriminate between samples or to match them with a particular provenance; for example, to match archaeological artefacts with a metallogenic or lithological source, or to determine the source of sedimentary particulates.^15,56,57 However, for these isotope systems to be effective as a discriminant between samples requires either that there is a suitable spread of isotope compositions, or that the precision of the measurement technique is high enough to provide a sound statistical difference. These two parameters are linked, in that if the isotope system has a large natural range, then high measurement precision may not needed, but a small compositional range requires a high resolution to enable discrimination.

Recent improvements in the analytical precision via Tl-spike and poly-spiking have the potential to change the way in which Pb isotopes can be applied to scientific problems. To demonstrate this, Fig. 8 makes a comparison between each of the key radiogenic isotope systems. This plot expresses the precision of each isotope system relative to the range of isotope ratios in Earth materials. For simplicity, the isotopic range is calculated from the approximate extent of compositions found in mantle-derived rocks. In particular, Fig. 8 illustrates the ability for each isotope ratio to effectively distinguish between any two sample compositions; in other words the effective resolving power of the isotope system. Resolving power is expressed here as the precision (2sd) as a percentage of the isotopic range of compositions. Conventional external methods of correcting Pb mass fractionation (f = c) mean that its effective resolution is around 1%, placing Pb between Sr (0.6%) and Nd (2%). However, mass fractionation correction using the double spike technique promotes Pb to the most highly resolving (∼0.1%) of the radiogenic isotope systems – a factor of ten better than conventional Pb. The result is that double spike data can be viewed on enlarged areas of Pb–Pb ratio plots and still enable points to be separated outside measurement precision. Ultra-high resolution Pb measurement, either by multiple analysis or increasing peak to background ratios has the potential to increase the resolving power to ∼0.03%.

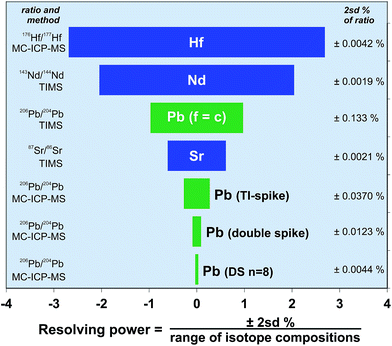Fig. 8 Comparison of analytical precision for radiogenic isotope systems expressed as a percentage of the spread of isotope compositions found in mantle-derived rocks. Each precision bar is calculated as e.g. ±2sd/(Δ¹⁴³Nd/¹⁴⁴Nd), where Δ = (max ¹⁴³Nd/¹⁴⁴Nd − min ¹⁴³Nd/¹⁴⁴Nd) in mantle rocks. End member mantle isotope compositions were chosen from the representative rocks: ED-DR34-1-3;⁶⁰ 98SM15.⁶¹ Column to the left of the chart includes the relevant isotope ratio and the measurement method, and the right column provides the typical 2sd% of the technique.

Actual precision for each system, expressed as a percentage of the isotope ratio, is given in the column on the right of Fig. 8. Hf, Sr and Nd have precision in the range ∼0.004–0.002%. The exact precision being controlled by the relative size of the smallest isotope needed to generate the fractionation-corrected ratio (e.g.⁸⁷Sr from ^86,87,88Sr), and the minimization and effectiveness of isobaric interference corrections (e.g.¹⁴⁴Sm on ¹⁴⁴Nd). Despite double spike Pb having the greatest resolving power of the radiogenic systems, the others are still capable of generating isotope ratios that are around 3–4 times more precise. As interference corrections on double spike Pb are generally minimal, and mass fractionation is effectively removed, the reason for the relative imprecision relates to ²⁰⁴Pb. When this is minimized, as for the n = 8 replicate double spike analysis shown in Fig. 8, the value approaches that of the Hf, Sr and Nd systems, demonstrating the potential for future improvements in Pb resolving power.

4.8 Converged values for NIST SRM 981

Table 1 also provides a re-assessment of the NIST SRM 981 standard, termed the poly-spike average. This is a compilation of mean values from 13 different TIMS and MC-ICP-MS instruments, all measured by poly-spike techniques (double, triple and 2× double spiking). The compilation includes mass fractionation correction via linear, power law and exponential systems and comprises 5 different spikes: in the case of SBL74 spike, calibrated at three separate laboratories. All spikes are calibrated relative to the reference measurement standard certified value of NIST SRM 982 ²⁰⁸Pb/²⁰⁶Pb = 1.00016.⁴⁹

Data from all laboratories are within their stated reproducibility of the poly-spike average. Fig. 9 shows that individual laboratory determinations cluster around the poly-spike average, with some tendency for the array to be aligned with a mass fractionation vector. The analysis from Galer and Abouchami⁶ lies to lower ²⁰⁷Pb/²⁰⁴Pb than the other poly-spike data, which may be related to the anomalous behavior of ²⁰⁷Pb on TIMS reported by Thirlwall.¹⁶ Notably, later data from the same laboratory – the Mainz average 2000–2008 in Table 1 – are coincident with the other poly-spike data. Original certification data⁴⁹ and later re-analysis of the standard^58,37 are excluded from the compilation, and all lie to lighter ratios roughly along the mass fractionation vector.

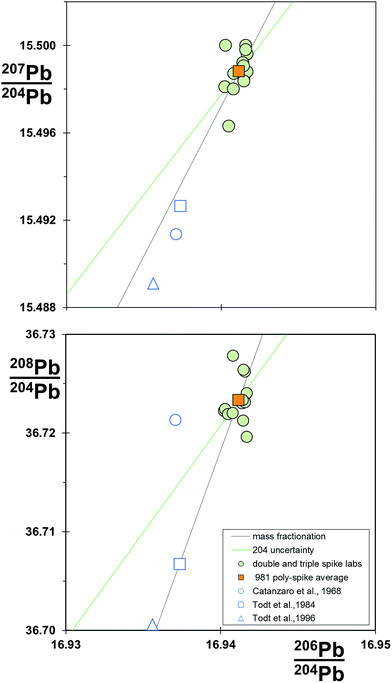Fig. 9 ²⁰⁶Pb/²⁰⁴Pb vs.²⁰⁷Pb/²⁰⁴Pb and ²⁰⁶Pb/²⁰⁴Pb vs.²⁰⁸Pb/²⁰⁴Pb for compilation of NIST SRM 981 standard data. Data for poly-spike laboratories (double, triple and 2× double spikes) and the poly-spike average are from Table 1. Linear law mass fractionation and ²⁰⁴Pb uncertainty vectors are shown relative to the poly-spike average.

Poly-spike determinations in the compilation are based on the same reference datum and all produce consistent isotope ratios for NIST SRM 981. This suggests that each spike is a valid secondary measurement standard. Furthermore, in the absence of any systematic measurements, the poly-spike average ratios for NIST SRM 981 are estimated to be accurate values.

5. Conclusions

Different mass fractionation correction techniques for Pb isotope determination have been assessed using data from a variety of mass spectrometers. Pre-double spike (or poly-spike) data for Pb was corrected by f = c, and has been previously recognised as significantly compromised in terms of their precision.¹⁶ Data from this study match these observations and highlight the potential inaccuracy of f = c related to the measurement of samples with remaining matrix. Double spike, data can be quantified as at least 10 times more precise, and has no discernible effects of matrix interference on the quantification of the ratios of interest.

Tl-spike corrected data can be measured during a double spike acquisition, and has provided a robust comparison between the techniques. Even attending to the defective relationship between Tl and Pb fractionation across the range of mass differences, and ensuring solution stability, Tl-spike corrected data has 2–3 times worse precision than double spiking. Examination of equivalent data in which mass fractionation is corrected by sample–standard bracketing shows that this is more precise than Tl-spiking when instrumental drift is stable and consistent, and is not significantly affected by matrix effects.

Double spike reproducibility data defines an uncertainty ellipse for each Pb–Pb isotope ratio that is scattered according to variance of the minor ²⁰⁴Pb isotope. Uncertainties induced by mass fractionation correction are minor and appear to be related to periodic instrumental changes. This suggests that data from temporally-constrained measurement periods have the potential to be internally consistent and have tighter precision. Such scatter can potentially be reduced using high-impedance amplifiers, or by 2× double spiking.³⁶ Alternatively, multiple analysis of individual samples can replicate this increase in precision, with a 2–3 times improvement depending on the number of replicates. Simulations of this ultra-high precision Pb analysis indicate that it has the potential to enhance geochemical and geochronological applications.

If an appreciation of differences in the uncertainty magnitude between alternative measurement protocols is maintained, then Pb isotopes can provide a usable discrimination tool between sample types. High-precision Pb isotopes are now the most resolving of all of the radiogenic isotope systems, and have the potential to make further advances for applications in Earth sciences, archaeometry and forensic science.

Acknowledgements

The authors thank all users of the isotope facilities at Southampton for their contribution to the standards dataset. In particular the assistance in the laboratory from Matt Cooper, Posy Boella, Tina Hayes, April Lloyd, Laura Hepburn and Loraine Foley. Laure Dosso collaborated in the creation of SBL74. Leah Carwithen and Sarah Munday carefully analysed the comparative samples during studies at Southampton. The authors appreciate a Japan–UK bilateral grant provided by JSPS, and a Royal Society travel grant to RNT. This paper also benefited from discussions with the Southampton geochemistry group and from the comments of two anonymous reviewers.

References

1. T. Elliott, T. Plank, A. Zindler, W. White and B. Bourdon, J. Geophys. Res.: Solid Earth, 1997, 102, 14991–15019.
2. Y. Niu, K. D. Collerson, R. Batiza, J. I. Wendt and M. Regelous, J. Geophys. Res.: Solid Earth, 1999, 104, 7067–7087.
3. M. H. Dodson, J. Sci. Instrum., 1963, 40, 289.
4. N. H. Gale, Chem. Geol., 1970, 6, 305–310.
5. J. D. Woodhead, F. Volker and M. T. McCulloch, Analyst, 1995, 120, 35–39.
6. S. J. G. Galer and W. Abouchami, Mineral. Mag., 1998, 62A, 491–492.
7. R. N. Taylor, M. F. Thirlwall, B. J. Murton, D. R. Hilton and M. A. M. Gee, Earth Planet. Sci. Lett., 1997, 148, E1–E8.
8. B. J. Murton, R. N. Taylor and M. F. Thirlwall, J. Petrol., 2002, 43, 1987–2012.
9. M. F. Thirlwall, M. A. M. Gee, R. N. Taylor and B. J. Murton, Geochim. Cosmochim. Acta, 2004, 68, 361–386.
10. P. E. Janney and P. R. Castillo, J. Geophys. Res.: Solid Earth, 1999, 104, 10571–10589.
11. R. N. Taylor, I. W. Croudace, P. E. Warwick and S. J. Dee, Chem. Geol., 1998, 144, 73–80.
12. D. Suzuki, Y. Saito-Kokubu, S. Sakurai, C.-G. Lee, M. Magara, K. Iguchi and T. Kimura, Int. J. Mass Spectrom., 2010, 294, 23–27.
13. M. D. Feigenson, M. J. Carr, S. V. Maharaj, S. Juliano and L. L. Bolge, Geochem., Geophys., Geosyst., 2004, 5, Q06001.
14. S. M. Straub, S. L. Goldstein, C. Class, A. Schmidt and A. Gomez-Tuena, J. Petrol., 2010, 51, 993–1026.
15. Z. A. Stos-Gale and N. H. Gale, Archaeol. Anthropol. Sci., 2009, 1, 195–213.
16. M. F. Thirlwall, Chem. Geol., 2000, 163, 299–322.
17. A. Hofmann, Earth Planet. Sci. Lett., 1971, 10, 397–402.
18. V. M. Oversby, Geochim. Cosmochim. Acta, 1973, 37, 2693–2696.
19. B. Hamelin, G. Manhes, F. Albarede and C. J. Allegre, Geochim. Cosmochim. Acta, 1985, 49, 173–182.
20. S. J. G. Galer, Chem. Geol., 1999, 157, 255–274.
21. J. BlichertToft, C. Chauvel and F. Albarede, Contrib. Mineral. Petrol., 1997, 127, 248–260.
22. R. N. Taylor, T. Warneke, J. A. Milton, I. W. Croudace, P. E. Warwick and R. W. Nesbitt, J. Anal. At. Spectrom., 2001, 16, 279–284.
23. R. N. Taylor, T. Warneke, J. A. Milton, I. W. Croudace, P. E. Warwick and R. W. Nesbitt, J. Anal. At. Spectrom., 2003, 18, 480–484.
24. N. C. Chu, R. N. Taylor, V. Chavagnac, R. W. Nesbitt, R. M. Boella, J. A. Milton, C. R. German, G. Bayon and K. Burton, J. Anal. At. Spectrom., 2002, 17, 1567–1574.
25. D. Vance and M. Thirlwall, Chem. Geol., 2002, 185, 227–240.
26. T. Warneke, I. W. Croudace, P. E. Warwick and R. N. Taylor, Earth Planet. Sci. Lett., 2002, 203, 1047–1057.
27. M. Bizzarro, J. A. Baker, H. Haack, D. Ulfbeck and M. Rosing, Nature, 2003, 421, 931–933.
28. M. F. Thirlwall, Chem. Geol., 2002, 184, 255–279.
29. O. Ishizuka, R. N. Taylor, J. A. Milton and R. W. Nesbitt, Earth Planet. Sci. Lett., 2003, 211, 221–236.
30. J. Baker, D. Peate, T. Waight and C. Meyzen, Chem. Geol., 2004, 211, 275–303.
31. M. F. Thirlwall, M. A. M. Gee, R. N. Taylor and B. J. Murton, Geochim. Cosmochim. Acta, 2004, 68, 361–386.
32. W. Abouchami, A. W. Hofmann, S. J. G. Galer, F. A. Frey, J. Eisele and M. Feigenson, Nature, 2005, 434, 851–856.
33. A. Makishima and E. Nakamura, J. Anal. At. Spectrom., 2010, 25, 1712–1716.
34. Y. Amelin and W. J. Davis, J. Anal. At. Spectrom., 2006, 21, 1053–1061.
35. J. M. Koornneef, C. Bouman, J. B. Schwieters and G. R. Davies, Anal. Chim. Acta, 2014, 819, 49–55.
36. T. Kuritani and E. Nakamura, J. Anal. At. Spectrom., 2003, 18, 1464–1470.
37. W. Todt, R. A. Cliff, A. Hanser and A. W. Hofmann, in Earth Processes: Reading the Isotopic Code, American Geophysical Union, 1996, pp. 429–437.
38. W. M. White, F. Albarède and P. Télouk, Chem. Geol., 2000, 167, 257–270.
39. N. S. Belshaw, P. A. Freedman, R. K. O'Nions, M. Frank and Y. Guo, Int. J. Mass Spectrom., 1998, 181, 51–58.
40. M. Rehkamper and A. N. Halliday, Int. J. Mass Spectrom., 1998, 181, 123–133.
41. M. Rehkamper and K. Mezger, J. Anal. At. Spectrom., 2000, 15, 1451–1460.
42. S. G. Nielsen, M. Rehkamper, A. D. Brandon, M. D. Norman, S. Turner and S. Y. O'Reilly, Earth Planet. Sci. Lett., 2007, 264, 332–345.
43. R. N. Taylor and O. Ishizuka, EOS Trans. Am. Geophys. Union, 2001, 82 , abstract V22B-1024.
44. J. Barling and D. Weis, J. Anal. At. Spectrom., 2008, 23, 1017–1025.
45. G. D. Kamenov, P. A. Mueller and M. R. Perfit, J. Anal. At. Spectrom., 2004, 19, 1262–1267.
46. J. Woodhead, J. Anal. At. Spectrom., 2002, 17, 1381–1385.
47. F. Albarede, P. Telouk, J. Blichert-Toft, M. Boyet, A. Agranier and B. Nelson, Geochim. Cosmochim. Acta, 2004, 68, 2725–2744.
48. I. G. Nobre Silva, D. Weis, J. Barling and J. S. Scoates, Geochem., Geophys., Geosyst., 2009, 10, Q08012.
49. E. J. Catanzaro, T. J. Murphy and W. R. Shields, J. Res. Natl. Bur. Stand., Sect. A, 1968, 72, 261.
50. H. Gerstenberger and G. Haase, Chem. Geol., 1997, 136, 309–312.
51. C. M. Johnson and B. L. Beard, Int. J. Mass Spectrom., 1999, 193, 87–99.
52. L. P. Dunstan, J. W. Gramlich, I. L. Barnes and W. C. Purdy, J. Res. Natl. Bur. Stand., 1980, 85, 1–10.
53. K. R. Ludwig, Earth Planet. Sci. Lett., 1980, 46, 212–220.
54. J. R. Adams, A. Antoniadou, C. O. Hunt, P. Bennett, I. W. Croudace, R. N. Taylor, R. B. Pearce, G. P. Earl, N. C. Flemming, J. Moggeridge, T. Whiteside, K. Oliver and A. J. Parker, Int. J. Naut. Archaeol., 2013, 42, 60–75.
55. S. R. Hart, Nature, 1984, 309(5971), 753–757.
56. J. Baker, S. Stos and T. Waight, Archaeometry, 2006, 48, 45–56.
57. H. Miller, I. W. Croudace, J. M. Bull, C. J. Cotterill, J. K. Dix and R. N. Taylor, Environ. Sci. Technol., 2014, 48, 7254–7263.
58. W. Todt, R. A. Cliff, A. Hanser and A. Hofmann, Terra cognita, 1984, 4(2), 209.
59. K. R. Ludwig, in Berkeley Geochronology Center. Special Publication, Berkeley, CA, USA, 1999, vol. 1a, p. 47.
60. C. M. Meyzen, J. N. Ludden, E. Humler, B. Luais, M. J. Toplis, C. Mevel and M. Storey, Geochem., Geophys., Geosyst., 2005, 6, Q11K11.
61. T. Elliott, J. Blichert-Toft, A. Heumann, G. Koetsier and V. Forjaz, Geochim. Cosmochim. Acta, 2007, 71, 219–240.
62. K. Hoernle, F. Hauff, T. F. Kokfelt, K. Haase, D. Garbe-Schönberg and R. Werner, Earth Planet. Sci. Lett., 2011, 306, 86–97.
63. I. Vlastelic, W. Abouchami, S. J. G. Galer and A. W. Hofmann, Geochim. Cosmochim. Acta, 2001, 65, 4303–4319.
64. J. Eisele, M. Sharma, S. J. G. Galer, J. Blichert-Toft, C. W. Devey and A. W. Hofmann, Earth Planet. Sci. Lett., 2002, 196, 197–212.
65. W. Abouchami, S. J. G. Galer and A. W. Hofmann, Chem. Geol., 2000, 169, 187–209.
66. M. Regelous, A. W. Hofmann, W. Abouchami and S. J. G. Galer, J. Petrol., 2003, 44, 113–140.
67. S. Pichat, W. Abouchami and S. J. G. Galer, Earth Planet. Sci. Lett., 2014, 388, 293–305.
68. F. Nauret, W. Abouchami, S. J. G. Galer, A. W. Hofmann, C. Hémond, C. Chauvel and J. Dyment, Earth Planet. Sci. Lett., 2006, 245, 137–152.
69. Z. Fekiacova, W. Abouchami, S. J. G. Galer, M. O. Garcia and A. W. Hofmann, Earth Planet. Sci. Lett., 2007, 261, 65–83.
70. J. Moore, W. M. White, D. Paul, R. A. Duncan, W. Abouchami and S. J. G. Galer, J. Volcanol. Geotherm. Res., 2011, 207, 47–66.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c4ja00279b

---