Distinguishing the influence of structural and energetic disorder on electron transport in fullerene multi-adducts†
Florian
Steiner
,
Samuel
Foster
,
Arthur
Losquin
,
John
Labram
,
Thomas D.
Anthopoulos
,
Jarvist M.
Frost‡
* and
Jenny
Nelson
*
Department of Physics and Centre for Plastic Electronics, Imperial College London, London SW7 2AZ, UK. E-mail: jenny.nelson@imperial.ac.uk; j.m.frost@bath.ac.uk
First published on 29th October 2014
Abstract
Fullerene multi-adducts offer a method to tune the open-circuit voltage of organic solar cells but generally lead to poor photocurrent generation which has been linked to poor electron transport in the fullerenes. The poor electron transport may result from the effect of multiple side chains in hindering close packing of the fullerene cages or from disorder in energy levels due to the presence of multiple isomers. Here, we present time-of-flight and field-effect transistor measurements of mobility in [6,6]-phenyl-C-61-butyric acid methyl ester (PCBM) and its higher adducts. To understand the origin of the poor electron mobility, we develop a coarse-grained molecular dynamics model to build isomeric mixes of the multi-adducts. The coarse grained model massively speeds up the simulation relative to atomistic molecular dynamics, enabling assemblies of 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 molecules to be studied. We simulate electron transport in the structures using a kinetic Monte Carlo method, accounting for variations in site energy using electronic structure calculations. This allows us to separate the influence of packing disorder (poorer contact between fullerenes due to steric hindrance) from the influence of energetic disorder (due to varying acceptor energies of the isomers) on electron mobility. We find that energetic disorder due to different isomers dominates the trend in charge transport. Consequently, pure isomeric samples of higher fullerene adducts should enable higher efficiency solar cells.
000 molecules to be studied. We simulate electron transport in the structures using a kinetic Monte Carlo method, accounting for variations in site energy using electronic structure calculations. This allows us to separate the influence of packing disorder (poorer contact between fullerenes due to steric hindrance) from the influence of energetic disorder (due to varying acceptor energies of the isomers) on electron mobility. We find that energetic disorder due to different isomers dominates the trend in charge transport. Consequently, pure isomeric samples of higher fullerene adducts should enable higher efficiency solar cells.
Conceptual insightsFullerenes are a technologically important class of materials and scientifically interesting because of the possibility of modulating the energy levels through functionalisation, but without otherwise changing the electronic structure. Simulation of electronic properties of experimentally relevant sizes of molecular assemblies is difficult from an atomistic perspective because of computer time constraints. In this paper we overcome those constraints by developing and using a coarse grained approach to the film growth, which incorporates disorder due to multiple isomers. The method is capable of distinguishing clearly between the effects of disorder in molecular packing and disorder in chemical structure on charge transport. The results are consistent with experimental time-of-flight and field-effect transistor measurements. The methodology can be translated to a wide range of other molecular materials, can be applied to investigate energy transport and spin transport, and has implications for chemists and material scientists. |
Introduction
Higher adducts of fullerene derivatives such as [6,6]-phenyl-C-61-butyric acid methyl ester (PCBM) and the indene-C60 mono-adduct (ICMA) have attracted interest as a means to raise the open-circuit voltage VOC of polymer solar cells. The most widely used acceptor is a derivative of C60, [6,6]-phenyl-C-61-butyric acid methyl ester (PCBM), and its C70 based analogue. These fullerene derivatives offer many advantageous features such as high acceptor strength, the ability to self organise into partly crystalline charge transport networks and a sufficiently high electron mobility to avoid recombination in optically thick films.1–3There are various routes to manipulate the LUMO energy by changing (a) the chemical structure of side chains,4 (b) the bonding between side chain and fullerene5 (c) the number of side chains. Examples for the latter are the indene-C60 bis-adduct (ICBA)6 and the higher adducts of PCBM, bis-PCBM and tris-PCBM, with two and three phenyl butyric acid methyl ester (PBM) side chains respectively.7,8
Although bis-adducts succeed in increasing the power conversion efficiency when substituted for PCBM in poly(3-hexylthiophen-2,5-diyl) (P3HT):fullerene blends,6,7 higher-fullerene adducts fail in general to improve upon PCBM mainly due to poor short-circuit current densities JSC.9,10 Lenes et al. proposed that the origin of the diminished JSC is a low electron mobility in the fullerene phase. This is supported by observations of efficient charge separation in blends of polymers with PCBM multi-adducts despite poor photocurrent.3,11
We identify two potential mechanisms by which electron transport in multi-adducts may be influenced, namely, (a) packing disorder leading to variation in electronic wavefunction overlap between neighbouring molecules and (b) energetic disorder resulting from variations in energy of electron transport states. We investigate the relative importance of structural and energetic disorder on charge carrier transport in PCBM and the multi-adducts bis- and tris-PCBM with the aim of separating the relative influence of the two mechanisms.
Previously we showed that the LUMO energy of different PCBM multi-adduct isomers varies by hundreds of meV.12 The successive cyclo-addition of fullerenes to form higher adducts raises the reduction potential by removing successive electrons from the π-system to form side-chain bonds. The location of the side chains relative to each other profoundly affects the electronic structure of the fullerene leading to variations in the reduction potential (and hence the LUMO energy) of hundreds of meV. By connecting the side chains of bis-PCBM, Bouwer et al. could isolate single bis-isomer derivatives and obtained higher short-circuit currents; this study indicates the value of eliminating energetic disorder in higher fullerene adducts.13 This observation is shared with Wong et al. who isolated single isomers of ICBA.14 On the other hand, it is suggested that the packing disorder results from the greater volume taken up by phenyl butyric acid methyl ester (PBM) side chains in higher fullerene adducts which ultimately reduces the number of available pathways for charge carriers.15
In this work we present experimental charge transport data from field-effect transistor (FET) and time-of-flight (ToF) measurements quantifying the difference in electron mobilities in PCBM, bis-PCBM and tris-PCBM and estimating energetic disorder from fits to the experimental data. In order to relate those findings to the relative influence of structural and energetic disorder, kinetic Monte Carlo transport simulations are carried out on molecular assemblies constructed using coarse-grained molecular dynamics. A computationally efficient algorithm is developed to enumerate the different isomers, construct their coarse grained representations and assemble starting configurations with given distributions of isomers. To describe hopping transport, electronic transfer integrals, internal reorganisation energies and site energies are calculated using semi-empirical quantum chemical calculations.
Experimental
Temperature-dependent time-of-flight measurements are an effective tool to determine the energetic disorder influencing charge transport. In order to prepare optically thick (>1 μm) films of PCBM we dispersed the fullerene in a matrix of polystyrene (33 wt% PCBM) by codeposition16 and extracted electron mobilities using the integral method of time-of-flight photocurrent.17 From the Gaussian Disorder Model (GDM)18 we derive an energetic disorder of σGDM = 77 meV which is in good accordance with literature.19 Transients obtained for similar samples of bis- and tris-PCBM were too dispersive to obtain reliable mobilities.To compare electron mobilities in all three fullerene types we measured FET mobility in top-contact bottom-gate FET structures20 as a function of temperature. At room temperature and at a gate voltage VG of 30 V, PCBM exhibits a mobility of 5 × 10−2 cm2 V−1 s−1; bis-PCBM, 3 × 10−3 cm2 V−1 s−1; and tris-PCBM, 3 × 10−5 cm2 V−1 s−1 (see Fig. 1). The mobilities follow an Arrhenius type temperature dependence with increasing activation energy in the order PCBM < bis-PCBM < tris-PCBM (see also ESI†). This indicates increasing energetic disorder with adduct number but it is not possible to extract a Gaussian disorder from the data.
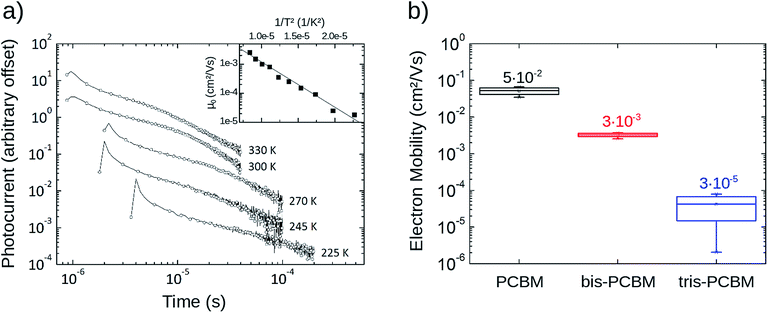 | ||
| Fig. 1 Experimental transport data. (a) Temperature-dependent time-of-flight electron mobilities of PCBM dispersed in polystyrene (33 wt% PCBM). Using the Gaussian Disorder Model, an energetic disorder of σGDM = 77 meV can be extracted. (b) Field-effect electron mobilities of pristine PCBM, bis-PCBM and tris-PCBM films at room temperature (300 K) for several gate-voltages VG (between 20 V and 80 V) (see also ESI1†). At room temperature and VG = 30 V, PCBM shows a mobility of 5 × 10−2 cm2 V−1 s−1, bis-PCBM a mobility of 3 × 10−3 cm2 V−1 s−1 and tris-PCBM a mobility of 3 × 10−5 cm2 V−1 s−1 (also shown in figure). | ||
Generating molecular assemblies
Charge transport simulation requires large representative morphologies to avoid finite size effects. Here we generate a minimalist, coarse-grained molecular-dynamics forcefield for the fullerene adducts which allows isomer-specific intermolecular side chain interactions to be included explicitly. Our intent is to simulate the various PCBM adducts, modelling the fullerene cage as a bead and each side chain as an additional bead, and allowing beads to interact only through a Lennard–Jones potential for computational efficiency. This model for the side chain of a single spherical super-atom is likely to be more accurate for more spherically symmetric side chains such as indene-functionalised fullerenes than PCBM.For the fullerene cage we adopt the Girifalco21 coarse-grain buckminsterfullerene (C60) potential. In doing so we assume that the smearing out of the effective Lennard–Jones interactions of 60 graphitic-like carbons over the surface of the C60 cage is a valid approximation for the interaction of the fullerene cages in functionalised adducts.
For the PBM side chain bead we choose the interaction energy to be the same as the Girifalco parameter for the fullerene site, scaled by the mass of the side-chain (190 Da for PBM versus 720.6 Da for C60), making the approximation that the side chain interacts as graphitic carbon. We consider the bond between the fullerene cage and side chain super-atoms to be arbitrarily stiff (though some flexibility of the side-chain is parametrised into its Lennard–Jones parameter), thus bond lengths and angles for the cage-sidechain attachments in the multi-adducts are fixed at the values of the relaxed geometry of each isomer. We are then left with two free parameters – one describing the sidechain-to-other distance minimum of the inter-molecular Lennard–Jones parameter (σPBM), the other being the fullerene-sidechain bond length (rC60-PBM).
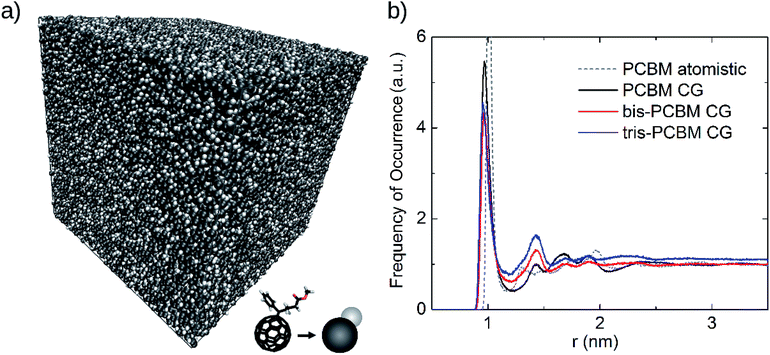 | ||
| Fig. 2 (a) Coarse-grained molecular-dynamics (MD) structures of PCBM. The side length of the cube is 45.4 nm. The C60 cage (black) and the side chains (white) have been replaced by pearls. (b) Radial distribution function of coarse-grained (CG) PCBM, bis-PCBM, tris-PCBM (structures of (a) and ESI1†) and of atomistic PCBM. Atomistic MD and coarse-grained MD structures of PCBM have been compared (see dashed grey and black line) and the parameters of the Lennard–Jones interaction for the coarse-grained model have been fitted accordingly. An identical set of parameters has been used for the coarse-grained bis- and tris-PCBM structures. | ||
To fit these parameters we generate pair distribution functions for mono-PCBM using atomistic MD. Our atomistic model for mono-PCBM is based on the OPLS22 empirical force-field, with the reference geometry from a gas-phase quantum chemistry calculation (b3lyp/6-31g*) and the fullerene cage simulated as arbitrarily stiff. We then generate a coarse-grained assembly of mono-PCBM using the atomistic structures as a starting configuration and fit the coarse-grain model parameters to reproduce the atomistic pair distribution function between fullerene cage centers (see Fig. 2 and ESI4†). The parameters used for the PBM sidechains in the atomistic MD are given in ESI5.†
For the Lennard–Jones potential, VLJ = 4ε[(σ/r)12 − (σ/r)6] with ε being the depth of the potential well, σ referring to the finite distance where the potential is zero and r being the distance between sites. The C60 parameters εC60 = 26.823 kJ mol−1 and σC60 = 0.895 nm are taken from the work of Girifalco et al.21 and εPBM is set to the C60 value weighted by relative mass of the sidechain, hence εPBM = 10.0 kJ mol−1. Fitting of the coarse grained to the atomistic pair distribution function yields the remaining parameters, σPBM = 0.704 nm and for the C60-PBM bond rC60-PBM = 0.64 nm. Having fitted a coarse-grained model for PCBM, we extend this to the various fullerene adduct isomers by adding extra PBM side chains, with the same interaction parameters, at the bonded locations of the side chains. The parameters for the irreducible set of eight bis and 45 tris isomers were generated by computationally efficient direct enumeration of all possible bonding configurations. Reduction of the set by point group symmetry was made by a simple canonical representation.
We generate both single-isomeric (of PCBM, bis-E1-PCBM and tris-EEE-PCBM) and uniform mixes of all possible isomers (for bis-PCBM and tris-PCBM). All MD configurations contain 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 molecules, initially randomly packed loosely. The assemblies are compressed and equilibrated by simulated annealing with a barostat and then representative equilibrium configurations are sampled from a NPT ensemble (300 K, 1 atm). As expected, the volume of the equilibrated MD configurations increases with the number of side chains (mono-PCBM: 0.094 μm3, bis-PCBM: 0.118 μm3 and tris-PCBM: 0.155 μm3) and is slightly larger for the selected single isomer configurations (bis-E1-PCBM: 0.121 μm3 and tris-EEE-PCBM: 0.180 μm3) than for isomeric mixes. Densities of around 1.5 g cm−3 and an average displacement of molecules of less than 0.2 Å (over a time period of 500 ps) indicate that all structures are solid at room temperature. All structures appear amorphous.
000 molecules, initially randomly packed loosely. The assemblies are compressed and equilibrated by simulated annealing with a barostat and then representative equilibrium configurations are sampled from a NPT ensemble (300 K, 1 atm). As expected, the volume of the equilibrated MD configurations increases with the number of side chains (mono-PCBM: 0.094 μm3, bis-PCBM: 0.118 μm3 and tris-PCBM: 0.155 μm3) and is slightly larger for the selected single isomer configurations (bis-E1-PCBM: 0.121 μm3 and tris-EEE-PCBM: 0.180 μm3) than for isomeric mixes. Densities of around 1.5 g cm−3 and an average displacement of molecules of less than 0.2 Å (over a time period of 500 ps) indicate that all structures are solid at room temperature. All structures appear amorphous.
Using the fitted coarse grained molecular dynamics model in place of an atomistic model accelerates the structure generation by around three orders of magnitude. This advantage results from the reduced number of sites in the system, the neglect of charge interactions, (only Lennard–Jones inter-molecular parameters are needed), and the use of a longer time step, enabled by the greater mass of the pseudo-atoms. The coarse graining sacrifices any knowledge of the microscopic orientation of the fullerenes, preserving only information about the C60–C60 separations and coordination number. The separation data remains useful because of the approximately spherical symmetry of the fullerene frontier orbitals23 which leads to an electronic transfer integral that depends only on separation, rather than on six degrees of freedom as in the general atomistic case, and is rapidly evaluated.
The size of the resulting coarse-grained MD generated assemblies, at 40–50 nm thick, is of relevant thickness for solar cells and is considerably larger than achievable assemblies from atomistic MD. In order to evaluate the influence of the system size on simulated charge carrier mobilities, we also generated smaller assemblies (1000 molecules) of mono-, bis- and tris-PCBM (see ESI6†).
Charge transport simulations
We use the ToFeT package23 to simulate charge transport across the coarse-grained fullerene assemblies. This uses a kinetic Monte Carlo algorithm with rates from semi-classical Marcus theory. The hopping rate Γij is defined as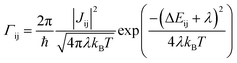 | (1) |
We approximate the electron transfer integral J between fullerenes with the isotropic expression J(r) ∝ α![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−d/β) where d is inter-fullerene cage distance, α is 15 keV and β is 0.5 Å. This functional relationship is based on a calculation of electron transfer integral as a function of separation for pairs of PCBM, bis-PCBM and tris-PCBM molecules (see ESI8†). The values of α and β extracted are in good agreement with previous calculations of J(r) for C60.27 Gajdos et al. found that transfer integrals between two PCBM molecules depend on their mutual orientation only for very small distances.28 It is known that for slightly larger distances the influence of specific molecular structure weakens and the transfer integral follows an exponential relationship.25,27 We therefore expect our isotropic expression for J to be an appropriate approximation.
exp(−d/β) where d is inter-fullerene cage distance, α is 15 keV and β is 0.5 Å. This functional relationship is based on a calculation of electron transfer integral as a function of separation for pairs of PCBM, bis-PCBM and tris-PCBM molecules (see ESI8†). The values of α and β extracted are in good agreement with previous calculations of J(r) for C60.27 Gajdos et al. found that transfer integrals between two PCBM molecules depend on their mutual orientation only for very small distances.28 It is known that for slightly larger distances the influence of specific molecular structure weakens and the transfer integral follows an exponential relationship.25,27 We therefore expect our isotropic expression for J to be an appropriate approximation.
The different distributions of LUMO energies for bis-PCBM and tris-PCBM are approximated by Gaussian distributions of width σisom of 56 meV and 121 meV respectively, following our previous work.12 For completeness we also study discrete, isomer-specific energy levels (ESI9†). We refer to this type of energetic disorder as isomeric disorder. For tris-PCBM we also consider a distribution with σisom = 72 meV which neglects two outlier isomers. PCBM has no energetically distinct isomers and therefore has σisom = 0 meV.
Despite possessing no isomeric disorder, in practice PCBM shows a temperature dependent mobility consistent with a degree of energetic disorder σGDM = 77 meV as determined from GDM analysis of our ToF mobility measurements and similar to a previous study of SCLC mobility measurements.19 This energetic disorder may arise from chemical impurities or from inductive effects of neighbouring fullerenes on the orbital energies.18,29,30 In the following transport calculations we will refer to this component of disorder as intrinsic disorder σintr. Since the experimental disorder σGDM is determined using the GDM which is based on Miller–Abrahams transfer rates and our transport simulations invoke hopping rates from semiclassical Marcus theory, we have to convert the empirical quantity before it can be integrated into the disorder parameter used in transport simulations. This is done by extracting an empirical value from simulated temperature and field dependent mobilities using the GDM and comparing with the width of a Gaussian density of states input into the simulation (see ESI10†). By this method the empirical (GDM) disorder of 77 meV is converted into a density of states broadening of σintr = 135 meV.
For all transport simulations we use 10 frozen representations or ‘snapshots’, separated by 50 ps, extracted from the 1 ns equilibrium 100 kDa coarse grain molecular dynamics trajectory. During the time-of-flight simulation an electric field of 0.01 V nm−1 is applied and we use regenerative contacts. The mobilities are calculated from collection times after convergence of the simulation. Coulomb interactions are neglected since simulations are run in the limit of low charge carrier concentrations. We consider three different regimes of energetic disorder. First, we assign the same energy to all sites (σ = 0) to study the role of molecular packing alone. Second, we introduce isomeric disorder (σ = σisom) for the bis and tris assemblies. Third, we combine isomeric and intrinsic disorder in all cases by convolution of the Gaussian distributions (σ2 = σisom2 + σintr2). We assume the same intrinsic disorder σintr for all fullerene multi-adducts.
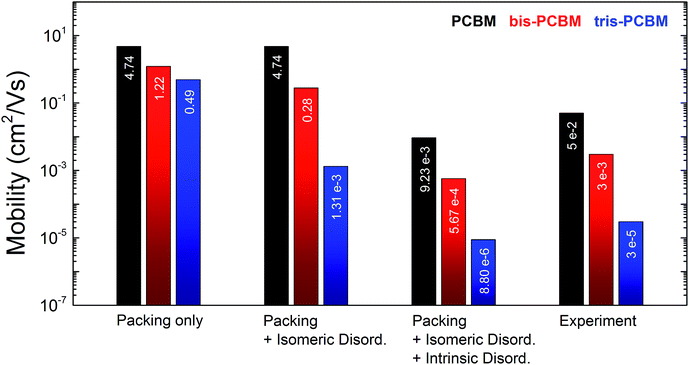
The simulated electron mobility values for λ = 200 meV are shown in Fig. 3. In the case of no energetic disorder the mobility difference between the fullerene derivatives depends only on the effect of packing on connectivity and transfer integral. Compared to the experiment, the relative differences between PCBM, bis-PCBM and tris-PCBM are too small (μmono/μbis = 4 and μmono/μtris = 10). Structures comprising only one isomer type (bis-E1-PCBM and tris-EEE-PCBM) exhibit slightly lower mobilities than corresponding structures with mixed isomers (see ESI11†), which is not surprising as the isomers we chose produce larger volume MD structures. The results indicate that packing is important, but not sufficient to explain the experimental observations.
Including isomeric disorder σisom increases the mobility ratios between the fullerenes close to the experimental finding (μmono/μbis = 17 and μmono/μtris = 3600). Neglecting the two deep trap-forming isomers for tris-PCBM the isomeric disorder drops from 121 meV to 72 meV. The relative mobility difference between PCBM and tris-PCBM would be reduced to 120 revealing the importance of such deep trap forming isomers. For the following calculations we retain the isomeric disorder of 121 meV for tris-PCBM.
Transport calculations combining packing, isomeric and intrinsic disorder with λ = 0.2 eV yield absolute electron mobilities close to our FET measurements. We obtain for PCBM, (9.3 ± 0.2) × 10−3 cm2 V−1 s−1; for bis-PCBM, (5.7 ± 0.1) × 10−4 cm2 V−1 s−1; and for tris-PCBM, (8.8 ± 0.3) × 10−6 cm2 V−1 s−1. The mobility ratios between PCBM and its higher adducts are marginally reduced compared to the case considering exclusively isomeric disorder (μmono/μbis = 16 and μmono/μtris = 1100) and are still in good accordance with the experimental ratios.
Charge transport calculations with reorganisation energies of λ = 0.5 eV lead to similar trends as for 200 meV (see ESI11†). The absolute mobility values are reduced by a factor of three however the relative mobility ratios are preserved. Simulations based on small molecular assemblies (1000 molecules) show a greatly increased variance in resulting mobilities but the mean values compare surprisingly well with mobilities from large structure simulations (see ESI6†). Standard deviations of simulated mobilities stay below 7% (relative to the average value) for the large structures while they can exceed 100% for small structures due to low mobility outliers.
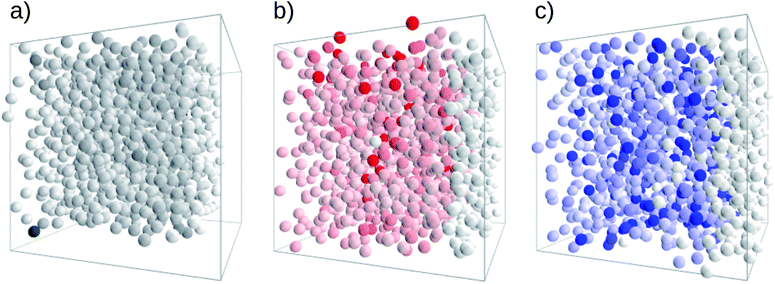
A visual representation of the general transport characteristics is provided in Fig. 4. It refers to a study on small molecular assemblies (1000 molecules) where the colour intensity corresponds to the time that a transport site is visited. A uniform colour intensity indicates good transport where all molecules participate in the transport process (PCBM in Fig. 4a). Poor transport behaviour is apparent for high contrast where traps appear as isolated, intensely coloured sites (tris-PCBM in Fig. 4c).
Conclusions
By building a multi-scale model up from an atomistic basis, with careful consideration of what physically justifiable approximations can be made at each level, we are able to reproduce quantitatively experimental values and trends in electron mobility. The separation of structural and energetic disorder in our model allows us to conclude that the low electron mobility observed in higher fullerene adducts is primarily due to the energetic disorder that results from the presence of different isomers. The relative insensitivity of mobility to structural disorder is assigned to the unique spherical symmetry of the electronic coupling in fullerene derivatives. On the basis of these results we predict that single isomer samples of the higher fullerenes will have mobilities within an order of magnitude of PCBM and, in some cases, will be capable of delivering greater power conversion efficiencies than PCBM. The coarse grained method saves several orders of magnitude in computing time relative to fully atomistic simulations. A similar approach can be recommended for transport simulations in other molecular materials provided that the most significant degrees of freedom in molecular packing and conformation can be identified.Acknowledgements
Florian Steiner would like thank Xerox Foundation/Xerox Research Centre of Canada (XRCC) for helpful discussions and their financial support and the DAAD for their financial support. Jarvist M. Frost, Samuel Foster and Jenny Nelson acknowledge the support of the Engineering and Physical Science Research Council (grant numbers EP/J500021, EP/F061757, EP/J017361 and EP/G031088). John G. Labram and Thomas D. Anthopoulos acknowledge the support of the the Engineering and Physical Sciences Research Council (EPSRC) grant number EP/F023200 and Research Councils UK (RCUK) for financial support. Jenny Nelson acknowledges the Royal Society for the award of a Wolfson Merit Award. Computer time was provided by the Imperial High Performance Computing Service.31Notes and references
- F. C. Jamieson, E. B. Domingo, T. McCarthy-Ward, M. Heeney, N. Stingelin and J. R. Durrant, Chem. Sci., 2012, 3, 485 RSC.
- M. A. Faist, T. Kirchartz, W. Gong, R. S. Ashraf, I. McCulloch, J. C. de Mello, N. J. Ekins-Daukes, D. D. C. Bradley and J. Nelson, J. Am. Chem. Soc., 2011, 134, 685 CrossRef PubMed.
- M. A. Faist, P. E. Keivanidis, S. Foster, P. H. Woebkenberg, T. D. Anthopoulos, D. D. C. Bradley, J. R. Durrant and J. Nelson, J. Polym. Sci., Part B: Polym. Phys., 2011, 49, 45 CrossRef CAS.
- P. A. Troshin, H. Hoppe, J. Renz, M. Egginger, J. Y. Mayorova, A. E. Goryachev, A. S. Peregudov, R. N. Lyubovskaya, G. Gobsch, N. S. Sariciftci and V. F. Razumov, Adv. Funct. Mater., 2009, 19, 779 CrossRef CAS.
- C. Zhang, S. Chen, Z. Xiao, Q. Zuo and L. Ding, Org. Lett., 2012, 14, 1508 CrossRef CAS PubMed.
- Y. He, H. Y. Chen, J. Hou and Y. Li, J. Am. Chem. Soc., 2010, 132, 1377 CrossRef CAS PubMed.
- M. Lenes, G.-J. A. H. Wetzelaer, F. B. Kooistra, S. C. Veenstra, J. C. Hummelen and P. W. M. Blom, Adv. Mater., 2008, 20, 211 CrossRef.
- M. Lenes, S. W. Shelton, A. B. Sieval, D. F. Kronholm, J. C. Hummelen and P. W. M. Blom, Adv. Funct. Mater., 2009, 19, 3002 CrossRef CAS.
- N. C. Cates, R. Gysel, Z. Beiley, C. E. Miller, M. F. Toney, M. Heeney, I. McCulloch and M. D. McGehee, Nano Lett., 2009, 9, 4153 CrossRef CAS PubMed.
- H. Azimi, A. Senes, M. C. Scharber, K. Hingerl and C. J. Brabec, Adv. Energy Mater., 2011, 1, 1162 CrossRef CAS.
- M. A. Faist, S. Shoaee, S. Tuladhar, G. F. A. Dibb, S. Foster, W. Gong, T. Kirchartz, D. D. C. Bradley, J. R. Durrant and J. Nelson, Adv. Energy Mater., 2013, 3, 744 CrossRef CAS.
- J. M. Frost, M. A. Faist and J. Nelson, Adv. Mater., 2010, 22, 4881 CrossRef CAS PubMed.
- R. K. M. Bouwer, G. J. A. H. Wetzelaer, P. W. M. Blom and J. C. Hummelen, J. Mater. Chem., 2012, 2, 15412 RSC.
- W. W. H. Wong, J. Subbiah, J. M. White, H. Seyler, B. Zhang, D. J. Jones and A. B. Holmes, Chem. Mater., 2014, 26, 1686 CrossRef CAS.
- X. Meng, G. Zhao, Q. Xu, Z. Tan, Z. Zhang, L. Jiang, C. Shu, C. Wang and Y. Li, Adv. Funct. Mater., 2013, 24, 158 CrossRef.
- S. M. Tuladhar, D. Poplavskyy, S. A. Choulis, J. R. Durrant, D. D. C. Bradley and J. Nelson, Adv. Funct. Mater., 2005, 15, 1171 CrossRef CAS.
- A. J. Campbell, D. D. C. Bradley and H. Antoniadis, Appl. Phys. Lett., 2001, 79, 2133 CrossRef CAS.
- H. Bässler, Phys. Status Solidi B, 1993, 175, 15 CrossRef.
- V. D. Mihailetchi, J. K. J. van Duren, P. W. M. Blom, J. C. Hummelen, R. A. J. Janssen, J. M. Kroon, M. T. Rispens, E. J. H. Verhees and M. M. Wienk, Adv. Funct. Mater., 2003, 13, 43 CrossRef CAS.
- J. Zaumseil and H. Sirringhaus, Chem. Rev., 2007, 107, 1296 CrossRef CAS PubMed.
- L. A. Girifalco, M. Hodak and R. S. Lee, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 13104 CrossRef CAS.
- W. L. Jorgensen, D. S. Maxwell and J. Tirado-Rives, J. Am. Chem. Soc., 1996, 118, 11225 CrossRef CAS.
- J. J. Kwiatkowski, J. Nelson, H. Li, J. L. Bredas, W. Wenzel and C. Lennartz, Phys. Chem. Chem. Phys., 2008, 10, 1852 RSC.
- K. Sakanoue, M. Motoda, M. Sugimoto and S. Sakaki, J. Phys. Chem. A, 1999, 103, 5551 CrossRef CAS.
- V. Rühle, A. Lukyanov, F. May, M. Schrader, T. Vehoff, J. Kirkpatrick, B. Baumeier and D. Andrienko, J. Chem. Theory Comput., 2011, 7, 3335 CrossRef PubMed.
- C. Poelking, E. Cho, A. Malafeev, V. A. Ivanov, K. Kremer, C. Risko, J. L. Bredas and D. Andrienko, J. Phys. Chem. C, 2013, 117, 1633 CAS.
- J. J. Kwiatkowski, J. M. Frost and J. Nelson, Nano Lett., 2009, 9, 1085 CrossRef CAS PubMed.
- F. Gajdos, H. Oberhofer, M. Dupuis and J. Blumberger, J. Phys. Chem. Lett., 2013, 4, 1012 CrossRef CAS PubMed.
- O. D. Jurchescu, J. Baas and T. T. M. Palstra, Appl. Phys. Lett., 2004, 84, 3061 CrossRef CAS.
- D. P. McMahon, D. L. Cheung, L. Goris, J. Dacuna, A. Salleo and A. Troisi, J. Phys. Chem. C, 2011, 115, 19386 CAS.
- Imperial College High Performance Computing Service, URL: http://www.imperial.ac.uk/ict/services/teachingandresearchservices/highperformancecomputing.
Footnotes |
| † Electronic supplementary information (ESI) available: ESI1 temperature-dependent field-effect-transistor measurements of electron-mobilities, ESI2 time of flight measurements, ESI3 MD-structures of PCBM, bis-PCBM and tris-PCBM, ESI4 coarse-grained vs. atomistic RDF, ESI5 fullerene side-chain enumeration, ESI6 small MD structures, ESI7 reorganisation energy, ESI8 charge transfer integrals, ESI9 discrete energy levels for isomers, ESI10 disorder conversion, ESI11 full table of charge-carrier mobilities for large MD structures, ESI12 coarse grain fullerene force field. See DOI: 10.1039/c4mh00173g |
| ‡ Present address: Department of Chemistry, University of Bath, Bath BA2 7AY, UK. |
| This journal is © The Royal Society of Chemistry 2015 |