Global minimization of gold clusters by combining neural network potentials and the basin-hopping method

Abstract

Neural network potentials trained by first-principles density functional theory total energies were applied to search for global minima of gold nanoclusters within the basin-hopping method. Using Au₅₈ as an example, we found a new putative global minimum which has a core–shell structure of Au₁₀@Au₄₈ and C₄ symmetry. This new structure of Au₅₈ is 0.24 eV per formula more stable than the best previous model that has C₁ symmetry. This work demonstrates that neural network potentials combined with the basin-hopping method could be very useful in global minimization for medium-sized metal clusters which might be computationally prohibitive for first principles density functional theory.

---

Gold nanoclusters and nanoparticles have attracted great research interest due to their novel physical and chemical properties in contrast with their bulk counterpart. Pioneered by Haruta, catalysis by nanogold has been one of the most active research areas in heterogeneous catalysis.^1–3 Understanding the structures of gold nanoclusters and nanoparticles can help elucidate their catalytic actives. Because of their small sizes, gold nanoclusters and nanoparticles are usually stabilized by an oxide support or a ligand monolayer.^2,4–6 Synthesis and structure determination of ligand-protected gold nanoclusters have advanced greatly in the past decade,^6–10 while structural understanding of oxide-supported gold nanoparticles has been hampered by their complexity (size dispersion, metal-support interaction, oxygen vacancies, etc.).^2,11,12

Au clusters in the gas phase, on the other hand, offer a simpler and interesting playground for both theorists and experimentalists to explore the evolution of their intrinsic structures and properties with size.¹³ For example, it was found that very small Au_n clusters with n < 13 for anion,¹⁴ <8 for cation,¹⁵ and <12 for neutral¹⁶ adopt planar configurations; clusters from Au₁₆ to Au₁₈ have cage configuration, while Au₁₉ and Au₂₀ have a pyramid shape.^17–21 From Au₂₁ to Au₃₅ the structure evolves from pyramidal to tubular, and then to core–shell structure.¹³ The global minimum of Au₄₀ has been predicted by first principles basin hopping to have a twisted pyramid structure with a tetrahedral Au₄ core.²² One of the largest Au clusters explored by DFT is Au₅₈ and the putative global minimum was found to have a double-shell structure of Au₁₀@Au₄₄ of C₁ symmetry.²³

It becomes increasingly difficult to do global minimization for larger size Au clusters (say, n > 50) using first principles methods such as density functional theory (DFT) due to the exponential increase of the local minima number with size^24,25 and the nonlinear scaling of the computational cost (roughly ∼n³ for DFT). In this context, alternative methods such as empirical potentials were often employed,^26–30 such as the Rosato–Guillope–Legrand potentials for Au clusters up to 318 atoms,²⁶ Sutton–Chen embedded atom potentials for Pt₅₅ and Au₅₅,²⁷ and effective-medium-theory potentials for Au₁₄₇ and Au₃₀₉.³⁰ Most empirical potentials, however, are not accurate enough, and sometimes could lead to unreliable predictions.^{13,25,27–29}

One promising way to overcome this difficulty is to use the artificial neural network (NN) potentials, trained by large data sets of first principles total energies. As a major approach of machine learning, an artificial NN is a group of interconnected nodes mimicking how neurons in the brain work. In the context of NN potentials for a chemical system (for example, a nanocluster), the goal is to construct a parameterized analytical expression for the potential-energy surface (PES) of the system by using an artificial NN. The details about how to construct such a NN PES based on DFT datasets can be found from the recent literature.^31–33 The NN potentials combine the advantages of the speed of empirical potentials and the accuracy of the first principles methods. A number of recent papers have already shown the success of NN potentials in geometry optimization and molecular dynamics of large systems, such as free standing metal particles, oxide supported metal particles, and solution systems.^32,34,35 However, NN-potential-based global minimization has not been demonstrated.

In this work, we apply the DFT-trained NN potentials to the global minimum search of Au nanoclusters for the first time. The Au₅₈ was chosen here because it was reported to be highly stable and robust as observed from experiment.^36,37 The basin-hopping method has been demonstrated to be a highly efficient algorithm for global minimization of clusters.^38,39 Therefore, the basin-hopping method combined with the NN potentials (the NN–BH method for short) was employed in this work for global minimization of Au₅₈. Stable structures found by NN–BH were then validated by DFT. For DFT calculations, we employed the Vienna Ab Initio Simulation (VASP) code,⁴⁰ with projector augmented wave⁴¹ for the description of core–valence electronic interaction, Perdew–Burke–Ernzerhof⁴² (PBE) functional for electron exchange–correlation, and plane wave for the basis set. Unless mentioned otherwise, calculations were done in normal precision with a cubic box of size 20 × 20 × 20 Å for the Au₅₈. Only Γ-point was used to sample the Brillouin zone. Conjugate-gradient algorithm was employed for geometry optimization with force convergence criterion of 0.03 eV Å⁻¹.

The flow chart to construct accurate NN potentials is shown in Fig. 1. The construction was started from the generation of 400 random initial structures of Au₅₈, which were created by randomizing the 58 Au atoms within a sphere of certain radius and with a constraint of minimal Au–Au bond length of 2.4 Å. These random structures were then optimized by DFT calculations, and the structures and energies during all the relaxations (totally 23 358 configurations spanning 10 eV) were then used as initial reference data to train the NN potentials. A feed-forward NN was used which is a nested sum of activation functions and contains many weight parameters.^31–33 Construction of NN potentials is to fit the weight parameters to known reference potential surfaces. The DFT data set was split randomly into 80% for the training and 20% for the test. The NN architecture of 56-30-30-1 (one input layer of 56 nodes, two hidden layers of 30 nodes each, and one output layer of 1 node which is just the energy) was adopted, which is reasonable to avoid inadequate or over fitting.^32,35 The constructed NN potentials were then used to calculate energy and force of given structures. To further refine the NN potentials, we used the NN–BH method to generate some new structures. Their energies were then checked by DFT: if the NN energies were in poor agreement with the DFT energies, these new structures would then be incorporated into the reference data set to refine the NN potentials. The final adopted NN potentials have a root mean square error (RMSE) of 0.60 meV per atom for the training set and 0.66 meV per atom for the test set, indicating that the quality of the NN potentials is acceptable. Fig. 2 shows the validation of the NN potentials on new structures from BH. Although some deviation can be as large as 0.6 eV, the overall agreement is good between NN potentials and DFT.

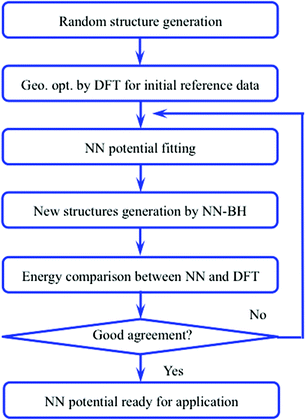Fig. 1 Flow chart of the NN potential construction. BH: basin-hopping algorithm; NN: neural network potential; DFT: density functional theory.

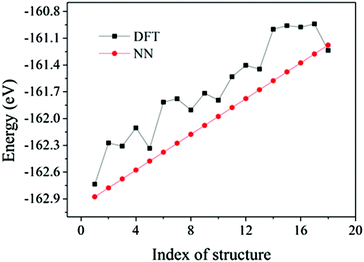Fig. 2 Comparison between NN and DFT energies of 18 Au₅₈ structures spanning a 1.8 eV energy window. The NN energies were chosen intentionally to be equally spaced.

Armed with the NN potentials, we applied the BH method to search the global minimum of Au₅₈. 20 NN–BH jobs (that is, Monte-Carlo walkers) were started from 20 random initial structures, each running for 6500 Monte-Carlo steps. The energy landscape from the 20 NN–BH jobs totaling 120 000 Monte-Carlo steps is plotted together in Fig. 3. Fig. 4 shows an example NN–BH run. It can be seen that combining the BH runs and many random initial structures is an effective way to explore the complex configuration space of the Au₅₈ cluster. Fig. 3 labels the seven low energy isomers of (a)–(g), whose energy order has been checked by DFT (Table 1).

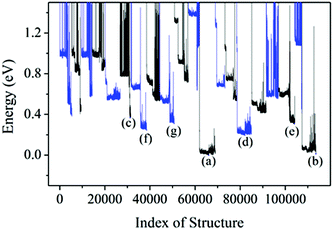Fig. 3 The energy landscape of 20 BH runs based on NN potential. Adjacent BH runs are indicated by different colour (blue or black). (a)–(g) are the local minima with their structure shown in Fig. 5.

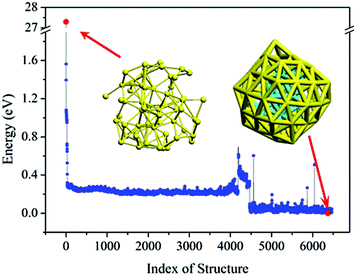Fig. 4 Energy landscape of an example single BH run based on NN potential with 6500 steps. The two red dots denote the initial random structure and the most stable structure found by the BH.

Table 1 Total energy (eV) of isomer (a)–(g) from NN potentials and DFT calculation

	(a)	(b)	(c)	(d)	(e)	(f)	(g)
NN	−162.88	−162.86	−162.51	−162.68	−162.57	−162.63	−162.56
DFT	−162.80	−162.49	−162.47	−162.43	−162.36	−162.35	−162.27

---

Isomer (a) was confirmed by DFT to be the most stable structure of Au₅₈ found from this work: we further optimized it with a tighter force tolerance (0.001 eV Å⁻¹) and finite-difference analysis of the normal modes found no imaginary frequencies (see the ESI† for the coordinates and the calculated IR spectrum). The structure of isomer (a) is shown together with the other six low-energy isomers in Fig. 5. Isomer (a) has C₄ symmetry and is of a prolate spheroid shape with two squares at the top and bottom. It comprises a 48-atom outer shell and a 10-atom inner core. The other isomers also have a core–shell structure but they are less symmetric and less stable by at least 0.30 eV than isomer (a).

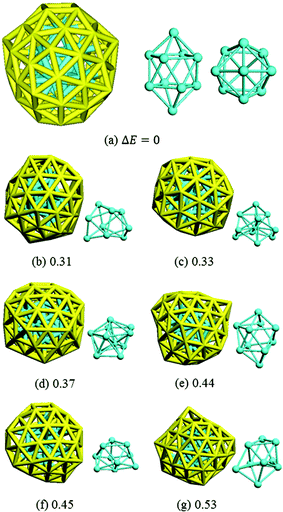Fig. 5 The most stable isomer (a) and other less stable ones as labeled in Fig. 3. Core structures are also shown (cyan). The number shows the DFT total energy (eV) relative to isomer (a).

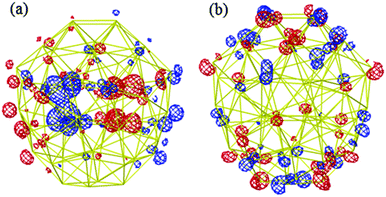
The HOMO and LUMO orbitals of the most stable Au₅₈ structure (Fig. 5a) are shown in Fig. 6. One can see that the HOMO orbital primarily distributes at the core and the waist of the shell, whereas the LUMO orbital populates the top and bottom of the outer shell. This indicates the spatial specific reactivity^43–45 of the Au₅₈ cluster, which could be interesting to explore in further studies. Isomer (a) has the largest HOMO–LUMO gap of 0.82 eV, while isomers (b)–(g) have gaps between 0.4–0.7 eV.

Fig. 6 (a) HOMO and (b) LUMO of isomer (a) of Au₅₈: positive, blue; negative, red.

It is interesting to compare our best Au₅₈ structure with previous models. In an earlier theoretical work, Dong and Gong (DG) performed global minimum search using genetic algorithm based on empirical potential, and then examined the found structures by DFT.²³ Their best model also has the construction of a 10-atom core and 48-atom shell. We compared the energy between their structure and ours by DFT. We tested various functionals (PBE,⁴² PBEsol,⁴⁶ and TPSS⁴⁷) and also employed a large box size of 30 × 30 × 30 Å in order to accurately evaluate the energy difference. We found that our structure is more stable than theirs for all functionals; for the TPSS functional which is known to be good for gold, our structure is 0.24 eV more stable. Geometrically, the two structures are quite similar, having a similar Au₁₀ core, but the Au₅₈ from this work is of C₄ symmetry, whereas the DG structure is of C₁ symmetry, which may explain the higher stability of our structure. The main difference lies in the shell structure as shown in Fig. 7. The outer shell of isomer (a) from this work has two squares at the two ends (top and bottom) of the prolate spheroid (Fig. 7a) and eight five-coordinated Au atoms symmetrically distributed on the shell (Fig. 7a and 7c). In contrast, the outer shell of the DG structure has a diamond at one end and a square at the other end (Fig. 7b); there are 10 five-coordinated Au atoms on the shell (Fig. 7b and 7d). We think that the higher symmetry of our structure leads to its higher stability. The electronic density of states (DOS) of the two structures near the Fermi level also shows small differences (Fig. 8): the higher symmetry of our structure leads to sharper peaks in the DOS.

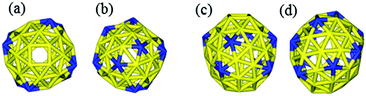Fig. 7 Comparison of the Au₅₈ shell structures between the best structure from this work (a, top view; c, side view) and the best structure (the DG structure) from ref. 23 (b, top view; d, side view). Blue, five-coordinated Au atoms.

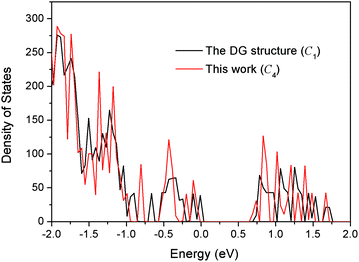Fig. 8 Comparison of the total electronic density of states between the DG structure (ref. 23) and the best structure (isomer a in Fig. 5) from the present work.

In summary, neural network (NN) potentials have been used to search for the global minimum of Au₅₈ in combination with the basin-hopping (BH) algorithm. NN potentials were trained and refined by DFT data sets. Then 20 NN–BH runs with 20 random initial structures were performed with a total of 120 000 Monte-Carlo steps. The putative global minimum of Au₅₈ was found to have C₄ symmetry and a core–shell configuration of a 10-atom core and 48-atom shell. Its stability was confirmed by DFT and found to be 0.24 eV more stable than the best previous model of a similar construction but of lower symmetry (C₁). This work shows that the neural network potentials can be used for global minimization of nanoclusters beyond the capability of the conventional first principles method.

Acknowledgements

This work was supported by the University of California, Riverside. This research used resources of the National Energy Research Scientific Computing Center, a DOE Office of Science User Facility supported by the Office of Science of the U.S. Department of Energy under Contract No. DE-AC02-05CH11231. We thank Dr C. D. Dong for providing us their structure for comparison.

References

1. M. Valden, X. Lai and D. W. Goodman, Science, 1998, 281, 1647–1650.
2. M. Haruta, CATTECH, 2002, 6, 102–115.
3. C. H. Christensen and J. K. Nørskov, Science, 2010, 327, 278–279.
4. M. S. Chen and D. W. Goodman, Science, 2004, 306, 252–255.
5. L. Gao and R. Jin, Acc. Chem. Res., 2012, 46, 1749–1758.
6. D.-e. Jiang, Nanoscale, 2013, 5, 7149–7160.
7. P. Maity, S. Xie, M. Yamauchi and T. Tsukuda, Nanoscale, 2012, 4, 4027–4037.
8. R. Jin, Nanoscale, 2010, 2, 343–362.
9. Y. Pei and X. C. Zeng, Nanoscale, 2012, 4, 4054–4072.
10. A. Fernando, K. L. D. M. Weerawardene, N. V. Karimova and C. M. Aikens, Chem. Rev., 2015, 115, 6112–6216.
11. R. Coquet, K. L. Howard and D. J. Willock, Chem. Soc. Rev., 2008, 37, 2046–2076.
12. M. S. Chen and D. W. Goodman, Catal. Today, 2006, 111, 22–33.
13. L.-M. Wang and L.-S. Wang, Nanoscale, 2012, 4, 4038–4053.
14. F. Furche, R. Ahlrichs, P. Weis, C. Jacob, S. Gilb, T. Bierweiler and M. M. Kappes, J. Chem. Phys., 2002, 117, 6982–6990.
15. S. Gilb, P. Weis, F. Furche, R. Ahlrichs and M. M. Kappes, J. Chem. Phys., 2002, 116, 4094–4101.
16. E. Fernández, J. Soler, I. Garzón and L. Balbás, Phys. Rev. B: Condens. Matter, 2004, 70, 165403.
17. P. Gruene, D. M. Rayner, B. Redlich, A. F. G. van der Meer, J. T. Lyon, G. Meijer and A. Fielicke, Science, 2008, 321, 674–676.
18. A. Lechtken, C. Neiss, M. M. Kappes and D. Schooss, Phys. Chem. Chem. Phys., 2009, 11, 4344–4350.
19. J. Li, X. Li, H. J. Zhai and L.-S. Wang, Science, 2003, 299, 864–867.
20. X. Xing, B. Yoon, U. Landman and J. H. Parks, Phys. Rev. B: Condens. Matter., 2006, 74, 165423.
21. B. Yoon, P. Koskinen, B. Huber, O. Kostko, B. von Issendorff, H. Hakkinen, M. Moseler and U. Landman, ChemPhysChem, 2007, 8, 157–161.
22. D.-e. Jiang and M. Walter, Phys. Rev. B: Condens. Matter, 2011, 84, 193042.
23. C. D. Dong and X. G. Gong, J. Chem. Phys., 2010, 132, 104301.
24. C. J. Pickard and R. J. Needs, J. Phys.: Condens. Matter, 2011, 23, 053201.
25. S. Heiles and R. L. Johnston, Int. J. Quantum Chem., 2013, 113, 2091–2109.
26. K. Bao, S. Goedecker, K. Koga, F. Lançon and A. Neelov, Phys. Rev. B: Condens. Matter, 2009, 79, 041405.
27. J. L. F. Da Silva, H. G. Kim, M. J. Piotrowski, M. J. Prieto and G. Tremiliosi-Filho, Phys. Rev. B: Condens. Matter, 2010, 82, 205424.
28. J. P. K. Doyea and D. J. Wales, New J. Chem., 1998, 773–744.
29. N. T. Wilson and R. L. Johnstona, Eur. Phys. J. D, 2000, 12, 161–169.
30. H. Li, L. Li, A. Pedersen, Y. Gao, N. Khetrapal, H. Jónsson and X. C. Zeng, Nano Lett., 2015, 15, 682–688.
31. N. Artrith and J. Behler, Phys. Rev. B: Condens. Matter, 2012, 85, 045439.
32. N. Artrith, B. Hiller and J. Behler, Phys. Status Solidi B, 2013, 250, 1191–1203.
33. J. Behler, Phys. Chem. Chem. Phys., 2011, 13, 17930–17955.
34. P. Geiger and C. Dellago, J. Chem. Phys., 2013, 139, 164105.
35. N. Artrith and A. M. Kolpak, Nano Lett., 2014, 14, 2670–2676.
36. K. J. Taylor, C. L. Pettiette-Hall, O. Cheshnovsky and R. E. Smalley, J. Chem. Phys., 1992, 96, 3319–3329.
37. W. Huang, M. Ji, C. D. Dong, X. Gu, L.-M. Wang, X. G. Gong and L.-S. Wang, ACS Nano, 2008, 5, 897–904.
38. D. J. Wales and J. P. K. Doye, J. Phys. Chem. A, 1997, 101, 5111–5116.
39. J. P. K. Doye and D. J. Wales, Phys. Rev. Lett., 1998, 80, 1357–1360.
40. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter, 1996, 54, 11169–11186.
41. P. E. Blöchl, Phys. Rev. B: Condens. Matter, 1994, 50, 17953–17979.
42. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
43. R. Ouyang and W.-X. Li, Phys. Rev. B: Condens. Matter, 2011, 84, 165403.
44. L. M. Molina and B. Hammer, J. Chem. Phys., 2005, 123, 161104.
45. L. M. Molina and J. A. Alonso, J. Phys. Chem. C, 2007, 111, 6668–6677.
46. J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406.
47. J. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Phys. Rev. Lett., 2003, 91, 146401.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c5nr03903g

---