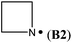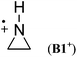The stability of nitrogen-centered radicals

Abstract

Radical stabilization energies (RSEs) for a wide variety of nitrogen-centered radicals and their protonated counterparts have been calculated at G3(MP2)-RAD and G3B3 level. The calculated RSE values can be rationalized through the combined effects of resonance delocalization of the unpaired spin, electron donation through adjacent alkyl groups or lone pairs, and through inductive electron donation/electron withdrawal. The influence of ring strain effects as well as the synergistic combination of individual substituent effects (captodatively stabilized N-radicals) have also been explored. In symmetric N-radicals the substituents may also affect the relative ordering of electronic states. In most cases the π-type radical (unpaired spin distribution perpendicular to the plane of the N-radical) is found to be most stable. Closed shell precursors of biological and pharmaceutical relevance, for which neither experimental nor theoretical results on radical stabilities exist, have been included.

---

Introduction

Nitrogen-centered radicals play an important role in a variety of reactions, including processes as diverse as the degradation of proteins and peptides,¹ the environmental fate of pharmaceuticals,² and the targeted synthesis of amines and amides.³ Following a strategy also used in carbon-centered radicals the stability of these species can be defined quantitatively using hydrogen-transfer reactions with well known reference compounds such as ammonia (NH₃, 1H). The reaction energy for this type of process as defined in eqn (1) is often referred to as the radical stabilization energy (RSE) of radical ˙NR′R′′ (Scheme 1).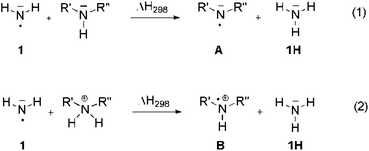

Scheme 1 Hydrogen transfer reaction used to define the stability of N-radicals (A) and N-radical cations (B).

However, in contrast to carbon-centered radicals, the substituents R′ and R′′ present in aminyl radical A interact with both the unpaired spin and the non-bonding electron pair located at the nitrogen atom. RSE values obtained from hydrogen transfer reaction (1) can thus only rarely be understood as the stabilizing or destabilizing effects of the substituents on the unpaired spin alone. Moreover, the stability of aminyl radicals will also depend on the interaction of the lone pair electrons with the surrounding. These interactions may range from weak solvation effects in apolar organic solvents all the way to (reactive) complexation with cationic species such as the proton. This latter case is described in eqn (2), where formal hydrogen abstraction now occurs from ammonium ions and generates amine radical cations B as the products. In order to identify systematic substituent effects for the situations described in eqn (1) and (2) we have now used a combination of theoretically calculated and experimentally measured enthalpies to calculate RSE values for radicals A and B with a selection of substituents R′ and R′′. These include alkyl groups such as R = CH₃ known to act on adjacent radical centers through inductive electron donation, aryl groups such as R = Ph known to stabilize radical centers through resonant delocalization of unpaired spin, and lone-pair donors such as R = OCH₃ or N(CH₃)₂ interacting with radical centers through electron-donation. Of particular importance for aminyl radicals are carbonyl substituents such as R = C(O)CH₃, mimicking the situation in peptide and protein radicals. Finally, when comparing theoretically calculated and experimentally measured⁴ RSE values, it is important to recall that the reaction enthalpy for reaction (1) is identical to the difference in the N–H bond dissociation energy (BDE) of the two participating amines NH₃ (1H) and HNR′R′′. This can be quantitatively expressed with eqn (3).

RSE(˙NR₂) = BDE(H-NR′R′′) − BDE(H-NH₂) (3)

From previous theoretical studies of radical stabilities and bond dissociation energies⁵ a clear hierarchy of theoretical methods with systematically increasing predictive power has emerged, which has recently been summarized by Radom et al.⁶ For the systems considered here relative energies can be calculated in a reliable manner with aid of the G3(MP2)-RAD scheme and all results discussed in the text refer to this level of theory (if not mentioned otherwise). This compound method combines geometry optimizations at DFT level with a series of single point calculations at ROMP2 and URCCSD(T) level to yield stability data for open shell species with an accuracy of around 5 kJ mol⁻¹.⁷ For selected systems calculations have also been performed at the slightly more accurate G3B3 level.⁸ Of critical importance in applying any of these theoretical methods to aminyl radicals is the identification of the lowest-lying electronic state. The simultaneous presence of one unpaired electron and the lone-pair electrons at (formally) the same nitrogen atom makes this step clearly more challenging than in other open-shell species.⁵

Results and discussion

The stability of neutral aminyl radicals

Following earlier attempts to categorize substituent effects in carbon-centered radicals, the discussion will first address the effects of alkyl substituents, followed by systems positioning the nitrogen-centered radical directly adjacent to π-systems and lone-pair donors. The interplay of individual effects in multiply-substituted systems will be addressed in a final section.

Stabilization through inductive effects. The stabilization of alkylaminyl radicals occurs through interaction of the unpaired spin with adjacent C–H (or C–C) bonds. This type of hyperconjugation leads to stabilizing effects of moderate size. In methylaminyl radical (A1), for example, hyperconjugation results from overlap between the unpaired electron in a 2p atomic orbital on nitrogen with the occupied σ_CH bond orbitals on the methyl group and leads to a stabilization of approx. 30 kJ mol⁻¹ (Table 1). The stability of alkylaminyl radicals increases with the number of alkyl substituents attached to the N-radical center. However, the addition of the second alkyl group is less stabilizing as compared to the first one, showing the same saturation behavior as already described for C-centered radicals.⁹ Increasing the size of the attached alkyl group leads to less efficient stabilization as can be seen from the RSE values (at G3B3 level) calculated for the series of the ˙NH-R radicals, where R is Me (−30.4 kJ mol⁻¹), Et (−30.1 kJ mol⁻¹), i-Pr (−24.9 kJ mol⁻¹), or t-Bu (−24.5 kJ mol⁻¹). A similar trend has been observed for oxygen-, sulfur-, and carbon-centered radicals and interpreted as the less efficient hyperconjugative efficiency of C–C as compared to C–H bonds.¹⁰ The introduction of cycloalkyl substituents (A7–A10) results in RSE values similar to those calculated for acyclic alkyl groups. Interestingly, larger ring sizes correlate with smaller RSE values. The cyclopropyl substituent present in cyclopropylmethylaminyl radical A7 shows a considerable stabilizing effect (−44.4 kJ mol⁻¹), which suggests that the three-membered ring is a much stronger partner in hyperconjugative interactions with the radical center. Therefore, it was of theoretical interest to calculate the stabilizing effect of two cyclopropyl groups attached to the N-centered radical. Indeed, a strong stabilization for A11 is predicted and the calculated RSE amounts to −78.9 kJ mol⁻¹, which is close to the RSE values for urea-derived radicals in which captodative effects are operative (see below).

Table 1 Radical stabilization enthalpies (RSE, in kJ mol⁻¹) at 298.15 K of alkyl and cycloalkyl substituted aminyl radicals calculated according to eqn (1)

N-centered radical^a	G3(MP2)-RAD	G3B3	Other	Exp. (RSE)	Exp. (BDE)^b
a All N-centered radicals exist in the π electronic ground state. b Experimental values from ref. 4 unless otherwise noted. c Ref. 13a. d Ref. 13b. e Ref. 6e. f Ref. 6b. g Ref. 11. h Ref. 12.
˙NH2 (A0)	0.0	0.0	0.0	0.0	+450.08 ± 0.24
˙NHC(CH3)3 (A6)	−23.7	−24.5	−25.1 (CBS-4M)^c	−52.6 ± 8.4^c	+397.5 ± 8.4
				−31.7 ± 12.6^d	+418.4 ± 12.6
˙NHCH(CH3)2 (A5)	−24.2	−24.9	—	—	—
˙NHCH(CH2)5 (A10)	−25.3	−26.1	—	—	—
˙NHCH2CH3 (A2)	−26.2	−30.1	−26.0 (CBS-4M)^c	—	—
˙NHCH(CH2)4 (A9)	−26.4	−27.3	—	—	—
˙NHCH(CH2)3 (A8)	−27.9	−28.7	—	—	—
˙NHCH3 (A1)	−30.0	−30.4	−31.8 (W1w)^e	−25.0 ± 8.4	+425.1 ± 8.4
			−32.1 (0 K, W2w)^f
			−32.2 (298 K, G4)^f
˙NHCH(CH2)2 (A7)	−41.1	−44.4	—	—	—
˙N(CH2CH3)2 (A4)	−51.9	−52.8	−48.1 (CBS-4M)^e	—	—
˙N(CH3)2 (A3)	−52.6	−53.2	−55.4 (W1w)^e	−52.6 ± 10.5^g	+397.5 ± 10.5
			−56.6 (0 K, W2w)^e	−67.3 ± 10.5^h	+382.8 ± 10.5
˙N(CH(CH2)2)2 (A11)	−77.6	−78.9	—	—	—

---

For two of the systems studied here conflicting experimental results have been published. The first concerns dimethylaminyl radical A3, whose stability according to eqn (1) has been quantified as either −52.6 (ref. 11) or −67.3 kJ mol⁻¹ (ref. 12). At G3B3 and G3(MP2)-RAD levels the calculated RSE values for A3 are −53.2 and −52.6 kJ mol⁻¹, respectively. This suggests that in this case the experimental RSE value obtained by very low pressure pyrolysis¹¹ (−52.6 kJ mol⁻¹) is more reliable than the RSE value derived indirectly from thermochemical data (electron affinity and ΔH° of acidity).¹² A similar situation exists for t-butyl substituted aminyl radical A6, where the two currently available experimental RSE values (−31.7 vs. −52.6 kJ mol⁻¹)¹³ differ significantly. The results obtained at G3B3 and G3(MP2)-RAD level clearly support the lower of these values (see Table 1).

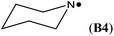
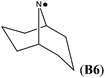
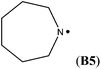
In cyclic aminyl radicals the substituent effects are modified through the more or less strained ring systems. The stability of cycloaminyl radicals of various ring sizes (n = 3–7) are collected in Table 2. It appears that, in comparison to the corresponding series of C-centered cycloalkyl radicals, the ring strain is less important in determining the stability of the cyclic aminyl radical.¹⁰ All the calculated RSE values are between −50 and −64 kJ mol⁻¹, whereas the corresponding RSE values for cycloalkyl radicals span a range of ca. 46 kJ mol⁻¹. The ease of formation of a radical center in the three (aziridinyl radical, RSE = −53.7 kJ mol⁻¹) or four (azetidinyl radical, RSE = −52.2 kJ mol⁻¹) membered ring systems is thus similar to that of the six (piperidinyl radical, RSE = −49.7 kJ mol⁻¹) or seven (azepinyl radical, RSE = −51.9 kJ mol⁻¹) membered systems. In addition, comparable relative stabilization effects (RSEs between −50 and −55 kJ mol⁻¹) have been calculated for a series of bicyclic aminyl radical, such as B6, B7, and B8, suggesting that the effects of added ring strain are not evident in these bridged systems.

Table 2 Radical stabilization enthalpies (RSE, in kJ mol⁻¹) at 298.15 K of cyclic and bicyclic aminyl radicals calculated according to eqn (1)

N-centered radical^a	G3(MP2)-RAD	G3B3
a All N-centered radicals exist in the π electronic ground state.
	−42.0	−47.7
	−43.4	−44.2
	−47.8	−48.7
	−48.1	−49.3
	−49.7	−55.7
	−49.9	−51.1
	−51.9	−52.7
	−52.2	−52.6
	−53.2	−54.1
	−53.7	−54.3
	−54.6	−55.5
	−57.2	−57.8
	−63.7	−64.5
	−73.4	−74.7
	−85.3	−86.9

---

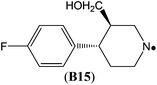
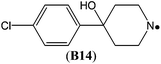
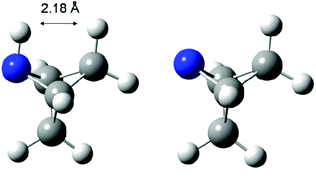
The highest stability is calculated for the bicyclic system B9 with RSE = −73.4 kJ mol⁻¹, which may be taken as a reflection of differences in steric hindrance between the radical and its closed shell precursor. It is clear (see Fig. 1) that the steric repulsion between the N- and C3-hydrogen atoms (a H–H distance of 2.18 Å is calculated at the B3LYP/6-31G(d) level) in the parent 2-aza-bicyclo[1.1.1]pentane does not exist in the corresponding N-centered radical. As expected, more strain energy is released on going from unsubstituted radical B9 to the methyl-substituted bicyclic radical B10. A number of the cycloaminyl radicals shown in Table 2 derive from heterocycles frequently associated with biologically active natural products and are often incorporated as the key structural motif in a vast array of pharmaceuticals. As two prominent examples we include open-shell metabolites derived from haloperidol (B14) and paroxetine (B15), both of which may be involved in biotransformations and environmental degradations of the respective parent compounds.^14–16

Fig. 1 B3LYP/6-31G(d) optimized geometry of 2-aza-bicyclo[1.1.1]pentane (left) and the corresponding N-centered radical B9 (right).

The effects of resonance stabilization. The attachment of carbonyl groups to the amino radical center (presented here as amidyl radicals ˙NHC(X)O; C1–C5) are usually destabilizing in nature.¹⁷ This is already exemplified for the smallest radicals in this group such as acetamidyl (C2; X = CH₃) and formamidyl (C1; X = H) radical with RSE values of +22.2 and +28.8 kJ mol⁻¹, respectively (Table 3).

Table 3 Radical stabilization enthalpies (RSE, in kJ mol⁻¹) at 298.15 K of resonance (de)stabilized radicals calculated according to eqn (1)

N-centered radical (electronic state in parentheses)	G3(MP2)-RAD	G3B3	Other	Exp. (RSE)	Exp. (BDE)^a
a Experimental values from ref. 4 unless otherwise noted. b Ref. 21a. c Ref. 6b. d Ref. 27. e Ref. 26.
	+73.0	+66.2	+56.9 (298 K, G4)^b	+43.6 ± 12.6	+493.7 ± 12.6
				−66.4 ± 12.6	+383.7 ± 12.6
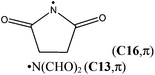
˙N(CHO)2 (C13,π)	+60.7	+48.9	+50.8 (0 K, W2w)^c	—	—
			+43.9 (298 K, G4)^b
	+53.4	+53.2	—	+31.1 ± 12.6	—
	+37.0	+34.0	—	—	—
˙NHCHO (C1,π)	+28.8	+29.2	+29.9 (0 K, W2w)^c	+3.9 ± 12.6	+454.0 ± 12.6
			+26.9 (298 K, G4)^c
˙NHCOOH (C5,π)	+23.7	+29.7	—	—	—
˙NHCOCH3 (C2,π)	+22.2	+19.9	+22.6	−0.3 ± 12.6	+449.8 ± 12.6
˙NHCONH2 (C3,π)	+8.2	+7.0	+7.7 (0 K, W2w)^c	+14.3 ± 12.6	+464.4 ± 12.6
˙NHCOPh (C4,π)	+7.0	+16.9	—	+2.4 ± 12.6	+452.5 ± 12.6
˙NHCOC(CH3)3 (C18,π)	+17.9	+15.8		+6.0 ± 12.6	+456.1 ± 12.6
˙NHCH=NH (C9,π)	−26.4	−24.1	−24.4 (0 K, W2w)^c	—	—
˙NHCHS (C6,π)	−42.0	−35.9	—	—	—
˙NHCSNH2 (C7,π)	−42.7	−39.0	—	−60.9 ± 12.6	+389.2 ± 12.6
˙NHC≡N (C19,π)	−46.5	−47.0	—	−45.9 ± 10.9	+404.2 ± 10.9
				−35.9 ± 12.6	+414.2 ± 12.6
˙N=CPh2 (C22,σ)	−59.8	−59.6	−66.4 (ROB3LYP)^d	+39.4 ± 12.6	+489.5 ± 12.6
˙N=C(CH3)2 (C21,σ)	−67.5	−72.1	−73.9 (CBS-QB3)^d	—	—
			−70.4 (W1w)^e
˙NHCH=CH2 (C10a,π)	−75.3	−75.7	—	—	—
˙N=CH2 (C20,σ)	−78.0	−79.9	−80.4 (W1w)^e	−86 ± 25.0	+364 ± 25.0
˙NHC≡CH (C8,π)	−81.8	−83.9	—	—	—
˙NHCH=CHPh (C11,π)	−101.1	−93.9	—	—	—
˙NHCH=CHCH=CH2 (C10b,π)	−106.3	−104.5	—	—	—
˙N(CH=CH2)2 (C12,π)	−110.9	−103.1	—	—	—
˙NH(CH=CH)2CH=CH2 (C10c,π)	−121.0	−116.3	—	—	—
˙NH(CH=CH)3CH=CH2 (C10d,π)	−130.0	−120.5	—	—	—
˙N(CH=CHCH=CH2)2 (C12a,π)	−138.6	−125.1	—	—	—
	−140.6	−142.9	—	—	—

---

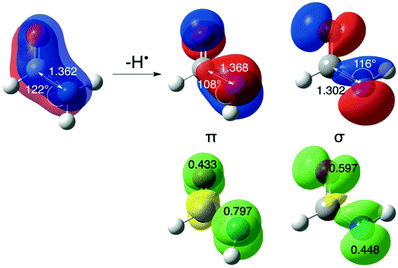
Destabilizing effects are even larger once a second carbonyl group is attached to the amino radical center (+60.7 kJ mol⁻¹ for N-formylformidyl radical, OHC–N˙–CHO (C13)), demonstrating the cumulative effect of multiple substituents. In the parent compounds H₂NC(X)=O (see Fig. 2), the acyl substituents participate in conjugation with the nitrogen lone pair, which leads to stabilization of the closed shell structure. In contrast, in the open shell counterparts the delocalization of the unpaired spin into the π-system of the carbonyl group is accompanied by the loss of resonant interaction between the carbonyl group and the nitrogen lone pair.¹⁸ The odd electron on nitrogen is involved in this conjugation, because it lies perpendicular to the N–C–O framework (if the amidyl radical exists in its π ground electronic state), while the nitrogen lone-pair electrons lie in the symmetry plane of the radical.

Fig. 2 HOMO/SOMO orbitals (red/blue surfaces) in formamide (left), π-radical (cis-isomer, NImag = 0), and σ-radical (trans-isomer, NImag = 0). The CNH bond angles, N–C bond lengths (in angstroms), spin distributions (NPA values), and spin SCF densities (green/yellow surfaces) for π- and σ-radicals have been calculated at UB3LYP/6-31G(d) level.

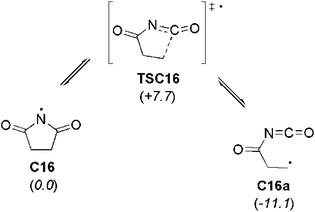
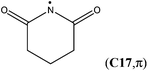
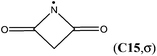
The attachment of an electron-withdrawing acyl group(s) to the nitrogen atom of an aminyl radical decreases the energy separation of the respective σ and π states. Diacylaminyl radicals (malonimidyl (C15), succinimidyl (C16)¹⁹ or glutarimidyl radical (C17)) would appear likely candidates for a σ ground state, in which the nitrogen lone-pair electrons are localized in π-type molecular orbitals. At the G3B3 level the calculated energy gap between the two electronic states for C17 (C₂ point group) is 16.1 kJ mol⁻¹, and only 4.1 kJ mol⁻¹ for C16 (C_s point group). In the case of C15 (C_2v point group), the σ-radical has been calculated to be 21.8 kJ mol⁻¹ more stable than the π-radical. These results imply that the lowest lying A′ and A′′ states together with their respective energy splitting have to be determined for all C_s symmetric radicals for the correct assignment of the electronic configuration.

In the case of succinimidyl radical (C16) a large discrepancy (over 100 kJ mol⁻¹) between the two experimental BDE values can be observed. This may be due to a fast equilibrium between cyclic and acyclic forms of the succinimidyl radical (Scheme 2). It has been shown that succinimidyl radical readily undergoes ring opening yielding the more stable β-(isocyanatocarbonyl)ethyl radical C16a (Scheme 2).²⁰ At the G3B3 level this carbon-centered radical is 11.1 kJ mol⁻¹ more stable than succinimidyl radical C16. In addition, the transition state structure TSC16 connecting C16 and C16a is located only 7.7 kJ mol⁻¹ above succinimidyl radical C16, implying a very low barrier for the ring opening process. This issue has already been raised in several previous studies of succinimidyl radical C16.²¹

Scheme 2 Ring-opening reaction of succinimidyl radical (C16) yielding C-centered β-(isocyanatocarbonyl)ethyl radical (C16a). Relative energies (italics, in kJ mol⁻¹) have been calculated at G3B3 level.

A similar interpretation can be invoked to rationalize the discrepancies between the calculated and experimental BDE values for amidyl radicals C1, C2, and C18. The calculated RSE values for these radicals are underestimated by ca. 10–20 kJ mol⁻¹. In the case of formamidyl radical (C1) the formation of three additional isomers is conceivable after hydrogen atom abstraction from the parent compound: the iminolic form C1a and the C-centered carbamoyl radicals C1b and C1c (Scheme 3).²² All three isomers are σ-type radicals and are more stable (−12.6, −81.0 and −19.9 kJ mol⁻¹, resp.) than formamidyl radical in its π-electronic state. Similar results have also been obtained for amidyl radicals C2, C4, and C18 (Table 4). However, the calculated energy barriers (ΔG^#₂₉₈) for isomerization processes C1 → C1a (1,3N↔O-hydrogen shift), C1 → C1b (1,2C↔N-hydrogen shift), and C1 → C1c (1,2C↔O-hydrogen shift) are very high (140.1, 134.8 and 133.7 kJ mol⁻¹, resp.), suggesting that formamidyl radical C1 is kinetically quite stable. Therefore, it is probable that amidyl radical C1 is the only species that exists under experimental conditions employed.

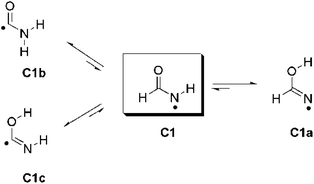Scheme 3 Isomerization of formamidyl radical (C1). For clarity, equilibria between isomers C1a, C1b, and C1c are not shown.

Table 4 Relative energies (ΔH₂₉₈) for isomers of amidyl radicals C1, C2, C4 and C18 (G3B3 level)

N-radical	α-Substituent R	ΔH298
		Amidic form	Iminolic form (a)	C-radical form (b)	C-radical form (c)
a CH2C(=O)NH2 and ˙CH2C(=NH)OH. b CH2C(CH3)2C(=O)NH2 and ˙CH2C(CH3)2C(=NH)OH.
C1	H	0.0	−12.6	−81.0	−19.9
C2	CH3	0.0	−9.6	−54.8^a	−7.6^a
C18	C(CH3)3	0.0	−9.5	−31.7^b	+18.8^b
C4	Ph	0.0	−3.7	—	—

---

Contrary to the carbonyl group effect, the attachment of thiocarbonyl groups (as in C6 and C7), ethynyl groups (as in C8), cyano groups (as in C19), or imine groups (as in C9) to the amino radical center leads to stabilization of nitrogen-centered radicals (see Table 3). A stabilizing effect of −75.3 kJ mol⁻¹ has been calculated for the vinyl-substituted amine radical (C10a), in which extension of the substituent π-system as in radicals C10b–C10d leads to RSE values as high as −130 kJ mol⁻¹. Taken together the RSE values of N-centered radicals can be tuned broadly through substitution containing small π-systems.²³

The actual magnitude of these substituent effects depends on several components such as the interaction of the substituent with the nitrogen lone pair in the close-shell parent system, the interaction of the substituent with the nitrogen lone pair in the radical, and the interaction of the substituent with the unpaired spin at the radical stage. This interplay of individual components is thus significantly more complex than in C-centered radicals and limits the possibilities of equating RSE values to individual bonding schemes.

In agreement with previous findings^24,25 iminyl radicals C20, C21, and C22 (Table 3) were located to exist in the σ-electronic state. The corresponding π-radicals were calculated to be 355.7, 309.2, and 242.7 kJ mol⁻¹ less stable, resp. The calculated RSE for the parent methaniminyl radical (C20) is −79.9 kJ mol⁻¹ (G3B3 level), which is in good agreement with the experimental value (−86 ± 25 kJ mol⁻¹). This stabilization may be attributed to the existence of a hyperconjugative interaction, which involves electron donation from σ_C–H orbitals to the half-filled orbital at the nitrogen radical center.^24,26 For diphenyl substituted iminyl radical (C22), in contrast, a destabilization effect has been observed experimentally (RSE = +39.4 kJ mol⁻¹). However, we could not reproduce this result computationally. The calculated RSE value for C22 is −59.6 kJ mol⁻¹, which suggests the opposite (i.e. stabilization) effect. A very similar RSE for C22 (−66.4 kJ mol⁻¹) has been calculated earlier by Blake et al. who have questioned the reliability of the experimental result claiming that “it is obviously much too large”.²⁷

The stabilizing effects of aryl substituents as present in arylaminyl radicals exceed those of substituents with smaller π-systems and lead to stable spin-delocalized systems (Table 5). The RSE values for para-substituted phenylaminyl radicals (D2–D7) range from −53 to −90 kJ mol⁻¹, depending on the ring-substituents. Electron-donating groups (e.g. OCH₃, CH₃) are more stabilizing than electron-acceptor substituents (e.g. CN, CF₃). All the investigated phenylaminyl radicals have a planar geometry with a plane of symmetry (C_s point group). Unlike alkyl aminyl radicals, which are expected to exist in a π electronic ground state (see above), phenylaminyl radicals may posses a σ ground state (²A′ state in C_s symmetry) if sufficiently electronegative substituents X are attached to preferentially delocalize the nitrogen lone-pair electrons (Scheme 4).

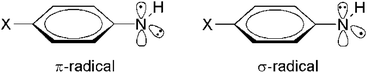Scheme 4 Two different electronic states for para-substituted phenylaminyl radical (²A′′ (left) and ²A′ (right) ground state of C_s symmetry).

Table 5 Radical stabilization enthalpies (RSE, in kJ mol⁻¹) at 298.15 K of arylaminyl radicals calculated according to eqn (1)

N-centered radical^a	G3(MP2)-RAD	G3B3	Other^b	Exp. (RSE)	Exp. (BDE)^c
a All N-centered radicals exist in the π electronic ground state. b All values have been calculated at the ROMP2/6-311+G(2d,2p) level; from ref. 30b. c Experimental values from ref. 4 unless otherwise noted. d Estimated experimental error from ref. 28a. e Experimental error reported in ref. 28b. f No value for experimental error is available in ref. 28c.
˙NH(p-NO2)C6H5 (D8)	−53.9	−45.2	−47.2	−45.5 ± 12.6	+404.6 ± 12.6
˙NH(p-SO2NH2)C6H5 (D10)	−54.2	−47.9	—	—	—
˙NH(p-CF3)C6H5 (D5)	−56.8	−49.1	−50.1	−45.6 ± 12.6	+404.2 ± 12.6
				−60.1 ± 6.3^d	+390.0 ± 6.3^d
˙NH(p-CN)C6H5 (D4)	−57.8	−48.9	−50.1	−51.8 ± 12.6	+398.3 ± 12.6
				−66.1 ± 4.0	+384.0 ± 4.0
˙NHC6H5 (D1)	−65.7	−59.3	−59.7	−64.3 ± 12.6	+385.8 ± 12.6
				−81.9 ± 8.4	+368.2 ± 8.4
˙NH(p-CH3)C6H5 (D2)	−70.9	−64.2	−64.7	−65.2 ± 12.6	+384.9 ± 12.6
				−84.0 ± 6.3^e	+366.1 ± 6.3^e
˙NH(p-OH)C6H5 (D3)	−78.0	−71.5	−72.3	—	—
˙NH(2,4,6-(NO2)3)C6H5 (D11)	−84.6	—	—	—	—
˙NH(p-NH2)C6H5 (D6)	−85.2	−79.4	−79.4	−87.8^f	+362.3^f
				−90.1 ± 6.3^d	+360.0 ± 6.3^d
˙NH(p-N(CH3)2)C6H5 (D7)	−87.7	−82.8	—	—	—
˙N(C6H5)2 (D9)	−89.7	−75.7	—	−85.3 ± 6.3^e	+364.8 ± 6.3^e
				−91.1 ± 2.9	+359.0 ± 2.9

---

For all substituted phenylaminyl radicals in Table 5 the A′′ state (π-radical) is energetically preferred over the A′ state (σ-radical) (assuming a C_s symmetric structure for both states). The σ-radicals actually correspond to first-order saddle points (NImag = 1) on the potential energy surface. The calculated A′′ − A′ splitting (ΔH₂₉₈) for the parent phenylaminyl radical amounts to 157.9 kJ mol⁻¹, but varies with the substitution pattern. While substituents with negative Brown σ_p⁺ values increase the energy gap between the two states (e.g. for X = OH, ΔH_(σ–π) = 176.2 kJ mol⁻¹), substituents with positive σ_p⁺ values provide relative stabilization to the A′ state (e.g. for X = NO₂, ΔH_(σ–π) = 137.5 kJ mol⁻¹). If the picryl (that is 2,4,6-trinitrophenyl) substituent is attached to the aminyl radical (D11), the energy gap between the two states amounts to only 22.3 kJ mol⁻¹. Other candidates, in which the A′ electronic state could be favored, are aromatic amidyl radicals. It has, for example, been shown recently that N-phenylacetamidyl radicals possess a σ ground state if appropriately substituted at the ring moiety.²⁹

The calculated RSE values for phenylaminyl radicals correlate well with Brown substituent constants (σ_p⁺), in line with earlier observation.^30b The linear relationship (r = 0.994) of the RSE and Brown's σ_p⁺ values displayed in Fig. 3 indicates that the stabilization effects of substituted phenylaminyl radicals are related to the electron-donating properties of the ring substituent X. In terms of Walter's criteria³¹ for radical behavior, the para-substituted phenylaminyl radicals belong to the “Class O” (where O denotes the opposite direction of effect for electron donation and releasing substituents) radicals which display a Hammett behavior.

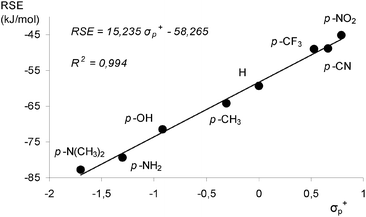Fig. 3 Hammett plot of calculated RSE values (G3B3 level) for para-substituted phenylaminyl radicals versus Brown σ_p⁺ values.

Interestingly, all investigated arylaminyl radicals are found to have lower RSE values than the strongly stabilized radicals derived from hydroxamic acid or urea (see below). Only the phenylaminyl radical D7 and the diaryl substituted aminyl radical D9 have comparable stabilities with the calculated RSE values of −87.7 and −89.7 kJ mol⁻¹, respectively.

In several cases where experimental RSE values for substituted phenylaminyl radicals differ significantly (>15 kJ mol⁻¹), the use of the calculated results is straightforward. Thus, for the parent phenylaminyl radical (D1) and its substituted derivatives (e.g. p-Me and p-CN), the calculated results support the lower experimental RSE value in each case (see Table 5).

All lone-pair donor substituents studied here (F, Cl, OH, OCH₃, SH, NH₂, N(CH₃)₂) are strongly stabilizing in nature. While the effects are large already for halide substituents such as chlorine and fluorine, RSE values beyond 100 kJ mol⁻¹ are found for hydrazinyl radicals such as E11 or E13 (Table 6). Stabilization of N-centered radicals through lone-pair donation is significantly more effective than in C-centered radicals, and somewhat less effective than in O-centered radicals. For example, the stabilizing effect of the hydroxyl group in hydroxymethyl radical with RSE(˙CH₂OH) = −37.4 kJ mol⁻¹ is lower than the corresponding effect in hydroxyaminyl radical with RSE(˙NHOH) = −110.4 kJ mol⁻¹, or in perhydroxyl radical with RSE(˙OOH) = −110.4 kJ mol⁻¹ (using the experimental data from ref. 4). This trend is correctly reproduced by calculations at the G3(MP2)-RAD and G3B3 levels.¹⁰

Table 6 Radical stabilization enthalpies (RSE, in kJ mol⁻¹) at 298.15 K of N-centered radicals substituted with lone pair donors calculated according to eqn (1)

N-centered radical^a	G3(MP2) RAD	G3B3	Exp. (RSE)	Exp. (BDE)^b
a All N-centered radicals exist in the π electronic ground state. b Experimental values from ref. 4.
˙NHCl (E3)	−60.3	−62.4	—	—
˙NHF (E1)	−68.0	−68.5	—	—
˙NHSH (E9)	−83.1	−85.7	—	—
˙NHOH (E5)	−90.2	−91.5	−110 ± 4	+340.1 ± 4
˙NHOCH3 (E7)	−96.2	−98.0	—	—
˙NHNH2 (E11)	−99.1	−101.1	−84 ± 5	+366.1 ± 5
			−112 ± 1	+338.1 ± 1
˙NHN(CH3)2 (E13)	−104.9	−106.9	−94 ± 21	+356 ± 21
˙NCl2 (E4)	−108.4	−110.9	—	—
˙N(SH)2 (E10)	−116.6	−117.3	—	—
˙N(N(CH3)2)2 (E14)	−132.2	−134.9	—	—
˙NF2 (E2)	−134.7	−135.3	−133 ± 10.5	+316.7 ± 10.5
˙N(OH)2 (E6)	−135.9	−136.6	—	—
˙N(OCH3)2 (E8)	−141.6	−140.9	—	—
˙N(NH2)2 (E12)	−149.7	−143.8	—	—

---

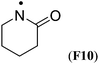
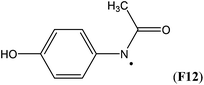
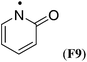
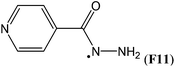
Simultaneous attachment of donor- and acceptor-substituents to the aminyl radical center leads to the class of push/pull- or captodatively substituted aminyl radicals. The highly stabilizing nature of this type of substituent pattern is well known for carbon-centered radicals, but the extent to which this effect is also present in aminyl radicals is not well established.³² The captodative effect may be operative in both acylic (e.g.F1a or F6) or cyclic open-shell systems (F9 or F10). This class of aminyl radicals also includes F11 and F12 derived from pharmaceutically important compounds. The formation of N-centered radical F11 has been linked to the mechanism of action of isoniazid, which is used to treat tuberculosis.³³ The formation of N-centered radical F12 has been implicated in the toxicity mechanism of analgesic acetaminophen (Table 7).³⁴

Table 7 Radical stabilization enthalpies (RSE, in kJ mol⁻¹) at 298.15 K of push/pull-substituted radicals calculated according to eqn (1)

N-centered radical^a	G3(MP2)-RAD	G3B3	Exp. (RSE)	Exp. (BDE)^b
a All N-centered radicals exist in π electronic ground state. b Experimental values from ref. 4 unless otherwise noted. c Experimental error reported in ref. 35d. d IMOMO(G3(MP2)-RAD,ROB2PLYP/Def2-TZVPP); this work (see ESI).
˙N(CH3)CHO (F1)	+7.6	+8.7	—	—
	+4.0	+6.6	+8.0 ± 12.6	+458.1 ± 12.6
˙N(CH3)COCH3 (F1a)	+2.2	−0.5	−4.5 ± 12.6	+445.6 ± 12.6
			−15.4 ± 12.6	+434.7
	−29.8	−24.0	—	—
˙N(Cl)CHO (F2)	−42.7	−43.0	—	—
	−42.0	−36.9	−40.5 ± 12.6	+410.0 ± 12.6
˙N(OH)CF3 (F7)	−79.9	−80.8	—	—
˙N(OCH3)CONH2 (F6)	−82.0	−80.3	—	—
˙N(OH)CHO (F3)	−93.2	−85.0	—	—
˙N(OH)COCH3 (F4)	−95.1	−93.0	−81.9 ± 12.6	+368.2 ± 12.6
˙N(NH2)COCH3 (F8)	−103.0	−105.3	−107.0 ± 12.6	+343.1 ± 12.6
˙N(OH)CONH2 (F5)	−103.8	−101.9	−110.0 ± 10.0^c	+340.1 ± 10.0^c
	−109.0	−110.8	—	—
	−119.4^d	—	−115.4 ± 12.6	+334.7 ± 12.6

---

The most prominent systems, in which captodative effects may be expected, are radicals derived from hydroxamic acids, the N-hydroxyformamidyl radical (F3) being a typical case. The RSE of this radical amounts to −93.2 kJ mol⁻¹, indicating a substantial degree of stabilization (Table 7). The geometry of radical F3 is symmetrical (C_s point group) and therefore two low-lying electronic states can be distinguished: a π electronic state (²A′′) with the unpaired electron in a nitrogen 2p orbital perpendicular to the molecular plane, and a σ state (²A′) with the spin on the molecular plane in a p-type atomic orbital on the carbonyl oxygen. The ²A′′ state in C_s symmetry (NImag = 0) corresponds to the global minimum, while the C_s²A′ structure (NImag = 0) is 119.7 kJ mol⁻¹ less stable (at the G3B3 level). The π electronic state corresponds to a nitrogen-centered radical (SD_N = 0.663; SD_O = 0.272), whereas in the σ radical the unpaired electron is mainly localized on the carbonyl oxygen atom (SD_N = 0.090; SD_O = 0.810). In order to calculate the exact RSE value for this captodative radical, the correct ground state is to be used.

An almost identical RSE value of −95.1 kJ mol⁻¹ is obtained for N-hydroxyacetamidyl radical (F4). In how far this value reflects true synergies between the two attached substituents can be seen by comparing to the two individual substituent effects of the attached hydroxy group as is present in radical E5 (with RSE = −90.2 kJ mol⁻¹) and the acetyl group present in radical C2 (with RSE = +22.2 kJ mol⁻¹). If these effects were additive, an overall stabilization of −90.2 + 22.2 = −68.0 kJ mol⁻¹ would be obtained. Comparison to the true value obtained for radical F4 of −95.1 kJ mol⁻¹ indicates, that the “synergistic gain” in substituent effects amounts to −95.1 + 68.0 = −27.1 kJ mol⁻¹. This degree of synergy is significantly larger as compared to similarly substituted carbon-centered radicals. In more general terms the captodative effect largely depends on the nature of the donor substituent present, with large stability enhancements being observed for strongly electron-donating substituents such as the amino group, and only weak (if any) enhancements for weak donors such as alkyl substituents.

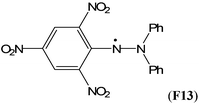
The captodative effect is even more pronounced in radicals derived from urea analogues. Favorable RSE values have been calculated for hydroxy-(F5) and methoxy-substituted (F6) ureas (−103.8 and −82.0 kJ mol⁻¹, resp.). It has been shown that the substantial stabilization effects of these radicals are of utmost importance for their biological and pharmacological properties.³⁵ Not surprisingly, the largest RSE value of −119.4 kJ mol⁻¹ has been calculated for 2,2-diphenyl-1-picrylhydrazyl radical (DPPH, F13), a well-known free radical trap. Scavenging of this stable radical is the basis of a common antioxidant assay.³⁶

The stability of protonated aminyl radicals

The protonation of aminyl radicals is known to strongly affect both their overall reactivity and the selectivity of their reactions, which makes aminium radicals considerably more attractive for synthetic purposes than their neutral counterparts.³⁷ Known reactivity data indicate that aminium radicals are more electrophilic than aminyl radicals, readily add to alkenes and arenes, and undergo synthetically useful intramolecular hydrogen atom abstraction reactions to form cyclic amines (the Hofmann–Löffler–Freytag reaction). In addition, the protonation state of N-centered radicals is of utmost importance in radical-mediated reactions of bioactive compounds in the environment in that the rate of radical rearrangement in amine-containing pharmaceuticals is significantly increased in the protonated state.^2,38

In the following we will investigate the effect of protonation on the stability of N-centered radicals by calculating RSE values of aminium radicals according to eqn (2). For the sake of brevity we will limit this analysis to (cyclo)alkyl- and aryl-substituted aminium radical cations together with their cyclic variants. In aminium radicals carrying lone-pair donor substituents or other protonable groups the analysis is obscured by a multitude of additional factors such as the site of protonation, fast rearrangements to C- and O-centered radical cations, and close lying electronic states. These latter systems will therefore not be considered here.

Alkyl-substituted aminium radicals. Protonation of the parent aminly radical ˙NH₂ (A0) decreases its stability by 72.0 kJ mol⁻¹, which is consistent with the greater s character in the SOMO. However, stabilization of aminium radicals through hyperconjugation is significantly more effective than that of neutral aminyl radicals. For example, the stabilizing effect of the methyl group in methylaminium radical A1⁺ of −60.9 kJ mol⁻¹ is much larger than in methylamine radical with RSE(˙NHCH₃) = −30.0 kJ mol⁻¹ (Table 8).

Table 8 Radical stabilization enthalpies (RSE, in kJ mol⁻¹) at 298.15 K of alkyl- and cycloalkyl-substituted aminium radicals calculated according to eqn (2)

N-centered radical cation^a	G3(MP2)-RAD	G3B3	Other^b
a All N-centered radicals exist in a π electronic ground state. b Ref. 21a.
˙NH2 (A0)	0.0	0.0	0.0
^+˙NH3 (A0^+)	+72.0	+73.2	+73.0 (0 K, W2w)
^+˙NH2CH3 (A1^+)	+11.1	+13.7	+10.7 (0 K, W2w)
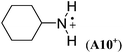
	−0.6	−1.6	—
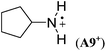
	−9.2	−10.1	—
^+˙NH(CH3)2 (A3^+)	−23.6	−23.7	−27.9 (0 K, W2w)
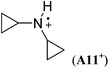
	−95.4	−96.4	—

---

The stabilizing effects of cyclopentyl (as in A9⁺) and cyclohexyl substituents (as in A10⁺) are larger than the effect of the methyl group in A1⁺. The stabilizing effects of cyclobutyl and cyclopropyl groups cannot easily be determined, because ring-opening to acyclic C-centered radicals occurs on geometry optimization in both cases (Scheme 5). However, in the presence of two cyclopropyl substituents no ring-opening occurs during geometry optimization, and a large RSE value of −96.4 kJ mol⁻¹ can be calculated for A11⁺.

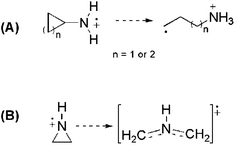Scheme 5 Ring-opening process occurs during geometry optimization (at B3LYP/6-31G(d) level) of some cycloalkyl-substituted aminium radicals (A) and the aziridine radical cation (B).

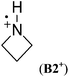
Cyclic aminium radicals (B2⁺–B5⁺) are stabilized, except the three-membered cyclic system B1⁺ (Table 9). The aziridine radical cation is strongly destabilized by 48.8 kJ mol⁻¹ mostly due to the ring strain. Its π electronic state (C_s point group) corresponds to a nitrogen-centered radical (SD_N = 0.691; SD_C = 0.123), whereas the cyclic structure of the σ state (C₂ point group) converges to an open structure (Scheme 5), in which positive charge and spin density are localized on the two carbon atoms (SD_C = 0.670; q_C = +0.460). The carbon-centered radical cation obtained during geometry optimization is calculated to be >130 kJ mol⁻¹ more stable than aziridine radical B1⁺. All other cyclic aminium radicals exist as π-radicals, whereas the corresponding σ-radicals represent first-order stationary points (NImag = 1).

Table 9 Radical stabilization enthalpies (RSE, in kJ mol⁻¹) at 298.15 K of cyclic and bicyclic aminium radicals calculated according to eqn (2)

N-centered radical cation^a	G3(MP2)-RAD	G3B3
a All N-centered radicals exist in π electronic ground state.
	+48.8	+48.6
	−15.5	−15.7
	−28.0	−28.9
	−35.3	−35.8
	−35.6	−37.0

---

In comparison to their neutral counterparts (Table 5), arylaminium radicals D1⁺–D8⁺ are stabilized to a much larger degree (Table 10). In this latter group the calculated RSE values span a range of ca. 100 kJ mol⁻¹, which is three times the range of RSE values calculated for neutral arylaminyl radicals. In contrast to arylaminyl radicals (Fig. 3), a poor correlation (R = 0.943) exists between the calculated RSE values of arylaminium radicals and Brown substituent constants σ_p⁺.

Table 10 Radical stabilization enthalpies (RSE, in kJ mol⁻¹) at 298.15 K of protonated arylamine radical cations calculated according to eqn (2)

N-centered radical cation^a	G3(MP2)-RAD	G3B3
a All N-centered radicals exist in π electronic ground state.
^+˙NH2(p-CF3)C6H5 (D5^+)	−114.3	−119.6
^+˙NH2(p-NO2)C6H5 (D8^+)	−119.1	−117.8
^+˙NH2(p-CN)C6H5 (D4^+)	−124.6	−125.1
^+˙NH2C6H5 (D1^+)	−131.3	−130.0
^+˙NH2(p-CH3)C6H5 (D2^+)	−136.7	−145.3
^+˙NH2(p-OH)C6H5 (D3^+)	−160.7	−163.1
^+˙NH2(p-N(CH3)2)C6H5 (D7^+)	−212.3	−211.6

---

Conclusions

Substituent effects in N-centered radicals vary systematically from those observed for O- and C-centered radicals (Fig. 4). Taking the methyl group as the simple-most alkyl substituent we note that the stabilizing effect on the aminyl radical (RSE = −30.4 kJ mol⁻¹) is intermediate to that observed for the methyl radical (RSE = −13.8 kJ mol⁻¹) and the hydroxyl radical of RSE = −55.7 kJ mol⁻¹. This ordering obviously follows the electronegativity of the radical center and it is tempting to rationalize this trend with the degree of electron donation from the substituent to the formal radical center. This conclusion is supported by population analysis results (NBO analysis).³⁹ By summing the charges of atoms in the methyl substituent, one can find the highest positive charge (q_Me = +0.29) for the methoxy radical, followed by the methylaminyl radical (q_Me = +0.12) and ethyl radical (q_Me = −0.04). A similar trend, but of enhanced magnitude, is observed for substituents acting as formal lone-pair donors such as the amino group. The radical stabilization energy is again smallest for the C-centered radical ˙CH₂NH₂ (−46.7 kJ mol⁻¹), larger for the N-centered radical ˙NHNH₂ (−101.1 kJ mol⁻¹) and largest for the O-centered radical ˙ONH₂ (−164.6 kJ mol⁻¹). This is in line with calculated NPA (Natural population analysis)³⁹ charges for the amino group in C-(q_NH2 = −0.06), N-(q_NH2 = +0.13), and O-centered radical (q_NH2 = +0.34).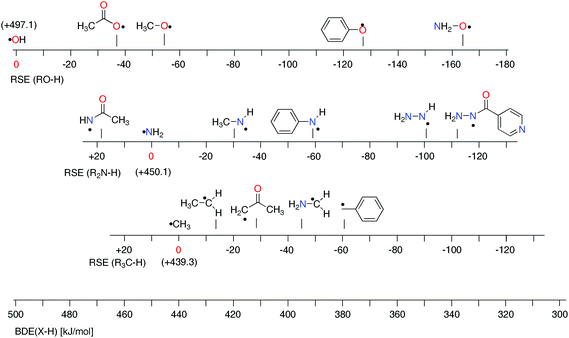

Fig. 4 Stability scales for selected O-, N-, and C-centered radicals together with a common BDE scale (G3B3 results).

The situation becomes more complex once the attached substituents interact notably with both, the unpaired spin as well as the lone pair electrons present at the radical center. Together with the fact that lone pair/substituent interactions can be sizeable already in the closed shell parent molecules, it is clear that a simple picture for the overall substituent effect is unlikely to emerge. This is apparent for the phenyl substituent, which leads to RSE = −61.2 kJ mol⁻¹ in the benzyl radical. The stabilizing effects for the N-centered radical is slightly smaller at RSE = −59.3 kJ mol⁻¹, while that for the O-centered radical is much larger at RSE = −128.1 kJ mol⁻¹. A complex interplay of factors also determines the influence of acyl substituents such as C(O)CH₃. For acetamidyl radical ˙NHC(O)CH₃ the calculated RSE = +19.9 kJ mol⁻¹ suggests that the attachment of acyl groups to the amino radical center is destabilizing,¹⁷ whereas for ˙OC(O)CH₃ (−37.6 kJ mol⁻¹) and ˙CH₂C(O)CH₃ (−29.1 kJ mol⁻¹) the effect is stabilizing. The above mentioned RSE values can be combined with the X–H BDE values of the respective reference compounds to put O/N/C-centered radicals on a common scale of BDE values. For the ethyl radical this implies a BDE(C–H) value of +439.3–13.8 = +425.5 kJ mol⁻¹. This value is larger than for most of the N-centered radicals shown in Fig. 4 and implies that hydrogen transfer is exothermic between the ethyl radical and the amino groups in methyl amine (CH₃NH₂), aniline (PhNH₂), and hydrazine (NH₂NH₂). This is also true for hydrogen abstraction from the hydroxyl groups in phenol (PhOH) and hydroxylamine (NH₂OH). The reductive properties of these two latter compounds and of hydrazines are, of course, well known, but it is usually not anticipated that a favorable driving force also exists for aliphatic and aromatic amines. The H-donor abilities of hydrazine derivatives is well demonstrated in isoniazid (F11, RSE = −110.8 kJ mol⁻¹), the first-line antituberculosis therapeutic agent. Isoniazid reacts in the active site of a mycobacterial catalase enzyme with a wide range of oxidants and turns into the corresponding isonicotinoyl radical. The open-shell intermediate forms adducts with NAD⁺ and NADP⁺, which inhibit cell wall lipid and nucleic acid synthesis.^33,40 These examples illustrate that the thermodynamics of hydrogen-transfer reactions involving nitrogen-centered radicals can be quantified for a variety of amines, including closed-shell precursors of biological and pharmaceutical relevance.⁴¹

Computational details

DFT calculations are employed for geometry optimizations and frequency calculations for open-shell systems and closed-shell systems at the unrestricted UB3LYP/6-31G(d) level and restricted B3LYP/6-31G(d) level, respectively. All energies are reported for the structures in gas-phase at 298.15 K where thermal corrections to enthalpies have been calculated at the same level of theory using the rigid rotor/harmonic oscillator model (in kJ mol⁻¹). Improved relative energies were obtained with the G3(MP2)-RAD method developed by Radom et al. for open shell systems in combination with the same (unscaled) thermochemical corrections as before.⁷ These results were confirmed by calculations at the even more accurate G3B3 approach.⁸ Wavefunction stability is checked at each level of theory. All the calculations were done using the Gaussian 09⁴² software package. URCCSD(T) calculations were performed with either MOLPRO or Gaussian 09, the differences between the calculated energies being negligible. A suitable manipulation of the initial guess was required to obtain optimized σ- and π-radical electronic states. In order to obtain the desired σ- or π- radical state, the “guess = alter” and “scf = symm” keywords along with definition of the list of orbital exchanges were used in the input. The σ- or π-nature of a radical was assigned on the basis of the unpaired spin SCF density (depicted in ESI† for selected molecules) and spin distributions (NPA values) calculated at the B3LYP/6-31G(d) level. The spin SCF densities of molecules were plotted (0.004 electron per bohr³) using the GaussView program.⁴³ Natural population analysis (NPA) was done using NBO 3.1. program,³⁹ as included in the Gaussian package.

Acknowledgements

Financial support by the Alexander von Humboldt Foundation (for the research group linkage project “Computational Life Sciences on Open Shell Intermediates”) and the SFB 749 on “Dynamics and Intermediates of Molecular Transformations” sponsored by the Deutsche Forschungsgemeinschaft (DFG) is gratefully acknowledged. We thank the Computing Centre SRCE of the University of Zagreb for allocating computer time on the Isabella cluster, where part of the calculations were performed.

Notes and references

1. (a) W. M. Garrison, Chem. Rev., 1987, 87, 381–398; (b) C. J. Easton, Chem. Rev., 1997, 97, 53–82; (c) H.-F. Lu, F.-Y. Li and S. H. Lin, J. Comput. Chem., 2007, 28, 783–794; (d) Z. I. Watts and C. J. Easton, J. Am. Chem. Soc., 2009, 131, 11323–11325; (e) S. Scheiner and T. Kar, J. Am. Chem. Soc., 2010, 132, 16450–16459; (f) B. Chan, R. J. O'Reilly, C. J. Easton and L. Radom, J. Org. Chem., 2012, 77, 9807–9812.
2. (a) H. Zhang and C.-H. Huang, Environ. Sci. Technol., 2005, 39, 4474–4483; (b) V. Vrcek and H. Zipse, J. Org. Chem., 2009, 74, 2947–2957.
3. (a) L. Stella, Angew. Chem., Int. Ed. Engl., 1983, 22, 337–350; (b) A. Gansäuer, T. Lauterbach and S. Narayan, Angew. Chem., Int. Ed., 2003, 42, 5556–5573; (c) W. R. Bowman, A. J. Fletcher and G. B. S. Potts, J. Chem. Soc., Perkin Trans. 1, 2002, 2747–2762.
4. Y.-R. Luo, Comprehensive Handbook of Chemical Bond Energies, CRC Press, London, 2007.
5. (a) K.-S. Song, Y.-H. Cheng, Y. Fu, L. Liu, X.-S. Li and Q. X. Guo, J. Phys. Chem. A, 2002, 106, 6651–6658; (b) G. P. F. Wood, D. J. Henry and L. Radom, J. Phys. Chem. A, 2003, 107, 7985–7990; (c) G. P. F. Wood, D. Moran, R. Jacob and L. Radom, J. Phys. Chem. A, 2005, 109, 6318–6325.
6. (a) B. Chan and L. Radom, Theor. Chem. Acc., 2011, 130, 251–260; (b) B. Chan and L. Radom, J. Phys. Chem. A, 2011, 115, 5496–5504; (c) B. Chan and L. Radom, J. Phys. Chem. A, 2012, 116, 3745–3752; (d) B. Chan and L. Radom, J. Phys. Chem. A, 2012, 116, 4975–4986; (e) R. J. O'Reilly, A. Karton and L. Radom, Int. J. Quantum Chem., 2012, 112, 1862–1878.
7. (a) D. J. Henry, C. J. Parkinson and L. Radom, J. Phys. Chem. A, 2002, 106, 7927–7936; (b) D. J. Henry, M. B. Sullivan and L. Radom, J. Chem. Phys., 2003, 118, 4849–4860.
8. A. G. Baboul, L. A. Curtiss, P. C. Redfern and K. Raghavachari, J. Chem. Phys., 1999, 110, 7650–7657.
9. H. Zipse, Top. Curr. Chem., 2006, 263, 163–189.
10. J. Hioe and H. Zipse, in Encyclopedia of Radical in Chemistry, Biology and Materials, ed. C. Chatgilialoglu and A. Studer, John Wiley & Sons Ltd, Chichester, 2012, pp. 449–476.
11. D. M. Golden, R. K. Solly, N. A. Gac and S. W. Benson, J. Am. Chem. Soc., 1972, 94, 363–369.
12. L. S. Sunderlin, D. Panu, D. B. Puranik, A. J. Ashe III and R. R. Squires, Organometallics, 1994, 13, 4732–4740.
13. (a) J. Lalevee, X. Allonas and J.-P. Fouassier, J. Am. Chem. Soc., 2002, 124, 9613–9621; (b) F. G. Bordwell and W.-Z. Liu, J. Phys. Org. Chem., 1998, 11, 397–406.
14. D. Sakic, F. Achreiner, V. Vrcek and H. Zipse, Org. Biomol. Chem., 2013, 11, 4232–4239.
15. T. J. Mali'n, L. Weidolf, N. Castagnoli Jr. and U. Jurva, Rapid Commun. Mass Spectrom., 2010, 24, 1231–1240.
16. F. P. Guengerich and E. M. Isin, in Handbook of Metabolic Pathways of Xenobiotics, ed. P. W. Lee, Wiley-VCH, Weinheim, 2014, pp. 147–197.
17. For a detailed discussion see: W. C. Danen and F. A. Neugebauer, Angew. Chem., Int. Ed. Engl., 1975, 14, 783–789.
18. (a) H. M. Muchall, N. H. Werstiuk and J. Lessard, J. Mol. Struct. (THEOCHEM), 1999, 469, 135–142; (b) R. Sutcliffe, D. Griller, J. Lessard and K. U. Ingold, J. Am. Chem. Soc., 1981, 103, 624–628.
19. (a) A. Lund, P. O. Samskog, L. Eberson and S. Lunell, J. Phys. Chem., 1982, 86, 2458–2462; (b) P. H. Kasai, J. Am. Chem. Soc., 1992, 114, 2875–2880; (c) Y. Apeloig and R. Schreiber, J. Am. Chem. Soc., 1980, 102, 6146–6147.
20. J. C. Martin and P. D. Bartlett, J. Am. Chem. Soc., 1957, 79, 2533–2541.
21. (a) D. I. Pattison, R. J. O'Reilly, O. Skaff, L. Radom, R. F. Anderson and M. J. Davies, Chem. Res. Toxicol., 2011, 24, 371–382; (b) J. Lind, M. Jonsson, T. E. Eriksen, G. Merenyi and L. Eberson, J. Phys. Chem., 1993, 97, 1610–1614.
22. T. Yonezawa, I. Noda and T. Kawamura, Bull. Chem. Soc. Jpn., 1969, 42, 650–657.
23. Y. H. Hu and E. Ruckenstein, J. Phys. Chem. B, 2007, 111, 5040–5042.
24. D. Griller, G. D. Mendenhall, W. Van Hoof and K. U. Ingold, J. Am. Chem. Soc., 1974, 96, 6068–6070.
25. M. C. R. Symons, Tetrahedron, 1973, 29, 615–619.
26. R. J. O'Reilly, A. Karton and L. Radom, J. Phys. Chem. A, 2013, 117, 460–472.
27. J. A. Blake, D. A. Pratt, S. Lin, J. C. Walton, P. Mulder and K. U. Ingold, J. Org. Chem., 2004, 69, 3112–3120.
28. (a) M. Jonsson, J. Lind, G. Merenyi and T. E. Eriksen, J. Chem. Soc., Perkin Trans. 2, 1995, 61–65; (b) P. A. MacFaul, D. D. M. Wayner and K. U. Ingold, J. Org. Chem., 1997, 62, 3413–3414; (c) T. Denisov and V. E. Tumanov, Russ. Chem. Rev., 2005, 74, 825–858.
29. P. Naumov, Y. Topcu, M. Eckert-Maksic, Z. Glasovac, F. Pavosevic, M. Kochunnoonny and H. Hara, J. Phys. Chem. A, 2011, 115, 7834–7848.
30. (a) C. Hansch, A. Leo and R. W. Taft, Chem. Rev., 1991, 91, 165–195; (b) Z. Li and J.-P. Cheng, J. Org. Chem., 2003, 68, 7350–7360.
31. R. I. Walter, J. Am. Chem. Soc., 1966, 88, 1923–1930.
32. For the only theoretical study, see: D. Kost, M. Raban and K. Aviram, J. Chem. Soc., Chem. Commun., 1986, 346–348.
33. K. A. Rickman, K. T. Swancutt, S. P. Mezyk and J. J. Kiddle, Bioorg. Med. Chem. Lett., 2013, 23, 3096–3100.
34. (a) L. Koymans, J. H. van Lenthe, R. van de Straat, G. M. D.-O. den Kelder and N. P. E. Vermeulen, Chem. Res. Toxicol., 1989, 2, 60–66; (b) C. N. Alves, R. S. Borges and A. B. F. Da Silva, Int. J. Quantum Chem., 2006, 106, 2617–2623.
35. (a) S. L. Vankayala, J. C. Hargis and H. L. Woodcock, J. Chem. Inf. Model., 2012, 52, 1288–1297; (b) J. Huang, Z. Zou, D. B. Kim-Shapiro, S. K. Ballas and S. B. King, J. Med. Chem., 2003, 46, 3748–3753; (c) I. Vinkovic Vrcek, D. Sakic, V. Vrcek, H. Zipse and M. Birus, Org. Biomol. Chem., 2012, 10, 1196–1206; (d) A. Budimir, E. Besic and M. Birus, Croat. Chem. Acta, 2009, 82, 807–818.
36. (a) J. Xie and K. M. Schaich, J. Agric. Food Chem., 2014, 62, 4251–4260; (b) Z.-Q. Liu, Chem. Rev., 2010, 110, 5675–5691.
37. J. L. Esker and M. Newcomb, Advances in Heterocyclic Chemistry, ed. A. R. Katritzky, Academic, San Diego, 1993, vol. 58, pp. 1–45.
38. V. K. Sharma, S. K. Mishra and N. Nesnas, Environ. Sci. Technol., 2006, 40, 7222–7227.
39. E. D. Glendening, A. E. Reed, J. E. Carpenter and F. Weinhold, NBO Version 3.1, Theoretical Chemistry Institute, University of Wisconsin, Madison WI, 1996.
40. G. S. Timmins and V. Deretic, Mol. Microbiol., 2006, 62, 1220–1227.
41. J. Hioe and H. Zipse, Chem. – Eur. J., 2012, 18, 16463–16472.
42. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford CT, 2009.
43. GaussView, Gaussian, Inc., Pittsburgh, PA, 2003.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c4ob01656d

---