Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
RAFT polymerization and associated reactivity ratios of methacrylate-functionalized mixed bio-oil constituents†
Angela L.
Holmberg
a,
Michael G.
Karavolias
a and
Thomas H.
Epps
III
*ab
aDepartment of Chemical and Biomolecular Engineering, University of Delaware, Newark, Delaware 19716, USA. E-mail: thepps@udel.edu
bDepartment of Materials Science and Engineering, University of Delaware, Newark, Delaware 19716, USA
First published on 22nd April 2015
Abstract
This work features a new suite of correlations for estimating kinetic parameters from multicomponent reversible addition–fragmentation chain-transfer (RAFT) polymerizations and an improved methodology for determining reactivity ratios in the pursuit of cost-effective and renewable plastics prepared from moderately processed bio-oils. Select monomers representing possible derivatives of compounds found in renewable bio-oils, such as pyrolyzed Kraft lignin and vegetable oils, were polymerized to investigate the consequences of structural diversity on the kinetics of RAFT polymerization. To facilitate predictions of heteropolymer dispersities and molecular weights, apparent chain-transfer coefficients (Capptr's) and propagation rate constants (kappp's) from homopolymerizations were correlated to kinetic parameters associated with the polymerization of bio-oil mixtures. Capptr depended on the reactivity ratios of the bio-oil components and the composition of the bio-oil feed, whereas kappp was related to only the composition of the bio-oil feed. A modified approach for analyzing Mayo–Lewis plots resulted in more accurate reactivity ratios and with greater precision in comparison to conventional nonlinear fitting procedures and traditional linearization fitting methods, respectively. The measured compositional data readily mapped onto the predicted monomer distribution profiles in multicomponent polymers, confirming the validity of the improved method described herein to determine reactivity ratios. Altogether, this manuscript offers a strategy for improving the viability of biobased polymers, addressing two key factors: minimizing separations costs by polymerizing bio-oil mixtures and preventing batch-to-batch inconsistencies in polymer properties by applying a priori knowledge about the bio-oil constituents’ individual kinetic parameters.
Introduction
Interest in the controlled polymerization of multicomponent monomer mixtures is gaining traction due to the numerous opportunities afforded by the resultant polymers. These multicomponent mixtures are precursors to heteropolymers, a generic term for random, statistical, gradient, or blocky polymers containing at least three chemically distinct monomers. Historically, mixtures of monomers have been polymerized to adjust a material's solubility, adhesion, chemical resistance, flame retardancy, processability, and other characteristics.1,2 More recently, heteropolymers with controlled monomer distributions have found application in drug-delivery vehicles, hydrogel systems, and biodegradable polyesters, as monomer mixtures provide a simple means for adding stimuli-responsive behavior and tunable end-of-life characteristics into a polymer.3–9 Homopolymers are less ideal for accessing these traits due to their comparably limited parameter space for manipulating polymer architecture and behavior. Instead, a heteropolymer can be tailored to meet specific design requirements simply by adjusting the monomer feed composition and/or the feed rate to the polymerization mixture.Yet another advantage offered by heteropolymers often is overlooked: polymerized mixtures can provide cost savings by reducing separations needs. Such an approach can ameliorate some of the economic challenges associated with biobased plastics. These renewable materials tend to be expensive largely due to the costs of separating complex mixtures (i.e., bio-oils) into purer individual components.10,11 Renewable bio-oil mixtures could be incorporated into plastics directly (or after minimal processing) as heteropolymers, thereby eliminating many separation steps, reducing costs, and subsequently enabling novel bio-based polymers to compete economically with well-established petroleum-based polymers.
Coupling the advantages of heteropolymers with controlled reversible-deactivation radical polymerization techniques, such as reversible addition–fragmentation chain-transfer (RAFT) polymerization, further improves the polymer's utility. Materials synthesized via controlled methods exhibit reproducibly narrow molecular weight distributions and predictable molecular weights. The resulting polymers subsequently can be chain-extended into self-assembling block polymers for numerous applications that benefit from nanostructure formation.12–14 For biobased polymers, these controlled methods are employed predominantly to synthesize materials for thermoplastic elastomers and pressure-sensitive adhesives,10,15 and RAFT potentially is ideal due to its sustainability benefits.16
Despite the above advantages, employing mixtures of monomers in the synthesis of polymers comes with numerous challenges attributable to the multivariate nature of the polymerization feedstocks,1,17 in which the properties of an n-component heteropolymer depend minimally on n − 1 mole-fractions of monomers and n!/(n − 2)! reactivity ratios. Bio-oils come with additional difficulties. Not only are bio-oils naturally complex, but their compositions also can vary significantly depending on the feedstock source, type, season, processing method, etc.18–21 This variability can hinder the practicality of bio-oil-based heteropolymers due to the possibility of generating materials with different monomer distributions (or polymer compositions) and consequently inconsistent properties between batches.
The concern of variability in bio-oil composition can be mitigated if controls are enacted to manage the polymerization kinetics and keep the monomer segment distributions and overall polymer compositions in an acceptable range for property consistency. Of utmost importance for reproducible properties is the monomer distribution profile; different glass transition temperatures and mechanical properties, among other traits, are displayed by gradient, statistical, blocky, and random segment distribution types.22–29 Control over these characteristics results from knowing the composition of the bio-oil, the kinetic parameters for the homopolymerization of each constituent, and how those kinetic parameters impact the heteropolymerization of corresponding mixtures.
In this work, we investigate the RAFT homopolymerization behavior of a library of potentially biobased methacrylates, as well as the polymerization behavior and resulting monomer segment distributions when producing heteropolymers from model bio-oil mixtures. To the authors’ knowledge, this report uniquely investigates equations that correlate select kinetic parameters from RAFT polymerizations containing more than two monomers to kinetic parameters from the homopolymerizations of the individual components. Additionally, this study features an elegant approach for fitting Mayo–Lewis reactivity ratio data with an appropriate level of precision, and it contributes to the growing library of biobased monomers10 available for block polymer syntheses. The correlations presented in this work for the apparent chain-transfer coefficient (Capptr) and the apparent propagation rate constant (kappp) in heteropolymerizations, as well as the structural differences between the monomers, help define the relative values of the kinetic parameters. The reported nonlinear Mayo–Lewis fitting procedure for determining reactivity ratios is an improvement over traditional methods as it accounts for variable level of confidence in the individual data points to enhance measurement credibility. The resulting reactivity ratios are employed to predict monomer distributions, providing insight into the separations that may be required in bio-oil processing for polymers applications. Finally, the structurally diverse collection of monomers in this work, combined with the insight into their kinetic behavior, provides exciting pathways to designer polymers with precise molecular weights and compositions.
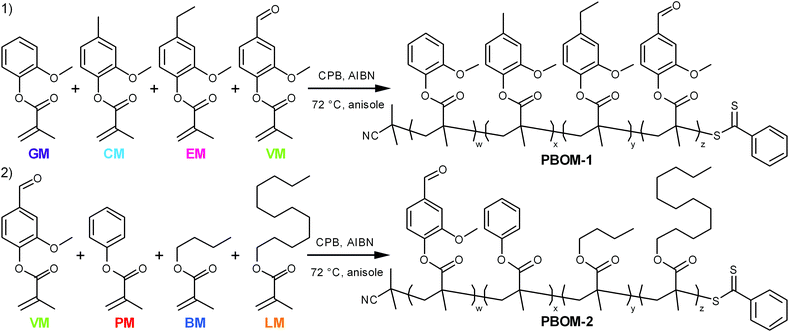
The monomers investigated in this work (Scheme 1) are derivatives of compounds that can found in some processed biomasses, such as pyrolyzed Kraft lignin,18,19,30 fermented biomass,31,32 and certain plant oils.10,33 The representative bio-oil constituents include guaiacol, creosol, 4-ethylguaiacol, vanillin, and phenol, which can comprise depolymerized softwood lignin;18,19,30n-butanol, which is a sought-after fermentation product;32 and lauric acid, which is a major constituent of coconut oil.33 Each of these chemicals can be converted to guaiacol methacrylate (GM, 2-methoxyphenyl methacrylate), creosol methacrylate (CM, 4-methyl-2-methoxyphenyl methacrylate), 4-ethylguaiacol methacrylate (EM, 4-ethyl-2-methoxyphenyl methacrylate), vanillin methacrylate (VM, 3-methoxy-4-methacryloyloxybenzaldehyde), phenyl methacrylate (PM), n-butyl methacrylate (BM), and lauryl methacrylate (LM, dodecyl methacrylate).34–36 Ideally, these renewable bio-oil methacrylate (BOM) monomers would be obtained from minimally processed mixtures and subsequently polymerized, with non-reactive species in the bio-oil serving as the polymerization solvent. The composition of the bio-oil or BOM could be assessed by partial fractionation of the components and subsequent characterization of the resulting fractions by advanced methods,37 such as two-dimensional gas chromatography coupled with time-of-flight mass spectrometry38 or various NMR techniques.39 The chemical makeup of the mixture could be refined as necessary by distillation, solvent extraction, blending, or other techniques. However, in this model study, petroleum-based versions of the individual components are mixed prior to polymerization, and the composition of the idealized BOM is confirmed by NMR spectroscopy. Anisole is the representative polymerization solvent, as its chemical structure is similar to other inert lignin pyrolysis products19,30 and it is considered reasonably ‘green’.40
The first model bio-oil methacrylate polymer (poly[bio-oil methacrylate]-1 or PBOM-1) investigated in this work is composed solely of compounds that can be generated from the pyrolysis products (bio-oil) of softwood Kraft lignin.18,30 These 2-methoxyphenol (guaiacol) derivatives are structurally identical except for the p-position moiety, which is a hydrogen atom (GM), methyl group (CM), ethyl group (EM), or formyl group (VM) depending on the monomer, and provide insight into the assumptions that can be made regarding the RAFT polymerization behavior of reasonably homogeneous bio-oils. The second model poly(bio-oil methacrylate) (PBOM-2) comprises possible derivatives of compounds found in multiple different processed biomasses: vanillin, a common aromatic target of lignin pyrolysis; phenol, an aromatic component of more deoxygenated lignin-based bio-oils;30n-butanol, a short-chained fatty alcohol from some fermentations; and lauric acid or lauryl alcohol, a long-chained fatty acid or alcohol found in many plant oils.10 The polymerization of BOM-2 serves to model situations in which bio-oils are mixed or are less structurally homogeneous. Furthermore, mixing dissimilar bio-oils is an attractive approach for tuning polymer properties and compositions.
The kinetic parameters we chose to investigate, viz., reactivity ratios, kappp, and Capptr, provide a means for controlling polymerization behavior and resulting polymer characteristics. Reactivity ratios (ri,j's) define the relative rate constants for a radical of monomer i self-propagating with monomer i vs. cross-propagating with monomer j, and allow one to calculate the expected monomer distribution profile in a polymer, whether it is gradient, statistical, blocky, or random.17 In RAFT polymerizations, kappp influences the polymerization rate and therefore the ‘livingness’ of a polymerization (i.e., the propensity for reversible deactivation during a polymerization); slow rates can lead to low fractions of ‘living’ chains (i.e., polymers with retained RAFT-enabling end groups) at high molecular weights or conversions.12,41 Additionally, Capptr correlates the rate of monomer consumption to the rate of chain-transfer agent consumption and helps define the dispersity (Đ) of the resulting polymer.12,42 Increasing values of Capptr correspond to narrowing polymer Đ's, faster consumption rates of the chain-transfer agent, and consequently more accurate molecular weight predictions at low monomer conversions. The value of Capptr depends on numerous factors including reaction solvents and temperatures, reagent choice, and certain reagent concentrations.12,42
Experimental
Reagents
Methacrylic anhydride (94%, inhibited with 200 ppm Topanol A, Sigma-Aldrich), 2-cyano-2-propyl benzodithioate (CPB, 97%, STREM Chemicals), and isopropyl acetate (98%, Sigma-Aldrich) were used as received. 2,2′-Azobisisobutyronitrile (AIBN, Sigma-Aldrich) was recrystallized twice from methanol and stored at −2 °C until use. The polymerization solvent [anisole (≥99.7%) with 4.9 wt% N,N-dimethylformamide (DMF, ≥99.9%) as an internal standard] was prepared in advance using reagents from Sigma-Aldrich and stored on molecular sieves to minimize water uptake. All additional reagents were purchased from Fisher Scientific and used as received, unless stated otherwise.Monomers
Lauryl methacrylate (LM, 96%, 500 ppm MEHQ inhibitor, Sigma-Aldrich) was purified by passage through neutral alumina to remove inhibitors prior to use. GM, CM, EM, VM, and PM of ∼95% purity were prepared via a base-catalyzed acylation reaction between methacrylic anhydride and the corresponding phenol as described and characterized elsewhere.34,35 BM is available commercially, but for this work, it was synthesized using a modified version of the aforementioned base-catalyzed reaction with methacrylic anhydride, for which n-butanol (≥99.8%) was the reactive alcohol.35 The major differences in the BM preparation, relative to the other methacrylates, include that the reaction temperature was reduced to 45 °C and that the reaction time was increased to 72 h.All synthesized monomers were purified to >98 mol% as described below. GM, CM, and EM were subjected to flash chromatography on silica gel (Sorbent Technologies, Standard Grade, 230 × 400 mesh, 60 Å) with a ‘green’ tripartite eluent43 (0.9/0.075/0.025 v/v/v heptane/isopropyl acetate/methanol), dried under reduced pressure, and stored at −2 °C until use. VM was purified as previously reported44via serial recrystallizations from hexanes (or n-heptane as a ‘green’ alternative) and stored at −2 °C until use. BM was purified to >99 mol% by vacuum distillation from calcium hydride at 0 °C, and PM was purified to >99 mol% by fractional vacuum distillation from calcium hydride at 40 °C. Unreacted methacrylic anhydride and methacrylic acid byproducts were removed in the first fraction of distilled PM, and both monomers were stored at −2 °C until use. Caution: calcium hydride reacts violently with water and should be deactivated carefully over ice prior to disposal. Purified BM was stored at −2 °C for ∼two weeks before auto-polymerization was noted.
Polymerization of monomers for kinetic studies
The same general procedure was used to synthesize each polymer, involving the mixing of a stock solution of CPB, AIBN, and solvent (4.9 wt% DMF in anisole) with known amounts of monomer (usually ∼2 g) and more solvent. The resulting mixtures, referred to as ‘monomer stock’ solutions, were prepared to target a predetermined mole-ratio of monomer![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CPB (usually 230
CPB (usually 230![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) and mass-ratio of monomer
1) and mass-ratio of monomer![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) solvent of 0.94
solvent of 0.94![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. Fractions of monomer stock solutions were mixed to prepare model functionalized bio-oil samples (BOM-1 and BOM-2). Each sample then was degassed by at least three freeze–pump–thaw cycles and either backfilled with argon for immediate use or transferred into a glovebox for storage under argon at −2 °C. Reference aliquots were taken from each monomer solution immediately prior to polymerization, after which the vessel was pressurized with argon (∼3 psig, 99.998%, Keen Compressed Gas), sealed, and heated to 72 °C. Additional aliquots for molecular analyses were extracted under argon flow at predetermined times after quenching the reaction mixture in liquid nitrogen and thawing the contents to room temperature. The reaction vessel was repressurized with argon and returned to 72 °C within ∼10 min of aliquot extraction. The collected fraction was divided into two parts, one part for immediate NMR characterization and the remainder for precipitation, drying, and subsequent size-exclusion chromatography (SEC) analyses. The precipitation solvent was methanol in all cases except for polymers containing VM, which can react with methanol.44 Thus, VM-containing polymers were precipitated into hexanes (PVM and PBOM-1) or ethanol (PBOM-2). Ethanol was chosen over hexanes in PBOM-2 to avoid dissolving any potential PLM and PBM homopolymer contaminants or other polymer chains with high LM or BM content.
1. Fractions of monomer stock solutions were mixed to prepare model functionalized bio-oil samples (BOM-1 and BOM-2). Each sample then was degassed by at least three freeze–pump–thaw cycles and either backfilled with argon for immediate use or transferred into a glovebox for storage under argon at −2 °C. Reference aliquots were taken from each monomer solution immediately prior to polymerization, after which the vessel was pressurized with argon (∼3 psig, 99.998%, Keen Compressed Gas), sealed, and heated to 72 °C. Additional aliquots for molecular analyses were extracted under argon flow at predetermined times after quenching the reaction mixture in liquid nitrogen and thawing the contents to room temperature. The reaction vessel was repressurized with argon and returned to 72 °C within ∼10 min of aliquot extraction. The collected fraction was divided into two parts, one part for immediate NMR characterization and the remainder for precipitation, drying, and subsequent size-exclusion chromatography (SEC) analyses. The precipitation solvent was methanol in all cases except for polymers containing VM, which can react with methanol.44 Thus, VM-containing polymers were precipitated into hexanes (PVM and PBOM-1) or ethanol (PBOM-2). Ethanol was chosen over hexanes in PBOM-2 to avoid dissolving any potential PLM and PBM homopolymer contaminants or other polymer chains with high LM or BM content.
Polymerization of monomer pairs for reactivity ratio measurements
Samples for determining reactivity ratios were prepared while using an argon-atmosphere glovebox by mixing predetermined volumes of monomer stock solutions (see the previous section) in a glass autosampler vial equipped with a stir bar for a total volume of 60–120 μL. Typically, eight samples with different mole-fractions of monomer spanning ∼0.1–0.9 were prepared for each monomer pair. Approximately 20 μL of each mixture was placed into an NMR tube to determine the composition of the monomer solution prior to polymerization (fi). The remaining solution was tightly sealed in the vial using a screw cap with a hole and Teflon/silicone septum, Teflon-side down. Five to eight sealed vials then were removed from the glovebox and suspended simultaneously in a preheated (72 °C) oil bath for at least 1.5 h. Longer times (up to 4 h) were necessary to get appropriate levels of conversion in samples that were predominantly LM or PM. After polymerization, samples were cooled to room temperature, and aliquots were taken for NMR characterization. All reported data are from samples with monomer-to-polymer conversions between 6 mol% and 20 mol%. The specified conversion window was thought to minimize possible effects of initiation or compositional drift that may distort reactivity ratio measurements.Characterization of polymerization aliquots
Number-average molecular weight (Mn), weight-average molecular weight (Mw), and Đ data were determined in reference to polystyrene standards (1.63–205 kg mol−1, Polymer Laboratories) using SEC with tetrahydrofuran (1.0 mL min−1) as the eluent. SEC data were collected using a Viscotek VE 2001 instrument equipped with Waters Styragel HR1 and HR4 columns (7.8 × 300 mm) in series with a Viscotek VE 3580 refractive index (RI) detector. The number-average degree of polymerization (Xn) was calculated from SEC data by subtracting the molecular weight of the chain-transfer agent (221.34 g mol−1) from Mn and dividing that difference by the monomer molecular weight. The same procedure gave the weight-average degree of polymerization (Xw), except using Mw instead of Mn. For the bio-oil polymers, an average monomer molecular weight was employed for each Xn and Xw calculation, for which the average was weighted by the experimentally determined mass-fraction of each component in the polymer. Composition and conversion data for each reaction were determined from 1H NMR data collected with CDCl3 (0.03 v/v% TMS) as the solvent. The NMR spectrometer (AVIII 600 MHz) used for these studies was equipped with a 5 mm Bruker SMART probe and Bruker SampleXpress autosampler.The molar monomer-to-polymer conversion (x) for each sample was calculated using 1H NMR data by tracking the change in area of the allyl peaks (6.45–5.45 ppm, see ESI† for individual peak assignments) relative to the peaks in the reference aliquot that were normalized to an internal standard. Anisole peaks (methoxy: 3.79 ppm singlet and aromatics: 6.97–6.88 ppm multiplets) served as the internal standard for the homopolymerizations of PM (methoxy), BM (aromatics), and LM (aromatics), whereas DMF peaks (8.01 ppm singlet and 2.91 ppm doublet) served as the internal standard for the polymerizations of all other monomers (GM, CM, EM) and reactivity ratio samples. For VM-containing polymerizations, the cumulative area of the aldehyde peak in VM and PVM (10.10–9.60 ppm) was the internal standard (i.e., VM, BOM-1, and BOM-2). The composition of each BOM aliquot and reactivity ratio sample also was determined using 1H NMR in CDCl3, and the corresponding characteristic NMR spectra and analysis methods are presented in the ESI.†
Quantification of reactivity ratios
Reactivity ratios for each monomer pair were measured by fitting compositional data with the Mayo–Lewis equation:45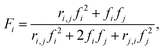 | (1) |
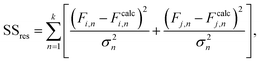 | (2) |
The mean standard error in Ficalc for the resulting fit equation was estimated using the following equation:
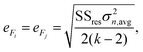 | (3) |
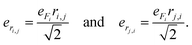 | (4) |
Estimation of kinetic parameters
To estimate reactivity data, the polymerizations were assumed to exhibit pseudo-first-order kinetic behavior for the first few hours of polymerization. Pseudo-first-order kinetic plots, ln{[M]0/[M]t} vs. t plots (in which [M]0 is the starting monomer concentration, and [M]t is the concentration of monomer at time t), were constructed with linear regressions fit to three hours to four hours of polymerization data, beginning with the first non-zero monomer conversion measurement and ending before the data deviated from linearity due to the molecular-weight dependence of the kinetic parameters.12 The apparent propagation rate constant for the polymerizations, kappp, was taken as the slope of the linear regression, and the pre-equilibrium time (or time to initiation), tinit, was taken as the x-intercept of the linear regression.C apptr for each polymerization was estimated from SEC data (Xn and Xw), the fractional conversion of monomer (x), and the following form of the Mayo equation:42,46
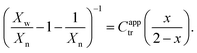 | (5) |
In addition to measuring Capptr for each polymerization, an average apparent chain-transfer coefficient (![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) apptr) was estimated for each heteropolymerization using a nonlinear combination of the apparent chain-transfer coefficient Capptr,i from each of the homopolymerizations of monomer i, the mole-fraction of each monomer in the feed, and the reactivity ratios between each of the monomers. The generic equation that we used to calculate
apptr) was estimated for each heteropolymerization using a nonlinear combination of the apparent chain-transfer coefficient Capptr,i from each of the homopolymerizations of monomer i, the mole-fraction of each monomer in the feed, and the reactivity ratios between each of the monomers. The generic equation that we used to calculate ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) apptr for the polymerization of a mixture of j chemically distinct monomers was as follows:
apptr for the polymerization of a mixture of j chemically distinct monomers was as follows:
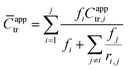 | (6) |
![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) apptr that did not accurately capture our data,52 as shown in the Results and Discussion section.
apptr that did not accurately capture our data,52 as shown in the Results and Discussion section.
Prediction of monomer distributions in heteropolymers
Cumulative and positional monomer distributions in PBOM-1 and PBOM-2 were predicted as a function of monomer conversion using the computational procedure outlined by Ting et al.17 The approach numerically solves the combined Walling–Briggs53 and Skeist54 models using fourth-order Runge–Kutta predictor–corrector methods (see the ESI† for more details).55 The solver code outputs positional and cumulative compositions of the polymer as a function of monomer conversion given starting compositions, reactivity ratios, and a step size (h = 0.0001). The code provided the data in this manuscript, and it also successfully reproduced compositional profiles reported by Ting et al.17Results and discussion
Control and kinetics of RAFT polymerizations
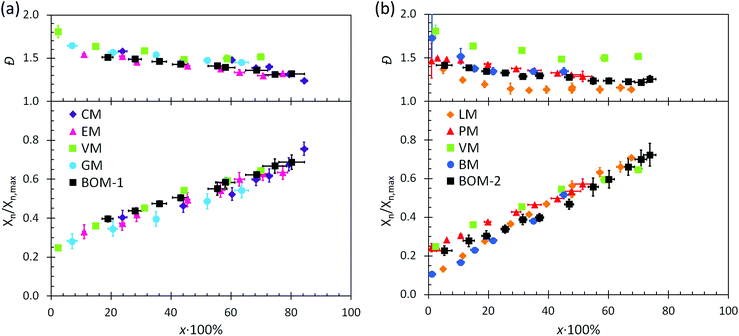
The utility of RAFT polymerization for each of the bio-oil constituents was established by investigating whether the reactions were controlled. The relevant data from reaction aliquots are presented in Fig. 1 for each homopolymerization and heteropolymerization, and additional information (SEC traces) from the syntheses of PBOM-1 and PBOM-2 are located in the ESI.† In all cases, Đ decreased with increasing conversion and was between 1.0 and 1.5 in the final product. Additionally, Xn increased linearly with conversion. These trends suggested that all polymerizations proceeded in a controlled manner. Furthermore, we previously reported the RAFT polymerization of VM and proposed that the same polymerization scheme could be extended to other lignin-based methacrylates (e.g., GM, EM, and CM) with similar levels of control.44 Data in Fig. 1a support this hypothesis as the data are consistent in the approximate slopes and y-intercepts.In this work, we determined that eqn (6) could be applied accurately to estimate ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) apptr from each heteropolymerization, thus providing information about the expected Đ of a heteropolymer prior to synthesis. Using eqn (6) with j = 4 and the other relevant parameters (the reactivity ratios and monomer feed compositions are in the following sections), the expected
apptr from each heteropolymerization, thus providing information about the expected Đ of a heteropolymer prior to synthesis. Using eqn (6) with j = 4 and the other relevant parameters (the reactivity ratios and monomer feed compositions are in the following sections), the expected ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) apptr for BOM-1 and BOM-2 was 2.4 ± 0.4 and 7.0 ± 0.6, respectively. These estimates are statistically indistinguishable from the measured values of 2.1 ± 0.3 and 7.4 ± 0.5 reported in Table 1, indicating that eqn (6) is appropriate for estimating
apptr for BOM-1 and BOM-2 was 2.4 ± 0.4 and 7.0 ± 0.6, respectively. These estimates are statistically indistinguishable from the measured values of 2.1 ± 0.3 and 7.4 ± 0.5 reported in Table 1, indicating that eqn (6) is appropriate for estimating ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) apptr in multicomponent RAFT polymerizations. Note that one variation of the two-component equation weights each fj in the denominator of eqn (6) by the product of ri,j instead of the quotient;52 however, that weighting does not accurately capture
apptr in multicomponent RAFT polymerizations. Note that one variation of the two-component equation weights each fj in the denominator of eqn (6) by the product of ri,j instead of the quotient;52 however, that weighting does not accurately capture ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) apptr in BOM-2, significantly overestimating the value as 11.9 ± 1.3. A simple mole-weighted average also overestimates
apptr in BOM-2, significantly overestimating the value as 11.9 ± 1.3. A simple mole-weighted average also overestimates ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) apptr for BOM-2 as 9.5 ± 0.2. More complicated models might improve the accuracy of the estimate for
apptr for BOM-2 as 9.5 ± 0.2. More complicated models might improve the accuracy of the estimate for ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) apptr if extended beyond the binary case, but they require additional parameters and measurements.51 Thus, eqn (6) provides a good estimate for
apptr if extended beyond the binary case, but they require additional parameters and measurements.51 Thus, eqn (6) provides a good estimate for ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) apptr without requiring excessive experimentation.
apptr without requiring excessive experimentation.
| M | [M]/[T]b | [I]/[T]c | t init (h) |
k
appp![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) d (h−1) d (h−1) |
C apptr |
|---|---|---|---|---|---|
a Reactions were performed at 72 °C in anisole (4.9 wt% DMF) with a monomer (M)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) solvent mass ratio of 0.94 solvent mass ratio of 0.94![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, AIBN as the initiator (I), and CPB as the chain-transfer agent (T). Error throughout the table is reported with 95% confidence.
b Equivalent to Xn,max with error of 0.3 unless specified.
c Error is 0.001 unless specified.
d Error is 0.01 unless specified.
e Values normalized to [I]/[T] = 0.10 using the proportionality of kappp or inverse proportionality of Capptr to the square root of the initiator concentration.56,57
f Refer to Table 4 for monomer compositions. 1, AIBN as the initiator (I), and CPB as the chain-transfer agent (T). Error throughout the table is reported with 95% confidence.
b Equivalent to Xn,max with error of 0.3 unless specified.
c Error is 0.001 unless specified.
d Error is 0.01 unless specified.
e Values normalized to [I]/[T] = 0.10 using the proportionality of kappp or inverse proportionality of Capptr to the square root of the initiator concentration.56,57
f Refer to Table 4 for monomer compositions.
|
|||||
| GM | 134 ± 16 | 0.12 ± 0.04 | 0.2 | 0.29 ± 0.07e | 1.4 ± 0.5e |
| CM | 144 ± 9 | 0.13 ± 0.02 | 0 | 0.22 ± 0.03e | 2.7 ± 1.1e |
| EM | 129 ± 16 | 0.09 ± 0.02 | 0 | 0.23 ± 0.04e | 2.5 ± 0.6e |
| VM | 230.3 | 0.100 | 2.1 | 0.21 | 2.8 ± 0.1 |
| PM | 229.9 | 0.100 | 1.0 | 0.11 | 4.6 ± 0.3 |
| BM | 229.7 | 0.100 | 0.4 | 0.17 | 14 ± 2 |
| LM | 224.4 | 0.100 | 2.6 | 0.09 | 19 ± 3 |
| BOM-1f | 232.9 | 0.100 | 0.4 | 0.24 | 2.1 ± 0.3 |
| BOM-2f | 230.0 | 0.100 | 0.1 | 0.16 | 7.4 ± 0.5 |
As indicated by eqn (6), an interesting implication of polymerizing mixtures is that ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) apptr can be lower for a heteropolymerization than any of the corresponding homopolymerizations (as demonstrated previously for binary cases51). Such low
apptr can be lower for a heteropolymerization than any of the corresponding homopolymerizations (as demonstrated previously for binary cases51). Such low ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) apptr's can result in materials that have broad Đ's (e.g., Xw/Xn from eqn (5)) and therefore ‘poor gradient quality’.58 Unfavorable
apptr's can result in materials that have broad Đ's (e.g., Xw/Xn from eqn (5)) and therefore ‘poor gradient quality’.58 Unfavorable ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) apptr's are most likely in systems that favor alternating monomer distributions (i.e., as any product of ri,j and rj,i approaches zero), which is not the case in the sets of monomers herein. An increase in
apptr's are most likely in systems that favor alternating monomer distributions (i.e., as any product of ri,j and rj,i approaches zero), which is not the case in the sets of monomers herein. An increase in ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) apptr and decrease in Đ relative to corresponding homopolymerizations and homopolymers would arise only if a significantly blocky monomer distribution is expected (i.e., if at least one product of ri,j and rj,i greatly exceeds unity and the rest approach unity), which is uncommon.59
apptr and decrease in Đ relative to corresponding homopolymerizations and homopolymers would arise only if a significantly blocky monomer distribution is expected (i.e., if at least one product of ri,j and rj,i greatly exceeds unity and the rest approach unity), which is uncommon.59
Additional kinetic parameters from the homopolymerizations and heteropolymerizations of interest to this work are tinit and kappp. Together, these parameters describe the time over which a reaction should proceed to reach a desired monomer conversion with an appropriate fraction of ‘living’ chains (L). Estimates for tinit and kappp were extracted from data in Fig. 2 and are reported in Table 1.
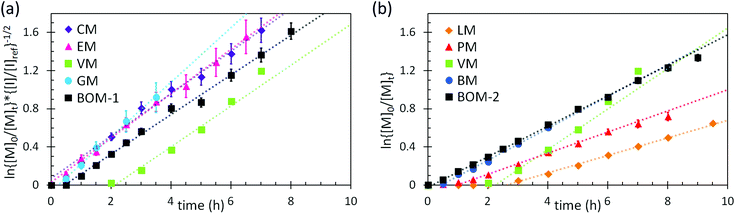 | ||
| Fig. 2 Kinetic data with pseudo-first-order linear fits (dashed lines) from the polymerizations of (a) the color-coded lignin-based monomers and bio-oil and (b) the remaining color-coded monomers and bio-oil. The data in (a) were normalized to an initiator/chain-transfer agent ([I]ref/[T]) ratio of 0.10, noting the proportionality of kappp (the slope) to the square-root of the initiator concentration.56 The data in (b) were all collected at [I]/[T] = 0.10, so normalization was unnecessary. Error bars represent 95% confidence limits on the basis of interpretation of the NMR data and the accuracy of the [I]/[T] ratio. | ||
No universal relationship can be gleaned from the tinit data, which is not unusual as this parameter is strongly affected by impurities in the reaction mixture, such as air or water, especially when benzodithioates are selected as the chain-transfer agents.12 The challenge of an unpredictable tinit is that the necessary reaction time for a polymerization to reach a desired conversion, and thus L (a function of reaction time), also is unpredictable. This problem can be mitigated by seeding the polymerizations with macromolecular or oligomeric chain-transfer agents, which typically have negligible pre-equilibrium times.12
The expected relationship between kappp in the polymerizations of the individual monomers and the BOM mixtures is complicated, possibly dependent on conversion and penultimate reactive chain ends, and unreported for systems with four or more chemically distinct monomers.60–62 Thus, we employ the simplest assumption, taking kappp as a molar composition-weighted average of the normalized kappp's from the homopolymerizations of each constituent (Table 1). This average allows one to estimate kappp's for BOM-1 (0.24 ± 0.02 h−1) and BOM-2 (0.15 ± 0.01 h−1), which agree closely with the measured values of 0.24 ± 0.01 h−1 and 0.16 ± 0.01 h−1, respectively, from Table 1. More experiments would be necessary to confirm whether this simplification of the kinetic behavior in heteropolymerizations is widely applicable, but these experiments suggest that an average gives an appropriate first-approximation for kappp in homogeneous mixtures of similarly structured monomers (e.g., miscible methacrylates).
In comparing each kappp from the individual homopolymerizations, polymerization behavior generally can be explained by steric effects. The constituents of the homogeneous bio-oil, BOM-1, polymerize at similar rates, whereas the short-chained and long-chained n-alkyl methacrylates, BM and LM, polymerize at different rates. However, one key exception is PM, which propagates more slowly than the guaiacol methacrylate derivatives (VM, GM, CM, and EM) despite the fact that PM is not hindered by an o-methoxy group. This reduced propagation rate may be explained by the electron-donating potential of methoxy moieties63 that promotes reactivity in substituted aromatic monomers relative to unsubstituted aromatic monomers.64 Overall, this comparison between PM and the components of BOM-1 may make lignin-based bio-oils with higher methoxy contents more favorable for polymerization than those that have been substantially deoxygenated.
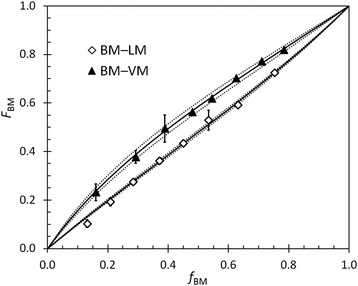
Reactivity ratios of monomers
Reactivity ratios for pairs of monomers in BOM-1 and BOM-2 were measured with generally high precision under reaction conditions similar to those used in the homopolymerizations and heteropolymerizations. Two example datasets overlaid by the Mayo–Lewis fits to the data are shown in Fig. 3. The remaining data sets are in the ESI.† The measured reactivity ratios for BOM-1 were near unity (rVM,EM = 0.97 ± 0.02, rEM,VM = 0.87 ± 0.02, rVM,CM = 0.95 ± 0.03, and rCM,VM = 0.92 ± 0.03), and the reactivity ratios for BOM-2 (BM–VM, BM–PM, BM–LM, VM–PM, VM–LM, and LM–PM) are compiled in Table 2.| i ↓ j→ | VM | PM | BM | LM |
|---|---|---|---|---|
| VM | — | 1.18 ± 0.08 | 1.21 ± 0.10 | 1.88 ± 0.10 |
| PM | 0.58 ± 0.04 | — | 1.10 ± 0.09 | 1.00 ± 0.11 |
| BM | 0.57 ± 0.05 | 0.45 ± 0.04 | — | 0.97 ± 0.04 |
| LM | 1.06 ± 0.05 | 0.44 ± 0.05 | 0.81 ± 0.03 | — |
One feature about the reactivity ratios is the similarity in values between monomers that have homologous structures (i.e., VM–EM, VM–CM, and BM–LM). VM, EM, and CM only differ structurally by the p-position formyl, ethyl, and methyl moiety, so their reactivity ratios are expected to be close to unity, which is indeed the case. Deviations from unity are either due to slight reactivity and steric differences between the monomers or minor systematic errors that arise from interpreting overlapping peaks in the NMR spectra. When the VM–EM and VM–CM data are fit assuming ri,j = rj,i = 1, the standard mean error estimates in ri,j only change from 0.02–0.03 to 0.03–0.04, and the coefficients of determination that describe the quality of the fit (r2) only decrease from 0.98 and 0.96 to 0.94 and 0.95 for VM–EM and VM–CM, respectively. These changes are trivial, indicating that a fair assumption for structurally homogeneous bio-oils is that all of the reactivity ratios are unity; hence, we assume that all ri,j in BOM-1 equal one throughout this work. This assumption was checked by select data in two other instances (EM–CM and GM–EM for the case in which fEM ≈ FEM ≈ 0.5 mole-fraction for both samples), further supporting its validity.
Similar assumptions did not apply to the components in BOM-2 as the structural, polarity, and reactivity differences between the monomers are significant. The Q–e model proposed by Alfrey and Price helps to explain the relative values for ri,j in Table 2,64,65 but the necessary information (i.e., the reactivity ratios between each monomer and a standard such as styrene or methyl methacrylate) for such a comparison currently is unavailable for this set of monomers under the employed RAFT polymerization conditions.
The uniquely rigorous, albeit simple, fitting and error analysis methods presented in this work permit calculation of the possible errors resulting from the systematic reduction in resolution (i.e., measurement accuracy) with respect to changes in composition. The development of this model was inspired by the BM–VM data in Fig. 3, in which the 95% confidence intervals from the 1H NMR data were broad at high VM content yet narrow at low VM content. We wanted to measure accurate ri,j while capturing the varying level of confidence in the reported error, which is oversimplified by most least squares fitting procedures.
An example set of ri,j data determined via multiple methods is reported in Table 3 and illustrates the significance of the newly reported analysis procedure (eqn (2)–(4)). As shown, wide-ranging values with non-overlapping confidence intervals were measured for the LM–VM data by traditional least squares fitting approaches. The discrepancies in the data are likely byproducts of the relative magnitudes of ri,j and rj,i, the range of compositions over which the reactivity data were measured, and the level of scatter in the data. In general, averages of the Fineman–Ross66 and Kelen–Tüdös67,68 data were accurate but imprecise, and the unaveraged data were unfavorable in both accuracy and precision. The conventional nonlinear fitting method, which follows eqn (2) but with σn2 = 1 and both Fj terms = 0, gave reasonable and precise values for ri,j, but the precision led to exaggerated error estimates (i.e., misleadingly narrow confidence intervals). Jaacks’ method,69 a linearization approach that can be attractive for its simplicity, was not tested in this work due to the model's dependence on samples of considerable compositional asymmetry (i.e., samples that are ∼95% one monomer),2 which was not representative of the systems studied herein. Eqn (2) provides an elegant and simple solution to these issues, yielding accurate and precise results with aptly represented and low error (eqn (4)). Accordingly, the reported method and equations improve the integrity of the resulting reactivity ratio measurements with minimal added effort.
| Method | r VM,LM | r LM,VM |
|---|---|---|
| a Conventional nonlinear and linear fitting methods disregard error in the individual data points and in this example are measured only for monomer 1 = VM; different values can be generated when monomer 2 = VM but are excluded for brevity. b Fineman and Ross report two linearized forms of the Mayo–Lewis equation that correspond to eqn (3) and (4) in ref. 66. c The confidence intervals from this method are misleadingly narrow. d Mean standard errors from Table 2 (eqn (4)) were converted to 95% confidence intervals using Student's t-distribution. | ||
| Fineman–Ross (3)b | 1.59 ± 0.07 | 0.90 ± 0.12 |
| Fineman–Ross (4)b | 1.95 ± 0.24 | 1.21 ± 0.12 |
| Fineman–Ross (average) | 1.77 ± 0.18 | 1.05 ± 0.12 |
| Kelen–Tüdös | 1.72 ± 0.24 | 1.03 ± 0.12 |
| Conventional nonlinear fitc | 2.12 ± 0.10 | 1.21 ± 0.05 |
| This work (error-weighted fit)d | 1.88 ± 0.06 | 1.06 ± 0.04 |
Compositional profiles of heteropolymers
In combination with the composition of the monomer feed (Table 4), the reactivity ratios from the previous section enabled predictions of the positional and cumulative compositions of monomers distributed along the heteropolymer chains. In BOM-1, all reactivity ratios were assumed to be unity, and the polymerization of this bio-oil thus was assumed to yield a fully random heteropolymer with unchanging positional and cumulative compositions as a function of conversion. The data in Fig. 4 support this hypothesis as the lines and data points overlay within error. Note that the larger error indicated for the EM and CM data relative to the VM and GM data are due to only a single distinct peak in the dried NMR spectra that was available to distinguish between the monomers.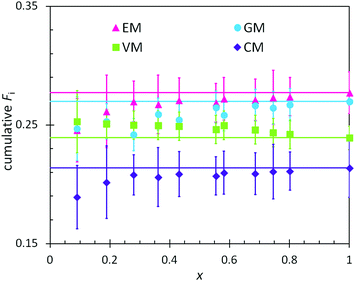 | ||
| Fig. 4 Measured (points) and predicted (lines) cumulative polymer compositions as a function of conversion (x) in the polymerization of BOM-1. The prediction assumes ri,j = 1 for every monomer pair. | ||
| Sample | i | f i,0 | F i,0 |
|---|---|---|---|
| a Monomer (fi) and polymer (Fi) compositions are mole-fractions. | |||
| BOM-1 | GM | 0.27 | 0.27 |
| CM | 0.21 | 0.21 | |
| EM | 0.28 | 0.28 | |
| VM | 0.24 | 0.24 | |
| BOM-2 | VM | 0.23 | 0.28 |
| PM | 0.29 | 0.34 | |
| BM | 0.30 | 0.25 | |
| LM | 0.18 | 0.13 | |
There are at least two features of note in the data from Fig. 4. First, the VM and GM compositions change slightly with conversion, with slopes of −0.01 and 0.03, respectively. This trend may result from the different electron densities in the p-position moieties for VM (formyl group) and GM (hydrogen) relative to CM and EM (alkyl groups); however, these changes with conversion are within experimental error and may be artificial. If real, the trend is captured by reactivity ratios spanning the measured values of 0.87–0.97 (see ESI†), yet trivial in comparison to the reactivity ratios from BOM-2 that span 0.4 to 1.9. Second, the data in Fig. 4 deviate from the expected trend at low molar conversions (x < 0.2). This deviation may be the result of initiator effects, in which one monomer is initiating and starting to propagate before the others, or concentration effects, in which the interpretation of the NMR spectra is least accurate at low conversions (i.e., when larger monomer peaks obscure smaller polymer peaks).
The positional and cumulative compositions of monomer units distributed along the polymer chain (i.e., monomer distribution profiles) predicted and measured for BOM-2 as a function of conversion are shown in Fig. 5. In this example, the reactivity ratios are not unity (Table 2), and the products of reactivity ratios are predominantly less than one, so a gradient polymer is expected. The profiles in Fig. 5a illustrate how the monomer units are distributed along the polymer chain, and the data in Fig. 5b support that a gradient heteropolymer was synthesized. The amounts of BM and LM could not be quantified individually as their characteristic NMR peaks were indistinguishable in the presence of VM and PM units. Nevertheless, the predicted positional compositions in Fig. 5a indicate that LM is consumed more slowly than BM, and both monomers are consumed more slowly than PM and VM. At full conversion, the heteropolymers would be terminated predominantly by LM units. These results are consistent with the reactivity and steric arguments presented in previous sections and validate the unique methods applied in this manuscript for determining ri,j.
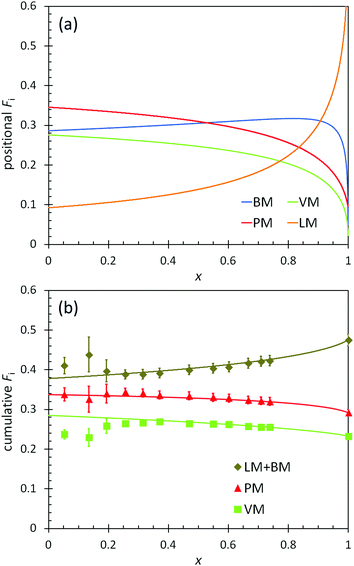 | ||
| Fig. 5 (a) Predicted positional polymer composition and (b) measured (points) and predicted (lines) cumulative polymer composition as a function of conversion (x) in the polymerization of BOM-2. The predictions utilize the reactivity ratios from Table 2. LM and BM data are combined in (b) as the individual compositions are indistinguishable by 1H NMR. | ||
Additional features apparent in Fig. 5b are the accuracy with which the predicted data overlap the measured data in the cumulative composition profiles at high molar conversions (x > 0.2), yet the distinct deviation in the data at low molar conversions (x ≤ 0.2). As with BOM-1, it is unclear whether the mismatch at low conversions was a byproduct of sample concentration (NMR resolution) or initiator effects. However, a reasonable assumption is that initiator effects are not significant, as was the case in Ting et al.'s four-component acrylate system.17 If initiator effects were substantial, the reactivity ratios that were all determined at low conversions (i.e., x = 0.06–0.20 mole-fraction, the compositions at which the data mismatch occurs in Fig. 4 and 5b) would not have depicted accurately either the monomer distribution profiles or the previously discussed ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) apptr data.
apptr data.
Altogether, these compositional profiles suggest that upon polymerization, bio-oils containing similarly structured chemicals will yield random heteropolymers, whereas bio-oils containing structurally diverse monomers will yield gradient, statistical, or blocky heteropolymers. The tendency for non-random monomer distributions can be avoided by applying a priori knowledge about the bio-oil's composition and the constituents’ polymerization behavior. One approach is to mix bio-oils of different compositions in a reactor via controlled feed rates. This tactic (albeit with single-component monomer streams) is employed regularly for synthesizing polymers with predetermined compositional profiles in tapered block copolymers and gradient copolymers.22–24,70–74 Extension of these methods to multicomponent bio-oils would allow for the synthesis of renewable heteropolymers with precise compositions and properties, greatly enhancing the feasibility of numerous bio-oil-based plastics for commercialization.
Conclusions and outlook
As demonstrated throughout this work, the ease of predicting the polymerization behavior of multicomponent mixtures and the resulting monomer distribution profiles depends on the structural diversity of the chemical inputs. For example, removing a methoxy group from a phenolic ring or exchanging the phenolic ring for an n-alkyl group was shown to affect monomer reactivity significantly. Hence, extensive kinetic studies potentially are necessary for preparing polymers with reproducible properties from structurally heterogeneous mixtures, such as unfractionated bio-oils prepared from lignocellulosic biomass instead of just the lignin component.Conversely, potentially biobased guaiacol methacrylate derivatives that vary only in the p-position substituent all exhibited similar polymerization behavior, with nearly identical kappp's and reactivity ratios near unity. Such structurally homogeneous bio-oils are ideal for the next chapter of cost-effective sustainable materials, as minimal data are necessary for controlling polymerization behavior and estimating resulting material characteristics prior to synthesis.
These examples together illustrated that seemingly subtle variations in potentially biobased monomer structure can have a significant impact on the polymerization behavior and the resulting polymer sequence distribution. Therefore, understanding structure–reactivity relationships between monomers is imperative for avoiding the oversimplification of kinetic models to the point of inaccuracy.
Finally, although the homogenous bio-oils have characteristics that are easier to predict, the heterogeneous bio-oils and mixtures can provide more exciting pathways to designer polymers once the necessary kinetic parameters have been evaluated. In this work, the necessary kinetic data were obtained for a set of potentially biobased monomers by determining kappp and ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) apptr, as well as using an improved method for determining ri,j. The reported equation for
apptr, as well as using an improved method for determining ri,j. The reported equation for ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) apptr also indicated that unfavorable mixture compositions may exist, in which multicomponent polymers could have larger Đ's than any corresponding homopolymer (a relevant problem for sets of monomers with especially low ri,j). Overall, these mixtures and newly reported correlations will assist future designs of versatile multicomponent polymers with on-demand properties, such as strength, processability, and possibly stimuli-responsiveness or self-healing behavior.
apptr also indicated that unfavorable mixture compositions may exist, in which multicomponent polymers could have larger Đ's than any corresponding homopolymer (a relevant problem for sets of monomers with especially low ri,j). Overall, these mixtures and newly reported correlations will assist future designs of versatile multicomponent polymers with on-demand properties, such as strength, processability, and possibly stimuli-responsiveness or self-healing behavior.
Acknowledgements
The authors acknowledge partial support from a DuPont Young Investigator Award to T.H.E., an AFOSR-PECASE grant (FA9550-09-1-0706), and the UD Office of Undergraduate Research and Experiential Learning's 2014 Summer Scholars Program (M.G.K). The NMR facility used for this project was supported by the Delaware COBRE program, with a grant from the National Institute of General Medical Sciences – NIGMS (1 P30 GM110758-01) from the National Institutes of Health. The authors thank Prof. Richard P. Wool, Kaleigh H. Reno, and Prof. Joseph P. Stanzione III for generously providing vanillin, ∼95% pure monomers (GM, CM, EM, and PM), and isopropyl acetate.References
- E. Saldívar-Guerra and I. Zapata-González, Macromol. Theory Simul., 2012, 21, 24–35 CrossRef PubMed
.
- S. Cousinet, A. Ghadban, I. Allaoua, F. Lortie, D. Portinha, E. Drockenmuller and J.-P. Pascault, J. Polym. Sci., Part A: Polym. Chem., 2014, 52, 3356–3364 CrossRef CAS PubMed
.
- J. M. Ting, T. S. Navale, F. S. Bates and T. M. Reineke, Macromolecules, 2014, 47, 6554–6565 CrossRef CAS
.
- Z. Zhao, H. Xie, S. An and Y. Jiang, J. Phys. Chem. B, 2014, 118, 14640–14647 CrossRef CAS PubMed
.
- E. G. Kelley, J. N. L. Albert, M. O. Sullivan and T. H. Epps, III, Chem. Soc. Rev., 2013, 42, 7057–7071 RSC
.
- J.-F. Lutz, M. Ouchi, D. R. Liu and M. Sawamoto, Science, 2013, 341, 1238149 CrossRef PubMed
.
- K. Matyjaszewski, Science, 2011, 333, 1104–1105 CrossRef CAS PubMed
.
- C. Romain and C. K. Williams, Angew. Chem., Int. Ed., 2014, 53, 1607–1610 CrossRef CAS PubMed
.
- J. A. Wilson, S. A. Hopkins, P. M. Wright and A. P. Dove, Macromolecules, 2015, 48, 950–958 CrossRef CAS
.
- A. L. Holmberg, K. H. Reno, R. P. Wool and T. H. Epps, III, Soft Matter, 2014, 10, 7405–7424 RSC
.
- R. Mülhaupt, Macromol. Chem. Phys., 2013, 214, 159–174 CrossRef PubMed
.
-
C. Barner-Kowollik, Handbook of RAFT Polymerization, Wiley-VCH, Weinheim, Germany, 2008 Search PubMed
.
- F. S. Bates and G. H. Fredrickson, Phys. Today, 1999, 52, 32–38 CrossRef CAS PubMed
.
- C. Park, J. Yoon and E. L. Thomas, Polymer, 2003, 44, 6725–6760 CrossRef CAS PubMed
.
- K. J. Yao and C. B. Tang, Macromolecules, 2013, 46, 1689–1712 CrossRef CAS
.
- M. Semsarilar and S. Perrier, Nat. Chem., 2010, 2, 811–820 CrossRef CAS PubMed
.
- J. M. Ting, T. S. Navale, F. S. Bates and T. M. Reineke, ACS Macro Lett., 2013, 2, 770–774 CrossRef CAS
.
- M. Asmadi, H. Kawamoto and S. Saka, J. Anal. Appl. Pyrolysis, 2011, 92, 417–425 CrossRef CAS PubMed
.
- A. J. Ragauskas, G. T. Beckham, M. J. Biddy, R. Chandra, F. Chen, M. F. Davis, B. H. Davison, R. A. Dixon, P. Gilna, M. Keller, P. Langan, A. K. Naskar, J. N. Saddler, T. J. Tschaplinski, G. A. Tuskan and C. E. Wyman, Science, 2014, 344, 1246843 CrossRef PubMed
.
- D. Mohan, C. U. Pittman and P. H. Steele, Energy Fuels, 2006, 20, 848–889 CrossRef CAS
.
- R. T. Mathers, J. Polym. Sci., Part A: Polym. Chem., 2012, 50, 1–15 CrossRef CAS PubMed
.
- M. Y. Zaremski, D. I. Kalugin and V. B. Golubev, Polym. Sci., Ser. A, 2009, 51, 103–122 CrossRef
.
- J. Kim, M. M. Mok, R. W. Sandoval, D. J. Woo and J. M. Torkelson, Macromolecules, 2006, 39, 6152–6160 CrossRef CAS
.
- R. Roy, J. K. Park, W.-S. Young, S. E. Mastroianni, M. S. Tureau and T. H. Epps, III, Macromolecules, 2011, 44, 3910–3915 CrossRef CAS PubMed
.
- J. Li, R. M. Stayshich and T. Y. Meyer, J. Am. Chem. Soc., 2011, 133, 6910–6913 CrossRef CAS PubMed
.
- B. N. Norris, S. Zhang, C. M. Campbell, J. T. Auletta, P. Calvo-Marzal, G. R. Hutchison and T. Y. Meyer, Macromolecules, 2013, 46, 1384–1392 CrossRef CAS
.
- P. Hodrokoukes, G. Floudas, S. Pispas and N. Hadjichristidis, Macromolecules, 2001, 34, 650–657 CrossRef CAS
.
- B. K. Denizli, J.-F. Lutz, L. Okrasa, T. Pakula, A. Guner and K. Matyjaszewski, J. Polym. Sci., Part A: Polym. Chem., 2005, 43, 3440–3446 CrossRef CAS PubMed
.
- W.-F. Kuan, R. Remy, M. E. Mackay and T. H. Epps, III, RSC Adv., 2015, 5, 12597–12604 RSC
.
- H. E. Jegers and M. T. Klein, Ind. Eng. Chem. Process Des. Dev., 1985, 24, 173–183 CAS
.
- M. M. Bomgardner, Chem. Eng. News, 2014, 92, 14 Search PubMed
.
-
P. R. Gruber, M. Kamm and B. Kamm, Biorefineries: Industrial Processes and Products: Status Quo and Future Directions, Wiley-VCH, Weinheim, Germany, 2006 Search PubMed
.
- F. M. Dayrit, J. Am. Oil Chem. Soc., 2015, 92, 1–15 CrossRef CAS
.
- J. F. Stanzione III, P. A. Giangiulio, J. M. Sadler, J. J. La Scala and R. P. Wool, ACS Sustainable Chem. Eng., 2013, 1, 419–426 CrossRef
.
- J. F. Stanzione III, J. M. Sadler, J. J. La Scala and R. P. Wool, ChemSusChem, 2012, 5, 1291–1297 CrossRef PubMed
.
- G. Çayli and M. A. R. Meier, Eur. J. Lipid Sci. Technol., 2008, 110, 853–859 CrossRef PubMed
.
- A. Oasmaa, E. Kuoppala and D. C. Elliott, Energy Fuels, 2012, 26, 2454–2460 CrossRef CAS
.
- N. S. Tessarolo, L. R. M. dos Santos, R. S. F. Silva and D. A. Azevedo, J. Chromatogr., A, 2013, 1279, 68–75 CrossRef CAS PubMed
.
- H. Ben and A. J. Ragauskas, Bioresour. Technol., 2013, 147, 577–584 CrossRef CAS PubMed
.
- D. Prat, J. Hayler and A. Wells, Green Chem., 2014, 16, 4546–4551 RSC
.
- G. Gody, T. Maschmeyer, P. B. Zetterlund and S. Perrier, Macromolecules, 2014, 47, 3451–3460 CrossRef CAS
.
- A. Goto and T. Fukuda, Prog. Polym. Sci., 2004, 29, 329–385 CrossRef CAS PubMed
.
- F. M. Chardon, N. Blaquiere, G. M. Castanedo and S. G. Koenig, Green Chem., 2014, 16, 4102–4105 RSC
.
- A. L. Holmberg, J. F. Stanzione III, R. P. Wool and T. H. Epps, III, ACS Sustainable Chem. Eng., 2014, 2, 569–573 CrossRef CAS
.
- F. R. Mayo and F. M. Lewis, J. Am. Chem. Soc., 1944, 66, 1594–1601 CrossRef CAS
.
- F. R. Mayo, J. Am. Chem. Soc., 1943, 65, 2324–2329 CrossRef CAS
.
- X. Han, J. Fan, J. He, J. Xu, D. Fan and Y. Yang, Macromolecules, 2007, 40, 5618–5624 CrossRef CAS
.
- T. Alfrey and V. Hardy, J. Polym. Sci., 1948, 3, 500–502 CrossRef CAS PubMed
.
- W. V. Smith, J. Am. Chem. Soc., 1946, 68, 2069–2071 CrossRef CAS
.
- J. Gao, Y. Luo, R. Wang, B. Li and S. Zhu, J. Polym. Sci., Part A: Polym. Chem., 2007, 45, 3098–3111 CrossRef CAS PubMed
.
- J. Gao, Y. Luo, R. Wang, X. Zhang, B.-G. Li and S. Zhu, Polymer, 2009, 50, 802–809 CrossRef CAS PubMed
.
- J. Chiefari, J. Jeffery, J. Krstina, C. L. Moad, G. Moad, A. Postma, E. Rizzardo and S. H. Thang, Macromolecules, 2005, 38, 9037–9054 CrossRef CAS
.
- C. Walling and E. R. Briggs, J. Am. Chem. Soc., 1945, 67, 1774–1778 CrossRef CAS
.
- I. Skeist, J. Am. Chem. Soc., 1946, 68, 1781–1784 CrossRef CAS
.
-
S. C. Chapra and R. P. Canale, in Numerical Methods for Engineers, McGraw-Hill, New York, 5th edn, 1985, ch. 25.3.3, pp. 707–708 Search PubMed
.
- W. A. Braunecker and K. Matyjaszewski, Prog. Polym. Sci., 2007, 32, 93–146 CrossRef CAS PubMed
.
- G. E. Roberts, J. P. A. Heuts and T. P. Davis, J. Polym. Sci., Part A: Polym. Chem., 2003, 41, 752–765 CrossRef CAS PubMed
.
- A. M. Elsen, Y. Li, Q. Li, S. S. Sheiko and K. Matyjaszewski, Macromol. Rapid Commun., 2014, 35, 133–140 CrossRef CAS PubMed
.
-
P. C. Hiemenz and T. P. Lodge, in Polymer Chemistry, Taylor & Francis, Boca Raton, Florida, 2nd edn, 2007, ch. 5.3.1, pp. 171–172 Search PubMed
.
- T. Fukuda, N. Ide and Y.-D. Ma, Macromol. Symp., 1996, 111, 305–315 CrossRef CAS PubMed
.
- Y.-D. Ma, K.-S. Sung, Y. Tsujii and T. Fukuda, Macromolecules, 2001, 34, 4749–4756 CrossRef CAS
.
- T. Fukuda, K. Kubo and Y.-D. Ma, Prog. Polym. Sci., 1992, 17, 875–916 CrossRef CAS
.
-
L. G. Wade, Organic Chemistry, Pearson Prentice Hall, Upper Saddle River, New Jersey, 6th edn, 2006 Search PubMed
.
- C. C. Price, J. Polym. Sci., 1948, 3, 772–775 CrossRef CAS PubMed
.
- T. Alfrey and C. C. Price, J. Polym. Sci., 1947, 2, 101–106 CrossRef CAS PubMed
.
- M. Fineman and S. D. Ross, J. Polym. Sci., 1950, 5, 259–262 CrossRef CAS PubMed
.
- T. Kelen and F. Tüdös, J. Macromol. Sci., Part A: Pure appl. Chem., 1975, 9, 1–27 CrossRef
.
- T. Kelen, F. Tüdös and B. Turcsányi, Polym. Bull., 1980, 2, 71–76 CrossRef CAS
.
- V. Jaacks, Makromol. Chem., 1972, 161, 161–172 CrossRef CAS PubMed
.
- X. Sun, Y. Luo, R. Wang, B.-G. Li and S. Zhu, AIChE J., 2008, 54, 1073–1087 CrossRef CAS PubMed
.
- N. Singh, M. S. Tureau and T. H. Epps, III, Soft Matter, 2009, 5, 4757–4762 RSC
.
- W.-F. Kuan, R. Roy, L. Rong, B. S. Hsiao and T. H. Epps, III, ACS Macro Lett., 2012, 1, 519–523 CrossRef CAS PubMed
.
- M. M. Mok, S. Pujari, W. R. Burghardt, C. M. Dettmer, S. T. Nguyen, C. J. Ellison and J. M. Torkelson, Macromolecules, 2008, 41, 5818–5829 CrossRef CAS
.
- M. M. Mok, J. Kim, C. L. H. Wong, S. R. Marrou, D. J. Woo, C. M. Dettmer, S. T. Nguyen, C. J. Ellison, K. R. Shull and J. M. Torkelson, Macromolecules, 2009, 42, 7863–7876 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5py00291e |
| This journal is © The Royal Society of Chemistry 2015 |