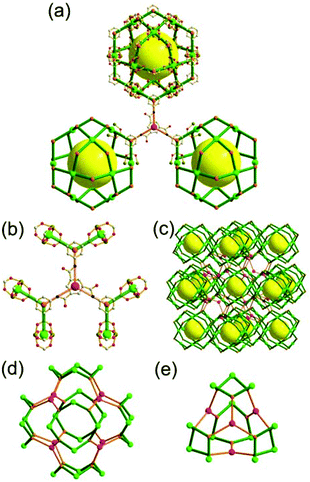
Topology analysis of metal–organic frameworks based on metal–organic polyhedra as secondary or tertiary building units

Abstract

The structural features of metal–organic frameworks (MOFs) can be analyzed based on the network structure (net) topology, composed of nodes and linkers. The connectivity and site symmetry of a node are probably the most important factors affecting the net topology of MOFs. Many MOFs with multiple nodes of different connectivity and site symmetry have complicated net topologies. However, the underlying net topology of some complicated MOFs could be analyzed using a hierarchical simplification approach. The underlying net topology of complicated MOFs with multi-connected nodes could be analyzed using a metal–organic polyhedron composed of multiple nodes as either a secondary building unit or a tertiary building unit. The simplified net topology provides better insight into the structural features of the complicated MOF structures and could be utilized in designing new MOF structures with known and/or unprecedented net topologies.

---

Dongwook Kim

Dongwook Kim was born in Korea in 1985. He received his bachelor's degree in chemistry from Hanyang University, Korea, in 2011. He is doing his PhD degree at Department of Chemistry, Ulsan National Institute of Science and Technology under the supervision of Prof. Myoung Soo Lah. He is currently working on the preparation of MOFs based on MOPs as supermolecular building blocks and studying their various properties including gas sorption behaviors.

Myoung Soo Lah

Myoung Soo Lah attended Seoul National University, Korea, for his BSc and MSc and earned his PhD in chemistry from the University of Michigan, Ann Arbor, in 1991. After his postdoctoral research in macromolecular crystallography from the same university, he became a faculty member of the Department of Chemistry, Hanyang University in 1992 and then moved to Ulsan National Institute of Science and Technology in 2010, where he is presently a professor of the Department of Chemistry. He is interested in the development of metal–organic systems such as MOPs and MOFs for applications in the areas of storage, capture/separation, and catalysis.

---

Introduction

Metal–organic frameworks (MOFs)¹ are an interesting class of materials because of inherent diversities in their structures and properties coming from the infinite number of combinations of organic and inorganic building blocks. The structural features of the MOFs can be analyzed based on the net topology composed of nodes (vertices) and linkers (edges), where metal ions (or metal clusters) and organic and inorganic ligands usually serve as secondary building units (SBUs).²

The prediction of the structure and net topology of an MOF from building components under given reaction conditions is not an easy task because of both the variability of metal coordination geometry and the diverse interconnectivities between the building components.³ Reactions of the same metal ions and organic ligands under slightly different reaction conditions often lead to MOFs of completely different structures and net topologies.⁴ When the building units have a strong tendency to form some specific metal centers such as the μ⁴-oxo tetranuclear Zn(II) cluster, [Zn₄O(COO)₆],⁵ as an octahedral 6-c SBU and a Cu(II) paddle-wheel cluster, [Cu₂(COO)₄],⁶ as a square planar 4-c SBU, reticular chemistry afforded a certain degree of success in predicting the final MOF.⁷

The structure of a network is affected by several factors such as building blocks, solvent, temperature, pH and so on and its topology is mainly dependent on the connectivity and the symmetry of the metal ions (or metal clusters) and organic nodes.⁸ Not only the number of possible network structures is infinite but even the number of possible net topologies is infinite because the number of topologically different vertices and the ways of linkage of the vertices are infinite. An enormous number of network structures with diverse and complicated net topologies have already been reported in the past two decades. The net topologies of many of those MOFs could be analyzed by the use of a hierarchical approach.⁹ The hierarchical simplification approach could help us to comprehend and to generalize the underlying net topology of complicated 3-D MOFs assembled from various building nodes.

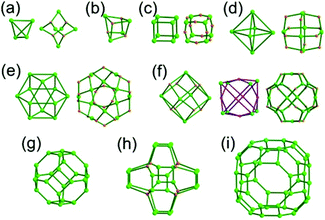
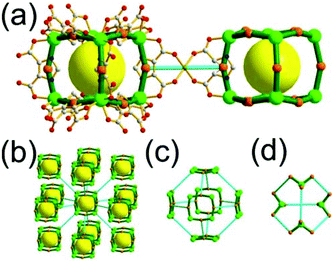
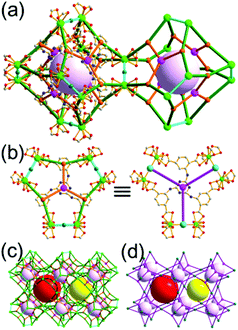
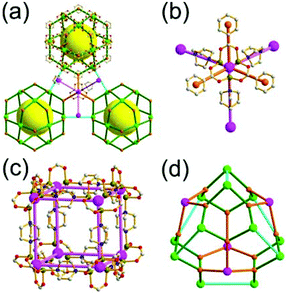
The focus of this review is on providing a better understanding of complicated MOFs based on metal–organic polyhedra (MOPs) as SBUs or TBUs comprising multiple organic and inorganic nodes (Fig. 1).¹⁰ Hierarchical analysis of the net topology of the MOFs could provide the topological characteristics of the networks and their underlying topologies, and the relationships between the net topologies. Besides the connectivity and symmetry properties of organic and inorganic building components, the connectivity and symmetry properties of the MOPs could also provide new insights into the factors playing important roles in the determination of the MOF structures, which could be utilized for the design of new MOFs based on various MOPs.

Fig. 1 Topologies of MOPs. (a) Tetrahedral MOPs of a 3⁴ face symbol and a 6⁴ face symbol. (b) A heterocubic MOP of a 4⁶ face symbol. (c) Cubic MOPs of a 4⁶ face symbol and an 8⁶ face symbol. (d) Octahedral MOPs of a 3⁸ face symbol and a 6⁸ face symbol. (e) Cuboctahedral MOPs of a 3⁸·4⁶ face symbol and a 6⁸·8⁶ face symbol. (f) Two rhombic dodecahedral MOPs of the same 4¹² face symbol and the other rhombic dodecahedral MOP of an 8¹² face symbol. (g) Truncated octahedral MOP (sod cage) of a 4⁶·6⁸ face symbol. (h) Partially truncated rhombic dodecahedral MOP of a 4⁶·6¹² face symbol. (i) Truncated cuboctahedral MOP (lta cage) of a 4¹²·6⁸·8⁶ face symbol.

It is well known that MOF-5^5a and its isoreticular structures^5b of pcu topology¹¹ † can be obtained by interconnecting the [Zn₄O(COO)₆] SBUs as a 6-c octahedral node using various rigid linear organic ligands as a 2-c linker. When planar 4-c [Cu₂(COO)₄] paddle-wheel SBUs are interconnected via various planar 3-c organic linkers, HKUST-1^6a and its isoreticular structures^6b,c can be obtained as a 3,4-c net of tbo topology. Although HKUST-1 of tbo topology is quite different from MOF-5 of pcu topology, HKUST-1 could be considered as a net of pcu underlying topology. In the network of HKUST-1, the topological tetrahedral metal–organic polyhedron (MOP) consisting of four trinodal organic nodes and six shared tetratopic nodes (4-c shared-edge-centers) as a supermolecular building block serves as a tertiary building unit (TBU) and the tetrahedral MOP shares its edge-centers with the six neighboring MOPs in a primitive cubic packing arrangement. The underlying topology of the network is pcu. On the other hand, the other 3,4-c network of bor topology, [Cu₃(TPT)₄](ClO₄)₃ (TPT = 2,4,6-tri(4-pyridyl)-1,3,5-triazine), can be obtained via the combination of the planar 3-c organic node, TPT, and the tetrahedral [Cu(I)(N_pyridyl)₄] 4-c inorganic node instead of the planar [Cu₂(COO)₄] 4-c node in the network structure of tbo topology.¹² The network structure of bor topology is also based on the tetrahedral MOP consisting of four trinodal organic nodes and six shared tetratopic nodes as a MOP, and the MOPs in a primitive cubic packing arrangement are interconnected via edge-center-sharing of the MOPs, and the underlying topology of the network is again pcu. The network structures of tbo and bor topologies are dictated by the symmetry properties of the 4-c nodes at the shared-edge-centers of the tetrahedral MOPs. When the shared-edge-center of the tetrahedral MOP is a planar 4-c node of D_2h (mmm) point symmetry, the net of tbo topology could be obtained. On the other hand, when the shared-edge-center of the tetrahedral MOP is a tetrahedral 4-c node of D_2d (−42m) point symmetry, the net of bor topology could be obtained. Table 1 lists all the MOFs covered in this review with their originally reported topologies and the underlying topologies analyzed using an MOP composed of multiple nodes as either an SBU or a TBU.

Table 1 MOFs with their reported topologies and the underlying topologies analyzed using an MOP as SBU or TBU

Network^a	Reported topology	Topology in this work	Underlying topology	Related sphere packing	Ref.
a ABDC = 5-amino-1,3-benzenedicarboxylate; abim = 5-azabenzimidazolate; ABTC = 3,3′,5,5′-azobenzenetetracarboxylate; Ac = acetate; amtz = 3-amino-5-mercapto-1,2,4-triazolate; atc = 3,5-dicarboxyl-(3′,5′-dicarboxylazophenyl)benzene; BBC = 4,4′,4′′-(benzene-1,3,5-triyl-tris(benzene-4,1-diyl))tribenzate; BC = benzoate; BDC = 1,4-benzene dicarboxylate; bipy = 4,4′-bipyridine; BPDC = 4,4′-biphenyldicarboxylate; BPE = cis-1,2-bis-4-pyridylethane; BTB = benzene-1,3,5-tribenzoate; BTC = 1,3,5-benzene tricarboxylate; btei = L^9 = 5,5′,5′′-benzene-1,3,5-triyltris(1-ethynyl-2-isophthalate); BTPCA = 1,1′,1′′-(benzene-1,3,5-triyl)tripiperidine-4-carboxylate; btt = benzene-1,3,5-tris(tetrazol-5-ylate); bttcd = 9,9′,9′′,9′′′-([1,1′-biphenyl]-3,3′,5,5′-tetrayl)tetrakis(9H-carbazole-3,6-dicarboxylate); BTTI = 5,5′,5′′-(4,4′,4′′-(benzene-1,3,5-triyl)tris(1H-1,2,3-triazole-4,1-diyl))triisophthalate; CDC = 9H-carbazole-3,6-dicarboxylate; dabco = 1,4-diazabicyclo-[2.2.2]octane; DTTDC = dithieno[3,2-b;2′,3′-d]thiophene-2,6-dicarboxylate; eim = 2-ethylimidazolate; G = guanidinium; hett = 5,5′,10,10′,15,15′-hexaethayltruxene-2,7,12-tricarboxylate; Him = imidazole; im = imidazolate; imdc = 4,5-imidazoledicarboxylate; MBDC = 5-methyl-1,3-benzenedicarboxylate; mbim = 5-methylbenzimidazole; mdip = 5,5′-methylene diisophthalate; Meim = 2-methylimidazolate; midc = 2-methyl-1H-imidazole-4,5-dicarboxylate; mim = 2-methylimidazolate; ntei = 5,5′,5′′-(4,4′,4′′-nitrilotris(benzene-4,1-diyl)tris(ethyne-2,1-diyl))triisophthalate; Phim = benzimidazolate; 3-ppp = 3-pyridylphosphonate; ptei = 5,5′-((5′-(4-((3,5-dicarboxyphenyl)ethynyl)phenyl)-[1,1′:3′,1′′-terphenyl]-4,4′-diyl)-bis(ethyne-2,1-diyl))diisophthalate; Pur = purinate; S = solvent; 5-SO3-BDC = 5-sulfonatoisophthalate; 5-SO3H-BDC = 5-sulfoisophthalate; SPh = benzenethiolate; SPhMe-3 = 3-methylbenzenethiol; TATAB = 4,4′,4′′-s-triazine-1,3,5-triyltri-p-aminobenzoate; TATB = 4,4′,4′′-s-triazine-2,4,6-triyltribenzoate; TBA = tetrabutylammonium; tdc = 2,5-thiophenedicarboxylate; TDPAT = 2,4,6-tris(3,5-dicarboxylphenylamino)-1,3,5-triazine; tib = 1,3,5-tris(1-imidazolyl) benzene; TMPyP = meso-tetra(N-methyl-4-pyridyl)porphine tetratosylate; TPBTM = L^8 = N,N′,N′′-tris(isophthalyl)-1,3,5-benzenetricarboxamide; TPT = 2,4,6-tri(4-pyridyl)-1,3,5-triazine; TTCA = triphenylene-2,6,10-tricarboxylate; ttei = 5,5′,5′′-(((benzene-1,3,5-triyltris(ethyne-2,1-diyl))tris(benzene-4,1-diyl))tris-(ethyne-2,1-diyl))triisophthalate; TZI = 5-tetrazolylisophthalate; L^1 = 5,5′,5′′,5′′′,-[1,2,4,5-benzenetetrayltetrakis(methyleneoxy)]tetra-1,3-benzenedicarboxylate; L^2 = 5,5′,5′′,5′′′-[1,2,4,5-benzenetetraylhexakis(methyleneoxy)]hexa-1,3-benzenedicarboxylate; L^3 = 5,5′,5′′,5′′′-[1,2,4,5-benzenetetrayltetrakis(4-methyleneoxyphenylazo)]tetra-1,3-benzenedicarboxylate; L^4 = 5-(2-carboxyvinyl)isophthalate; L^5 = 3,3′-(5-carboxy-1,3-phenylene)diacrylate; L^6 = 1,3-bis(5-methoxy-1,3-benzene dicarboxylic acid)benzene; L^7 = 1,3-bis(3,5-dicarboxylphenylethynyl)benzene; L^8 = 5,5′,5′′-[1,3,5-benzenetriyltris(carbonylimino)]tris-1,3-benzenedicarboxylic acid; L^9 = 1,3,5-tris(3,5-dicarboxylphenylethynyl)benzene; L^10 = 1,3,5-tris[(1,3-carboxylic acid-5-(4-(ethynyl)phenyl))ethynyl]-benzene; L^11 = 1,3,5-tris[(1,3-carboxylic acid-5-(4-(ethynyl)phenyl))butadiynyl]-benzene; L^12 = 1,3,5-tris[((1,3-carboxylic acid-5-(4-(ethynyl)phenyl))ethynyl)phenyl]-benzene; L^13 = 1,3,5-tris[(1,3-carboxylic acid-5-(4-(ethynyl)phenyl))butadiynyl]-benzene; L^14 = 1,3,5-tris(3′,5′-dicarboxy[1,1′-biphenyl]-4-yl)benzene; L^15 = 5-sulfoisophthalate; L^16 = 1, 3-bis (3,5-dicarboxylphenylethynyl) pyridine; L^17 = N,N′,N′′-tris(3-pyridinyl)-1,3,5-benzenetricarboxamide; L^18 = N,N′,N′′-tris(4-pyridinylmethyl)-1,3,5-benzenetricarboxamide; L^19 = N-phenyl-N′-phenyl bicyclo[2,2,2]oct-7-ene-2,3,5,6-tetracarboxdiimide tetracarboxylic acid; L^20 = 5,5′-(1,3-phenylenedi-2,1-ethynediyl)bis(1,3-benzenedicarboxylic acid); L^21 = 5,5′-[1,3-phenylenebis(carbonylimino)]bis(1,3-benzenedicarboxylic acid); L^22 = 5,5′,5′′-(2,4,6-trimethylbenzene-1,3,5-triyl) trismethylene-trisoxy-triisophthalic acid.
Tetrahedral MOP as SBU or TBU
[Cd4(SPh)6](SPh)2	—	4-c dia-a	4-c dia		13
[Pr(im)3(Him)]	—	6-c crs (dia-e)	4-c dia		14
Fe12O4(BPDC)6(SO4)12(BPE)6·[NH2(CH3)2]8 (MOF-500)	Related to β-cristobalite structure	6-c crs (dia-b-e)	4-c dia		15
[Cr3F(H2O)3O(BDC)3] (MIL-101)	MTN	6,6,6,6-c mtn-e	4,4,4-c mtn	Diamond-like packing	16
[Cu3(BTC)2(H2O)3] (HKUST-1)	—	3,4-c tbo	6-c pcu		6a
[Cu3(TATB)2(H2O)3] (PCN-6)	Interpenetrated 3,4-c net	3,4-c tbo-c	6-c pcu-c		6b
[Cu3(TATB)2(H2O)3] (PCN-6′)	Twisted boracite	3,4-c tbo	6-c pcu		6c
[(Co(SCN)2)3(TPT)4]	—	3,4-c tbo	6-c pcu		17a
					17b
[Cu4(L^1)(DMF)3(H2O)3S] (tbo-MOF-1)	tbo	3,4-c tbo	6-c pcu		17c
[Cu4(L^2)(DMF)3(H2O)3S] (tbo-MOF-2)
[Cu4(L^3)(DMF)3(H2O)3S] (tbo-MOF-3)
[Fe12(BTC)8S12]Cl6··x(FeTMPyPCl5) (porph@MOM-4)	tbo	3,4-c tbo	6-c pcu		17d
[Co12(BTC)8S12]·xCoTMPyPCl4 (porph@MOM-5)
[Mn12(BTC)8S12]·xMnTMPyPCl5 (porph@MOM-6)
[Ni10(BTC)8S24]·xNiTMPyP·(H3O)(4−4x) (porph@MOM-7)
[Mg10(BTC)8S24]·xMgTMPyP·(H3O)(4−4x) (porph@MOM-8)
[Zn18(OH)4(BTC)12S15]·xZnTMPyP·(H3O)(4−4x) (porph@MOM-9)
[Cu3(TATAB)2(H2O)3] (mesoMOF-1)	Twisted boracite	3,4-c tbo	6-c pcu		18a
[Cu3(TTCA)2(H2O)3] (PCN-20)	Twisted boracite	3,4-c tbo	6-c pcu		18b
[Cu3(BBC)2(H2O)3] (MOF-399)	tbo	3,4-c tbo	6-c pcu		19
[Cu3(L^4)2(H2O)3] (ZJU-35)	tbo	3,4-c tbo	6-c pcu		20
[Cu3(L^5)2(H2O)3] (ZJU-36)
[Cu3(TPT)4](CIO4)3	(6^3)4(6^28^4)3	3,4-c bor	6-c pcu		24a
[{(NH4)2[Cd17S4(SPhMe-3)24(SPhMe-3)4/2}]3	Boracite type	3,4-c bor	6-c pcu		24b
[{Cd17S4(SPhMe-3)24(SPhMe-3)3/2(SPhMe-3)]4}n]
[Zn3(BTPCA)2(H2O)3]	Primitive cubic network	3,4-c bor	6-c pcu		24c
[Zn3(tib)4](NO3)6	—	3,4-c bor	6-c pcu		25a
[Cu31Cl4(H1.55amtz)24](SO4)8	bor	3,4-c bor	6-c pcu		25b
[Cu31Br4(H1.55amtz)24](SO4)8
[Cu31I4(H1.55amtz)24](SO4)8
Na2Zn3(CO3)4·3H2O	Related to diamond type structure	3,4-c bor	6-c pcu		25c
[Cu2(bttcd)] (PCN-80)	3,3,4-c network (4,8-c scu)	3,3,4-c lwg	3,4-c tbo (6-c pcu)		26
Cubic/heterocubic MOP as SBU or TBU
[Cd(3-ppp)2]	—	3,6-c spn	4-c dia		27
[Cr3F(H2O)3O(BTC)2] (MIL-100)	MNT	3,3,3,3,3,3,6,6,6,6-c moo	4,4,4-c mtn	Diamond-like packing	28
[Zn(im)x(mbim)y], (x + y = 2) (TIF-3)	ACO	4-c pcb	8-c bcu		29
(G)8[Zn12(imdc)8(Himdc)4(DMF)8]·3H2O	AST-like	3,3-c xaa	12-c fcu		30
Li20(H2O)20[Ni8(imdc)12]	—	3,3,3-c rqz	6-c pcu		31
[Co(H2O)6]{Na6[Co8(Hmidc)12]}	—	3,3-c tfg/P	6-c pcu		32
Na20(H2O)28[Ni8(imdc)12]	—	—	8-c bcu		31
Octahedral MOP as SBU or TBU
[Cu2(CDC)2(bipy)(DMA)(EtOH)]6	pcu-a	5-c cab	6-c pcu		33
[Zr6O6(OH)2(DTTDC)4(BC)2(DMF)6] (DUT-51(Zr))	8-c reo	8-c reo (pcu-e)	6-c pcu		34a
[Hf6O6(OH)2(DTTDC)4(BC)2(DMF)6] (DUT-51(Hf))
[Zr6O6(OH)2(tdc)4(Ac)2] (DUT-67(Zr))	8-c reo	8-c reo (pcu-e)	6-c pcu		34b
[Hf6O6(OH)2(tdc)4(Ac)2] (DUT-67(Hf))
[Ni2(atc)(H2O)3]	Augmented fcu-like	3,4-c tfb	12-c fcu		35
Cuboctahedral MOP as SBU or TBU
[Zn4(MBDC)4(dabco)(OH2)2]	5-c net of the boron framework in UB12	5-c ubt	12-c fcu		37
[Cu24(ABDC)24(bipy)6(H2O)12]	fcu net	5-c ubt	12-c fcu		38
[(Cu2)12(5-SO3-BDC)16(5-SO3H-BDC)6 (4-methoxypyridine)6(MeOH)12x(H2O)18–12x]^24−	—	3,3,3,3,4,4,4,4-c gjm	8-c bcu		39
[Cu24(L^6)12(H2O)16(DMSO)8]	Primitive cubic network	3,3,4,4-c zmj	6-c pcu		40
[Cu24(L^7)12(DMF)8(H2O)16] (PMOF-3)	Simple cubic network	3,3,4,4,-c zmj	6-c pcu		41
[Cu6(mdip)3(H2O)6] (PCN-12)	—	3,3,3,3,4,4,4,4-c zhc	6-c pcu		42
[Zn24(L^8)8(H2O)24] (PMOF-1(Zn))	3,24-c network	3,3,4-c ntt	3,24-c rht	Cubic close packing	43
[Cu24(TPBTM)8(H2O)24]	3,24-c rht				44j
[Zn24(L^9)8(H2O)24] (PMOF-2(Zn))	3,24-c network	3,3,4-c ntt	3,24-c rht	Cubic close packing	44a
[Cu24(L^9)8(H2O)24] (PMOF-2(Cu))					44a
[Cu3(btei)(H2O)3] (PCN-61)					44b
[Cu3(ntei)(H2O)3] (PCN-66)	3,24-c network	3,3,4-c ntt	3,24-c rht	Cubic close packing	44b
[Cu3(ptei)(H2O)3] (PCN-68)	3,24-c network	3,3,4-c ntt	3,24-c rht	Cubic close packing	44c
[Cu3(ttei)(H2O)3] (PCN-610)
[Cu3(L^10)(H2O)3] (NU-100)	3,24-c network	3,3,4-c ntt	3,24-c rht	Cubic close packing	44d
[Cu3(L^11)(H2O)3] (NU-109)	3,24-c rht	3,3,4-c ntt	3,24-c rht	Cubic close packing	44e
[Cu3(L^12)(H2O)3] (NU-110)
[Cu3(L^13)(H2O)3] (NU-111)	3,24-c rht	3,3,4-c ntt	3,24-c rht	Cubic close packing	44f
[Cu3(L^14)(H2O)3)] (NOTT-112)	—	3,3,4-c ntt	3,24-c rht	Cubic close packing	44g
[Cu3(BTTI)(H2O)3] (NOTT-122)	3,24-c network (ubt type)	3,3,4-c ntt	3,24-c rht	Cubic close packing	44h
[Cu3(TDPAT)(H2O)3] (Cu-TDPAT)	3,24-c rht	3,3,4-c ntt	3,24-c rht	Cubic close packing	44i
[Cu6O(TZI)3(H2O)9(NO3)]	3,24-c rht	3,3,4-c ntt	3,24-c rht	Cubic close packing	45
Na12G4[Cu24(L^15)24G8(H2O)24]	3,24-c network	3,3,4-c ntt	3,24-c rht	Cubic close packing	46
Proposed network	3,4-c ucp	3,4-c ucp	6-c pcu		8b
[Cu24(L^16)12(H2O)12]	3,36-c network	3,3,5-c pzh	3,36-c txt	Primitive cubic packing	47
[Cu24(CN)4(BTC)12(dabco)9(H2O)6](NO3)8	3,5,6-c net	3,5,6-c ott		Cubic close packing	49
[(CH3)2NH2]15[(Cd2Cl)3(TATPT)4]	3,4-c tbo	3,3,5-c nut		Cubic close packing	48
mcp-d MOP as SBU or TBU
[(CH3)2NH2]15[(Cd2Cl)3(TATPT)4]	3,4-c tbo	3,3,5-c nut	3,4-c tbo (6-c pcu)		48
Rhombic dodecahedral MOP as SBU or TBU
[Cu6(L^17)8](NO3)12	Twofold interpenetrated simple cubic net	3,5-c jjp	6-c pcu		50
[Cu6(L^18)8](NO3)12
H2[Co4O(TATB)8/3] (PCN-9)	Twofold interpenetrated 3,8-c net	3,8-c the	6-c pcu		51
H[Cu(DMF)6][(Cu4Cl)3(btt)8(H2O)12]	3,8-c network	3,8-c the	6-c pcu		52a
Cd1.5(H3O)3[(Cd4O)3(hett)8]	3,8-c network	3,8-c the	6-c pcu		52b
Fe4(μ3-O)2(BTB)8/3(DMF)2(H2O)2·(DMF)10(H2O)2	3,8-c the	3,8-c the	6-c pcu		52c
(Mg12(H2O)12(μ2-(H2O)6)(BTB)8(dioxane)6) (MIL-123)	Twofold interpenetrated ReO3 net	3,8-c the	6-c pcu		52d
[In3O(ABTC)1.5(H2O)3](NO3)	4,6-c soc	3,6-c edq	4,6-c soc (8-c bcu)		53
[Zn7(L^19)3(H2O)7][Zn5(L^19)3(H2O)5]	pcu-like net	3,3,4-c zjz	6-c pcu		54
[Zn28(L^20)12(H2O)28](NO3)8 (PMOF-4)	3,3,4-c zjz	3,3,4-c zjz	6-c pcu		55
[Zn28(L^21)12(H2O)28](NO3)8 (PMOF-5)
[Zn2(BTC)1.333S2]12	—	3,3,4-c tfe	6-c pcu or 3,24-c rht	Primitive cubic packing or cubic close packing	4d
[Zn7(L^22)2(OH)2(H2O)9]	6,6,12,12-c net or 3,4,6-c net	3,3,4-c tfe	6-c pcu or 3,24-c rht	Primitive cubic packing or cubic close packing	57
[Zn(CN)(NO3)(TPT)2/3]	Cubic arrangement of eight partially augmented rhombic dodecahedra	3,4-c tfg	3,8-c the (6-c pcu)		58
Truncated octahedral MOP as SBU or TBU
Zn(Phim)2 (ZIF-7)	4-c sod	4-c sod	6-c pcu		60
Zn(Meim)2 (ZIF-8)
Co(Phim)2 (ZIF-9)
In(imdc)2(C3N2H5)(DMF)4(CH3CN)(H2O)4 (sod-ZMOF)	4-c sod	4-c sod	6-c pcu		61
Zn(Pur)2·(DMF)0.75(H2O)1.5 (ZIF-20)	4-c lta	4-c lta	6-c pcu		62
Co(Pur)2·(DMF)(H2O) (ZIF-21)
Truncated cuboctahedral MOP as SBU or TBU
Zn(Phim)2, (ZIF-11), Co(Phim)2, (ZIF-12), Zn(eim/mim)2	4-c rho	4-c rho	6-c pcu		60
In48(imdc)96(C7N3H15)24(DMF)36(H2O)192 (rho-ZMOF)	4-c rho	4-c rho	6-c pcu		61

---

MOFs based on MOPs as SBU or TBU

Networks based on tetrahedral MOP

Networks based on corner linkage of tetrahedral MOP.
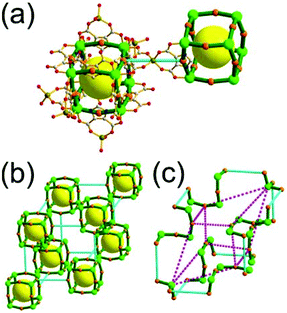
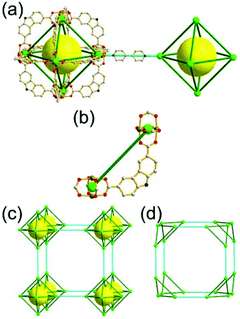
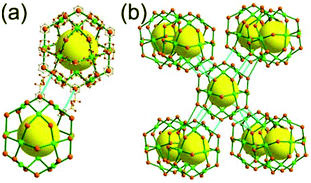
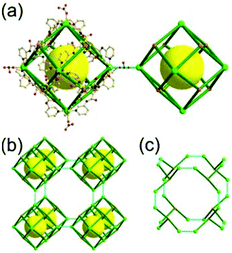
A 4-c net of dia-a topology. A 4-c net based on a corner-linked tetrahedral MOP could have dia-a topology. The network [Cd₄(SPh)₆](SPh)₂ (SPh = benzenethiolate) is an example having dia-a topology, where the tetrahedral MOP consisting of four corner-linked 4-c [Cu(I)(S_Ph)₄] nodes in a tetrahedral arrangement serves as a 4-c SBU, and the MOPs corner-shared in a staggered conformation are interconnected to a dia-a topology via the other bridging SPh group as a 2-c linker (Fig. 2).¹³ In the network, the 2-c SPh ligand serves both as the edges of the tetrahedral MOP and as a linker between the MOPs. The network of dia-a net topology has a supercage of a truncated tetrahedral geometry (a polyhedron of a 3⁴·12⁴ face symbol).

Fig. 2 A 3-D network of dia-a topology based on the tetrahedral MOP [Cd₄(SPh)₆]. (a) The tetrahedral MOP serves as a 4-c SBU through four outer SPh bridging ligands. (b) The adamantine cage of dia underlying topology based on the tetrahedral MOP. (c) The adamantinoid supercage of truncated tetrahedral geometry.

Networks based on corner-shared tetrahedral MOP.
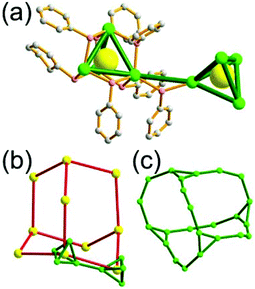
A 6-c net of crs (dia-e) topology. A crs (dia-e: an edge net of dia topology) net is a uninodal 6-c net based on a corner-shared tetrahedral MOP, where the MOPs are corner-shared in a staggered fashion. A lanthanide-based network, [Pr(im)₃(Him)] (Him = imidazole), has crs topology, where the Pr(III) serves as a 6-c node of D_3d (−3m) point symmetry and the imidazolate as a linker between the nodes (Fig. 3).¹⁴ In the network, the tetrahedral [Pr₄(im)₆] units are corner-shared in a staggered fashion, and the net is dia-e topology. The network of dia-e (crs) topology has a supercage of truncated tetrahedral geometry (a polyhedron of a 3⁴·6⁴ face symbol).

Fig. 3 A 3-D network of dia-e topology. (a) The tetrahedral MOP [Pr₄(im)₆]. (b) The 6-c crs net based on the tetrahedral MOP as a corner-shared SBU. (c) The truncated tetrahedral supercage.

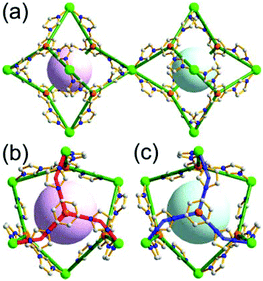
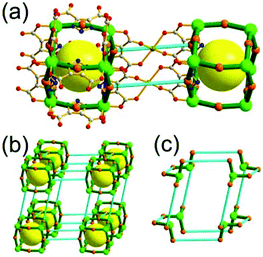
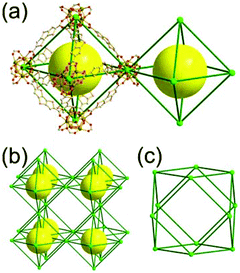
A 6-c net of crs (dia-b-e) topology. An Fe-based network, MOF-500, is also a net of crs topology with an [Fe₃O(COO)₃(py)₃] unit as a trigonal antiprismatic 6-c SBU, where the SBUs form two different kinds of corner-shared tetrahedral MOPs in a staggered fashion (Fig. 4).¹⁵ In the network, the 6-c [Fe₃O(COO)₃(N_py)₃] SBUs of C_3v (3m) point symmetry are interconnected via two different kinds of 2-c nodes, three 2-c bpdc ligands (H₂BPDC = 4,4′-biphenyldicarboxylic acid) and three 2-c bpe ligands (BPE = 1,2-bis-4-pyridylethane). Four corner-shared 6-c SBUs are interconnected via six BPDC ligands to a tetrahedral MOP, and the other four corner-shared 6-c SBUs are similarly interconnected via six BPE ligands to another tetrahedral MOP. These two different kinds of tetrahedral MOPs are corner-shared in a staggered fashion, and the topology of the network is dia-b-e (an edge net of dia-b (binary dia)). The net of dia-b-e topology has two different supercages of the same truncated tetrahedral geometry (a polyhedron of a 3⁴·6⁴ face symbol) (Fig. 4).

Fig. 4 A 3-D network of dia-b-e topology based on two kinds of tetrahedral MOPs. (a) The trinuclear [(Fe₃O(COO)₃(py)₃)] SBU. (b) The side view of the 6-c trigonal antiprismatic SBU of C_3v (3m) point symmetry. (c) The tetrahedral MOP made of six BPE ligands. (d) The tetrahedral MOP made of six BPDC ligands. (e) The two kinds of tetrahedral MOPs are corner-shared to a net of dia-b underlying topology. (f) and (g) The two different supercages of a truncated tetrahedral geometry.

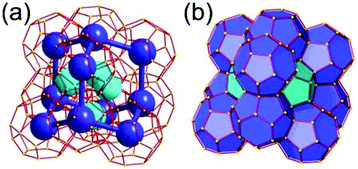
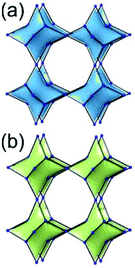
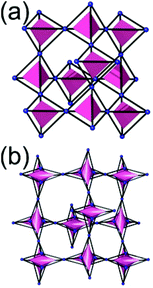
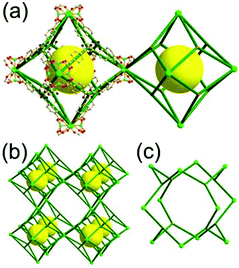
A 6,6,6,6-c net of mtn-e topology. A Cr(Fe,Al)-based extended framework, MIL-101, is a network containing an [M₃O(COO)₆] unit as a 6-c SBU (Fig. 5).¹⁶ The net topology of MIL-101 could be analyzed as a network based on corner-shared tetrahedral MOPs. The [M₃O(COO)₆] SBUs are interconnected via six 2-c 1,4-benzene dicarboxylate (BDC) ligands to a network of 6,6,6,6-c mtn-e topology (Fig. 5). In the network, the 6-c SBUs are interconnected to a tetrahedral MOP via BDC ligands. When the tetrahedral MOP is simplified as a 4-c tetrahedral TBU corner-shared in an eclipsed fashion, the underlying topology of the network is mtn. The net of mtn underlying topology contains two different kinds of supercages: an mtn cage of a 5¹²·6⁴ face symbol and a dodecahedral cage of a 5¹² face symbol.

Fig. 5 A 3-D network of mtn-e topology based on a tetrahedral MOP. (a) Four 6-c trinuclear [M₃O(COO)₆] SBUs are connected by six BDC ligands to a corner-shared tetrahedral MOP. (b) The linkage between the [M₃O(COO)₆] SBUs. (c) The tetrahedral MOPs are corner-shared to a net of mtn underlying topology.

In the network of mtn topology, an mtn cage is face-shared with four adjacent mtn cages via 6-membered hexagonal faces in dia underlying topology, and four face-sharing dodecahedral cages in a tetrahedral arrangement are in the adamantinoid supercage (Fig. 6).

Fig. 6 (a) Ball-and-stick and (b) tile-and-net models of a net of mtn topology with mtn cages (blue) in dia underlying topology and with the four dodecahedral cages (cyan) in an adamantinoid supercage.

Networks based on edge-center-shared tetrahedral MOP

Network based on a planar 4-c node as a shared-edge-center of a tetrahedral MOP.
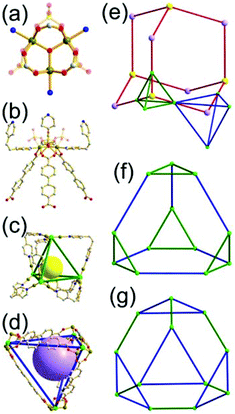
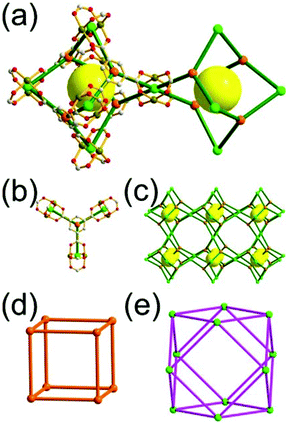
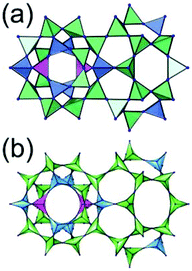
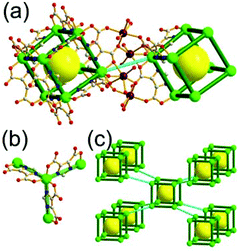
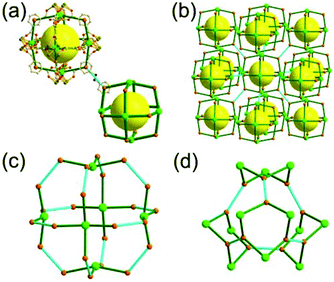
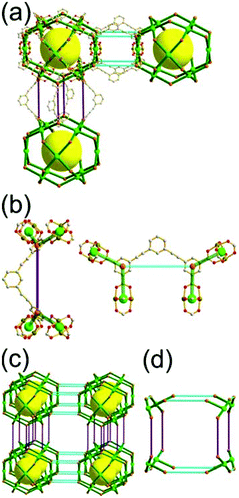
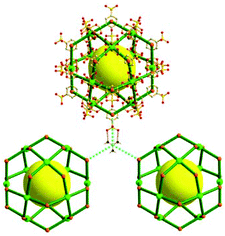
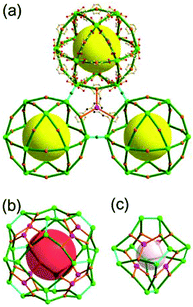
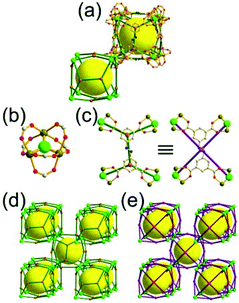
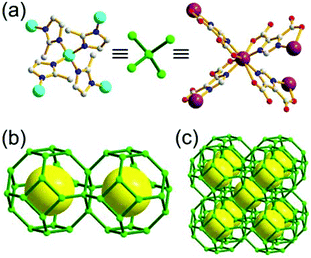
A 3,4-c net of tbo topology. A Cu(II)-based extended framework, [Cu₃(BTC)₂(H₂O)₃] (BTC = 1,3,5-benzene tricarboxylate) (HKUST-1), is a network of tbo topology containing a [Cu₂(COO)₄] paddle-wheel unit as a planar 4-c SBU of D_2h (mmm) point symmetry and BTC as a 3-c organic node of C_3v (3m) point symmetry.^6a In the network, six paddle-wheel SBUs are interconnected to a tetrahedral MOP via four 3-c BTC ligands (Fig. 7a and b). The six edge-centers of the tetrahedral MOP, the Cu paddle-wheel SBUs, are shared with the edge-centers of six adjacent MOPs in a primitive cubic packing arrangement (Fig. 7c). When the MOP is simplified as a 6-c octahedral TBU, the net is of pcu underlying topology. The arrangement of the tetrahedral MOPs in two different, alternating, orientations in the network generates two different supercages, supercage A and supercage B, of different topologies (Fig. 7d and e). Supercage A is a cube of an 8⁶ face symbol, and supercage B is a cuboctahedron of a 6⁸·8⁶ face symbol. Several isoreticular networks of the same tbo net topology have been reported using 3-c organic ligands of C_3v point symmetry and 4-c planar inorganic nodes of D_2h point symmetry.^6b,c,17

Fig. 7 A 3-D network of tbo topology based on a tetrahedral MOP. (a) The BTC ligand as a 3-c vertex and the [Cu₂(COO)₄] SBU as a 4-c shared edge-center of the tetrahedral MOP. The MOPs are corner-shared via the [Cu₂(COO)₄] SBU. (b) The planar BTC ligand is linked to three [Cu₂(COO)₄] SBUs. (c) The edge-center-shared tetrahedral MOPs with 3,4-c tbo topology could be considered as a net of pcu underlying topology based on a tetrahedral MOP as a TBU. (d) and (e) The two kinds of supercages of cubic and cuboctahedral geometries.

The combination of a planar 4-c node of D_2h point symmetry with a 3-c node of C₃ point symmetry (with no σ_v symmetry), instead of a C_3v point symmetry, could also yield a net of tbo topology by adopting the alternating tetrahedral MOPs, MOP-A and MOP-B, either with the C₃ point symmetry ligands of a right-handed C₃ rotational symmetry and a left-handed C₃ rotational symmetry (Fig. 8)¹⁸ or with disordered C₃ point symmetry ligands of right- and left-handed C₃ rotational symmetry.¹⁹ Even the combination with a flexible 3-c ligand (with no C₃ and σ_v symmetries) could also yield a net of tbo topology by adopting the alternating tetrahedral MOPs with the statistically disordered 3-c ligands at the C_3v point symmetry site.²⁰

Fig. 8 A 3-D network of tbo topology based on the 3-c node of C₃ point symmetry. (a) The alternating tetrahedral MOPs in the network of tbo topology. (b) A view showing the C₃ point symmetry ligand of a right-handed C₃ rotational symmetry in MOP-A. (c) A view showing the C₃ point symmetry ligand of a left-handed C₃ rotational symmetry in MOP-B.

Comparison between the nets of tbo topology and pto topology^19,21. While the reaction of the tricarboxylate ligand, BTC, with the Cu(II), having a strong preference for a planar 4-c [Cu₂(COO)₄] SBU, led to Cu-HKUST-1 of a 3,4-c net of tbo topology, a similar reaction of the other tricarboxylate ligand, 1,3,5-benzenetribenzoate (BTB), with the Cu(II) afforded MOF-14 of another 3,4-c net of pto topology.²² The net of tbo topology requires the point symmetry of its 3-c node as a C_3v point symmetry, and the planar BTC can satisfy the symmetry requirement of the net of tbo topology.²³ On the other hand, the BTB ligand of D₃ point symmetry with three benzoate groups twisted from the ligand plane lacks the symmetry property (m (σ_v) symmetry) required for the 3-c node in the net of tbo topology but it can satisfy the symmetry property of the 3-c node of the net of pto topology: a D₃ point symmetry. MOF-14 of pto topology could be obtained when the BTB ligand is combined with the 4-c [Cu₂(COO)₄] SBU.²³

Network based on a tetrahedral 4-c node as a shared-edge-center of a tetrahedral MOP.
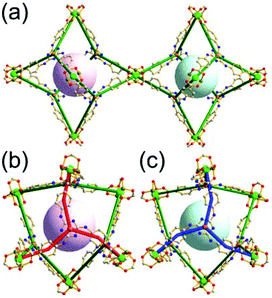
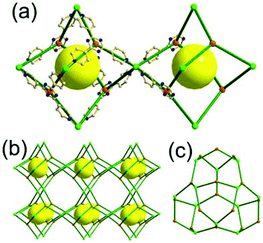
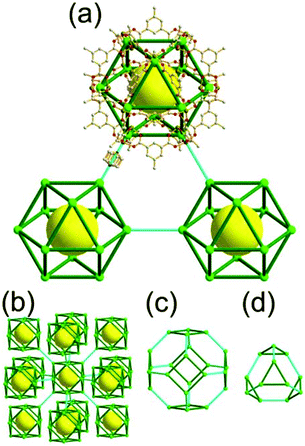
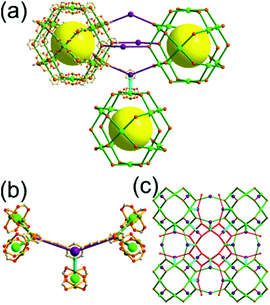
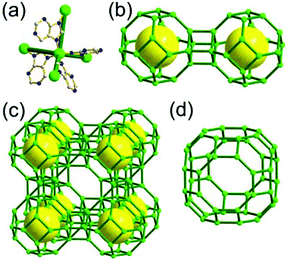
A 3,4-c net of bor topology. A Cu(I)-based extended framework, [Cu₃(TPT)₄](ClO₄)₃ (TPT = 2,4,6-tri(4-pyridyl)-1,3,5-triazine), is a net of bor topology containing a tetrahedral Cu(I) as a 4-c node of D_2d (−42m) point symmetry and a TPT ligand as a 3-c organic node of C_3v (3m) point symmetry (Fig. 9).^24a In the network, six Cu(I) centers are interconnected via four 3-c TPT ligands to form a tetrahedral MOP. As in the networks of tbo topology, six tetrahedral 4-c Cu(I) centers as the six edge-centers of the tetrahedral MOP are shared with the edge-centers of the six adjacent MOPs in a primitive cubic packing arrangement. Contrary to the D_2h (mmm) point symmetry of the 4-c node in tbo topology, the point symmetry of the 4-c node in bor topology is D_2d.²³ When the MOP is simplified as a 6-c octahedral SBU, the net of bor topology could be considered as a net of the same pcu underlying topology as the net of tbo topology. The net of pcu underlying topology generates a supercage of partially decorated heterocubic geometry (a polyhedron of a 6⁴·8⁶ face symbol) at the body-center of the cube. Several isoreticular networks of the same bor net topology have been reported using the 3-c nodes of C_3v point symmetry and the 4-c tetrahedral nodes of D_2d point symmetry.^24b,c

Fig. 9 A 3-D network of bor topology based on a tetrahedral MOP. (a) The tetrahedral MOP with a TPT ligand as a 3-c vertex and copper ions as a 4-c shared edge-center. (b) The planar 3-c ligand is linked to three tetrahedral 4-c nodes. (c) A 3,4-c bor net with the edge-center-shared tetrahedral MOPs could be considered as a net of pcu underlying topology based on a tetrahedral MOP as a SBU. (d) The supercage of partially truncated heterocubic geometry.

As in the 3,4-c net of tbo topology, combination of the 4-c tetrahedral nodes of D_2d point symmetry with the 3-c nodes of C₃ point symmetry (with no σ_v symmetry), instead of a C_3v point symmetry, could also yield a net of bor topology by adopting the alternating tetrahedral MOPs, MOP-A and MOP-B, of the C₃ point symmetry ligands with right-handed and left-handed C₃ rotational symmetries, respectively (Fig. 10).²⁵

Fig. 10 A 3-D network of bor topology based on the 3-c node of C₃ point symmetry. (a) The alternating tetrahedral MOPs in the network of bor topology. (b) A view showing the C₃ point symmetry ligand with a right-handed C₃ rotational symmetry in MOP-A. (c) A view showing the C₃ point symmetry ligand with a left-handed C₃ rotational symmetry in MOP-B.

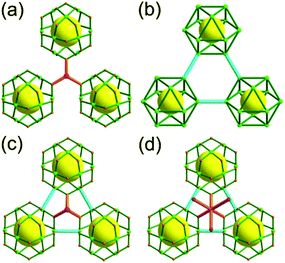
Comparison between the nets of tbo topology and bor topology. The networks of both tbo and bor topologies are based on the edge-center-shared tetrahedral MOPs (Fig. 11). While the shared edge-center in the tbo net is a planar 4-c node of D_2h point symmetry, the corresponding shared edge-center in the bor net is a tetrahedral 4-c node of D_2d point symmetry.

Fig. 11 A comparison of the two 3,4-c nets of (a) tbo topology and (b) bor topology based on the edge-center-shared tetrahedral MOPs.

Networks based on edge-center-sharing and edge-sharing of a tetrahedral MOP.
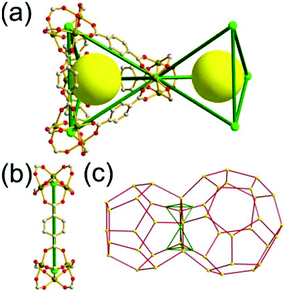
A 3,3,4-net of lwg topology. The solvothermal reaction of the Cu(II) and the octacarboxylic acid 9,9′,9′′,9′′′-([1,1′-biphenyl]-3,3′,5,5′-tetrayl)tetrakis(9H-carbazole-3,6-dicarboxylic acid) (H₈bttcd), as a 3,3-c organic node, resulted in the 3,3,4-c network (PCN-80) of lwg topology based on both the edge-center-shared and the edge-shared tetrahedral MOP of a 7⁴ face symbol (Fig. 12).²⁶ The tetrahedral MOP is connected to the six adjacent MOPs in a primitive cubic packing arrangement via edge-center-sharing of a 4-c inorganic node, [Cu₂(COO)₄] SBU (represented by green spheres), and edge-sharing of two adjacent 3-c nodes, the biphenyl group of bttcd (represented by two pink spheres). The net of lwg topology based on the MOP as a 6-c TBU is a net of pcu underlying topology. The network has two different kinds of supercages, supercage A and supercage B, both derived from the cubic geometry at the body-centers of the tetrahedral MOPs in the primitive cubic packing arrangement. The supercage A is a polyhedron of a 7⁸·8⁶ face symbol, and the supercage B is a cube of an 8⁶ face symbol. When the two adjacent 3-c nodes (the biphenyl group of the ligand) are combined as a single 4-c node, the network is a 3,4-c net of tbo underlying topology.

Fig. 12 A 3,3,4-c network of lwg topology based on a tetrahedral MOP. The tetrahedral MOP is interconnected via (a) edge-center-sharing of a tetrahedral MOP and (b) edge-sharing of a tetrahedral MOP. (c) The ligand consisting of two different kinds of six 3-c nodes (orange and pink spheres) is connected to eight 4-c [Cu₂(COO)₄] inorganic nodes (green spheres). (d) The MOP is interconnected to the six adjacent MOPs in a primitive cubic packing arrangement via edge-center-sharing and edge-sharing. (e) The supercage A derived from a cubic cavity is a polyhedron of a 7⁸·8⁶ face symbol. (f) The supercage B derived from the other cubic cavity is a cube of an 8⁶ face symbol. (g) and (h) When the two adjacent 3-c nodes of the ligand are simplified as one 4-c node, the 3,3,4-c net of lwg topology is a 3,4-c net of tbo topology.

Networks based on cubic MOP

Networks based on corner-shared heterocubic MOP.
A 3,6-c net of spn topology. Lin and co-workers reported a 3-D Cd network, [Cd(3-ppp)₂] (3-ppp = 3-pyridylphosphonate), using 3-ppp as an organic ligand.²⁷ The topology of the network is a 3,6-c spn net, where the Cd(II) center is an octahedral 6-c node and the tripodal 3-ppp is a 3-c organic node (Fig. 13). The network contains a partially corner-shared heterocubic MOP as a SBU, where 3-c 3-ppp serves as an organic 3-c node and the Cd(II) participates in the formation of another 3-c corner of the heterocubic MOP. The corner-shared 6-c Cd(II) ions are at the edge-centers of the net of dia underlying topology based on the heterocubic MOPs in a staggered fashion. The spn net is also an edge net of dia underlying topology, where the vertex of the net of dia topology is decorated by a heterocube rather than a tetrahedron. The spn net has a supercage derived from adamantinoid geometry (a polyhedron of a 4⁶·12⁴ face symbol).

Fig. 13 A 3-D network of spn topology based on a heterocubic MOP. (a) The partially corner-shared heterocubic MOPs, where the pink spheres represent 3-c 3-ppp ligands and the green spheres represent corner-shared 6-c cadmium ions. (b) A net of the corner-shared heterocubic MOPs of dia underlying topology. (c) The supercage of a 4⁶·12⁴ face symbol derived from adamantinoid geometry.

Comparison between the nets of crs topology and spn topology. The net of 3,6-c spn topology is closely related to the net of 6-c crs topology. Both are nets of the same dia underlying topology. While the net of crs topology is an edge net of dia topology based on the corner-shared tetrahedron as a SBU or TBU, the net of spn topology is an edge net of the same dia topology but based on the alternatively corner-shared heterocube (Fig. 14).

Fig. 14 A comparison between the nets of (a) crs topology and (b) spn topology.

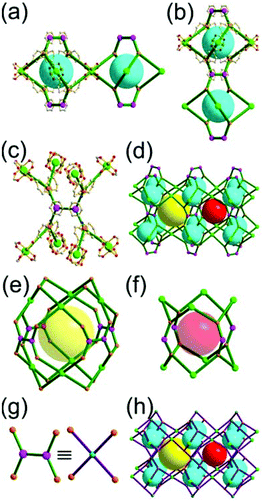
A 3,3,3,3,3,3,6,6,6,6-c net of moo topology. Another Cr(Fe,Al)-based extended network, MIL-100, could be analyzed as a network containing an [M₃O(COO)₆] unit as a 6-c SBU and BTC as a 3-c organic node.²⁸ Topology analysis reveals that the MOF is a net of extremely complex 3,3,3,3,3,3,6,6,6,6-c moo topology with 10 topologically different vertices. In the network, four 6-c SBUs are interconnected via four 3-c BTC ligands to a heterocubic MOP (Fig. 15). The heterocubic MOP in MIL-100 is composed of two different kinds of nodes, 3-c and corner-shared 6-c nodes. The four corner-shared 6-c trigonal prismatic nodes are interconnected to a heterocubic MOP via three 3-c organic nodes, BTC ligands. When the heterocubic MOP is simplified as an alternatively corner-shared 4-c heterocubic TBU in an eclipsed fashion, as in the case of MIL-101, the underlying net topology of MIL-100 is the same as that of MIL-101, mtn. The MIL-100 also has two different kinds of mesoporous supercages as in MIL-101.

Fig. 15 A 3-D network of moo topology based on a heterocubic MOP. (a) The heterocubic MOPs are corner-shared, where the orange spheres represent 3-c BTC ligands and the green spheres represent corner-shared 6-c SBUs. (b) The BTC ligand in the heterocubic MOP is linked to three 6-c SBUs. (c) The corner-shared heterocubic MOPs generate a net of mtn underlying topology based on a heterocubic MOP as a TBU.

Comparison between MIL-101 and MIL-100. While the trigonal prismatic 6-c [M₃O(COO)₆] SBUs in MIL-101 are interconnected via a 2-c BDC linker to a network of mtn-e topology, the same SBUs in MIL-100 are interconnected via a 3-c BTC linker to a network of moo topology. Both MIL-101 and MIL-100 contain MOPs made of four SBUs interconnected in a tetrahedral arrangement. While in MIL-101 the corner-shared tetrahedral MOPs are interconnected to the network of mtn underlying topology, in MIL-100 the alternatively corner-shared heterocubic MOPs are interconnected to the networks of the same mtn underlying topology (Fig. 16).

Fig. 16 A comparison between the nets of (a) mtn-e topology and (b) moo topology.

Networks based on corner-linked cubic MOP.
A 4-c net of pcb topology. The solvothermal reaction of Zn(II), Him and 5-methylbenzimidazole (Hmbim) in the presence of (±)-2-amino-1-butanol and benzene yielded the zeolitic network TIF-3 of pcb topology (ACO zeolite framework) based on the [Zn₈(im)₆(mbim)₆]⁴⁻ cluster as a cubic MOP (Fig. 17).²⁹ In the network, the eight tetrahedral 4-c [ZnN₄] inorganic nodes in a cubic arrangement are connected to a cubic MOP via the combination of 12 im and mbim ligands as bent 2-c linkers, where two 4-c inorganic nodes are the nodes of the [Zn(N_im)₄] co-ordination environment, and the remaining six 4-c inorganic nodes are the nodes of the [Zn(N_im)₂(N_mbim)₂] coordination environment. The cubic MOP is further linked to eight surrounding MOPs in a body-centered cubic packing arrangement to a net of pcb (bcu-a) topology via the im ligand as another 2-c linker.

Fig. 17 A 4-c zeolitic network of pcb topology based on the cubic MOP [Zn₈(im)₆(mbim)₆]⁴⁻. (a) Two cubic MOPs are corner-linked via a 2-c im linker. (b) The two 4-c nodes in two different coordination environments, the first tetrahedral 4-c node consists of two im ligands and two mbim ligands, and the second tetrahedral 4-c node consists of all four im ligands (the imidazolate, drawn using broken bonds, is disordered in the crystal structure). (c) The network based on corner-linked cubic MOPs in bcu underlying topology.

Networks based on single edge-center-linked cubic MOP.
A 3,3-c net of xaa topology. A network, Zn₄G₈[Zn₈(imdc)₈(Himdc)₄], based on an edge-center-linked cubic MOP, could be prepared by the reaction of 4,5-imidazoledicarboxylic acid (H₃imdc) and Zn(II) in the presence of a guanidinium cation (G⁺) (Fig. 18).³⁰ In the network, the eight tripodal 3-c [Zn(ON)_imdc)₃] inorganic nodes in a cubic arrangement are connected via the combination of 12 imdc and Himdc ligands as a linear 2-c linker to a cubic MOP, [Zn₈(imdc)₈(Himdc)₄]¹⁶⁻. The cubic MOP is further interconnected to 12 neighboring cubic MOPs in a cubic close packing arrangement via edge-center linkages through a ditopic [Zn(COO)₄] linker. When the edge-center-linked cubic MOP is considered as a 12-c node, the MOF is a net of fcu underlying topology. The cubic close packing arrangement of the cubic MOPs led to two different kinds of supercages derived from an octahedron and a tetrahedron: a polyhedron of an 8⁶·9⁸ face symbol and a polyhedron of a 9⁴ face symbol, respectively.

Fig. 18 A network of xaa topology based on a cubic MOP. (a) The cubic MOPs are interconnected via the edge-center through the ditopic linker [Zn(COO)₄]. (b) The network of fcu underlying topology showing the cubic close packing arrangement of the cubic MOPs. The two different kinds of supercages of (c) a polyhedron of an 8⁶·9⁸ face symbol and (d) a polyhedron of a 9⁴ face symbol.

Networks based on partial edge-center-linked cubic MOP.
A 3,3,3-c net of rqz topology. Zou et al. reported another network, Li₂₀(H₂O)₂₀[Ni₈(imdc)₁₂], based on an edge-center-linked cubic MOP, [Ni₈(imdc)₁₂]²⁰⁻, as a TBU.³¹ In the network, a Li⁺ bridges two adjacent cubic MOPs via the four O atoms from two edge-ligands of two adjacent cubic MOPs (Fig. 19). Among the 12 edges of the cubic MOP, only six alternative edges are linked to the six adjacent cubic MOPs in a primitive cubic packing arrangement by the Li⁺ ions, leading to a 3,3,3-c net of rqz topology. When the cubic MOP is considered as an octahedral 6-c node, the network could be considered as a net of pcu underlying topology. The primitive cubic packing arrangement of the cubic MOPs led to a polyhedral supercage derived from a cube, a polyhedron of an 18⁶ face symbol.

Fig. 19 A 3,3,3-c network of rqz topology based on a partially edge-center-linked cubic MOP. (a) The cubic MOPs are linked via the edge-centers of the cubic MOP. (b) The network of pcu underlying topology showing the primitive cubic close packing arrangement of the cubic MOPs. (c) The supercage of an 18⁶ face symbol. The pink dotted lines show the cubic geometry of the supercage.

Networks based on double edge-center-linked cubic MOP.
A 3,3-c net of tfg/P topology. Chen et al. reported a 3,3-c network of tfg/P topology (Fig. 20).³² The network, based on a doubly edge-center-linked cubic MOP, [Co(H₂O)₆]{Na₆[Co₈(Hmidc)₁₂]}, is a net of pcu underlying topology when the doubly linked cubic MOPs in a primitive cubic packing arrangement are considered as a 6-c octahedral node. The network contains a polyhedral supercage derived from a cube at the body-center, a polyhedron of a 12⁶ face symbol.

Fig. 20 A 3,3-c network of tfg/P topology based on a doubly edge-center-linked cubic MOP. (a) The cubic MOPs are doubly linked via the edge-centers of the cubic MOP. (b) The network of pcu underlying topology showing the primitive cubic close packing arrangement of the cubic MOPs. (c) A supercage of a 12⁶ face symbol.

Networks based on multiple edge-center-linked cubic MOP. A 3,4-c network based on a [Ni₈(imdc)₁₂]²⁰⁻ cluster as a cubic MOP has been reported (Fig. 21).³¹ The octahedral 3-c Ni(II) center as the corner of the cubic MOP is generated by three imdc ligands in the (ON)_imdc chelating binding mode. In the network of Na₂₀(H₂O)₂₈[Ni₈(imdc)₁₂], the eight tripodal 3-c [Ni((ON)_imdc)₃] inorganic nodes in a cubic arrangement are connected via 12 imdc ligands to a cubic MOP, [Ni₈(imdc)₁₂], and the cubic MOPs are further linked to eight surrounding MOPs in a body-centered cubic packing arrangement via multiple Na–O bonds to a 3,4-c net topology. The network based on the cubic MOP as an 8-c TBU is a net of bcu underlying topology.

Fig. 21 A 3,4-c network based on the cubic MOP [Ni₈(imdc)₁₂]²⁰⁻. (a) Two cubic MOPs are linked via multiple Na–O bonds. (b) An octahedral 3-c Ni(II) center. (c) The network based on the cubic MOPs in bcu underlying topology.

Networks based on octahedral MOP

Networks based on corner-linked octahedral MOP.
A 5-c net of cab topology. Zhou and co-workers reported an octahedron-based MOF, [Cu₂(CDC)₂(bipy)] (CDC = 9H-carbazole-3,6-dicarboxylate, bipy = 4,4′-bipyridine).³³ The network, adopting a net of cab-c (twofold catenated cab) topology, contains an octahedral MOP based on cdc as a 2-c 90°-bent linker and a square planar paddle-wheel cluster [Cu₂(COO)₄] as a 4-c SBU (Fig. 22). The octahedral MOP is further interconnected via a bipy linker to the network of cab (pcu-a) topology based on the octahedral MOP as a 6-c octahedral TBU. The MOF of pcu underlying topology has a truncated cubic supercage of a 3⁸·8⁶ face symbol.

Fig. 22 A 3-D network of cab topology based on an octahedral MOP. (a) The octahedral MOP assembled from 12 cdc ligands as a 90°-bent 2-c linker and six [Cu₂(COO)₄] SBUs as a planar 4-c corner is corner-linked via a linear 2-c bipy linker. (b) A 2-c 90°-bent linker. (c) Scheme of pcu-a topology with the octahedral MOP as a TBU. (d) The truncated cubic supercage of a 3⁸·8⁶ face symbol.

Networks based on corner-shared octahedral MOP.
An 8-c net of reo (pcu-e) topology. Kaskel and co-workers reported DUT-51(Zr) based on a [Zr₆O₆(OH)₂(COO)₈] cluster as a uninodal 8-c SBU (Fig. 23).^34a The 8-c SBU of a D_2h (mmm) point symmetry interconnected via the linear ditopic dithieno[3,2-b;20,30-d]-thiophene-2,6-dicarboxylate (DTTDC) linker of a C_s (m) point symmetry yields a network of a corner-shared octahedral MOP that adopts an edge net of pcu underlying topology (pcu-e: reo topology). The network of reo topology has a supercage of cuboctahedral geometry (a polyhedron of a 3⁸·4⁶ face symbol). Isoreticular DUT-67(Zr) has the same 8-c SBU of a D_2h point symmetry, but the SBUs are interconnected via the other linear ditopic linker, 2,5-thiophenedicarboxylate (tdc), of a C_s point symmetry.^34b

Fig. 23 A 3-D network of reo topology based on an octahedral MOP. (a) An octahedral MOP based on six [Zr₆O₆(OH)₂(COO)₈] clusters interlinked via 12 2-c dttdc linkers. (b) Scheme of pcu-e topology with the corner-shared octahedral MOP. (c) The cuboctahedral supercage of a 3⁸·4⁶ face symbol.

Networks based on edge-center-linked octahedral MOP.
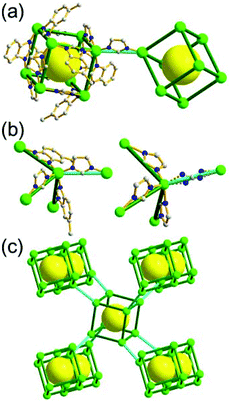
A 3,4-c net of tfb topology. Zaworotko and co-workers reported another type of octahedron-based MOF, [Ni₂(atc)(H₂O)₃] (H₄atc = 3,5-dicarboxyl-(3′,5′-dicarboxylazophenyl)benzene), of a 3,4-c net of tfb topology, using the atc ligand containing two 1,3-benzenedicarboxylate (1,3-BDC) units (Fig. 24).³⁵ Twelve 1,3-BDC groups of the atc ligands and six [Ni₂(COO)₄] SBUs as 2-c edges and 4-c corners, respectively, formed an octahedral MOP. The MOP as a TBU was further interconnected to the 12 surrounding MOPs in a cubic close packing arrangement to the 3,4-c network of tfb topology via the diaza group of the atc ligand through the 12 edge-centers of the octahedral MOP. When the edge-center-linked octahedral MOP is considered as a 12-c TBU, the network is a net of fcu underlying topology. The network of fcu underlying topology contains two different kinds of supercages, an octahedron of a 9⁸ face symbol and a polyhedron of a 6⁴·9⁴ face symbol. The octahedral MOP of the 9⁸ face symbol is based on the six paddle-wheel units as the 4-c vertices of an octahedron connected by the 12 2-c atc ligands. The second polyhedron of the 6⁴·9⁴ face symbol is the decorated tetrahedral cage with four 3-c corners replaced by the hexagons formed by the alternating [Ni₂(COO)₄] SBUs and the BDC units of the ligands. Another isoreticular network of the same tfb net topology was also reported using the other tetracarboxylate ligand, benzoimidephenanthroline tetracarboxylate, containing two 1,3-BDC units and 4-c inorganic nodes.³⁵

Fig. 24 A 3-D network of tfb topology based on an edge-center-linked octahedral MOP. (a) The octahedral MOP based on the [Ni₂(COO)₄] paddle wheel serves as a 12-c TBU interconnected via the diaza group of the atc ligand. (b) Scheme of the net of fcu underlying topology with the octahedral MOP as a TBU. The two different kinds of supercages are derived from (c) an octahedron and (d) a tetrahedron.

Networks based on cuboctahedral MOP

Networks based on corner-linked cuboctahedral MOP.
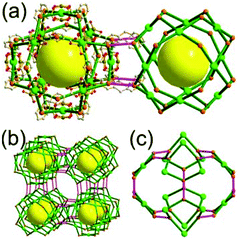
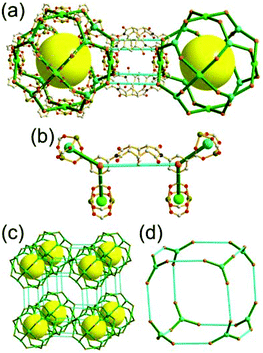
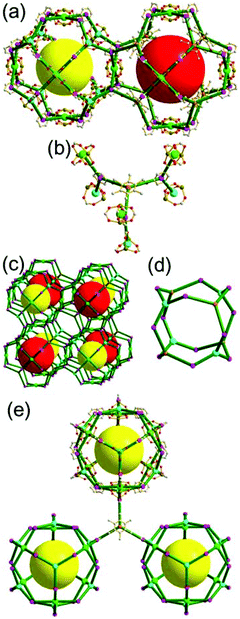
A 5-c net of ubt topology. It is well known that the reaction of a ligand containing the 1,3-BDC unit with either the Cu(II) or Mo(II) could lead to a cuboctahedral MOP based on the [M₂(COO)₄] paddle-wheel SBU as a square planar 4-c vertex and 1,3-BDC as a 120°-bent 2-c edge.³⁶ The solvothermal reaction of 5-methyl-1,3-benzenedicarboxylic acid (H₂MBDC) with Zn(II) in the presence of 1,4-diazabicyclo-[2.2.2]octane (dabco) led to a cuboctahedron-based Zn-MOF, [Zn₄(MBDC)₄(dabco)(OH₂)₂] (Fig. 25).³⁷ In the network, the [Zn₂(COO)₄] paddle wheel as SBU was connected to a cuboctahedral MOP via MBDC ligands, and the MOP is further linked via the ditopic dabco through the 12 corners of the cuboctahedral MOP. The network is an example of a uninodal 5-c net based on the [Zn₂(COO)₄] paddle wheel as a 5-c SBU, and the network is a net of ubt topology. When the cuboctahedral MOPs in a cubic close packing arrangement are treated as a 12-c TBU, the network is a net of fcu underlying topology. The six adjacent cuboctahedral MOPs, which are connected on the vertices of the square window of the cuboctahedral MOP, generate a supercage of a truncated octahedral geometry (a polyhedron of a 4⁶·6⁸ face symbol). The four adjacent cuboctahedral MOPs, which are connected to each other on the vertices of the triangular face of the cuboctahedral MOP, form a supercage of a truncated tetrahedral geometry (a polyhedron of a 3⁴·6⁴ face symbol). Several other isoreticular networks of the same ubt net topology are also reported.³⁸

Fig. 25 A 3-D network of ubt topology based on a cuboctahedral MOP. (a) The cuboctahedral MOPs are interconnected to the corners of the adjacent MOPs via 2-c dabco linkers. (b) Scheme of a net of fcu underlying topology with the corner-linked cuboctahedral MOP as a 12-c TBU. (c) and (d) The two kinds of supercages with truncated octahedral and truncated tetrahedral geometries, respectively.

The networks based on either a corner-shared or a singly edge-center-linked cuboctahedral MOP are yet to be reported. The network based on a corner-shared cuboctahedral MOP might lead to severe congestion of the MOPs around the shared 8-c corners. For all the 24 edges of a cuboctahedral MOP to be singly connected to the adjacent MOPs, the MOP must be surrounded by 24 MOPs, which will cause severe congestion of the MOPs unless they are connected by more than two different lengths of linkers.

Networks based on edge-center-linked cuboctahedral MOPs

A 3,4-c network based on doubly edge-center-linked cuboctahedral MOP.
A 3,3,3,3,4,4,4,4-c net of gjm topology. Zaworotko and co-workers reported the edge-center-linked cuboctahedron-based MOF, [(Cu₂)₁₂(5-SO₃-BDC)₁₆(5-SO₃H-BDC)₆(4-methoxypyridine)₆(MeOH)_12x(H₂O)_18–12x]²⁴⁻ (5-SO₃-BDC = 5-sulfonatoisophthalate; 5-SO₃H-BDC = 5-sulfoisophthalate), using 5-SO₃-BDC/5-SO₃H-BDC as the edge of the cuboctahedral MOP.³⁹ In the network, 16 of the 24 edge-centers of the cuboctahedral MOP are doubly interconnected to the edge-centers of the eight adjacent MOPs via coordination of the sulfonate group at an edge-center to a 2-c [Cu(methoxypyridine)₄] node. When the MOP is considered as a doubly linked 16-c TBU, the network is a net of bcu underlying topology (Fig. 26).

Fig. 26 A 3,3,3,3,4,4,4,4-c network of gjm topology based on a cuboctahedral MOP. (a) The cuboctahedral MOP is doubly interconnected to the adjacent MOP via edge-center linkages. (b) Scheme of the net of bcu underlying topology based on the cuboctahedral MOP as a TBU.

Networks based on quadruply edge-center-linked cuboctahedral MOP.
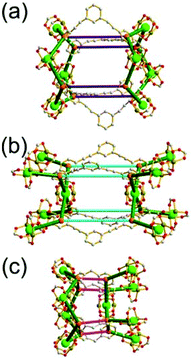
A 3,3,4,4-c net of zmj topology. When a ligand containing two 1,3-BDC units linked via a flexible linker was combined with Cu(II), a network of zmj-c (catenated zmj) topology was reported based on a quadruply edge-center-linked cuboctahedral MOP as a TBU.⁴⁰ A similar ligand containing a rigid bent linker, 1,3-bis(3,5-dicarboxylphenylethynyl)benzene, also led to the isoreticular twofold interpenetrated structure, PMOF-3.⁴¹ In the single network of PMOF-3, the cuboctahedral MOP is quadruply interlinked to the six neighboring MOPs in a primitive cubic packing arrangement via the 24 edge-centers of the MOP (Fig. 27). In the network of zmj topology, two different kinds of quadruple linkages, two AA-type linkages between the same two square faces of the cuboctahedral MOPs (represented by purple rods) and four BB-type linkages between the same two square nodes of the cuboctahedral MOPs (represented by cyan rods) were observed (Fig. 28).⁴¹ The network based on the quadruple edge-center-linked cuboctahedral MOP as a TBU is a net of pcu underlying topology. The primitive cubic packing arrangement of the MOPs contains a supercage at the body-center of the network, a polyhedron of a 3⁴·6⁴ face symbol derived from cubic geometry.

Fig. 27 A 3-D network of zmj topology based on a cuboctahedral MOP. (a) Two different kinds of quadruple linkages between the cuboctahedral MOPs (AA-type linkage (purple rods) between the same two square faces of the cuboctahedral MOPs and BB-type linkage (cyan rods) between the same two square nodes of the cuboctahedral MOPs). (b) The ligands are involved in two different kinds of quadruple linkages, where the ligand could be considered as two linked 3-c nodes participating as the edges of the cuboctahedral MOPs. (c) Scheme of the net of pcu underlying topology with the quadruply edge-center-linked cuboctahedral MOPs as a TBU. (d) The cubic supercage of a 3⁴·6⁴ face symbol.

Fig. 28 Three different kinds of quadruple linkages observed in the cuboctahedron-based networks of pcu underlying topology. (a) An AA-type (purple rods), (b) an BB-type (cyan rods) and (c) an AB-type (pink rods).

A 3,3,3,3,4,4,4,4-c net of zhc topology. PCN-12 is a 3,3,3,3,4,4,4,4-c network of zhc topology containing a quadruply edge-center-linked cuboctahedral MOP (Fig. 29). Reaction of the Cu(II) with a ligand containing a short methylene linker between the two 1,3-BDC residues yielded a network of zhc topology.⁴² Although the net of zhc topology has the same pcu underlying topology, based on the quadruply edge-center-linked cuboctahedral MOP as the net of zmj topology, the kinds of quadruple linkages in the zhc net are different from those in the zmj net. While two different kinds of quadruple edge-center linkages, AA-type and BB-type, were observed in the network of zmj topology, only one kind of quadruple edge-center linkage, AB-type, between the square face of the cuboctahedral MOP and the square node of the cuboctahedral MOP was observed in the network of zhc topology (Fig. 29). The supercage at the body-center of the pcu underlying net is a complicated cage of a 6⁶·8⁶ face symbol derived from a cube.

Fig. 29 A 3-D network of zhc topology based on a cuboctahedral MOP. (a) The cuboctahedral MOPs are quadruply linked via the edge-centers of the cuboctahedral MOP. (b) Scheme of the net of pcu underlying topology with the cuboctahedral MOP as TBU. (c) The supercage of a 6⁶·8⁶ face symbol.

Networks based on cuboctahedral MOP edge-center-linked via a 3-c node.
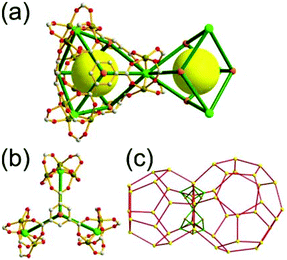
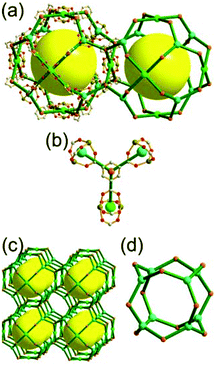
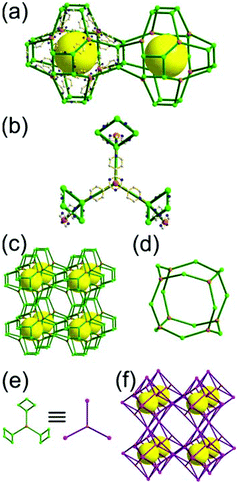
A 3,3,4-c net of ntt topology linked via a 3-c covalent node. When a hexacarboxylate ligand containing three 1,3-BDC units connected via a 3-c covalent node was combined with Zn(II), a 3,3,4-c net of ntt topology could be obtained (Fig. 30).⁴³ The 1,3-BDC unit combined with a Zn(II) generates a 4-c [Zn₂(COO)₄] square paddle-wheel SBU of a C_2h (mm2) point symmetry and the 12 4-c SBUs are linked via a 2-c BDC group to a cuboctahedral MOP as a TBU.‡ The cuboctahedral MOP was further interconnected to 12 adjacent cuboctahedral MOPs in a cubic close packing arrangement via a 3-c covalent node of the ligand through the 24 edge-centers of the cuboctahedral MOP. When the cuboctahedral MOP is considered as a 24-c TBU interconnected via the 3-c covalent node, the underlying net of ntt topology is a 3,24-c of rht topology. The cuboctahedral MOPs in a cubic close packing arrangement lead to two different kinds of supercages: a rhombic dodecahedron with the six 4-c corners decorated by octagons (a polyhedron of an 8¹⁸ face symbol) and a heterocube with the four alternating 3-c corners decorated by hexagons (a polyhedron of a 6⁴·8⁴ face symbol). Several isoreticular networks of the same 3,24-c rht underlying topology have been reported using similar hexacarboxylate ligands of a C_3v (or C₃) point symmetry containing three 1,3-BDC units linked via different 3-c covalent nodes.⁴⁴

Fig. 30 A 3,3,4-c network of ntt topology based on a cuboctahedral MOP. (a) The three cuboctahedral MOPs are linked by the 3-c organic node. (b) The ligand consisting of two different kinds of four 3-c nodes is connected to six 4-c inorganic nodes. (c) Scheme of a 3,24-c of rht underlying topology. (d) and (e) The two kinds of supercages derived from an octahedron and a tetrahedron, respectively.

A 3,3,4-c net of ntt topology linked via a coordination 3-c node and via a hydrogen bonding 3-c node. Another 3,3,4-c network of ntt topology could be prepared by linking the edge-centers of a cuboctahedral MOP via a 3-c coordination node.⁴⁵ The solvothermal reaction of 5-tetrazolylisophthalic acid (H₃TZI) and Cu(II) yielded a Cu-MOF, [Cu₃O(H₂O)₃]₂₄[Cu₂₄(TZI)₂₄(H₂O)₂₄]₃(NO₃)₂₄ (H₃TZI = 5-tetrazolylisophthalic acid). In the network, 24 1,3-BDC units of TZI ligands as edges and 12 Cu paddle-wheel SBUs as 4-c nodes self-assembled into a cuboctahedral MOP, and the MOPs as 24-c TBUs are interconnected to a 3,24-c of rht underlying topology via a 3-c node of coordination linkage, [Cu₃O(tetrazole)₃], of a C_3v point symmetry (Fig. 31).

Fig. 31 The three 24-c cuboctahedral MOPs in the net of ntt topology are linked by a 3-c [Cu₃O(tetrazole)₃] coordination linkage.

The other 3,3,4-c network of ntt topology could also be prepared by linking the edge-centers of a cuboctahedral MOP via a hydrogen-bonded 3-c node.⁴⁶ The reaction of Cu(II) with sodium 5-sulfoisophthalate (Na(5-SO₃-BDC)) in the presence of guanidinium (G⁺) yielded the network {G₈[Cu₂₄(5-SO₃-BDC)₂₄]}¹⁶⁻ of ntt topology based on the cuboctahedral MOP interconnected via a hydrogen-bonded 3-c G⁺ cation of a C_3v point symmetry (Fig. 32).

Fig. 32 The three 24-c cuboctahedral MOPs in the net of ntt topology are linked by a 3-c (G⁺)⋯(SO₃⁻)₃ hydrogen bond linkage.

Networks based on the combination of quadruple edge-center linkages and edge-center-to-corner linkages of cuboctahedral MOP.
A 3,3,5-c net of pzh topology. Zhang et al. reported a 3,3,5-c network of pzh topology using a ligand resembling 1,3-bis(3,5-dicarboxylphenylethynyl)benzene used for PMOF-3 of zmj topology but containing a pyridyl group at the site of the central benzene ring (Fig. 33).⁴⁷ The cuboctahedral MOP in the network is connected via the 24 edge-centers and the 12 corners of the MOP as a 36-c TBU and the pyridyl unit of the ligand as a 3-c organic node, and the network was described as a 3,36-c net of txt topology.¹¹ The network could alternatively be described as a 3,3,5-c net of pzh topology, where the ligand is considered as a 3,3,3-c node consisting of two different kinds of three 3-c nodes and the [Cu₂(COO)₄(pyridyl)] cluster as a 5-c node.¹⁰ The cuboctahedral MOP in the network is interconnected to six adjacent MOPs in primitive cubic arrangement via quadruple edge-center linkages as in the networks of PMOF-3 of zmj topology and of PCN-12 of zhc topology. However, the quadruple linkages between the cuboctahedral MOPs are different from those observed in the networks of zmj and zhc topologies. All six quadruple linkages in the network are of AA-type, with the linkage between the same two square faces of the cuboctahedral MOPs (Fig. 33). This 3,4-c subnet based on the quadruple edge-center linkages is a net of ucp topology proposed by O'Keeffe and Yaghi.^8b In the 3,3,5-c net of pzh topology, the 3,4-c subnets of ucp topology are twofold interpenetrated, and the central 2-c pyridyl group at the edge-center of one subnet is further linked to the 4-c [Cu₂(COO)₄] paddle-wheel corner of the MOP of the other subnet (Fig. 33).

Fig. 33 (a) The cuboctahedral MOPs with the AA-type quadruple edge-center linkage and the edge-center-to-corner linkage between the pyridyl group of the ligand and the corner of the MOP from the other interpenetrated network. (b) The ligand contains two linked 3-c nodes acting as the edges of the cuboctahedral MOPs and has a pyridyl residue between the two 3-c nodes as an additional linkage site. (c) The net shows the interconnection (cyan rods) between the twofold interpenetrated subnets of ucp topology.

Networks based on cuboctahedral MOPs interconnected via the combination of a 3-c edge-center linkage and a corner linkage.
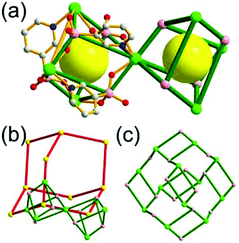
A 3,3,5-c net of nut topology. Sun et al. reported an anionic 3,3,5-c network of nut topology, [(Cd₂Cl)₃(TATPT)₄]¹⁵⁻ (H₆TATPT = 2,4,6-tris(2,5-dicarboxylphenylamino)-1,3,5-triazine), containing a cuboctahedral MOP, using the hexacarboxylate ligand, TATPT, as a 3,3-c organic node containing two different kinds of four 3-c nodes (Fig. 34).⁴⁸ The net of nut topology contains the characteristics of the nets of ubt and ntt topologies at the same time. The cuboctahedral MOP in the network consists of the BDC unit of the TATPT ligand as an edge and the [Cd(COO)₄] metal center as a corner. The [Cd(COO)₄] centers of the cuboctahedral MOP are interconnected to the 12 cuboctahedral MOPs in a cubic close packing arrangement via Cl⁻ bridging anions as in the network of the ubt topology, and the three adjacent cuboctahedral MOPs in the network are further interconnected via a 3-c tris(amino)-1,3,5-triazine unit of the ligand as in the network of ntt topology.§ The cubic close packing arrangement of the cuboctahedral MOPs in the net of nut topology contains two different kinds of supercages. The supercage at the octahedral cavity of the cubic close packing arrangement of the cuboctahedral MOPs is a polyhedron of a 5²⁴·8⁶ face symbol, and the other supercage at the tetrahedral cavity is an mcp-d polyhedron of a 5¹²·6⁴ face symbol.

Fig. 34 A 3,3,5-c network of nut topology based on a cuboctahedral MOP. (a) Three adjacent cuboctahedral MOPs in a cubic close packing arrangement are linked by a 3-c tris(amino)-1,3,5-triazine unit through the 24 edge-centers of the MOP and also linked by a 2-c Cl⁻ through the 12 corners of the MOP. (b) A supercage of a 5²⁴·8⁶ face symbol at the octahedral cavity. (c) The other mcp-d polyhedral supercage of a 5¹²·6⁴ face symbol at the tetrahedral cavity.

The net of nut topology could alternatively be described as a net based on edge-shared mcp-d MOPs in a primitive cubic packing arrangement (Fig. 35). When a 3,3-c node of the TATPT ligand is simplified as a 3-c node and the [Cd(COO)₄]₂Cl metal cluster as a 4-c node, the network of nut topology is a net of tbo underlying topology, as originally described.⁴⁸

Fig. 35 A 3,3,5-c network of nut topology based on an edge-shared mcp-d polyhedral MOP. (a) The mcp-d polyhedral MOP with pink and orange spheres representing two different kinds of 3-c nodes in the ligand and green spheres representing 5-c [Cd(COO)₄] centers is linked to the adjacent MOPs in a primitive cubic packing arrangement via edge-sharing. (b) When the TATPT ligand of two different kinds of four 3-c nodes is simplified as a ligand of one 3-c organic node, the [Cd(COO)₄]₂Cl metal cluster, the two Cl-linked [Cd(COO)₄] centers, is a 4-c inorganic node. (c) The 3,3,5-c net of nut topology based on an edge-shared mcp-d polyhedral MOP. (d) The 3,3,5-c net of nut topology could be simplified as a 3,4-c net of tbo underlying topology.

A 3,5,6-c net of ott topology. Lian et al. reported a 3,5,6-c network of ott topology, [Cu₂₄(CN)₄(BTC)₁₂(dabco)₉(H₂O)₆]·8(NO₃), containing a cuboctahedral MOP (Fig. 36).⁴⁹ The ott net also contains the characteristics of the nets of ubt and ntt topologies, and of nut topology, at the same time. The 1,3-BDC unit of a BTC ligand as an edge and a [Cu₂(COO)₄] paddle-wheel cluster as a 4-c SBU form a cuboctahedral MOP as a TBU. The 4-c [Cu₂(COO)₄] paddle-wheel clusters of the cuboctahedral MOP are interconnected to the 12 cuboctahedral MOPs in a cubic close packing arrangement via a dabco linker as in the network of ubt topology, and the three adjacent cuboctahedral MOPs in the network are further interconnected via a 3-c [Cu₃(CN)(COO)₃] cluster as in the network of ntt topology. In addition to the 3,3,5-c net of nut topology, the eight [Cu₃(CN)(COO)₃] clusters at the corners of a cube are further interlinked via dabco linkers to a cubic cage at the octahedral cavity of the cubic close packing arrangement of the cuboctahedral MOPs, leading to a 3,5,6-c net of ott topology (Fig. 36c). The other supercage at the tetrahedral cavity of the cubic close packing arrangement of the cuboctahedral MOPs is an mcp-d polyhedron of a 5¹²·6⁴ face symbol as in the net of nut topology.

Fig. 36 (a) Three adjacent cuboctahedral MOPs in a cubic close packing arrangement are linked by a [Cu₃(CN)(COO)₃] coordination linkage through the 24 edge-centers of the MOP and are also linked by a 2-c dabco through the 12 corners of the MOP as a 36-c TBU. (b) The [Cu₃(CN)(COO)₃] cluster is further linked to the other three [Cu₃(CN)(COO)₃] clusters by 2-c dabco linkers. (c) A cubic cage at the octahedral cavity of the cubic close packing arrangement of the cuboctahedral MOPs. (d) An mcp-d polyhedral cage at the tetrahedral cavity of the cubic close packing arrangement of the cuboctahedral MOPs.

Comparison of the nets of ntt topology, ubt topology, nut topology and ott topology. All the nets of ntt, ubt, nut and ott topologies are based on the same cuboctahedra in cubic close packing arrangement as a TBU (Fig. 37). While the three cuboctahedra in close contact in the 3,3,4-c net of ntt topology are interconnected via a 3-c node through the edge-centers of the cuboctahedron (Fig. 37a), the three cuboctahedra in the 5-c net of ubt topology are interconnected via a 2-c node through the corners of the cuboctahedron (Fig. 37b). In the 3,3,5-c net of nut topology, the three cuboctahedra are interconnected via both a 3-c node through the edge-centers of the cuboctahedron and a 2-c node through the corners of the cuboctahedron (Fig. 37c). In the 3,5,6-c net of ott topology, in addition to the two different kinds of linkages between the cuboctahedra in the net of nut topology, the eight 3-c nodes in a cubic arrangement at the octahedral cavity of the cubic close packing arrangement of the cuboctahedra are further interconnected via 2-c nodes (Fig. 38d).

Fig. 37 (a) Three adjacent cuboctahedra in a net of ntt topology are linked by a 3-c node through the 24 edge-centers of the MOP. (b) Three adjacent cuboctahedra in a net of ubt topology are linked by a 2-c node through the 12 corners of the MOP. (c) The cuboctahedra in a net of nut topology are linked both by a 3-c node and a 2-c node. (d) In the net of ott topology, the 3-c nodes in the net of nut topology are further linked to the other 3-c nodes by 2-c linkers.

Fig. 38 A 3,5-c network of jjp topology based on a partially corner-linked rhombic dodecahedral MOP. (a) Rhombic dodecahedral MOP with orange vertices representing 3-c organic nodes and green vertices representing 4-c copper ions is interlinked via the 4-c corners of the MOP. (b) The MOP as a 6-c SBU is connected via a 2-c nitrate anion to a net of pcu underlying topology. (c) The supercage of a cubic geometry.

Networks based on rhombic dodecahedral MOP

Networks based on corner-linked rhombic dodecahedral MOP.
A 3,5-c net of jjp topology. The combination of a 3-c organic node and a 4-c node could lead to an MOP of a 3,4-c rhombic dodecahedral geometry.⁵⁰ When the 4-c node of the MOP is further linked via an additional 2-c linker, the network based on a corner-linked rhombic dodecahedral MOP as a SBU could be achieved (Fig. 38). Combination of the organic ligand N,N′N′′-tris(3-pyridinyl)-1,3,5-benzenetricarboxamide (tpbc) or N,N′,N′′-tris(4-pyridinylmethyl)-1,3,5-benzenetricarboxamide (tpmbc) as a 3-c node and a Cu(II) as a 4-c corner component leads to a 3,4-c rhombic dodecahedral MOP as a SBU. The SBU could be further interconnected by a nitrate anion through the 4-c Cu(II) ion to a twofold interpenetrated 3,5-c network of jjp topology. When the rhombic dodecahedral MOP is considered as a 6-c SBU, the network is a net of pcu underlying topology. The supercage at the body-center of the MOPs in the primitive cubic arrangement is a polyhedron of cubic geometry (a polyhedron of a 12⁶ face symbol).

Networks based on corner-sharing of rhombic dodecahedral MOP.
A 3,8-c net of the topology. Ma and Zhou reported the 3,8-c network of the topology, PCN-9. The solvothermal reaction of 4,4′,4′′-s-triazine-2,4,6-triyltribenzoate (TATB) and Co(II) yielded a 3,8-c network based on the [Co₄(μ⁴-O)(COO)₈] cluster as an 8-c SBU and the TATB ligand as a 3-c organic node (Fig. 39).⁵¹ In the network, six 8-c SBUs of D_4h (4/mmm) point symmetry and eight 3-c organic nodes of C_3v (3m) point symmetry form a corner-shared rhombic dodecahedral MOP as a 6-c TBU in the net of pcu underlying topology. The supercage at the body-center of the MOPs in the primitive cubic packing arrangement is a polyhedron of cubic geometry (a polyhedron of an 8⁶ face symbol). Several isoreticular networks of the same the net topology have been reported using 3-c organic ligands and 8-c inorganic nodes.⁵²

Fig. 39 A 3,8-c network of the topology based on a partially corner-shared rhombic dodecahedral MOP. (a) Rhombic dodecahedral MOP with orange vertices representing 3-c organic nodes and green vertices representing cobalt clusters is interlinked via the 4-c corners of the MOP. (b) The MOPs are corner-shared via the 8-c SBU to a net of pcu underlying topology. (c) The supercage of cubic geometry.

A 3,6-c net of edq topology. The reaction of H₄ABTC and In(III) in a DMF–CH₃CN solution in the presence of piperazine yields a 3-D MOF, [In₃O(ABTC)_1.5(H₂O)₃] (ABTC = 3,3′,5,5′-azobenzenetetracarboxylate).⁵³ When the ligand is considered as a 3,3-c organic node and the trigonal prismatic [In₃O(CO₂)₆(H₂O)₃] cluster is considered as a 6-c inorganic SBU, the network is a 3,6-c net of edq topology (Fig. 40). In the network, eight 6-c SBUs as corners are combined with six 3,3-c organic nodes as faces to a cuboidal MOP (topologically dodecahedral MOP), and the cuboidal MOPs are corner-shared with eight adjacent cuboidal MOPs in a body-centered cubic packing arrangement. When the 3,3-c ligand is simplified as a 4-c organic node, the dodecahedral MOP could be considered as a rhombic dodecahedral MOP, and the network is a 4,6-c net of soc topology based on the corner-shared rhombic dodecahedral MOP. In the net of soc topology, the eight 3-c corners of the rhombic dodecahedral MOP are corner-shared to the eight adjacent rhombic dodecahedral MOPs in a body-centered cubic packing arrangement to a net of bcu underlying topology. On the other hand, in the net of the topology, the six 4-c corners of the rhombic dodecahedral MOP are corner-shared to the six adjacent rhombic dodecahedral MOPs in a primitive cubic arrangement to a net of pcu underlying topology.

Fig. 40 A 3,6-c network of edq topology based on a corner-shared cuboidal MOP (topologically dodecahedral MOP). (a) The topological dodecahedral MOP with orange spheres representing 3-c nodes and green spheres representing 6-c [In₃O(CO₂)₆] SBUs is interlinked via the 6-c shared-corners of the MOP. (b) The 6-c shared-corner of the MOP. (c) The atc ligand of two adjacent 3-c nodes could be simplified as a ligand of one 4-c organic node. (d) The 3,6-c net of edq topology based on the partially corner-shared dodecahedral MOP as an 8-c TBU is a net of bcu underlying topology. (e) The 4,6-c net of soc topology based on the partially corner-shared rhombic dodecahedral MOP as an 8-c TBU is a net of the same bcu underlying topology.

Networks based on quadruple edge-center linkage of rhombic dodecahedral MOP.
A 3,3,4-c net of zjz topology. Zhang et al. reported a network based on a quadruply edge-center-linked rhombic dodecahedral MOP (Fig. 41).⁵⁴ The network was prepared by a solvothermal reaction of the Zn(II) with the ligand containing two 1,3-BDC groups linked via the bent rigid organic residue (N-phenyl-N′′-phenylbicyclo[2,2,2]oct-7-ene-2,3,5,6-tetracarboxdiimide tetracarboxylic acid). In the network, the rhombic dodecahedral MOP was built using six [Zn₂(COO)₄] clusters as a 4-c SBU, eight [Zn₂(COO)₃] (or Zn(COO)₃) clusters as a 3-c SBU and the 1,3-BDC groups as the 24 edges of the rhombic dodecahedral MOP. The network based on rhombic dodecahedral MOP is a 3,3,4-c net of a zjz topology, where the rhombic dodecahedral MOPs are quadruply interconnected to six neighboring MOPs in a primitive cubic packing arrangement to a net of pcu underlying topology. This network differs from those of similar 3,3,4,4-c networks: PMOF-3 of a net of zmj topology and PCN-12 of a net of zhc topology. While the quadruple linkages in the nets of zmj and zhc topologies are between the cuboctahedral MOPs, the quadruple linkage in the net of zjz topology is between the rhombic dodecahedral MOPs. The type of all the linkages in the nets of zjz topology is the BB-type linkage between the same two square nodes of the rhombic dodecahedral MOPs. The net of pcu underlying topology contains the supercage of cubic geometry (a polyhedron of an 8⁶ face symbol) at the body-center of the MOPs in the primitive cubic arrangement (Fig. 41). Two other isoreticular networks of a zjz topology have been reported using tetracarboxylate ligands containing two 1,3-BDC units linked via bent residues.⁵⁵

Fig. 41 A 3,3,4-c network of zjz topology based on a rhombic dodecahedral MOP. (a) Rhombic dodecahedral MOPs are quadruply linked via edge-centers of the MOP, where the 3-c organic nodes are represented by orange spheres, 3-c inorganic nodes, [Zn₂(COO)₃], are represented by cyan spheres and 4-c inorganic nodes, [Zn₂(COO)₄], are represented by green spheres. (b) The two adjacent 3-c nodes of the ligand are interconnected to 3-c and 4-c inorganic nodes. (c) The rhombic dodecahedral MOP as a 6-c TBU is quadruply edge-center-linked to six neighboring MOPs in a primitive cubic packing arrangement to a net of pcu underlying topology. (d) The supercage of a cubic geometry.

Networks based on multiple edge-center-sharing of rhombic dodecahedral MOP.
A 3,3,4-c net of tfe topology. It is well known that the solvothermal reaction of the BTC ligand with the Cu(II) leads to Cu-HKUST-1, a 3,4-c network of tbo topology, based on the BTC ligand as an organic 3-c node and the [Cu₂(COO)₄] cluster as inorganic 4-c SBU. However, similar reactions of the same BTC ligand with the Zn(II) lead to either 3-c networks of srs topology based on both the BTC ligand and [Zn₂(COO)₃] cluster as a 3-c node^4b,c or a 3,4-c network of Zn-HKUST-1,^4a,56 which is isostructural to Cu-HKUST-1, based on the [Zn₂(COO)₄] cluster as an inorganic 4-c node instead of [Cu₂(COO)₄] in Cu-HKUST-1. A 3,3,4-c network of tfe topology was also reported based on the BTC ligand as a 3-c organic node and both [Zn₂(COO)₃] and [Zn₂(COO)₄] clusters as 3-c and 4-c inorganic SBUs (Fig. 42).^4d As in the network of a 3,3,4-c net of zjz topology, the rhombic dodecahedral MOP was built using six [Zn₂(COO)₄] clusters as a 4-c SBU, eight [Zn₂(COO)₃] (or Zn(COO)₃) clusters as a 3-c SBU and the 1,3-BDC part of the BTC ligand as the 24 edges of the rhombic dodecahedral MOP. In the network of zjz topology, the edge-centers of the rhombic dodecahedral MOPs are quadruply edge-center-linked to the adjacent rhombic dodecahedral MOPs. On the other hand, a 4-c SBU and four surrounding edge-centers are shared with the adjacent rhombic dodecahedral MOPs in the network of tfe topology. The 3,3,4-c net of tfe topology could also be considered as a net of multiple edge-center-shared rhombic dodecahedral MOPs in a primitive cubic packing arrangement of pcu underlying topology. The net of pcu underlying topology contains the supercage of cubic geometry (a polyhedron of an 8⁶ face symbol) at the body-center of the MOPs in the primitive cubic arrangement.

Fig. 42 A 3,3,4-c network of tfe topology based on a rhombic dodecahedral MOP. (a) Rhombic dodecahedral MOPs are linked via multiple edge-center-sharing of the MOP, where 3-c organic nodes are represented by orange spheres, 3-c inorganic nodes, [Zn₂(COO)₃], are represented by cyan spheres and 4-c inorganic nodes, [Zn₂(COO)₄], are represented by green spheres. (b) The 3-c node of the ligand is interconnected to two 3-c inorganic nodes and one 4-c inorganic node. (c) The rhombic dodecahedral MOP as a 6-c TBU is quadruply edge-center-shared to six neighboring MOPs in a primitive cubic packing arrangement to a net of pcu underlying topology. (d) The supercage of cubic geometry.

Another 3,3,4-c network of tfe topology has been reported based on the flexible hexacarboxylate ligand, 5,5′,5′′-(2,4,6-trimethylbenzene-1,3,5-triyl) trismethylene-trisoxy-triisophthalic acid, containing three 1,3-BDC units (Fig. 43).⁵⁷ The solvothermal reaction of the hexacarboxylate ligand with the Zn(II) in DMSO yielded a network containing both [Zn₂(COO)₃] and [Zn₂(COO)₄] clusters as 3-c and 4-c inorganic SBUs, respectively. The network has two different kinds of multiply edge-center-shared rhombic dodecahedral MOPs. One rhombic dodecahedral MOP was built using six [Zn₂(COO)₄] clusters as a 4-c SBU, eight [Zn₂(COO)₃] clusters as a 3-c SBU and the 1,3-BDC part of the ligand as the 24 edges of the rhombic dodecahedral MOP. On the other hand, while the same [Zn₂(COO)₄] clusters are used as a 4-c SBU of the other rhombic dodecahedral MOP, the 5,5′,5′′-(2,4,6-trimethylbenzene-1,3,5-triyl) trismethylene-trisoxy unit of the ligand was employed as a 3-c organic node instead of the [Zn₂(COO)₃] clusters. The network could be considered as a net of the alternating dodecahedral MOPs in a primitive cubic packing arrangement of pcu underlying topology and contains the supercage of cubic geometry (a polyhedron of an 8⁶ face symbol). The 3,3,4-c network of tfe topology could also be considered as a 3,24-c underlying net of rht topology. All the 24 edge-centers of the rhombic dodecahedral MOP based on the [Zn₂(COO)₄] clusters as a 4-c inorganic node and [Zn₂(COO)₃] clusters as a 3-c inorganic node are interconnected via the 5,5′,5′′-(2,4,6-trimethylbenzene-1,3,5-triyl) trismethylene-trisoxy unit of the ligand as a 3-c organic node (Fig. 43e).

Fig. 43 A 3,3,4-c network of tfe topology based on two different kinds of multiply edge-center-shared rhombic dodecahedral MOPs. (a) Two different kinds of rhombic dodecahedral MOPs are linked via multiple edge-center-sharing of the MOPs, where two different 3-c organic nodes of the ligand are represented by orange spheres and pink spheres, respectively; the 3-c inorganic nodes, [Zn₂(COO)₃], are represented by cyan spheres and the 4-c inorganic nodes, [Zn₂(COO)₄], are represented by green spheres. (b) The central 3-c node of the ligand is linked to three 1,3-BDC units, and each 1,3-BDC unit is further interconnected to both a 3-c inorganic node and a 4-c inorganic node. (c) The alternating rhombic dodecahedral MOPs as a 6-c TBU are quadruply edge-center-shared to six neighboring MOPs in a primitive cubic packing arrangement to a net of pcu underlying topology. (d) The supercage of cubic geometry. (e) The three rhombic dodecahedral MOPs serving as a 24-c node are linked by the 3-c organic node of C_3v point symmetry.

Networks based on face-shared partially augmented rhombic dodecahedral MOP.
A 3,4-c net of tfg topology. Batten et al. reported a network based on a face-shared partially augmented rhombic dodecahedral MOP (a polyhedron of a 4⁶·6¹² face symbol).⁵⁸ The reaction of a trigonal 3-c ligand, 2,4,6-tri(4-pyridyl)-1,3,5-triazine (TPT), with the Zn(II) in the presence of tetraethylammonium cyanide resulted in a twofold interpenetrated 3-D network, [Zn₃(CN)₃(NO₃)₃(TPT)₂]. The single network is a 3,4-c net of tfg topology based on the ligand as a 3-c organic node and the [Zn(CN)₂(N_pyridyl)₂] unit as a 4-c inorganic node (Fig. 44a). In the network, the partially augmented rhombic dodecahedral MOP in a primitive cubic packing arrangement is face-shared to the adjacent MOPs in a primitive cubic packing arrangement via the augmented 4-membered ring with the four 4-c nodes in a square arrangement. The network of tfg topology contains a supercage derived from a cubic cavity, a cube of an 8⁶ face symbol. When the four 4-c inorganic nodes in a square arrangement are combined with the metal cluster [Zn₄(CN)₄(N_pyridyl)₈] as an 8-c TBU of a D_4h point symmetry, the 8-c TBU is connected via the 3-c TPT ligand of a C_3v point symmetry to a 3,8-c net of the topology (Fig. 44). In the network of the underlying topology, eight TPT ligands as a 3-c node and six 8-c TBUs as a shared corner form a network based on a partially corner-shared rhombic dodecahedral MOP (Fig. 44e). The network with the rhombic dodecahedral MOPs in a primitive cubic arrangement could again be simplified as a net of pcu underlying topology, and the net also contains a supercage derived from a cubic cavity, a cube of an 8⁶ face symbol.

Fig. 44 A 3,4-c network of tfg topology based on a partially augmented rhombic dodecahedral MOP. (a) The MOP is interconnected via face-sharing of the MOP, where the orange spheres represent the 3-c organic nodes and the green spheres represent the 4-c tetrahedral inorganic nodes, [Zn(CN)₂(N_pyridyl)₂]. (b) The 3-c organic ligand is connected to three tetrahedral 4-c inorganic nodes. (c) In the net of tfg topology, the MOP is interlinked to six adjacent MOPs in a primitive cubic packing arrangement via sharing of the four 4-c nodes in a square arrangement. (d) A supercage of an 8⁶ face symbol. (e) The four 4-c nodes in a square arrangement are simplified as a corner-shared 8-c node. (f) A 3,8-c net of the underlying topology.

Networks based on truncated octahedral MOP

Networks based on multiple edge-shared truncated octahedral MOP.
A 4-c net of sod topology. While the reaction of a simple imidazole (Him) with divalent metal ions often leads to densely packed M(II)(im)₂ networks,⁵⁹ reaction of the 2-methyl-substituted ligand 2-methylimidazole (Hmeim) with Zn(OH)₂, in the presence of ammonia, yielded the zeolitic network of sod topology, [Zn(meim)₂], based on [Zn(N_meim)₄] as a tetrahedral 4-c node and the meim ligand as a bent 2-c linker, corresponding to the –O– linker in zeolite networks (Fig. 45).⁶⁰ In the network, a truncated octahedron (sod cage) is involved in the face-sharing with the six sod cages in a primitive cubic arrangement via the six 4-membered rings of the sod cage. The net of sod topology contains the same sod cage at the body-center of the face-shared sod cages in a primitive cubic arrangement. The 2-methyl group of the ligand plays the role of the structure directing agent for the network of sod topology.

Fig. 45 A 4-c zeolitic net of sod topology. (a) The meim or the Himdc ligand serves as a 2-c node and the [Zn(Nmeim)₄] unit or the In(III) center serves as a tetrahedral 4-c node. (b) The two truncated octahedral MOPs (sod cages) are interlinked via face-sharing of the four square-nodes of the sod cages in a square arrangement (4R linkage). (c) The net contains the same sod cage at the body-center of the face-shared sod cages.

The zeolitic network of sod topology, (H₂im)[In(Himdc)₂], could also be prepared via a solvothermal reaction using 4,5- imidazoledicarboxylic acid (H₃imdc) as a 2-c linker and the In(III) as a potential 4-c node in the presence of imidazole (Him) as a template.⁶¹ In the network, the In(III) center with four ligands in chelating binding mode serves as a tetrahedral 4-c node, and the ligand serves as a bent 2-c linker. While the zeolitic network based on [Zn(meim)₂] is a neutral network, the zeolitic network based on [In(Himdc)₂] is an anionic framework. The protonated form of the imidazole is used as a template. H₂im serves as a charge-balancing counter monocation.

Networks based on quadruple corner-linked truncated octahedral MOP.
A 4-c net of lta topology. The zeolitic networks of lta topology, [Zn(pur)₂] (ZIF-20), [Co(pur)₂] (ZIF-21) and [Zn(abim)₂] (ZIF-22), were prepared by a solvothermal reaction of Zn(II) or Co(II) and an excess of purine (Hpur) or 5-azabenzimidazole (Habim) (Fig. 46).⁶² The nitrogen atom at the 5-position of the purinate or 5-azabenzimidazolate linker is involved in a dipole–dipole interaction. Such an interaction is proposed for the favourable formation of the quadruple corner linkage (d4R cage) at the early stage of crystallization of the network of lta topology.

Fig. 46 A 4-c zeolitic net of lta topology. (a) The pur ligand serves as a 2-c node and the [Zn(N_pur)₄] unit serves as tetrahedral 4-c node. (b) The two truncated octahedral MOPs (sod cages) are interconnected via quadruple corner linkage between the four 4-c nodes of the sod cages in a square arrangement (d4R linkage). (c) In the network, the sod cages in a primitive cubic arrangement are interconnected via quadruple corner linkages to a net of pcu underlying topology. (d) The net contains an lta cage at the body-center.

Networks based on truncated cuboctahedral MOP

Networks based on octuple corner-linked truncated cuboctahedral MOP.
A 4-c net of rho topology. While the reaction of 2-methylimidazole with the Zn(II) results in the zeolitic network of sod topology, [Zn(meim)₂], a similar reaction using 2-ethylimidazole (Heim) as a ligand yielded another type of zeolitic network; namely, a net of rho topology, as a minor product, where a truncated cuboctahedron (lta cage) is octuply corner-linked via the six 8-membered rings (d8R cage) with the six lta cages in a primitive cubic arrangement (Fig. 47).^60b The net of rho topology contains the same lta cage at the body-center of the octuply corner-linked lta cages in a primitive cubic arrangement. Another zeolitic network of rho topology, [In(phim)₂], could be prepared as a pure form via a solvothermal reaction using benzimidazole (Hphim) as a 2-c linker instead of purine (Hpur) or Habim and the Zn(II) (or Co(II)) as a potential 4-c node.^60a The phenyl residue of the benzimidazole that lacks the nitrogen atom at the 5-position of the ligand, unlike Hpur or Habim, only led to the zeolitic network of rho topology.

Fig. 47 A 4-c zeolitic net of rho topology. (a) The eim or the phim or the Himdc ligand serves as a 2-c node and the [Zn(N_eim)₄] or the [Zn(N_phim)₄] or the [In((N–O)_Himdc)₄] unit serves as a tetrahedral 4-c node. (b) The two lta cages are interconnected via octuple corner linkage between the eight 4-c nodes of the lta cages in an octagonal arrangement (d8R linkage). (c) The net contains the same lta cage at the body-center.

The other zeolitic network of rho topology, (H₂hpp)_0.5[In(Himdc)₂], could also be prepared via a solvothermal reaction using 4,5-imidazoledicarboxylic acid (H₃imdc) as a 2-c linker and the In(III) as a potential 4-c node in the presence of 1,3,4,6,7,8-hexahydro-2H-pyrimido[1,2-a]pyrimidine (hpp) as a structure-directing agent.⁶¹ In the anionic framework, the doubly protonated form of the structure-directing hpp, H₂hpp, serves as a charge-balancing counter dication.

Conclusions

Connectivity and site symmetry of a node are probably the most important factors affecting the network structures of MOFs. Many MOFs with multiple nodes of different connectivity and of different site symmetry have complicated net topologies. Some of these MOFs can be analyzed as networks having simple underlying net topologies when the MOPs composed of multiple nodes are considered as TBUs, using a hierarchical simplification approach.

When a MOP in a network is a uninodal TBU, the connectivity and site symmetry of the MOP play major roles in determining the underlying net topology. When 4-c tetrahedral MOPs are corner-linked or corner-shared in the networks, the networks can have a variety of net topologies depending on the topology of the MOPs and the type of connectivity between the MOPs. They can be simplified either as a net of dia topology or as nets of zeolitic topology. When MOFs have an edge-center-shared tetrahedral MOP or corner-linked octahedral/rhombic dodecahedral MOP or corner-shared rhombic dodecahedral MOP, a variety of net topologies are observed. However, all of them can be simplified as a net of pcu underlying topology when the TBU in the networks has a 6-c octahedral (O_h) site symmetry. Similarly, MOPs as an 8-c node have been encountered in networks that can be simplified as a net of bcu underlying topology, and MOPs as a 12-c node have been encountered in networks that can be simplified as a net of fcu underlying topology. More than 200 zeolitic net topologies have been reported;⁶³ however, only a few have been realized in MOFs. Further investigations into MOFs with zeolitic net topologies, especially zeolitic MOFs augmented by tetrahedral MOPs as TBUs, are required.

Network interpenetration is very important for the control of the pore size and shape of MOFs; it is also related to the network stability. The MOFs of self-dual net topology generated with long and rigid linkers are prone to interpenetration because the centers of the pores (tiles) of a network can be occupied by nodes of the other interpenetrating dual network of the same net topology, and these nodes are interconnected through the centers of the faces of the network. The MOFs of an underlying self-dual net topology with large enough supercages will be susceptible to interpenetration.

In this review, we have analyzed the underlying net topologies of complicated MOFs using hierarchical simplification. The simplified net topology provides better insight into the structural features of complicated MOF structures and could be utilized in designing new MOF structures with known and/or unprecedented net topologies.

Acknowledgements

This work was supported by NRF-2010-0019408 and NRF-2012R1A2A2A01003077 from the National Research Foundation of Korea.

Notes and references

1. (a) J. R. Long and O. M. Yaghi, Chem. Soc. Rev., 2009, 38, 1213–1214; (b) H.-C. Zhou, J. R. Long and O. M. Yaghi, Chem. Rev., 2012, 112, 673–674.
2. (a) M. O'Keeffe, M. Eddaoudi, H. Li, T. Reineke and O. M. Yaghi, J. Solid State Chem., 2000, 152, 3–20; (b) M. O'Keeffe, M. A. Peskov, S. J. Ramsden and O. M. Yaghi, Acc. Chem. Res., 2008, 41, 1782–1789.
3. M. G. Goesten, F. Kapteijn and J. Gascon, CrystEngComm, 2013, 15, 9249–9257.
4. (a) J. I. Feldblyum, M. Liu, D. W. Gidley and A. J. Matzger, J. Am. Chem. Soc., 2011, 133, 18257–18263; (b) O. M. Yaghi, C. E. Davis, G. Li and H. Li, J. Am. Chem. Soc., 1997, 119, 2861–2868; (c) X.-R. Hao, X.-L. Wang, K.-Z. Shao, G.-S. Yang, Z.-M. Su and G. Yuan, CrystEngComm, 2012, 14, 5596–5603; (d) J. Lu, A. Mondal, B. Moulton and M. J. Zaworotko, Angew. Chem., Int. Ed., 2001, 40, 2113–2116.
5. (a) H. Li, M. Eddaoudi, M. O'Keeffe and O. M. Yaghi, Nature, 1999, 402, 276–279; (b) M. Eddaoudi, J. Kim, N. Rosi, D. Vodak, J. Wachter, M. O'Keeffe and O. M. Yaghi, Science, 2002, 295, 469–472.
6. (a) S. S.-Y. Chui, S. M.-F. Lo, J. P. H. Charmant, A. G. Orpen and I. D. Williams, Science, 1999, 283, 1148–1150; (b) S. Ma, D. Sun, M. Ambrogio, J. A. Fillinger, S. Parkin and H.-C. Zhou, J. Am. Chem. Soc., 2006, 129, 1858–1859; (c) X.-S. Wang, S. Ma, D. Sun, S. Parkin and H.-C. Zhou, J. Am. Chem. Soc., 2006, 128, 16474–16475.
7. O. M. Yaghi, M. O'Keeffe, N. W. Ockwig, H. K. Chae, M. Eddaoudi and J. Kim, Nature, 2003, 423, 705–714.
8. (a) D. Zhao, D. J. Timmons, D. Yuan and H.-C. Zhou, Acc. Chem. Res., 2011, 44, 123–133; (b) M. O'Keeffe and O. M. Yaghi, Chem. Rev., 2012, 112, 675–702.
9. M. Li, D. Li, M. O'Keeffe and O. M. Yaghi, Chem. Rev., 2014, 114, 1343–1370.
10. (a) J. J. Perry IV, J. A. Perman and M. J. Zaworotko, Chem. Soc. Rev., 2009, 38, 1400–1417; (b) V. Guillerm, D. Kim, X. Liu, K. Adil, R. Luebke, J. F. Eubank, M. S. Lah and M. Eddaoudi, Chem. Soc. Rev., 2014, 43, 6141–6172.
11. RCSR database at http://rcsr.anu.edu.au.
12. B. F. Abrahams, S. R. Batten, H. Hamit, B. F. Hoskins and R. Robson, Angew. Chem., Int. Ed., Engl., 1996, 35, 1690–1692.
13. I. G. Dance, R. G. Garbutt, D. C. Craig and M. L. Scudder, Inorg. Chem., 1987, 26, 4057–4064.
14. (a) K. Müller-Buschbaum, Z. Naturforsch., B: Chem. Sci., 2006, 61, 792–798; (b) H. Li, M. Eddaoudi, A. Laine, M. O'Keeffe and O. M. Yaghi, J. Am. Chem. Soc., 1999, 121, 6096–6097.
15. A. C. Sudik, A. P. Côté, A. G. Wong-Foy, M. O'Keeffe and O. M. Yaghi, Angew. Chem., Int. Ed., 2006, 45, 2528–2533.
16. G. Férey, C. Mellot-Draznieks, C. Serre, F. Millange, J. Dutour, S. Surblé and I. Margiolaki, Science, 2005, 309, 2040–2042.
17. (a) Y. Inokuma, T. Arai and M. Fujita, Nat. Chem., 2010, 2, 780–783; (b) Y. Inokuma, S. Yoshioka, J. Ariyoshi, T. Arai, Y. Hitora, K. Takada, S. Matsunaga, K. Rissanen and M. Fujita, Nature, 2013, 495, 461–466; (c) J. F. Eubank, H. Mouttaki, A. J. Cairns, Y. Belmabkhout, L. Wojtas, R. Luebke, M. Alkordi and M. Eddaoudi, J. Am. Chem. Soc., 2011, 133, 14204–14207; (d) Z. Zhang, L. Zhang, L. Wojtas, M. Eddaoudi and M. J. Zaworotko, J. Am. Chem. Soc., 2012, 134, 928–933.
18. (a) D. Sun, S. Ma, Y. Ke, D. J. Collins and H.-C. Zhou, J. Am. Chem. Soc., 2006, 128, 3896–3897; (b) X.-S. Wang, S. Ma, D. Yuan, J. W. Yoon, Y. K. Hwang, J.-S. Chang, X. Wang, M. R. Jørgensen, Y.-S. Chen and H.-C. Zhou, Inorg. Chem., 2009, 48, 7519–7521.
19. H. Furukawa, Y. B. Go, N. Ko, Y. K. Park, F. J. Uribe-Romo, J. Kim, M. O'Keeffe and O. M. Yaghi, Inorg. Chem., 2011, 50, 9147–9152.
20. G.-Q. Kong, Z.-D. Han, Y. He, S. Ou, W. Zhou, T. Yildirim, R. Krishna, C. Zou, B. Chen and C.-D. Wu, Chem. – Eur. J., 2013, 19, 14886–14894.
21. S. Amirjalayer, M. Tafipolsky and R. Schmid, J. Phys. Chem. C, 2011, 115, 15133–15139.
22. B. Chen, M. Eddaoudi, S. T. Hyde, M. O'Keeffe and O. M. Yaghi, Science, 2001, 291, 1021–1023.
23. O. Delgado-Friedrichs, M. O'Keeffe and O. M. Yaghi, Acta Crystallogr., Sect. A: Fundam. Crystallogr., 2006, 62, 350–355.
24. (a) B. F. Abrahams, S. R. Batten, H. Hamit, B. F. Hoskins and R. Robson, Angew. Chem., Int. Ed., Engl., 1996, 35, 1690–1692; (b) Q. Zhang, Y. Liu, X. Bu, T. Wu and P. Feng, Angew. Chem., Int. Ed., 2008, 47, 113–116; (c) X. Zhao, H. He, T. Hu, F. Dai and D. Sun, Inorg. Chem., 2009, 48, 8057–8059.
25. (a) Z.-Z. Xue, T.-L. Sheng, Q.-L. Zhu, D.-Q. Yuan, Y.-L. Wang, C.-H. Tan, S.-M. Hu, Y.-H. Wen, Y. Wang, R.-B. Fu and X.-T. Wu, CrystEngComm, 2013, 15, 8139–8145; (b) Z.-M. Hao, C.-H. Guo, H.-S. Wu and X.-M. Zhang, CrystEngComm, 2010, 12, 55–58; (c) T. E. Gier, X. Bu, S.-L. Wang and G. D. Stucky, J. Am. Chem. Soc., 1996, 118, 3039–3040.
26. W. Lu, D. Yuan, T. A. Makal, J.-R. Li and H.-C. Zhou, Angew. Chem., Int. Ed., 2012, 51, 1580–1584.
27. P. Ayyappan, O. R. Evans, B. M. Foxman, K. A. Wheeler, T. H. Warren and W. Lin, Inorg. Chem., 2001, 40, 5954–5961.
28. G. Férey, C. Serre, C. Mellot-Draznieks, F. Millange, S. Surblé, J. Dutour and I. Margiolaki, Angew. Chem., Int. Ed., 2004, 43, 6296–6301.
29. T. Wu, X. Bu, J. Zhang and P. Feng, Chem. Mater., 2008, 20, 7377–7382.
30. M. H. Alkordi, J. A. Brant, L. Wojtas, V. Ch. Kravtsov, A. J. Cairns and M. Eddaoudi, J. Am. Chem. Soc., 2009, 131, 17753–17755.
31. R.-Q. Zou, H. Sakurai and Q. Xu, Angew. Chem., Int. Ed., 2006, 45, 2542–2546.
32. J.-Z. Chen, Y.-G. Tu and X.-L. Nie, Chin. J. Synth. Chem., 2011, 19, 359–362.
33. J.-R. Li, D. J. Timmons and H.-C. Zhou, J. Am. Chem. Soc., 2009, 131, 6368–6369.
34. (a) V. Bon, V. Senkovskyy, I. Senkovska and S. Kaskel, Chem. Commun., 2012, 48, 8407–8409; (b) V. Bon, I. Senkovska, I. A. Baburin and S. Kaskel, Cryst. Growth Des., 2013, 13, 1231–1237.
35. A. J. Cairns, J. A. Perman, L. Wojtas, V. Ch. Kravtsov, M. H. Alkordi, M. Eddaoudi and M. J. Zaworotko, J. Am. Chem. Soc., 2008, 130, 1560–1561.
36. (a) M. Eddaoudi, J. Kim, J. B. Wachter, H. K. Chae, M. O'Keeffe and O. M. Yaghi, J. Am. Chem. Soc., 2001, 123, 4368–4369; (b) B. Moulton, J. Lu, A. Mondal and M. J. Zaworotko, Chem. Commun., 2001, 863–864; (c) Y. Ke, D. J. Collins and H.-C. Zhou, Inorg. Chem., 2005, 44, 4154–4156.
37. H. Chun, J. Am. Chem. Soc., 2008, 130, 800–801.
38. H.-N. Wang, X. Meng, G.-S. Yang, X.-L. Wang, K.-Z Shao, Z.-M. Su and C.-G. Wang, Chem. Commum., 2011, 47, 7128–7130.
39. G. J. McManus, Z. Wang and M. J. Zaworotko, Cryst. Growth Des., 2004, 4, 11–13.
40. J. J. Perry IV, V. Ch. Kravtsov, G. J. McManus and M. J. Zaworotko, J. Am. Chem. Soc., 2007, 129, 10076–10077.
41. X. Liu, M. Park, S. Hong, M. Oh, J. W. Yoon, J.-S. Chang and M. S. Lah, Inorg. Chem., 2009, 48, 11507–11509.
42. X.-S. Wang, S. Ma, P. M. Forster, D. Yuan, J. Eckert, J. J. López, B. J. Murphy, J. B. Parise and H.-C. Zhou, Angew. Chem., Int. Ed., 2008, 47, 7263–7266.
43. Y. Zou, M. Park, S. Hong and M. S. Lah, Chem. Commun., 2008, 2340–2342.
44. (a) S. Hong, M. Oh, M. Park, J. W. Yoon, J.-S. Chang and M. S. Lah, Chem. Commun., 2009, 5397–5399; (b) D. Zhao, D. Yuan, D. Sun and H.-C. Zhou, J. Am. Chem. Soc., 2009, 131, 9186–9188; (c) D. Yuan, D. Zhao, D. Sun and H.-C. Zhou, Angew. Chem., Int. Ed., 2010, 49, 5357–5361; (d) O. K. Farha, A. O. Yazaydın, I. Eryazici, C. D. Malliakas, B. G. Hauser, M. G. Kanatzidis, S. T. Nguyen, R. Q. Snurr and J. T. Hupp, Nat. Chem., 2010, 2, 944–948; (e) O. K. Farha, I. Eryazici, N. C. Jeong, B. G. Hauser, C. E. Wilmer, A. A. Sarjeant, R. Q. Snurr, S. T. Nguyen, A. O. Yazaydın and J. T. Hupp, J. Am. Chem. Soc., 2012, 134, 15016–15021; (f) O. K. Farha, C. E. Wilmer, I. Eryazici, B. G. Hauser, P. A. Parilla, K. O'Neill, A. A. Sarjeant, S. T. Nguyen, R. Q. Snurr and J. T. Hupp, J. Am. Chem. Soc., 2012, 134, 9860–9863; (g) Y. Yan, X. Lin, S. Yang, A. J. Blake, A. Dailly, N. R. Champness, P. Hubberstey and M. Schröder, Chem. Commun., 2009, 1025–1027; (h) Y. Yan, M. Suyetin, E. Bichoutskaia, A. J. Blake, D. R. Allan, S. A. Barnett and M. Schröder, Chem. Sci., 2013, 4, 1731–1736; (i) B. Li, Z. Zhang, Y. Li, K. Yao, Y. Zhu, Z. Deng, F. Yang, X. Zhou, G. Li, H. Wu, N. Nijem, Y. J. Chabal, Z. Lai, Y. Han, Z. Shi, S. Feng and J. Li, Angew. Chem., Int. Ed., 2012, 51, 1412–1415; (j) B. Zheng, J. Bai, J. Duan, L. Wojtas and M. J. Zaworotko, J. Am. Chem. Soc., 2011, 133, 748–751.
45. F. Nouar, J. F. Eubank, T. Bousquet, L. Wojtas, M. J. Zaworotko and M. Eddaoudi, J. Am. Chem. Soc., 2008, 130, 1833–1835.
46. W. Wei, W. Li, X. Wang and J. He, Cryst. Growth Des., 2013, 13, 3843–3846.
47. P. Zhang, B. Li, Y. Zhao, X. Meng and T. Zhang, Chem. Commun., 2011, 47, 7722–7724.
48. C.-Y. Sun, X.-L. Wang, X. Zhang, C. Qin, P. Li, Z.-M. Su, D.-X. Zhu, G.-G. Shan, K.-Z. Shao, H. Wu and J. Li, Nat. Commun., 2013, 4(2717), 1–8.
49. T.-T. Lian, S.-M. Chen, F. Wang and J. Zhang, CrystEngComm, 2013, 15, 1036–1038.
50. J. Park, S. Hong, D. Moon, M. Park, K. Lee, S. Kang, Y. Zou, R. P. John, G. H. Kim and M. S. Lah, Inorg. Chem., 2007, 46, 10208–10213.
51. S. Ma and H.-C. Zhou, J. Am. Chem. Soc., 2006, 128, 11734–11735.
52. (a) M. Dincă, W. S. Han, Y. Liu, A. Dailly, C. M. Brown and J. R. Long, Angew. Chem., Int. Ed., 2007, 46, 1419–1422; (b) S. Das, H. Kim and K. Kim, J. Am. Chem. Soc., 2009, 131, 3814–3815; (c) S. B. Choi, M. J. Seo, M. Cho, Y. Kim, M. K. Jin, D.-Y. Jung, J.-S. Choi, W.-S. Ahn, J. L. C. Rowsell and J. Kim, Cryst. Growth Des., 2007, 7, 2290–2293; (d) Hydrogen bonding net: C. Volkringer, T. Loiseau, J. Marrot and G. Férey, CrystEngComm, 2009, 11, 58–60.
53. Y. Liu, J. F. Eubank, A. J. Cairns, J. Eckert, V. Ch. Kravtsov, R. Luebke and M. Eddaoudi, Angew. Chem., Int. Ed., 2007, 46, 3278–3283.
54. Z.-J. Zhang, W. Shi, Z. Niu, H.-H. Li, B. Zhao, P. Cheng, D.-Z. Liao and S.-P. Yan, Chem. Commun., 2011, 47, 6425–6427.
55. D. Kim, X. Liu, M. Oh, X. Song, Y. Zou, D. Singh, K. S. Kim and M. S. Lah, CrystEngComm, 2014, 16, 6391–6397.
56. (a) X. Song, S. Jeong, D. Kim and M. S. Lah, CrystEngComm, 2012, 14, 5753–5756; (b) Q.-R. Fang, G.-S. Zhu, M.-H. Xin, D.-L. Zhang, X. Shi, G. Wu, G. Tian, L.-L. Tang, M. Xue and S.-L. Qiu, Chem. J. Chin. Univ.-Chin., 2004, 25, 1016–2018.
57. M. Wu, F. Jiang, W. Wei, Q. Gao, Y. Huang, L. Chen and M. Hong, Cryst. Growth Des., 2009, 9, 2559–2561.
58. S. R. Batten, B. F. Hoskins and R. Robson, J. Am. Chem. Soc., 1995, 117, 5385–5386.
59. (a) R. Lehnert and F. Seel, Z. Anorg. Allg. Chem., 1980, 464, 187–194; (b) M. Sturm, F. Bromdl, D. Engel and W. Hoppe, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1975, 31, 2369–2378; (c) N. Masciocchi, S. Bruni, E. Cariati, F. Cariati, S. Galli and A. Sironi, Inorg. Chem., 2001, 40, 5897–5905.
60. (a) K. S. Park, Z. Ni, A. P. Côté, J. Y. Choi, R. Huang, F. J. Uribe-Romo, H. K. Chae, M. O'Keeffe and O. M. Yaghi, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 10186–10191; (b) X.-C. Huang, Y.-Y. Lin, J.-P. Zhang and X.-M. Chen, Angew. Chem., Int. Ed., 2006, 45, 1557–1559.
61. Y. Liu, V. Ch. Kravtsov, R. Larsen and M. Eddaoudi, Chem. Commun., 2006, 1488–1490.
62. H. Hayashi, A. P. Côté, H. Furukawa, M. O'Keeffe and O. M. Yaghi, Nat. Mater., 2007, 6, 501–506.
63. Database of zeolite structures at http://www.iza-structure.org/databases/.

---

Footnotes

† See ref. 2b for the explanation of the three letter RCSR symbol of a net.

‡ The absence of a σ_v symmetry in the ligand needed for the site symmetry of the 3-c node (C_3v point symmetry) of the net of ntt topology leads to the statistical disorder of the three amide linkages between the central 3-c node and the three terminal 3-c nodes of the ligand.

§ The absence of a σ_v symmetry in the ligand needed for the site symmetry of the 3-c node (C_3v point symmetry) of the net of nut topology also leads to the statistical disorder of the tris(amino)-1,3,5-triazine unit.

---