Field-induced dynamic magnetic behaviour of a canted weak ferromagnetic chain material†
Jun-Liang
Liu
 ,
Guo-Zhang
Huang
and
Ming-Liang
Tong
*
,
Guo-Zhang
Huang
and
Ming-Liang
Tong
*
Key Laboratory of Bioinorganic and Synthetic Chemistry of Ministry of Education, School of Chemistry & Chemical Engineering, Sun Yat-Sen University, Guangzhou, 510275, P. R. China. E-mail: tongml@mail.sysu.edu.cn; Fax: (+)86 20 8411-2245
First published on 12th February 2015
Abstract
An interesting 1-D magnetic chain material was facilely synthesized with a one-pot route. The [MnIII3O] based chain shows slow relaxation of magnetization under different applied magnetic fields, even in the antiferromagnetic ordered phase. Furthermore, the material amazingly exhibits the coexistence of spin glass, spin canting, and metamagnetic behaviours.
Introduction
Low-dimensional materials with slow relaxation of magnetization, such as 0-D single-molecule magnets (SMMs)1 and single-ion magnets (SIMs),2 as well as 1-D single-chain magnets (SCMs),3,4 have attained ongoing and great interest for their potential applications in information storage and academic research on molecular magnetism. Furthermore, 1-D magnets can also provide appropriate examples to investigate a few fundamental phenomena in magnetism, such as spin canting,5–10 metamagnetic transition,6,7,10 spin flop (SF) transition,6,10 and spin glass (SG) behaviour.8–11Non-collinear spin arrangements on two sublattices lead to spin canting, where spins are canted by a small angle due to the asymmetric exchange. As for spin glass, the spins are randomly distributed due to the competing interactions, and the metastable frozen state appears at a particular temperature without conventional magnetic long-range ordering.5,10,11 Apart from the superparamagnetism, spin glass also exhibits slow relaxation behavior, which may have potential applications in information theory, associative memory, and combinatorial optimization.9 If the magnetic moments are dominantly antiferromagnetical (AF) arrangement and with magnetic anisotropy as well, the spin flop could happen under the applied magnetic field along with the easy axis, giving rise that the spins first flop to the direction perpendicular to the field, and then tilt closer and closer parallel to the field.5,6,10 If the preference of the magnetic moments is strong enough, spin flip should occur instead of spin flop.5
Although these phenomena (spin canting, spin glass behaviour, and metamagnetism) are distinguishable in many aspects, they also share some common points in nature, such as the existence of magnetic anisotropy.5 The coexistence of two of them is particularly rare,8a,10 not to mention the simultaneous presence of all of them in one single magnetic system.
Herein, we report an interesting 1-D chain material based on [MnIII3O] units that exhibits different magnetic behaviours (spin canting, spin glass, and metamagnetism) under different magnetic fields and at different temperatures. At zero field, the coexistence of weak ferromagnetism and slow relaxation behaviour (spin glass behaviour) dominates. Although antiferromagnetic ordering is clearly observed in the spin flop phase, the slow magnetic relaxation does not disappear, suggesting that 3-D antiferromagnetic order cannot prevent the slow relaxation of the magnetization.16 In addition, under a strong enough magnetic field, we can observe metamagnetic transitions, suggesting that a large field can overwhelm the AF interactions and force the spins to align parallel to the field. Consequently, the antiferromagnetic ordering disappears whereas the slow relaxation behaviour still exists.
Experimental section
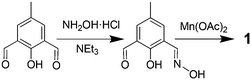
Synthesis of 1: a mixture of 2-hydroxy-5-methylisophthalaldehyde (33 mg, 0.2 mmol), hydroxylamine hydrochloride (28 mg, 0.4 mmol) and triethylamine (61 mg, 0.6 mmol) in CH3OH (20 mL) was stirred for half an hour. Then Mn(OAc)2·4H2O (49 mg, 0.2 mmol) was added. The resulting solution turned greenish black after stirring under ambient conditions for more than 2 hours, and then it was filtered. Lamellate greenish black crystals of 1 (∼33% yield) were obtained when the solution nearly dried. Anal. calcd for C30H38.5Mn3N3O18 (911.47): C 39.53, H 4.42, N 4.61; found: C 39.18, H 4.61, N 4.97. IR (KBr): ν = 3416 (br), 2922 (m), 2515 (w), 2361 (s), 1663 (s), 1547 (vs), 1448 (vs), 1313 (s), 1230 (s), 1049 (s), 879 (m), 771 (m), 667 (s), 540 (w).The intensity data of 1 were recorded on a Rigaku R-AXIS SPIDE IP system with MoKα radiation (λ = 0.71073 Å). The structures were solved by direct methods and refined by full-matrix least-squares on F2 using SHELXTL.17a The disordered water and methanol molecules could not be modelled properly; thus, the program SQUEEZE,17b a part of the PLATON package of crystallographic software, was used to calculate the solvent disorder area and remove its contribution to the overall intensity data.
Crystal data of 1: C30H40Mn3N3O19, M = 911.47, monoclinic, a = 58.419(6) Å, b = 20.302(2) Å, c = 7.4801(8) Å, β = 91.105(3)°, V = 8870.1(17) Å3, T = 100(2) K, space group C2/c, Z = 8, μ(MoKα) = 0.911 mm−1, 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 929 reflections measured, 8360 independent reflections (Rint = 0.0979). The final R1 value was 0.0800 (I > 2σ(I)). The final wR(F2) value was 0.2236 (all data). The goodness of fit on F2 was 0.905.
929 reflections measured, 8360 independent reflections (Rint = 0.0979). The final R1 value was 0.0800 (I > 2σ(I)). The final wR(F2) value was 0.2236 (all data). The goodness of fit on F2 was 0.905.
CCDC 832674 contains the supplementary crystallographic data for this paper.
Results and discussion
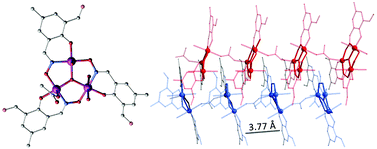
After the oxime was synthesized in situ, it was added to Mn(OAc)2·4H2O and triethylamine in methanol (Scheme 1 and the Experimental section). Compound 1 crystallizes in the monoclinic space group, C2/c (see the Experimental section). All the manganese ions are trivalent, which are confirmed by bond-valence-sum (BVS) calculations (Table S1†),12 charge considerations, and the observation of Jahn–Teller distortion around the MnIII centers.As can be seen in Fig. 1, compound 1 is composed of anti–anti acetate bridged [MnIII3O(mpox)3(H2O)3]− trigonal units, which are formed by one sharing μ3-oxo center and three oxime-group (NO) edges. An acetate bridge coordinates two different MnIII ions in the neighbouring [MnIII3O] units. Two of the three MnIII ions adopt the distorted octahedral geometries, while the third one adopts a distorted square pyramidal geometry. No symmetry elements can be found in the [MnIII3O] unit. Interestingly, the dihedral angle between the adjacent [MnIII3] planes within the chain is 0°, in other words they are completely parallel, and the Jahn–Teller axes of MnIII ions are nearly perpendicular to the plane. It is quite different from the previously reported 1-D chains based on [MnIII3O].13 Supramolecular interactions are also observed – the dimer-like double chain structures are formed during aggregation of neighbouring chains through π–π interactions (3.77 Å, Fig. 1). The shortest interchain distance based on the nearest central oxygen atom of the [MnIII3O] units is 7.373 Å. Moreover, the dihedral angle between each [MnIII3O] plane of the neighbouring chain, namely the dimer-double chain, is 54.8° and they are not parallel to each other.
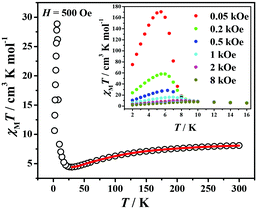
The χMT product under 500 Oe applied dc field in the temperature range of 2–300 K is shown in Fig. 2. The χMT value decreases from 8.09 cm3 K mol−1 at 300 K, which is somewhat smaller than the expected value for three spin-only MnIII ions (9.00 cm3 K mol−1, taking g = 2.0),5a,5b,14 to 4.40 cm3 K mol−1 at 30 K, suggesting the dominant antiferromagnetic interactions. On further lowering the temperature, the χMT product increases to a maximum of 28.86 cm3 K mol−1 at 6.3 K and then drops down to 10.62 cm3 K mol−1 at 2 K. The magnetic exchange constants were extracted using the isosceles triangle model5a,5b,14 in the temperature range of 30–300 K:
| Ĥ = −2J1(Ŝ1·Ŝ2 + Ŝ1·Ŝ3) − 2J2Ŝ2·Ŝ3 |
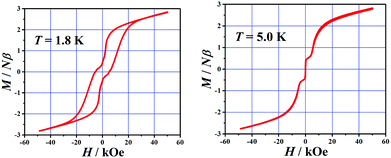
To investigate the phase transition at low temperatures, the field-cooled (FC) and zero-field-cooled (ZFC) susceptibility measurements were performed at 10 Oe in the 1.8–15 K range (Fig. S2†). The FC curve shows an abrupt increase with decreasing temperature below 8 K, reaching saturation at lower temperatures, while the ZFC curve shows a peak. The FC and ZFC data are divergent below the critical temperature TC = 6.4 K, which indicates the occurrence of irreversibility of magnetization below this temperature. FC magnetization was measured under different applied fields and is obviously field-dependent: the products of susceptibilities increase as the measuring fields decrease. This is an important feature of weak ferromagnetism due to spin canting, which is attributed to the existence of an antisymmetrical component of the superexchange interaction (Dzyaloshinsky–Moriya interaction) and/or the appropriate magnetic anisotropy, arising from the non-collinear spin arrangements.5 A remarkable hysteresis loop can be clearly seen at 1.8 K (Fig. 3), confirming the occurrence of spontaneous magnetization, in agreement with the observed spin canting behavior. The coercive field and the remnant magnetization are very large, reaching respectively HC = 5.4 kOe and MR = 0.44μB. Thus the canting angle α is estimated to be around 2.1° from the equation sin(α) = MR/MS (taking MS = 12μB).5
The field-dependence magnetization at different temperatures displays a pronounced sigmoidal shape (Fig. 4), owing to the field-induced metamagnetic behaviour (spin flop or spin flip). The calculated derivatives of dM/dH also show a field-induced spin-reorientation transition at a critical field (Fig. S3†). On closer inspection of the field dependence of the magnetization, something interesting can be found: (1) the magnetization increases nearly linearly at high temperatures, thus no phase transitions are observed; (2) in the temperature range of 8–5 K, the magnetization increases rapidly at the very beginning, and then increases very slowly and remains roughly constant. On applying a magnetic field larger than HC obtained from the maximum (∼5.5 kOe) of dM/dH, the magnetization increases again; (3) in the low temperature range (4–3 K), the demonstration of the double sigmoidal shape of magnetization and two peaks in dM/dH suggests that two step magnetic phase transitions occurred, or the transitions which are originated from applying fields on the different eigen directions (easy, intermediate, or hard axis) for the polycrystalline sample. In order to clarify this behaviour, a lot of magnetic measurements like orienting a single big crystal in the eigen directions, are necessary in the follow-up work. We observed the presence of metamagnetic transitions accompanied by the increasing magnetic field, and finally the antiferromagnetic interactions among MnIII ions are overwhelmed by the field; (4) a typical sigmoidal shape magnetization is shown at 2 K, also suggesting the presence of metamagnetism.
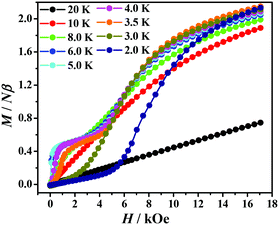 | ||
| Fig. 4 The field dependence of the magnetization of a powder sample of 1 obtained at the indicated temperatures. The lines are a guide to the eye. | ||
In order to further investigate the phase transitions as well as the slow dynamic behaviours of compound 1, the ac susceptibilities were measured under different dc fields (Fig. 5, S4 and S5†). Under zero dc field, both the in-phase (χM′) and out-of-phase signals (χM′′) display a small but significant frequency-dependent behaviour. According to φ = (ΔTp/Tp)/Δ(log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) f), the value of φ is 0.06 (Fig. S6†), suggesting a slow relaxation process of spin-glass-like behaviour.11 The least-squares fitting of the experimental data to the Arrhenius law typically gives values of τ0 = 2.94 × 10−19 s and Δ/kB = 245(5) K (Fig. S7†). The unusually small pre-exponential factor suggests that the domain walls are difficult to move, and confirms the spin glass behavior.10,13 The Cole–Cole plots are shown in Fig. S8,† yielding the α values in the range of 0.21–0.38 with a generalized Debye model, which corresponds to moderate distribution of relaxation times.15 As the simultaneous ferromagnetic and antiferromagnetic exchange couplings exist, especially the antiferromagnetic exchange within the [MnIII3O] asymmetric triangle, it may display some degree of frustration in the magnetic lattice. The randomness in the magnetic lattice is also likely to come from the comparable antiferro/ferromagnetic interactions, crystal defects and/or the presence of two different coordination environments of the MnIII ions. Thus it makes sense that the material exhibits spin-glass behaviour under zero dc field.
f), the value of φ is 0.06 (Fig. S6†), suggesting a slow relaxation process of spin-glass-like behaviour.11 The least-squares fitting of the experimental data to the Arrhenius law typically gives values of τ0 = 2.94 × 10−19 s and Δ/kB = 245(5) K (Fig. S7†). The unusually small pre-exponential factor suggests that the domain walls are difficult to move, and confirms the spin glass behavior.10,13 The Cole–Cole plots are shown in Fig. S8,† yielding the α values in the range of 0.21–0.38 with a generalized Debye model, which corresponds to moderate distribution of relaxation times.15 As the simultaneous ferromagnetic and antiferromagnetic exchange couplings exist, especially the antiferromagnetic exchange within the [MnIII3O] asymmetric triangle, it may display some degree of frustration in the magnetic lattice. The randomness in the magnetic lattice is also likely to come from the comparable antiferro/ferromagnetic interactions, crystal defects and/or the presence of two different coordination environments of the MnIII ions. Thus it makes sense that the material exhibits spin-glass behaviour under zero dc field.
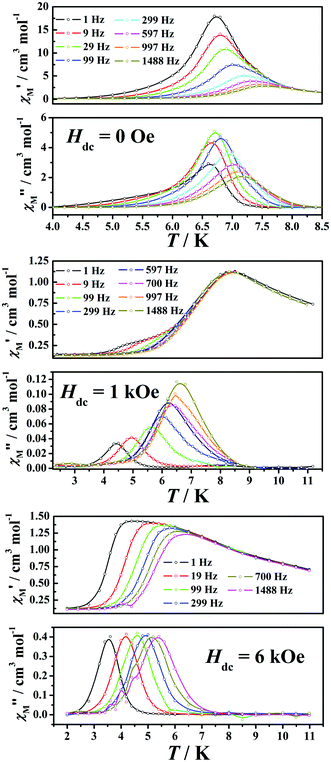 | ||
| Fig. 5 Temperature dependence of the ac susceptibilities under 0 Oe (top), 1 kOe (middle) and 6 kOe (bottom) dc fields. | ||
When 1 kOe dc field was applied, a strong frequency-dependent behaviour was observed. Moreover, a non-frequency-dependent cusp appears at 8.35 K in the in-phase susceptibilities, indicating the occurrence of long-range ordering below the Néel temperature (TN) due to the antiferromagnetic inter-chain interaction and the field-induced spin flop transition. It is reasonable that a small external field can force the magnetization direction to tilt slightly along with the applied field instead of showing randomness. After being free from the spin glass state, a spin flop occurs: an applied magnetic field parallel to the easy axis forces the spins to flop in the direction perpendicular to it, and then the magnetic moments get progressively tilted until they line up with the external field. Surprisingly, obvious frequency-dependent out-of-phase signals were still observed. And the calculated φ value is 0.11 (Fig. S6†), which is close to the superparamagnet-like behaviour. It once again confirms that the magnetic field overcomes the randomness of the magnetization. So, it is likely that this compound falls in the category of materials displaying both a magnetic ordered and a magnet-type behaviour. The magnet-type behaviour originates from the chains exhibiting SCM-like behaviour if the chains are isolated, while the antiferromagnetic inter-chain interaction results from antiferromagnetic ordering.10b,13b,16 The best-fit parameters τ0 and Δ/kB of respectively 5.21 × 10−11 s and 96.5(2) K (Fig. S7†) are acceptable for the SCM-like compounds.3,10b,13b The α values extracted by a generalized Debye model are in a moderate distribution of relaxation times in the range of 0.24–0.34 (Fig. S8†).
When the magnetic field increases up to 6 kOe, the non-frequency-dependent cusps in the in-phase susceptibilities disappear, whereas the strong frequency-dependent signals in both in-phase and out-of-phase susceptibilities appear.10b,13b,16 When a large enough external field (critical field, HC) was employed, the magnetization direction progressively turns parallel to the field, finally resulting in the SF-PM transition. In order to check whether the compound behaves like a superparamagnet or not at 6 kOe, the φ value is calculated, which is the same as the value at 1 kOe (0.11) (Fig. S6†), revealing the superparamagnet-like dynamics behavior. The peak temperatures of χM′′ can be fitted well to the Arrhenius law, with physically reasonable values of τ0 = 1.13 × 10−10 s and Δ/kB = 76(4) K (Fig. S7†). The α values extracted by a generalized Debye model are also in a moderate distribution of relaxation times in the range of 0.24–0.34 (Fig. S8†). In this case, the material also exhibits slow relaxation of magnetization under the magnetic fields larger than HC.
Hence, we can preliminarily conclude as follows: (1) at high temperatures or high magnetic fields (see Fig. 6, PM phase regime), the thermal perturbation or a strong magnetic field provides a large enough energy to overcome the spontaneous alignment of the spins, so the material behaves as a paramagnet or superparamagnet; (2) at a medium temperature and a medium field (see Fig. 6, SF phase regime), the spin flop transition as well as slow magnetization relaxation clearly occurs in the antiferromagnetic ordered phase; (3) at a very low magnetic field (see Fig. 6, SG phase regime), as a result of the possible Dzyaloshinsky–Moriya interaction or the magnetic anisotropy of MnIII ions which lead to spin canting and some degree of frustration due to the competing interactions, both the random alignment of the spins and the creation of the domain walls make the material behave as spin glass; (4) at a very low temperature (see Fig. 6, PM phase regime), although the spins are frozen, they can suddenly flip parallel to the magnetic field, triggering the metamagnetic transition in the case of the increasing applied field.
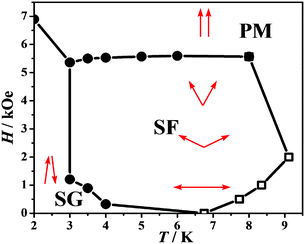 | ||
| Fig. 6 H–T phase diagram for 1. ●: Location of the maximum of temperature-dependent differential susceptibility from dM/dH vs. H data (Fig. S3†); □: Location of the maximum of ac susceptibility from field-dependent χM′ vs. T data (Fig. S4†). | ||
Conclusions
In this study, we facilely synthesized a 1-D chain with a one-pot route. The [MnIII3O] based chain shows slow magnetic relaxation with/without different applied fields, even in the antiferromagnetic ordered phase. Furthermore, the material amazingly exhibits complicated behaviours: the coexistence of spin glass, spin canting, and metamagnetic behaviours. More experiments and further investigations are necessary to deepen our understanding on this interesting material.Acknowledgements
This work was supported by the “973 Project” (2014CB845602 and 2012CB821704), the NSFC (grant no. 91122032, 21371183 and 91422302), the NSF of Guangdong (S2013020013002), the Program for Changjiang Scholars and Innovative Research Team in University of China and the Fundamental Research Funds for the Central Universities. We are grateful to Dr Rodolphe Clérac for meaningful discussions.Notes and references
- (a) R. Sessoli, H.-L. Tsai, A. R. Schake, S. Wang, J. B. Vincent, K. Folting, D. Gatteschi, G. Christou and D. N. Hendrickson, J. Am. Chem. Soc., 1993, 115, 1804 CrossRef CAS; (b) R. Sessoli, D. Gatteschi, A. Caneschi and M. A. Novak, Nature, 1993, 365, 141 CrossRef CAS; (c) D. Gatteschi and R. Sessoli, Angew. Chem., Int. Ed., 2003, 42, 268 CrossRef CAS PubMed; (d) J.-L. Liu, J.-Y. Wu, Y.-C. Chen, V. Mereacre, A. K. Powell, L. Ungur, L. F. Chibotaru, X.-M. Chen and M.-L. Tong, Angew. Chem., Int. Ed., 2014, 53, 12966 CrossRef CAS PubMed.
- (a) N. Ishikawa, M. Sugita, T. Ishikawa, S. Koshiharaand and Y. Kaizu, J. Am. Chem. Soc., 2003, 125, 8694 CrossRef CAS PubMed; (b) S.-D. Jiang, B.-W. Wang, H.-L. Sun, Z.-M. Wangand and S. Gao, J. Am. Chem. Soc., 2011, 133, 4730 CrossRef CAS PubMed; (c) J.-L. Liu, Y.-C. Chen, Y.-Z. Zhen, W.-Q. Lin, L. Ungur, W. Wernsdorfer, L. F. Chibotaru and M.-L. Tong, Chem. Sci., 2013, 4, 3310 RSC.
- (a) R. J. Glauber, J. Math. Phys., 1963, 4, 294 CrossRef PubMed; (b) R. Georges, J. J. Borrás-Almenar, E. Coronado, J. Curély and M. Drillon, One-dimensional Magnetism: An Overview of the Models, in Magnetism: Molecules to Materials, ed. J. S. Miller and M. Drillon, Wiley-VCH Verlag, Berlin, 2001, vol. I, pp. 1–47 Search PubMed; (c) A. Caneschi, D. Gatteschi, N. Lalioti, C. Sangregorio, R. Sessoli, G. Venturi, A. Vindigni, A. Rettori, M. G. Pini and M. A. Novak, Angew. Chem., Int. Ed., 2001, 40, 1760 CrossRef CAS; (d) T.-F. Liu, D. Fu, S. Gao, Y.-Z. Zhang, H.-L. Sun, G. Su and Y.-J. Liu, J. Am. Chem. Soc., 2003, 125, 13976 CrossRef CAS PubMed; (e) M. Ferbinteanu, H. Miyasaka, W. Wernsdorfer, K. Nakata, K. Sugiura, M. Yamashita, C. Coulon and R. Clérac, J. Am. Chem. Soc., 2005, 127, 3090 CrossRef CAS PubMed; (f) Z.-M. Sun, A. V. Prosvirin, H.-H. Zhao, J.-G. Mao and K. R. Dunbar, J. Appl. Phys., 2005, 97, 10B305 Search PubMed; (g) Y.-Z. Zheng, M.-L. Tong, W.-X. Zhang and X.-M. Chen, Angew. Chem., Int. Ed., 2006, 45, 6310 CrossRef CAS PubMed; (h) H.-L. Sun, Z.-M. Wang and S. Gao, Coord. Chem. Rev., 2010, 254, 1081 CrossRef CAS PubMed; (i) Z.-J. Lin and M.-L. Tong, Coord. Chem. Rev., 2011, 255, 421 CrossRef CAS PubMed.
- (a) R. Clérac, H. Miyasaka, M. Yamashita and C. Coulon, J. Am. Chem. Soc., 2002, 124, 12837 CrossRef PubMed; (b) C. Coulon, H. Miyasaka and R. Clérac, Struct. Bonding, 2006, 122, 163 CrossRef CAS; (c) L. Bogani, A. Vindigni, R. Sessoli and D. Gatteschi, J. Mater. Chem., 2008, 18, 4750 RSC; (d) L. Bogani, A. Caneschi, M. Fedi, D. Gatteschi, M. Massi, M. A. Novak, M. G. Pini, A. Rettori, R. Sessoli and A. Vindigni, Phys. Rev. Lett., 2004, 92, 207204 CrossRef CAS; (e) H. Miyasaka, M. Julve, M. Yamashita and R. Clérac, Inorg. Chem., 2009, 48, 3420 CrossRef CAS PubMed.
- (a) R. L. Carlin and A. J. van Duyneveldt, Magnetic Properties of Transition Metal Compounds, Springer-Verlag, New York, 1977 Search PubMed; (b) R. L. Carlin, Magnetochemistry, Springer-Verlag, Berlin, 1986 Search PubMed; (c) S. Blundell, Magnetism in Condensed Matter, Oxford University Press, New York, 2001 Search PubMed.
- (a) M. Kurmoo, H. Kumagai, M. A. Green, B. W. Lovett, S. J. Blundell, A. Ardavan and J. J. Singleton, J. Solid State Chem., 2001, 159, 343 CrossRef CAS; (b) E. Q. Gao, Z.-M. Wang and C.-H. Yan, Chem. Commun., 2003, 1748 RSC; (c) M.-H. Zeng, W.-X. Zhang, X.-Z. Sun and X.-M. Chen, Angew. Chem., Int. Ed., 2005, 44, 3079 CrossRef CAS PubMed; (d) E. Stryjewski and N. Giordano, Adv. Phys., 1977, 26, 487 CrossRef CAS.
- (a) A. Herweijer, W. J. M. de Jonge, A. C. Botterman, A. L. M. Bongaarts and J. A. Cowen, Phys. Rev. B: Solid State, 1972, 5, 4618 CrossRef; (b) J. A. Basten, Q. A. G. van Vlimmeren and W. J. M. de Jonge, Phys. Rev. B: Solid State, 1978, 18, 2179 CrossRef CAS; (c) Y.-Q. Tian, C.-X. Cai, X.-M. Ren, C. Y. Duan, Y. Xu, S. Gao and X.-Z. You, Chem. – Eur. J., 2003, 9, 5673 CrossRef CAS PubMed; (d) Y.-Z. Zheng, W. Xue, M.-L. Tong, W.-X. Zhang, X.-M. Chen, F. Grandjean and G. J. Long, Inorg. Chem., 2008, 47, 4077 CrossRef CAS PubMed; (e) Y.-Z. Zheng, W. Xue, M.-L. Tong, X.-M. Chen and S.-L. Zheng, Inorg. Chem., 2008, 47, 11202 CrossRef CAS PubMed; (f) S. Hu, L. Yun, Y.-Z. Zheng, Y.-H. Lan, A. K. Powell and M.-L. Tong, Dalton Trans., 2009, 1897 RSC; (g) Y.-Z. Zheng, W. Xue, W.-X. Zhang, M.-L. Tong, X.-M. Chen, F. Grandjean, G. J. Long, S.-W. Ng, P. Panissod and M. Drillon, Inorg. Chem., 2009, 48, 2028 CrossRef CAS PubMed; (h) D.-R. Xiao, G.-J. Zhang, J.-L. Liu, R. Yuan, L.-L. Fan and M.-L. Tong, Dalton Trans., 2011, 40, 5680 RSC.
- (a) X.-T. Liu, X.-Y. Wang, W.-X. Zhang, P. Cui and S. Gao, Adv. Mater., 2006, 18, 2852 CrossRef CAS; (b) D.-K. Cao, Y.-Z. Li and L.-M. Zheng, Inorg. Chem., 2007, 46, 7571 CrossRef CAS PubMed.
- (a) T. Taniguchi, K. Yamanaka, H. Sumioka, T. Yamazaki, Y. Tabata and S. Kawarazaki, Phys. Rev. Lett., 2004, 93, 246605 CrossRef; (b) N. Sourlas, Nature, 1989, 339, 693 CrossRef.
- (a) X.-Y. Wang, L. Wang, Z.-M. Wang, G. Su and S. Gao, Chem. Mater., 2005, 17, 6369 CrossRef CAS; (b) Y.-Z. Zheng, W. Xue, M.-L. Tong, X.-M. Chen, F. Grandjean and G. J. Long, Inorg. Chem., 2008, 47, 4077 CrossRef CAS PubMed; (c) J. H. Yoon, D. W. Ryu, H. C. Kim, S. W. Yoon, B. J. Suh and C. S. Hong, Chem. – Eur. J., 2009, 15, 3661 CrossRef CAS PubMed; (d) J. H. Yoon, J. W. Lee, D. W. Ryu, S. W. Yoon, B. J. Suh, H. C. Kim and C. S. Hong, Chem. – Eur. J., 2011, 17, 3028 CrossRef CAS PubMed; (e) F.-P. Huang, J.-L. Tian, D.-D. Li, G.-J. Chen, W. Gu, S.-P. Yan, X. Liu, D.-Z. Liao and P. Cheng, Inorg. Chem., 2010, 49, 2525 CrossRef CAS PubMed; (f) H. Miyasaka, K. Takayama, A. Saitoh, S. Furukawa, M. Yamashita and R. Clérac, Chem. – Eur. J., 2010, 16, 3656 CrossRef CAS PubMed.
- J. A. Mydosh, Spin Glasses: An Experimental Introduction, Taylor and Francis, London, 1993 Search PubMed.
- (a) I. D. Brown and D. Altermatt, Acta Crystallogr., Sect. B: Struct. Sci., 1985, 41, 244 CrossRef; (b) W. Liu and H. H. Thorp, Inorg. Chem., 1993, 32, 4102 CrossRef CAS.
- (a) H.-B. Xu, B.-W. Wang, F. Pan, Z.-M. Wang and S. Gao, Angew. Chem., Int. Ed., 2007, 46, 7388 CrossRef CAS PubMed; (b) C.-M. Liu, D.-Q. Zhang and D.-B. Zhu, Chem. Commun., 2008, 368 RSC; (c) C.-M. Liu, D.-Q. Zhang and D.-B. Zhu, Inorg. Chem., 2009, 48, 4980 CrossRef CAS PubMed; (d) J. Tao, Y.-Z. Zhang, Y.-L. Bai and O. Sato, Inorg. Chem., 2006, 45, 4877 CrossRef CAS PubMed.
- O. Kahn, Molecular Magnetism, VCH Publishers, New York, 1993 Search PubMed.
- K. S. Cole and R. H. Cole, J. Chem. Phys., 1941, 9, 341 CrossRef CAS PubMed.
- (a) C. Coulon, R. Clérac, W. Wernsdorfer, T. Colin, A. Saitoh, N. Motokawa and H. Miyasaka, Phys. Rev. B: Condens. Matter, 2007, 76, 214422 CrossRef; (b) C. Cloulon, R. Clérac, W. Wernsdorfer, T. Colin and H. Miyasaka, Phys. Rev. Lett., 2009, 102, 167204 CrossRef.
- (a) G. M. Sheldrick, Acta Crystallogr., Sect. A: Fundam. Crystallogr., 2008, 64, 112 CrossRef CAS PubMed; (b) P. van der Sluis and A. L. Spek, Acta Crystallogr., Sect. A: Fundam. Crystallogr., 1990, 46, 194 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Additional crystallography tables and figures for magnetic properties. CCDC 832674. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c5qi00004a |
| This journal is © the Partner Organisations 2015 |