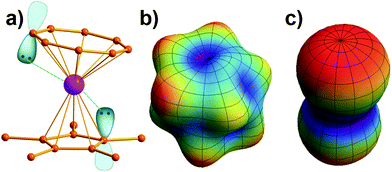Prediction of the quantized axis of rare-earth ions: the electrostatic model with displaced point charges†‡
Shang-Da
Jiang
*ab and
Si-Xue
Qin
c
a1. Physikalisches Institut, Universität Stuttgart, Pfaffenwaldring 57, D-70569 Stuttgart, Germany
bLNCMI-CNRS, 25 rue des Martyrs BP 166, 38042 Grenoble Cedex 9, France. E-mail: jiang@lncmi.cnrs.fr
cInstitute for Theoretical Physics, Johann Wolfgang Goethe Universität, D-60438 Frankfurt am Main, Germany
First published on 18th May 2015
Abstract
An electrostatic model based on the effective-point-charge approach is proposed to predict the quantized axis of rare-earth ions, even in low symmetry. The effective charges of coordination atoms create an electrostatic potential interacting with the aspherical 4f electron cloud of the rare-earth ion. The quantized axis can be determined by minimizing the electrostatic energy. The effective charge displacements must be considered according to the nature of the coordination bond, which can be calculated by the atomic orbital wavefunctions for the σ- and π-bonds, respectively. Using our model, the experimentally determined magnetic easy axis of some complexes with Tb3+, Dy3+ and Er3+ can be very well reproduced.
Introduction
Rare earth elements have fascinated scientists for decades because of their numerous promising properties and applications. Due to their largely unquenched orbital momentum and corresponding spin–orbit coupling, some of the rare-earth ions exhibit vast magnetic anisotropy in certain crystal-field environments, making possible the construction of single-molecule magnets (SMMs),1 especially mononuclear ones.2–6 The strong spin–orbit interaction, however, makes the investigation of the magnetic properties of rare-earth ions very difficult. The spin Hamiltonian approach breaks down while the crystal-field Hamiltonian (CFH) has to be applied to fully describe the spectroscopic and magnetic properties of rare-earth ions.7 Recent research has suggested that structural–magneto relationships can fail to predict the behavior of the magnetic easy axis based on a simple structural approximation.8The CFH approach was first proposed by Bethe with considerations of placing the metal ion in the point-charge environment and parameterizing the charge effect into crystal-field parameters (CFPs) together with the corresponding spherical-harmonic tensors to build up the CFH matrix.9 Neglecting the multiplets’ interaction, the total momentum J can be assumed as a well-defined quantum number and the spherical harmonics can then be substituted with equivalent operators, which largely reduce the calculation complexity.10 Nevertheless, determining CFPs is nontrivial because of the large number of parameters in low symmetry. Generally, spectroscopists extract the CFPs from the optical, infrared, inelastic neutron scattering, and magneto-circular dichroism spectra. Recently, scientists have also proposed fitting the magnetization data at various temperatures and in various directions to determine the CFPs. Lueken and his coworkers have compiled a CONDON code to fit the magnetic-susceptibility data to obtain the CFPs,11,12 while Sessoli's group has proposed to fit the magneto-torque data of a single-crystal sample to determine the CFPs.13 Theoretically, one can calculate the electronic structures by ab initio methods and therefore obtain the phenomenological CFPs.14 Coronado and his coworkers have constructed a semi-empirical method to calculate the CFPs directly from the molecular structure,15 and a SIMPRE code was compiled for this purpose.16
Instead of determining the CFPs, Winpenny and Soncini's groups suggested going back to the original idea of CFH, i.e., minimizing the electrostatic potential of anisotropic dysprosium ions by varying its quantized axis in the Cartesian space to determine the magnetic easy axis.17 This method has been proven to be successful and efficient, providing an intuitive understanding of the orientation of the magnetic easy axis. This idea was compiled into the MAGELLAN code in Fortran. One of the significant drawbacks of this approach, however, is the assumption that the negative charges sit on the atom. This was amply argued by the effective-charge18 and the simple-overlap models,19,20 considering that the negative charges are in the middle of the coordination bond, accounting for the covalency. In contrast, with charge-shifting consideration, the SIMPRE code was compiled to obtain the CFPs by fitting with the magnetic susceptibility data. To validate the theoretical model, it is necessary to compare the predicted quantized axis orientation with the results from experiment determination. Herein, we propose to improve Winpenny and Soncini's approach by shifting the negative charges according to the average radius of the atomic orbital of the coordination atoms to improve the prediction accuracy and overcome the problem encountered when dealing with the π-coordination system. We also generalize this electrostatic method to all the rare-earth ions of all the pure eigenstates. We then verify this improved model using our results from single-crystal magnetometer measurement.
Method
The asphericity of 4f shells
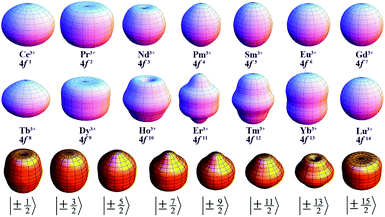
Since the 4f electrons are shielded by the 5d and 6s orbitals and do not play important roles in the coordination bonds,21 one can safely consider the crystal-field effect as a perturbation on the 4f shell. The phenomenological understanding of the single-ion magnetic anisotropy can be viewed from the asphericity of the electron cloud. Skomski has proposed a simplified anisotropy distribution of the 4f electron density by a quadrupole moment, where the electron cloud of rare-earth ions in the Ising-limit state can be viewed as prolate (Pm3+, Sm3+, Er3+, Tm3+, Yb3+) and oblate (Ce3+, Pr3+, Nd3+, Tb3+, Dy3+, Ho3+).22 Rinehart and Long have extended this model to qualitatively maximize the anisotropy of rare-earth ions by orienting the quantized axis (oblate ions) or the equator plane (prolate ion) to the negative charge dense direction.23Sievers has analytically calculated the asphericity of 4f shell by 2k-multipolemoment expansion, where k denotes the rank of spherical harmonics (k = 2, 4, and 6).24 The rotational symmetry of the pure eigenstate of MJ requires q = 0 in Yqk, and therefore only axial terms of Y02, Y04 and Y06 contribute. The Y0k coefficients of light (1a) and heavy (1b) lanthanides in the electron configuration of MJ = M in the Russell–Saunders multiplet 2S+1LJ can be calculated using
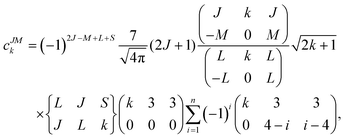 | (1a) |
 | (1b) |
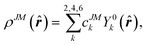 | (2) |
![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) denotes the unit vector of 4f-shell electron coordinates.
denotes the unit vector of 4f-shell electron coordinates.
The coefficients of the spherical harmonics are similar to those in Skomski's model which describe the anisotropy type of rare-earth ions. The negative c2 indicates an oblate anisotropy type and vice versa. The detailed shape of the anisotropic electron cloud is determined by the higher-rank coefficients.
Note that it is inadequate to simply attribute, e.g., Dy3+ to an oblate ion or Er3+ to a prolate ion. The geometry of the electron-density distribution for a certain lanthanide ion depends on the MJ state. As shown in the last row of Fig. 1, the electron-density distribution of the Dy3+ ion changes gradually from typically oblate (MJ = ±15/2) to typically prolate (MJ = ±1/2).
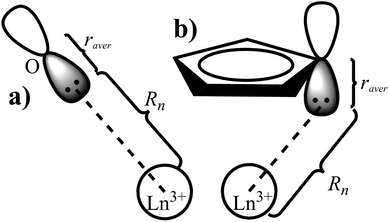
The displacement of the charges
Similarly to the radial effective-charge model (REC) and the lone-pair effective-charge model (LPEC) compiled in SIMPRE,15 the displacements of the negative charges on the ligand in the two types of coordination bonds (i.e., σ- and π-bonds) can differ. As shown in Fig. 2, in the σ-coordination complex, the negative charges of the coordinating atoms originate from the valence atomic orbitals and localize on the σ-bond. One can therefore identify the location of the charge by shifting the atom coordinates along the σ-bond vector to the rare-earth ion by the length of the corresponding average atomic-orbital radius. For the π-coordinating bond, however, the spin polarizations of the negative charges are not individually shifted along the ligand–metal vector, but integrally along the normal of the aromatic plane. The displacement magnitude is determined by the same approach as in the former case. Here, our definition is different from the two-vector (Dr and Dh) one in the LPEC model, since we assume that the p orbital is perpendicular to the aromatic plane and is rather robust due to the conjugation effect.Considering a negative charge Qn on the 2p orbital of an oxygen atom, we express the normalized radial wavefunction as
 | (3) |
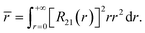 | (4) |
With the average radius and according to the coordination bond type, we can then determine the displaced coordinates of the negative charges.
The electrostatic potential energy
The quantized axis direction with respect to the crystal field is characterized by the wavefunction of the system |ψi〉. Apparently, the ground state of the crystal-field splitting is the one with the lowest expected value of energy,| Eψi = 〈ψi|HCF|ψi〉, | (5) |
In the point-charge model, the crystal field can be described by the approach proposed by Griffith,28 where the infinite series of Legendre polynomials is truncated by the spherical-harmonic summation, which limits the harmonics’ rank to 6 for lanthanide ions. Then, the crystal-field potential is simplified to
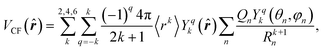 | (6) |
The potential energy of the system can then be calculated, instead of eqn (5), by the integral of the product of 4f shell electron cloud distribution and the crystal field,
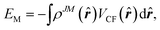 | (7) |
![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) ) depends on the polar angle θ and azimuth angle φ of the quantized axis. Equivalently, we can rewrite eqn (7) in the central-ion coordination system by rotating the charge positions (θn, φn). In this case, VCF(
) depends on the polar angle θ and azimuth angle φ of the quantized axis. Equivalently, we can rewrite eqn (7) in the central-ion coordination system by rotating the charge positions (θn, φn). In this case, VCF(![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) ) is accordingly a function of (θ, φ). Using the orthonormal condition of spherical harmonics, the integral in eqn (7) can be easily evaluated. Therefore, the potential energy is written as the summation
) is accordingly a function of (θ, φ). Using the orthonormal condition of spherical harmonics, the integral in eqn (7) can be easily evaluated. Therefore, the potential energy is written as the summation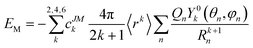 | (8) |
This simple expression allows us to calculate the potential energy of the system when the quantized axis orients in various directions of the molecular coordinate system. Moreover, as we are not interested in the absolute value of the potential energy but the relative value in various directions, the ratio of the charges rather than their magnitudes determines the quantized axis direction.
Note that the higher-rank terms, corresponding to the detailed shape of the electron cloud, contribute a smaller fraction of the potential energy (see eqn (8) for example, where all terms are proportional to 1/Rk+1n). In the on-nuclei point charge model, Rn is overestimated, leading to underestimated higher-rank-term potentials and vice versa. In our model, the drawback is improved, since Rn is reduced by the charge displacement. This is in agreement with the previous research.31
With the expression of the potential energy (eqn (8)), one can plot the potential surface in terms of the polar angle θ and azimuth angle φ of the quantized axis. The direction corresponding to the minimum potential energy is supposed to be the quantized axis of the rare-earth ion.
Results and discussion§
Oblate Tb3+ ions
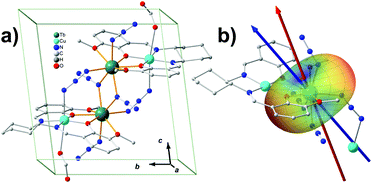
The prediction of magnetic easy axis for terbium ions was not included in MAGELLAN. In the present work, we first apply our model to a tetranuclear SMM containing terbium ions (Fig. 3a).32 The target molecule [CuTb]2 is a chiral molecule crystalized in the P1 space group with only one cluster in the unit cell, which is very similar to a previously reported compound.33 The two azide-bridged [CuTb] units are related to each other by a pseudo-inversion center. The molecule is characterized by strong Ising-type anisotropic behaviour and magnetic hysteresis is present up to 4.0 K. Since the Cu2+ are normally considered to be isotropic, it is reasonable to infer that the two nearly identical Tb3+ ions dominate the overall magnetic-anisotropy behaviour. Taking advantage of the pseudo-inversion center, the colinearity of the easy axes from the two Tb3+ ensures that the magnetization principal axes may be determined from angular-dependence magnetometry on single-crystal samples.34 The single-crystal measurement provides that the effective g value of Tb3+ along easy axis is 18.3. This deviation from the 7F6-multiplet theoretical Ising-limit value of 18 is probably because of the weak ferromagnetic coupling effect between the Tb3+ ions. Ab initio calculations are performed to characterize the magnetic anisotropy of the Tb3+ center as well. The two nearly degenerate ground states, with a splitting of 10−3 cm−1, are very well isolated from the first excited state (200 cm−1 energy gap). We calculated the ground-state effective g value to be 17.9. The calculated easy axis and the experimental one make an angle of 12.6°. Both the experiment and the ab initio calculation show that the ground state of the Tb3+ is dominated by the Ising limit MJ = ±6, and the ground states are a pseudo doublet.The model prediction of the quantized axis for Tb3+ was performed with considering all the atoms behaving non-zero charges, based on the valence-bond resonant structure analysis, which assumes the side and center nitrogen atoms in azide contribute −1 and +1 charges, respectively, and the copper and terbium ions +2 and +3, respectively. The charges of the atoms directly bonding to the Tb3+ are displaced from the corresponding nuclei position to the Tb3+ as described previously, while those which do not interact with Tb3+ directly are considered to be on the nuclei for simplicity (calculation details are listed in Table S2.1‡). The result shows that the predicted quantized axis of Tb3+ in the MJ = ±6 state deviates from the experimental and ab initio easy axis by 18.5° and 6.6°, respectively. The deviations can be larger (22.2° and 10.6° to experimental and ab initio ones, respectively), however, once the charge displacements are not considered. This illustrates that the displacement of the charges indeed improves the prediction accuracy. The electron-cloud shape of Tb3+ in MJ = ±6 is typical oblate, indicating that the negative charges lying along the quantized axis can efficiently stabilize the Ising-limit state. In this case, the potential energy near the azide N and phenolic O is relatively low (see the blue areas in Fig. 3b). The reason is that the contributed negative charges from these atoms are more than the ones from methoxy oxygen atoms, and the displacements of the negative charges forward to the Tb3+ lower the potential energy further.
Oblate Dy3+ ions
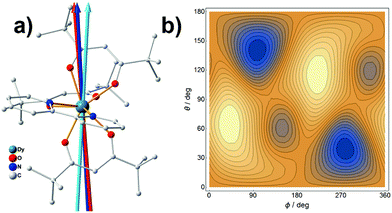
The application of the electrostatic method on Dy3+ easy-axis prediction has been detailedly discussed in previous publications.17,35 In this paper, we would like to address the role of the charge displacement. The Dy/β-diketonate system is generally a well-defined mononuclear SMMs with a dominated |±15/2〉 ground state.36 We have recently synthesized a mononuclear complex,37 as shown in Fig. 4a, crystallized in a P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) space group, making it possible to determine the magnetic easy axis. The experimental easy axis was found to lie in the plane made by the two trans-side β-diketonate ligands, consistent with a previous finding.38 By employing each coordinating oxygen atom with a negative charge of −1/3 according to the previous discussion, we predicted the quantized axes with and without charge displacement will deviate from the experimental easy axis by 3.1° and 7.8°, respectively (calculation details are listed in Table S3.1‡). This result is very similar to the Tb3+ case, which has demonstrated the importance of charge displacement.
space group, making it possible to determine the magnetic easy axis. The experimental easy axis was found to lie in the plane made by the two trans-side β-diketonate ligands, consistent with a previous finding.38 By employing each coordinating oxygen atom with a negative charge of −1/3 according to the previous discussion, we predicted the quantized axes with and without charge displacement will deviate from the experimental easy axis by 3.1° and 7.8°, respectively (calculation details are listed in Table S3.1‡). This result is very similar to the Tb3+ case, which has demonstrated the importance of charge displacement.
We also carried out SIMPRE analysis on the system, while offering a relatively large deviation of 9.2° from the experimental one. This is probably because SIMPRE is a semi-empirical approach based on a single-ion CFH. The possible interaction, however, may contribute to the magnetic data, in which the fitted parameters could deviate from the real results. Nevertheless, we adapt the parameters obtained from SIMPRE analysis into the electrostatic model with Dr = 1.30 Å, Zi = −0.025 for N and Dr = 0.57 Å, Zi = −0.677 for O, while an angle of 5.1° still exists between the REC and the electrostatic model with displaced charges. This is entirely due to the pure-ground-state assumption in the present model, while the SIMPRE calculation provides a ground-state wavefunction composed by 86% |±15/2〉 and 13% |±11/2〉. As a qualitative approach, the electrostatic model is not designed to provide such detailed information.
Prolate Er3+ ions
The Ising-limit 4f-shell of Er3+ is of prolate type, unlike the previous two cases. The negative charges on the equator plane are able to stabilize the easy-axial anisotropy. According to this strategy, Tang's group has synthesized a series of Er-based mononuclear SMMs, with three negatively charged N atoms in the equator plane and two neutral O atoms along the axis.6 Within the electrostatic model, both the displaced and on-nuclei negative charges can stabilize the |±15/2〉 state as along the geometry pseudo-C3 axis very well, in consistent with the experimental result (see Table S4.1 and Fig. S4.1‡).The power of our new model can be demonstrated by the complexes containing π-coordination bonds. We have reported an Er3+-based mixed sandwiched mononuclear SMM (Fig. 5a). Theoretical and experimental investigations have revealed that the ground state of the Er3+ is |±15/2〉, and the magnetic easy axis is along the normal of the aromatic plane.5,13,39,40 The on-nuclei negative charges, however, are not able to stabilize the quantized axis of the Ising-limit state along the pseudo-rotation axis (Fig. 5c). The states with lowest energy along the axis are the ones with the quantum number |MJ| < 7/2, indicating an easy-plane anisotropy. Considering the displacements of the negative charges from the 13 coordinating carbon atoms by the average radius of 2p orbital along the aromatic plane (Fig. 5a and Table S5.1‡), the quantized axis of |±15/2〉 is stabilized along the symmetric axis with a deviation of 8°, which is comparable to the included angle of the two unparalleled aromatic planes (Fig. 5b). It is remarkable that this charge displacement plays such an important role in stabilizing the |±15/2〉 state as the ground state, which describes actually the nature of the π-coordination systems. The SIMPRE research reveals a similar result, claiming that the REC model is very poor to reproduce the magnetic-susceptibility data, but only the LPEC is able to conclude similar results with the single-crystal data and the Ising-limit ground state.41
Comments on the model
Before moving to the conclusion, there are a few comments on the present model. First and most importantly, this electrostatic model is basically a classical approach, where the fundamental degrees of freedom are the polar angle θ and azimuth angle φ of the quantized axis (see eqn (7) and (8)). In contrast, eqn (5) in terms of quantum mechanics, requires a Hamiltonian matrix, which is generally complicated. This is why the present method is much less expensive than the quantum-chemistry approach. For a ground state which is dominated by a pure state (e.g., SMM behaviour molecules), one is able to provide a well-defined electron-density cloud according to eqn (1) and (2). For a mixed ground state that exists in low symmetry, however, the asphericity of electron clouds generally has a non-trivial expression. Accordingly, the electrostatic model may become complicated.Secondly, the chemical neutral atoms are assumed not to contribute to the electrostatic potential, which is not exactly true. In the molecular-orbital picture, the electrons are shared by all the atoms in the molecule. Effective charges, though possibly small, can be found around neutral atoms. This is supported by both ab initio calculations and high-resolution X-ray diffraction. Therefore, neglecting the neutral coordination atoms could lead to some unrealistic results, especially when such neglecting alters the symmetry of the system. One may overcome this problem by taking the charges from an ab initio or semi-empirical approach. It is, however, necessary to note that the charges taken from ab initio calculations are not supposed to be displaced, as suggested in this work, since those charges are calculated to be net charges on the nucleic positions.
Lastly, the locations of the charges are assumed to be on the atomic orbital, and the average value of the atomic orbital is calculated with the effective nuclear charge, which is just a phenomenological value for a neutral single atom and varies with the interactions within the ligand and with the metal ions. The magnitude of the displacement can thus deviate from what we report here. Hypothetically, the effective negative charge is delocalized on the resonance hybrid structures, while the atomic electronegativities can be different from each other. Accordingly, the negative charges on the hybrid structures are not necessarily distributed uniformly.
Even though the eigenstates beyond the Ising limit are not discussed herein, the orientation of the quantized axis for pure states can also be analysed in the same way, though the model is not applicable to mixed states.
Conclusions
Based on the electrostatic model, the qualitative method of investigating magnetic anisotropy can only provide limited information on the system. Unlike CONDON, SIMPRE, or more expensive ab initio calculations, the present method is not able to tell the wavefunction and the crystal-field splitting. It also fails to predict the quantized axis orientation of heavily mixed states. Nevertheless, one of its remarkable advantages compared to other approaches is its high efficiency. With the available molecular structure, one can, on a personal computer, rapidly interpret the quantized axis orientation of a pure state within a few seconds. Moreover, the electrostatic model can provide an intuitive picture for the roles that each coordination atom plays in the complex. Manipulating the magnitudes or the positions of the effective negative charges, one can investigate their effects on the potential energy surface and thus the quantized axis to gain clues to their effects on the magnetic anisotropy.Acknowledgements
J.S.-D. and Q.S.-X. were supported by the Alexander von Humboldt Stiftung in the postdoc research fellow actions. We thank the AvH offering us the freedom in doing our research, the possibility to know each other and to work together. We appreciate the helpful discussions with M.-Y. Tsang from Princeton University.Notes and references
- D. N. Woodruff, R. E. P. Winpenny and R. A. Layfield, Chem. Rev., 2013, 113, 5110–5148 CrossRef CAS PubMed.
- N. Ishikawa, M. Sugita, T. Ishikawa, S. Koshihara and Y. Kaizu, J. Am. Chem. Soc., 2003, 125, 8694–8695 CrossRef CAS PubMed.
- M. A. AlDamen, J. M. Clemente-Juan, E. Coronado, C. Marti-Gastaldo and A. Gaita-Arino, J. Am. Chem. Soc., 2008, 130, 8874–8875 CrossRef CAS PubMed.
- S.-D. Jiang, B.-W. Wang, G. Su, Z.-M. Wang and S. Gao, Angew. Chem., Int. Ed., 2010, 49, 7448–7451 CrossRef CAS PubMed.
- S.-D. Jiang, B.-W. Wang, H.-L. Sun, Z.-M. Wang and S. Gao, J. Am. Chem. Soc., 2011, 133, 4730–4733 CrossRef CAS PubMed.
- P. Zhang, L. Zhang, C. Wang, S. F. Xue, S. Y. Lin and J. K. Tang, J. Am. Chem. Soc., 2014, 136, 4484–4487 CrossRef CAS PubMed.
- L. Sorace, C. Benelli and D. Gatteschi, Chem. Soc. Rev., 2011, 40, 3092–3104 RSC.
- G. Cucinotta, M. Perfetti, J. Luzon, M. Etienne, P. E. Car, A. Caneschi, G. Calvez, K. Bernot and R. Sessoli, Angew. Chem., Int. Ed., 2012, 51, 1606–1610 CrossRef CAS PubMed.
- H. Bethe, Ann. Phys., 1929, 3, 133–208 CrossRef CAS PubMed.
- K. W. H. Stevens, Proc. R. Soc. London, Ser. A, 1952, 65, 209–215 CrossRef.
- H. Schilder and H. Lueken, J. Magn. Magn. Mater., 2004, 281, 17–26 CrossRef CAS PubMed.
- J. van Leusen, M. Speldrich, H. Schilder and P. Kögerler, Coord. Chem. Rev., 2015, 289–290, 137–148 CrossRef CAS PubMed.
- M. Perfetti, G. Cucinotta, M. E. Boulon, F. El Hallak, S. Gao and R. Sessoli, Chem. – Eur. J., 2014, 20, 14051–14056 CrossRef CAS PubMed.
- L. F. Chibotaru and L. Ungur, J. Chem. Phys., 2012, 137, 064112 CrossRef CAS PubMed.
- J. J. Baldovi, J. J. Borras-Almenar, J. M. Clemente-Juan, E. Coronado and A. Gaita-Arino, Dalton Trans., 2012, 41, 13705–13710 RSC.
- J. J. Baldovi, S. Cardona-Serra, J. M. Clemente-Juan, E. Coronado, A. Gaita-Arino and A. Palii, J. Comput. Chem., 2013, 34, 1961–1967 CrossRef CAS PubMed.
- N. F. Chilton, D. Collison, E. J. L. McInnes, R. E. P. Winpenny and A. Soncini, Nat. Commun., 2013, 4, 2551 Search PubMed.
- C. A. Morrison, Lectures on Crystal Field Theory, Tech. Rep. HDL-SR-82-2, Harry Diamonds Laboratory, 1982.
- O. L. Malta, Chem. Phys. Lett., 1982, 87, 27–29 CrossRef CAS.
- O. L. Malta, Chem. Phys. Lett., 1982, 88, 353–356 CrossRef CAS.
- L. Maron and O. Eisenstein, J. Phys. Chem. A, 2000, 104, 7140–7143 CrossRef CAS.
- R. Skomski, in Simple Models of Magnetism, Oxford University Press, New York, 2008, pp. 91–95 Search PubMed.
- J. D. Rinehart and J. R. Long, Chem. Sci., 2011, 2, 2078–2085 RSC.
- J. Sievers, Z. Phys. B: Condens. Matter, 1982, 45, 289–296 CrossRef CAS.
- J. C. Slater, Phys. Rev., 1930, 36, 57–64 CrossRef CAS.
- E. Clementi and D. L. Raimondi, J. Chem. Phys., 1963, 38, 2686 CrossRef CAS PubMed.
- E. Clementi, D. L. Raimondi and W. p. Reinhard, J. Chem. Phys., 1967, 47, 1300 CrossRef CAS PubMed.
- J. S. Griffith, The Theory of Transition-metal Ions, Cambridge University Press, London, New York, 1961, pp. 199–202 Search PubMed.
- A. J. Freeman and R. E. Watson, Phys. Rev., 1962, 127, 2058–2075 CrossRef CAS.
- S. Edvardsson and M. Klintenberg, J. Alloys Compd., 1998, 275, 230–233 CrossRef.
- P. Porcher, M. C. Dos Santos and O. Malta, Phys. Chem. Chem. Phys., 1999, 1, 397–405 RSC.
- X.-C. Huang, V. Vieru, L. F. Chibotaru, W. Wernsdorfer, S.-D. Jiang and X.-Y. Wang, Chem. Commun., 2015 10.1039/C5CC03089G.
- X. C. Huang, C. Zhou, H. Y. Wei and X. Y. Wang, Inorg. Chem., 2013, 52, 7314–7316 CrossRef CAS PubMed.
- S.-D. Jiang, B.-W. Wang and S. Gao, Advances in Lanthanide Single-Ion Magnets, in Molecular Nanomagnets and Related Phenomena, in Series: Structure and Bonding, ed. S. Gao, Springer, Berlin Heidelberg, 2014, DOI:10.1007/430_2014_153.
- Q. Chen, Y. S. Meng, Y. Q. Zhang, S. D. Jiang, H. L. Sun and S. Gao, Chem. Commun., 2014, 50, 10434–10437 RSC.
- P. Zhang, Y. N. Guo and J. K. Tang, Coord. Chem. Rev., 2013, 257, 1728–1763 CrossRef CAS PubMed.
- K. Qian, J. J. Baldovi, S.-D. Jiang, A. Gaita-Arino, Y.-Q. Zhang, J. Overgaard, B.-W. Wang, E. Coronado and S. Gao, Chem. Sci. 10.1039/C5SC01245G.
- T. T. da Cunha, J. Jung, M. E. Boulon, G. Campo, F. Pointillart, C. L. M. Pereira, B. Le Guennic, O. Cador, K. Bernot, F. Pineider, S. Golhen and L. Ouahab, J. Am. Chem. Soc., 2013, 135, 16332–16335 CrossRef CAS PubMed.
- S.-D. Jiang, S.-S. Liu, L.-N. Zhou, B.-W. Wang, Z.-M. Wang and S. Gao, Inorg. Chem., 2012, 51, 3079–3087 CrossRef CAS PubMed.
- M. E. Boulon, G. Cucinotta, S. S. Liu, S. D. Jiang, L. Ungur, L. F. Chibotaru, S. Gao and R. Sessoli, Chem. – Eur. J., 2013, 19, 13726–13731 CrossRef CAS PubMed.
- J. J. Baldovi, J. M. Clemente-Juan, E. Coronado and A. Gaita-Arino, Inorg. Chem., 2014, 53, 11323–11327 CrossRef CAS PubMed.
Footnotes |
| † Dedicated to Prof. Dr Guang-Xian Xu, Father of China Rare Earth. |
| ‡ Electronic supplementary information (ESI) available. See DOI: 10.1039/c5qi00052a |
| § The electrostatic calculations with and without the charge displacement were carried out on a Wolfram Mathematica code, which is available from the authors on demand. |
| This journal is © the Partner Organisations 2015 |