A theoretical prediction on CN6O: structure, stability and performance†
Tao
Yu
ab and
Bo
Wu
*a
aMultiscale Computational Materials Facility, School of Materials Science and Engineering, Fuzhou University, Fuzhou 350100, P. R. China. E-mail: wubo@fzu.edu.cn; Tel: +86-591-22866532
bComputer-Aided Energetic Materials Design Group, Xi'an Modern Chemistry Research Institute, Xi'an 710065, P. R. China
First published on 1st September 2015
Abstract
The potential energy surfaces of CN6O isomers were calculated at the B3LYP/aug-cc-pVDZ level and the key decomposition pathways were calculated at the G3B3 level. The optimum pathway for the decomposition of carbonyl diazide to OCN4 and N2 has a barrier of about 30 kcal mol−1. Except for carbonyl diazide, no isomer of CN6O crosses a higher decomposition barrier than 20 kcal mol−1. The specific impulse of carbonyl diazide is close to those of RDX (cyclotrimethylene trinitramine), HMX (cyclotetramethylene tetranitramine) and CL-20 (hexanitrohexaazaisowurtzitane), and the specific impulses of many other CN6O isomers are greater than that of FTDO ([1,2,5]oxadizolo[3,4-4][1,2,3,4]tetrazine-4,6-di-N-dioxide). The CN6O system has a higher combustion temperature than RDX, HMX, CL-20 and FTDO at comparable specific impulses. The detonation velocity and pressure of most of CN6O isomers are lower than that of CL-20.
I. Introduction
Geminal diazides are much more powerful than monoazides and vicinal azides. They are extremely sensitive, explosive, and dangerous either as byproducts or pure substances.1 The chemical community is interested in these marginally stable compounds. Carbonyl diazide with a sum formula of CN6O was synthesized in situ using carbonyl dihydrazide, hydrogen chloride, and sodium nitrite in the 1920s.2,3 Banert et al. discovered carbonyl diazide as the hydrolysis product of tetraazidomethane spectroscopically in 2007.4 Zeng et al. synthesized carbonyl diazide via the nucleophilic substitution reaction between chlorofluorocarbonyl and sodium azide, the pure compound was firstly isolated and the crystal structure was obtained in 2010.5 Nolan et al. improved the synthetic process using less toxic triphosgene instead of chlorofluorocarbonyl in 2012.6 The specific energy of carbonyl diazide, decomposition into carbon monoxide and dinitrogen, does not come up to expectation. Compared with the general energetic compounds such as TNT (trinitrotoluene), RDX (cyclotrimethylene trinitramine), and HMX (cyclotetramethylene tetranitramine), there is not much difference in the specific energy of carbonyl diazide.7 In addition, carbonyl diazide has a very common density (1.712 g cm−3)5 which is higher than TNT (1.654 g cm−3), but lower than RDX (1.816 g cm−3) and HMX (1.910 g cm−3).8However, carbonyl diazide possesses some unique characteristics as a rocket fuel or an explosive, e.g., high nitrogen content and zero oxygen balance for carbon monoxide. According to Tsiolkovsky9 and Kamlet–Jacobs10 equations, the acceleration of a single-stage rocket and the detonation velocity of an explosive depend on combustion energy and density. Unlike explosives, the manufacture of huge or multi-stage rockets may compensate for the loss in fuel density. Thus CN6O is probably more applicable as a rocket fuel than an explosive. The most challenging issue in space application is the energy content of CN6O, although some other obstacles may emerge in the future.
Most recently, we investigated the N7O+ cation which is the isoelectronic species of carbonyl diazide, computationally and experimentally, and found that the 1-oxo-N7O+ component is formed in the reaction of NF2O+ with excess HN3, and 4-oxo-N7O+ is much more stable than 1-oxo-N7O+.11 Both carbonyl diazide and the 4-oxo-N7O+ cation impart W-shape, geminal diazide structure, eight atoms and 56 electrons, but a hetero carbon atom is located at the center of the carbonyl diazide chain. As the energy of 1-oxo-N7O+ is higher than that of 4-oxo-N7O+ by 18.6 kcal mol−1, the atomic arrangements of CN6O should offer more possibilities due to the replacement of nitrogen by carbon.
In this paper, several typical CN6O isomers were explored by studying the potential surfaces around the electronic structures of different carbon positions in order to increase the energy content, see Fig. 1. The existence of novel CN6O isomers was demonstrated by geometry optimization, and the stability was estimated by decomposition (or isomerization) barrier. Then we figure out the dependence of structure, enthalpy of formation and stability, and evaluate the potential application of CN6O as a rocket fuel and an explosive. The feasibilities presented herein are expected to assist chemists and engineers in molecular design and synthesis.
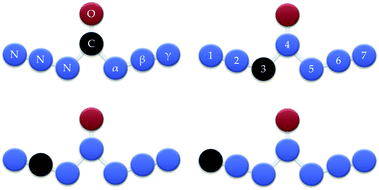 | ||
| Fig. 1 W-shaped CN6O. The oxygen atom fixed beyond the central position and carbon atom at different positions. | ||
II. Computational methods
The optimized geometries and harmonic frequencies for the reactants, intermediates, transition states and products were calculated using the B3LYP12,13 method and Dunning's aug-cc-pVDZ14 basis set. All reactants, intermediates and products have true minima on their potential energy surfaces without any imaginary frequencies, and the transition states have only one imaginary frequency. To check the connection of each transition state, intrinsic reaction coordinate (IRC)15,16 calculations were carried out. The correlative energies of key pathways were also calculated at the composite G3B3 level17,18 (a G3 variant using B3LYP geometries). The standard enthalpies of formation were calculated by the atomic method in which the target compounds are formed from their constituent atoms in the gaseous phase. The experimental atomic enthalpies were referred from NIST Chemistry Web book.19 The free energy activation barriers were derived by the differences between the transition states and reactants (or products) at 0 and 298.15 K, respectively. Numbering schemes for the compounds are shown in Fig. S1.† Unless otherwise specified, the barriers of 0 K were mainly used in this paper. The reliabilities of B3LYP and G3B3 methods have been verified in the N7O+ system.11 All quantum chemistry calculations were carried out using the Gaussian 09 program package.20The specific impulse and the chamber combustion temperature were estimated by NASA's CEA code.21,22 The equilibrium composition, heat, phase and velocity were supposed during expansion of combustion products from an infinite area combustor. The exhaust gases expand from chamber to exit. The chamber and exit pressures were set to 70 and 1 atm, respectively.
The detonation velocity and pressure were calculated by the Kamlet–Jacobs equation for CHNO explosives.10 For more detail on this equation, see ESI.†
III. Results and discussion
A. Potential energy surfaces around 4-carbonic-CN6O
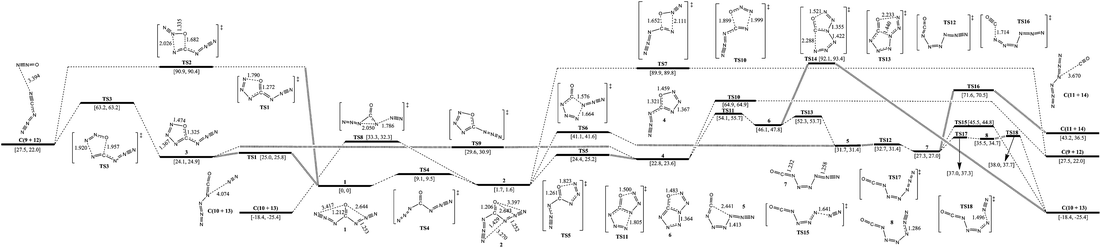
The isomerization and dissociation pathways of carbonyl diazide (1 and 2) are shown in Fig. 2. The oxygen is attached to the central carbon atom, and the two azido ligands point either in the same direction as the oxygen in 1 (syn–syn), or one in the same direction and the other one in the opposite direction in 2 (syn–anti). 1 lies 1.7 kcal mol−1 below 2, and isomerization barrier for conversion from 2 to 1 is 7.4 kcal mol−1. The computational results are consistent with the previous investigations.5–7,23,24 According to ref. 6, 7, 23 and 24, anti–anti carbonyl diazide is rather unstable and was not involved in further consideration.There are two pathways for the dissociation of 1 to cyanogen azide (NCN3, 9) and nitrous oxide (N2O, 12): one is stepwise, and the other one is concerted. The stepwise pathway involves an intermediate (3, z-5-azido-oxatriazole) with a five-membered ring. The first step is cyclization of 1 to 3 with a barrier of 25.0 kcal mol−1, and the second step is the dissociation of 3 to 9 and 12 with a barrier of 39.1 kcal mol−1. Intermediate 3 is located in a potential well and its isomerization barrier to 1 is only 0.9 kcal mol−1. 3 lies 1.3 kcal mol−1 above 4 (e-5-azido-oxatriazole), and the isomerization viaTS9 crosses a barrier of 5.5 kcal mol−1. It tends to isomerize rather than dissociate because the barrier of isomerization to 1 is lower than that of dissociation to 9 and 12 by 38.2 kcal mol−1. The concerted pathway involving only one transition state with a four-membered ring, TS2, has a very high barrier of 90.9 kcal mol−1. At the onset of synthesis, 1 can be formed by 9 and 12, and the pathway viaTS3 crosses a barrier of 35.7 kcal mol−1.
For the dissociation of 2 to 9 and 12, there are also two similar pathways. The concerted pathway involving TS7 crosses a barrier of 88.2 kcal mol−1. The stepwise pathway involving an intermediate (4) crosses a barrier of 22.7 kcal mol−1 at the first step and 42.1 kcal mol−1 at the second step. 4 tends to isomerize to 2 with a barrier of 1.6 kcal mol−1. There are other possible pathways for the decomposition of 2 to OCN4 (10) and N6 (11). 2 decomposes to 10 with evolution of N2 (13) viaTS8. It undergoes breakage of the α-N–β-N bond on one side and an azide group shifts from carbonyl to α-N on the other side with a barrier of 31.6 kcal mol−1. The isomerization of 2 to 5 involving attachment of α-N of an azide group to γ-N of the other azide group viaTS6 crosses a barrier of 39.4 kcal mol−1. 5 transfers to 7 (z-1-azido-2-isocyanatodiazene) with a barrier of 1.0 kcal mol−1. The dissociation of 7 can proceed along three different pathways: (1) dissociation to 10 and 13viaTS15 crossing a barrier of 18.2 kcal mol−1; transformation to 8 with a barrier of 9.7 kcal mol−1 and dissociation of 8 to 10 and 13 with a barrier of 2.5 kcal mol−1; (2) dissociation to 11 (N6) and 14 (CO) viaTS16 crossing a barrier of 44.3 kcal mol−1 and (3) 2 cyclizes to 4, then 4 isomerizes to 6 (tetrazolo[1,5-d][1,2,3,4]oxatriazole) viaTS11 with a barrier of 31.3 kcal mol−1, but the total barrier from 2 to TS11 is 52.4 kcal mol−1. Accordingly, it is not an optimum pathway for isomerization of 1 or 2 to 6. The dissociation of 6 to 10 and 13viaTS14 crosses a barrier of 46.0 kcal mol−1. 6 can also isomerize to 5viaTS13 crossing a barrier of 6.2 kcal mol−1, and 5 decomposes to 10 or 11 ultimately.
Although 1 is a thermodynamically dominant isomer, its decomposition goes through 2, and the optimum pathway of decomposition is 1 → TS4 → 2 → TS8 → C(10+13) with a maximum barrier of 31.6 kcal mol−1 (from 2 to TS8). The pathway viaTS8 is similar to our previous report on the self-dissociation of N7O+, and 4-oxo-N7O+ dissociates to N5O+ and N2 with a barrier of about 20 kcal mol−1. The mechanism also supports the matrix isolation of OCN4 by decomposition of carbonyl diazide experimentally.25
B. Potential energy surfaces around 3-carbonic-CN6O
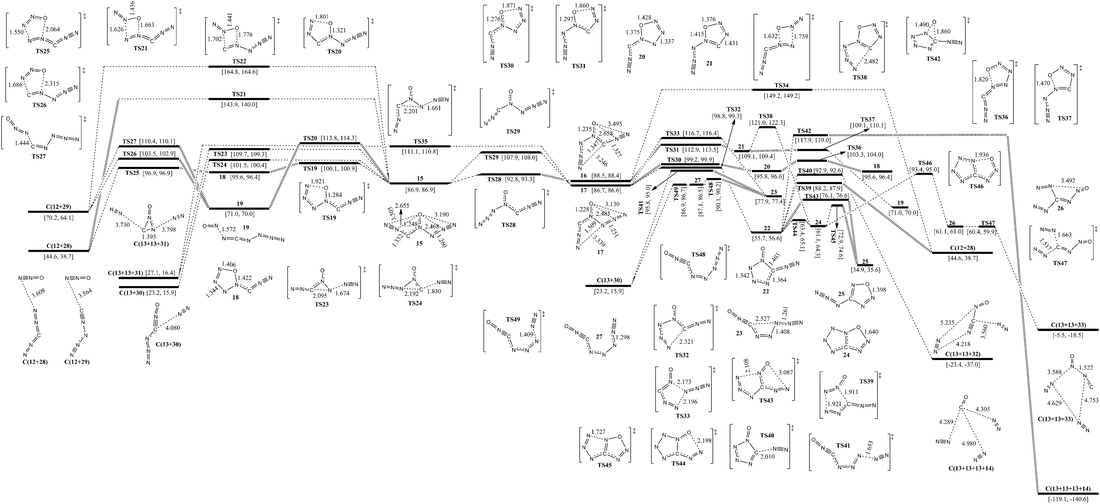
The isomerization and dissociation pathways of 3-carbonic-CN6O (15, 16 and 17) are shown in Fig. 3. 15, 16 and 17 are the three possible 3-carbonic isomers, i.e., oxygen is attached to the central nitrogen atom, and both 3-carbonic and azido ligands point in the same direction as oxygen (15), 3-carbonic in the same direction and azido in the opposite direction (16), or azido in the same direction and 3-carbonic in the opposite direction (17). The isomers 15, 16 and 17 lie 86.9, 88.5 and 86.7 kcal mol−1 above 1, respectively. The isomerization barriers for conversion of 15 to 16 and 15 to 17 are 21.0 and 5.9 kcal mol−1, respectively.Except for the pathways to 16 and 17, the dissociation and isomerization of 15 can proceed along six different pathways: (1) a stepwise pathway to N2O (12) and N2CN2 (28) involving an intermediate (18) with a five-membered ring crossing a limiting barrier (from 15 to TS19) of 13.2 kcal mol−1; (2) a pathway to 19 involving the TS20 transition state with a five-membered ring and a barrier of 26.9 kcal mol−1; (3) the formation of a new N–O bond between the 6-N and O viaTS21 with a four-membered ring, producing 12 and 28, and a barrier of 57.0 kcal mol−1; (4) the formation of a new N–O bond between the 2-N and O viaTS22 with a four-membered ring, producing N2O (12) and CNN3 (isocyanogen azide, 29) and a barrier of 77.9 kcal mol−1; (5) a pathway to 13 and 31 going through a transition state (TS23) involving the breakage of a 5-N–6-N bond and a 3-C approaching 5-N with a decomposition barrier of 22.8 kcal mol−1; (6) a pathway to 13 and 30 going through a transition state (TS24) involving the breakage of a 2-N–3-C bond and a 5-N approaching 3-C with a decomposition barrier of 14.6 kcal mol−1. The optimum pathway of dissociation for 15 is 15 → TS19 → 18 → TS25 → C(12+28) with a maximum barrier of 13.2 kcal mol−1 (from 15 to TS19).
Except for the pathways to 15 and 17, there are three pathways for the dissociation and isomerization of 16: (1) a pathway to 19 involving an intermediate (21) with a five-membered ring crossing a limiting barrier (from 16 to TS31) of 24.2 kcal mol−1; (2) a pathway to 24 involving an intermediate (21), and a higher barrier viaTS38 than viaTS37 by 11.9 kcal mol−1; (3) the formation of a new N–O bond between the 6-N and O viaTS34 with a four-membered ring, producing 12 and 28, and a barrier of 60.7 kcal mol−1. Because the direct dissociation pathway of 16 crosses a higher barrier than that of 15, the optimum pathway of dissociation for 16 is 16 → TS28 → 15 → TS19 → 18 → TS25 → C(12+28).
Except for the pathways to 15 and 16, the dissociation and isomerization of 17 can proceed along four pathways: (1) an isomerization pathway to 18 involving an intermediate (20) with a five-membered ring crossing a limiting barrier (from 17 to TS30) of 12.5 kcal mol−1; (2) an isomerization pathway to 23 involving the TS33 transition state with a five-membered ring, a barrier of 30.0 kcal mol−1, and the optimal dissociation of 23 to 13 and 30 crossing a limiting barrier of 12.2 kcal mol−1 (from 23 to TS48); (3) a pathway to 13 and 31 undergoing a transition state (TS35) involving the breakage of a 5-N–6-N bond and a 3-C approaching 5-N with a decomposition barrier of 24.4 kcal mol−1; (4) an isomerization pathway to 22 involving attachment of 1-N to 3-C viaTS32, and a barrier of 12.1 kcal mol−1. There are six possible pathways for the dissociation and isomerization of 22: (1) it decomposes to 28 with evolution of 13viaTS39 with a barrier of 32.5 kcal mol−1; (2) it decomposes to ONCN (32) with evolution of 13viaTS40 with a barrier of 37.2 kcal mol−1; (3) the O shifts from N to C viaTS42 with the evolution of 13 and 14 crossing a barrier of 62.2 kcal mol−1; (4) the multi-step pathway of decomposition to 13 and 33 goes through two intermediates, 24 (tetrazolo[5,1-d][1,2,3,5]oxatriazole) and 26, with a limiting barrier (from 24 to TS46) of 32.3 kcal mol−1; (5) the concerted pathway of isomerization to z-4-azido-oxatriazole (25) viaTS43 crosses a barrier of 20.4 kcal mol−1; (6) the stepwise pathway of isomerization to 25 goes through an intermediate (24) with a bicyclic five-membered ring crossing a limiting barrier (from 24 to TS45) of 11.6 kcal mol−1. For more details of reaction pathways of 4-azido-oxatriazole, see section E. The optimum pathway of dissociation of 17 is 17 → TS30 → 20 → TS36 → 18 → TS25 → C(12+28) with a maximum barrier of 12.5 kcal mol−1 (from 17 to TS30).
C. Potential energy surfaces around 2-carbonic-CN6O
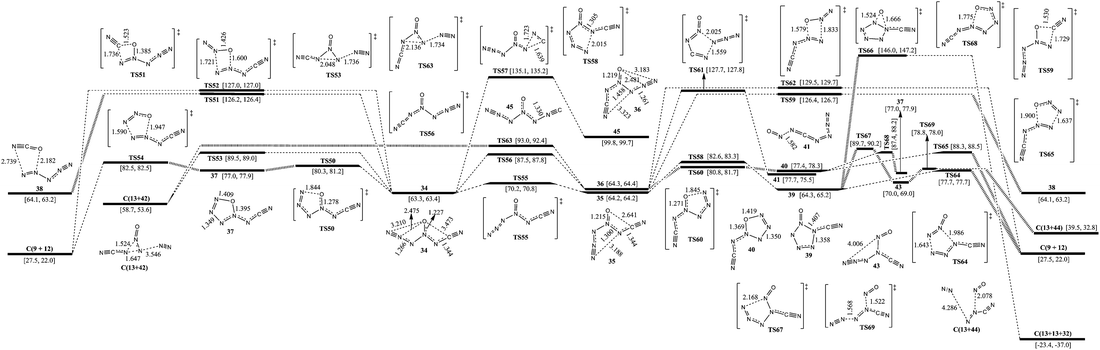
The corresponding pathways of 2-carbonic-CN6O are shown in Fig. 4. According to the directions of ligands of 4-N as O, there are three 3-carbonic isomers (34, 35, and 36). 34 lies 0.9 and 1.0 kcal mol−1 below 35 and 36, respectively. The barriers for conversion of 34 to 35 and 34 to 36 are 6.9 and 24.2 kcal mol−1, respectively.Except for the pathways to 35 and 36, the dissociation and isomerization of 34 can proceed along five different pathways: (1) a stepwise pathway to 9 and 12 involving an intermediate (37) with a five-membered ring crossing a limiting barrier (from 34 to TS50) of 17.0 kcal mol−1; (2) a pathway to 13 and 42 going through a transition state (TS53) involving the breakage of a 5-N–6-N bond and a 3-N approaching 5-N with a decomposition barrier of 26.2 kcal mol−1; (3) the formation of a new N–O bond between the 6-N and O viaTS52 with a four-membered ring, producing 9 and 12, and a barrier of 63.7 kcal mol−1; (4) the formation of a new N–O bond between the 2-C and O viaTS51 with a four-membered ring, producing 38 (N5+OCN−) and a barrier of 62.9 kcal mol−1; (5) a pathway to 45 (1-carbonic-CN6O) viaTS57 involving the breakage of 2-C–3-N and formation of a new 2-N–3-N bond with a barrier of 71.8 kcal mol−1. The optimum pathway of dissociation for 34 is 34 → TS50 → 37 → TS54 → C(9+12) with a maximum barrier of 17.0 kcal mol−1 (from 34 to TS50).
Except for the pathways to 34 and 36, the dissociation and isomerization of 35 have two pathways: (1) a pathway to 38 involving a transition state (TS59) with a four-membered ring crossing a barrier of 62.2 kcal mol−1; (2) an isomerization pathway to 39 involving attachment of 1-N to 5-N viaTS58 crossing a barrier of 18.4 kcal mol−1. There exist three possible pathways for the dissociation of 39: (1) it decomposes to 9 with evolution of 12viaTS64 with a barrier of 13.4 kcal mol−1; (2) the O shifts to N which links the cyanogen group viaTS66, and 39 dissociates to 13 and 32 crossing a barrier of 81.7 kcal mol−1; (3) a stepwise pathway to 13 and 44 involving an intermediate (43), the center N with three arms, and it crosses a limiting barrier (from 39 to TS67) of 25.4 kcal mol−1. The optimum pathway of dissociation for 35 is 35 → TS58 → 39 → TS64 → C(9+12) with a maximum barrier of 18.4 kcal mol−1 (from 35 to TS58).
Except for the pathways to 34 and 35, there are four dissociation and isomerization pathways for 36: (1) an isomerization pathway to 41 involving breakage of a 4-N–5-N bond and attachment of 1-N to 5-N viaTS57 crossing a barrier of 63.4 kcal mol−1; (2) a pathway to 9 with evolution of 12 involving a transition state (TS62) with a four-membered ring crossing a barrier of 65.2 kcal mol−1; (3) a pathway to 13 and 42 undergoing a transition state (TS63) involving the breakage of a 5-N–6-N bond and a 3-N approaching 5-N crossing a barrier of 28.7 kcal mol−1; (4) a stepwise pathway to 9 and 12 involving an intermediate (40) with a five-membered ring crossing a limiting barrier (from 36 to TS60) of 16.5 kcal mol−1 or transformation from 40 to 37viaTS68. The optimum pathway of dissociation for 36 is 36 → TS60 → 40 → TS65 → C(9+12) with a maximum barrier of 16.5 kcal mol−1 (from 36 to TS60).
D. Potential energy surfaces around 1-carbonic-CN6O
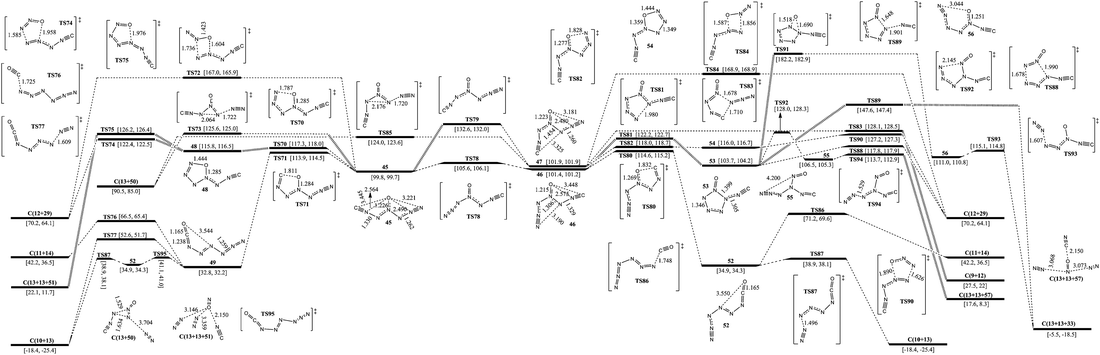
The isomerization and dissociation pathways of 1-carbonic-CN6O are shown in Fig. 5. According to the directions of ligands of 4-N as O, there are three 1-carbonic isomers (45, 46, and 47). 45 lies 1.6 and 2.1 kcal mol−1 below 46 and 47 respectively. The barriers for transformation of 45 to 46 and 45 to 47 are 5.8 and 32.8 kcal mol−1, respectively. It is difficult to twist the multi-bond of 3-N–4-N in 47. Whether forward or reverse, the isomerizations between cyanogen and isocyanogen, such as 34 and 45 in Fig. 4, cross ultra-high barriers exceeding 35 kcal mol−1 and these pathways were excluded for further consideration.Except for the pathways to 46 and 47, the dissociation and isomerization of 45 can proceed along four different pathways: (1) the stepwise pathway involving an intermediate (48) with a five-membered ring, decomposition of 48viaTS74 (to 12 and 29) or TS75 (to 13 and 51), and crossing a limiting barrier of 17.5 kcal mol−1 (from 45 to TS70); (2) the stepwise pathway involving an intermediate (49) with a linear chain, the isomerization viaTS71 with a barrier of 14.1 kcal mol−1, and decomposition of 49viaTS76 (to 11 and 14), TS77 (to 10 and 13) or 52 (to 10 and 13); (3) the formation of a new N–O bond between the 6-N and O viaTS72 with a four-membered ring, producing 12 and 29, and a barrier of 67.2 kcal mol−1; (4) a pathway to 13 and 50 going through a transition state (TS73) involving the breakage of a 5-N–6-N bond and a 3-N approaching 5-N with a decomposition barrier of 25.8 kcal mol−1. The optimum pathway of dissociation for 45 is 45 → TS71 → 49 → TS95 → 52 → TS87 → C(10+13) with a maximum barrier of 14.1 kcal mol−1 (from 45 to TS71). There is an pathway for isomerizing 49 (e) to 7 (z). As shown in Fig. S2,† an energy barrier of 47.5 kcal mol−1 needs to be crossed. N5+NCO− (38) is not stable, and its transformation to 49 crosses a barrier of not more than 1 kcal mol−1, also see Fig. S2.†
Except for the pathways to 45 and 47, there are two pathways for the dissociation and isomerization of 46: (1) the stepwise pathway involving an intermediate (52, e-1-azido-2-isocyanatodiazene) with a linear chain, the isomerization viaTS80 with a barrier of 13.2 kcal mol−1, and decomposition of 52viaTS86 (to 11 and 14) or TS87 (to 10 and 13); (2) an isomerization pathway to 53 involving attachment of 3-N to 7-N viaTS81, and a barrier of 20.8 kcal mol−1. There are four possible pathways for the dissociation and isomerization of 53: (1) it decomposes to 33 with evolution of 13viaTS88 with a barrier of 14.1 kcal mol−1; (2) it decomposes to 29 with evolution of 12viaTS89 with a barrier of 43.9 kcal mol−1; (3) the O shifts to N which links the isocyanogen group viaTS91 with the formation of 56 crossing a barrier of 78.5 kcal mol−1, and 56 dissociates to 13 and 33 with a barrier of 4.1 kcal mol−1; (4) a stepwise pathway to 13 and 57 involving an intermediate (55), the center N with three arms, and it crosses a limiting barrier (from 53 to TS92) of 24.3 kcal mol−1. The optimum pathway of dissociation for 46 is 46 → TS80 → 52 → TS87 → C(10+13) with a maximum barrier of 13.2 kcal mol−1 (from 46 to TS80).
Except for the pathways to 45 and 46, there are four pathways for the dissociation of 47: (1) a stepwise pathway to 12 and 29 involving an intermediate (54) with a five-membered ring crossing a limiting barrier (from 47 to TS82) of 16.1 kcal mol−1; (2) a decomposition pathway to 9 and 12 involving breakage of a 4-N–5-N bond and attachment of 1-C to 5-N viaTS83 crossing a barrier of 26.2 kcal mol−1; (3) a pathway to 29 with evolution of 12 involving a transition state (TS84) with a four-membered ring crossing a barrier of 67.0 kcal mol−1; (4) a pathway to 13 and 50 going through a transition state (TS85) involving the breakage of a 5-N–6-N bond and a 3-N approaching 5-N crossing a barrier of 22.1 kcal mol−1. The optimum pathway of dissociation for 47 is 47 → TS82 → 54 → TS90 → C(12+29) with a maximum barrier of 16.1 kcal mol−1 (from 47 to TS82).
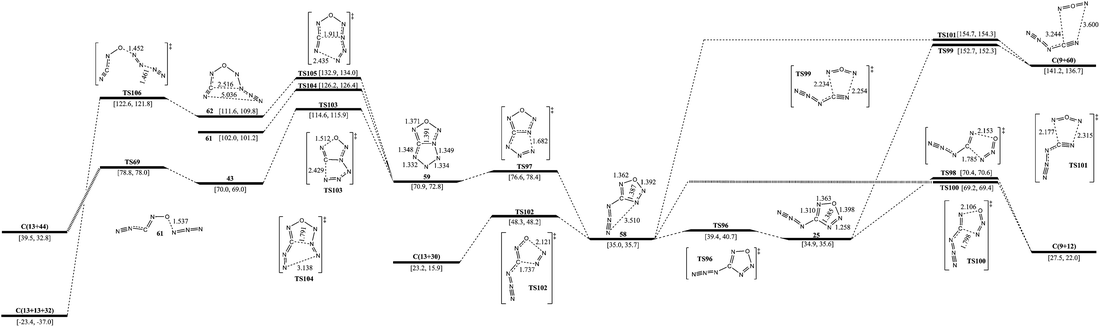
E. Potential energy surfaces around 4-azido-oxatriazole
The isomerization and dissociation pathways of 25 are shown in Fig. 3 and 6. The pathway of 25 to 22 has been discussed in section B already. 25 can produce 9 with evolution of 12 (N2O) or 60 (NON). The barrier of formation of 9 and 12 is 35.5 kcal mol−1, while the formation of 9 and 60 crosses a higher barrier of 117.8 kcal mol−1. The isomerization from 25 to 58 crosses a barrier of 4.5 kcal mol−1, and their energies are almost the same. 58 has two similar decomposition pathways viaTS100 and TS101, and the barriers are 34.2 and 119.7 kcal mol−1, respectively. Unlike 25, 58 can decompose to 13 and 30viaTS102 with a barrier of 13.3 kcal mol−1. Another pathway for isomerization of 58 is the formation of 59 with a bicyclic five-membered ring. The barrier for opening the ring is only 5.7 kcal mol−1. 59 can break the N–O and C–N bonds viaTS103 with a barrier of 43.7 kcal mol−1, and form a three arm isomer (43). 43 dissociates to 13 and 44 crossing a barrier of 8.8 kcal mol−1. The pathway from 59 to 61 with the breakage of the C–N and N–N bonds crosses a barrier of 55.3 kcal mol−1. Breakage of the C–N bond and the other N–N bonds form an intermediate (62) with a barrier of 62.0 kcal mol−1. 62 decomposes to 13 and 32viaTS106 crossing a barrier of 11.0 kcal mol−1. The optimum pathway of dissociation for 25 is 25 → TS96 → 58 → TS102 → C(13+30) with a maximum barrier of 13.3 kcal mol−1 (from 58 to TS102).F. Energy barrier, enthalpy of formation and performance
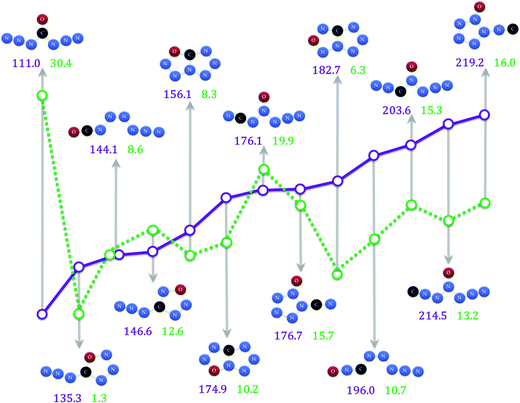
In this study, the potential energy surfaces of CN6O have been calculated intensively. Many isomers and conversion mechanisms were acquired. We can extract five noticeable kinds of CN6O isomers from the potential energy surfaces. (1) W-shaped CN6O (oxygen atom fixed beyond the 4-position), such as 1 (4-carbonic), 15 (3-carbonic), 34 (2-carbonic) and 45 (1-carbonic). The dissociation pathway of 1, undergoing evolution of N2 and shift of the azide group, crosses a barrier of 31.3 kcal mol−1 at the G3B3 level. The dissociations of 15, 34 and 45 go through the transition states with the five-membered rings, and the barriers at the G3B3 level are 14.5, 19.1 and 13.8 kcal mol−1, respectively. (2) Azido-oxatriazoles, such as 3 (5-) and 25 (4-). 3 isomerize to 1 with a very low barrier of 1.2 kcal mol−1 at the G3B3 level. 25 should transfer to its e-isomer (58), and the decomposition barrier from 58 to TS102 is 13.5 kcal mol−1 at the G3B3 level. If 25 can form a solid state with strong lattice interaction, the conversion to 58 will be avoided. The decomposition barrier should rise to about 35 kcal mol−1 (from 25 to TS98). The reaction between oxime groups is a probable pathway for the synthesis of 25. (3) Azido-diazenes, such as 7 and 23. The dissociations of 7 and 23 with evolution of dinitrogen cross the barriers of 7.9 (from 7 to TS17) and 10.3 (from 23 to TS48) kcal mol−1 at the G3B3 level, respectively. (4) Tetrazolo oxatriazoles, such as 6, 24, and 59. The barriers for opening the rings are 8.7, 10.1 and 6.4 kcal mol−1 at the G3B3 level, respectively. (5) Oxo-pentazoles, such as 39 and 53. The dissociations of 39 and 53 with evolution of N2O cross the barriers of 16.6 and 16.4 kcal mol−1 at the G3B3 level, respectively.The optimum conversion barriers and enthalpies of formation for aforementioned CN6O isomers are shown in Fig. 7. The detailed pathways for dissociations and their barriers at the B3LYP and G3B3 levels are presented in Table S1.† The detailed standard enthalpies of formation in the gaseous phase are presented in Table S2.† Compared with 111.4 (G2), 113.9 (G3) and 109.2 (G4) kcal mol−1,7 the enthalpy of formation of 1 is 115.7 kcal mol−1 at the B3LYP level, and 110.0 kcal mol−1 at the G3B3 level. 1 possesses the highest limiting barrier and lowest enthalpy of formation. Although the other isomers contain more enthalpies, they cannot reach the kinetic stability of 1. The frontier orbital energies of CN6O isomers provided in Table S3† show that 1 imparts the maximum gap between the LUMO (lowest unoccupied molecular orbital) and HOMO (highest occupied molecular orbital). It demonstrates the stability of 1 from another viewpoint. The result, shown in Fig. 7, is not a strong inverse correlation between the barrier and enthalpy. 53 possesses a very high enthalpy of formation (about 220 kcal mol−1), but not a lowest limiting barrier. Except for 1, the barrier of 34 is relatively high (about 20 kcal mol−1).
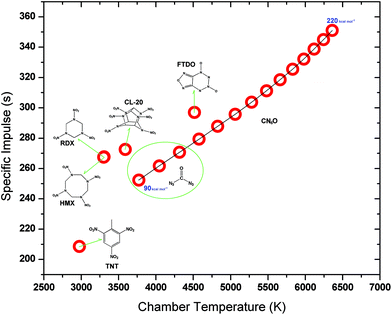
The relationship between enthalpy of formation and rocket performance for CN6O is presented in Fig. 8. More detailed data for rocket performances of CN6O is shown in Table S4.† The enthalpies of formation and rocket performances of comparative set, TNT, RDX, HMX, CL-20 (hexanitrohexaazaisowurtzitane) and FTDO ([1,2,5]oxadizolo[3,4-4][1,2,3,4]tetrazine-4,6-di-N-dioxide), are shown in Table S5.† With the increase of enthalpy of formation of CN6O, both specific impulse and combustion temperature tend to increase simultaneously. But the growth becomes slow in the high enthalpy area. If the condensed energy is taken into account, the specific impulse of carbonyl diazide is in the range of 252.3–270.7 s. It is close to those of RDX (267.7 s), HMX (267.5 s) and CL-20 (272.6 s), and much higher than that of TNT (208.6 s). When a CN6O compound has a 140 kcal mol−1 enthalpy of formation, its specific impulse will get to the level of FTDO (297.0 s), which keeps the record of theoretical specific impulse as a known CHNO compound.26 Our previous study on the FTDO indicated that its limiting barrier for decomposition is only 13 kcal mol−1 at the B3LYP/cc-pVDZ level.27 The enthalpies of formation of 23, 25 and 34 are at 190, 140 and 170 kcal mol−1 levels, respectively, and the corresponding specific impulses are 332.2, 295.8 and 318.5 s. If 53 is an existing compound, its specific impulse will amazingly reach the level of 350 s. The low chamber combustion temperature can enhance sustainability of working of a rocket engine, but the CN6O system has a higher combustion temperature than RDX, HMX, CL-20 and FTDO at the same levels of specific impulses.
To calculate the detonation performances of CN6O, the densities were deduced by molecular volumes inside a contour of 0.003 electrons Bohr−3 density and 73.6% space occupancy (the unit cell volume per molecule divided by isolated molecular volume for 1). As shown in Table S6,† the upper and lower limits are 1.817 and 1.644 g cm−3, respectively. The detonation performances of CN6O are presented in Fig. 9. The densities and detonation performances of the comparative set are shown in Table S7.† With the increase of enthalpy of formation and density, the detonation velocity and pressure of CN6O tend to increase. The detonation velocity of carbonyl diazide is greater than that of TNT (6997 m s−1) by about 1000 m s−1, but it is much less than those of RDX (8872 m s−1), HMX (9191 m s−1), CL-20 (9414 m s−1) and FTDO (9309 m s−1). Only if the enthalpy of formation exceeds 200 kcal mol−1, and the density reaches the upper limit, the detonation velocity and pressure of CN6O will be greater than CL-20. It can be easily understood by comparing FTDO with CL-20. Although the specific impulse of FTDO is superior to that of CL-20, the detonation velocity and pressure of FTDO are inferior to those of CL-20, because the detonation performances are sensitive to density (1.850 g cm−3 FTDO versus 1.970 g cm−3 CL-20). Compared with CL-20, CN6O isomers as explosives have little advantage.
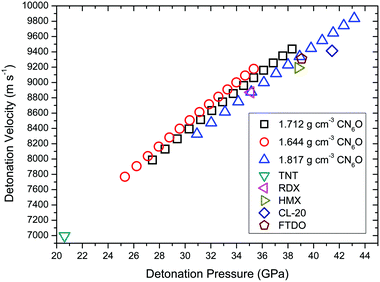 | ||
| Fig. 9 Detonation velocities for TNT, RDX, HMX, CL-20, FTDO and CN6O versus their detonation pressure. The enthalpies of formation of CN6O from 90 to 220 kcal mol−1 with an interval of 10 kcal mol−1. | ||
IV. Conclusions
The study on potential energy surfaces of ground state CN6O demonstrates that carbonyl diazide has the same dissociation mechanism as 4-oxo-N7O+, the predictive pathway supports the matrix isolation of OCN4, the dissociation barrier is about 30 kcal mol−1, and its isomers have more energy content but lower decomposition barriers. Except for carbonyl diazide, no isomer of CN6O has a higher barrier than 20 kcal mol−1, just as the linear CN6O isomers have low barriers as their isoelectronic 1-oxo-N7O+. The specific impulse of carbonyl diazide is near to those of RDX, HMX and CL-20. The W-shaped 2-carbonic-CN6O crosses a decomposition barrier of 19.1 kcal mol−1 at the G3B3 level, and its specific impulse is greater than that of carbonyl diazide by about 60 s. The dissociation barrier of 4-azido-oxatriazole is 13.5 kcal mol−1 at the G3B3 level which is significantly lower than that of carbonyl diazide but same as that of FTDO, and its specific impulse is comparable to FTDO. As a result, the isomers of carbonyl diazide can win the specific impulse but lose stability. It will be a great challenge for synthesis and storage. The explosives need long-term preservation and adaptation to various environments. The requirement for stability of rocket fuels, by contrast, is not so severe. The rocket engine can be loaded with fuel at the launch site, and the fuel can maintain stability with external conditions. Another obstacle is relatively high combustion temperature for structural materials of a rocket engine. The perspective for CN6O isomers as explosives is not bright, because they impart low density and instability. The polymeric (CN6O)n (n ≥ 2) may increase the density, and additives may partly improve the stability. We have revealed the nature of CN6O, and further experimental work will be required to identify the theoretical prediction.Acknowledgements
The work was partially supported by the National Natural Science Foundation of China (no. 51171046, 21303133 and 21403162).Notes and references
- K. O. Christe, R. Haiges, W. W. Wilson and J. A. Boatz, Inorg. Chem., 2010, 49, 1245 CrossRef CAS.
- W. Kesting, Ber. Dtsch. Chem. Ges B, 1924, 57, 1321 CrossRef PubMed.
- T. Curtius and A. Bertho, Ber. Dtsch. Chem. Ges B, 1926, 59, 565 CrossRef PubMed.
- K. Banert, Y.-H. Joo, T. Rüffer, B. Walfort and H. Lang, Angew. Chem., Int. Ed., 2007, 46, 1168 CrossRef CAS PubMed.
- X. Zeng, M. Gerken, H. Beckers and H. Willner, Inorg. Chem., 2010, 49, 9694 CrossRef CAS PubMed.
- A. M. Nolan, B. K. Amberger, B. J. Esselman, V. S. Thimmakondu, J. F. Stanton, R. C. Woods and R. J. McMahon, Inorg. Chem., 2012, 51, 9846 CrossRef CAS PubMed.
- D. W. Ball, Comput. Theor. Chem., 2011, 965, 176 CrossRef CAS.
- H. Shekhar, Cent. Eur. J. Energ. Mater., 2012, 9, 39 CAS.
- Wikipedia entry on Tsiolkovsky rocket equation.
- M. J. Kamlet and S. J. Jacobs, J. Chem. Phys., 1968, 48, 23 CrossRef CAS.
- T. Yu, Y.-Z. Liu, R. Haiges, K. O. Christe, W.-P. Lai and B. Wu, RSC Adv., 2014, 4, 28377 RSC.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648 CrossRef CAS PubMed.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785 CrossRef CAS.
- T. H. Dunning Jr., J. Chem. Phys., 1989, 90, 1007 CrossRef PubMed.
- C. Gonzalez and H. B. Schlegel, J. Chem. Phys., 1989, 90, 2154 CrossRef CAS PubMed.
- C. Gonzalez and H. B. Schlegel, J. Chem. Phys., 1991, 95, 5853 CrossRef CAS PubMed.
- A. G. Baboul, L. A. Curtiss, P. C. Redfern and K. Raghavachari, J. Chem. Phys., 1999, 110, 7650 CrossRef CAS PubMed.
- L. A. Curtiss, K. Raghavachari, P. C. Redfern, V. Rassolov and J. A. Pople, J. Chem. Phys., 1998, 109, 7764 CrossRef CAS PubMed.
- http://webbook.nist.gov/chemistry .
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision B. 01, Gaussian, Inc., Wallingford, CT, 2009 Search PubMed.
- S. Gordon and B. J. McBride, Computer program for calculation of complex chemical equilibrium compositions and applications. I. Analysis, NASA, 1994 Search PubMed.
- B. J. McBride and S. Gordon, Computer program for calculation of complex chemical equilibrium compositions and applications. II. User's manual and program description, NASA, 1996 Search PubMed.
- B. Napolion, J. D. Watts, M.-J. Huang, F. M. McFarland, E. E. McClendon, W. L. Walters and Q. L. Williams, Chem. Phys. Lett., 2013, 559, 18 CrossRef CAS PubMed.
- B. K. Amberger, B. J. Esselman, R. C. Woods and R. J. McMahon, J. Mol. Spectrosc., 2014, 295, 15 CrossRef CAS PubMed.
- X. Zeng, M. Gerken, H. Beckers and H. Willner, Angew. Chem., Int. Ed., 2011, 50, 482 CrossRef CAS PubMed.
- D. Lempert and A. Shastin, Triazines as a basis for new energetic compound creation, Lecture in Xi'an Modern Chemistry Research Institute, May 20th, 2014, Prof. Lempert's e-mail: lempert@icp.ac.ru.
- W.-P. Lai, P. Lian, T. Yu, J.-H. Bu, Y.-Z. Liu, W.-L. Zhu, J. Lv and Z.-X. Ge, J. Mol. Model, 2014, 20, 2343 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Compounds mapping list for their serial numbers, Kamlet–Jacobs equation, supplementary reaction pathways, barriers of limiting pathways for different isomers of CN6O, gas phase enthalpies of formation for different isomers of CN6O, frontier orbital energies for different isomers of CN6O, enthalpy of formation effect on specific impulse and combustion temperature for CN6O, calculated rocket performances of comparative set (TNT, RDX, HMX, CL-20 and FTDO), molecular volumes for different isomers of CN6O, and calculated detonation performances of comparative set. See DOI: 10.1039/c5qi00120j |
| This journal is © the Partner Organisations 2015 |