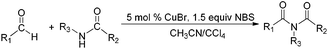Density functional study on the mechanism of direct N-acylation reaction of lactams with aldehydes catalyzed by Shvo's catalyst†
Qian
Liu
a,
Xi
Lu
*bc,
Xiaomin
Sun
d and
Xian
Zhao
*a
aState Key Laboratory of Crystal Materials, Shandong University, Jinan 250100, China. E-mail: zhaoxian@sdu.edu.cn
bDepartment of Chemical and Materials Engineering, University of Alberta, Edmonton, AB T6G 2V4, Canada. E-mail: xlu2@ualberta.ca
cPetroleum Exploration and Production Research Institute, Sinopec, Beijing 100083, People's Republic of China
dEnvironment Research Institute, Shandong University, Jinan, 250100, People's Republic of China
First published on 8th June 2015
Abstract
Density functional theory (DFT) was used to explore the mechanism of the direct N-acylation of lactams with aldehydes under the catalysis of Shvo's catalyst. The most kinetically and thermodynamically feasible mechanism was proposed in this study. The lactam–lactim tautomerism was firstly achieved by means of a concerted intermolecular hydrogen exchange between two molecules of 2-pyrrolidinone, 1. Then, the formed lactim 2 and an aldehyde reacted to yield a hemiaminal 3via a nucleophilic reaction and a hydrogen transfer. Finally, the product 5 was generated through a dehydrogenation of the hemiaminal 3, catalyzed by ruthenium complex 4. The total Gibbs energy barrier in the catalytic cycle of N-acylation is 23.9 kcal mol−1, and the generation of the hemiaminal 3 is the rate-determining step.
Introduction
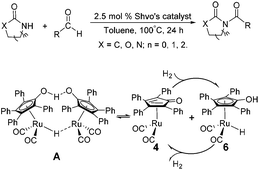
Due to their significant biological activity,1N-acylated lactams, oxazolidinones and imidazolidinones are widely applied in natural products and medication.2–6 Thus, an effective and economic method for the synthesis of these amide compounds is urgent and essential. As shown in previous reports, a classical method for the N-acylation reaction employs acyl chlorides or anhydrides with the aid of alkyl lithium reagents.7 Some facile approaches were subsequently developed, such as the synthesis of N-acylated oxazolidinones using acid fluorides and mild bases like iPr2NEt and NEt3 (Scheme 1),8 and the copper-catalyzed C–H activation of aldehydes with amides in the presence of N-bromosuccinimide (NBS) (Scheme 2).9Although these improved methods make the synthetic process more facile and convenient, the rigorous reaction conditions are difficult to achieve and the stoichiometric reagents are also expensive for bulk producing. By comparison, the reported transition-metal-catalyzed oxidative amidation of aldehydes with amines is a desired atom economical transformation,10–16 due to a much higher catalytic dehydrogenation efficiency. Recently, Zhang and Hong demonstrated a direct method for N-acylation of lactams, oxazolidinones, and imidazolidinones with aldehydes, catalyzed by Shvo's catalyst, without any stoichiometric reagent (Scheme 3),17–19 which also showed a great functional group tolerance for substrates. This enhancement is more “green” for the environment and more atom-economical, reducing synthesis costs. More recently, Lei et al. also successfully developed an iron-catalyzed coupling reaction between aldehydes and amides, which possibly involves a radical process (Scheme 4).20
 | ||
| Scheme 3 Direct N-acylation of lactams, oxazolidinones, and imidazolidinones with aldehydes is achieved under the catalysis of Shvo's catalyst A. | ||
 | ||
| Scheme 4 An oxidative C–H/N–H coupling of aldehydes with simple amides, catalyzed by an iron catalyst. | ||
However, to develop wider applications of the N-acylation reaction and an appreciable range of substrates, only depending on experiments is very difficult and expensive considering the synthesis time of the substrates and catalysts. Here, a deep and detailed study of the mechanism and the elementary steps involved in the direct N-acylation of lactams, oxazolidinones, and imidazolidinones with aldehydes is offered as a prerequisite for the further improvement. Density functional theory (DFT) was used to perform a detailed theoretical study of the mechanism of Zhang and Hong's method. The calculated results were then analyzed to clarify the relationships between the structures and reactivities in order to supply more reliable and accessible information for experimental studies.
Computational details
To obtain a more reasonable computational result, the substrates of 2-pyrrolidinone and benzaldehyde were derived from Zhang and Hong's experiments.17 The original structure of Shvo's catalyst A is also used here without any simplification.18 All optimizations were performed at the density functional theory (DFT) level by means of the M06-2X functional. Zhao and Truhlar reported that the M06-2X method can achieve a high accuracy for the calculation of the thermochemistry and kinetics of transition metals and main-group elements.21,22 In addition, the effective core potential LANL2DZ,23 along with its associated basis set, was employed for ruthenium and the main group elements (C, O, H, and Si) were calculated using the 6-31G* basis set. All calculations were performed without any geometrical constraints. Frequency calculations were carried out for all stationary points under the same computational level in order to identify the minima (zero imaginary frequency) and transition states (TSs, only one imaginary frequency) and to provide Gibbs energies at 298.15 K and 1 atm. Intrinsic reaction coordinate (IRC)24 analysis was carried out to confirm that all stationary states were smoothly connected to each other. Solvent effects (in toluene) were included using the SMD model25,26 with the same method by performing single-point calculations via the optimized-geometries in the gas phase at a higher level of basis set, where the def2-TZVP basis set was employed for Ru and the 6-31++G** basis set was used for main group elements.27,28 A correction term of 1.8943 kcal mol−1 must be added to the G(sol) calculations to convert the gas-phase standard Gibbs energies at a standard state of 1 atm to the appropriate standard state for a solution of 1 mol L−1.29,30 Solvation Gibbs energies ΔG(sol) were used to explore the reaction mechanism in order to consider both entropic and solvent effects. Calculations for all geometries were carried out using the Gaussian 09 software package.31Results and discussion
The acylation mechanism via unimolecular lactam
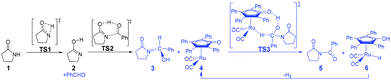
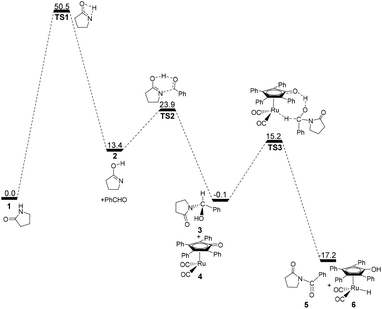
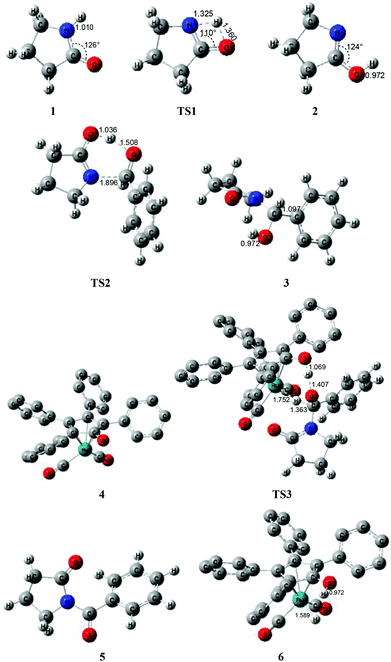
According to Zhang and Hong's proposal,17N-acylation of lactams is possibly achieved via a unimolecular nucleophilic attack mechanism (Scheme 5). In this route, the 2-pyrrolidinone 1 firstly transforms to the lactim 2via an intramolecular lactam–lactim tautomerism. Then, a nucleophilic attack of lactim 2 on the carbonyl group of the aldehyde generates a hemiaminal intermediate 3, which can be further dehydrogenated with the help of ruthenium complex 4. Finally, the acylation product 5 and another ruthenium species 6 are produced by β-hydride elimination and proton transfer.Fig. 1 shows that the substrate 1 transfers to the lactim 2via the transition state TS1 with a very high Gibbs energy barrier of 50.5 kcal mol−1. In this intramolecular lactam–lactim tautomerism, the bond angle of OCN is firstly reduced to 110° in the transition state TS1 from 126° in the substrate 1 in order to allow hydrogen atom transfer to the carbonyl oxygen from nitrogen. Moreover, the H–N bond length was increased to 1.325 Å, whereas the H–O distance was shortened to 1.360 Å. Here, the four-member ring of OHNC was shaped like a diamond, by which an exceedingly high ring strain force was correspondingly induced in the geometry of TS1. Thus, the Gibbs energy barrier of the first step was significantly enhanced. Although the geometry of 2 did not cause an intramolecular geometric stain, its thermodynamic stability was still reduced due to the activated N-atom.
 | ||
| Fig. 1 Gibbs energy ΔG(sol) profiles (kcal mol−1) of the acylation mechanism via a unimolecular lactam. Relative to Gibbs energies of 1, PhCHO and 4. | ||
In the next step, the lactim 2 reacted with the carbonyl carbon of the benzaldehyde, where the corresponding transition state TS2 had a Gibbs energy barrier of 10.5 kcal mol−1. From the structure of TS2, the N–C bond length of 1.896 Å indicates that the N-atom is attacking the carbonyl carbon atom. In addition, the two H–O bond lengths of 1.036 and 1.508 Å correspond to the hydroxyl hydrogen concertedly transferring to the oxygen of PhCHO. After this process, a hemiaminal intermediate 3 was then formed and its geometry resembled a tetrahedron (Fig. 2). Here, the 1 + PhCHO → 3 reaction was exergonic by 0.1 kcal mol−1, which indicated that this hemiaminal 3 has a better thermodynamic stability compared with the reactants of 1 and PhCHO. This is also in agreement with the experimental results.17
 | ||
| Fig. 2 Optimized structures for the acylation via a unimolecular lactam. Distances in Å. Hydrogen atoms of the Cp group of Shvo's catalyst are omitted for clarity. | ||
Due to the presence of Shvo's catalyst, an oxidized ruthenium complex 4 can be generated following the dissociation of the diruthenium-bridging hydride.32–37 Thus, the hemiaminal 3 can be further hydrogenated under the catalysis of ruthenium complex 4. According to numerous experimental and theoretical studies,38–42 the concerted hydrogen transfer mechanism is demonstrated to be the most thermodynamically and kinetically reasonable pathway. From the transition state TS3, the two bond distances of O⋯H–O (1.069 Å) and Ru⋯H–C (1.752 Å) indicate that the two hydrogen atoms of the CH–OH of 3 are concertedly transferring to the oxygen atom of the CpO substituent and the ruthenium center of 4 in the form of a proton and hydride ion, respectively. The Gibbs energy barrier ΔG≠(sol) was 15.3 kcal mol−1 for the 3 + 4 → 5 + 6 reaction, which was exergonic by 17.1 kcal mol−1.
For this mechanism, the processes are kinetically and thermodynamically facile, except for the first step. However, the initial intramolecular lactam–lactim tautomerism causes a large Gibbs energy barrier of 50.5 kcal mol−1, due to the very large structural strain force. This barrier cannot be kinetically overcome under the experimental conditions, because it is generally required to heat the reaction up to a very high temperature that far exceeds the boiling point of toluene.
Ruthenium-mediated acylation mechanism
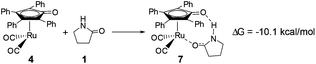
As mentioned above, a ruthenium complex 4 can exist in the reaction system after the dissociation of Shvo's catalyst. Due to it having an unoccupied d-orbital, the Ru-complex 4 is also a very good electron acceptor. As a donor, the substrate 1 possibly forms another ruthenium complex 7 by presenting its carbonyl oxygen atom to the vacant site of ruthenium of 4. Scheme 6 shows that this complexation reaction is exergonic by 10.1 kcal mol−1, although there is an entropic penalty. In Ru-complex 7 (see Fig. 3), there is also a hydrogen bonding interaction between the oxygen of the Cp-ring group and H–N of 2-pyrrolidinone, besides a coordination bond, due to the distance of O⋯HN being 1.878 Å. Both factors are favorable to increase the thermodynamic stability of Ru-complex 7. This means that the substrate 1 is possibly captured by Ru-complex 4 due to the higher thermodynamic stability of Ru-complex 7.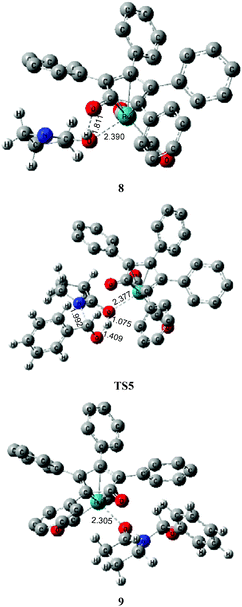 | ||
| Fig. 3 Optimized structures for the ruthenium-mediated acylation mechanism. Distances in Å. Hydrogen atoms of the Cp group of Shvo's catalyst are omitted for clarity. | ||
Next, the intramolecular lactam–lactim tautomerism occurs with the aid of ruthenium coordination using the transition state TS4. From the geometries of TS4, there is also a four-membered ring strain as in TS1. In addition, the protophilicity of the oxygen of substrate 1 is also reduced due to the coordination to ruthenium compared with TS1. Therefore, the Gibbs energy barrier is increased to a higher value of 55.5 kcal mol−1 (see Fig. 4). Compared with the structure of 7, the bond length of O–Ru is nearly increased by 0.1 Å, which indicates that the O–Ru coordination bond is being impaired. This causes the intermediate 7 to become more thermodynamically unstable, so that the process of 7 → 8 is correspondingly endergonic by 21.2 kcal mol−1.
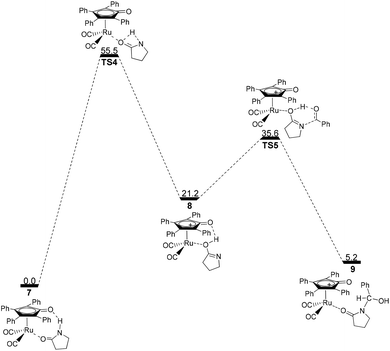 | ||
| Fig. 4 Gibbs energy ΔG(sol) profiles (kcal mol−1) for the ruthenium-mediated acylation mechanism. Relative to Gibbs energies of 7 and PhCHO. | ||
The further nucleophilic attack and hydrogen transfer between 8 and PhCHO can produce the hemiaminal–ruthenium complex 9via transition state TS5 with a Gibbs energy barrier of 14.4 kcal mol−1, which is higher than the value of 10.5 kcal mol−1 for 2 → TS2. This is because the coordinated ruthenium complex induces a steric hindrance when PhCHO approaches the substrate. This fact eventually gives rise to a reduction in the thermodynamic stability of hemiaminal–ruthenium complex 9, of which the ΔG(sol) is increased to 5.2 kcal mol−1 compared with the reactants of 1 and PhCHO.
By far, the participation of the ruthenium complex does not display an expected action in the acylation of a lactam with an aldehyde. In contrast, the total Gibbs energy barrier of this route and the ΔG(sol) of product 9 are increased to 55.5 kcal mol−1 and 5.2 kcal mol−1, respectively, which indicates that this mechanism is kinetically and thermodynamically unfeasible. From this mechanism, it can be found that the substrate 1 can coordinate to Ru-complex 4 and form a ruthenium complex 7 prior to the lactam–lactim tautomerism when Shvo's catalyst is added to the reaction system. However, the generation of Ru-complex 7 is unfavorable for the further catalytic dehydrogenation reaction.
Bimolecular lactam-mediated acylation mechanism
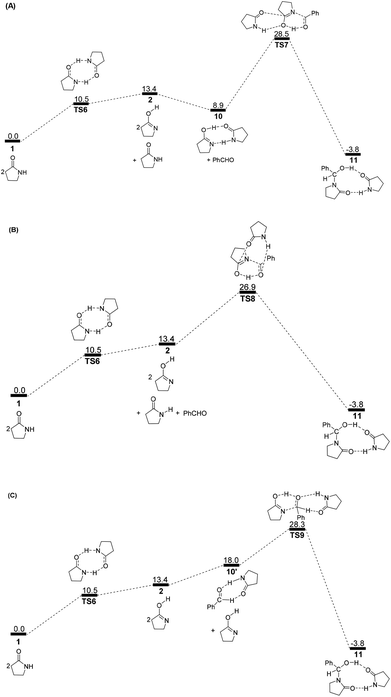
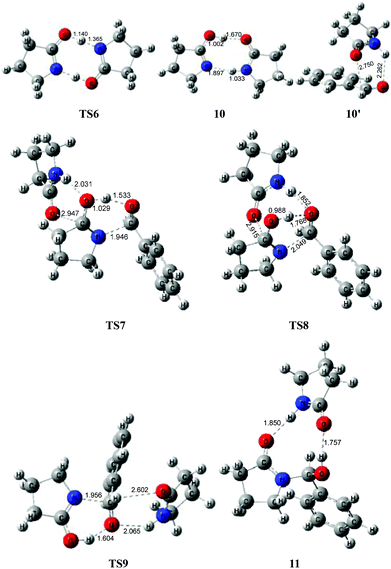
To avoid the geometric strain, there is actually another potential means by which the lactam–lactim tautomerism can be achieved, via an intermolecular hydrogen exchange between two molecules of substrate 1. As shown in Fig. 5, two molecules of lactam 1 exchange two hydrogen atoms each other via the transition state TS6, having a six-membered ring, which corresponds to a Gibbs energy barrier of only 10.5 kcal mol−1. Fig. 6 shows that the geometry of 1 is retained to a large extent in the transition state TS6. Therefore, this indicates that the intermolecular hydrogen exchange can effectively eliminate the impact of strain.Correspondingly, two lactims 2 are also generated through the transition state TS6, which was endergonic by 13.4 kcal mol−1 from 1 to 10. In particular, the Gibbs energy of the produced lactim 2 is 2.9 kcal mol−1 higher than that of TS6. As per Shaik's theory,43 the reaction of 1 → TS6 → 2 is a continued endothermic process, where the real Gibbs energy should be 13.4 kcal mol−1 instead of 10.5 kcal mol−1. In this case, a more stable intermediate 10 is then generated with an exergonic 4.5 kcal mol−1 from 2 to 10. The intermediate 10 is actually a bimolecular complex involving the lactim 2 and lactam 1. Fig. 6 shows that the OH⋯O and N⋯HN distances are 1.670 and 1.897 Å, respectively. This indicates that two strong hydrogen bonding interactions are formed in 10, which is favorable for improving the thermodynamic stability.
However, there are three possible pathways, (a), (b) and (c), in the next step, which corresponds to three different transition states, TS7, TS8 and TS9, respectively. In these transition states, the function of substrate 1 is mainly to increase both the electropositivity of the carbon and the electronegativity of the oxygen that participate in the nucleophilic reaction. By comparison, the transition state TS8 in the (b) route corresponds to a lowest Gibbs energy barrier of 26.9 kcal mol−1, where the oxygen of PhCHO is more favoured to accept the proton from the OH of 10. Then, an intermediate 11 was produced, which is a molecular pair of the hemiaminal 3 and substrate 1 connected by hydrogen bonds.
The total Gibbs energy barrier is 26.9 kcal mol−1 from 1 to 11 in this mechanism, which is exergonic by 3.8 kcal mol−1. Compared with 1 → TS1 → 2 of the first route, a bimolecular hydrogen exchange viaTS6 is much more kinetically feasible to achieve the lactam–lactim tautomerism. This calculated conclusion is also in agreement with the previous theoretical and experimental results.44 Although the finally produced molecular pair 11 also has a higher thermodynamic stability compared with a single hemiaminal 3, the Gibbs energy barrier of TS8 is 3.0 kcal mol−1 higher than that of TS2. Thus, the unimolecular 2 is more kinetically favorable to make a nucleophilic attack on PhCHO. This means that the dimer 10 is again dissociated to the monomer 2, and then lactim 2 further produces the hemiaminal 3viaTS2.
According to the above analyses, the most reasonable mechanism is that shown in Fig. 7. Here, the Gibbs energy shows an increasing tendency for 1 → TS1 → 2 + PhCHO → TS2, which is a continuously endergonic process.43 Therefore, the actual Gibbs energy barrier is 23.9 kcal mol−1 for the generation of hemiaminal 3. Adding Shvo's catalyst with the substrates into the reaction system can cause a higher Gibbs energy barrier of 25.6 kcal mol−1 for the first catalytic cycle, due to the formation of a more thermodynamically stable Ru-complex 7. After the first cycle, the Ru-complex 6 is initially regenerated to the active catalyst 4,28 and then the following dehydrogenation of the hemiaminal can be directly catalyzed by the Ru-catalyst 4. This is because a lower Gibbs energy barrier of 15.4 kcal mol−1 has a preponderant kinetic favorability compared with Ru-complex 7. Here, the Gibbs energy barrier of hemiaminal formation is 23.9 kcal mol−1, which is higher than that of 15.3 kcal mol−1 for the dehydrogenation of 3. This means that the rate-determining step is 2 + PhCHO → TS2 → 3 in the real catalytic cycle, which is also in agreement with experimental results. The total Gibbs energy barrier becomes 23.9 kcal mol−1 for the N-acylation of the lactam with the aldehyde. Furthermore, according to this mechanism the crucial factor in further developing this method is improving the nucleophilicity of the lactam or the electrophilic ability of the aldehyde.
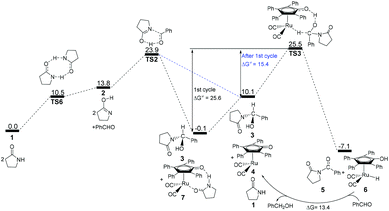 | ||
| Fig. 7 Gibbs energy ΔG(sol) profiles (kcal mol−1) for the most reasonable acylation mechanism. Relative to Gibbs energies of 1, PhCHO, and 7. | ||
Conclusions
The mechanism of the direct N-acylation of a lactam with an aldehyde using Shvo's catalyst was studied in detail using the DFT method. Solvation effects in toluene were also considered and were included in the calculated Gibbs energy profiles. In the acylation process, the substrate 1 can isomerize to the lactim 2 by means of an intermolecular lactam–lactim tautomerism. The formed monomer 2 can generate a hemiaminal 3 with an aldehyde via a nucleophilic reaction and a hydrogen transfer. Finally, this hemiaminal 3 is dehydrogenated to obtain the product 5 under the catalysis of ruthenium complex 4. The highest Gibbs energy barrier for the catalytic cycle is 23.9 kcal mol−1, where the generation of the hemiaminal 3 is the rate-determining step. In paricular, adding Shvo's catalyst to the substrates can increase the Gibbs energy barrier for the first cycle of N-acylation. In addition, increasing the nucleophilicity of the lactam or the electrophilic ability of the aldehyde is favorable to further develop this synthesis method.Acknowledgements
This work is supported by the National Natural Science Foundation of China (no. 21277082 and 21337001), Marie Curie International Research Staff Exchange Scheme Fellowship within the 7th European Community Framework Programme (no. 295132) and Program for New Century Excellent Talents in University (NCET-13-0349).Notes and references
- (a) T. Cupido, J. Tulla-Puche, J. Spengler and F. Albericio, Curr. Opin. Drug Discovery Dev., 2007, 10, 768–783 CAS; (b) J. W. Bode, Curr. Opin. Drug Discovery Dev., 2006, 9, 765–775 CAS.
- J. M. Humphrey and A. R. Chamberlin, Chem. Rev., 1997, 97, 2243–2266 CrossRef CAS PubMed.
- (a) K. Hayashi, K. Nunami, J. Kato, N. Yoneda, M. Kubo, T. Ochiai and R. Ishida, J. Med. Chem., 1989, 32, 289–297 CrossRef CAS; (b) D. M. Robinson, M. P. Curran and K. A. Lyseng-Williamson, Drugs, 2007, 67, 1359–1378 CrossRef CAS PubMed.
- (a) M. Sakakiba and M. Matsui, Agric. Biol. Chem., 1973, 37, 911–914 CrossRef; (b) A. Ishida and T. Mukaiyama, Bull. Chem. Soc. Jpn., 1978, 51, 2077–2081 CrossRef CAS.
- (a) G. Bandoli, M. Nicolini, H. Lumbroso, A. Grassi and G. C. Pappalardo, J. Mol. Struct., 1987, 160, 297–309 CrossRef CAS; (b) C. M. Tang, Q. Y. Shi, A. Katchman and G. Lynch, Science, 1991, 254, 288–290 CAS.
- C. Y. Li, W. Tsai, A. G. Damu, E. J. Lee, T. S. Wu, N. X. Dung, T. D. Thang and L. Thanh, J. Agric. Food Chem., 2007, 55, 9436–9442 CrossRef CAS PubMed.
- (a) A. Giovannini, D. Savoia and A. Umani-Ronchi, J. Org. Chem., 1989, 54, 228–234 CrossRef CAS; (b) D. Savoia, V. Concialini, S. Roffia and L. Tarsi, J. Org. Chem., 1991, 56, 1822–1827 CrossRef CAS.
- C. S. Schindler, P. M. Forster and E. M. Carreira, Org. Lett., 2010, 12, 4102–4105 CrossRef CAS PubMed.
- L. Wang, H. Fu, Y. Y. Jiang and Y. F. Zhao, Chem. – Eur. J., 2008, 14, 10722–10726 CrossRef CAS PubMed.
- W.-J. Yoo and C.-J. Li, J. Am. Chem. Soc., 2006, 128, 13064–13065 CrossRef CAS PubMed.
- (a) Y. Suto, N. Yamagiwa and Y. Torisawa, Tetrahedron Lett., 2008, 49, 5732–5735 CrossRef CAS PubMed; (b) Y. Tamaru, Y. Yamada and Z. Yoshida, Synthesis, 1983, 474–476 CrossRef CAS.
- (a) A. Tillack, I. Rudloff and M. Beller, Eur. J. Org. Chem., 2001, 523–528 CrossRef CAS; (b) W.-K. Chan, C.-M. Ho, M.-K. Wong and C.-M. Che, J. Am. Chem. Soc., 2006, 128, 14796–14797 CrossRef CAS PubMed.
- T. Naota and S.-I. Murahashi, Synlett, 1991, 693–694 CrossRef CAS.
- (a) S. Seo and T. J. Marks, Org. Lett., 2008, 10, 317–319 CrossRef CAS PubMed; (b) C. Qian, X. Zhang, J. Li, F. Xu, Y. Zhang and Q. Shen, Organometallics, 2009, 28, 3856–3862 CrossRef CAS.
- J. M. Li, F. Xu, Y. Zhang and Q. Shen, J. Org. Chem., 2009, 74, 2575–2577 CrossRef CAS PubMed.
- S. Muthaiah, S. C. Ghosh, J. E. Jee, C. Chen, J. Zhang and S. H. Hong, J. Org. Chem., 2010, 75, 3002–3006 CrossRef CAS PubMed.
- J. Zhang and S. H. Hong, Org. Lett., 2012, 14, 4646–4649 CrossRef CAS PubMed.
- Y. Shvo, D. Czarkie, Y. Rahamim and D. F. Chodosh, J. Am. Chem. Soc., 1986, 108, 7400–7402 CrossRef CAS.
- (a) R. Karvemu, R. Prabhakaran and K. Natarajan, Coord. Chem. Rev., 2005, 249, 911–918 CrossRef PubMed; (b) S. Gladiali and E. Alberico, Chem. Soc. Rev., 2006, 35, 226–236 RSC.
- J. Wang, C. Liu, J. Yuan and A. Lei, Chem. Commun., 2014, 50, 4736–4739 RSC.
- Y. Zhao and D. G. Truhlar, Acc. Chem. Res., 2008, 41, 157–167 CrossRef CAS PubMed.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 CrossRef CAS.
- (a) P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 270–283 CrossRef CAS PubMed; (b) P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 299–310 CrossRef CAS PubMed.
- (a) K. Fukui, J. Phys. Chem., 1970, 74, 4161–4163 CrossRef CAS; (b) K. Fukui, Acc. Chem. Res., 1981, 14, 363–368 CrossRef CAS.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 4538–4543 CrossRef CAS PubMed.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396 CrossRef CAS PubMed.
- X. Xu and D. G. Truhlar, J. Chem. Theory Comput., 2012, 8, 80–90 CrossRef CAS.
- X. Lu, Q. Liu, X. Wang, R. Cheng, M. Zhang and X. Sun, RSC Adv., 2015, 5, 2827–2836 RSC.
- L. M. Pratt, S. Merry, S. C. Nguyen, P. Quan and B. T. Thanh, Tetrahedron, 2006, 62, 10821–10828 CrossRef CAS PubMed.
- L. M. Pratt, D. G. Truhlar, C. J. Cramer, S. R. Kass, J. D. Thompson and J. D. Xidos, J. Org. Chem., 2007, 72, 2962–2966 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, J. E. Peralta Jr., F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09 (Revision B.01), Gaussian, Inc., Wallingford, CT, 2009 Search PubMed.
- C. P. Casey, S. W. Singer, D. R. Powell, R. K. Hayashi and M. Kavana, J. Am. Chem. Soc., 2001, 123, 1090–1100 CrossRef CAS PubMed.
- L. S. M. Samec, J.-E. Bäckvall, P. G. Andersson and P. Brant, Chem. Soc. Rev., 2006, 35, 237–248 RSC.
- S. E. Clapham, A. Hadzovic and R. H. Morris, Coord. Chem. Rev., 2004, 248, 2201–2237 CrossRef CAS PubMed.
- G. Csjernyk, A. H. Éll, L. Fadini, B. Pugin and J.-E. Bäckvall, J. Org. Chem., 2002, 67, 1657–1662 CrossRef PubMed.
- C. P. Casey, G. A. Bikzhanova, Q. Cui and I. A. Guzei, J. Am. Chem. Soc., 2005, 127, 14062–14071 CrossRef CAS PubMed.
- J. B. Johnson and J.-E. Bäckvall, J. Org. Chem., 2003, 68, 7681–7684 CrossRef CAS PubMed.
- C. P. Casey and H. Guan, J. Am. Chem. Soc., 2007, 129, 5816–5817 CrossRef CAS PubMed.
- C. P. Casey and H. Guan, Organometallics, 2012, 31, 2631–2638 CrossRef CAS PubMed.
- A. Comas-Vives, G. Ujaque and A. Lledós, Organometallics, 2007, 26, 4135–4144 CrossRef CAS.
- H. Zhang, D. Chen, Y. Zhang, G. Zhang and J. Liu, Dalton Trans., 2010, 39, 1972–1978 RSC.
- (a) X. Lu, Y. Zhang, P. Yun, M. Zhang and T. Li, Org. Biomol. Chem., 2013, 11, 5264–5277 RSC; (b) X. Lu, R. Cheng, N. Turner, Q. Liu, M. Zhang and X. Sun, J. Org. Chem., 2014, 79, 9355–9364 CrossRef CAS PubMed.
- S. Kozuch and S. Shaik, Acc. Chem. Res., 2011, 44, 101–110 CrossRef CAS PubMed.
- (a) S. Tolosa, N. Mora-Diez, A. Hidalgoa and J. A. Sansóna, RSC Adv., 2014, 4, 44757–44768 RSC; (b) C. S. Peng, C. R. Baiz and A. Tokmakoff, Proc. Natl. Acad. Sci. U. S. A., 2013, 23, 9243–9248 CrossRef PubMed; (c) D. Ray, A. Pramanik and N. Guchhait, J. Photochem. Photobiol., A, 2014, 274, 33–42 CrossRef CAS PubMed; (d) H. I. Abdulla and M. F. El-Bermani, Spectrochim. Acta, Part A, 2001, 57, 2659–2671 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Total electronic energies, thermal corrections to Gibbs energies and Cartesian coordinates, and so on. See DOI: 10.1039/c5qo00082c |
| This journal is © the Partner Organisations 2015 |