Effect of two-color laser pulse intensity ratio on intense terahertz generation
Chenhui Luab,
Shian Zhang*a,
Yunhua Yaoa,
Shuwu Xuac,
Tianqing Jiaa,
Jingxin Dinga and
Zhenrong Sun*a
aState Key Laboratory of Precision Spectroscopy, Department of Physics, East China Normal University, Shanghai 200062, People's Republic of China. E-mail: sazhang@phy.ecnu.edu.cn; zrsun@phy.ecnu.edu.cn
bCollege of Mechanical Engineering, Shanghai University of Engineering Science, Shanghai 201620, People's Republic of China
cSchool of Science, Nantong University, Nantong 226007, People's Republic of China
First published on 26th November 2014
Abstract
We theoretically demonstrate the effect of the intensity ratio of the two-color laser field on the terahertz generation based on a transient photocurrent model. We show that the terahertz generation depends on the intensity ratio of the two-color laser field at a given total laser intensity, and the optimal intensity ratio for the maximum terahertz generation will decrease with the increase of the total laser intensity. We also show that the final ionization degree can be used to explain the optimal intensity ratio change at different laser intensities. Furthermore, we utilize the increasing rate of electron density and the electron drift velocity to illustrate the physical mechanism of the maximum terahertz radiation generation.
1. Introduction
Terahertz (THz) pulse has been widely applied to various related fields, such as noninvasive imaging,1,2 optical communications,3,4 molecular spectroscopy,5 high-speed optical signal processing,6 biological and medical imaging,7,8 and non-destructive evaluation (NDE).9 For some specific applications, such as remote sensing,10 it is crucial to generate the intense THz radiation. Conventional THz sources were usually achieved by semiconductor photoconductive switches11,12 or optical rectification in nonlinear crystals,13 while the THz field intensity by the two schemes is relatively low and its spectral range is narrow. Recently, as an alternative approach, two-color laser field has been proposed to generate the intense and broadband THz pulse.14–16 In this two-color scheme, a fundamental femtosecond laser field combining with its second harmonic field are focused in air to generate gaseous plasma, and an intense THz pulse can be irradiated in the forward direction. This intense THz generation created by the two-color laser field has attracted considerable attention in both its related application and physical mechanism.17–26Initially, this intense THz generation was understood as a four-wave mixing process, but it was soon found that the Kerr nonlinearity is too small to explain the high THz field intensity.27 In addition, several experimental results confirmed that the THz intensity threshold was coincident with the ionization threshold of gas molecules, which indicated that the plasma formation plays an important role in the THz generation process.18,27 Recently, a transient photocurrent model proposed by Kim et al. was used to elucidate such THz generation in the two-color laser field,15,19 and has been studied in many experiments and theoretical simulations.15–28 In this model, tunneling ionization and subsequent electron motion will form a directional current, which is responsible for the intense THz generation. The intensity ratio of the second harmonic field to the fundamental laser field is an important parameter to affect tunneling ionization and subsequent electron motion, and consequently the THz generation. In previous works, this intensity ratio was usually controlled by varying the fundamental laser field intensity (or second harmonic field intensity) while keeping the second harmonic field intensity (or fundamental laser field intensity).19,29–32 However, in this paper we demonstrate the effect of the intensity ratio of the second harmonic field to the fundamental laser field at a given total laser intensity on the THz generation, that is to say, both the fundamental laser field and its second harmonic field are simultaneously varied while the total laser intensity keeps a constant, which is different from the previous studies. We utilize the transient photocurrent model to simulate the THz generation in the two-color laser field. It is shown that the THz amplitude depends on the intensity ratio of the two-color laser field at a given total laser intensity and reaches to its maximal value at an optimal intensity ratio, while the optimal intensity ratio will decrease as the total laser intensity increases. It is also shown that the final ionization degree can explain the optimal intensity ratio change at different laser intensities. Furthermore, the physical mechanism of the maximal THz generation is also discussed and analyzed on the basis of the increasing rate of the electron density and the electron drift velocity.
2. Theoretical model
Our theoretical simulation is based on the transient photocurrent model,15,16 and a two-color laser field with a superposition of the fundamental laser field and its second harmonic field is given by
E(t) = exp(−2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2t2/τ2)[E1 2t2/τ2)[E1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ω0t + E2 ω0t + E2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(2ω0t + ϕ)], cos(2ω0t + ϕ)],
| (1) |
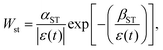 | (2) |
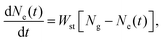 | (3) |
| Wfi = Ne(t = ∞)/Ng. | (4) |
Here, Wfi also can represent the final electron density after the passage of laser pulse. Once ionized, the electron will oscillate with the laser field, and the electron velocity at a subsequent time can be written as
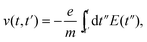 | (5) |
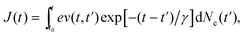 | (6) |
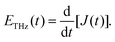 | (7) |
Finally, the THz radiation spectrum is obtained by the Fourier transform of ETHz(t), i.e. ETHz(ω) = FFT[ETHz(t)]. In our simulation, the central frequency of the fundamental laser field is set to be ω0 = 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 cm−1, and the pulse duration is τ = 50 fs. Iω and I2ω respectively represent the laser intensity of the fundamental laser field and its second harmonic field, Itotal represents the total laser intensity of the two-color laser field, and RI = I2ω/Iω is the intensity ratio of the two laser fields.
500 cm−1, and the pulse duration is τ = 50 fs. Iω and I2ω respectively represent the laser intensity of the fundamental laser field and its second harmonic field, Itotal represents the total laser intensity of the two-color laser field, and RI = I2ω/Iω is the intensity ratio of the two laser fields.
3. Results and discussion
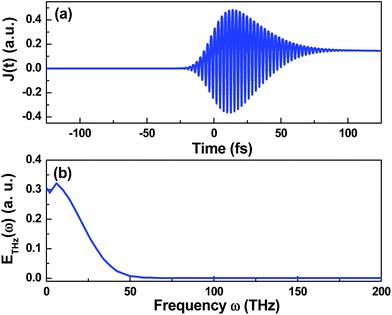
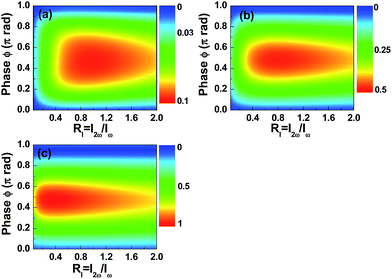
Fig. 1 shows the time-dependent electron current J(t) calculated from eqn (6) (a) and its corresponding THz radiation spectrum ETHz(ω) (b) with the relative phase of ϕ = 0.5π, the relative intensity ratio of RI = 0.2 and the total laser intensity of Itotal = 180 TW cm−2. As can be seen, the electron current J(t) is asymmetric distribution and a quasi-DC current arises after the laser pulse (see Fig. 1(a)). This current surge occurs in the time scale of photoionization process (<100 fs in the general case), which leads to the generation of electromagnetic radiation at THz frequencies (see Fig. 1(b)). The electromagnetic radiation spectrum also contains the fundamental laser field, its second harmonic field and their mixing fields, but here only the components at THz frequencies are our concern. As shown in Fig. 1(b), the THz spectrum has a wide range up to ∼50 THz, and the maximal value is at about ω = 6 THz.In our work, we focus on the effect of the intensity ratio RI of the two-color laser field on the THz generation at a given total laser intensity. Fig. 2 shows the contour plot of THz amplitude as a function of the intensity ratio RI and the relative phase ϕ with the total laser intensities of Itotal = 120 (a), 180 (b), and 360 TW cm−2 (c). It can be seen that the THz radiation is maximally obtained with the relative phase of ϕ = π/2 at all total laser intensities, and this result is the same as previous studies.15–17,19 However, the THz radiation is maximally obtained at different intensity ratios for different laser intensities. As shown in Fig. 2, the THz amplitude reaches the maximum value at the intensity ratios of RI = 1, 0.8 and 0.35 for the total laser intensities of Itotal = 120, 180 and 360 TW cm−2, respectively. That is to say, the optimal intensity ratio decreases with the increase of the total laser intensity.
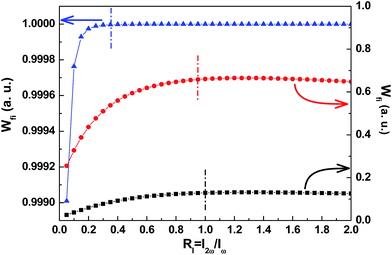
Generally, the field amplitude of THz pulse relies on the ionization rate of gas molecules when the electric field of the two-color laser pulse is given.37 Therefore, next we demonstrate the effect of the relative intensity ratio RI and the total laser intensity Itotal on the ionization rate. Fig. 3 shows the final ionization degree Wfi as the function of the intensity ratio RI with the total laser intensities of Itotal = 120 (squares), 180 (circles) and 360 TW cm−2 (triangles). As can be seen, the final ionization degree Wfi increases with the increase of the total laser intensity and almost reaches saturation at the total laser intensity of Itotal = 360 TW cm−2. Furthermore, the final ionization degree Wfi shows a fast increase and then slow decrease process with the increase of the intensity ratio RI, and is close to the maximal value at the intensity ratios of RI = 1, 0.8 and 0.35 for the total laser intensities of Itotal = 120, 180 and 360 TW cm−2, respectively. It's noteworthy that the optimal intensity ratio for the maximal ionization degree is almost the same as that for the maximal THz amplitude, which further indicates that the THz generation is correlated with the plasma density. Obviously, the final ionization degree can explain why the optimal intensity ratio for maximal THz generation decreases with the increase of the total laser intensity in Fig. 2.
In this two-color laser field, the free electron is produced through tunneling ionization and then accelerated by the laser field, which results in the formation of transient electron current. Furthermore, these electrons not only oscillate with the laser field but also drift in the transverse direction. As a result, some residual-current density (RCD) remains in the produced plasma when the laser pulse is passed. This residual-current density RCD is an initial impetus to the plasma polarization and the excitation of transverse dipole oscillations, and therefore determines the THz emission.38,39 The dependence of THz generation on residual-current density RCD has been demonstrated in many experimental and theoretical studies.23,30,38–40 Similarly, our results in Fig. 2 can also be explained by analyzing the residual-current density RCD. Here, we rewrite the eqn (5) as
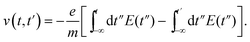 | (8) |
The first term in eqn (8) is the electron oscillation velocity at laser frequency, and is constant when the laser pulse is passed. Therefore, after the passage of the laser pulse (i.e., t → ∞), the velocity of electron is only determined by the second term in eqn (8), which is usually defined as drift velocity
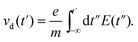 | (9) |
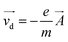 (ref. 19,23,25 and 40). So residual-current density RCD can be written as
(ref. 19,23,25 and 40). So residual-current density RCD can be written as
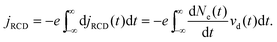 | (10) |
The peak amplitude of THz pulse is proportional to residual-current density RCD jRCD, and written as
| ETHz ∝ jRCD. | (11) |
As shown in eqn (11), the THz amplitude depends on the drift velocity vd(t) and the increasing rate of electron density dNe(t)/dt, and therefore this simple model can be used to explore the physical mechanism of the THz amplitude modulation in Fig. 2.
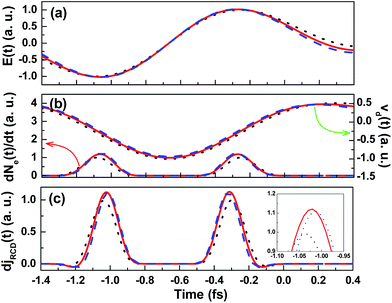
Since the THz amplitude depends on the intensity ratio of the two-color laser field, we discuss the THz generation by analyzing the drift velocity vd(t) and the increasing rate of the electron density dNe(t)/dt at the optimal intensity ratio and it's both sides. Fig. 4(a) shows the field amplitude of the two-color laser pulse in an half optical period with the intensity ratios of RI = 0.6 (black dotted line), 1 (red solid line) and 1.4 (blue dashed line) for the total laser intensity of Itotal = 120 TW cm−2 and the relative phase of ϕ = 0.5π. As can be seen, the field amplitude increases with the increase of the intensity ratio RI. As shown in eqn (2), the ionization process only occurs near extreme of the electric field and the ionization rate Wst depends on the amplitude of electric field, and thus the stronger laser pulse will produce the more free electrons. Fig. 4(b) shows the drift velocity vd(t) and the increasing rate of electron density dNe(t)/dt in the optical period for the three intensity ratios. One can see that the increasing rate of electron density dNe(t)/dt shows the same evolution behavior with the field amplitude in Fig. 4(a), which is consistent with our above prediction. However, the absolute value of drift velocity vd(t) shows an opposite behavior, which decreases as the intensity ratio RI increases, here the minus sign only indicate that direction of electron current. Since the THz amplitude depends on both the drift velocity vd(t) and the increasing rate of the electron density dNe(t)/dt (see eqn (10) and (11)), the former decreases while the latter increases with the increase of the intensity ratio, and therefore there will be a maximal THz amplitude at an appropriate intensity ratio. Fig. 4(c) shows the transition residual-current density RCD djRCD(t) at the three intensity ratios calculated from Fig. 4(b) based on eqn (10). One can see that the transition residual-current density RCD djRCD(t) is maximally obtained at the intensity ratio of RI = 1 (see inset of Fig. 4(c)). Since the transition residual-current density RCD djRCD(t) has the same behavior in each optical period at the three intensity ratios, the whole residual-current density RCD jRCD is maximal value at the intensity ratio RI = 1, which can radiate the maximal THz emission. Consequently, one can conclude that the THz amplitude at the optimal intensity ratio benefits from lager electron density comparing with the lower intensity ratio, while benefits from lager drift velocity comparing with the higher intensity ratio.
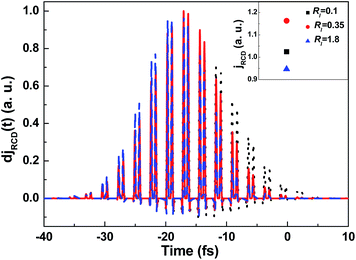
In above analysis, the laser intensity is relatively low, and therefore only a part of gas molecules are ionized. As shown in eqn (3), the increasing rate of the electron density is given by dNe(t)/dt = Wst[Ng − Ne(t)], where Ng − Ne(t) is density of neutral gas at time t. Since Ne(t) is rather small at low laser intensity, the increasing rate of electron density can be further expressed by dNe(t)/dt ≈ WstNg, and thus its decrease in each optical period can be neglected. In this case, the electron current change in one optical period by varying the intensity ratio of the two-color laser field can directly reflect the whole electron current modulation. However, when the laser intensity is high enough, the gas molecules can be completely ionized in a few optical periods, above analysis method cannot be utilized, it need to consider the transition residual-current density RCD djRCD(t) in each optical period. Fig. 5 shows the transition residual-current density RCD djRCD(t) in the range of the whole laser pulse duration with the total laser intensity of Itotal = 360 TW cm−2 for the intensity ratios of RI = 0.1 (black solid line), 0.35 (red dashed line) and 1.8 (blue dotted line). As can be seen, the gas molecules will be completely ionized within about fifteen optical periods in this high laser intensity. With the increase of the intensity ratio RI, the transition residual-current density RCD djRCD(t) increases in the first optical few optical periods, while decreases in the last few optical periods, and thus the whole residual-current density RCD jRCD is maximally obtained at a approximate intensity ratio. We also present the whole residual-current density RCD jRCD by integrating the transition RCD djRCD(t) over the entire laser pulse for the three intensity ratios, as shown in inset of Fig. 5. As can be seen, the whole residual-current density RCD jRCD obtains the maximal value at the intensity ratio of RI = 0.35, which results in the maximal THz radiation.
Finally, we present the dependence of the THz amplitude on the total laser intensity Itotal at the optimal intensity ratio, as shown in Fig. 6. One can see that the THz output first increases and then approaches to saturation with the increase of the total laser intensity Itotal. Obviously, such intensity dependence is similar to the previous report.15,17 In previous studies, the intensity ratio is kept a constant, but here we present the THz amplitude at the optimal intensity ratio, and therefore it represents the maximally attainable THz output at each given laser intensity. The THz amplitude saturation in the high laser intensity can be attributed to the complete ionization in the gaseous molecules, as shown in Fig. 3 and 5.
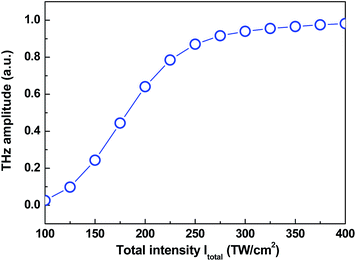 | ||
| Fig. 6 (Color online) The THz amplitude as a function of the total laser intensity Itotal at the optimal intensity ratio. | ||
4. Conclusions
In conclusion, we have theoretically shown that the intensity ratio of the two-color laser field at a given total laser intensity will affect the THz generation. Our results showed that the optimal intensity ratio for the maximal THz generation decreases with the increase of the total laser intensity, and the final ionization degree can explain the optimal intensity ratio change at different laser intensities. Furthermore, the physical mechanisms of the maximal THz generation at low and high laser intensities were discussed and analyzed by considering the drift velocity and the increasing rate of the electron density. Our results will be very useful for further understanding the intense THz generation and its control, and are expect to be applied in various related fields.Acknowledgements
This work was partly supported by National Natural Science Fund (nos 51132004 and 11474096) and Shanghai Municipal Science and Technology Commission (no. 14JC1401500).References
- P. Y. Han, G. C. Cho and X.-C. Zhang, Time-domain transillumination of biological tissues with terahertz pulses, Opt. Lett., 2000, 25, 242 CrossRef CAS.
- J. L. Johnson, T. D. Dorney and D. M. Mittleman, Enhanced depth resolution in terahertz imaging using phase-shift interferometry, Appl. Phys. Lett., 2001, 78, 835 CrossRef CAS PubMed.
- T. Kleine-Ostmann and T. Nagatsuma, A review on terahertz communications research, J. Infrared, Millimeter, Terahertz Waves, 2011, 32(2), 143 CrossRef.
- H. J. Song and T. Nagatsuma, Present and future of terahertz communications, IEEE Trans. Terahertz Sci. Technol., 2011, 1, 256 CrossRef.
- E. Knoesel, M. Bonn, J. Shan and T. F. Heinz, Charge transport and carrier dynamics in liquids probed by THz time-domain spectroscopy, Phys. Rev. Lett., 2001, 86, 340 CrossRef CAS.
- D. S. Citrin, Picosecond dynamics of terahertz-sideband generation in far-infrared illuminated quantum wells, Appl. Phys. Lett., 2000, 76, 3176 CrossRef CAS PubMed.
- D. D. Arnone, C. M. Ciesla, A. Corchia, S. Egusa, M. Pepper, J. M. Chamberlain, C. Bezant and E. H. Linfield, Applications of terahertz (THz) technology to medical imaging, Proc. SPIE, 1999, 3828, 209 CrossRef PubMed.
- Z. D. Taylor, R. S. Singh, D. B. Bennett, P. Tewari, C. P. Kealey, N. Bajwa, M. O. Culjat, A. Stojadinovic, H. Lee, J.-P. Hubschman, E. R. Brown and W. S. Grundfest, THz medical imaging: in vivo hydration sensing, IEEE Trans. Terahertz Sci. Technol., 2011, 1, 201 CrossRef CAS.
- J. B. Jackson, M. Mourou, J. F. Whitaker, I. N. Duling III, S. L. Williamson, M. Menu and G. A. Mourou, Terahertz imaging for non-destructive evaluation of mural paintings, Opt. Commun., 2008, 281, 527 CrossRef CAS PubMed.
- J. Liu, J. Dai, S. L. Chin and X.-C. Zhang, Broadband terahertz wave remote sensing using coherent manipulation of fluorescence from asymmetrically ionized gases, Nat. Photonics, 2010, 4, 627 CrossRef CAS.
- D. H. Auston and P. R. Smith, Generation and detection of millimeter waves by picosecond photoconductivity, Appl. Phys. Lett., 1983, 43, 631 CrossRef CAS PubMed.
- C. Fattinger and D. Grischkowsky, Terahertz beams, Appl. Phys. Lett., 1989, 54, 490 CrossRef PubMed.
- D. H. Auston, K. P. Cheung, J. A. Valdmanis and D. A. Kleinman, Cherenkov radiation from femtosecond optical pulses in electro-optic media, Phys. Rev. Lett., 1984, 53, 1555 CrossRef CAS.
- D. J. Cook and R. M. Hochstrasser, Intense terahertz pulses by four-wave rectification in air, Opt. Lett., 2000, 25, 1210 CrossRef CAS.
- K. Y. Kim, J. H. Glownia, A. J. Taylor and G. Rodriguez, Terahertz emission from ultrafast ionizing air in symmetry-broken laser fields, Opt. Express, 2007, 15, 4577 CrossRef CAS.
- T. I. Oh, Y. S. You, N. Jhajj, E. W. Rosenthal, H. M. Milchberg and K. Y. Kim, Intense terahertz generation in two-color laser filamentation: energy scaling with terawatt laser systems, New J. Phys., 2013, 15, 75002 CrossRef.
- H. G. Roskos, M. D. Thomson, M. Kreß and T. Löffler, Broadband THz emission from gas plasmas induced by femtosecond optical pulses: from fundamentals to applications, Laser Photonics Rev., 2007, 1, 349 CrossRef.
- N. Karpowicz, X. Lu and X.-C. Zhang, Terahertz gas photonics, J. Mod. Opt., 2009, 56(10), 1137 CrossRef CAS.
- K. Y. Kim, Generation of coherent terahertz radiation in ultrafast laser-gas interactions, Phys. Plasmas, 2009, 16(5), 56706 CrossRef PubMed.
- I. Babushkin, W. Kuehn, C. Köhler, S. Skupin, L. Bergé, K. Reimann, M. Woerner, J. Herrmann and T. Elsaesser, Ultrafast spatiotemporal dynamics of terahertz generation by ionizing two-color femtosecond pulses in gases, Phys. Rev. Lett., 2010, 105(5), 53903 CrossRef CAS.
- H. Dai and J. Liu, Phase dependence of the generation of terahertz waves from two-color laser-induced gas plasma, J. Opt., 2011, 13(5), 55201 CrossRef.
- I. Babushkin, S. Skupin, A. Husakou, C. Köhler, E. Cabrera-Granado, L. Bergé and J. Herrmann, Tailoring terahertz radiation by controlling tunnel photoionization events in gases, New J. Phys., 2011, 13(12), 123029 CrossRef.
- H.-C. Wu, J. Meyer-ter-Vehn and Z.-H. Sheng, Phase-sensitive terahertz emission from gas targets irradiated by few-cycle laser pulses, New J. Phys., 2008, 10(4), 43001 CrossRef.
- D. Zhang, Z. Lü, C. Meng, X. Du, Z. Zhou, Z. Zhao and J. Yuan, Synchronizing terahertz wave generation with attosecond bursts, Phys. Rev. Lett., 2012, 109(24), 243002 CrossRef.
- J. Das and M. Yamaguchi, Tunable narrow band THz wave generation from laser induced gas plasma, Opt. Express, 2010, 18(7), 7038 CrossRef CAS PubMed.
- A. V. Borodin, N. A. Panov, O. G. Kosareva, V. A. Andreeva, M. N. Esaulkov, V. A. Makarov, A. P. Shkurinov, S. L. Chin and X.-C. Zhang, Transformation of terahertz spectra emitted from dual-frequency femtosecond pulse interaction in gases, Opt. Lett., 2013, 38(11), 1906 CrossRef CAS PubMed.
- M. Kress, T. Löffler, S. Eden, M. Thomson and H. G. Roskos, Terahertz-pulse generation by photoionization of air with laser pulses composed of both fundamental and second-harmonic waves, Opt. Lett., 2004, 29(10), 1120 CrossRef CAS.
- K. Y. Kim, A. J. Taylor, J. H. Glownia and G. Rodriguez, Coherent control of terahertz supercontinuum generation in ultrafast laser–gas interactions, Nat. Photonics, 2008, 2(10), 605 CrossRef CAS.
- X. Xie, J. Dai and X.-C. Zhang, Coherent control of THz wave generation in ambient air, Phys. Rev. Lett., 2006, 96, 075005 CrossRef.
- N. V. Vvedenskii, A. I. Korytin, V. A. Kostin, A. A. Murzanev, A. A. Silaev and A. N. Stepanov, Two-color laser-plasma generation of terahertz radiation using a frequency-tunable half harmonic of a femtosecond pulse, Phys. Rev. Lett., 2014, 112, 055004 CrossRef CAS.
- I. Babushkin, S. Skupin and J. Herrmann, Generation of terahertz radiation from ionizing two-color laser pulses in Ar filled metallic hollow waveguides, Opt. Express, 2010, 18, 9658 CrossRef CAS PubMed.
- W. Zhang, S.-F. Guo, S.-Q. Duan and X.-G. Zhao, Terahertz wave generation from hyper-Raman lines in two-level quantum systems driven by two-color lasers, Opt. Express, 2013, 21, 21349 CrossRef PubMed.
- D. W. Schumacher and P. H. Bucksbaum, Phase dependence of intense-field ionization, Phys. Rev. A: At., Mol., Opt. Phys., 1996, 54(5), 4271 CrossRef CAS.
- P. B. Corkum, N. H. Burnett and F. Brunel, Above-threshold ionization in the long-wavelength limit, Phys. Rev. Lett., 1989, 62, 1259 CrossRef CAS.
- P. B. Corkum, Plasma perspective on strong field multiphoton ionization, Phys. Rev. Lett., 1993, 71(13), 1994 CrossRef CAS.
- S. C. Rae and K. Burnett, Detailed simulations of plasma-induced spectral blueshifting, Phys. Rev. A: At., Mol., Opt. Phys., 1992, 46(2), 1084 CrossRef CAS.
- X. Sun and X.-C. Zhang, Terahertz radiation in alkali vapor plasmas, Appl. Phys. Lett., 2014, 104, 191106 CrossRef PubMed.
- V. B. Gildenburge and N. V. Vvedenskii, Optical-to-THz wave conversion via excitation of plasma oscillations in the tunneling ionization process, Phys. Rev. Lett., 2007, 98, 245002 CrossRef.
- A. A. Silaev and N. V. Vvedenskii, Residual-current excitation in plasmas produced by few-cycle laser pulse, Phys. Rev. Lett., 2009, 102, 115005 CrossRef CAS.
- C. S. Liu and V. K. Tripathi, Tunable terahertz radiation from a tunnel ionized magnetized plasma cylinder, J. Appl. Phys., 2009, 105, 013313 CrossRef PubMed.
| This journal is © The Royal Society of Chemistry 2015 |