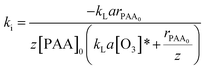Kinetics and mechanism study of direct ozonation organics in aqueous solution
Qizhou Dai,
Liling Chen,
Shijie Zhou and
Jianmeng Chen*
College of Biological and Environmental Engineering, Zhejiang University of Technology, Hangzhou 310032, China. E-mail: jchen@zjut.edu.cn; Fax: +86 571 88320882; Tel: +86 571 88320276
First published on 10th February 2015
Abstract
In this study, the kinetics and mechanism of direct ozonation organics in aqueous solution were explored. Phenoxyacetic acid was selected as the model pollutant and ozonation experiments were performed in a bubble batch reactor to determine the rate constants for the direct reaction. Two kinetic methods were used for determination of different kinetic rate constants (kapp and ki). The first group of results showed that degradation of phenoxyacetic acid followed pseudo-first-order kinetics. A simplified model was derived related to the operational parameters on phenoxyacetic acid degradation, and the apparent rate constant kapp was obtained. The reaction was proved in the slow kinetics of the gas–liquid reaction, and the kinetic constant ki was built. Influence of pH on kapp and ki, the O3 dosage, and the initial phenoxyacetic acid concentration were carefully analyzed.
1. Introduction
Development in industrial production has caused amounts and categories of pharmaceutical production to increase. Some pharmaceuticals, such as antibiotics and pharmaceutical intermediates, are persisting organic pollutants and cannot be treated with traditional biological technology if directly discharged into the environment.1–4 Thus, identifying a suitable method for pharmaceutical wastewater treatment is one of the focuses of environmental workers and the government, with the aim of reducing the intolerable burden on the environment.5–8Some effective efforts have been made in reduction of the toxicity of pharmaceutical wastewater, such as advanced oxidation processes (AOPs).9–11 Ozonation is a useful AOP in water treatment technology because ozone is an oxidizing agent showing high reactivity with different kinds of pharmaceuticals.12,13 During ozonation, ozone either reacts selectively with organic pollutant or decomposes in water to form free hydroxyl radical, which is another stronger oxidizing agent with high potential (2.80 eV) leading to indirect reactions.14
The reaction of target pollutant B with molecular ozone (O3) and hydroxyl radicals (˙OH) during ozonation is expressed in eqn (1) and (2) parallel reactions:15
| B + O3 → products | (1) |
| B + ˙OH → products | (2) |
Thus, for an ozone-reacting compound B, the chemical reaction rate rB can be expressed as follows:
| rB = −(zkO3[B][O3] + kOH˙[B][˙OH]) | (3) |
The stoichiometric ratio z is the number of moles of compound B consumed per mole of ozone consumed. kO3 is the second-order rate constant between ozone and compound B, and kOH is the second-order rate constant between hydroxyl radical and compound B. [B], [O3], and [˙OH] are the concentrations of target compound B, ozone, and hydroxyl radical, respectively.
Ozonation is a heterogeneous reaction and the kinetics of heterogeneous reactions are governed by absorption theories of gases in liquids along with chemical reactions.16 So far, the two most commonly applied absorption theories are the film and surface renewal theories. Two-film theory is relatively mature and has been widely applied. The basis of the theory is mainly diffusion law and the gas–liquid mass transfer model. Thus the main aim of ozonation kinetics is to derive the mass transfer coefficients and reaction rate constants. Eqn (4) represents the mass transfer of ozone from the gas phase to the liquid phase, where kLa is the volumetric mass transfer coefficient.
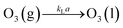 | (4) |
In view of the competition between ozone decomposition and the intermediates produced in the processes, absorption rate equations are unsuitable for irreversible second-order reactions.17 It is necessary to add a radical scavenger into the reactor to avoid ozone decomposition. The ozone decomposition mechanism involves an initiation reaction, a propagation reaction, and a termination reaction. The free radical species are exactly formed in the initiation or propagation reactions of ozone with agents such as hydroxyl and hydroperoxide ion. Among these, the hydroxyl radical is the main threat.18 tert-Butyl alcohol (TBA) reacts with hydroxyl radicals quickly (k = 5 × 108 M−1 s−1) and O3 slowly (k = 0.03 M−1 s−1),15,19 therefore, TBA can be used as a hydroxyl radical scavenger.
Although there have been some studies on oxidation of relevant pharmaceuticals,12 the developing kinetic aspects are still limited. In this study, phenoxyacetic acid (PAA) is selected as the model pollutant because it is an important pharmaceutical intermediate and widely applied in the pharmaceutical industry. It can be used as the parent molecule of herbicides, highly toxic compounds applied in the agricultural fields, and also in preparation of cefazolin, penicillin, and meclofenoxate.
The aim of this study was to establish a database with kinetic rate constants for the direct reaction of PAA degradation. Two kinetic methods for PAA degradation in the ozonation system were used and corresponding models were built. One relatively macroscopic kinetics model was established with the ozone dosage, the initial concentration of phenoxyacetic acid, and the pH value, which could be used easily in highly concentrated organic wastewater pollution treatment with ozonation. Another model studying the characteristics of the initial kinetic to reflect the reaction rate constant was also discussed. This paper provides basic data and kinetic reference for ozonation of pharmaceutical wastewater.
2. Experimental
2.1 Materials and reagents
Phenoxyacetic acid was purchased from Shanghai J&K Scientific Ltd. (China), (purity 99%). tert-Butyl alcohol (TBA) was chosen as the radical scavenger and purchased from Shanghai Lingfeng Chemical Reagent (China) Co., Ltd.All other chemicals used in the experimental process were analytical reagent or guaranteed reagent. Ultra-pure water was used as experimental water. The pH value of the solutions was adjusted with sodium hydroxide.
2.2 Apparatus and methods
Ozone was produced by an ozone generator (CFY-3) with high purity oxygen (99.999%). The experiments were carried out in a cylindrical Pyrex glass reactor (inner circulation) with a capacity of 1.5 L at room temperature. Sample connection was set on top of the reactor. An aeration head was fixed at the center of the bottom of the reactor for gas distribution. At the beginning of the reaction, small bubbles of ozone were placed in sufficient contact with the solution through the aeration head, thus forming the gas–liquid two-phase. Samples were withdrawn at fixed times, filtered through 0.45 μm pore size membrane filters, and analyzed.2.3 Analytical methods
Phenoxyacetic acid (PAA) was detected by high performance liquid chromatography (1200, Agilent Technologies, USA) with a UV-detector at 210 nm using a C18 reversed phase column. The column temperature was 30 °C. The mobile phase was a mixture of ammonium biphosphate (pH = 7, adjusted by ammonia water) and acetonitrile at 85![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 15 (v/v) at 0.8 mL min−1 flow rate. The injection volume was 5 μL. Intermediates produced in the ozonation/TBA system were detected using HPLC, IC, and GC-MS technologies. The methods were performed as described previously.17
15 (v/v) at 0.8 mL min−1 flow rate. The injection volume was 5 μL. Intermediates produced in the ozonation/TBA system were detected using HPLC, IC, and GC-MS technologies. The methods were performed as described previously.17
3. Results and discussion
3.1 Effect of tert-butyl alcohol on PAA removal
Fig. 1 shows the effect of the presence and absence of tert-butyl alcohol (TBA) in acid, neutral, and alkaline conditions for PAA removal. The initial pH was investigated in the range of 3.0–11.0. The effect of pH from 3.0 to 7.0 on PAA removal was non-significant, but showed a rising trend in alkaline environment without addition of TBA. The presence of TBA caused a negative acceleration of PAA removal compared with experiments carried out under the same operating conditions in the absence of TBA. It is likely that when pH is lower than 12.0, the ozone decomposition has to compete for the available ozone that reacts with pollutants.18 After 50 min at pH 3.0 without TBA, 79.22% of PAA was removed, compared with 67.14% with TBA. This is evident of a competitive effect of ozone decomposition. In this case, the ozone decomposition can be stopped by addition of a scavenger of hydroxyl radicals (TBA).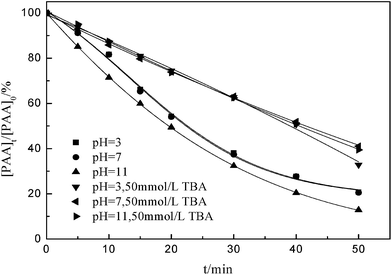 | ||
| Fig. 1 Effect of presence and absence of TBA on degradation of phenoxyacetic acid. Experimental conditions: [PAA]0 = 1000 mg L−1, ozone dosage = 40 mg min−1. | ||
Intermediates formed during ozonation with TBA were identified by HPLC, IC, and GC-MS technologies. By comparison with intermediates formed during ozonation alone, as described in a previous article,17 it was found that TBA rarely affected the categories of intermediates.
3.2 Kinetic model of pseudo first-order reaction
Ozonation experiments were performed in the presence of scavengers of hydroxyl radicals to guarantee direct ozonation in the environment, and aimed at studying the kinetic models of direct ozone reactions between ozone and phenoxyacetic acid (PAA). It can be assumed that the second term on the right side in eqn (3) is negligible under experimental conditions with ozone in great excess.| rPAA = −kapp[PAA] | (5) |
Integration of the apparent rate constant leads to
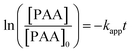 | (6) |
| No. | T/K | pH | [PAA]0/mg L−1 | TBA/mmol L−1 | QO3/mg min−1 | R2 | kapp/min−1 |
|---|---|---|---|---|---|---|---|
| 1 | 298 | 3 | 200 | 50 | 40 | 0.9915 | 9.68 × 10−2 |
| 2 | 298 | 3 | 500 | 50 | 40 | 0.9939 | 3.64 × 10−2 |
| 3 | 298 | 3 | 1000 | 50 | 40 | 0.9934 | 1.68 × 10−2 |
| 4 | 298 | 3 | 2000 | 50 | 40 | 0.9962 | 0.62 × 10−2 |
| 5 | 298 | 3 | 1000 | 50 | 16 | 0.9970 | 0.51 × 10−2 |
| 6 | 298 | 3 | 1000 | 50 | 24 | 0.9971 | 0.79 × 10−2 |
| 7 | 298 | 3 | 1000 | 50 | 32 | 0.9976 | 1.28 × 10−2 |
| 8 | 298 | 5 | 1000 | 50 | 40 | 0.9952 | 1.75 × 10−2 |
| 9 | 298 | 7 | 1000 | 50 | 40 | 0.9973 | 1.61 × 10−2 |
| 10 | 298 | 9 | 1000 | 50 | 40 | 0.9967 | 1.70 × 10−2 |
| 11 | 298 | 11 | 1000 | 50 | 40 | 0.9952 | 1.70 × 10−2 |
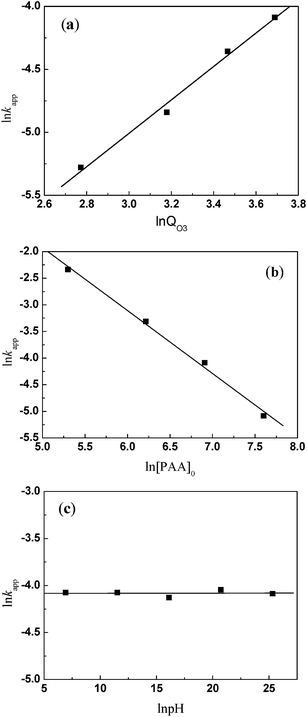
If relatively macroscopic kinetics are established with optimization of operational factors, this will allow control of the highly concentrated organic wastewater pollution by ozonation. As dissolved ozone concentration is difficult to calculate, a relationship between kapp and O3 dosage is supposed. Therefore, an empirical equation forms as suggested by Dai et al.:21
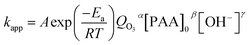 | (7) |
Eqn (7) expressed in logarithmic form becomes
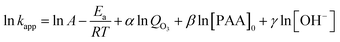 | (8) |
Regression analysis was conducted between the first item and the O3 dosage, the initial concentration of PAA, and the pH value, respectively. Corresponding α and β were equal to 1.3273 and −1.1816 (Fig. 2a and b) with linear correlation coefficients of 0.9918 and 0.9948, respectively. As a result of the nonlinear relationship between ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kapp and ln[OH−], γ was regarded as 0 (Fig. 2c).
kapp and ln[OH−], γ was regarded as 0 (Fig. 2c).
Thus eqn (8) can be converted to
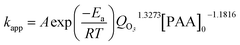 | (9) |
As the experiments were done at room temperature, A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−Ea/RT) was obtained from substitution of all experimental data into eqn (9). The result was equal to 0.51. Finally, the kinetic model turns into
exp(−Ea/RT) was obtained from substitution of all experimental data into eqn (9). The result was equal to 0.51. Finally, the kinetic model turns into
| [PAA]t = [PAA]0exp(−0.51QO31.3273[PAA]−1.18160t) | (10) |
3.3 Kinetic model in initial stage
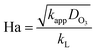 | (11) |
Some research23–25 has been done to study DO3. In the ozonation process, the empirical correlation of Johnson and Davis25 can be used to determine DO3:
| DO3 = (5.9 ± 0.04) × 10−10T/μs | (12) |
Determination of the individual mass transfer coefficient kL in liquid phase is dependent on type of reactors. For the bubble batch reactor in the experiment, kL could be determined by detecting mass transfer of CO2. Based on the absorption reaction of CO2 in the Na2CO3–NaHCO3 system, with hypochlorite ion and NaAsO2 as the catalysts, k′L, the individual mass transfer coefficient of CO2, could be obtained using the plot method of Roberts and Danckwerts.26 The basic requirement was that the absorption reaction of CO2 was the pseudo first-order reaction. The absorption rate is defined as follows:
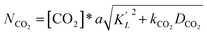 | (13) |
Then eqn (13) can be converted into
| (NCO2/[CO2]*)2 = (ak′L)2 + a2kCO2DCO2 | (14) |
From eqn (14), it can be seen that (NCO2/[CO2]*)2 ∼ kCO2DCO2 shows a linear relationship. k′L could be attained by variation of kCO2DCO2. DCO2 was equal to 1.58 × 10−9 m2 s−1. Finally, kL is determined by the calculation of eqn (15).27
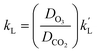 | (15) |
| No. | T/K | pH | [PAA]0/mg L−1 | QO3/mg min−1 | kL/m s−1 | a | Ha number |
|---|---|---|---|---|---|---|---|
| 1 | 298 | 3 | 200 | 40 | 8.10 × 10−5 | 95.3 | 1.86 × 10−2 |
| 2 | 298 | 3 | 500 | 40 | 8.10 × 10−5 | 95.3 | 1.14 × 10−2 |
| 3 | 298 | 3 | 1000 | 40 | 8.10 × 10−5 | 95.3 | 0.77 × 10−2 |
| 4 | 298 | 3 | 2000 | 40 | 8.10 × 10−5 | 95.3 | 0.47 × 10−2 |
| 5 | 298 | 3 | 1000 | 16 | 6.90 × 10−5 | 50.2 | 0.50 × 10−2 |
| 6 | 298 | 3 | 1000 | 24 | 7.20 × 10−5 | 62.8 | 0.60 × 10−2 |
| 7 | 298 | 3 | 1000 | 32 | 7.60 × 10−5 | 87.4 | 0.72 × 10−2 |
| 8 | 298 | 5 | 1000 | 40 | 8.10 × 10−5 | 95.3 | 0.79 × 10−2 |
| 9 | 298 | 7 | 1000 | 40 | 8.10 × 10−5 | 95.3 | 0.76 × 10−2 |
| 10 | 298 | 9 | 1000 | 40 | 8.10 × 10−5 | 95.3 | 0.78 × 10−2 |
| 11 | 298 | 11 | 1000 | 40 | 8.10 × 10−5 | 95.3 | 0.78 × 10−2 |
| rPAA = −zki[PAA]b[O3]b | (16) |
The presence of dissolved ozone in water is a symbol of the slow kinetic regime. For the slow kinetic regime, the reaction factor E (eqn (17)) is 1, which is perceived as the ratio between the actual chemical absorption rate and that of physical absorption in the gas–liquid reaction.18
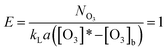 | (17) |
This method has a disadvantage in that the value of the ozone concentration is vague. Actually, the concentration of dissolved ozone is theoretically zero at the beginning of reaction. Nonetheless, application of the mass balance of ozone in water is handled well with this problem. Eqn (18), in the case of a semi-batch reactor, is as follows:18
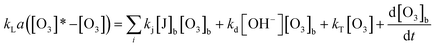 | (18) |
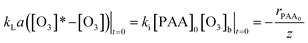 | (19) |
From the change of eqn (19), the concentration of ozone in the initial reaction is
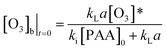 | (20) |
Combining eqn (17) and (20) allows us to determine kinetic constant ki in the initial stage:
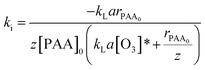 | (21) |
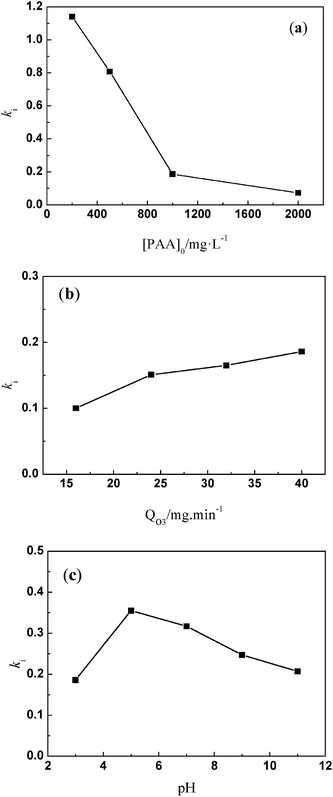
Table 2 shows that some parameters, such as individual mass transfer coefficients and the Hatta number, are useful to determine kinetic constant ki in the initial stage. Comparison of ki with different parameters, such as pH value, the initial concentration of PAA, and the ozone dosage is shown in Fig. 3. Fig. 3a shows the effect of different initial concentrations of PAA ([PAA]0) on ki. The greater the initial concentration of PAA, the less was ki, which was the same as the variation of kapp with increasing initial concentration of PAA. Fig. 3b shows the effect of the ozone dosage (QO3) on ki. When the ozone dosage increased from 16 to 40 mg L−1, ki could be regarded as independent of the value of the stable ozone concentration in agreement with Leitner et al.29 It is clear that the effect of ozone dosage on kapp is larger than on ki. Fig. 3c shows the effect of pH on ki. Increasing the pH value from 3.0 to 11.0, variation tendency of ki was not evident which is almost identical to that of kapp. This explained directly that the main sites of reaction result from molecular ozone only, and that ozone decomposition was inhibited well by TBA. Results shown in Tables 1 and 2 confirmed that the relationship between kapp and ki. kapp changed with variation of ki and the concentration of ozone.
4. Conclusions
Kinetic models of PAA degradation by ozonation were discussed and two rate constants kapp and ki were carefully explored. The apparent rate constant kapp was supposed to be related to the pH value, the initial concentration of PAA, the O3 dosage, and the temperature. A kinetics model was proposed as an exponential function of [PAA]t = [PAA]0exp(−0.51QO31.3273[PAA]−1.18160t).The calculated results showed that all Ha constants are lower than 0.3 in PAA degradation by ozonation, so the reaction was proved to be in the slow kinetic regime of gas–liquid reaction. In kinetic study of the initial stage, establishment of the mass balance equation of ozone and PAA in water determined the kinetic constant ki.
Comparing ki and kapp under different conditions, the results implied that there were effects of PAA initial concentration on kapp and ki, and that these followed the same trend. The ozone dosage did not make any difference to ki, but did to kapp. Increasing the pH value from 3.0 to 11.0, variation tendency of ki was not evident which is almost identical to that of kapp and proved ozone decomposition was inhibited well by TBA. The mathematical models are able to reproduce the experimental observations concerning the reaction rate of direct ozonation. This paper provides basic data and kinetic reference for ozonation of pharmaceutical wastewater.
Acknowledgements
The authors are grateful for the financial support provided by the National Natural Science Foundation of China (21306175) and the Project of Science and Technology Office of Zhejiang Province (2008C13014-6).Notes and references
- B. I. Escher, R. Baumgartner, M. Koller, K. Treyer, J. Lienert and C. S. McArdell, Water Res., 2011, 45, 75–92 CrossRef CAS PubMed.
- A. Joss, H. Siegrist and T. A. Ternes, Water Sci. Technol., 2008, 57, 251–255 CrossRef CAS PubMed.
- I. M. Sebastine and R. J. Wakeman, Process Saf. Environ. Prot., 2003, 81, 229–235 CrossRef CAS.
- K. Kümmerer, Chemosphere, 2001, 45, 957–969 CrossRef.
- J. L. Zhou, Z. L. Zhang, E. Banks, D. Grover and J. Q. Jiang, J. Hazard. Mater., 2009, 166, 655–661 CrossRef CAS PubMed.
- Q. Z. Dai, J. Y. Wang, J. Chen and J. M. Chen, Sep. Purif. Technol., 2014, 127, 112–120 CrossRef CAS PubMed.
- H. K. Singh, M. Saquib, M. M. Haque, M. Muneer and D. W. Bahnemann, J. Mol. Catal. A: Chem., 2007, 264, 66–72 CrossRef CAS PubMed.
- S. P. Kamble, S. B. Sawant and V. G. Pangarkar, Chem. Eng. Res. Des., 2006, 84, 355–362 CrossRef CAS.
- F. J. Beltrán, A. Aguinaco, J. F. García-Araya and A. Oropesa, Water Res., 2008, 42, 3799–3808 CrossRef PubMed.
- X. Liu, T. Garoma, Z. Chen, L. Wang and Y. Wu, Chemosphere, 2012, 87, 1134–1140 CrossRef CAS PubMed.
- F. J. Beltrán, A. Aguinaco and J. F. García-Araya, Water Res., 2009, 43, 1359–1369 CrossRef PubMed.
- J. Rivas, O. Gimeno, A. Encinas and F. Beltrán, Chemosphere, 2009, 76, 651–656 CrossRef CAS PubMed.
- V. Farines, S. Baig, J. Albet, J. Molinier and C. Legay, Chem. Eng. J., 2003, 91, 67–73 CrossRef CAS.
- L. Zhong and C. H. Kuo, Chin. J. Chem. Eng., 2000, 8, 272–275 CAS.
- Z. Q. Zeng, H. K. Zou, X. Li, M. Arowo, B. C. Sun, J. F. Chen, G. W. Chu and L. Shao, Chem. Eng. J., 2013, 229, 404–411 CrossRef CAS PubMed.
- C. N. Satterfield, Mass transfer in heterogeneous catalysis, Massachusetts Institute of Technology Press, Cambridge, 1970 Search PubMed.
- Q. Z. Dai, L. L. Chen, W. Chen and J. M. Chen, Sep. Purif. Technol., 2015, 142, 287–292 CrossRef CAS PubMed.
- F. J. Beltrán, Ozone reaction kinetics for water and wastewater systems, Taylor & Francis e-library, 2005 Search PubMed.
- J. Staehelin and J. Hoigné, Environ. Sci. Technol., 1985, 19, 1206–1213 CrossRef CAS PubMed.
- Z. Q. He, S. Song, H. M. Zhou, H. P. Ying and J. M. Chen, J. Chem. Ind. Eng., 2006, 57, 2965–2969 Search PubMed.
- Q. Z. Dai, J. Y. Wang, L. L. Chen and J. M. Chen, Ind. Eng. Chem. Res., 2014, 53, 11593–11600 CrossRef CAS.
- J. C. Charpentier, Adv. Chem. Eng., 1981, 11, 1–133 CAS.
- C. R. Wilke and P. Chang, AIChE J., 1955, 1, 264–270 CrossRef CAS.
- R. G. Utter, J. B. Burkholder, C. J. Howard and A. R. Ravishankara, J. Phys. Chem., 1992, 96, 4973–4979 CrossRef CAS.
- P. N. Johnson and R. A. Davis, J. Chem. Eng. Data, 1996, 41, 1485–1487 CrossRef CAS.
- D. Roberts and P. V. Danckwerts, Chem. Eng. Sci., 1962, 17, 961–969 CrossRef CAS.
- W. R. Zhao, Z. B. Wu and D. H. Wang, J. Hazard. Mater., 2006, 137, 1859–1865 CrossRef CAS PubMed.
- F. J. Beltrán, G. Ovejero, J. M. Encinar and J. Rivas, Ind. Eng. Chem. Res., 1995, 34, 1596–1606 CrossRef.
- N. K. V. Leitner and B. Roshani, Water Res., 2010, 44, 2058–2066 CrossRef PubMed.
| This journal is © The Royal Society of Chemistry 2015 |