A microdevice for producing monodispersed droplets under a jetting flow

Abstract

A new microdevice by extending capillaries into a step microchannel for generating monodispersed droplets was specially designed. A much wider narrowing jetting flow regime can be easily realized in this new device. The new microchannel and the operating regime make it possible to produce monodispersed microdroplets that are one to two magnitudes smaller than the main channel size. Scaling laws of jet diameters and droplet sizes are developed in both theory and experiments. The device turns out to be a good platform for tiny droplet preparation under the jetting flow compared with conventional microchannels.

---

Introduction

Monodispersed microdroplets have many applications in biomedicine and biochemical analysis, such as drug delivery,^1,2 complex multiple emulsions,^3–5 enzyme molecule analysis⁶ and nucleic acid detection.⁷ Among the various methods, microfluidics is one of the most popular ways for producing monodispersed microdroplets. Different methods have been developed with microfluidic devices, such as cross-flowing shearing,^8,9 perpendicular flowing shearing,¹⁰ hydrodynamic flow focusing,^11,12 coflowing rupturing,^13,14 and geometry-dominated breakup.¹⁵ But it is still considered to be a challenging job to control the drop size in the range of 1–100 μm until now.

In recent research, droplet formation is normally achieved by dripping regime for its highly stable breakup process. Nevertheless, the droplet sizes are normally in the same of magnitude of the structure sizes of microchannels under dripping.^16,17 Some researchers fabricated smaller microdevices and thus prepared tiny droplets.¹⁸ The techniques of embedding capillaries was used to decrease the structure sizes and droplets with sizes one order of magnitude smaller were produced.¹⁹ To avoid the limitation of dripping-to-jetting transition, microchannels with complex structures were made.²⁰ Unfortunately, small sizes and complex structure microchannels require a high level of fabrication and tend to clog, and the operating range is very narrow as well, which is difficult for large-scale preparation.

To realize microdroplet preparation in large scales, we need to reduce the feature size of disperse phase, but not the structure size. Jetting is a considerable choice to reduce the feature sizes. However, the jets often tend to break into polydispersed droplets for the uncontrollable Rayleigh instability.²¹ To stabilize the breakup process of jetting, researchers developed flow focusing (FF) devices. FF devices come up with an orifice to control the droplet behaviors. Gañán-Calvo and Gordillo²² produced highly monodispersed gas bubbles using a technique called capillary flow focusing. They found a simple scaling law for the prediction of droplet sizes. The capillary flow focusing device was implemented by Anna to form droplets in planar microchannels. They found that the drop size is dictated by the diameter of a thin focused thread which is much smaller than the width of the orifice.¹¹ Notably, the jetting regime in FF devices possesses more advantages than that in other types of devices. Co-flow in FF devices at the orifice deforms the interface and fuels a tip-streaming process,^23,24 giving rise to the steady emission of thin jets.²⁵ In recent research, flexible FF devices enabling tuning of the droplet breakup regime and high-pressure endured 3D FF devices have been fabricated.^26,27 Many kinds of functional materials by flow-focusing regime were produced.^28–30 Phase change process was introduced in FF devices to prepare tiny and complex droplets.^31,32 However, it should be noted that the operating range for produce uniform microdroplets under jetting in FF devices is still narrow. Due to the difficulty of the alignment of the injection tube with the exit orifice, as well as the fabrication of planar channel, the parallelization of flow focusing devices is not straightforward. Tedious chip-fabrication processes and costly materials hinder the development of FF devices²⁷ and the cost can dramatically increase with a channel geometry required for unique applications.³³

In FF devices, the jet is broken up at a stable frequency in a narrow operating range because of the difficulty to control the Rayleigh instability and we need to strengthen the absolute instability of the jets. In our previous work, we developed capillary embedded T-junction microchannels.¹⁹ This microchannel reduces the structure sizes of the channel. By means of extending capillaries into the main channel, we obtained small droplets³⁴ and microspheres with controllable structures³⁵ under dripping. Based on further analysis, the asymmetric structure of capillary embedded T-junction would strengthen the instability downstream the injecting position of disperse phase, providing us with a novel process to achieve a stable breakup frequency under jetting.

In this paper we introduce a newly designed capillary embedded step T-junction microchannel for the production of microdroplets. More specifically, we propose a novel method for the production of 10 to 100 μm monodispersed droplets under jetting by controlling the instability downstream the injecting position of disperse phase. We will present the scaling law for droplet sizes in the step T-junction channels. The flow fields and operating range in the new device will be studied. The comparison of the new device with the previous capillary embedded straight T-junction microchannel will be presented.

Materials and methods

The step T-junction devices were fabricated on polymethyl methacrylate (PMMA) chips using end mills. The main channel upstream was W′ = 1150 μm in width and h = 750 μm in height. The main channel downstream and the side channel with W = 750 μm both in width and height were fabricated. A quartz capillary with an inner diameter of 530 μm and outer diameter of 740 μm was embedded in the side channel and extended into the main channel. The devices were sealed using another PMMA chip and cured at 75 °C for 3 min using a high-pressure thermal sealing technique. With the quartz capillary extending into the main channel, different extending lengths l = 520, 600, 670 μm were studied respectively. Fig. 1 shows the structure of the channel and the droplets prepared in this device. In the experiments, the disperse phase was injected into the main channel from the quartz capillary. For the extreme large phase ratio as well as the high flow rate of the continuous phase in the system, a stable oblique interface is formed. Downstream the orifice, a steady liquid ligament issues from the apex of the interface in the capillary. The liquid ligament breaks up very soon into homogeneous size droplets (see Fig. 1a).

Fig. 1 (Color online) Sketch view of capillary embedded T-junction step microchannel and the prepared microdroplets: (a) high speed CMOS photograph of the droplet formation process in the microchannel. The outer phase flow forces the inner phase to issue a thin ligament that breaks up very soon into homogeneous size droplets. (b) Monodispersed microdroplets.

In this work, n-hexane was used as the disperse phase and deionized water was used as the continuous phase for the liquid/liquid (L/L) dispersion. Sodium dodecyl sulfate (SDS) used as the surfactants were added into the water phase with a concentration of 1 wt%. Glycerol was used to control the viscosities of the water phase with different concentrations. The physical properties of the working systems at 20 °C are given in Table 1. The viscosities were measured with an Ubbelohde viscometer. The interfacial tensions were measured with a pendent drop interfacial tension meter (OCAH200, DataPhysics Instruments GmbH, Germany).

Table 1 Physical properties of the working systems (20 °C)

Concentration of glycerol (wt%)	0	10	50
μc (mPa s)	1.42	1.58	6.92
γ (mN m^−1)	3.44	3.45	3.71

---

In the experiment, all the fluids were delivered by syringe pumps (PHD ultra, Harvard Apparatus, USA) with gastight syringes. The feed flow rates of disperse phase were controlled from 1 μL min⁻¹ to 20 μL min⁻¹, while those of continuous phase from 100 to 5000 μL min⁻¹. After changing any of the flow parameters, we allowed at least 1 min of equilibration time. The process was captured by a microscope (BX51, Olympus) and a high-speed CMOS camera (i-SPEED TR, Olympus, capture frame frequencies of 1000–10 000 fps). Using the recorded pictures, the jet lengths, jet diameters and droplet diameters were measured and their variation rules were carefully analyzed. The apparent average diameters (d_d) were determined by measuring at least 50 droplets. Polydispersity index (PDI) (σ) is defined as the equation below:

σ = δ/d_d × 100% (1)

where δ is the standard deviation of the apparent droplet diameters. All the PDIs at different experimental conditions were less than 5% in this work. Microparticle image velocimetry technique (micro-PIV, Dantec Dynamics, Denmark) was applied to measure the flow fields in the continuous phase. The aqueous continuous phase was seeded with latex particles whose diameter is 2 μm (LIFANGTIANDI Corporation, China).

Results and discussions

Comparison of different structures of capillary embedded microchannels

In the previous studies of T-junction microfluidic devices, the channel structures are either rigid T-shaped or simply modified structure. For researchers focused on the dripping regime in the past, T-junction microchannels for the jetting regime have not been carefully designed. In this part, dispersion variations (including the flow pattern maps, flow fields and interface structures) of conventional capillary straight embedded T-junction microchannels and our newly designed step microchannels are compared.

Comparison of flow pattern maps in different microchannels. In previous work on droplet formation process, the capillary number (Ca) was introduced to describe the force balance between the shear force induced by continuous-phase flow and Laplace pressure caused by interfacial tension:

Ca = μ_cu_c/γ (2)

where μ_c is the viscosity of the continuous phase; u_c is the shear velocity of the continuous phase. In the experiments, u_c in straight channels is calculated based on the projected area of the extended capillary in the flow direction, similar to that in literatures.³⁴ However, u_c in the step channel is modified by a theory analysis, which would be illustrated in detail in the section ‘Modification of the shear velocity’.

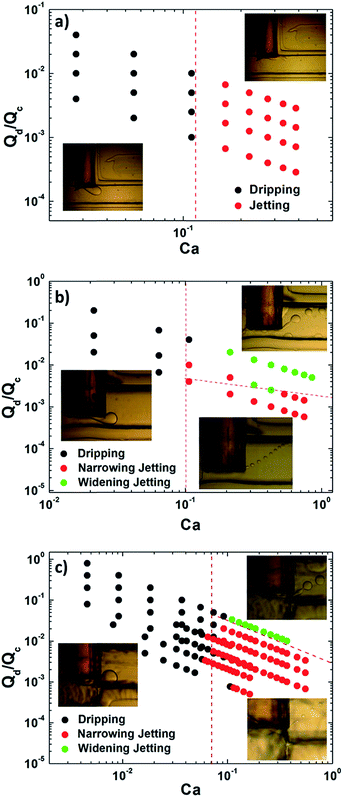
There are three different flow patterns with different operating parameters: dripping, narrowing jetting and widening jetting. When the two phase flow rates and phase ratio are not so large, droplet formation is dominated by shear force and the dripping regime is formed. Dripping is characterized by the periodic droplet formation pinching off at the tip of the capillary. As the flow rates increase, jets arise and the droplets pinch off at the end of the jet, dominated by Rayleigh instability. Actually, two jetting regimes exist.¹⁴ First, for the case that the inner fluid flow rates are low and the outer large, the jet thins as it moves downstream. The jet develops undulations driven by the Rayleigh instability and induces the formation of droplets slightly larger than the width of the jets, which is defined as ‘narrowing regime’. Second, when Ca of continuous phase above a critical number, the jet would retract back and form a spherical end at the tip of the jet as the disperse phase flow rates increase. This regime is known as the ‘widening regime’. It should be noted that the jet would breakup into polydispersed droplets under widening jetting.

As shown in Fig. 2, the transition from dripping to jetting is found to be in the range Ca = 0.07–0.12, coinciding with the measurement and calculation by former researchers.^36,37 But for the capillary embedded T-junction microchannels (see Fig. 2a), droplet formation under jetting is unstable and jets break into polydispersed droplets, which is undesirable.

Fig. 2 (Color online) Comparison of flow pattern maps in different microchannels. Flow pattern maps in capillary embedded T-junction microchannel, capillary extended straight microchannel and capillary extended step T-junction microchannel are compared. Flow rates of disperse phase range from 1 μL min⁻¹ to 20 μL min⁻¹, while those of continuous phase from 100 to 5000 μL min⁻¹.

As for the capillary extended straight microchannels, stable breakup process and monodispersed droplets would be achieved under proper conditions. Nevertheless, the variations are quite different between the step channel and the straight channel (see Fig. 2b and c). The system in straight channels would tend to fall in widening jetting even at low flow rates of the disperse phase. Thus the droplet formation frequencies would be lower than that of the step channel. While, the droplet breakup formation in step channels is stable and stay in narrowing jetting regime in a larger operating range (see Fig. 3). This phenomena would be illustrated by different flow fields and different positions of the maximum shear velocity determined by the different structures. Flow fields in both capillary extended channel would be presented in the following sections.

Fig. 3 (Color online) Droplet formation frequencies under different conditions. Droplet formation frequencies are extracted from the image analysis of the high speed video. Formation frequencies in the step channel go larger with the increase of continuous phase flow rates. However, the frequencies in the straight channel decrease when continuous flow rates become higher, illustrated by the arise of widening jetting regime induced by the different flow fields.

Comparison of flow fields and interface structures in different microchannels by micro-PIV technique. As discussed above, flow fields determine the flow patterns and play a fundamental role in the droplet breakup process. Micro-PIV technique is introduced to describe the continuous phase flow fields in the step/straight channels. For the extreme large phase ratio and formation of tiny droplets in the system, disperse phase flow influences little on the outer phase flow fields (see Fig. 4).

Fig. 4 (Color online) Velocity fields of the continuous phase measured by micro-PIV. The flow rates are 5 μL min⁻¹ and 4000 μL min⁻¹ for disperse phase and continuous phase respectively in both channels. Darker areas stand for higher velocities. (a) Velocity fields in the straight microchannel. (b) Velocity fields in the step microchannel. For the low flow rates of the disperse phase and the small sizes of droplets, the measured velocity fields depend little on the disperse phase flow.

Velocity fields measured by micro-PIV technique indicate that the positions of maximum shear velocity are quite different in two channels: for straight channels it locates upstream the capillary underside and for step channels it is absolutely fixed at the orifice. This illustrates the differences of flow pattern maps. Furthermore, different interface structures are found in the two microchannels for different velocity fields (see Fig. 5). As shown in the figures, the interface structures in straight channels are undulant while those in step channels are gentle. It proves that the flow/pressure fields in straight channels are chaotic while those in step channels are gradual, coinciding with the results presented by micro-PIV. Especially, when flow rates of the continuous phase are so high that the drop formation process is unstable owing to the high pressure drop in the straight channel, while, the system could remain stable in the step channel.

Fig. 5 (Color online) Comparison of different interface structures in step and straight microchannels. Flow rate of disperse phase is fixed at 5 μL min⁻¹. Similar extending lengths are applied to step and straight channels and different interface structures are observed by high speed CMOS camera.

Dispersion rules in capillary extended step microchannels

According to the analysis above, the capillary extended step microchannel proves to be an effective platform for the preparation of tiny monodispersed droplets under jetting flow. In this section, we would focus on the dispersion rules in this microchannel. The shear velocity would first be modified and the influences of the capillary extending length on the dispersion process would be discussed. Second, the operating range of the devices would be determined. Third, the jet diameters and the drop sizes would be calculated and measured in both theory and experimental.

The average droplet size variations with the flow rates of two phases are shown in Fig. 6. We observe the formation of monodispersed droplets under low disperse phase flow rates and high continuous phase flow rates (but also upper limits exist to avoid an overlong jet). Obviously, in dripping regime the droplet sizes vary little with the disperse phase flow rates, but in jetting regime the disperse phase flow rates influence the drop sizes much.

Fig. 6 (Color online) Droplet formation and average droplet size variation diagram. For the droplet size variation diagram, 50 wt% glycerol solution is chosen as the continuous phase as an example and the variation under jetting is extracted especially.

Modification of the shear velocity. The shear force when droplet formation is decided by the shear velocity in situ. Researchers modified the shear velocity influenced by the block of the large droplet⁸ and decreased the deviation by the velocity calculation based on the main channel sizes. In our previous work, the shear velocity in straight channels was calculated relying on the projected area in the flow direction.³⁴ However, in our newly designed step channel, the orifice structure is neither rigidly square nor rigidly circular, but a 3D structure, so the shear velocity should be carefully modified to reflect real process. We build a theoretical model based on flow resistance analysis. 3D area integration with flow resistance formula is invited and the calculated velocity fits well with the measured one (see section ESI†). We demonstrate the calculated shear velocity variation under different extending capillary lengths (see Fig. 7).

Fig. 7 (Color online) Model shear velocity variation under different extending capillary lengths. Inlet figure represents the velocity variation when l/W ranges from 0.01 to 1 and the velocity of u_m1 falls to 0 when l/W reaches 1. Main figure demonstrates the variation from l/W = 0.01 to l/W = 0.9.

In Fig. 7, l is the capillary extending length while W is the main channel width (750 μm in experimental). There are three kinds of shear velocities u. Among them, u_m1 stands for the calculated velocity in our model, u_m2 is the velocity based on the integration area and u_m3 is the calculated velocity by projected areas.

Based on the model velocities, it is apparent that the shear velocity in step channels would not increase much with the extension of the capillary, different from that in straight channels (see u_m3). When l/W is large (especially larger than 0.7), the shear velocity would not change a lot, which is proper for the parallelization of this kind of channels. A structure parameter α, which stands for the equivalent extending length (leading to the same calculated shear velocity) in step channels with straight channels, is invited to simplify the modelling process. Values of structure parameter α with different capillary extending lengths are demonstrated in Table 2.

Table 2 Values of structure parameter α with different capillary extending lengths

l/W	0.7	0.75	0.8	0.85	0.9
α	0.345	0.31	0.275	0.255	0.25

---

In analysis below, we take the step channel with l/W = 0.77 and α = 0.29 as the example for the discussion of the dispersion rules. Droplet breakup dynamics in channels with other extending lengths would be similarly analyzed when we consider the modification of shear velocities.

It should be stressed that the model velocities in the step channel is only related to the channel structure and has nothing to do with the fluid properties (see eqn (S13)†). In addition, the velocity increases linearly with the increase of the continuous phase flow rates, as that in straight channel (see Fig. S2†). Both features above validate our assumption that a structure parameter α with a fixed value exists in a fixed step microchannel (see Fig. 7).

Operating range for the narrowing jetting flow. The narrowing jetting flow would be achieved under proper operating parameters (see Fig. 6). According to those discussed above, we conclude three restrict conditions for this regime. First, the stable narrowing jetting regime would be reached when Ca of the continuous phase above a critical threshold, in this work namely

Ca_c ≥ 0.07 (3)

which is close to the transition Ca_c number in rigid T-junction microchannels.

Second, the restriction is made by the transition from narrowing jetting to widening jetting, which is mainly determined by the large inertial forces of the inner fluid. In previous study, researchers distinguished the widening jetting from dripping by means of the inner phase We_d number in co-flowing microchannels.¹⁴ We_d is defined as: We_d = ρ_dd_cu_d²/γ, where ρ_d is the density of the inner disperse phase, d_c is the inner diameter of the capillary and u_d is the inner disperse phase flow velocity in the capillary. When We_d is larger than 1, system would transfer from dripping to widening jetting. In this paper, the We_d is also introduced to describe the transition from narrowing jetting to widening jetting. Unfortunately, we cannot calculate the We_d by the capillary diameter. On the one hand, flow velocity of the disperse phase in the capillary is so small that the We_d based on the capillary diameter is minuscule (<10⁻⁵). On the other hand, the interface structures determine that the momentum of the disperse phase relies on the actual velocity in the jet and the jet diameter, but not the capillary diameter. So in this work, we assume the jet cylinder and calculate the We_d based on the measured jet diameter. Similar to that in co-flowing devices, transition from narrowing jetting to widening jetting occurs when We_d = O(1), namely

We_d ≤ 1 (4)

here we calculate the We_d as We_d = ρ_dd_ju_d²/γ, where d_j is the measured jet diameter and u_d is the velocity in the jet.

Third, as we've discussed above, overlong jets would lead to unstable dispersion process, which can be illustrated by the asymmetry of flow fields. There are some studies on the jet length under jetting regime in co-flowing and flow focusing devices.^21,38 Researchers indicated that the jet length is influenced by both inner and outer fluids. Based on the Ca_c of the continuous phase and the We_d of the disperse phase, a semi-empirical correlation for jet lengths is presented (see Fig. 8):

L_l/W = 10.60Ca_c^2.15We_d^0.27 (5)

where L_l is the jet length and W is the width of the main channel. It should be noted that the correlation applies under both narrowing jetting and widening jetting.

Fig. 8 (Color online) Predicted values of the jet lengths: jet lengths under both narrowing jetting and widening jetting are measured. Inlet figure shows the measured region at the orifice.

In this work, the length of the jet is restricted to 25% of the width of the main channel. From the eqn (5), the third restriction condition is achieved:

We_d ≤ 9 × 10⁻⁷ Ca_c⁻⁸ (6)

As depicted in Fig. 9, different experiments considered in this study satisfy well with the conditions given by eqn (3), (4) and (6).

Fig. 9 (Color online) Operating range for the narrowing jetting flow. Red dots indicate the experiment values in this study. Stable narrowing jetting are achieved under Ca_c = 0.07–0.21 and We_d = 0–1.

Scaling of the jet diameters. In this work, we restrict the system in the narrowing jetting regime. The Reynolds number (Re) at the orifice ranges from 0.01 to 40, which guarantees the effective diffusion of momentum across the jet.³⁹ As a result, the velocities of disperse phase and continuous phase reach equal downstream the orifice:where d_j is the diameter of the jet, U_c is the shear velocity of the continuous phase at the orifice and Q_d is the flow rate of the disperse phase.

As shown in ‘Modification of the shear velocity’, the shear velocity at the orifice satisfies U_c = Q_c/(αW²), and thus

For the step channel with l/W = 0.77 and α = 0.29, eqn (8) can be solved as:

We measure the jet diameters in this step channel, and a semi-empirical correlation is presented as:

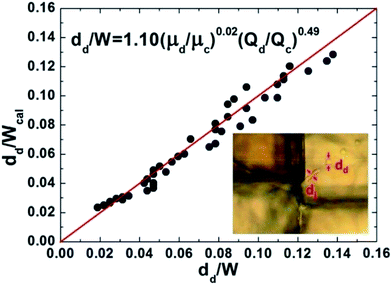
The semi-empirical correlation (10) is in good accordance with the theoretical eqn (9), validating our physical reasoning. Fig. 10 presents the measured diameters with the predicted ones and both fit well.

Fig. 10 (Color online) Predicted values of the jet diameters. Jet diameters are measured under narrowing jetting and inlet figure shows the measured region at the orifice.

Scaling of the droplet diameters. We've got the scaling rules of the jet diameters. To get the variation rules for droplet sizes, we must find the relationship between jet diameters and the droplet sizes. Based on mass balance, the droplet sizes satisfy and ω is the drop formation frequency and d_d is the diameters of the droplets.

The jets in narrowing jetting regime are under Rayleigh instability. We can assume that the droplet formation time is equal to that needed to elongate the jet to reach the wavelength of the maximum growth rate.³⁹ The corresponding maximum growth rate wavelength can be calculated as πd_j/k*, where k* is the dimensionless wavenumber and . Oh is Ohnesorge number and defined as . In our work, Oh ∼ O(10⁻¹) and k* is in little correlation with Oh in this range.³⁹ So the relationship can be described as . Considering that the flow velocity in the jet is assumed to be equivalent to the continuous phase velocity, we can calculate the drop formation frequency as 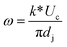where .

Combined these equations, we get:

For the step channel with l/W = 0.77 and α = 0.29, eqn (11) can be solved as:

The droplet diameters are measured in this step channel and a semi-empirical correlation is presented as:

The semi-empirical correlation (13) follows closely to the theoretical eqn (12). As shown in Fig. 11, the predicted values of the droplet sizes and the measured ones match very well.

Fig. 11 (Color online) Predicted values of the droplet diameters. Droplet diameters are measured under narrowing jetting and inlet figure shows the measured region at the orifice.

From eqn (12) and (13), we can derive that . By comparing the correlations for jet diameters and droplet sizes, we find d_d ≈ 2d_j, as reported in FF devices.^14,40

Even though dispersion rules in the step microchannel appear similar to those in co-flowing and FF devices, the operating range for stable narrowing jetting regime is much larger in the step channel due to the asymmetric flow fields (see Fig. 9). In addition, the channels are much cheaper and easier for parallelization.

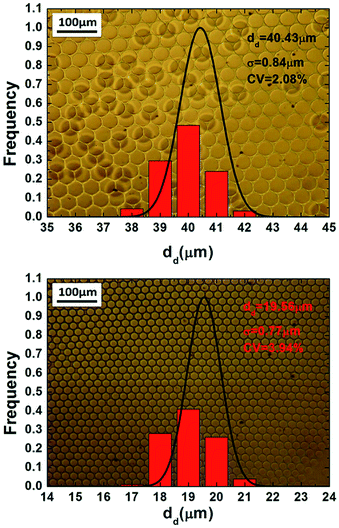
By adjusting the operating parameters, especially the two phase flow rates, different sizes of monodispersed droplets are achieved exactly. Fig. 12 shows the droplets we made with sizes of 20 μm and 40 μm. Both CVs are below 5%.

Fig. 12 (Color online) Droplets with different sizes. Average diameters, standard deviations and coefficients of variation are presented. Size distribution figures are compared with normal distribution curves.

An operation logic chart for precise control of droplet sizes in the step channel can be established as Fig. 13 under the results from theoretical analysis without experimental.

Fig. 13 Operation logic chart for precise control of droplet sizes.

Conclusions and outlook

We developed a new capillary embedded & extended step microchannel for microdroplet preparation. With the new channel, we successfully prepared monodispersed droplets with sizes from 10 to 100 μm, one to two magnitudes smaller than the main channel width, which has not been reported in literatures. Our new step channels are easy to fabricate and parallelize. Common commercial materials are needed and thus the cost of the channels is much lower than FF devices'.

Moreover, we established theoretical models for the dispersion process in the step channel. The shear velocities are carefully modified, the correlations predicting the jet lengths are presented and thus the operating range is precisely restricted. We built models to predict jet and droplet diameters, which matches well with the experimental results. There are some similarities of dispersion rules in this new channel with former FF device, but the operating range in the new one is much larger than the other, illustrated by the asymmetric flow fields.

This newly designed channel represents a novel method to produce monodispersed tiny droplets, which can benefit the preparation of microspheres. However, the systems for particle preparation are diverse. In future work, the dispersion rules of different systems including non-newtonian fluid, which is widely used in food and pharmaceutical industries,⁴¹ would be investigated carefully. Considering the similarities of the formation of bubbles and droplets, similar regime may apply to the preparation of microbubbles. And thus, the dispersion rules of bubbles in the step channel would also be studied.

Acknowledgements

We gratefully acknowledge the supports of the National Natural Science Foundation of China (91334201, U1463208) on this work.

Notes and references

1. J. Cejkova and F. Stepanek, Curr. Pharm. Des., 2013, 19, 6298–6314.
2. K. Tang and A. Gomez, J. Aerosol Sci., 1994, 25, 1237–1249.
3. W. Wei, X. Rui, J. Xiao-Jie, L. Tao, L. Li, D. A. Weitz and C. Liang-Yin, Lab Chip, 2011, 11, 1587–1592.
4. N. Deng, Z. Meng, R. Xie, X. Ju, C. Mou, W. Wang and L. Chu, Lab Chip, 2011, 11, 3963–3969.
5. R. Chen, P. Dong, J. Xu, Y. Wang and G. Luo, Lab Chip, 2012, 12, 3858–3860.
6. R. B. Liebherr and H. H. Gorris, Molecules, 2014, 19, 14417–14445.
7. S. Roediger, C. Liebsch, C. Schmidt, W. Lehmann, U. Resch-Genger, U. Schedler and P. Schierack, Microchim. Acta, 2014, 181, 1151–1168.
8. J. H. Xu, S. W. Li, J. Tan and G. S. Luo, Microfluid. Nanofluid., 2008, 5, 711–717.
9. P. Garstecki, M. J. Fuerstman, H. A. Stone and G. M. Whitesides, Lab Chip, 2006, 6, 437–446.
10. J. Tan, J. H. Xu, S. W. Li and G. S. Luo, Chem. Eng. J., 2008, 136, 306–311.
11. S. L. Anna, N. Bontoux and H. A. Stone, Appl. Phys. Lett., 2003, 82, 364–366.
12. A. G. Marin, F. Campo-Cortes and J. M. Gordillo, Colloids Surf., A, 2009, 344, 2–7.
13. P. B. Umbanhowar, V. Prasad and D. A. Weitz, Langmuir, 2000, 16, 347–351.
14. A. S. Utada, A. Fernandez-Nieves, H. A. Stone and D. A. Weitz, Phys. Rev. Lett., 2007, 99, 094502.
15. D. R. Link, S. L. Anna, D. A. Weitz and H. A. Stone, Phys. Rev. Lett., 2004, 92, 054503.
16. B. Ambravaneswaran, H. J. Subramani, S. D. Phillips and O. A. Basaran, Phys. Rev. Lett., 2004, 93, 034501.
17. V. Cristini and Y. C. Tan, Lab Chip, 2004, 4, 257–264.
18. S. Sugiura, M. Nakajima, H. Itou and M. Seki, Macromol. Rapid Commun., 2001, 22, 773–778.
19. J. H. Xu, S. W. Li, J. Tan, Y. J. Wang and G. S. Luo, AIChE J., 2006, 52, 3005–3010.
20. A. R. Abate and D. A. Weitz, Lab Chip, 2011, 11, 1713–1716.
21. M. L. Cordero, F. Gallaire and C. N. Baroud, Phys. Fluids, 2011, 23, 094111.
22. A. M. Gañán-Calvo and J. M. Gordillo, Phys. Rev. Lett., 2001, 87, 274501.
23. W. Jeong, J. Lim, J. Choi, J. Kim, Y. Lee, S. Kim, G. Lee, J. Kim, G. Yi and S. Yang, Lab Chip, 2012, 12, 1446–1453.
24. T. M. Moyle, L. M. Walker and S. L. Anna, Lab Chip, 2013, 13, 4534–4541.
25. A. M. Gañán-Calvo, J. M. Montanero, L. Martin-Banderas and M. Flores-Mosquera, Adv. Drug Delivery Rev., 2013, 65, 1447–1469.
26. B. R. Benson, H. A. Stone and R. K. Prud'Homme, Lab Chip, 2013, 13, 4507–4511.
27. W. Ping, W. Yong, L. Zhaofeng, L. Muting, L. Minfei and H. Liqun, Lab Chip, 2014, 14, 795–798.
28. Q. Wang, D. Zhang, H. Xu, X. Yang, A. Q. Shen and Y. Yang, Lab Chip, 2012, 12, 4781–4786.
29. A. S. Utada, E. Lorenceau, D. R. Link, P. D. Kaplan, H. A. Stone and D. A. Weitz, Science, 2005, 308, 537–541.
30. D. J. Han, J. H. Jung, J. S. Choi, Y. T. Kim and T. S. Seo, Lab Chip, 2013, 13, 4006–4010.
31. W. Jeong, M. Choi, C. H. Lim and S. Yang, Lab Chip, 2012, 12, 5262–5271.
32. Q. Zhang, X. Liu, D. Liub and H. Gai, Lab Chip, 2014, 14, 1395–1400.
33. S. Focaroli, S. Mazzitelli, M. Falconi, G. Luca and C. Nastruzzi, Lab Chip, 2014, 14, 4007–4016.
34. K. Wang, Y. C. Lu, J. H. Xu, J. Tan and G. S. Luo, AIChE J., 2011, 57, 299–306.
35. J. Xu, H. Zhao, W. Lan and G. Luo, Adv. Healthcare Mater., 2012, 1, 106–111.
36. A. Gupta and R. Kumar, Phys. Fluids, 2010, 22, 112001.
37. M. De Menech, P. Garstecki, F. Jousse and H. A. Stone, J. Fluid Mech., 2008, 595, 141–161.
38. S. L. Anna and H. C. Mayer, Phys. Fluids, 2006, 18, 121512.
39. E. Castro-Hernandez, V. Gundabala, A. Fernandez-Nieves and J. M. Gordillo, New J. Phys., 2009, 11, 075021.
40. T. Cubaud and T. G. Mason, Phys. Fluids, 2008, 20, 053302.
41. Y. Ren, Z. Liu and H. C. Shum, Lab Chip, 2014, 15, 121–134.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c5ra02397a

---