Structure and magnetic properties of open-ended silicon carbide nanotubes

Abstract

Nanotubes with open ends have been found to offer interesting opportunities in many applications. In this paper, the structures and magnetic properties of a series of open-ended SiCNTs have been studied through first-principles simulation. Our results reveal that the structures and magnetic properties of the open-ended SiCNT are strongly dependent on the tube diameter and chirality: (i) the open-ended armchair SiCNT is nonmagnetic due to the formation of spin-antiparallel pairs between the Si and C atoms at the tube mouth, and the self-closure behavior occurs at the tube mouth; (ii) the magnetic moment of the C-rich-ended zigzag or chiral SiCNT is nearly equal to the number of dangling bonds on the tube mouth; (iii) for the Si-rich-ended zigzag or chiral SiCNT, the spin density mainly locates on the isolated Si atoms at the tube mouth, the magnetic moment of each Si atom at the tube mouth is strongly dependent on the tube diameters. Our results might be helpful in deeply understanding the magnetic properties of SiCNTs, as well as provide guidance to design novel SiCNT-based nanodevices such as spintronic or field-emission display devices.

---

1. Introduction

The recently synthesized silicon carbide nanotube (SiCNT)¹ has attracted considerable attention due to its unique properties and potential applications. SiCNT is a structural analogue of a carbon nanotube (CNT) in nature, but is quite different from its carbon counterpart in properties. For example, the SiCNT is a semiconductor, weakly dependent on the tube chirality,^2,3 and has higher reactivity than CNT or the boron nitride nanotube (BNNT) due to its great polarity.^4–8 These unique properties of SiCNT make it a promising candidate for the design of electronic devices, gas sensors, metal-free catalysts in harsh environments. For example, it is found that the electronic properties of SiCNT could be modified by heteroatom (B, N, Fe or Al) doping,^3,9,10 and the chemical functionalization with H, CH₃, SiH₃, NH_x (x = 1, 2).^11,12 In addition, SiCNT has been predicted to be a promising sensor for some molecules (such as CO₂, CO, NO₂, NO, HCN, SO₂) in view of an appreciable adsorption energy and considerable amount of charge transfer between SiCNT and these molecules.^4,6,13,14 Sahimi et al.'s studies revealed that SiCNTs provide larger water flow enhancements than those reported for the CNTs, and they predicted that SiCNT could be used to develop polymeric membranes that can withstand harsh conditions at elevated pressures and temperatures.^15,16 Our previous results have shown that SiCNT could be a promising catalyst to cleave the N–H bonds in NH₃ and C–Cls bond in CCl₂.^17,18

On the other hand, nanotubes with open end are testified to offer interesting opportunities in the design of field-emission display (FED) or metal-free catalyst due to the local spin-polarizations at the tube edges or high reactivity as compared with pristine nanotubes. For example, theoretical studies have shown that open-ended CNT is a promising material for field emitter when functionalized by H₂O (ref. 19), and it could be used to cleave the chemical bond in H₂O, H₂ and O₂.¹⁹ Duan et al. proposed that the open-ended BNNT²⁰ or functionalized by carbon atoms²¹ presents the tremendous spin-splitting, which makes BNNT significant for applications of spintronic. It is also found that the open-ended BNNT is able to cleave the chemical bond in NH₃, H₂O, H₂ and O₂.^22,23 Hou et al. revealed that the open-ended AlN nanotube (AlNNT) with Al termination is more efficient for field emission than that of N-termination,²⁴ and Liu et al. pointed out that H₂ and H₂O dissociate when they are chemisorbed on the open-ended AlNNT.²⁵

In view of the unique properties of SiCNT and the potential applications of open-ended nanotube, we feel that it is highly desirable to explore the properties of open-ended SiCNT. In the present paper, we have studied the structure and magnetic properties of a series of open-ended SiCNTs by first-principle simulation. Our results reveal that magnetic properties of the open-ended SiCNT are strongly dependent on the atomic structures at the tube mouth. All the open-ended armchair SiCNT is a closing mouth structure without magnetism; the magnetism on C-rich-ended SiCNT is close to the number of dangling bonds at the tube mouth; the spin density on Si-rich-ended SiCNT mainly locates on the C (and Si) atoms at the tube end (and mouth), and the magnetic moment on these Si atoms is strongly dependent on the structure at the tube mouth.

2. Computational method

The density functional theory (DFT) calculation was performed using the Vienna Ab-Initio Simulation Package.^26,27 The electron–ion interaction was described by projector augmented-wave (PAW)²⁸ pseudopotentials. For the exchange and correlation functionals, we use the Perdew–Burke–Ernzerhof (PBE) version of the generalized gradient approximation (GGA).²⁹ The energy cutoff of 400 eV was used for the wave functions expansion. The same method also has been used in the previous studies on the SiCNT system.^30–32 K-point of 1 × 1 × 1 grid was used for Brillouin-zone integrations. The geometries were fully optimized until the forces on each atom is less than 0.01 eV Å⁻¹. The structure of SiCNT has been decoupled by a vacuum thickness larger than 15 Å (along a, b and c directions).

The molecular dynamics (MD) simulation and ionization potential (IP) calculation were carried out by using DMOL³ package.³³ In detail, the GGA-PBE method was considered, and all-electron calculations were undertaken with double numerical basis sets plus a polarization functional (DNP). The same method also has been used in the previous studies on the SiCNT system.^7,17,23 MD simulation was performed in the NVT ensemble, and the time step was set to be 2 fs. The Nosé–Hoover chain method³⁴ was used for temperature control. A default Nosé Q ratio of 2.0 and a default Nosé chain length of 2 were selected. It should be noted that, in this work, the SiCNT system contains about 100 atoms, and has a relatively large supercell (a = b = 25 Å, and c = 32 Å), which is quite time-consuming for the first-principle MD simulation by using VASP. Alternately, DMOL³ package could deal with the non-periodic system, and the time-consumption of MD simulation on SiCNT by using this package is obviously less than that in the case of VASP. Thus, DMOL³ package has been considered to perform the MD simulation on open-ended SiCNT.

The ionization potential (IP) value is defined as IP = E(N − 1) − E(N), where E(N) and E(N − 1) are the total ground-state energy in neutral (N) and singly positive charged (N − 1) systems. We choose a series of finite-length SiCNTs with different chiralities, where one mouth is opened and the other is terminated by hydrogen atoms to saturate the dangling bond. The lengths of the studied armchair, zigzag and chiral SiCNTs are 7 atomic layers.

3. Results and discussions

3.1 The structures of open-ended SiCNTs

Taking the pristine (8, 0) SiCNT as an example, two types of Si–C bonds could be found: one has the bond length of 1.78 Å and is in parallel with the tube axis, and another has the bond length of 1.80 Å, but is not in parallel with the tube axis. The structural parameters are in good agreement with previous studies.^{7,17,23,30–32} Initially, each Si or C atom at the open end of SiCNTs has one unpaired electron, corresponding to one dangling bond, similar to the case in the open-ended CNT or BNNT. After the relaxation, the open end structures of SiCNTs have changed in various ways as shown in Fig. 1. For the armchair open-ended (n, n) SiCNT (n = 4, 5, 6, and 7), two types of structures have been found after the relaxation: (i) for the open-ended (4, 4) and (5, 5) SiCNT, a completed closing mouth is obtained as shown in Fig. 1a, which is similar to the case in the open-ended armchair AlN nanotube (AlNNT).²⁴ Taking open-ended (5, 5) SiCNT as an example, Si–C pairs at the tube mouth interact with their nearest-neighbor ones during the structure relaxation, the dangling bonds of these atoms are saturated, and a hexagonal and quadrilateral alternating network is formed. The Si–C bond lengths at the hexagonal and quadrilateral sites are 1.83 Å and 1.76 Å, respectively. The nearest Si–Si bond length at the tube mouth is about 2.42 Å, which is slightly larger than that of the Si–Si single bond (2.36 Å),³⁵ indicating that a chemical bond might be formed between the two Si atoms; (ii) for the open-ended (6, 6) or (7, 7) SiCNTs with larger diameter, the structure of the tube mouth is very different from that of the open-ended (4, 4) or (5, 5) after the relaxation. In these structures, the Si–C bonds at the tube mouth have been drastically buckled, which is similar to the case in open-ended armchair BNNTs.²⁰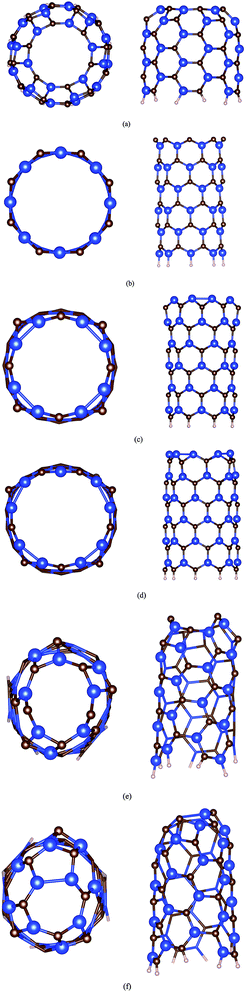

Fig. 1 Top and side view structures of (a) open-ended (6, 6), (b) C-rich-ended (8, 0), (c) Si-rich-ended (8, 0), (d) Si-rich-ended (9, 0), (e) C-rich-ended (5, 3) and (f) Si-rich-ended (5, 3) SiCNT.

Interestingly, the open-ended (6, 6) and (7, 7) SiCNTs with closed-mouth structure are also obtained, which is energetically much more stable than that of buckled-mouth structure. Thus, it is highly desirable to examine the phase transition of open-ended (6, 6) and (7, 7) SiCNTs from buckled-mouth structure to closed-mouth structure. To do this, the molecular dynamics (MD) simulations have been performed on the open-ended (6, 6) and (7, 7) SiCNTs with buckled-mouth structure under the room temperature. In MD simulation, the time step is 2 fs, and the total time is 5 ps. After only 1 ps, the buckled-mouth structure has dramatically changed into the closed-mouth structure, and such closed-mouth structure could sustain after another 4 ps MD simulation. Thus, for the open-ended (n, n) SiCNT (n = 4, 5, 6, and 7), the closed-mouth structure is always the most stable.

Next, we consider the structures of the open-ended zigzag (n, 0) SiCNT with n = 6, 7, 8, and 9. Two different atomic terminations could be found at the tube mouth: C-rich-ended and Si-rich-ended SiCNT. For the C-rich-ended SiCNT as shown in Fig. 1b, the position of C atoms at the tube mouth moves outward the tube axis, leading to a slightly broader opening of the tube mouth. This is mainly due to the repulsion between the localized electron stats of C atoms preventing the unpaired electrons of two neighboring C atoms from bonding. In this case, the spin-parallel configuration of unpaired electrons of C atoms is energetically favorable as shown in Fig. 2a. Taking the C-rich-ended (8, 0) SiCNT as an example, the length between the nearest two C atoms at the tube mouth increases into 3.21 Å as compared with the parent tube (3.13 Å), which results from the strong repulsion between the nearest C atoms at the tube mouth. The Si-rich-ended SiCNT is always energetically more stable than the C-rich-ended one, i.e., the total energy of Si-rich-ended (8, 0) SiCNT is 11.31 eV lower than the C-rich-ended (8, 0) SiCNT. As shown in Fig. 1c and d, the structures at the tube mouth of Si-rich-ended SiCNT have been significantly changed, the nearest Si atoms at the tube mouth spontaneously dimerize with the length of Si–Si bonds ranging from 2.20 to 2.41 Å. As a result, Si–C–Si triangles are formed at the tube mouth, which is similar to the case in B-rich-ended BNNTs.²¹ For the Si-rich-ended (7, 0) or (9, 0) SiCNT, there is one isolated Si atom left with a little shift inward radially after the Si–Si dimerizations.

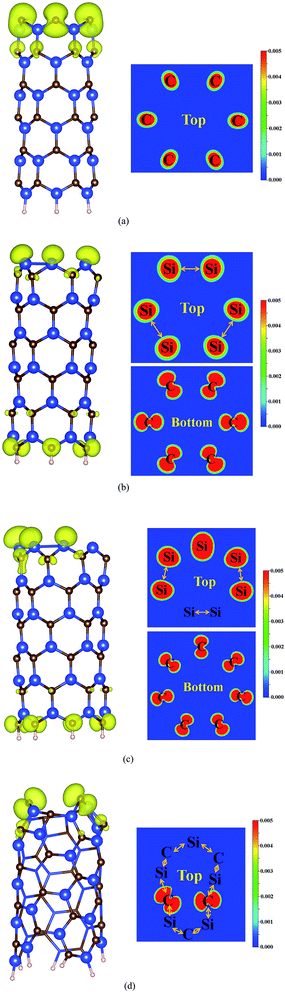Fig. 2 Top and side view of spin density of (a) C-rich-ended (6, 0), (b) Si-rich-ended (6, 0), (c) Si-rich-ended (7, 0) and (d) C-rich-ended (5, 3) SiCNT.

At last, the structure of open-ended chiral (n, m) SiCNT has been considered with n = 4 or 5, and m = 3. For an open (n, m) SiCNT, the open mouth consists of m Si–C pairs and |n − m| isolated Si (or C) atoms. Similar to the case in the open-ended zigzag and armchair SiCNT as have been mentioned above, the isolated C atoms and self-closure Si–C pairs could be found in C-rich-ended (n, m) SiCNT as shown in Fig. 1e. In the Si-rich-ended (n, m) SiCNT (Fig. 1f), the dimeric Si atoms (when |n − m| is even number) or isolated Si atoms (when |n − m| is odd number), and self-closure Si–C pairs are formed at the tube mouth.

3.2 The magnetic properties of the open-ended SiCNT

In this Section, we mainly focus on the magnetic properties of the open-ended SiCNT. The net magnetic moment of open-ended SiCNT is summarized in Table 1. Our results reveal that the net magnetic moment is dramatically dependent on the structures at the tube mouth of open-ended SiCNTs. In detail, for the armchair open-ended SiCNT, the electron clouds between the Si and C atoms in the Si–C pairs at the tube mouth have the large overlap, and the spin direction of the nearest two unpaired electrons is antiparallel. Thus, the open-ended armchair SiCNT is nonmagnetic. For the C-rich-ended SiCNT as shown in Fig. 2a, the slightly enhanced Si–C bonds will counteract only a small quantity of the unpaired electrons in the C atoms at the tube mouth, and thus the net magnetic moment at the mouth of each C atom is closed to 1 μ_B, which is similar to the case in N-rich-ended BNNT.²⁰

Table 1 Ionization potential (IP) and magnetism (μ_B) of the open-ended SiCNTs

Chiral	IP (eV)		μB
	Si-rich-end	C-rich-end	Si-rich-end	C-rich-end
(6, 0)	5.91	6.17	3.80	7.60
(7, 0)	5.77	6.04	4.85	8.72
(8, 0)	5.66	5.93	4.83	8.91
(9, 0)	5.58	5.84	6.37	11.00
(4, 3)	6.21	6.22	1.03	1.00
(5, 3)	5.62	5.86	0	2.00
(4, 4)	5.78		0
(5, 5)	5.61		0
(6, 6)	5.53		0
(7, 7)	5.38		0

---

For the Si-rich-ended SiCNT, the system exhibits a spin-polarized ground state, where spin density mainly localizes on both edges of the tube as shown in Fig. 2b and c. It should be noted that, in CNT and graphene, the C termination saturated by H atom usually induces unpaired electrons on these C atoms,^36,37 which is similar to the case in Si-rich-ended SiCNT. For all the Si-rich-ended (n, 0) SiCNT (n = 6, 7, 8, and 9), the magnetic moment per C atom at the tube end is close to 0.3 μ_B, irrespective to the tube diameters. However, Si atoms with various spin densities could be found at the tube mouth as shown in Fig. 2b and c, they could be categorized into three groups: (i) isolated Si atom with big magnetic moment (∼0.5 μ_B), it usually exists in the (n, 0) Si-rich-ended SiCNT when n is odd number, such as in (7, 0) and (9, 0) Si-rich-ended SiCNT; (ii) Si atom in weak Si–Si dimerization, which has a relatively small magnetic moment (∼0.3 μ_B), in this case, the Si–Si bond length is close to 2.41 Å, which is slightly longer than that of Si–Si single bond length (2.36 Å); (iii) Si atom in strong Si–Si dimerization, which has no magnetic moment, in this case, the Si–Si bond length is close to 2.20 Å, which is smaller than that of Si–Si single bond length.

In the open-ended chiral (n, m) SiCNT, the electron clouds between the Si and C atoms in the Si–C pairs at the tube mouth have the large overlap, and the Si–C pairs is nonmagnetic. As a consequence, the magnetic moment of open-ended chiral (n, m) SiCNT is dependent on the numbers of isolated C atoms or Si atoms at the tube mouth. In detail, for the C-rich-ended (n, m) SiCNT, the net magnetic moment at the tube mouth of each isolated C atom is closed to 1 μ_B as shown in Fig. 2d, which is similar to the case in C-rich-ended zigzag SiCNT and N-rich-ended BNNT.²⁰ In the case of Si-rich-ended (n, m) SiCNT, the strong Si–Si dimerizations are formed when |n − m| is even number, and thus the tube has no magnetic moment. In contrast, the isolated Si atom with magnetic moment of ∼0.5 μ_B could be found in the Si-rich-ended (n, m) SiCNT when |n − m| is odd number.

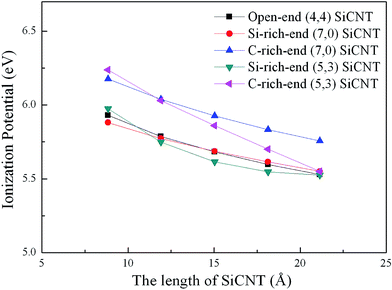
To determine the intension of the field emission in open-ended SiCNTs, we calculate the ionization potential (IP) defined as the energy difference between a system with +1 charge and the parent system with zero charge. The lower the IP, the easier it is to extract an electron to the vacuum, and the higher the expected field-emission current at a given operating voltage. As have been mentioned in finite-length CNT and BNNT cases,^38,39 IP value is strong dependent on the tube diameters and lengths. In Table 1, we describe the IP values in various open-ended SiCNTs with the similar tube length. The results reveal that the IP values decrease with the increase of tube diameters. Moreover, the IP values of open-ended (7, 0), (4, 4) and (5, 3) SiCNTs (with the similar diameters) dependent on the tube lengths have been considered as shown in Fig. 3. It is found that the IP value decreases with the increase of tube lengths, and the IP value of C-rich-ended (7, 0) SiCNT is always larger than that in the other cases with the similar tube length, which implies that the C-rich-ended zigzag SiCNT might not be suitable to be used as the field-emission device as compared with the other open-ended SiCNTs.

Fig. 3 The IP values of open-ended (7, 0), (4, 4) and (5, 3) SiCNTs dependent on the tube lengths.

4. Conclusion

In this paper, we present a detailed analysis of the structures and the magnetic properties of a series of open-ended SiCNTs using density functional theory methods. For the open-ended armchair SiCNT, the self-closure behavior occurs at the tube mouth, and the system shows no magnetism. For the C-rich-ended zigzag or chiral SiCNT, the position of C atoms at the tube mouth moves outward the tube axis slightly, and each of these C atoms has the same magnetic moment approximated to 1 μ_B. For the Si-rich-ended zigzag SiCNT, the spin density mainly locates on C (and Si) atoms at the tube end (and mouth). At the tube end, the magnetic moment on each C atom is always close to 0.3 μ_B. At the tube mouth, three types of Si atoms could be identified, (i) isolated Si atom (magnetic moment of ∼0.5 μ_B) in (n, 0) open-ended SiCNT when n is odd number; (ii) Si atom in strong Si–Si dimmer structure with no magnetism, and (iii) Si atom in weak Si–Si dimmer structure with the magnetic moment of ∼0.3 μ_B. In the Si-rich-ended chiral (n, m) SiCNT, the tube has no magnetic moment when |n − m| is even number, which is due to the formation of strong Si–Si dimerizations. In contrast, the isolated Si atom could be found in the Si-rich-ended (n, m) SiCNT when |n − m| is odd number, with the magnetic moment on each isolated Si atom of ∼0.5 μ_B.

References

1. S. H. Barghi, T. T. Tsotsis and M. Sahimi, Int. J. Hydrogen Energy, 2014, 39, 21107.
2. M. W. Zhao, F. Xia, F. Li, R. Q. Zhao and S. T. Lee, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 085312.
3. A. Gali, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 245415.
4. J. X. Zhao and Y. H. Ding, J. Chem. Theory Comput., 2009, 5, 1099.
5. H. S. Kang and G. H. Gao, J. Chem. Theory Comput., 2008, 4, 1690.
6. R. Q. Wu, M. Yang, Y. H. Lu and Y. P. Feng, J. Phys. Chem. C, 2008, 112, 15985.
7. J. X. Zhao and Y. H. Ding, J. Phys. Chem. C, 2008, 112, 2558.
8. G. G. Gao, S. H. Park and H. S. Kang, Chem. Phys., 2009, 355, 50.
9. K. M. Alam and A. K. Ray, J. Nanopart. Res., 2008, 11, 1405.
10. F. M. Gao, W. Y. Yang, H. T. Wang, Y. Fan, Z. P. Xie and L. N. An, Cryst. Growth Des, 2008, 8, 1461.
11. F. Li, Y. Y. Xia, M. W. Zhao, X. D. Liu, B. D. Huang, Z. H. Yang, Y. J. Ji and C. Song, J. Appl. Phys., 2005, 97, 104311.
12. T. He, M. W. Zhao, Y. Y. Xia, W. F. Li, C. Song, X. H. Lin, X. D. Liu and L. M. Mei, J. Chem. Phys., 2006, 125, 94710.
13. R. X. Ding, Y. T. Yang and L. X. Liu, J. Semicond., 2009, 30, 114010.
14. Y. B. Jia, G. L. Zhuang and J. G. Wang, J. Phys. D: Appl. Phys., 2012, 45, 065305.
15. M. Khademi and M. Sahimi, J. Chem. Phys., 2011, 135, 204509.
16. K. Malek and M. Sahimi, J. Chem. Phys., 2010, 132, 014310.
17. J. X. Zhao, B. Xiao and Y. H. Ding, J. Phys. Chem. C, 2009, 113, 16736.
18. B. Xiao, H. Hu, J. X. Zhao and Y. H. Ding, Phys. E, 2014, 56, 377.
19. C. Kim, Y. S. Choi, S. M. Lee, B. K. Park and Y. H. Lee, J. Am. Chem. Soc., 2002, 124, 9906.
20. S. G. Hao, G. Zhou, W. H. Duan, J. Wu and B. L. Gu, J. Am. Chem. Soc., 2006, 128, 8453.
21. G. Zhou and W. H. Duan, Chem. Phys. Lett., 2007, 437, 83.
22. A. Ahmadi, J. Beheshtian and N. Hadipour, Struct. Chem., 2011, 22, 183.
23. J. X. Zhao and Y. H. Ding, J. Phys. Chem. C, 2008, 112, 20206.
24. S. M. Hou, J. X. Zhang, Z. Y. Shen, X. Y. Zhao and Z. Q. Xue, Phys. E, 2005, 27, 45.
25. W. G. Liu, G. H. Chen, X. C. Huang, D. Wu and Y. P. Yu, J. Phys. Chem. C, 2012, 116, 4957.
26. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15.
27. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169.
28. G. Kresse and J. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758.
29. Y. Wang and J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44, 13298.
30. G. X. Chen, D. D. Wang, X. Yang, H. X. Chen and J. M. Zhang, J. Supercond. Novel Magn., 2015 DOI:10.1007/s10948-015-3083-9.
31. F. W. Zheng, Y. Yang and P. Zhang, Appl. Phys. Lett., 2010, 97, 263105.
32. R. L. Liang, Y. Zhang, J. M. Zhang and V. Ji, Phys. B, 2010, 405, 2673.
33. B. Delley, J. Chem. Phys., 1990, 92, 508; B. Delley, J. Chem. Phys., 2000, 113, 7756.
34. G. J. Martyna, M. L. Klein and M. E. Tuckerman, J. Chem. Phys., 1992, 97, 2635.
35. X. D. Wen, T. J. Cahill and R. Hoffmann, Chem.–Eur. J, 2010, 16, 6555.
36. O. Hod and G. E. Scuseria, ACS Nano, 2008, 2, 2243.
37. Y.-W. Son, M. L. Cohen and S. G. Louie, Nature, 2006, 444, 347.
38. L. K. Petrushenko and N. A. Ivanov, Phys. E, 2013, 54, 262.
39. H. Roohi and S. Bagheri, J. Mol. Struct. Theochem, 2008, 856, 46.

---