Microscopic study of the equation of state of β-HMX using reactive molecular dynamics simulations
Guang Yu Wang*a,
Qing Peng*b,
Gui Rong Liua and
Suvranu Deb
aDepartment of Aerospace Engineering and Engineering Mechanics, University of Cincinnati, Cincinnati, OH 45221-0070, USA. E-mail: wangg3@mail.uc.edu
bDepartment of Mechanical, Aerospace and Nuclear Engineering, Rensselaer Polytechnic Institute, Troy, NY 12180, USA. E-mail: qpeng.org@gmail.com
First published on 19th June 2015
Abstract
The equation of state (EoS) is the relation between physical quantities describing thermodynamic states of materials under a given set of conditions such as pressure, temperature, and volume. The EoS plays a significant role in determining the characteristics of energetic materials, including Chapman–Jouguet point and detonation velocity. Furthermore, the EoS is the key to connect microscopic and macroscopic phenomena in the study of energetic materials. For instance, the foundation of the ignition and growth model for high explosives is two Jones–Wilkins–Lee (JWL) EoSs, one for unreacted explosive and the other for reacted explosive. Thus, an accurate calculation of the EoS is required for the study of energetic materials. In this paper, the EoSs for both unreacted and reacted β-HMX are calculated using molecular dynamics simulations with the ReaxFF-lg potential. The microscopic simulation results are compared with experiments, first-principles calculations, and a continuum ignition and growth model. Good agreement is observed. Our result indicates that molecular dynamics simulations are a reliable alternative method to experiments to generate the EoS for energetic materials.
1. Introduction
Due to the extreme conditions (very short time, high pressure, high temperature, phase transformation, and chemical reaction) that are hard to achieve,1,2 it still remains difficult to investigate the details of the detonation of high explosives through experiments today. As a result, the simulation of high explosives has long been an interest of researchers and various numerical models have been proposed to simulate the detonation process.3–7 The equation of state (EoS), which describes the relation of the state variables in detonation, is a significant tool to determine the characteristics (Chapman–Jouguet point, detonation velocity, etc.) of high explosives. The EoS also plays a critical role in many numerical models for high explosives,3,4,6,7 for instance, the foundation of ignition and growth models for high explosives is two Jones–Wilkins–Lee (JWL) EoSs, one for unreacted explosive and one for reacted explosive.3,4 Generally, to obtain the data needed for fitting parameters of reacted JWL EoSs, a cylinder test needs to be conducted. The cylinder test consists of detonating a cylinder of explosive confined by copper and measuring the velocity of the expanding copper wall. Thus, it is complicated and also costly to conduct cylinder tests for various high explosives.The EoS for unreacted high explosives is obtained using Rankine–Hugoniot conditions, which are a set of conservation equations of mass, momentum, and energy. Much research has been done on the Hugoniot curve of solids. Walsh and Christian initiated the idea in 1955 to use planar shock waves to determine the EoS of condensed materials.8 After that, shock wave experiments have been widely applied to calculate the EoS for a wide range of materials, including elements, compounds, alloys, porous materials, etc.9–13 Some researchers have successfully applied planar shock waves in the study of Hugoniot curve of explosives.14,15
Molecular dynamics is a powerful tool that can be used to investigate many microscopic processes. In recent years, the detonation of high explosives has been explored much more profoundly with the introduction of reactive force fields (ReaxFF) in molecular dynamics. Van Duin and S. Dasgupta first proposed ReaxFF for hydrocarbons,16 which enables convenient and fast molecular dynamics simulations of large-scale reactive chemical systems. Furthermore, Liu et al. introduced an additional vdW-like interaction to ReaxFF, which enables ReaxFF to obtain the correct density of molecular crystals.17 The reactive force field with van der Waals interaction corrections at low gradient regions, the so-called ReaxFF-lg, is used in this study.
A lot of research has been conducted on high explosives (such as TNT, HMX, and RDX) since the introduction of ReaxFF. Strachan, Kober, and Van Duin et al. studied thermal decomposition of RDX under various temperature and densities.18 Chenoweth, Cheung et al. studied thermal decomposition of a poly polymer with ReaxFF.19 Zhang et al. studied the thermal decomposition of 1,3,5-trinitrohexahydro-s-triazine (RDX) bonded with polyurethane (Estane) using molecular dynamics simulation equipped with ReaxFF.20 Zhou et al. studied the thermal and chemical response of shock induced HMX with ReaxFF.21 However, these papers mainly focus on the thermal decomposition of high explosives. We have studied the EoS22 and elastic properties23 of unreacted β-HMX using first-principles calculations at zero temperature. To the authors' best knowledge there is no report on molecular dynamics simulations of the reacted EoS of high explosives yet. Thus, in this paper, we propose a method of molecular dynamics with ReaxFF-lg to calculate the EoSs for both unreacted and reacted HMX.
2. Method
2.1 Hugoniot EoS
The Hugoniot EoS describes the locus of thermodynamic states of unreacted high explosives after a shock passing through. It can be derived from the conservation of mass, momentum, and energy, known as Rankine–Hugoniot conditions:24| ρ1us = ρ2(us − u2) conservation of mass | (1) |
| p2 − p1 = ρ2u2(us − u2) = ρ1usu2 conservation of momentum | (2) |
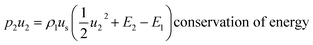 | (3) |
From eqn (1) and (2), the following relations can be obtained:
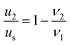 | (4) |
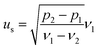 | (5) |
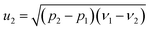 | (6) |
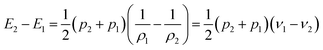 | (7) |
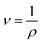 | (8) |
In the ignition and growth model of high explosives, the equation of state of the unreacted explosive has a simple form, which can be expressed as follow:4
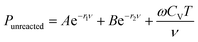 | (9) |
The parameters of the unreacted JWL EoS of PBX 9501 are listed in Table 1.25 PBX 9501 is chosen because it consists of 95 weight% HMX, 2.5 weight% estane binder, and 2.5 weight% BDNPA/F.
| A (GPa) | B (GPa) | r1 | r2 | ω | CV (J kg−1 K−1) | T0 (K) | |
|---|---|---|---|---|---|---|---|
| Unreacted PBX 9501 | 732![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
−5.2654 | 14.1 | 1.41 | 0.8867 | 2.7806 × 106 | 298 |
2.2 JWL EoS
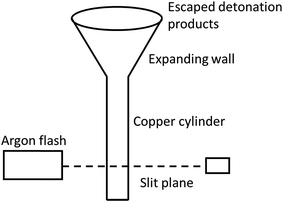
The expansion of the detonation products of high explosives is considered to be an isentropic process. It consists of complicated chemical reactions, occurring over very small time interval. The cylinder test has long been the principal method to obtain the data needed for fitting parameters of the JWL EoS of explosive detonation products.26 It consists of detonating a cylinder of explosive confined by copper and measuring the velocity of the expanding copper wall. The standard tube has a 1-inch internal diameter, 0.1-inch copper wall, and is 12 inches long. The configuration of cylinder test is shown in Fig. 1.In the ignition and growth model, the reacted JWL EoS of high explosives has a similar form as the unreacted JWL EoS:
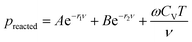 | (10) |
preacted is the pressure of the detonation products. The other parameters have a similar meaning as those in eqn (9).
The parameters of the reacted JWL EoS of PBX 9501 are listed in Table 2.25
| A (GPa) | B (GPa) | r1 | r2 | ω | CV (J kg−1 K−1) | T0 (K) | |
|---|---|---|---|---|---|---|---|
| Reacted PBX 9501 | 1668.9 | 59.69 | 5.9 | 2.1 | 0.45 | 1.0 × 106 | 298 |
3. Molecular dynamics simulation
3.1 Structure and relaxation of β-HMX
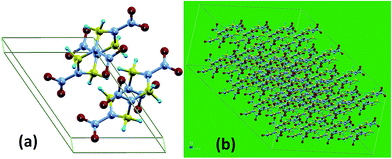
We focus on the β-HMX (octahydro-1,3,5,7-tetranitro-1,3,5,7-tetrazocine), a typical secondary explosive with chemical formula of C4H8N8O8. The geometry of the primitive unit cell of the β-HMX is shown in Fig. 2(a) with the cell box, which was obtained from our previous DFT-D2 study.22 The β-HMX is a P21/c monoclinic crystal with space group number 14. The lattice parameters are listed in Table 3. Replication of the primitive unit cell of HMX, is shown in Fig. 2(b). We tested three different systems with 4 × 2 × 4, 5 × 3 × 5, and 8 × 5 × 7 primitive unit cells, with 1792, 4200, and 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 680 atoms, respectively. We found that the results are converged at the system with 1792 atoms. Therefore, we report our results from the simulation cells with 1792 atoms as depicted in Fig. 2(b).
680 atoms, respectively. We found that the results are converged at the system with 1792 atoms. Therefore, we report our results from the simulation cells with 1792 atoms as depicted in Fig. 2(b).
The structure of β-HMX at zero temperature was obtained from our previous DFT-D2 (ref. 22) calculations. The system is firstly relaxed using the NPT, NVT, and NVE ensembles successively with ReaxFF-lg. Due to the inadequate consideration of van der Waals (vdW) attractions, when using original ReaxFF to relax the solid molecule, the equilibrium volume will be about 10–15% higher than experiment.17 This disadvantage is overcome by ReaxFF-lg, which gives sufficient consideration of vdW interactions in its description of reactive force fields. In the structural of relaxation, the time step is set to be 0.25 fs while the simulation time is set to be 50 ps for each ensemble.
The lattice constants for the unit cell of β-HMX from experiment,27 DFT-D2 (ref. 22) studies are listed in Table 3.
The supercell of β-HMX consists of 64 β-HMX molecules, which contains 1792 atoms in total. The density of β-HMX before relaxation is 1893.4 kg m−3.
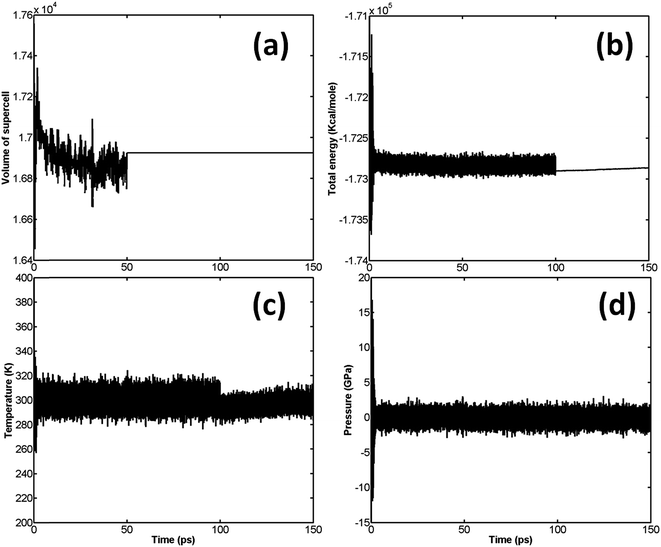
The variation of volume, pressure, temperature, and total energy is shown in Fig. 3.
It is well known that β-HMX is very sensitive to fluctuations in temperature. It will transform from β-HMX to δ-HMX above 436 K.28 Therefore, it is critical to control these temperature fluctuations. It can be seen from Fig. 3(c) that, during the relaxation, the temperature is limited to around 300 K, which ensures no phase transformations during relaxation. According to Fig. 3(a), the volume of the supercell fluctuates significantly in the NPT stage, and the maximum volume of the supercell reaches 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 558.66 Å3. In the successive NVT and NVE stages, the volume stabilizes at 16
558.66 Å3. In the successive NVT and NVE stages, the volume stabilizes at 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 924.73 Å3 (or 528.9 Å3 per primitive unit cell). After relaxation, the density of β-HMX is 1893.4 kg m−3, which is very close to the experimental value (1.838 kg m−3) at ambient conditions. According to Fig. 3(b), after the initial fluctuation, the pressure of the system fluctuates around 0 GPa.
924.73 Å3 (or 528.9 Å3 per primitive unit cell). After relaxation, the density of β-HMX is 1893.4 kg m−3, which is very close to the experimental value (1.838 kg m−3) at ambient conditions. According to Fig. 3(b), after the initial fluctuation, the pressure of the system fluctuates around 0 GPa.
3.2 Unreacted equation of state
The unreacted EoS of β-HMX is obtained through a series of NVT simulations. NVT is preferred because as mentioned in Section 2, the effect of temperature is introduced in the unreacted JWL EoS of high explosives. Furthermore, according to Yoo,29 the pressure–volume relation calculated under hydrostatic conditions should be in good agreement with Hugoniot curve. The simulation scheme is as follows: compress the β-HMX along a-direction of the supercell to a predefined volume and temperature, thus, for each set of volumes and temperatures, there is a corresponding pressure. In the implementation of each NVT simulation, the time step is set to be 0.1 fs and the total simulation time is set to be 15 ps. The variation of volume, pressure, temperature, and total energy is shown in Fig. 4, where the compression direction is a-direction of the supercell and the predefined volume ratio is 0.5 (compress the volume to 0.5 its original volume) while the predefined temperature is 1000 K.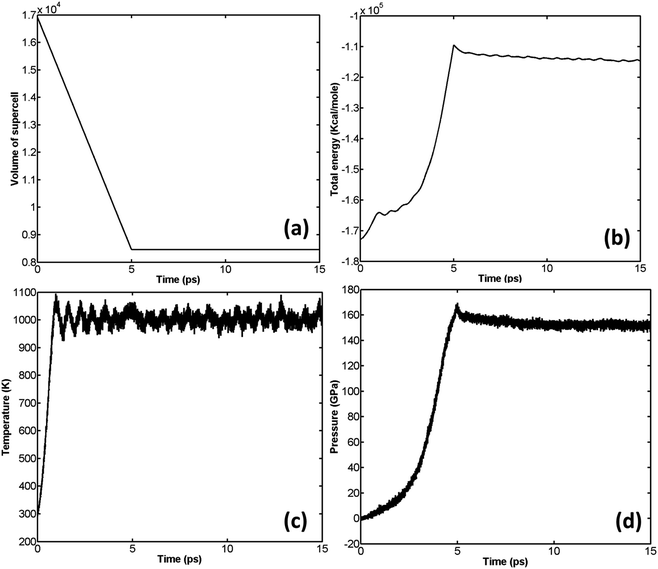 | ||
Fig. 4 Variation of volume (a), total energy (b), temperature (c), and pressure (d) of β-HMX under compression at T = 1000 K, 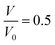 . . | ||
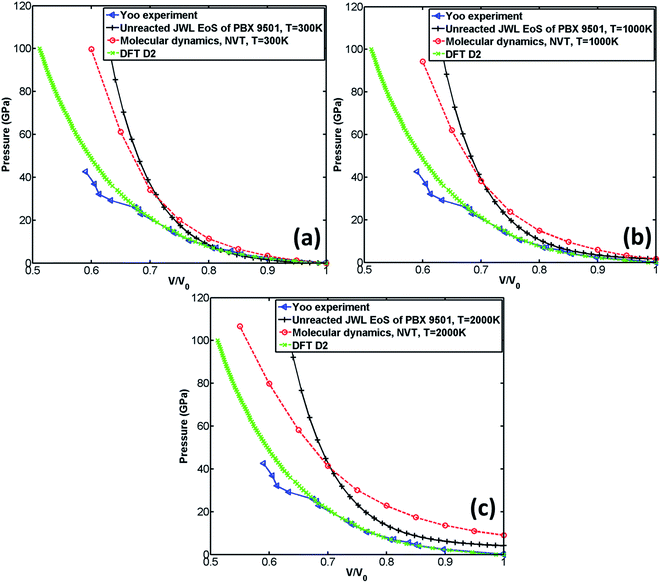
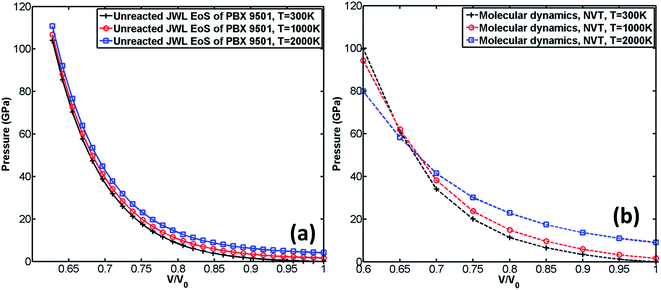
The comparison of the EoS calculated by MD with those obtained from experiment,29 DFT-D2,22 and unreacted JWL EoS of PBX 9501 is shown in Fig. 5. It should be noted that the experiment was performed at room temperature, and DFT-D2 was performed at 0 K.
According to Fig. 5(a), the EoS calculated by DFT-D2 is very close to experiment29 when volume ratio is greater than 0.72. It can also be observed from Fig. 5(a) that when the volume ratio is greater than 0.8, all three calculated EoSs are close to experiment. However, substantial deviation from experiment is found for both unreacted JWL EoS and MD EoS when the volume ratio is less than 0.8, which implies that both numerical predictions fail at high compression. A possible reason for the failing prediction made by MD simulation is that Reaxff-lg may be not suitable for simulating unreacted process.
According to Fig. 5(a–c), when the volume ratio is greater than 0.7, the EoS calculated by MD is greater than the unreacted JWL EoS at all predefined temperatures (300 K, 1000 K, 2000 K). However, when the volume ratio is less than 0.7, the pressure calculated by the unreacted JWL EoS becomes much larger than that obtained from MD simulations and others.
The influence of temperature on unreacted JWL EoS and EoS calculated by MD is shown in Fig. 6. It can be observed from Fig. 6(a) that unreacted JWL EoSs under different temperature are close to each other, especially when volume ratio is small, which indicates that for unreacted JWL EoS in ignition and growth model, the pressure is not sensitive to variation of temperature. However, the situation is quite different for EoS calculated by MD. According to Fig. 6(b), the pressure of the supercell is significantly influenced by temperature. When volume ratio is greater than 0.65, the pressure at high temperature is larger than that at low temperature, while in low volume ratio zone, the situation is opposite.
3.3 JWL equation of state
Similar to unreacted EoS, the JWL equation of state of β-HMX was also obtained through NVT simulations. Prior to the NVT simulation, NPHUG is used to compress the system to around 64 GPa. NPHUG performs a time integration of the Hugoniotstat equations of motion developed by Ravelo.30 Afterwards, the system expands from the compressed state. The simulation scheme is similar: expand the β-HMX along a specific direction (a-direction of the supercell) to reach a predefined volume and temperature, thus, for each set of volume and temperature, there is a corresponding pressure. The time step is set to be 0.1 fs and the total simulation time is set to be 15 ps. The variation of volume, pressure, temperature, and total energy is shown in Fig. 7, where the expansion direction is a-direction of the supercell, the predefined volume ratio is 2.621 (expand the volume to 2.621 its original relaxed volume), and the predefined temperature is 1000 K.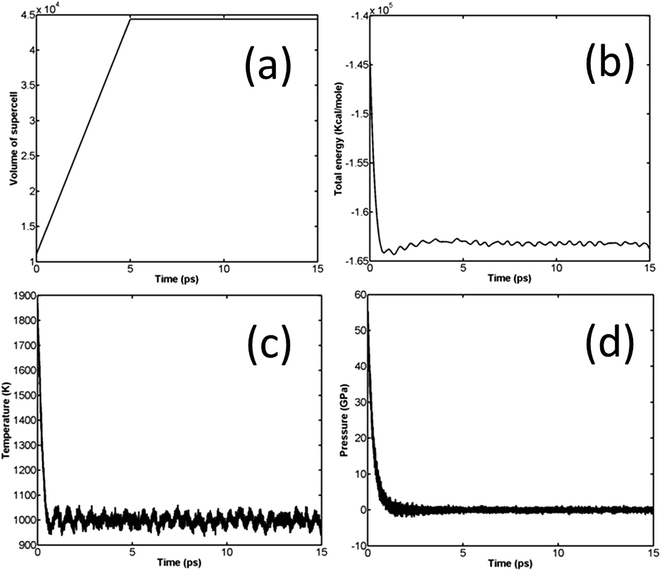 | ||
Fig. 7 Variation of volume (a), total energy (b), temperature (c), and pressure (d) of β-HMX in NVT expansion, T = 1000 K,  . . | ||
The comparison of the reacted JWL EoS of PBX 9501 with that obtained through MD is shown in Fig. 8.
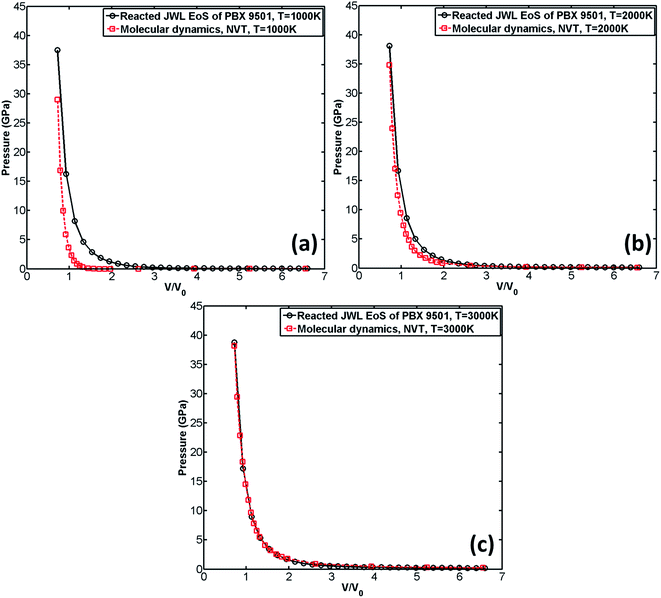 | ||
| Fig. 8 Comparison of the reacted JWL EoS with the EoS obtained from MD. Temperature is set to be 1000 K (a), 2000 K (b), and 3000 K (c) respectively. | ||
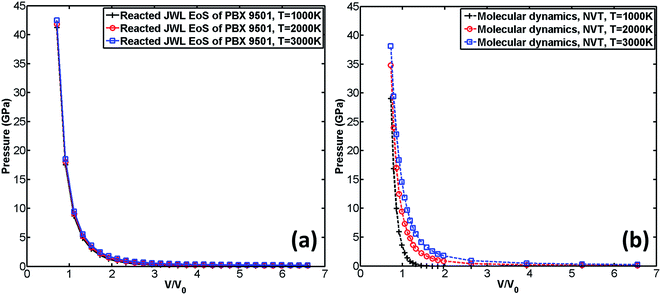
It can be observed from Fig. 8(c) that when the predefined temperature is set to be 3000 K, the MD result agrees very well with the reacted JWL EoS. However, when temperature is decreased, the MD result gradually deviates from the reacted JWL EoS. The lower the temperature is, the greater the MD result deviates from reacted JWL EoS. It indicates that ReaxFF-lg excels in describing chemical reactions at high temperature (for example, at 3000 K, which is close to the temperature of detonation products of PBX 9501 right after explosion) where chemical reactions occur violently.
Similarly, the influence of temperature on reacted JWL EoS and EoS calculated by MD is shown in Fig. 9.
It can also be observed from Fig. 9(a) that the three reacted JWL EoSs almost coincide, which indicates that in the ignition and growth model, temperature has little influence on the shape of reacted JWL EoS. However, as shown in Fig. 9(b), in MD simulation, the influence of temperature on EoS is significant. When temperature increases, the pressure of the system increases correspondingly. Larger amount of increments are observed at low volume ratio zone than at high volume ratio zone. It seems that in ignition and growth model, the effect of temperature is not thoroughly considered, and that is probably why the reacted JWL EoSs under three different temperature nearly coincide with each other.
4. Conclusion
In summary, we have studied the unreacted JWL EoS of β-HMX and reacted JWL EoS of PBX 9501 using reactive molecular dynamics simulations with ReaxFF-lg potentials. For the unreacted case, the pressure–volume relation obtained from MD simulations is compared with experiment, DFT-D2, and unreacted JWL EoS of PBX 9501 in the ignition and growth model. It is found that when temperature is low (300 K), the MD result agrees relatively well with unreacted JWL EoS in ignition and growth model. However, when temperature is increased, the MD result gradually deviates from unreacted JWL EoS. In addition, the pressure of compressed supercell calculated by both MD and unreacted JWL EoS are higher than that obtained from experiment. It suggests that the unreacted JWL EoS in ignition and growth model is not capable to describe the pressure of the compressed system well at high compression ratio. Furthermore, the influence of temperature on EoS is investigated. It is found that unreacted JWL EoS is not sensitive to the variation of temperature, in other words, when temperature changes substantially, the unreacted JWL EoS only changes a little. The situation is quite different for MD simulation. The unreacted EoS calculated by MD is significantly influenced by temperature.For the reacted case, it is found that when temperature is as high as 3000 K where the chemical reaction is violent (3000 K is close to the temperature of detonation products of PBX 9501 right after explosion), the EoS calculated by MD agrees very well with the reacted JWL EoS in ignition and growth model. However, when temperature becomes lower, the EoS calculated by MD gradually deviates from the reacted JWL EoS. Furthermore, the influence of temperature on reacted JWL EoS is studied. It is found that reacted JWL EoS is not sensitive to temperature. When temperature increases from 1000 K to 3000 K, the reacted JWL EoS only have insignificant change, opposite to the situation happening to MD simulations. Therefore, we conclude that in current ignition and growth model, temperature only plays trivial role in EoS.
Acknowledgements
The authors appreciate the financial support from the United States DoD (DTRA): Grant # HDTRA1-13-1-0025. This work was supported in part by an allocation of computing time from the Ohio Supercomputer Center.References
- P. W. Cooper and S. R. Kurowski, Introduction to the Technology of Explosives, VCH, New York, 1996 Search PubMed.
- P. W. Cooper, Explosives engineering, VCH, New York, 1996 Search PubMed.
- E. L. Lee and C. M. Tarver, Phenomenological model of shock initiation in heterogeneous explosives, Phys. Fluids, 1980, 23(12), 2362–2372 CrossRef CAS PubMed.
- C. M. Tarver, Ignition and Growth Modeling of LX-17 Hockey Puck Experiments, Propellants, Explos., Pyrotech., 2005, 30(2), 109–117 CrossRef CAS PubMed.
- P. C. Souers and L. C. Haselman Jr, Detonation equation of state at LLNL, 1993, No. UCRL-ID-116113, Lawrence Livermore National Lab., CA, United States, 1994.
- P. C. Souers, S. Anderson and J. Mercer, et al., JWL++: a simple reactive flow code package for detonation, Propellants, Explos., Pyrotech., 2000, 25(2), 54–58 CrossRef CAS.
- P. C. Souers, R. Garza and P. Vitello, Ignition & growth and JWL++ detonation models in coarse zones, Propellants, Explos., Pyrotech., 2002, 27(2), 62–71 CrossRef CAS.
- J. M. Walsh and R. H. Christian, Equation of state of metals from shock wave measurements, Phys. Rev., 1955, 97, 1544 CrossRef CAS.
- R. G. McQueen and S. P. Marsh, Equation of State for Nineteen Metallic Elements from Shock-Wave Measurements to Two Megabars, J. Appl. Phys., 1960, 31(7), 1253–1269 CrossRef CAS PubMed.
- R. G. McQueen, S. P. Marsh and J. W. Taylor, et al., The equation of state of solids from shock wave studies, High-Velocity Impact Phenom., 1970, 293 Search PubMed.
- A. C. Mitchell and W. J. Nellis, Equation of state and electrical conductivity of water and ammonia shocked to the 100 GPa (1 Mbar) pressure range, J. Chem. Phys., 1982, 76(12), 6273–6281 CrossRef CAS PubMed.
- E. N. Avrorin, B. K. Vodolaga and N. P. Voloshin, et al., Experimental confirmation of shell effects on the shock adiabats of aluminum and lead, JETP Lett., 1986, 43(5), 308–311 Search PubMed.
- L. B. Da Silva, P. Celliers and G. W. Collins, et al., Absolute equation of state measurements on shocked liquid deuterium up to 200 GPa (2 Mbar), Phys. Rev. Lett., 1997, 78(3), 483 CrossRef CAS.
- N. L. Coleburn and T. P. Liddiard Jr, Hugoniot equations of state of several unreacted explosives, J. Chem. Phys., 1966, 44(5), 1929–1936 CrossRef CAS PubMed.
- J. J. Dick and C. A. Forest, The Hugoniot and shock sensitivity of a plastic-bonded TATB explosive PBX 9502, J. Appl. Phys., 1988, 63(10), 4881–4888 CrossRef CAS PubMed.
- A. C. T. Van Duin, S. Dasgupta and F. Lorant, et al., ReaxFF: a reactive force field for hydrocarbons, J. Phys. Chem. A, 2001, 105(41), 9396–9409 CrossRef CAS.
- L. Liu, Y. Liu and S. V. Zybin, et al., ReaxFF-lg: correction of the ReaxFF reactive force field for London dispersion, with applications to the equations of state for energetic materials, J. Phys. Chem. A, 2011, 115(40), 11016–11022 CrossRef CAS PubMed.
- A. Strachan, E. M. Kober, A. C. Van Duin, et al., Thermal decomposition of RDX from reactive molecular dynamics, California Inst of Tech Pasadena Materials and Processes Simulation Center, 2005 Search PubMed.
- K. Chenoweth, S. Cheung and A. C. T. Du Van, et al., Simulations on the thermal decomposition of a poly (dimethylsiloxane) polymer using the ReaxFF reactive force field, J. Am. Chem. Soc., 2005, 127(19), 7192–7202 CrossRef CAS PubMed.
- L. Zhang, S. V. Zybin, A. C. T. V. Duin, et al., Thermal decomposition of energetic materials by ReaxFF reactive molecular dynamics, Shock Compression of Condensed Matter-2005: Proceedings of the Conference of the American Physical Society Topical Group on Shock Compression of Condensed Matter, American Institute of Physics Conference Proceedings, No. 845, American Institute of Physics, Melville, NY, 2005, pp. 589–592 Search PubMed.
- T. Zhou, H. Song and Y. Liu, et al., Shock initiated thermal and chemical responses of HMX crystal from ReaxFF molecular dynamics simulation, Phys. Chem. Chem. Phys., 2014, 16, 13914–13931 RSC.
- Q. Peng, Rahul, G. Wang, G. R. Liu and S. De, Structures, Mechanical Properties, Equations of State, and Electronic Properties of β-HMX under Hydrostatic Pressures: A DFT-D2 study, Phys. Chem. Chem. Phys., 2014, 16, 19972–19983 CAS.
- Q. Peng, Rahul, G. Wang, G. R. Liu, S. Grimme and S. De, Predicting Elastic Properties of β-HMX from First-principles calculations, J. Phys. Chem. B, 2015, 119, 5896–5903 CrossRef CAS PubMed.
- M. D. Salas, The curious events leading to the theory of shock waves, Shock Waves, 2007, 16(6), 477–487 CrossRef.
- C. M. Tarver, J. W. Forbes, F. Garcia, et al., Manganin gauge and reactive flow modeling study of the shock initiation of PBX 9501, in AIP Conference Proceedings. No. 2, IOP Institute of Physics Publishing Ltd, 2002 Search PubMed.
- L. L. Davis and L. G. Hill, ANFO cylinder tests, AIP Conference Proceedings. No. 1, IOP Institute of Physics Publishing Ltd, 2002 Search PubMed.
- J. M. Zaug, Elastic constants of β-HMX and tantalum, equations of state of supercritical fluids and fluid mixtures and thermal transport determinations, Proceedings of the 11th detonation symposium, vol. 498, 1998 Search PubMed.
- R. J. Karpowicz and T. B. Brill, The beta to delta transformation of HMX-Its thermal analysis and relationship to propellants, AIAA J., 1982, 20(11), 1586–1591 CrossRef CAS PubMed.
- C. S. Yoo and H. Cynn, Equation of state, phase transition, decomposition of β-HMX (octahydro-1,3,5,7-tetranitro-1,3,5,7-tetrazocine) at high pressures, J. Chem. Phys., 1999, 111(22), 10229–10235 CrossRef CAS PubMed.
- R. Ravelo, B. L. Holian and T. C. Germann, et al., Constant-stress Hugoniot method for following the dynamical evolution of shocked matter, Phys. Rev. B, 2004, 70(1), 014103 CrossRef.
| This journal is © The Royal Society of Chemistry 2015 |