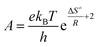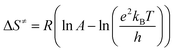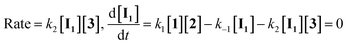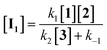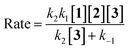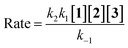DOI:
10.1039/C5RA09717G
(Paper)
RSC Adv., 2015,
5, 52508-52515
Effect of different substituents on the one-pot formation of 3,4,5-substituted furan-2(5H)-ones: a kinetics and mechanism study†
Received
23rd May 2015
, Accepted 9th June 2015
First published on 9th June 2015
Abstract
The kinetics of reactions between benzaldehyde and diethyl acetylenedicarboxylate with para-substituted anilines for the one-pot formation of 3,4,5-substituted furan-2(5H)-ones have been studied spectrally at different temperatures in formic acid. For all substituents at the para position of the aniline ring, the reaction followed second-order kinetics. The partial orders with respect to substituted aniline and diethyl acetylenedicarboxylate were one and one, and the reactions also revealed zero-order kinetics in relation to benzaldehyde. Para-electron donating substituents on the aniline ring increased the rate of reaction. On the basis of experimental data, a three step mechanism has been proposed. Kinetic values (k and Ea) and associated activation parameters (ΔH≠, ΔG≠ and ΔS≠) of the reactions were determined.
1. Introduction
A multicomponent reaction (MCR) is a process in which three or more accessible components combine to produce a final product that displays the features of all inputs and thus offers greater possibilities for molecular diversity per step with a minimum of synthetic time and effort in a single reaction.
Synthesis of furan-2(5H)-ones as subunits in a large number of natural products1–5 is a significant target for organic and medicinal chemists. Highly substituted furans are a structural component of a vast number of biologically active natural and synthetic compounds such as anticancer,6,7 anti-inflammatory,8 antifungal,9,10 antimicrobial,11,12 and antiviral HIV-1.13–15 The reactions leading to the formation of furanones are frequently reported by several research groups, however, they have proposed the reactions mechanism without offering evidence to support them.16–20 There are a number of reasons for tendency to know reaction mechanisms. Knowledge of mechanisms aids the synthetic chemist in predicting by products and improving reaction conditions, the most powerful tool for the experimental study of reaction mechanisms is chemical kinetics. Kinetics is the study of the speed with which a chemical reaction occurs, and with all of the factors which influence these rates.21
The spectroscopic technique is the largest and important techniques used in chemistry. The most widely method used for kinetic and mechanistic studies of chemical reactions is ultraviolet-visible (UV-visible) spectroscopy. Several research studies have documented over a large area of different reactions which have previously been reported using the UV-visible spectrophotometry technique.22–30 In our previous work, experimental and theoretical kinetics studies and mechanism investigation have fully been discussed for various reactions.31–37 In continuing our investigations on the kinetic of the organic reactions, we focused on 3,4,5-substituted furan-2(5H)-ones by one-pot multicomponent reaction that was reported by MT Maghsoodlou and coworkers.38 Depending upon the stoichiometry and conditions, other products have also been reported for this reaction.39–42 However, under optimized conditions reported by M. T. Maghsoodlou and et al. (Fig. 1),38 3,4,5-substituted furan-2(5H)-ones are obtained in high ylides (%90–98). In the current work for the first time, we describe kinetic results together with the detailed mechanistic studies for the mentioned reactions based on a global kinetic analysis methodology using the UV-vis spectrophotometry apparatus. Also, this work focused especially on the effects of temperature, different para-substituted anilines on the activation parameters of preparation reaction of 3,4,5-substituted furan-2(5H)-ones.
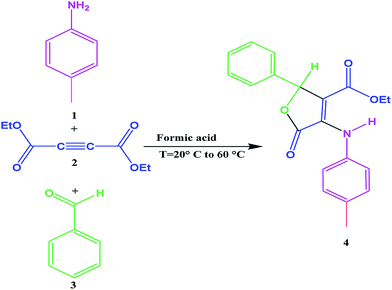 |
| | Fig. 1 The three-component synthesis of furan-2(5H)-ones.38 | |
2. Experimental
2.1. Chemicals and apparatus used
All chemicals were used without further purification. Substituted-aniline 1, diethyl acetylenedicarboxylate 2 and benzaldehyde 3 were supplied by Merck (Darmstadt, Germany), Acros (Geel, Belgium) and Fluka (Buchs, Switzerland). Extra pure formic acid and acetic acid were also obtained from Merck (Darmstadt, Germany).
A Cary UV-vis spectrophotometer model Bio-300 with a 10 mm light-path quartz spectrophotometer cell equipped with thermostated housing cell was used to record absorption spectra in order to follow reaction kinetics.
2.2. General procedure
The first experiment is performed with 10−2 M solutions of aniline 1, diethyl acetylenedicarboxylate 2 and benzaldehyde 3 in formic acid solvent. The progress of reaction is monitored by the absorbance changes as a function of wavelengths (Fig. 2). Since at wavelength of 420 nm, reactants 1, 2 and 3 have no relatively absorbance values, it provides the opportunity to fully investigate the kinetics and mechanism of the reaction. Hence, the product absorbance changes with time are undertaken under the same condition at wavelength of 420 nm (Fig. 3) at 20 °C. As can be seen in Fig. 3, the original experimental absorbance curve versus time (dotted line) is exactly fitted to second order fit curve (solid line). So the reaction is second order (α + β + γ = 2), the overall reaction rate is described by the kinetic equation:| | |
Rate = kovr[1]γ[2]β[3]α
| (1) |
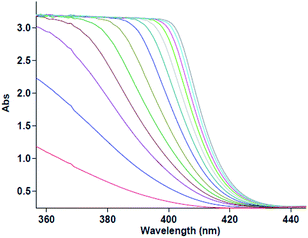 |
| | Fig. 2 Absorption changes versus wavelength for the reaction between 1 (10−2 M), 2 (10−2 M) and 3 (10−2 M) in formic acid for generation of product 4. | |
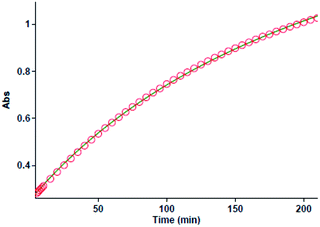 |
| | Fig. 3 The original experimental absorbance curve versus time at selected wavelength of 420 nm for the reaction between 1 (10−2 M) and 2 (10−2 M) with 3 (10−2 M) in formic acid. Dotted line is experimental values and the solid line is a fit curve. | |
Then the second-order rate constant (kovr = 3.50 min−1 M−2) is automatically calculated using the standard equations within the program at 20 °C.34
3. Results and discussion
3.1. Effects of concentration
In order to obtain partial order with respect to aniline 1, pseudo-order condition is performed for the reaction. So in the second experiment, we followed the reaction kinetics by plotting the UV-vis absorbance versus time at wavelength of 420 nm with 1 (10−3 M), 2 (10−2 M) and 3 (10−2 M) at 20.0 °C in formic acid. For this case the rate law can be expressed:
All kinetic mathematical fits (the zero, first or second fit curve) are done using the software43 associated with the UV-Vis spectrophotometer instrument. The original experimental absorbance against time data make a pseudo-first-order available fit curve at 420 nm, which exactly fits the experimental curve, Fig. 4A. Herein, observation rate constant (kobs) is automatically calculated for the eqn (2) by the software associated within the UV-vis instrument. It is obviously that the reaction is of the first order type with respect to aniline 1 (α = 1).
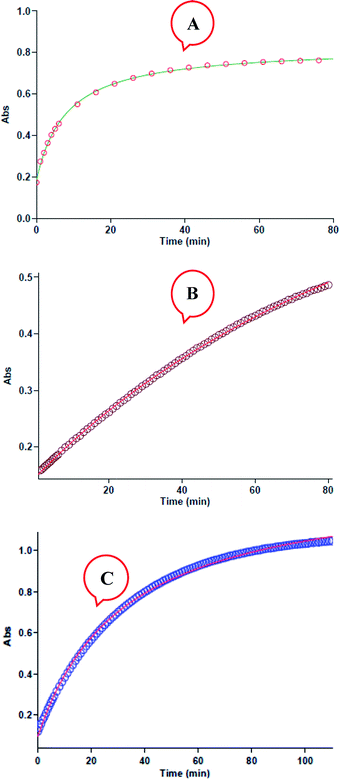 |
| | Fig. 4 (A) Plot of absorbance versus time at 420 nm for the reaction between 1 (10−2 M), 2 (10−2 M) and 3 (10−3 M) in formic acid. Dotted line is experimental values, and the solid line is fit curve. (B) Plot of absorbance versus time at 420 nm for the reaction between 1 (10−3 M), 2 (10−2 M) and 3 (10−2 M) in formic acid. Dotted line is experimental values, and the solid line is fit curve. (C) Plot of absorbance versus time at 420 nm for the reaction between 1 (10−2 mol L−1), 2 (10−3 mol L−1) and 3 (10−2 mol L−1) in formic acid, dotted line is experimental values, and the solid line is fit curve. | |
Also, to gain the partial order of reaction with respect to reactant 3, third experiment is done under pseudo-order condition [(10−2 M, 1), [(10−2 M, 2) and [(10−3 M, 3)]. In this experiment the original experimental absorbance versus time provides a second-order curve (kovr = 3.49 min−1 M−2, Fig. 4B) like the first experiment. Due to the concentration changes of reactant 3 had no effect on the reaction rate, then reaction is zero-order with respect to reactant 3 (γ = 0). Also, in fourth experiment, we followed kinetics under pseudo order condition of reactant 2. As can be seen in Fig. 4C, the reaction shows first order kinetics that it means the partial order with respect to reactant 2 is one (β = 1). So, the reaction between aniline 1 and diethyl acetylenedicarboxylate 2 with benzaldehyde 3 follows second-order kinetics.
According to the obtained results from the four experiments, the rate law of reaction can be written:
| From the first experiment: α + β + γ = 2 |
| From the second experiment: α = 1 |
| From the third experiment: α + β = 2 and γ = 0 |
| From the fourth experiment: β = 1 |
3.2. Effect of solvents and temperature
The solvent dielectric constant and polarity are important parameters that influence rate constants. Solvent effects on the rate of reaction depend on the relative stabilization of the starting materials and the corresponding transition state through solvation.44,45 For investigation of the effect of medium dielectric constant on the rate of reaction, the same kinetic procedure is followed in the presence of acetic acid in 20 °C.
It is found that as medium dielectric constant decreased, the reaction rate reduced from formic acid (kovr = 3.50 min−1 M−2) to acetic acid (kovr = 0.713 min−1 M−2).
Temperature is considered a major factor that affects the rate of a chemical reaction. The influences of temperature on the reaction rate were studied in the range of 20 °C to 60 °C with 10 °C intervals for each reaction and the values of second-order rate constants are determined. Kinetic data are shown in Table 1. Reaction rate constant has a temperature dependency, which is usually given by the Arrhenius equation.
Table 1 Reaction rate constant (kovr (min−1 M−2)) in different temperatures and different substituted-aniline under the same conditions for the reaction between 1 (10−2 M) and 2 (10−2 M) with 3 (10−2 M) in formic acid
| (λ) (nm) |
Substituted-aniline |
20.0 °C |
30.0 °C |
40.0 °C |
50.0 °C |
60.0 °C |
| Standard deviation (SD). |
| 420 |
OMe-aniline |
8.10 (0.0028)a |
24.31 (0.0057) |
52.53 (0.0063) |
115.42 (0.0023) |
210.31 (0.0039) |
| 420 |
Ethyl-aniline |
6.16 (0.0026) |
15.9 (0.0068) |
34.88 (0.0074) |
91.97 (0.0064) |
174.10 (0.0075) |
| 420 |
Aniline |
3.50 (0.0046) |
9.06 (0.0038) |
20.40 (0.0038) |
48.45 (0.0025) |
115.35 (0.0037) |
| 420 |
F-aniline |
0.75 (0.0029) |
2.10 (0.0057) |
5.12 (0.0037) |
12.87 (0.0010) |
32.938 (0.0037) |
| 420 |
NO2-aniline |
0.44 (0.0022) |
1.40 (0.0029) |
3.42 (0.0026) |
9.33 (0.0021) |
23.84 (0.0072) |
Most reactions are found to obey the Arrhenius equation:
| |
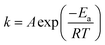 | (3) |
Taking the natural logarithm of both sides of the equation provides:
| |
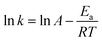 | (4) |
where
Ea is the activation energy of reaction,
R is universal gas constant (8.314 J K
−1 mol
−1), and
A is frequency factor.
The activation energy of reaction is usually determined experimentally by plotting the graph of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k versus the reciprocal of the temperature 1/T, which will yield a straight line with a slope of
k versus the reciprocal of the temperature 1/T, which will yield a straight line with a slope of 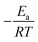 and an intercept ln
and an intercept ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A (Fig. 5). The highest activation energy (Ea = 80.12 kJ mol−1) is obtained for NO2-aniline, that means reaction will occur slower than alone aniline and para-donating substituent-aniline. Nevertheless, the differences in activation energies are not much, because the substituents on aniline ring are far from the center of reaction. The Eyring equation is used in chemical kinetics to describe the variance of the rate of a chemical reaction with temperature and was used to evaluate activation parameters involving ΔH≠ (activation enthalpy), ΔS≠ (activation entropy).46
A (Fig. 5). The highest activation energy (Ea = 80.12 kJ mol−1) is obtained for NO2-aniline, that means reaction will occur slower than alone aniline and para-donating substituent-aniline. Nevertheless, the differences in activation energies are not much, because the substituents on aniline ring are far from the center of reaction. The Eyring equation is used in chemical kinetics to describe the variance of the rate of a chemical reaction with temperature and was used to evaluate activation parameters involving ΔH≠ (activation enthalpy), ΔS≠ (activation entropy).46
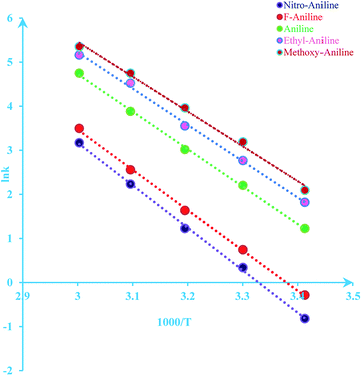 |
| | Fig. 5 Dependence of second order (ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kovr = ln kovr = ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k1) on reciprocal temperature for the reaction between reactants 1, 2 and 3 in formic acid measured at wavelength 420 nm in accordance with Arrhenius equation. k1) on reciprocal temperature for the reaction between reactants 1, 2 and 3 in formic acid measured at wavelength 420 nm in accordance with Arrhenius equation. | |
The linear form of the Eyring equation is given below:
| |
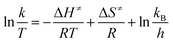 | (5) |
that
kB = Boltzmann's constant,
T = temperature,
h = Planck's constant and
R = universal gas constant.
The values for ΔH≠ (activation enthalpy), ΔS≠ (activation entropy) can be determined from slopes and intercepts of 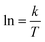 versus 1/T plot (Fig. 6). Obtained activation parameters for para-substituted aniline are given in Tables 2 and 3.
versus 1/T plot (Fig. 6). Obtained activation parameters for para-substituted aniline are given in Tables 2 and 3.
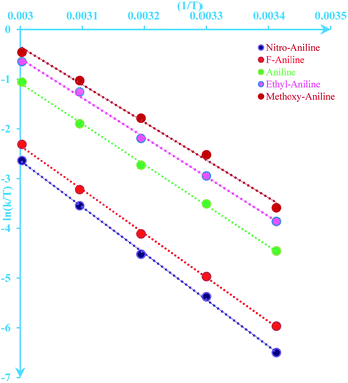 |
| | Fig. 6 Eyring plot (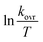 versus T) according to eqn (5) for the reaction between 1, 2 and 3 in formic acid. versus T) according to eqn (5) for the reaction between 1, 2 and 3 in formic acid. | |
Table 2 Activation parameters (ΔS≠, ΔH≠, ΔG≠ and Ea) using the Arrhenius eqn (3) and Eyring eqn (5) and (6) in 20 °C
| Substituted-aniline |
ΔH≠ (kJ mol−1) |
ΔS≠ (J mol−1 K−1) |
ΔG≠ (kJ mol−1) |
Ea (kJ mol−1) |
| OMe-aniline |
63.08 |
−11.20 |
59.24 |
65.67 |
| Ethyl-aniline |
65.91 |
−4.67 |
64.92 |
68.51 |
| Aniline |
68.17 |
−2.01 |
68.76 |
70.76 |
| F-aniline |
73.46 |
3.40 |
74.83 |
76.05 |
| NO2-aniline |
77.53 |
13.10 |
80.81 |
80.12 |
Table 3 Activation parameters (ΔS≠, ΔH≠, ΔG≠ and ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A) using the Arrhenius eqn (3) and The transition state eqn (6)–(8) in 20 °C
A) using the Arrhenius eqn (3) and The transition state eqn (6)–(8) in 20 °C
| Substituted-aniline |
ΔH≠ (kJ mol−1) |
ΔS≠ (J mol−1 K−1) |
ΔG≠ (kJ mol−1) |
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A A |
| OMe-aniline |
60.71 |
−18.87 |
66.34 |
29.15 |
| Ethyl-aniline |
63.55 |
−12.36 |
67.24 |
29.94 |
| Aniline |
65.80 |
−9.68 |
68.69 |
30.26 |
| F-aniline |
71.09 |
−4.27 |
72.37 |
30.91 |
| NO2-aniline |
75.16 |
5.42 |
73.55 |
32.08 |
Also, the transition state equation was used to calculate activation parameters ΔH≠, ΔS≠ in order to check the results obtained from the two methods (Eyring and the transition state theory). According to the transition state theory, activation energy can be related to activation enthalpy (eqn (6)) and also pre-exponential factor is relevant to activation entropy according to eqn (8) and (9), respectively:46
| |
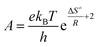 | (7) |
| |
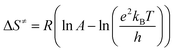 | (8) |
The values obtained on the basis of transition state theory inferred that the activation enthalpy is the lowest for donating substituent-aniline that have the higher reaction rates and the highest for withdrawing substituent-aniline with the lowest reaction rates (Table 3). Note that the negative activation entropy indicated a greater degree of ordering in the transition state than in the initial state. These results suggest that the transition state in first step of reaction, Fig. 8, involving donating substituent-aniline is ordered more effectively stabilized than the transition state containing withdrawing substituent-aniline (Tables 2 and 3). The activation Gibbs free energy has also been evaluated from the following form of the Gibbs–Helmholtz equation:
The activation free energy is essentially the energy requirement to get a molecule (or a mole of them) to undergo the reaction. It is of interest to note that activation free energies ΔG≠ for the different substituents are positive. The value of the activation free energy for donating substituent-aniline is lower than withdrawing substituent-aniline that means the reaction will occur harder for withdrawing substituent-aniline.
To investigate the impact of the different substituents on the rate constant of reaction and activation parameters, we changed the substituents R on aniline from the electron donating (methoxy, ethyl) to the electron withdrawing (fluorine, nitro) group. The reaction provides respective Schiff base and is reversible in absence of reactant 3. The first step of reaction consists of Michael addition. According to the experimental observations, the first step is slow (please see Mechanism section 3.3). Then, electron donating groups cause the aniline more nucleophilic and accelerate the reaction.
3.3. Mechanism
In separate experiments, reactions between aniline 1 and diethyl acetylenedicarboxylate 2 (Re. (1)), aniline 1 and benzaldehyde 3 (Re. (2)), and then diethyl acetylenedicarboxylate 2 and benzaldehyde 3 (Re. (3)) are performed under the same concentration of each reactant (10−2 M) at 20 °C. The Re. (1) is monitored by recording scans of the entire spectra with 5 min intervals in 45 min reaction time at 20 °C (Fig. 7A). The Re. (2) was monitored by recording scans of the entire spectra with 1 min intervals during the whole reaction time (5 min) at 20 °C (Fig. 7B). There are no reactions between reactants 2 and 3 due to the lack of any progress. Moreover, some 1HNMR information about the reaction products is presented in ESI file,† and also the about first intermediate I1 was reported previously.47,48 According to these references, the first step of the reaction consists of Michael addition and is slow which respective diethyl 2-aryloamino-fumarate I1 can be readily synthesize and characterized according to known protocols and can be purified by convenient distillation, then, I1 can be used for subsequent steps.49,50 As a result of these preliminary investigations and experimental observations, the speculative mechanism containing three steps with starting reaction between reactants 1 and 2 (the more rapidly occurring reaction amongst competing reactions) is proposed in Fig. 8.
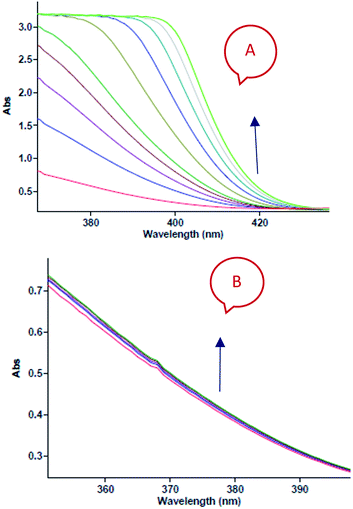 |
| | Fig. 7 (A) Changes in absorption spectra vs. wavelength in 20 °C for the reaction between aniline 1 and diethyl acetylenedicarboxylate 2 in formic acid as reaction proceeds into a 10 mm light-path cell. The total acquisition time was 45 min; the time increment was set to 5 min. Herein, the upward of direction of the arrow indicate that the progress of reaction. (B) Changes in absorption spectra vs. wavelength in 20 °C for the reaction between aniline 1 and benzaldehyde 3 in formic acid as reaction proceeds into a 10 mm light-path cell. The total acquisition time was 5 min; the time increment was set to 1 min. Herein, the upward of direction of the arrow indicate that the progress of reaction. | |
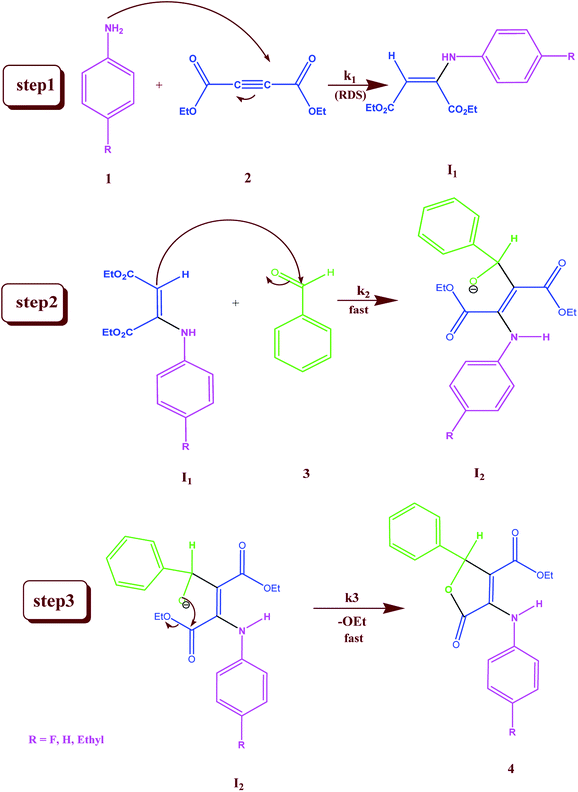 |
| | Fig. 8 Speculative mechanism for the reaction between aniline 1 and diethyl acetylenedicarboxylate 2 with para-substituted benzaldehyde 3 for generation of product 4 in formic acid. | |
For the reaction, a steady state treatment is coupled with the kinetic observations. So, the rate law is written using the final step of the proposed mechanism in Fig. 8 for the generation of product 4:
Also, the overall reaction can be written as:
This makes it possible to accept that the first step is the rate-determining step (RDS) of the reaction and the overall order of reaction is two since k1 is the only rate constant which appeared in the eqn (11). This equation, obtained from the proposed mechanism, is same with the rate law that resulted from UV-vis experiment (rate = kovr [1][2]). It is possible to analyze the effect of the solvent on the reaction, because the first step (k1) is the rate determining step, in this case in both solvents the transition state partially charged, in solvent with higher dielectric constant the transition state is highly solvated relative to the reactant molecules that have no any charge.
If the second step to be a rate determining step, therefore, the first step is fast with forward rate constant (k1) and return rate constant (k−1). We can write the rate law:
| |
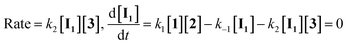 | (12) |
| |
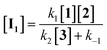 | (13) |
| |
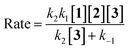 | (14) |
According to the above assumption, k2 is a rate determining step, therefore it is logical to express k−1 ≫ k2[3].
As a result, rate law becomes:
| |
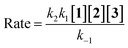 | (15) |
herein, the overall order of recent rate law is three and is not compatible with the rate law arising from UV-vis experiment (rate =
kovr[
1][
2]), so the second step could not be a rate determining step.
4. Conclusions
Kinetics and mechanism of the reactions between para-substituted anilines 1 and diethyl acetylenedicarboxylate 2 with benzaldehyde 3 were investigated in formic acid and the below results were obtained:
A mechanism involving three steps was proposed for the reactions. The overall order of reaction followed second-order kinetics and the partial orders with respect to para-substituted aniline, diethyl acetylenedicarboxylate and benzaldehyde were one, one and zero, respectively. Also, the first step of the reaction is recognized as a rate-limiting step according to the experimental data. The electron donating group on substituted aniline more stabilized the transition state than the electron withdrawing group and with decreasing the activation energy the value of rate constant (k1) was speed up. The rate of reaction was also accelerated by increasing the temperature and was in agreement with Arrhenius, Eyring equations and the transition state equations.
Acknowledgements
We gratefully acknowledge financial support from the Research Council of the University of Sistan and Baluchestan.
References
- N. B. Carter, A. E. Nadany and J. B. Sweeney, J. Chem. Soc., Perkin Trans. 1, 2002, 2324 RSC.
- Q. H. Chen, P. N. Praveen and E. E. Knaus, Bioorg. Med. Chem., 2006, 14, 7898 CrossRef CAS PubMed.
- J. Boukouvalas, S. Cote and B. Ndzi, Tetrahedron Lett., 2007, 48, 105 CrossRef CAS PubMed.
- A. Zarghi, P. N. Praveen and E. E. Knaus, Bioorg. Med. Chem., 2007, 15, 1056 CrossRef CAS PubMed.
- M. Braun, A. Hohmann, J. Rahematpura, C. Buhne and S. Grimme, Chem.–Eur. J., 2004, 10, 4584 CrossRef CAS PubMed.
- F. Bellina, E. Falchi and R. Rossi, Tetrahedron, 2003, 59, 9091 CrossRef CAS PubMed.
- S. Takahashi, A. Kubota and T. Nakata, Tetrahedron Lett., 2002, 43, 8661 CrossRef CAS.
- S. Padakanti, M. Pal and K. R. Yeleswarapu, Tetrahedron, 2003, 59, 7915 CrossRef CAS PubMed.
- S. M. Hein, J. B. Gloer, B. Koster and D. J. Malloch, Nat. Prod., 2001, 64, 809 CrossRef CAS PubMed.
- M. Pour, M. Spulak, V. Balsanek, J. Kunes, P. Kubanova and V. Butcha, Bioorg. Med. Chem., 2003, 11, 2843 CrossRef CAS.
- L. M. Levy, G. M. Cabrera, J. E. Wright and A. M. Seldes, Phytochemistry, 2003, 62, 239 CrossRef CAS.
- G. Grossmann, M. Poncioni, M. Bornand, B. Jolivet, M. Neuburger and U. Sequin, Tetrahedron, 2003, 59, 3237 CrossRef CAS.
- S. Hanessian, R. Y. Park and R. Y. Yang, Synlett, 1997, 4, 351 CrossRef PubMed.
- S. Hanessian, R. Y. Park and R. Y. Yang, Synlett, 1997, 4, 353 CrossRef PubMed.
- A. Choudhury, F. Jin, D. Wang, Z. Wang, G. Xu, D. Nguyen, J. Castoro, M. E. Pierce and P. N. Confalone, Tetrahedron Lett., 2003, 44, 247 CrossRef CAS.
- N. Hazeri, M. T. Maghsoodlou, N. Mahmoudabadi, R. Doostmohammadi and S. Salahi, Curr. Organocatal., 2014, 1, 45–50 CrossRef CAS.
- R. Doostmohammadi, M. T. Maghsoodlou, N. Hazeri and S. M. Habibi-Khorassani, Res. Chem. Intermed., 2013, 39, 4061 CrossRef CAS.
- R. Doostmohammadi and N. Hazeri, Lett. Org. Chem., 2013, 10, 199 CrossRef CAS.
- M. S. Narayana, et al., Tetrahedron, 2009, 65, 5251 CrossRef PubMed.
- R. M. Mohammad, et al., C. R. Chim., 2014, 17, 131 CrossRef PubMed.
- F. A. Carey and R. J. Sundberg, Advanced Organic Chemistry, Part A, Structure Mechanisms Kluwer Academic Press, New York, 2000 Search PubMed.
- O. J. Nielsen, J. Sehested, S. Langer, E. Ljungström and I. Wängberg, Chem. Phys. Lett., 1995, 238, 359 CrossRef.
- V. V. Ivanov and C. Decker, Polym. Int., 2001, 50, 113 CrossRef CAS.
- M. C. Almandoz, Y. A. Dávila, M. I. Sancho, E. I. Gasull and S. E. Blanco, Spectrochim. Acta, Part A, 2010, 77, 51 CrossRef CAS PubMed.
- L. L. Lu, Y. H. Li and X. Y. Lu, Spectrochim. Acta, Part A, 2009, 74, 829 CrossRef PubMed.
- J. J. C. Erasmus, M. M. Conradie and J. Conradie, React. Kinet., Mech. Catal., 2012, 105, 233 CrossRef CAS.
- B. P. Kalyan and K. S. Gupta, Transition Met. Chem., 2012, 37, 671 CrossRef.
- A. K. Chandra, J. Mol. Model., 2012, 18, 4239 CrossRef CAS PubMed.
- L. Sandhiya, P. Kolandaivel and K. Senthilkumar, Struct. Chem., 2012, 23, 1475 CrossRef CAS PubMed.
- M. Pandeeswaran and K. P. Elango, J. Solution Chem., 2009, 38, 1558 CrossRef CAS.
- S. M. Habibi Khorassani, A. Ebrahimi, M. T. Maghsoodlou, M. Shahraki and D. Price, Analyst, 2011, 136, 1713 RSC.
- M. Dehdab, S. M. Habibi-Khorassani and M. Shahraki, Catal. Lett., 2014, 144, 1790 CrossRef CAS PubMed.
- S. M. Habibi-Khorassani, M. T. Maghsoodlou, E. Aghdaei and M. Shahraki, Prog. React. Kinet. Mech., 2012, 37, 301 CrossRef.
- M. Shaharaki, S. M. Habibi-Khorassani, A. Ebrahimi, M. T. Maghsoodlou and A. Paknahad, Prog. React. Kinet. Mech., 2012, 37, 321 CrossRef.
- M. Shahraki and S. M. Habibi-Khorassani, J. Phys. Org. Chem., 2015, 28, 396 CrossRef CAS PubMed.
- S. M. Habibi-Khorassani, A. Ebrahimi, M. T. Maghsoodlou, O. Asheri, M. Shahraki, N. Akbarzadeh and Y. Ghalandarzehi, Int. J. Chem. Kinet., 2013, 45, 596 CrossRef CAS PubMed.
- S. S. Pourpanah, S. M. Habibi-Khorassani and M. Shahraki, Chin. J. Catal., 2015, 36, 757 CrossRef CAS.
- R. Doostmohammadi, M. T. Maghsoodlou and S. M. Habibi-Khorassani, Iran J. Org. Chem., 2012, 4, 939 Search PubMed.
- L. Longyun, et al., ACS Comb. Sci., 2013, 15, 183 CrossRef PubMed.
- R. Sarkar and C. Mukhopadhyay, Tetrahedron Lett., 2013, 54, 3706 CrossRef CAS PubMed.
- M. Zhang and J. Huan-Feng, Eur. J. Org. Chem., 2008, 20, 3519 CrossRef PubMed.
- M. Zhang, et al., Synlett, 2007, 20, 3214 Search PubMed.
- O. J. Nielsen, J. Sehested, S. Langer, E. Ljungström and I. Wängberg, Chem. Phys. Lett., 1995, 238, 359 CrossRef.
- C. Lerveny and V. Ruzicka, Adv. Catal., 1981, 30, 335 Search PubMed.
- M. Mortimer and P. Taylor, Chemical Kinetics and Mechanism, The Royal Society of Chemistry, Thomas Graham House, Science Park, Milton Road, Cambridge, CB4 OWF, UK, 2002 Search PubMed.
- K. J. Laidler, Theories of Chemical Reaction Rates, McGraw-Hill, New York, 1941 Search PubMed.
- M. M. Mashaly, S. R. El-Gogary and T. R. Kosbar, J. Heterocycl. Chem., 2014, 51, 1078 CrossRef CAS PubMed.
- C. Huang, Y. Yin, J. Guo, J. Wang, B. Fan and L. Yang, RSC Adv., 2014, 4, 10188 RSC.
- J. Safaei-Ghomi, F. Salimi, A. Ramazani, F. Z. Nasrabadi and Y. Ahmadi, Turk. J. Chem., 2012, 36, 485 CAS.
- G. Domschke, Inz. Chem., 1980, 20, 16 CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5ra09717g |
|
| This journal is © The Royal Society of Chemistry 2015 |
Click here to see how this site uses Cookies. View our privacy policy here. 

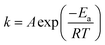
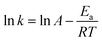
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k versus the reciprocal of the temperature 1/T, which will yield a straight line with a slope of
k versus the reciprocal of the temperature 1/T, which will yield a straight line with a slope of 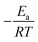 and an intercept ln
and an intercept ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A (Fig. 5). The highest activation energy (Ea = 80.12 kJ mol−1) is obtained for NO2-aniline, that means reaction will occur slower than alone aniline and para-donating substituent-aniline. Nevertheless, the differences in activation energies are not much, because the substituents on aniline ring are far from the center of reaction. The Eyring equation is used in chemical kinetics to describe the variance of the rate of a chemical reaction with temperature and was used to evaluate activation parameters involving ΔH≠ (activation enthalpy), ΔS≠ (activation entropy).46
A (Fig. 5). The highest activation energy (Ea = 80.12 kJ mol−1) is obtained for NO2-aniline, that means reaction will occur slower than alone aniline and para-donating substituent-aniline. Nevertheless, the differences in activation energies are not much, because the substituents on aniline ring are far from the center of reaction. The Eyring equation is used in chemical kinetics to describe the variance of the rate of a chemical reaction with temperature and was used to evaluate activation parameters involving ΔH≠ (activation enthalpy), ΔS≠ (activation entropy).46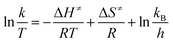
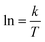 versus 1/T plot (Fig. 6). Obtained activation parameters for para-substituted aniline are given in Tables 2 and 3.
versus 1/T plot (Fig. 6). Obtained activation parameters for para-substituted aniline are given in Tables 2 and 3.
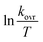 versus T) according to eqn (5) for the reaction between 1, 2 and 3 in formic acid.
versus T) according to eqn (5) for the reaction between 1, 2 and 3 in formic acid.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A) using the Arrhenius eqn (3) and The transition state eqn (6)–(8) in 20 °C
A) using the Arrhenius eqn (3) and The transition state eqn (6)–(8) in 20 °C
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A
A