Open Access Article
Open Access ArticleThe role of xylulose as an intermediate in xylose conversion to furfural: insights via experiments and kinetic modelling
O.
Ershova
a,
J.
Kanervo
b,
S.
Hellsten
a and
H.
Sixta
*a
aDepartment of Forest Products Technology, Aalto University, Finland. E-mail: herbert.sixta@aalto.fi
bDepartment of Biotechnology and Chemical Technology, Aalto University, Finland
First published on 30th July 2015
Abstract
An experimental work has been performed to study the relevance of xylulose as an intermediate in xylose conversion to furfural in aqueous solution. The furfural formation was investigated at the temperature range from 180 to 220 °C during non-catalyzed and acid-catalyzed conversion of xylose in a stirred microwave-assisted batch reactor. The separate experiments on xylulose and furfural conversions were carried out under similar conditions. The maximum furfural yields obtained from xylose were 48 mol% and 65 mol% for the non-catalyzed and the acid-catalyzed processes, respectively. It was shown that the furfural yield is significantly lower from xylulose than from xylose. Furthermore, the effects of initial xylose concentration and the formation of xylulose were investigated in a mechanistic modeling study. A new reaction mechanism was developed taking into account the xylulose formation from xylose. Based on the experimental results and the proposed reaction model, it was concluded that xylose isomerization to xylulose with subsequent furfural formation is not a primary reaction pathway. The obtained kinetic parameters were further used for plug flow reactor simulations to evaluate furfural yields achievable by an optimized continuous operation.
Introduction
Furfural is a platform chemical utilized in the chemical industry for synthesizing solvents, adhesives, medicines, and plastics.1 It is mainly obtained in acidic aqueous solution by direct dehydration of pentosans derived from different biomass such as corncob, bagasse, wheat and rice straw. Xylose is the most utilized monosaccharide in furfural production. It is a pentose which can be formed either by direct degradation of polymeric xylan in lignocellulosic material or by depolymerization of the solubilized oligomeric xylan.2 In addition, several studies describe the furfural formation from other pentoses3–6 or hexoses.5 Furfural can be also obtained as a by-product of different biomass treatment processes.7–9Currently, furfural is produced industrially with about 50 mol% yield10,11 utilizing sulfuric or hydrochloric acid as a catalyst. The replacement of these wasteful and energy-inefficient mineral acid catalysts by solid acid catalysts bearing different acidic functionalities, which are able to achieve a sufficient improving in the furfural yield, has a growing interest. However, an understanding of the reaction pathways as well as the kinetics of furfural formation in aqueous media in the presence or absence of acids is crucial for the successful development of the efficient catalytic system and the obtaining of the target product in high yields.
Currently, the kinetics of furfural formation under different conditions are widely studied in order to create a scientific basis for improving the production efficiency. However, it is challenging to reconcile all the published kinetic data presented in the literature due to the different reaction conditions and conflicting modelling approaches used. Different reaction mechanisms of the furfural formation from pentoses have been proposed in scientific literature based on different analysis and reaction modellings. In the majority of research papers, the kinetics of xylose dehydration to furfural is based on a simplified reaction scheme with a direct pathway from xylose to furfural.12–14 The current knowledge on the kinetics of side and loss reactions has been identified as insufficient as well.15
One of the open questions in the furfural formation reaction is whether the mechanism proceeds via a cyclic or an acyclic form of xylose. Antal and co-workers claim that the furfural formation proceeds from the pyranose form of xylose without a ring opening stage.16,17 However, most researchers have adopted a reaction mechanism hypothesis that involves the formation of an acyclic xylose form, even though this mechanism is not able to fully explain the formation of some side products.4,15 Antal et al.17 have also proposed the formation of both acyclic and cyclic forms of xylose at temperatures above 250 °C.
Irrespective whether the reaction proceeds via cyclic or acyclic forms of xylose, the existence of some intermediate compounds is not questionable. The formation of intermediates has been considered as the rate-limiting stage in the reaction of furfural formation from xylose.15,18 Firstly, it was stated that an essential intermediate is a 2,3-(α,β-)unsaturated aldehyde as formed by a β-elimination reaction from pentose sugars.10,19,20 Several other authors explained the reaction to take place via a 1,2-enediol intermediate with subsequent dehydration.4,18 More recently, the isomerization of aldopentoses to ketose sugar (luxose17,21 or xylulose22–24) as an intermediate step in furfural formation has been studied intensively. The current developments of bi-functional catalysts24–28 and other catalytic systems29 consider an implementation of such two stage process which includes the xylose isomerization as the first step followed by the second step – the ketose sugar dehydration to furfural. However, the role of these intermediate ketose sugars (luxose or xylulose) in the furfural formation reactions remains unclear. Only few studies have focused on the determination of the intermediate xylulose concentration during the process4,27,29 and considered its formation and conversion for kinetic parameters evaluation.22 The formation of xylulose during xylose conversion in high temperature water has been confirmed in a study made by Aida et al.22 with implementation of GC-MS analysis. They observed the formation of about 20% of D-xylulose at 350–400 °C after 0.5–1 s reaction time.
In addition to conventional reactor systems, microwave irradiation can be utilized as an alternative rapid and efficient heating method during furfural production. It has been shown to accelerate reaction rates and to give a slightly higher furfural yield, which is, nonetheless, comparable to the conventional heating methods.12 The aim of this study is to devise kinetic models for the non-catalyzed and acid-catalyzed dehydration of xylose to furfural under microwave irradiation at the temperature range 180–220 °C. A special focus is placed to address the role of xylulose in the total reaction scheme.
Experimental
Materials
D-Xylose powder (≥99%, Sigma Aldrich), D-xylulose (≥98%, syrup, HPLC grade, Sigma Aldrich), furfural (99%, Sigma Aldrich), sulfuric acid (49–51%, HPLC grade, Sigma Aldrich) were used in the experiments and as calibration standards as purchased, without further purification. Formic acid (98%, Sigma Aldrich) and acetic acid (99%, HPLC grade, Sigma Aldrich) were used for the preparation of calibration standards for HPLC analysis. Millipore grade water was used for the solutions preparation.Methods
Single component solutions of D-xylose (51, 196, 498 mmol l−1), D-xylulose (7 mmol l−1) and furfural (85 mmol l−1) were freshly prepared before experiments. The first set of experiments was performed without addition of sulfuric acid as catalysts. These experiments can be considered as auto-catalyzed reaction system where some side products (namely carboxylic acids) or intermediates, formed during the treatment, may have a catalytic effect. The second set of experiments was performed using 0.1 mol l−1 H2SO4 as a catalyst.The samples were prepared by heating 3 ml of the reaction mixture in a Monowave 300 single-mode microwave reactor (Anton Paar GmbH, Graz, Austria) using a borosilicate glass vial of 10 ml capacity. A magnetic stirrer at 600 rpm utilized to mix the solution during the reaction. Time-to-maximum temperature was set to 1.5 min with 850 W maximum output power employed. The temperature inside the reaction vessel was controlled by a fiber optic sensor. The prepared solutions were tested for furfural yield and monosugars conversion at the treatment temperatures of 220, 200 and 180 °C with different reaction times in the range of 1–240 min. The reaction vial was rapidly cooled after the treatment by compressed air inside the reactor. The highest temperature and the longest reaction time studied at the present work were limited to 220 °C and 240 min, respectively, due to the technical limitations of the Monowave 300 reactor.
The liquid samples were analyzed by High Performance Liquid Chromatography (HPLC) using a Dionex UltiMate 3000 HPLC (Dionex, Sunnyvale, CA, USA) device equipped with refractive index (RI) and ultraviolet (UV) diode array detectors and HyperREZ XP Carbohydrate Ca+ column (Thermo Scientific, Waltham, MA, USA). 0.0025 mol l−1 sulfuric acid solution was used as eluent at a flow rate of 0.8 ml min−1. The column temperature and the RI detector temperature were set to 70 °C and 55 °C, respectively. The furfural concentration in the liquid samples was determined by UV-detector at wavelength 280 nm, and the residual xylose concentration was analyzed by RI detector. The xylulose concentration was measured by RI-detector with a crosscheck using UV detector at 210 nm.30 The HPLC system was calibrated within the compounds concentrations from 10 to 150 mg l−1.
The following equations have been used for the mathematical evaluation of the obtained results:
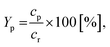 | (1) |
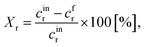 | (2) |
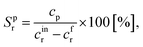 | (3) |
Reaction kinetics were modelled by nonlinear regression analysis by fitting the simulated ideal batch reactor composition to the experimental one covering xylose, xylulose and furfural molar concentrations. All the computations were implemented in MATLAB 2013b (Mathworks Inc.). The ordinary differential equations were numerically solved by ‘ode15s’ (variable order method for stiff odes) and optimization to minimize the weighed sum of squared residuals was done by ‘fminsearch’ (Nelder-Mead algorithm). Weighing factors were applied to compensate the weight of the experiments with very dilute concentration scale.
The kinetic parameters for each tested reaction temperature were expressed by the following equation:
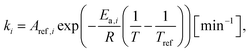 | (4) |
The plug flow reactor simulations were implemented in MATLAB 2013b. The set of boundary value equations were numerically solved by ‘ode23’. Optimization of the temperature and the residence time to maximize the simulated furfural yield was carried out using ‘fminsearch’ routine.
Results and discussions
Experimental results
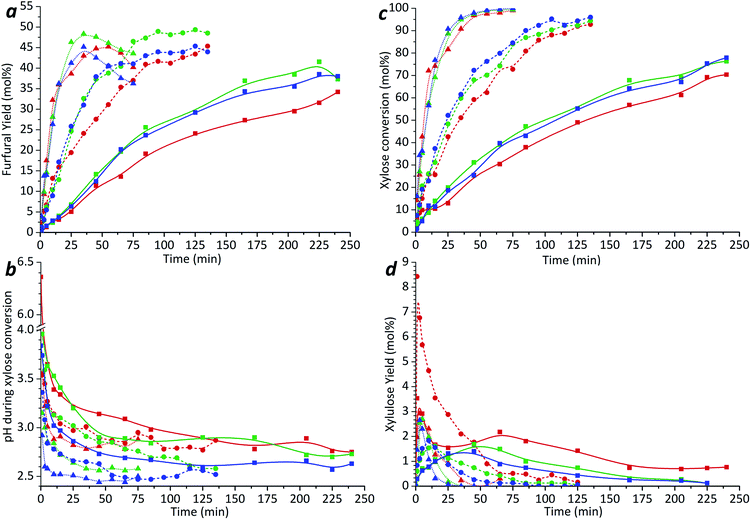
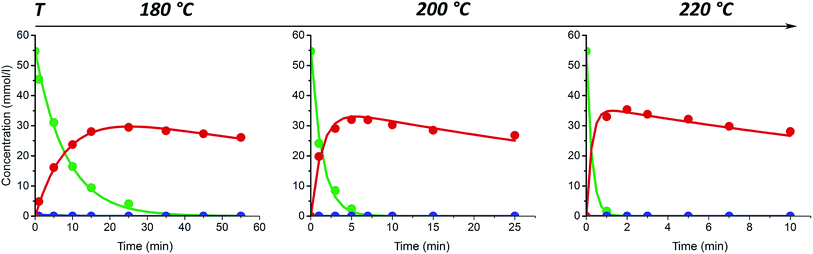
In agreement with previous studies,31–33 furfural yield and xylose conversion were observed to be strongly influenced by the treatment temperature. As seen in Fig. 1a, after the first 25–35 min of the treatment the furfural yield was increased up to 4.5–5 times by increasing the temperature from 180 to 200 °C. A further 2–2.5-fold increase was observed with the temperature change from 200 to 220 °C.
It was observed that at the highest temperature studied (220 °C) the furfural yield from xylose dehydration goes through a maximum and thereafter decreases with increasing reaction time. The maximum furfural yield (45–48%) was reached after the first 35 min at 220 °C, corresponding to a xylose conversion of 96% (Fig. 1c). However, at the temperature 200 °C the same conversion was achieved only after 115–125 min resulting in similar maximum furfural yield.
These results are in close agreement with those reported by Möller and Schröder.34 The decrease of furfural yield with a further increase in the reaction time can occur due to decomposition35–37 and polymerization with char formation.10,38
At the lower reaction temperatures (180 and 200 °C), no rapid decrease in the furfural yield after certain reaction time was observed during the reaction time range studied. It is, however, possible that a yield decrease similar to that observed at 220 °C could be observed also at these temperatures during prolonged treatment times. Nevertheless, the maximum yield clearly shifts to a longer reaction time with a decline of the treatment temperature.
The maximum selectivity to furfural formation during un-catalyzed xylose conversion was around 48–52% in the studied range of reaction temperatures. These results are in agreement with the previous reports,31,34 indicating either a small or even a negligible effect of microwave irradiation on furfural formation.
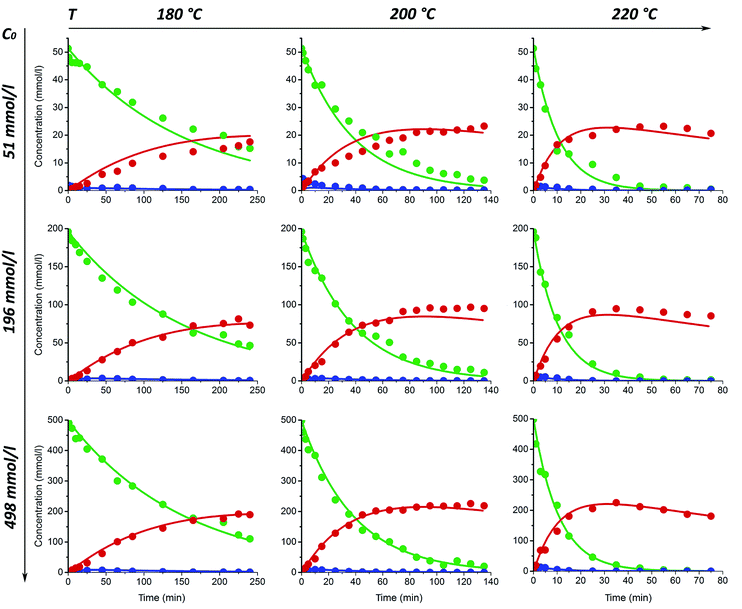
The xylose conversion and furfural yield are also dependent on the initial xylose concentration as seen in Fig. 1a and c. The dependence of xylose conversion on the initial concentration is, however, less significant at higher temperatures. During the first 15–25 min of the experiment, both furfural yield and xylose conversion seem to be independent of the initial xylose concentration. However, with extended reaction times, a clear concentration dependence can be observed. The furfural yield increased by 12% after 100 min at 200 °C and 14% after 175 min at 180 °C when the initial concentration of xylose was increased from 51 to 196 mmol l−1. A further increase of the initial xylose concentration to 498 mmol l−1 did not lead to higher furfural production; but, at the temperatures of 200 and 220 °C, it led to a reduction of 5–7% in the furfural yield in comparison to the experiments with a xylose concentration of 196 mmol l−1 (Fig. 1a). Fig. 1a also shows that at 220 °C, the furfural yield starts to decrease earlier in the solution with increasing initial xylose concentration. This phenomenon could be well explained by a side reaction between furfural and xylose (or intermediate compounds),10,38 which is, probably, promoted by increasing temperature. These results suggest that differences in reaction temperature and other conditions might explain the contradiction between previous reports either concluding the furfural yield to be independent on the xylose concentration12 or observing an almost linear decline in furfural yield when initial xylose concentration was increased.14,39 In the work published by Weingarten et al.,12 the experiments were performed at relatively low temperatures and very short experimental time, while other authors investigated the furfural formation at more severe conditions including higher temperature, pressure and prolonged reaction time.14,39
As can be seen in Fig. 1b, the pH of the solution decreases rapidly during the first 5 min of the experiment and levels off at about 3–2.5 in all of the temperatures studied. A similar decrease in pH has been earlier reported for the xylose degradation in subcritical6,40 or high temperature41 water, and it can be explained by the formation of acidic compounds such as formic, glycolic, lactic and acetic acids41 during the degradation of the pentose sugars and furfural. The final pH is observed to be dependent on the reagents concentrations in the solution. A lower final pH was obtained in the solution with higher initial xylose concentration, supporting the results of Oefner et al.,41 who observed the formation of these organic acids with a yield of about 15% of all xylose conversion products. The generated acidic conditions may promote further furfural formation as well as the formation of side products.41,42
The xylulose formation was monitored by means of HPLC utilizing a pure xylulose solution as a reference. No detectable amounts of xylulose were observed in the initial xylose solutions. Fig. 1d shows that the highest amount of xylulose (3–3.5%) was formed during the initial stage (the first 1–3 min) of the process. At the temperature of 180 °C, some amount of xylulose was present even after a 4 h treatment. The extent of xylulose formation was highest for the solution with the lowest initial xylose concentration. As can be seen from Fig. 1d, the highest amount of xylulose formed was experimentally found at 200 °C with the initial xylose concentration 51 mmol l−1. The obtained results show that the xylulose formation is accelerated by increasing the reaction temperature, particularly from 180 °C to 200 °C. However, at 220 °C the presence of furfural in a sufficient amount increases the probability of condensation reactions with xylulose.
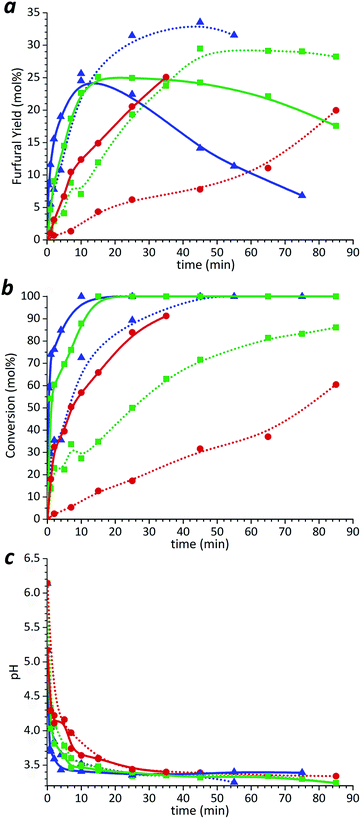
The maximum furfural yield from xylulose obtained during the un-catalyzed process was 25%, which is almost 10 mol% lower than the furfural yield obtained from solution with similar concentration of xylose (Fig. 2a). Xylulose was completely transformed into products after 10–15 min at 220 and 200 °C, respectively (Fig. 2b), while no formation of xylose was detected. However, it is possible that its amount was below the HPLC detection limit. At the same time, the full conversion of xylose was achieved only after 55 min at 220 °C. The results show that the xylulose is more reactive and converts to furfural and other products faster than xylose giving lower pH during first 10 min of the reaction. However, the final pH of the obtained solutions was very similar in both cases with equal initial concentrations of the xylose and xylulose. This implies that almost equal amount of acids were generated from pentoses during degradation experiments.
The formation of solid products was observed at the latest stages of the reaction experiments. These so-called humin-like substances are formed either by resinification and polymerization reactions of furfural10 or by condensation reactions between furfural and pentose.38 The obtained results show that xylulose is not a key intermediate in the un-catalyzed furfural formation. Xylulose rather leads to a loss reaction than to furfural formation.
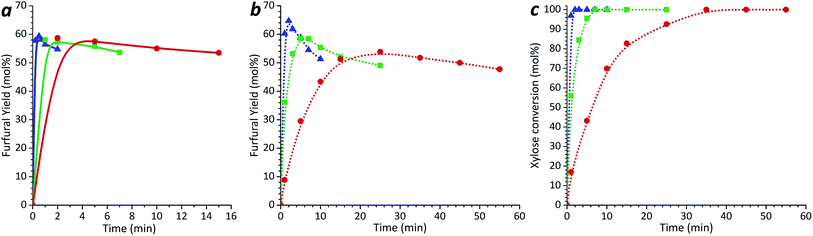
During acid-catalyzed xylose conversion, the maximum selectivity to the furfural formation was around 64% in contrast to 50–51% obtained in un-catalyzed reaction system. To investigate the possible furfural formation from xylulose in the presence of the acid catalyst, a solution containing 6.6 mmol l−1 of xylulose and 0.1 mol l−1 H2SO4 was tested using the same procedure as for the xylose solution. The results are shown in Fig. 3a. For all the tested temperatures, the maximum furfural yield produced was 58–59% and it was obtained in less than 2 min. This maximum yield is almost 2.4 times higher than in the case of the un-catalyzed system. In the range of the studied reaction temperatures, the complete xylulose conversion during the acid-catalyzed reaction was achieved already after 1 min treatment. At the time when all the xylulose was converted, a part of formed furfural was already degraded. The furfural yields from xylulose in acid-catalyzed reactions obtained in previous studies were 40–50% (ref. 4) at 96 °C, 50–65% (ref. 27) at temperatures 105–135 °C using 0.1 mol l−1 HCl, and 70% (ref. 29) at 110–130 °C with HCl at pH 1.
After acid-catalyzed conversion, neither formation of xylulose from xylose nor formation of xylose from xylulose was detected by HPLC. However, it is possible that the amounts were below the detection limit.
The results of the acid-catalyzed process suggest that two different reaction pathways of furfural formation from pentoses possibly coexist. In the un-catalyzed xylose conversion, the intermediate xylulose seemingly leads to the side products formation, while with the addition of sulfuric acid a prevailing mechanism includes fast ketose dehydration to furfural.
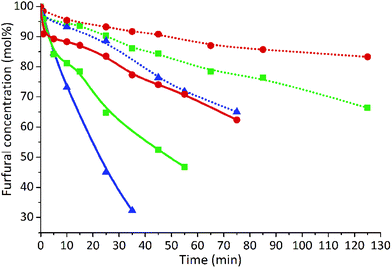
Fig. 4 illustrates the effect of the treatment temperature and the usage of 0.1 mol l−1 H2SO4 as catalyst on the degradation rate of furfural. The results show a clear dependency of furfural degradation on the temperature, similarly to the data presented in earlier reports.31,36,37,42,43 It can be seen that the implementation of a higher temperature increases the furfural degradation for both un-catalyzed and acid-catalyzed reactions. In addition, the results show that furfural is decomposed more rapidly in the presence of 0.1 mol l−1 H2SO4. The highest degree of degradation, 68%, was observed at 220 °C after 35 min in 0.1 mol l−1 sulfuric acid solution. Without the acid catalyst, only 15% of furfural was converted at the same temperature and reaction time. The formation of furfural resinification products – humins – was observed at the late stages of both un-catalyzed and acid-catalyzed degradation. The acetic and formic acids were also found in the solution during non-catalyzed and acid-catalyzed furfural degradation reactions.
Reaction mechanism and its mathematical modelling
Based on the obtained experimental results, several reaction mechanisms were screened in order to find the optimal kinetic model explaining the xylose dehydration and furfural formation. The model screening was performed by formulating mechanism candidates, implementing corresponding mathematical models and by carrying out nonlinear regression analysis to test the compatibility of a model to the experimental data and to receive values for kinetic parameters. These reaction mechanisms considered a pathway of furfural formation pathways from xylose via intermediate xylulose or tentatively via some other intermediates to furfural. Using the xylose conversion data only in the modeling resulted in multiple equally well-fitting models with differing mechanistic assumptions. Therefore, the data set was appended with the independent xylulose conversion and furfural degradation experiments that enabled the model screening and mathematical identification of the values for all the related rate constants. Finally, the best fitting of the model to experimental data was obtained taking into account pathways via xylulose and via another intermediate compound leading to the formation of furfural in the un-catalyzed and the acid-catalyzed reactions. The developed reaction mechanism taking into account the xylulose formation from xylose is as follows: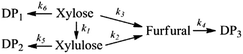 | (5) |
In the reaction model presented in eqn (5), xylose can be converted to furfural either stepwise with xylulose as an intermediate product (k1 + k2), or via a direct or pseudo-direct reaction pathway (k3), which may involve the formation of some other intermediate compound but not xylulose. The produced furfural further forms degradation products (DP3). At the same time, some parts of the xylose and xylulose form degradation products, DP1 and DP2, respectively. The possible side reactions between xylose and furfural10,44 and the isomerization of xylulose back to xylose were not identifiable from the present data.
Assuming a sequence of pseudo-first order reactions,22,41 the proposed reaction model can be expressed by differential equations as follows:
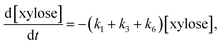 | (6) |
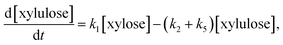 | (7) |
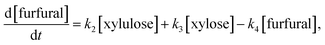 | (8) |
The fits of the proposed kinetic model for acid-catalyzed and un-catalyzed reactions are shown in Fig. 5 and 6, respectively. The fitting is relatively good for all experimental series with different initial xylose concentration ranging from 50 to 500 mmol l−1. The model reconciles all the xylose conversion data as well as the independent experiments for xylulose conversion and furfural degradation. This indicates that the reaction behavior of furfural and monosugars at high temperatures can be adequately predicted by first order kinetic model. It should be noted that the validity of first-order models may be attributed to the relatively dilute concentrations and non-simultaneous presence of abundance of furfural and sugars. To the author's knowledge in some solutions, relevant in industry, the high xylose concentration, e.g. 1.5–2 mol l−1, have a strong impact on the furfural yield. Future experiments targeting at the investigation of the influence of the initial xylose concentration on furfural formation encompassing a much broader concentration range need to be carried out in order to elucidate the effect of initial xylose concentration on furfural formation.
The obtained kinetic parameters and the activation energies for the each reaction step are shown in Tables 1–3. Some literature data for the kinetic parameters related to similar reaction steps are shown for comparison in Tables 2 and 3.
As seen from Table 1, the implementation of sulfuric acid as a catalyst leads to an increase of more than one order of magnitude for all the reaction rates in comparison to the respective step in the un-catalyzed process. As an exception, the rate constants for the xylose isomerization to xylulose (k1) are of the same order of magnitude in both catalytic and non-catalytic systems. This observation is supported by the fact that sugar isomerization reactions are catalyzed by Lewis acids24,26 or bases18 but not by sulfuric acid.
| T, (°C) | Acid | k 1 | k 2 | k 3 | k 4 | k 5 | k 6 | k 3/k1 | k 2/k3 | k 2/k1 | k 5/k6 | k 5/k2 | k 5/k4 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 220 | − | 0.039 | 0.268 | 0.042 | 0.0059 | 1.016 | 0.013 | 1.1 | 6.4 | 6.9 | 79.8 | 3.8 | 172.1 |
| 200 | − | 0.009 | 0.081 | 0.013 | 0.0034 | 0.270 | 0.004 | 1.5 | 6.2 | 9.1 | 73.0 | 3.3 | 79.4 |
| 180 | − | 0.002 | 0.022 | 0.004 | 0.0019 | 0.064 | 0.001 | 2.0 | 6.0 | 12.3 | 66.2 | 2.9 | 34.2 |
| 220 | + | 0.056 | 16.151 | 2.499 | 0.0315 | 11.214 | 1.235 | 44.5 | 6.5 | 287.8 | 9.1 | 0.69 | 355.7 |
| 200 | + | 0.028 | 4.100 | 0.450 | 0.0150 | 2.800 | 0.230 | 16.1 | 9.1 | 146.4 | 12.2 | 0.68 | 186.7 |
| 180 | + | 0.013 | 0.922 | 0.070 | 0.0067 | 0.619 | 0.037 | 5.3 | 13.2 | 70.2 | 16.7 | 0.67 | 92.5 |
The rate constants for un-catalyzed and catalyzed reactions are evaluated at experimental temperatures to be able to elucidate relative contributions of individual steps (Table 1). The temperature dependence of ki is more pronounced in the acid-catalyzed processes, indicating that the reaction rates in the absence of sulfuric acid are less sensitive to the reaction temperature.
This is in line with the activation energies given in Table 2. The ratio of the reaction rate constants k2/k3 shows that in both reaction types furfural formation is more than six times faster from xylulose than from xylose. At the same time, the high ratio k2/k1 indicates that the xylulose formation from xylose can be considered as the rate-limiting step in furfural production via this reaction pathway. The values of k3/k1 show a substantial difference between the un-catalyzed and acid-catalyzed processes. The rate of the xylose isomerization to xylulose during un-catalyzed process is comparable to the rate of furfural formation from xylose (k3/k1 is near to 1), whereas in the acid-catalyzed process isomerization is substantially slower in these two competing reactions (k3/k1 values from 44.5 to 5.3).
| i | A ref,i | E a,i | E a,i, literature data |
|---|---|---|---|
| 1 | 0.0089 | 143.2 | — |
| 2 | 0.0810 | 116.1 | — |
| 3 | 0.0130 | 113.2 | 76.6 (ref. 14), 111.5 (ref. 31), 110–127 (ref. 40), 119.4 (ref. 41), 129.9 (ref. 13) |
| 4 | 0.0034 | 53.5 | 24.2 (ref. 14), 36.5 (ref. 6), 58.8 (ref. 31), 75.5 (ref. 47) |
| 5 | 0.2700 | 128.5 | — |
| 6 | 0.0037 | 119.8 | 58.8 (ref. 14), 101–119 (ref. 22), 143.1 (ref. 31), 168.5 (ref. 13) |
From these results, it can be concluded that the addition of 0.1 mol l−1 H2SO4 shifts the xylose conversion reaction towards furfural formation via some other intermediate than xylulose. For the acid-catalyzed reactions, the role of xylulose formation in the furfural production is insignificant in the range of studied reaction conditions.
The ratios k5/k6 and k5/k4 for the un-catalyzed and acid-catalyzed reactions reveals that at temperatures 180–220 °C xylulose is intend to degradation reaction more than xylose and furfural. Moreover, the ratio k5/k2 indicates that in un-catalyzed process the degradation of xylulose is three times more preferable than its conversion to furfural. However, when sulfuric acid is added as a catalyst, about 70% of the reacting xylulose is dehydrated to furfural. However, as the isomerization rate from xylose to xylulose is rather low in the acid catalyzed case the overall role of xylulose as an intermediate remains modest.
The calculated frequency factors and activation energies for proposed kinetic model for un-catalyzed and acid-catalyzed conversions are presented in Tables 2 and 3, respectively.
To the authors' knowledge, the activation energies of xylose isomerization to xylulose, furfural and degradation products formation from xylulose have not been previously reported in literature for neither un-catalyzed nor acid-catalyzed reactions. Aida et al.22 have presented respective rate constants, but only for the temperatures of 350 and 400 °C. The high temperature difference and implementation of high pressure by Aida et al. makes their results incomparable with the values obtained in this work.
As seen from Tables 2 and 3 the higher activation energies of steps 2 and 3 in case of the catalysed reactions in comparison to the uncatalysed ones reveals that furfural formation is favored at higher temperatures in the case of catalyzed reactions. This fact is supported by the results in Fig. 1 and 3a and b.
As seen in Table 3, the activation energy of furfural formation from xylose (113.2 kJ mol−1) obtained in our work is in a good agreement with the results previously published by Jing and Lü31 and Chen et al.40 The activation energy of furfural degradation (53.5 kJ mol−1) is also in a good agreement with data published by Jing and Lü,31 which can be expected because of the similarity in the experimental and procedure design.
As it can be seen from Table 3, the activation energies calculated for the acid-catalyzed process in the present study are much higher than those published earlier.3,12,41,45 These discrepancies between data could be possibly explained by either utilization of simplified reaction mechanism3,12–14,31,41,45 or implementation of subcritical and supercritical reaction conditions22 in the earlier studies.
Plug flow reactor simulations for xylose conversion
The determined kinetics for uncatalyzed and acid-catalyzed system (Table 1) were utilised to simulate a flow reactor system described by the plug flow reactor model (PFR). The objective was to assess possibilities to maximize the furfural yield by adjusting the reactor residence time and the temperature. A steady state and isothermal operation were assumed. The PFR model with the determined kinetics incorporated for each component is expressed as: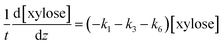 | (9) |
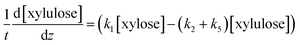 | (10) |
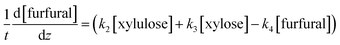 | (11) |
Simulation results revealed that for the uncatalyzed system the optimal process parameters are T = 218 °C and t = 34.8 min which resulted in 44.34% furfural yield. Fig. 7 illustrates the furfural yield as a function of the residence time and the reaction temperature. As can be seen, in addition to the reported optimum, there is a relatively wide region of temperature and time combinations that provide a furfural yield above 40%.
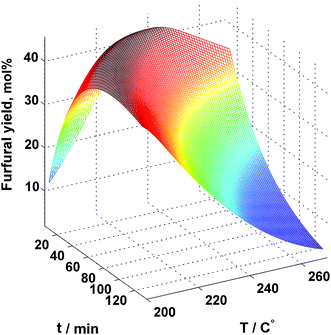 | ||
| Fig. 7 Simulated furfural yield as a function of residence time and temperature for uncatalyzed xylose conversion in plug flow reactor. | ||
In comparison to the un-catalyzed system, the strong acid-catalyzed system behaved differently in PFR simulations. The highest furfural yield was calculated for the maximum allowed temperature and with extremely short residence time. Table 4 displays the maximum furfural yields at selected temperatures and the required residence times for each temperature for attaining the optimal yield. The simulation results suggest that operating a PFR for 65% furfural yield requires the residence time slightly below 40 seconds at the temperature of 230 °C. Further increase in temperature and decrease in residence time can promote the furfural yield further up to 68%, provided that the extrapolation from 220 °C and 280 °C is valid. The dynamics of the strong acid catalyzed xylose conversion in a flow system would call for small-diameter-devices such as millireactors or, alternatively, an efficiently heat-controlled section in a tubular reactor followed by an efficient effluent cooling.
| T, °C | t, min | Y(furfural) mol% |
|---|---|---|
| 200 | 5.3 | 60.4 |
| 220 | 1.3 | 64.0 |
| 230 | 0.62 = 37 s | 65.1 |
| 240 | 0.31 = 18.6 s | 66.1 |
| 250 | 0.16 = 9.6 s | 66.7 |
| 260 | 0.084 = 5.0 s | 67.4 |
| 270 | 0.045 = 2.7 s | 67.9 |
| 280 | 0.025 = 1.5 s | 68.3 |
The plug flow reactor simulations underline how the un-catalyzed and strong acid catalyzed kinetics define the theoretical bounds for harnessing the intrinsic kinetics for furfural production, and they simply illustrate the interplay between the temperature and the residence time in flow systems for optimizing the furfural yield. If a yield of 44 mol% is considered acceptable, furfural production could be implemented without catalysts. On the other hand, 68 mol% cannot likely be exceeded without either inventive furfural recovery strategies or the inhibition of the loss reactions related to furfural and xylose.
Conclusions
The broad and informative experimental data were collected under well-controlled conditions and utilized for kinetic modeling of both the non-catalyzed and acid-catalyzed dehydration of xylose. A reaction mechanism with six kinetically relevant steps was found to be the most compatible with all the collected experimental data under microwave irradiation in the temperature range of 180–220 °C. The reaction steps were best described with the first order dynamics. The determined kinetic parameters were well identified and of physically meaningful order of magnitudes. Mechanism and parameter identification relied on the versatility in the experimental data: independent xylulose conversion and furfural degradation experiments provided a critical additional information in the combination with the xylose conversion experiments started at three initial concentrations and at three reaction temperatures.Xylulose was identified during the xylose conversion in varying yields depending on the reaction conditions, especially on the temperature. In the light of the results obtained, the role of xylulose as a key intermediate for furfural production from xylose was rejected under the tested reaction conditions. The experimental data obtained for the un-catalyzed xylose conversion as such ruled out the possibility of xylulose being the key intermediate. Modeling helped to establish the role of xylulose along a parallel reaction pathway. The primary reaction route involves another short-living intermediate that reacts rapidly to the furfural.
The results of the batch reactor experiments in conjunction with the plug-flow reactor simulations suggest that the maximum obtained furfural yield for the un-catalyzed system remains below 50% and requires approximately 35 minutes at 220 °C or 90 minutes at 200 °C. The presence of a strong acid accelerates most of the reaction steps and increases the maximum furfural yield. In the batch reactor experiments the maximum furfural yield of 62–65 mol% was obtained corresponding to 2–3 min reaction time at 220 °C in the acid catalyzed case. The plug flow reactor simulations for the acid catalyzed conversion suggested furfural yields up to 68 mol% with further increase in the reaction temperature along with an appropriate reduction in the residence time in the continuous operation.
Acknowledgements
The authors would like to acknowledge financial support from The International Doctoral Programme in Bioproducts Technology (PaPSaT) and from the Academy of Finland. We also sincerely thank Rita Hatakka for her contribution in the HPLC method development.References
- D. Win, AU Journal of Technology, 2005, 8, 185–190 Search PubMed.
- A. Mittal, S. G. Chatterjee, G. M. Scott and T. E. Amidon, Chem. Eng. Sci., 2009, 64, 3031–3041 CrossRef CAS.
- E. Garrett and B. Dvorchik, J. Pharm. Sci., 1969, 58, 813–820 CrossRef CAS PubMed.
- T. Ahmad, L. Kenne, K. Olsson and O. Theander, Carbohydr. Res., 1995, 276, 309–320 CrossRef CAS.
- X. Lü and S. Saka, J. Supercrit. Fluids, 2012, 61, 146–156 CrossRef.
- X. Bai, X. Liu, F. Xu and R. Li, Adv. Mater. Res., 2014, 512–515, 366–370 CrossRef.
- R. Lehnen, B. Saake and H. Nimz, Holzforschung, 2001, 55, 199–204 CrossRef CAS.
- K. C. Schuster, et al. , Nat. Fibers, Plast. Compos., 2004, 123–148 CAS.
- T. Zhang, R. Kumar and C. E. Wyman, RSC Adv., 2013, 3, 9809–9819 RSC.
- K. Zeitsch, The chemistry and technology of furfural and its many by-products, Elsevier Science B.V., 2000 Search PubMed.
- W. Jong de and G. Marcotullio, Int. J. Chem. React. Eng., 2010, 8, 1–25 Search PubMed.
- R. Weingarten, J. Cho, W. C. Conner, Jr and G. W. Huber, Green Chem., 2010, 12, 1423 RSC.
- M. Borrega, K. Nieminen and H. Sixta, Bioresour. Technol., 2011, 102, 10724–10732 CrossRef CAS PubMed.
- S. B. Kim, et al. , React. Kinet., Mech. Catal., 2011, 103, 267–277 CrossRef CAS.
- B. Danon, G. Marcotullio and W. de Jong, Green Chem., 2014, 16, 39 RSC.
- M. J. Antal, W. S. Mok and G. N. Richards, Carbohydr. Res., 1990, 199, 111–115 CrossRef CAS.
- M. J. Antal, T. Leesomboon and W. S. Mok, Carbohydr. Res., 1991, 217, 71–85 CrossRef CAS.
- M. Feather and J. Harris, Adv. Carbohydr. Chem. Biochem., 1973, 28, 161–224 CrossRef CAS.
- C. Hurd and L. Isenhour, J. Am. Chem. Soc., 1932, 54, 317–330 CrossRef CAS.
- W. Bonner and M. Roth, J. Am. Chem. Soc., 1959, 81, 5454–5456 CrossRef CAS.
- R. O'Neill, M. N. Ahmad, L. Vanoye and F. Aiouache, Ind. Eng. Chem. Res., 2009, 48, 4300–4306 CrossRef.
- T. M. Aida, N. Shiraishi, M. Kubo, M. Watanabe and R. L. Smith, J. Supercrit. Fluids, 2010, 55, 208–216 CrossRef CAS.
- J. Binder, J. Blank, A. Cefali and R. Raines, ChemSusChem, 2010, 3, 1268–1272 CrossRef CAS PubMed.
- V. Choudhary, S. Caratzoulas and D. G. Vlachos, Carbohydr. Res., 2013, 368, 89–95 CrossRef CAS PubMed.
- A. Takagaki, M. Ohara, S. Nishimura and K. Ebitani, Chem. Lett., 2010, 39, 838–840 CrossRef CAS.
- V. Choudhary, A. B. A. Pinar, S. I. S. Sandler, D. G. Vlachos and R. F. Lobo, ACS Catal., 2011, 1, 1724–1728 CrossRef CAS.
- V. Choudhary, S. I. Sandler and D. G. Vlachos, ACS Catal., 2012, 2, 2022–2028 CrossRef CAS.
- M. Shirotori, S. Nishimura and K. Ebitani, Catal. Sci. Technol., 2014, 4, 971 CAS.
- B. Li, S. Varanasi and P. Relue, Green Chem., 2013, 15, 2149 RSC.
- S. Givry, C. Bliard and F. Duchiron, Carbohydr. Res., 2007, 342, 859–864 CrossRef CAS PubMed.
- Q. Jing and X. Lü, Chin. J. Chem. Eng., 2007, 15, 666–669 CrossRef CAS.
- B. Shen, Y. Liu and J. Peng, Adv. Mater. Res., 2013, 690–693, 1382–1385 CrossRef.
- P. Brazdausks, N. Vedernikovs, M. Puke and I. Kruma, Key Eng. Mater., 2014, 604, 245–248 CrossRef CAS.
- M. Möller and U. Schröder, RSC Adv., 2013, 3, 22253 RSC.
- A. Dunlop, Ind. Eng. Chem., 1948, 40, 204–209 CrossRef CAS.
- D. Williams and A. Dunlop, Ind. Eng. Chem., 1948, 40, 239–241 CrossRef CAS.
- G. Marcotullio and M. Cardoso, Int. J. Chem. React. Eng., 2009, 7, 1–14 Search PubMed.
- I. V. Sumerskii, S. M. Krutov and M. Y. Zarubin, Russ. J. Appl. Chem., 2010, 83, 320–327 CrossRef CAS.
- K. Gairola and I. Smirnova, Bioresour. Technol., 2012, 123, 592–598 CrossRef CAS PubMed.
- X. Chen, X. Liu, F. Xu and X. Bai, Adv. Mater. Res., 2014, 450–451, 710–714 Search PubMed.
- P. J. Oefner, A. H. Lanziner, G. Bonn and O. Bobleter, Monatsh. Chem. Chem. Mon., 1992, 123, 547–556 CrossRef CAS.
- K. Lamminpää, J. Ahola and J. Tanskanen, RSC Adv., 2014, 4, 60243–60248 RSC.
- B. Danon, L. van der Aa and W. de Jong, Carbohydr. Res., 2013, 375, 145–152 CrossRef CAS PubMed.
- D. Root, J. F. Saeman, J. F. Harris and W. K. Neill, For. Prod. J., 1959, 158–165 CAS.
- E. S. Kim, S. Liu, M. M. Abu-Omar and N. S. Mosier, Energy Fuels, 2012, 26, 1298–1304 CrossRef CAS.
- I. C. Rose, N. Epstein and A. P. Watkinson, Ind. Eng. Chem. Res., 2000, 39, 843–845 CrossRef CAS.
- K. Lamminpää, J. Ahola and J. Tanskanen, Ind. Eng. Chem. Res., 2012, 51, 6297–6303 CrossRef.
| This journal is © The Royal Society of Chemistry 2015 |