Observation of high-temperature magnetic transition and existence of ferromagnetic short-range correlations above transition in double perovskite La₂FeMnO₆

Abstract

We present the observation of a high-temperature magnetic transition along with ferromagnetic short-range correlations (FSCs) in La₂FeMnO₆ perovskite system. XPS analysis confirmed the presence of Fe³⁺ and Mn³⁺ cations. Magnetization vs. temperature curves show two distinct transitions at T_C1 ∼ 60 K and T_C ∼ 425 K. Coercivity values of ∼1140 Oe and ∼35 Oe are observed at 2 K and 300 K respectively. Thermomagnetic analysis reveals the presence of FSCs in La₂FeMnO₆ up to T* = 570 K, well above the transition point, similar to a Griffiths-like phase (GP). The presence of ferromagnetic clusters in the paramagnetic region might be due to the intrinsic inhomogeneities associated with the structure, the quenched disorder related to the B-site cations and the antisite boundaries. The coefficient of lower temperature electronic specific heat is as high as 59.5 mJ mol⁻¹ K⁻². The electron spin resonance spectra show ferromagnetic resonance signals that point to the possibility of the presence of FSCs at room temperature. The material seems to be quite a promising candidate for some room temperature applications due to the possibility of the coexistence of functionalities like ferromagnetism, ferrimagnetism, GP, magnetotransport coupling, etc. in a single material.

---

Introduction

The perovskite oxides ABO₃ (A = alkaline or rare earth elements (R), B = transition elements) possess a vast variety of physical properties like ferromagnetism (FM), ferrimagnetism (FiM), half metallicity, magnetoresistance, magnetodielectric (MD) coupling, etc.^1–10 The manganite perovskites (AMnO₃) have received considerable attention due to their magnetic, transport and magnetotransport properties linked with the change in the spin state.^11,12 Introducing a second element to the B-site will provide further characteristics to the system [Double Perovskite (DP)] in accordance with the difference in cationic ordering, oxidation states, antiphase boundaries, multiple exchange interactions, lattice distortion, etc.^1–4 Enormous studies are being carried out in nowadays on rare earth (RE) manganites with DP structure that exhibit multifunctional properties by virtue of their wide B/Mn cationic range.^7–10 Among these compounds, La₂NiMnO₆ is quite attractive because it is a FM semiconductor with good magnetodielectricity and magnetoresistance at temperatures close to room temperature due to its frustrated spin system originating from Ni and Mn cations.^13,14 Among the RE manganites, La₂FeMnO₆, the Fe counterpart of La₂NiMnO₆, remains unexplored fully, to a large extent.

The perovskites LaFeO₃ and LaMnO₃ are antiferromagnetic (AFM) insulators in bulk form with Néel temperature (T_N) 740 K and 140 K respectively, in which the superexchange interactions Fe³⁺–O–Fe³⁺ and Mn³⁺–O–Mn³⁺ lead to AFM coupling.^15–17 There are reports pertaining to the preparation of La₂FeMnO₆ having perovskite structure.^18,19 Many researchers continued the work on La₂FeMnO₆ both experimentally and theoretically, but a clear magnetic transition was not identified experimentally on bulk La₂FeMnO₆. The present work presents the observation of a high-temperature magnetic transition and the evidence for the existence of ferromagnetic short-range correlations (FSCs) far above room temperature in La₂FeMnO₆.

Experimental

Polycrystalline La₂FeMnO₆ is synthesized by employing Pechini method.¹⁹ High purity chemicals La(NO₃)₃·6H₂O, Fe(NO₃)₃·9H₂O and Mn(NO₃)₂ (Sigma-Aldrich, purity ∼99.99%) were weighed according to stoichiometry. Citric acid was added to this mixture such that the citric acid and cation ratio is 1 : 3. The nitrates and citric acid were mixed in 1 L beaker in de-ionized water medium at 70 °C with continuous stirring. The temperature were slowly raised and finally the combustion happened at 200 °C. The powder was kept at same condition for one day. The precursor powder was ground well and loaded into a muffle furnace at 600 °C for 2 hours and 900 °C for 2 hours. The powders were ground well and pelletized using a hydraulic press. For pelletization, polyvinyl alcohol was used as a binder. The pellets were finally sintered at 900 °C for 6 hours. The sintered pellets were ground well, and the final material was confirmed as phase pure La₂FeMnO₆ by using the X-ray diffraction (XRD) data obtained by Philips PANalytical X'Pert Pro Powder X-Ray Diffractometer with a Ni filtered Cu Kα radiation (λ = 1.5406 Å). The Rietveld refinement of the XRD pattern was done using the software GSAS – EXPGUI.²⁰ The crystallographic structure is framed using CrystalMaker®.²¹ X-ray photoelectron spectroscopy (XPS) measurements were carried out using an Omicron Nanotechnology Multiprobe Instrument. The XPS spectra corresponding to Fe 2p and Mn 2p of La₂FeMnO₆ are recorded by using a high resolution hemisphere analyzer EA 125 HR equipped with a detection system consisting of seven channeltrons. A monochromatic Al Kα source of energy, hν = 1486.6 eV was used to probe the La₂FeMnO₆ pellets, attached by a double-sided tape to the molybdenum sample holder. The pressure in the XPS chamber during the measurements was 5 × 10⁻¹⁰ mbar. A wide scan was collected to ensure that no foreign materials were present on the sample surface. Narrow scans of Fe 2p and Mn 2p regions were collected at analyzer pass energy of 20 eV. The peaks are fitted using the XPS Peak Fit software. The magnetization measurements were carried out on La₂FeMnO₆ powders by using a Vibrating Sample Magnetometer (VSM) attached to a Physical Property Measurement System (Dynacool, Quantum Design). The specific heat (C) is measured for the temperature range of 10–150 K by using the heat capacity option attached to the PPMS (Dynacool, Quantum Design). The electron spin resonance (ESR) spectra obtained using JES-FA200 ESR Spectrometer (ESR-JEOL, Japan) at temperatures 100 K, 170 K, and 300 K.

Results and discussion

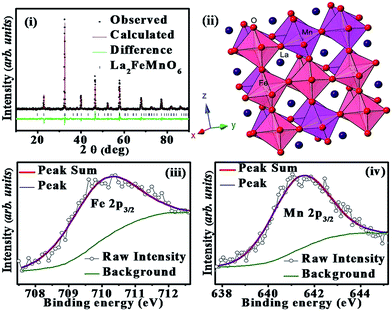
The orthorhombic, Pbnm crystal structure is confirmed for La₂FeMnO₆ by the Rietveld refinement using GSAS-EXPGUI²⁰ (WR_P = 4.64%). The observed, calculated and difference data are shown in Fig. 1(i) and the obtained lattice parameters are, a = 5.54 Å, b = 5.51 Å, c = 7.81 Å, and α, β, γ = 90° with 〈Fe–O–Mn〉 bond angle of 161.75°. The crystallographic structure framed using CrystalMaker® is shown in Fig. 1(ii).

Fig. 1 (i) Observed, calculated and the difference XRD pattern of La₂FeMnO₆ obtained from Rietveld refinement. (ii) A small portion of the crystallographic structure of La₂FeMnO₆ crystal framed using CrystalMaker®. (iii) XPS spectra of Fe 2p_3/2 in La₂FeMnO₆ along with the fitted curves. (iv) XPS spectra of Mn 2p_3/2 in La₂FeMnO₆ along with the fitted curves.

The XPS spectra corresponding to Fe 2p and Mn 2p of La₂FeMnO₆ are analyzed. The binding energies were corrected by C 1s as reference energy (C 1s = 284.8 eV). The peaks are fitted using the XPS Peak Fit software and the fitted curves are shown in Fig. 1(iii) and (iv). The fitted curves give single peak for Fe 2p_3/2 and Mn 2p_3/2 with peak positions at 710.14 eV and 641.36 eV respectively which confirms the oxidation states of cations as Fe³⁺ and Mn³⁺.^22,23.

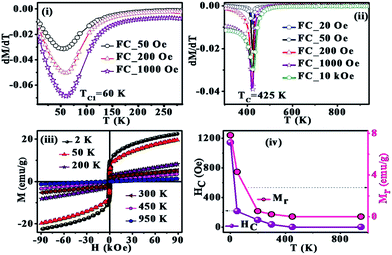
Based on the reported density-functional calculations, La₂FeMnO₆ could be either a FM semiconductor or a FM half-metal or a FM metal or a FiM semiconductor under different biaxial strain conditions.²⁴ Also, de Lima et al. reported the magnetic properties of La₂FeMnO₆ bulk with T_C = 65 K and coercivity (H_C) of 1160 Oe at 2 K and 170 Oe at 300 K.²⁵ Further, a hysteresis loop with small H_C and remanence (M_r) at 300 K was also reported for La₂FeMnO₆.²⁶ In the present study, zero field cooled (ZFC) and field cooled (FC) magnetizations were measured in the temperature range 5–385 K using the cryostat (inset of Fig. 2) and in the range 300–950 K using the oven (Fig. 2) in applied fields of 50, 200 and 1000 Oe. The temperature dependent magnetization (M–T) show irreversibility in magnetization as can be evidenced in the ZFC and FC bifurcation at lower temperatures and lower applied fields, which points towards the presence of spin frustration/spin glass state at lower temperatures in accordance with the previous reports on La₂FeMnO₆.^27–29 The derivative dM/dT vs. T plot (Fig. 3(i)) indicates a broad transition at T_C1 = 60 K, which corroborates the spin glass-like transition reported earlier.^25,27–29

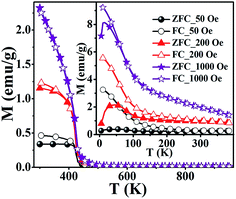Fig. 2 ZFC and FC curves at 50, 200, and 1000 Oe for 5–380 K. Inset: ZFC and FC curves at 50, 200, and 1000 Oe for 300–950 K.

Fig. 3 (i) Derivative of magnetization (FC) with respect to temperature vs. temperature for 5–300 K. (ii) Derivative of magnetization (FC) with respect to temperature vs. temperature for 300–950 K. (iii) M–H curves recorded at different temperatures. (iv) Variation of coercivity (H_C) and remanence (M_r) with temperature.

Bhame et al. observed positive values of Curie–Weiss constant (θ) as an indication of the presence of ferromagnetic exchange interactions and a H_C of 1170 Oe at 12 K for La₂FeMnO₆.³⁰ The M–T in the range 5–300 K is similar to that observed in previous cases, and a closer look at the plot shows that the moment does not go to zero even at room temperature.^30,31 Further, the room temperature hysteresis loop is also reported for La₂FeMnO₆.^25,26 Ueda et al. observed no transition in the M–T in the range of 50–400 K, and predicted that there might be an AFM transition above 400 K.³³ They have also fabricated thin films of La₂FeMnO₆, by artificially creating superlattices and by natural growth and showed a FM to PM transition (T_C) at ∼230 K and ∼380 K respectively.^32,33.

This instigated us to carry out higher temperature (300–950 K) M–T measurements (Fig. 2), which showed a transition at T_C ∼ 425 K as shown in dM/dT vs. T plot (Fig. 3(ii)). This evidence of the onset of a magnetic transition above room temperature is in line with the theoretical predictions and experimental observations in La₂FeMnO₆ thin films.^34,35 The disordered cation arrangements generate antisite boundaries leading to competing exchange interactions viz. Fe³⁺–O–Mn³⁺ FiM interactions, Fe³⁺–O–Fe³⁺, and Mn³⁺–O–Mn³⁺ AFM interactions and Mn³⁺–O–Mn³⁺ dynamic FM interactions.^17,26. Further, there is a key role played by the 〈B–O–B′〉 bond angle in determining the exchange interaction strength with the maximum in exchange interaction for 180°. The super exchange interaction is rather favored in this case since the 〈Fe–O–Mn〉 bond angle is as high as 161.75°.

Field dependent isothermal magnetization (M–H) was measured in the field range of −90 kOe to +90 kOe at different temperatures ranging from 2 to 950 K, and representative results are summarized in Fig. 3(iii). The M–H is non-saturating even at the highest field due to the inhomogeneities associated with its structure. Variations of H_C and M_r with temperature are shown in Fig. 3(iv). It shows a hysteresis with H_C = 1140 Oe and M_r = 7.8 emu g⁻¹ at 2 K and H_C = 35 Oe and M_r = 0.2 emu g⁻¹ at 300 K that are in agreement with the earlier report^25,30 and the loop disappears at higher temperatures. The room temperature loop is almost similar to that reported earlier.^25,26 The coercivity value of 1140 Oe drops to 215 Oe as the sample is warmed to 50 K from 2 K and then a slow rate of decrease in H_C with temperature is observed, which is an indication of the decrease of the strength of FM clusters and increase of the strength of PM matrix. The straight line plot at 950 K, with no H_C, and M_r, shows the complete PM state. The M–H curves show a non-linear behavior for low fields (<2 kOe) even above T_C, which is an indication of the presence of weak magnetization in the PM region.

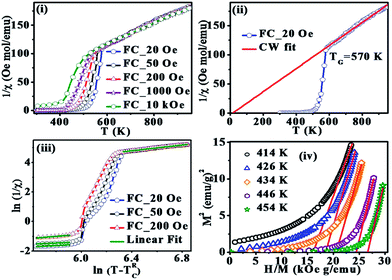
The inverse susceptibility derived from FC magnetization for 20, 50, 200, 1000 Oe and 10 kOe is shown in Fig. 4(i) and the fit to Curie–Weiss (CW) law 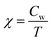for 20 Oe is shown in Fig. 4(ii). A CW fit is obtained only above T* = 570 K and the presence of FSC is clearly evidenced bye the plot as a sharp downturn below T*, which is gradually reduced as the field is increased. This feature is usually considered as a manifestation of typical Griffiths-like phases (GP).^36–51 GP was originally proposed as randomly distributed lsing FM regions with nearest neighbor exchange interactions J and 0 with probabilities p and (1 − p) respectively.⁵² The CW fit in PM region yields an effective magnetic moment, 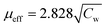(C_w is the Curie constant) as 6.5 μ_B per F.U. The XPS spectra confirmed Fe³⁺ and Mn³⁺ spin states in La₂FeMnO₆. The theoretically expected μ_eff for La₂FeMnO₆ with Fe³⁺ and Mn³⁺ are given in Table 1. The obtained μ_eff proclaims that the Fe³⁺ and Mn³⁺ are not in a low spin state (LS) simultaneously, and if spin-orbit coupling is present, Fe³⁺ should not be in LS. The FM state may arise from the high spin state (HS) Fe³⁺ (t³_2g, e²_g) and LS Mn³⁺ (t⁴_2g, e⁰_g), whereas the FiM state arises from LS Fe³⁺ (t⁵_2g, e⁰_g) and HS Mn³⁺ (t³_2g, e¹_g), under certain strain conditions.²⁴ A recent study on La₂FeMnO₆ thin film confirmed AFM coupling of HS Fe³⁺ and HS Mn³⁺, leading to FiM and observed an inverse relationship in between saturation magnetization and Fe/Mn-order.³⁴

Fig. 4 (i) Temperature dependence of inverse susceptibility (FC) at various fields. (ii) CW fit (solid red line) on 1/χ(T) (FC) at 20 Oe. (iii) ln(χ⁻¹) vs. ln(T − T_C^R) at 20, 50 and 200 Oe. The solid green line is the linear fit. (iv) The Arrot plot (M² vs. H/M) at different temperatures below and above T_C. The solid red line is the linear fit.

Table 1

Calculated μ_eff for La₂FeMnO₆ with Fe³⁺ and Mn³⁺

Spin-orbit coupling	Mn^3+ (HS)	Mn^3+ (LS)
Fe^3+ (HS)	5.916	5.916
Fe^3+ (LS)	1.732	1.732

---

Spin only interaction	Mn^3+ (HS)	Mn^3+ (LS)
Fe^3+ (HS)	7.681	6.16
Fe^3+ (LS)	5.196	3.317

---

The disordered perovskite causes a random dilution of FM with different exchange interactions viz. super exchange and double exchange interactions as described before and causes the evolution of FSCs above T_C. The presence of inhomogeneous magnetic states, magnetic clusters and random competing exchange interactions in La₂FeMnO₆ are well reported previously.^27–30 Moreover, the quenched disorder, triggered by the random chemical replacement of ions of different sizes can also induce intrinsic inhomogeneities in manganites.^53–55 The disorder is quenched within the distorted structure of La₂FeMnO₆ due to the strong coupling of Jahn–Teller distortion of the Fe³⁺/Mn³⁺ ions and orthorhombic crystal lattice so that the FM bonds can be assumed as fixed within the lattice that form clusters and FSCs.⁵⁴

Usually, the susceptibility of a Griffiths-like phase in low fields follows the power law,³⁶⁻⁴⁸ χ⁻¹ ∝ (T − T^R_C)^1−λ, where λ is the magnetic susceptibility exponent (0 ≤λ ≤1) and T^R_C is the random critical temperature. T^R_C is taken as the temperature for which the equation yields a λ (λ_PM) value close to zero above T*. The θ obtained from CW fit is 18 K for 20 Oe (Fig. 4(ii)), and assuming T^R_C at 18 K well establishes λ_PM ∼ 0.02. The linear part of the plot ln(χ⁻¹) vs. ln(T − T^R_C) (Fig. 4(iii)) is fitted with the power law and estimated the susceptibility exponent λ as 0.54 at 20 Oe and 0.29 at 200 Oe. The value of λ lies in between 0 and 1 and is decreasing with increase in the field, a signature of Griffiths-like phases.^36–48 The Arrot plots (M² vs. H/M) at five different temperatures, below and above T_C are shown in Fig. 4(iv). The linear extrapolation to the high field region of the Arrot plot gives a negative M² axis intercept confirming the absence of spontaneous magnetization (Fig. 4(iv)) with the existence of finite-sized FM interrelated spins without any static long-range magnetization.^40,41

The presence of inhomogeneous magnetic phases with co-existence of FM and AFM states in La₂FeMnO₆ was reported where, the FM phase originating from static Jahn–Teller distortions removed Mn³⁺–O–Mn³⁺ dynamic interactions and the AFM phase arising from Fe³⁺–O–Fe³⁺ interactions.²⁷ De et al. reported a glassy complex system at low temperatures with two dynamical freezing points below room temperature (at 20 K and 255 K), in La₂FeMnO₆ due to phase separation that was observed in many mixed valence manganites and also due to the existence of several competing magnetic interactions induced by antiphase boundaries ^28–29 Zhou et al. studied LaMn_1−xFe_xO₃ (0 < x < 1.0) system and concluded that Mn favors double exchange interaction whereas Fe favors AFM super exchange.³⁵ Bhame et al. reported the material as a spin glass, with Fe³⁺ and Mn³⁺ ions having Mn-rich and/or Fe-rich clusters of different sizes, causing predominant FM or AFM interactions respectively.³⁰ These clusters are distributed within the lattice according to the synthesis conditions; wherein the magnetism is predicted by a two-phase model.

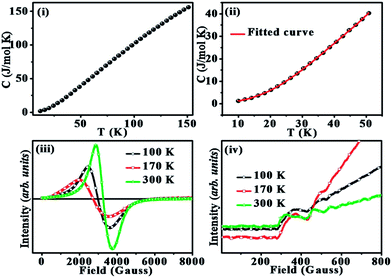
In order to get a clear idea about the inhomogeneities, the specific heat (C) was measured for the temperature range of 10–150 K as shown in Fig. 5(i). The low-temperature region from 10–50 K is fitted using the polynomial:⁴⁰ C = γT + β₃T³ + β₅T⁵ + β₇T⁷ as shown in Fig. 5(ii). The γ gives the coefficient of electronic specific heat due to free charge carriers. The higher order T terms are the lattice contribution arising from phonons. The obtained values are γ = 59.5 mJ mol⁻¹ K⁻² for the linear term, β₃ = 0.694 mJ mol⁻¹ K⁻⁴, β₅ = −2.54 × 10⁻⁴ mJ mol⁻¹ K⁻⁶ and β₇ = 3.69 × 10⁻⁸ mJ mol⁻¹ K⁻⁸. The high value of the electronic linear contribution to the low-temperature specific heat could be an indication of the coexistence of FM metallic and charge ordered state.⁴⁴ A higher value of γ is obtained for materials having FSC with GP.^40,43,44

Fig. 5 (i) Specific heat (C) as a function of temperature. (ii) Low temperature specific heat C fit. (iii) ESR spectra of La₂FeMnO₆ at different temperatures. (iv) Enlarged low field region of ESR spectra showing FMR signals.

The electron spin resonance spectra obtained at 100 K, 170 K, and 300 K are shown in Fig. 5(iii). ESR is highly sensitive to trivial magnetic correlations and is widely used for analyzing magnetic properties of manganites.^55–57 The ferromagnetic resonance signals, seen in the enlarged low field region of ESR spectra as shown in Fig. 5(iv) clearly show the presence of FSCs. The coexistence of PM resonance and FM resonance (FMR) signal is an indication of co-existence of PM and FM clusters.⁵⁷

Conclusions

In the present study, the disordered, orthorhombic La₂FeMnO₆ is found to possess double transition at T_C1 = 60 K and, T_C = 425 K. The inverse susceptibility show a sharp downturn with temperature, below T* = 570 K, as an indication of the occurrence of FSCs/GP. The oxidation states of cations are +3 (for Fe and Mn), and the effective PM moment is obtained as 6.5 μ_B per F.U. Fe³⁺–O–Mn³⁺, Fe³⁺–O–Fe³⁺ and Mn³⁺–O–Mn³⁺ super exchange interactions, and Mn³⁺–O–Mn³⁺ dynamic FM interactions could be present in the system. These competing interactions are responsible for the occurrence of glassy like transition at 60 K and Griffiths-like phase at higher temperatures. The total thermo-magnetic picture of La₂FeMnO₆ is as follows. At T^R_C = 18 K, random dilution of FM phases starts due to the transition of some of the magnetic phases. The FM clusters within the matrix interacts with each other and these clusters will undergo spin flipping with time and enters into a Griffiths-like phase above T^R_C. At T_C1 = 60 K, most of the FM phase will undergo magnetic transition into PM state and at T_C1 = 425 K, another magnetic transition occurs. Even though the T_C has reached, some of the FM clusters remain in the PM matrix and eventually transform completely into a PM state at T* = 570 K, similar to a Griffiths-like phase. The Griffiths analysis yields a λ value 0.54 at 20 Oe and decreases to 0.29 at 200 Oe. Below T_C, the FM clusters present themselves as a matrix in which PM clusters are embedded. Above T_C, it seems the FM clusters are distributed within the PM matrix and eventually completely transforms to PM state. The intrinsic inhomogeneities associated with the structure, quenched disorder related to the B-site cations and the antisite boundaries cause the presence of FSCs. The coefficient of low temperature electronic specific heat is as high as γ = 59.5 mJ mol⁻¹ K⁻², and such a high value can be argued to be responsible for FSCs. The electron spin resonance spectra show ferromagnetic resonance signals pointing the possibility of the presence of FSCs at room temperature. Normally, magneto-transport properties co-exist with GP, which can be explored in our future research, and the material is a promising candidate for room temperature applications. The coexistence of functionalities like FM, FiM, GP, magnetotransport coupling, etc. in a single material is of great interest for both the scientific aspects and for practical applications.

Acknowledgements

Jasnamol P. P. is thankful to the University Grants Commission (UGC), India and P. Neenu Lekshmi is thankful to the Council of Scientific and Industrial Research (CSIR), India for providing Senior Research Fellowships. S. Thomas acknowledge the financial support received from DST, India, via INSPIRE faculty award. M. R. Varma is pleased to acknowledge CSIR, India granted project SURE (No. CSC0132) and Kerala State Council for Science, Technology & Environment (KSCSTE) for financial support. The authors are thankful to Mr Ajeesh P Paulose for the technical support.

References

1. K.-I. Kobayashi, T. Kimura, H. Sawada, K. Terakura and Y. Tokura, Nature, 1998, 395, 677.
2. P. Baettig, C. Ederer and N. A. Spaldin, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 214105.
3. M. T. Anderson, K. B. Greenwood, G. A. Taylor and K. R. Poeppelmeiert, Prog. Solid State Chem., 1993, 22, 197.
4. Ll. Balcells, J. Navarro, M. Bibes, A. Roig, B. Martínez and J. Fontcuberta, Appl. Phys. Lett., 2001, 78, 781.
5. R. von Helmolt, J. Wecker, B. Holzapfel, L. Schultz and K. Samwer, Phys. Rev. Lett., 1993, 71, 2331.
6. M.-R. Li, M. Retuerto, Z. Deng, P. W. Stephens, M. Croft, Q. Huang, H. Wu, X. Deng, G. Kotliar, J. Sanchez-Benitez, J. Hadermann, D. Walker and M. Greenblatt, Angew. Chem., 2015, 127, 1.
7. P. Neenu Lekshmi, M. Vasundhara, M. R. Varma, K. G. Suresh and M. Valant, Phys. B, 2014, 448, 285.
8. Y. Mao, J. Parsons and J. S. Mc Cloy, Nanoscale, 2013, 5, 4720.
9. R. Yadav, H. S. Nair, A. Kumar, S. Adiga, H. L. Bhat, S. M. Yusuf and S. Elizabeth, J. Appl. Phys., 2015, 117, 093903.
10. P. Barrozo and J. Albino Aguiar, J. Appl. Phys., 2013, 113, 17E309.
11. J. M. D. Coey, M. Viret and L. Ranno, Phys. Rev. Lett., 1995, 75, 3910.
12. J. M. D. Coey and M. Viret, Adv. Phys., 1999, 48, 167.
13. D. Choudhury, P. Mandal, R. Mathieu, A. Hazarika, S. Rajan, A. Sundaresan, U. V. Waghmare, R. Knut, O. Karis, P. Nordblad and D. D. Sarma, Phys. Rev. Lett., 2012, 108, 127201.
14. Y. Guo, L. Shi, S. Zhou, J. Zhao and W. Liu, Appl. Phys. Lett., 2013, 102, 222401.
15. J. W. Seo, E. E. Fullerton, F. Nolting, A. Scholl, J. Fompeyrine and J.-P. Locquet, J. Phys.: Condens. Matter, 2008, 20, 264014.
16. P. Mondal, D. Bhattacharya, P. Choudhury and P. Mandal, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 172403.
17. J. Kanamori, J. Phys. Chem. Solids, 1959, 10, 87.
18. P. Ganguly, Bull. Mater. Sci., 1981, 3, 255.
19. Y. Wu, Z. Yu and S. Liu, J. Solid State Chem., 1994, 112, 157.
20. B. H. Toby, EXPGUI, a graphical user interface for GSAS, J. Appl. Crystallogr., 2001, 34, 210.
21. CrystalMaker Software Ltd, Oxford, England (www.crystalmaker.com).
22. J. Blomquist, U. Helgeson, L. C. Moberg, B. Folkesson and R. Larsson, Inorg. Chim. Acta, 1983, 69, 17.
23. J. C. Carver, G. K. Schweitzer and T. A. Carlson, J. Chem. Phys., 1972, 57, 973.
24. Y. Qian, H. Wu, E. Kan, J. Lu, R. Lu, Y. Liu, W. Tan, C. Xiao and K. Deng, J. Appl. Phys., 2013, 114, 063713.
25. O. F. de Lima, J. A. H. Coaquira, R. L. de Almeida, L. B. de Carvalho and S. K. Malik, J. Appl. Phys., 2009, 105, 013907.
26. Z.-X. Wei, Y. Wang, J.-P. Liua, C.-M. Xiao and W.-W. Zeng, Mater. Chem. Phys., 2012, 136, 755.
27. D. V. Karpinsky, I. O. Troyanchuk and V. V. Sikolenko, J. Phys.: Condens. Matter, 2007, 19, 036220.
28. K. de, M. Thakur, A. Manna and S. Giri, J. Appl. Phys., 2006, 99, 013908.
29. K. De, R. Ray, R. N. Panda, S. Giri, H. Nakamura and T. Kohara, J. Magn. Magn. Mater., 2005, 288, 339.
30. S. D. Bhame, V. L. Joseph Joly and P. A. Joy, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 054426.
31. P. Barrozo, N. O. Moreno and J. A. Aguiar, Adv. Mater. Res., 2014, 975, 122.
32. K. Ueda, H. Tabata and T. Kawai, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60, R12 561.
33. K. Ueda, Y. Muraoka, H. Tabata and T. Kawai, Appl. Phys. Lett., 2001, 78, 512.
34. K. Yoshimatsu, K. Nogami, K. Watarai, K. Horiba, H. Kumigashira, O. Sakata, T. Oshima and A. Ohtomo, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 054421.
35. X.-D. Zhou, L. R. Pederson, Q. Cai, J. Yang, B. J. Scarfino, M. Kim, W. B. Yelon, W. J. James, H. U. Anderson and C. Wang, J. Appl. Phys., 2006, 99, 08 M918.
36. S. K. Giri, S. M. Yusuf, M. D. Mukadam and T. K. Nath, J. Alloys Compd., 2014, 591, 181.
37. A. K. Pramanik and A. Banerjee, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 024431.
38. W. Jiang, X. Z. Zhou and G. Williams, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 064424.
39. P. Tong, B. Kim, D. Kwon, T. Qian, S. Lee, S.-W. Cheong and B. G. Kim, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 184432.
40. H. S. Nair, D. Swain, N. S. Hariharan, S. Adiga, C. Narayana and S. Elzabeth, J. Appl. Phys., 2011, 110, 123919.
41. A. Shahee, K. Singh, R. J. Choudhary and N. P. Lalla, Phys. Status Solidi B, 2015, 1, 1832.
42. S. Zhou, Y. Guo, J. Zhao, L. He and L. Shi, J. Phys. Chem. C, 2011, 115, 1535.
43. A. Slebarski, J. Goraus and M. Fijałkowski, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 075154.
44. C. L. Lu, K. F. Wang, S. Dong, J. G. Wan, J. M. Liu and Z. F. Ren, J. Appl. Phys., 2008, 103, 07F714.
45. S. Guo, D. P. Young, R. T. Macaluso, D. A. Browne, N. L. Henderson, J. Y. Chan, L. L. Henry and J. F. DiTusa, Phys. Rev. Lett., 2008, 100, 017209.
46. W. Jiang, X. Z. Zhou and G. Williams, Europhys. Lett., 2008, 84, 47009.
47. W. Jiang, X. Z. Zhou and G. Williams, Phys. Rev. Lett., 2007, 99, 177203.
48. C. Magen, P. A. Algarabel, L. Morellon, J. P. Araujo, C. Ritter, M. R. Ibarra, A. M. Pereira and J. B. Sousa, Phys. Rev. Lett., 2006, 96, 167201.
49. A. K. Pathak, D. Paudyal, W. T. Jayasekara, S. Calder, A. Kreyssig, A. I. Goldman, K. A. Gschneidner Jr and V. K. Pecharsky, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 224411.
50. O. Chauvet, G. Goglio, P. Molinie, B. Corraze and L. Brohan, Phys. Rev. Lett., 1998, 81, 1102.
51. R. B. Griffiths, Phys. Rev. Lett., 1969, 23, 17.
52. A. Moreo, M. Mayr, A. Feiguin, S. Yunoki and E. Dagotto, Phys. Rev. Lett., 2000, 84, 5568.
53. Y. Ren-Fu, Y. Sun, W. He, Q.-A. Li and C. Zhao-Hua, Appl. Phys. Lett., 2007, 90, 032502.
54. V. Markovich, R. Puzniak, I. Fita, A. Wisniewski, D. Mogilyansky, B. Dolgin, G. Gorodetsky and G. Jung, J. Appl. Phys., 2013, 113, 233911.
55. X. J. Liu, Z. Q. Li, A. Yu, M. L. Liu, W. R. Li, B. L. Li, P. Wu, H. L. Bai and E. Y. Jiang, J. Magn. Magn. Mater., 2007, 313, 354.
56. S. Zhou, L. Shi, H. Yang and J. Zhao, Appl. Phys. Lett., 2007, 91, 172505.
57. J. Deisenhofer, D. Braak, H.-A. Krug von Nidda, J. Hemberger, R. M. Eremina, V. A. Ivanshin, A. M. Balbashov, G. Jug, A. Loidl, T. Kimura and Y. Tokura, Phys. Rev. Lett., 2005, 95, 257202.

---