Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Mechanism, reactivity, and selectivity of the iridium-catalyzed C(sp3)–H borylation of chlorosilanes†
Genping
Huang
 ,
Marcin
Kalek
,
Rong-Zhen
Liao
and
Fahmi
Himo
*
,
Marcin
Kalek
,
Rong-Zhen
Liao
and
Fahmi
Himo
*
Department of Organic Chemistry, Arrhenius Laboratory, Stockholm University, SE-106 91 Stockholm, Sweden. E-mail: himo@organ.su.se
First published on 4th December 2014
Abstract
The iridium-catalyzed C(sp3)–H borylation of methylchlorosilanes is investigated by means of density functional theory, using the B3LYP and M06 functionals. The calculations establish that the resting state of the catalyst is a seven-coordinate Ir(V) species that has to be converted into an Ir(III)tris(boryl) complex in order to effect the oxidative addition of the C–H bond. This is then followed by a C–B reductive elimination to yield the borylated product, and the catalytic cycle is finally completed by the regeneration of the active catalyst over two facile steps. The two employed functionals give somewhat different conclusions concerning the nature of the rate-determining step, and whether reductive elimination occurs directly or after a prior isomerization of the Ir(V) hydride intermediate complex. The calculations reproduce quite well the experimentally-observed trends in the reactivities of substrates with different substituents. It is demonstrated that the reactivity can be correlated to the Ir–C bond dissociation energies of the corresponding Ir(V) hydride intermediates. The effect of the chlorosilyl group is identified to originate from the α-carbanion-stabilizing effect of the silicon, which is further reinforced by the presence of an electron-withdrawing chlorine substituent. Furthermore, the source of selectivity for the borylation of primary over secondary C(sp3)–H can be explained on a steric basis, by repulsion between the alkyl group and the Ir/ligand moiety. Finally, the difference in the reactivity between C(sp3)–H and C(sp2)–H borylation is investigated and rationalized in terms of distortion/interaction analysis.
1. Introduction
Transition metal-catalyzed C–H functionalizations are today some of the most pursued chemical transformations. Despite the tremendous progress in this area during the last ten years,1 development of these types of reactions remains a central challenge in organic chemistry. In particular, the activation of C(sp3)–H bonds with high efficiency and selectivity represents an important and long-standing goal.A number of approaches have been developed to achieve selective functionalization of a single C(sp3)–H bond in a molecule containing several CHn groups. Probably the most widespread strategy relies on the use of a coordinating moiety incorporated into the structure of the starting material that ligates the metal catalyst and thus directs the C–H cleavage.2 The selectivity of the C–H cleavage may also be governed by electronic effects. In this case a functional group present in the substrate molecule activates a certain C–H bond for the reaction with the metal. Classical examples of this approach are α-functionalizations of carbonyl compounds,3 and allylic4 and benzylic5 C–H functionalizations. Furthermore, some methods allow for the selective activation of C–H bonds based on steric criteria. Reactions occurring favorably at less hindered methyl groups6 and those preferentially functionalizing tertiary C–H bonds have been developed.7
Especially useful from a synthetic point of view are methods for C–H functionalization in which the employed directing group itself can be used in subsequent transformations. This way, a rapid increase of molecular complexity is possible during the synthesis, which in turn allows for the shortening of synthetic routes. In this context, an excellent contribution was recently made by Suginome and coworkers, who reported an iridium-catalyzed C(sp3)–H borylation of chlorosilanes (Scheme 1).8 C–H activation for the construction of the C–B bond has been achieved using a number of catalytic systems,9,10 but the novelty of the reaction shown in Scheme 1 stems from the fact that it makes use of a novel directing group for controlling the reactivity and selectivity. Namely, the reaction takes place at the methyl group adjacent to a chlorosilyl moiety, thus generating compounds containing 1-silyl-1-boryl-substituted methylene.11 Both the boronate functionality introduced in the reaction and the silyl group are synthetically very useful,10 as they can be employed in, for instance, Suzuki12 and Hiyama13 couplings, respectively. Since the silyl substituent is compatible with the conditions of the Suzuki reaction,14 a sequential application of these transformations opens access to non-symmetrical gem-difunctionalized methylenes.
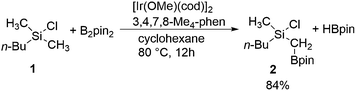 | ||
| Scheme 1 Iridium-catalyzed C(sp3)–H borylation of methylchlorosilane 1 (pin = (–OCMe2)2).8 | ||
Experimentally, it has been established that the reaction in Scheme 1 takes place selectively at the primary methyl C–H bond on the silicon atom, without a secondary borylation product being observed.8 Importantly, it was found that the presence of the chlorosilyl group is crucial for achieving a good reactivity under the mild reaction conditions used. Namely, no borylation product could be observed upon the replacement of the silicon by a carbon. Also, when changing the chlorine substituent to a methyl group, a much higher reaction temperature had to be applied in order to observe the formation of product.15 Moreover, replacing the chlorine by other substituents, such as chloromethyl or methoxy groups, led to a considerable decrease in the product yield.8 Based on these observations, it was proposed that the chlorine functions as a directing group by coordination to iridium or preferably to one of the boron atoms in the active species [(3,4,7,8-Me4-phen)Ir(Bpin)3] (3,4,7,8-Me4-phen = 3,4,7,8-tetramethylphenanthroline), thus positioning the reactant for a facile C–H activation.8
Due to the significance of this transformation, it is important to elucidate the detailed reaction mechanism, including the origins of the observed reactivity and selectivity. Although the C(sp2)–H borylation reaction has been studied extensively, both experimentally and theoretically,16,17 mechanistic insights into C(sp3)–H borylation remain scarce.18,19 Understanding the mechanism, especially the role of the chlorosilyl group, could have important implications for the future design of new catalytic systems for C–H functionalization. Therefore, we decided to investigate the details of the reaction mechanism using density functional theory (DFT) calculations. The generally accepted mechanism for Ir-catalyzed C(sp2)–H borylation involves Ir(III)/Ir(V) intermediates and consists of three steps: C–H oxidative addition, C–B reductive elimination, and regeneration of active catalyst.
In a very recent paper, Hartwig and coworkers used DFT calculations to investigate the mechanism and regioselectivity of the C(sp3)–H borylation of alkylamines and alkyl ethers using (η6-mes)Ir(Bpin)3 (mes = mesitylene) and the 3,4,7,8-Me4-phen ligand, i.e. involving the same catalytically active species that is engaged in the reaction studied herein.19 The mechanism was found to be very similar to the C(sp2)–H borylation. These results are very relevant to the current study and the similarities and differences compared to our findings will be discussed in the appropriate sections below.
2. Computational details
All the calculations were performed using the Gaussian 09 package.20 Geometry optimizations were carried out using the B3LYP functional21 with a combined basis set, in which Ir was described by LANL2DZ,22 and 6-31G(d,p) was used for all other atoms. Frequencies were computed analytically at the same level of theory to confirm whether the structures are minima (no imaginary frequencies) or transition states (only one imaginary frequency), and also to calculate the free energy corrections. Solvation effects were evaluated by performing single-point calculations with the polarizable continuum model (PCM).23 The parameters for cyclohexane (ε = 2.0165), corresponding to the experimental conditions, and UFF atomic radii were used in these calculations.To obtain better accuracy, single-point energies for the optimized geometries were recalculated using both the B3LYP and M06 functionals with a larger basis set, which is LANL2TZ(f) for Ir and 6-311+G(2d,2p) for all other atoms. The free energies reported in the article (ΔGsol) are the large basis set single-point energies corrected by a gas-phase Gibbs free energy correction (at 298.15 K) and solvation correction. For B3LYP, a dispersion correction using the D3 method developed by Grimme was added.24
In the reactivity analysis, the bond dissociation energies (BDEs) were calculated in a similar manner but including only the zero-point energy part of the Gibbs free energy correction.
It is important to point out that for each stationary point discussed in the paper there exists a number of rotamers of both the substrate and ligands. A thorough conformational analysis has therefore been performed in order to ensure that the lowest energy conformation is used.
3. Results and discussion
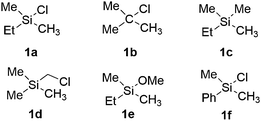
In this section, we first focus on the primary C(sp3)–H borylation of the model substrate EtMe2SiCl 1a (Scheme 2) and evaluate the mechanism step by step. The results calculated with both B3LYP and M06 are presented. Some details regarding the mechanism turned out to be somewhat different using the two methods and this will be discussed in detail below. Next, the energy profiles for substrates 1b–1e are calculated and compared with that for 1a in order to elucidate the origin of the observed reactivity differences. Then, the secondary C(sp3)–H borylation of 1a is studied and the 1° vs. 2° regioselectivity is rationalized. Finally, we present a comparison of the C(sp2)–H and C(sp3)–H borylation of substrate 1f and analyze the origins of the observed selectivity.3.1. Results with B3LYP
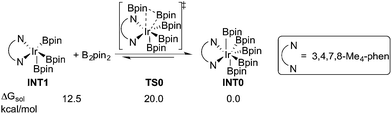
Experimentally, the iridium(I) complex [Ir(OMe)(cod)]2 (cod = 1,5-cyclooctadiene) is used as the catalyst precursor, and 3,4,7,8-Me4-phen as the ligand.8 It has been suggested that under the reaction conditions, the pre-catalyst undergoes an initiation process to generate an Ir(III)tris(boryl) complex, being the active catalytic species.16a,17,19 Thus, in the current calculations, we use INT1 (Scheme 3) as the starting point, in line with the previous studies.16a,17,19INT1 is a 16-electron complex that is able to effect the C–H bond cleavage. However, as discussed previously,16a it may also react with another molecule of B2pin2 to generate a seven-coordinate 18-electron Ir(V)-species INT0. The transformation of INT1 into INT0 is calculated to be exergonic by 12.5 kcal mol−1 and the energy of the transition state (TS0) is 7.5 kcal mol−1 higher than that of INT1 (Scheme 3). These results regarding the stability of the Ir(V) species are consistent with the previous findings in the case of C(sp2)–H borylation.16a As will be shown below, the coordinately saturated 18-electron Ir(V) complex INT0 is in fact the lowest lying intermediate, and thus constitutes the resting state of the catalyst.
In order for the reaction to take place, INT0 must thus first be converted into INT1 by a reversible reductive elimination of B2pin2. Therefore, we set the sum of the free energies of complex INT0 and the substrate to zero on the relative free energy scale.
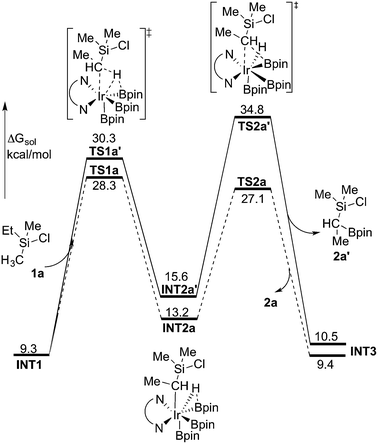
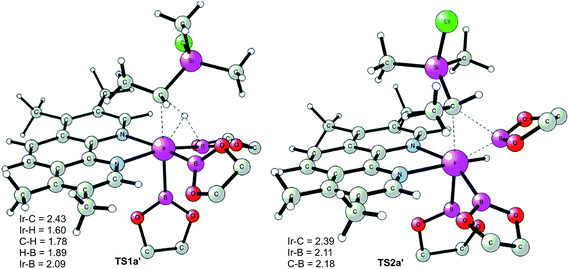
The first step of the mechanism is the oxidative addition of the C–H bond in the methyl group of 1a to the Ir(III) complex INT1. As mentioned in the introduction, it has been suggested that the C–H oxidative addition might be assisted by the coordination of the chlorine atom to the iridium or to the boron atom.8 However, such a scenario could not be confirmed by the calculations, as no coordination of the chlorine atom to the iridium complex could be observed, neither in the pre-complex nor in the C–H oxidative addition transition state. Instead, the calculations always converged to transition state TS1a, in which there is no direct interaction between the chlorine and the boron or the iridium (Fig. 1). The energy barrier is calculated to be 15.2 kcal mol−1 relative to INT1, i.e. 27.7 kcal mol−1 relative to INT0 (see Fig. 2 for energy profile).25
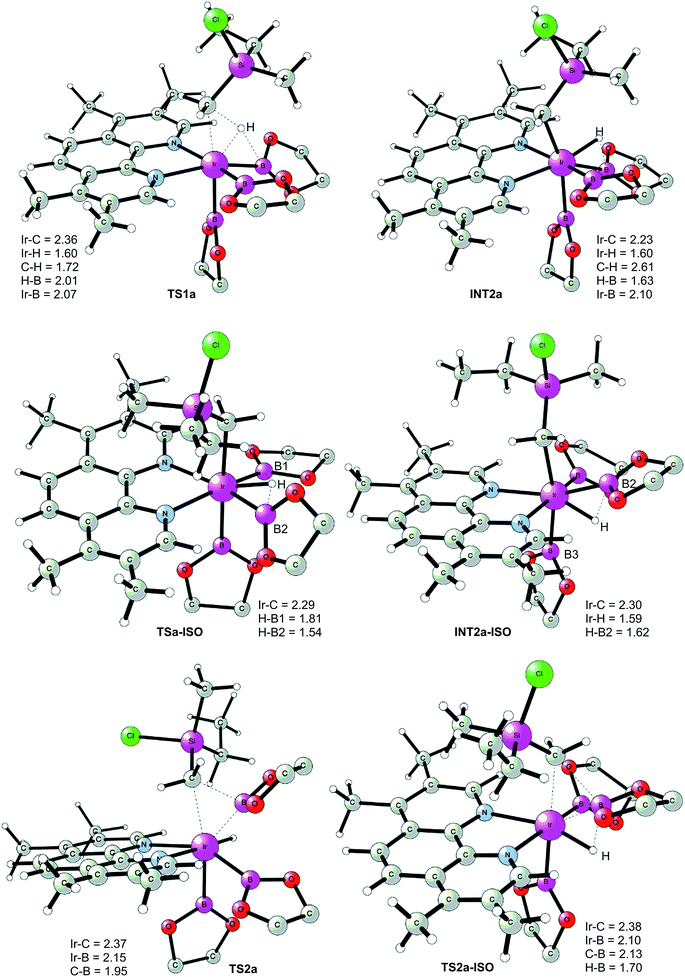 | ||
| Fig. 1 Optimized structures of stationary points for primary C–H borylation of 1a (distances are given in Å). The methyl groups on the Bpin ligands are omitted for clarity. | ||
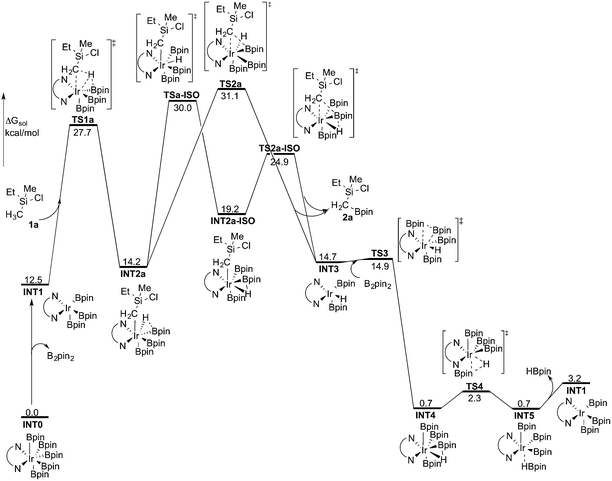 | ||
| Fig. 2 Overall energy profile calculated at the B3LYP-D3 level of theory for the Ir-catalyzed primary C(sp3)–H borylation of 1a. | ||
The C(sp3)–H oxidative addition transition state TS1a shows many similarities to transition states for C(sp2)–H oxidative additions reported before.16a,17 Importantly, the previously-observed multi-center interactions between the Ir, H, C, and B atoms are also found in TS1a, as seen from the C–H, Ir–H, Ir–C, and H–B distances being 1.72, 1.60, 2.36, and 2.01 Å, respectively (Fig. 1). This indicates that the interaction of the empty p orbital of boron with the hydride is important for a facile C–H oxidative addition to the iridium center.16a,18b,c,19,26
The oxidative addition is calculated to be endergonic by 1.7 kcal mol−1 relative to INT1 (14.2 kcal mol−1 relative to INT0, Fig. 2) and the resulting intermediate INT2a is a seven-coordinated Ir(V) hydride complex, which has a capped octahedron configuration.27 Importantly, an even stronger interaction between the hydride ligand and the boron center is found in INT2a compared to TS1a (H–B distance 1.63 vs. 2.01 Å).
Upon formation of INT2a, the subsequent step of the reaction is a C–B bond-forming reductive elimination, as in the case of the C(sp2)–H borylation.16a From INT2a the energy barrier for the reductive elimination viaTS2a was calculated to be 31.1 kcal mol−1 relative to INT0, i.e. 3.4 kcal mol−1 higher than that for the preceding TS1a for the oxidative addition.28 This is different from the case of the C(sp2)–B reductive elimination, for which previous calculations have shown that it is very facile, with a barrier lower than for the preceding C(sp2)–H oxidative addition.16a It is also different from the results of Hartwig and coworkers on the Ir-catalyzed C(sp3)–H borylation of triethylamine, where it was found that the transition state for the reductive elimination is 6.4 kcal mol−1 lower in energy than the transition state for the oxidative addition.19
This result was somewhat surprising and we therefore examined alternative pathways for this process, involving an initial ligand rearrangement in INT2a. Indeed, we found that the reductive elimination is more favorable from an isomeric Ir(V) complex INT2a-ISO, in which the hydride ligand occupies a coordination site adjacent to the B2 and B3 ligands, instead of the one adjacent to the alkyl group and B1 (see Fig. 1). INT2a-ISO is 5.0 kcal mol−1 higher in energy than INT2a, but the transition state for the reductive elimination from INT2a-ISO (TS2a-ISO) is 6.2 kcal mol−1 lower in energy than TS2a (Fig. 2), i.e. 24.9 kcal mol−1 relative to INT0. Comparison of the structures of TS2a and TS2a-ISO identifies two factors that may be responsible for the energy difference between these transition states. First, in TS2a-ISO the interaction between the hydride ligand and the empty p orbital of the B atom of one of the boryl ligands, which is present in both intermediates INT2a and INT2a-ISO, is maintained (H–B distance 1.70 Å, Fig. 1), while in TS2a it has to be broken in order for the reductive elimination to occur. Second, there is some steric repulsion between the two Bpin groups in TS2a, which can contribute to raising the energy of this transition state.
Nevertheless, although the C–B bond formation viaTS2a-ISO is facile, the prior isomerization of INT2a into INT2a-ISO has to take place. The isomerization was found to occur via transition state TSa-ISO, which has a pentagonal-bipyramidal configuration,27,29 in which the hydride ligand is practically coplanar with the 3,4,7,8-Me4-phen and boryl ligands, and it interacts with two boron centers simultaneously (B–H distances 1.81 and 1.54 Å).30TSa-ISO is calculated to be 15.8 kcal mol−1 higher in energy than INT2a, i.e. 30.0 kcal mol−1 higher in energy than INT0. The energy barrier is thus only 1.1 kcal mol−1 lower than that of TS2a, and it is therefore not possible on the basis of these calculations to conclude which one of these two options is the favored path for the reductive elimination step.
The reductive elimination results in the final reaction product 2a and the Ir(III) complex INT3, which is 0.5 kcal mol−1 higher in energy than INT2a (Fig. 2). The catalytic cycle is completed by the regeneration of active catalyst INT1. This process consists of two steps, namely an oxidative addition of B2pin2 to INT3viaTS3, followed by a reductive elimination of HBpin (TS4). The calculations show that both steps are very facile, with very low energy barriers, as shown in Fig. 2 (see ESI† for optimized structures of the TSs).
Here, it is important to emphasize that the proposed coordination of the silicon-bound chlorine atom to the catalyst could not be observed in our calculations at any stage of the mechanism. Therefore, such a scenario is apparently not responsible for the observed reactivity and selectivity of the reaction. A detailed investigation of these issues will be presented below.
3.2. Results with M06
As discussed above, the current results are somewhat different compared with the recent results of Hartwig and coworkers, where they used the M06 functional to study the borylation of alkylamines.19 To investigate whether this discrepancy is due to the employed functional, we recalculated the free energy graph using the M06 method by performing single-point calculations on the B3LYP-optimized geometries (see Fig. 3 for the calculated free energy profile). We also performed test geometry optimizations with M06, but the results were very similar, within 1 kcal mol−1.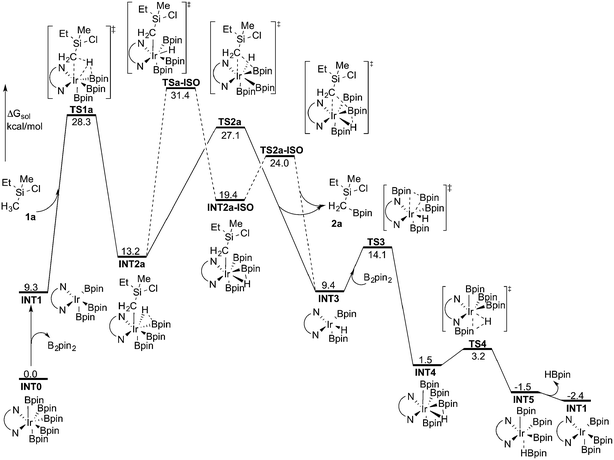 | ||
| Fig. 3 Overall energy profile calculated at the M06 level of theory for the Ir-catalyzed primary C(sp3)–H borylation of 1a. | ||
Indeed, the calculations show that the energy profile changes depending on the functional employed. A significant change is the energy difference between TSa-ISO and TS2a. In the B3LYP calculations, the energy of TS2a was 1.1 kcal mol−1 higher than that of TSa-ISO, whereas in the M06 calculations, the energy of TS2a is 4.3 kcal mol−1 lower than that of TSa-ISO. This indicates that the direct C–B reductive elimination pathway would be more favored compared to the isomerization step. Another difference compared to the B3LYP calculations is that the C–H oxidative addition with M06 turns out to be the highest point of the overall energy profile, as TS2a is calculated to be 1.2 kcal mol−1 lower in energy than TS1a. This result is more consistent with the calculations on the borylation of triethylamine.19 However, since the energy difference between oxidative addition and direct reductive elimination is rather small (only 1.2 kcal mol−1), and the results calculated using the B3LYP and M06 functionals point in somewhat different directions regarding the nature of the rate-determining step, it is not possible to draw definitive conclusions regarding this matter on the basis of the current calculations.
Nevertheless, taken together, both the B3LYP and M06 functionals give a quite similar overall picture of the reaction mechanism. Namely, both predict the resting state to be the seven-coordinate Ir(V) complex INT0. This saturated complex has to convert into the active catalyst INT1 in order to perform the C–H oxidative addition, which is then followed by C–B reductive elimination and regeneration of the active catalyst. The B3LYP results suggest that an isomerization step is needed prior to the C–B reductive elimination, while M06 suggests that the direct reductive elimination is preferred. It should also be noted that the energy difference between the oxidative addition and reductive elimination steps is rather small for both methods and falls within the accuracy limits.
3.3. Kinetic isotope effect
An important test of the validity of a calculated mechanism is whether it complies with the results of kinetic isotope effect (KIE) experiments. In the experimental report, when the substrate n-C6H13(CH3)(CD3)SiCl, containing one of the methyl groups labeled with deuterium, was used in the reaction, a 2.7 ratio of C–H![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C–D functionalization products was obtained.8
C–D functionalization products was obtained.8
To examine the KIE for the calculated mechanism we evaluated the zero-point energies (ZPE) with the deuterium incorporated in the appropriate positions according to the experiment (by using the deuterated 1a Et(CH3)(CD3)SiCl). For the oxidative addition transition state TS1a, the calculated ZPE difference is 0.78 kcal mol−1, corresponding to a normal KIE of 3.0 at the temperature used in the experiment (80 °C), which agrees very well with the experimentally-observed KIE. For the direct reductive elimination transition state TS2a, on the other hand, the calculated ZPE difference is only 0.23 kcal mol−1, corresponding to a KIE of only 1.4.
Interestingly, the ZPE difference for TSa-ISO was calculated to be 0.45 kcal mol−1, corresponding to a KIE of 1.9, which is also in reasonable agreement with the experimental value. This KIE originates mainly from the equilibrium isotope effect between INT1 and INT2a,31 since the calculated the ZPE difference for INT2a was 0.37 kcal mol−1, corresponding to a KIE value of 1.7.
The fact that the calculated KIE for TS1a agrees better with the experimental value as compared to TSa-ISO indicates that it is more likely that the oxidative addition is the rate-determining step, which would support the M06 results. However, considering that the values are quite close, a definitive assignment cannot be done on the basis of these results solely.
3.4. Reactivity of other substrates
Considering that there is no interaction between the chlorine atom and iridium or boron at any stage of the mechanism, the results presented above raise the question of how the chlorosilyl group facilitates the reaction. To rationalize this effect, we calculated the energy profiles for the borylation of substrates 1b–e (Scheme 2), at both the B3LYP and M06 levels. The energies are listed in Table 1.| Substrate | TS1 | INT2 | TS2 | TS-ISO | INT2-ISO | TS2-ISO | INT3 |
|---|---|---|---|---|---|---|---|
| B3LYP-D3 | |||||||
| 1a | 27.7 | 14.2 | 31.1 | 30.0 | 19.2 | 24.9 | 14.7 |
| 1b | 31.1 | 18.2 | 40.8 | 36.0 | 23.5 | 30.0 | 18.6 |
| 1c | 30.7 | 19.2 | 36.4 | 36.7 | 25.8 | 30.4 | 14.5 |
| 1d | 28.6 | 15.1 | 34.1 | 33.2 | 22.6 | 25.2 | 14.5 |
| 1e | 29.7 | 17.1 | 33.7 | 32.4 | 22.1 | 25.1 | 14.5 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||
| M06 | |||||||
| 1a | 28.3 | 13.2 | 27.1 | 31.4 | 19.4 | 24.0 | 9.4 |
| 1b | 31.0 | 17.0 | 36.7 | 36.9 | 23.0 | 27.7 | 13.1 |
| 1c | 30.9 | 17.7 | 32.5 | 37.6 | 26.2 | 29.1 | 8.9 |
| 1d | 28.8 | 13.7 | 30.5 | 34.6 | 23.4 | 24.4 | 9.1 |
| 1e | 30.0 | 15.9 | 30.5 | 33.7 | 23.6 | 24.0 | 8.9 |
For the B3LYP calculations, the results show that in all cases except for substrate 1c, the barriers of isomerization (TS-ISO) are slightly lower than those of direct C–B reductive elimination (TS2). For 1c, the direct C–B reductive elimination was found to be slightly favored, by only 0.3 kcal mol−1. Moreover, the barriers of isomerization are significantly higher than those of C–H oxidative addition, showing that the former is rate-determining. The results are thus in line with the energy profile for 1a using B3LYP.
For the M06 calculations, the direct C–B reductive elimination was found to be more favorable compared to the isomerization in all cases, in line with the results for substrate 1a. Very importantly, however, the reductive elimination step is found to be rate-determining for substrates 1b–e, which is different from the case of substrate 1a. One contributing factor for this could be the increased steric repulsion between the C and B groups that undergo direct C–B reductive elimination, as compared to the steric repulsion for the C–H oxidative addition (see structures of optimized transition states TS2a–e in ESI†).
Generally, both M06 and B3LYP calculations reproduce quite well the experimental trends in the relative reactivity of the different substrates (Table 1). Here, we will use the M06 results to compare and rationalize the reactivity. Note that, since no detailed kinetic experiments have been conducted, the comparison with the experimental results is only qualitative.
For substrate 1b, in which the silicon atom is replaced by a carbon atom, the overall energy barrier was calculated to be 36.7 kcal mol−1 (TS2b), which is 8.4 kcal mol−1 higher than that for substrate 1a. This is consistent with the fact that no desired product formation was observed experimentally for 1b.
Experimentally, the Cl substituent on silicon was found to be very important for the reactivity. In the original report, no reaction was observed with substrate n-C8H17SiMe3.8 However, as described in a subsequent article, the application of a much higher temperature led to the formation of the desired product for this substrate.15 The calculations show that the energy barrier for the reaction with model substrate 1c is 32.5 kcal mol−1 (TS2c), which is 4.2 kcal mol−1 higher than for 1a, thus in agreement with the experiments.
The reaction with 1d, in which the chlorine is substituted for a chloromethyl group and for which the product is formed in only a 20% yield experimentally, was calculated to have an overall barrier of 30.5 kcal mol−1 (TS2d), i.e. only 2.2 kcal mol−1 higher than for 1a.
Finally, the reaction with model substrate 1e, in which the Cl atom is replaced by a methoxide group, was also investigated and the results show that the energy barrier is 2.2 kcal mol−1 higher than that for 1a. This is qualitatively consistent with the experimentally observed yield of less than 5% for substrate n-BuMe2Si(OMe).
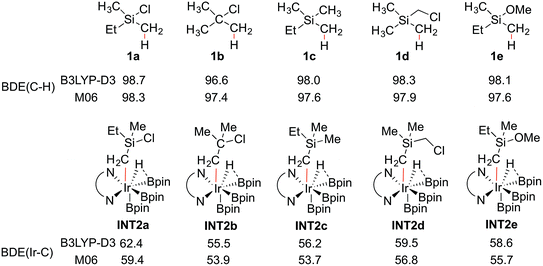
To shed light on the origin of the observed reactivity difference, the homolytic bond dissociation energies (BDEs) of the C–H bonds of substrates 1a–e, and the Ir–C bonds of intermediates INT2a–e were calculated (Scheme 4). Interestingly, the results show that the C–H BDEs of substrates containing a Si atom are almost identical, with energy differences within 0.7 kcal mol−1. The C–H BDE of 1b is the lowest, which does not correlate with the observed low reactivity of this substrate. In contrast, the Ir–C BDE in INT2 was found to be more sensitive to the substituent of the alkyl group, ranging from 53.7 to 59.4 kcal mol−1. Importantly, we find that there is a good correlation between the calculated barriers of the C–H oxidative addition step and the Ir–C BDEs (see ESI†). That is, the stronger the Ir–C bond, the lower the energy barrier. A similar trend can also be observed for the direct C–B reductive elimination step. These correlations are found for both the M06 and B3LYP functionals.
The trends of reactivity can thus be predicted by the stability of the Ir–C bond in INT2. The results of the current study on C(sp3)–H borylation are consistent with the results of Houk and coworkers, who very recently showed that in the Ir-catalyzed C(sp2)–H borylation, the Ir–C BDEs of the aryl iridium hydride intermediates, resulting from the C–H oxidative addition step, can be used to predict the regioselectivity of the reaction.32
In general, it has been found that the BDEs of M–C bonds correlate quite well with the M–C bond ionicity, where an increased bond ionicity leads to a larger BDE.33 Thus, an electron-withdrawing substituent on the alkyl group can polarize the Ir–C bond, which results in a higher BDE. In the current study, it is found that the Ir–C BDE of INT2a, with a Si atom, is higher than that of INT2b, with a C atom. The reason is that the Si atom is well-known to stabilize the negative charge at the α position (the so-called α-effect),34 which thus makes the Ir–C bond stronger. Furthermore, comparison of the Ir–C BDEs of INT2avs.INT2c–e indicates that the presence of the electron-withdrawing Cl substituent on the Si atom further reinforces this stabilization effect. This suggests that other substituents at the Si with even stronger electron-withdrawing ability could lead to an increased reactivity, although the balance between the electronic and steric effects must also be considered. It should be noted that an analogous dependence of reactivity on the stabilization of negative charge on the arene ligand was recently found for the related iridium-catalyzed C(sp2)–H borylation.17
3.5. Primary vs. secondary C(sp3)–H borylation
We now turn to the issue of the selective borylation of the primary position in the presence of secondary C(sp3)–hydrogens. Experimentally, it was shown that the reaction did not take place for substrates such as Et3SiCl, i.e. without a methyl group on silicon.8 To shed light on the origin of this selectivity, we calculated the full free energy profile for the C(sp3)–H borylation at the secondary position in substrate 1a (Fig. 4, solid line). Both M06 and B3LYP results reproduced well the observed selectivity. Here, the M06 results will be presented, and the B3LYP results are given in the ESI.†The calculations show that for the secondary C(sp3)–H borylation the direct C–B reductive elimination (TS2a′) is the rate-determining step, with an overall energy barrier of 34.8 kcal mol−1 relative to INT0 (Fig. 4). The activation energy difference of 6.5 kcal mol−1 between the primary and secondary borylation thus reproduces the experimentally observed exclusive formation of product 2a. Inspection of the optimized structures (Fig. 5) indicates that the selectivity is mainly caused by the steric repulsion between the alkyl group and the Ir/ligand moiety in TS2a′. A similar steric origin of the selectivity has been proposed for the Rh-catalyzed C(sp3)–H borylation of terminal methyl groups of unactivated alkanes.18a
3.6. C(sp3)–H vs. C(sp2)–H borylation
In general, it is considered that functionalizations of C(sp2)–H are easier than of C(sp3)–H.1a,g For the borylation reaction investigated in the present work, when substrate 1f was used (Scheme 2), C(sp2)–H borylation was exclusively observed (ortho![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) meta
meta![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) para = 0
para = 0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 67
67![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 33).8 In order to investigate the origin of this selectivity, we have examined both the C(sp2)–H and C(sp3)–H borylation of 1f at both M06 and B3LYP levels. The results for both functionals are in quite good agreement with the experimental observations. The energy profiles calculated using M06 for both C(sp2)–H and C(sp3)–H borylation of 1f are shown in Fig. 6 (see ESI† for B3LYP results).
33).8 In order to investigate the origin of this selectivity, we have examined both the C(sp2)–H and C(sp3)–H borylation of 1f at both M06 and B3LYP levels. The results for both functionals are in quite good agreement with the experimental observations. The energy profiles calculated using M06 for both C(sp2)–H and C(sp3)–H borylation of 1f are shown in Fig. 6 (see ESI† for B3LYP results).
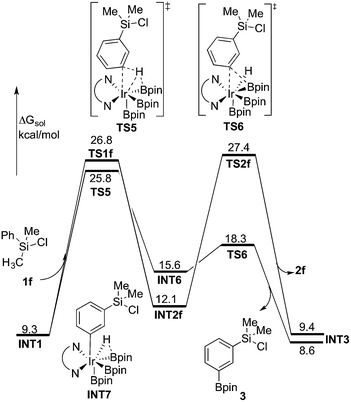 | ||
| Fig. 6 Energy profile calculated at M06 level of theory for the Ir-catalyzed C(sp3)–H and C(sp2)–H borylation of 1f. | ||
As shown in Fig. 6, the energy barrier for the C(sp2)–H oxidative addition at the meta position35 (TS5, 25.8 kcal mol−1 relative to INT0) was found to be 1.0 kcal mol−1 lower than that for the C(sp3)–H oxidative addition (TS1f, 26.8 kcal mol−1). However, in the former case, the resulting intermediate INT6 is higher in energy than INT2f, by 3.5 kcal mol−1. Interestingly, INT6 can undergo a facile direct reductive elimination (TS6) with an energy barrier of only 2.7 kcal mol−1 relative to INT6, i.e. 18.3 kcal mol−1 relative to INT0. Hence, the rate-determining step for the C(sp2)–H borylation is the C–H oxidative addition step, with an overall barrier of 25.8 kcal mol−1. In the case of the C(sp3)–H borylation, like for the substrates 1b–e, the direct C–B reductive elimination from INT2f (TS2f) constitutes the rate-determining step, with an overall barrier of 27.4 kcal mol−1. The calculated 1.6 kcal mol−1 energy difference between C(sp3)–H and C(sp2)–H borylation is in qualitative agreement with the experimental results.
According to these results, we find that a significant difference between C(sp2)–H and C(sp3)–H borylation originates from the different reactivity of the intermediates resulting from the C–H oxidative addition (INT6vs.INT2f) in the direct reductive elimination process (TS6vs.TS2f). In order to understand the origins of this difference, we performed a distortion/interaction analysis36 of TS2f and TS6 (see Fig. 7). It turns out that the total distortion energy of TS2f is 14.6 kcal mol−1 lower than that of TS6, while the interaction energy of TS6 was found to be higher than that of TS2f by as much as 20.1 kcal mol−1. Thus, a significant interaction energy difference between TS2f and TS6 determines the reactivity. One plausible explanation for such a large interaction energy difference is that in TS6 the presence of a Ph–B π* orbital can enhance the back-bonding interaction with the d orbital of iridium, while no such strong orbital interaction exists in TS2f. A similar explanation has been proposed by Lin and coworkers to account for the reactivity differences in the oxidative addition of alkyl and aryl halides to palladium.37
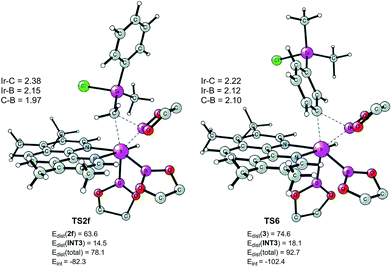 | ||
| Fig. 7 Optimized structures of reductive elimination transition states from INT2f and INT6. Distortion/interaction energies calculated using M06 are given in kcal mol−1. | ||
4. Conclusions
In the current study we have presented a detailed investigation of the iridium-catalyzed C(sp3)–H borylation of methylchlorosilanes by means of B3LYP and M06 density functional theory calculations. The two methods give quite a similar overall view of the catalytic mechanism, namely that the saturated seven-coordinate Ir(V) complex INT0 is the resting state of the catalyst and it has to be converted into the active catalyst INT1 to effect the oxidative addition of the C–H bond, which is then followed by C–B reductive elimination and regeneration of the active catalyst.The two methods differ, however, in that B3LYP predicts that an isomerization step is needed prior to the C–B reductive elimination, whereas M06 predicts that the direct reductive elimination is preferred. The energy difference between the two scenarios for both methods is quite small and therefore no definitive conclusion can be drawn regarding this issue. Furthermore, for the model substrate EtMe2SiCl (1a), B3LYP predicts the isomerization step to be rate-determining, whereas M06 predicts the oxidative addition to be rate-determining. Again, the energy differences are rather small and both scenarios are calculated to be consistent with the experimentally-observed kinetic isotope effect.
A number of substrates with different substituents were also examined in the present work, and the calculations reproduce quite well the experimentally-observed trends in reactivity. A good correlation was found between the Ir–C bond dissociation energies of the Ir(V) hydride intermediate complex and the calculated energy barriers for the reaction. The accelerating role of the chlorosilyl group was ascribed to its strong α-carbanion stabilizing property, stemming from a combination of the silicon α-effect and the high electronegativity of the chlorine substituent.
Additionally, the origin of selectivity for the borylation of primary over secondary C(sp3)–H was investigated and explained in terms of a steric repulsion between the alkyl group and the Ir/ligand moiety.
Finally, the difference between C(sp2)–H and C(sp3)–H borylation was considered and this was found to originate from the difference in the reductive elimination step, which is much more facile for the C(sp2) case. It is argued that the origin of this difference is due to the presence of a strong back-bonding interaction between the Ph–B π* orbital and the d orbital of iridium in the C(sp2) case, which stabilizes the transition state for direct reductive elimination.
The present calculations thus provide a number of important insights into the mechanism of iridium-catalyzed borylation reactions, in particular in terms of selectivity and reactivity, and could be extended to other related systems.38 Therefore, we believe that the results will have important implications for the design of more efficient catalytic systems and directing groups in the field of metal-catalyzed C–H functionalization.
Acknowledgements
We acknowledge financial support from the Swedish Research Council, the Göran Gustafsson Foundation and the Knut and Alice Wallenberg Foundation. G.H. thanks the Carl-Trygger Foundation for a postdoctoral fellowship. We thank Prof. Kálmán Szabó and Prof. Shigeyoshi Sakaki for valuable discussions. Computer time was generously provided by the Swedish National Infrastructure for Computing.References
- (a) J. A. Labinger and J. E. Bercaw, Nature, 2002, 417, 507–514 CrossRef CAS PubMed; (b) H. M. L. Davies and R. E. J. Beckwith, Chem. Rev., 2003, 103, 2861–2904 CrossRef CAS PubMed; (c) R. H. Crabtree, J. Organomet. Chem., 2004, 689, 4083–4091 CrossRef CAS PubMed; (d) A. R. Dick and M. S. Sanford, Tetrahedron, 2006, 62, 2439–2463 CrossRef CAS PubMed; (e) K. Godula and D. Sames, Science, 2006, 312, 67–72 CrossRef CAS PubMed; (f) X. Chen, K. M. Engle, D.-H. Wang and J.-Q. Yu, Angew. Chem., Int. Ed., 2009, 48, 5094–5115 CrossRef CAS PubMed; (g) R. Jazzar, J. Hitce, A. Renaudat, J. Sofack-Kreutzer and O. Baudoin, Chem.–Eur. J., 2010, 17, 2654–2672 CrossRef PubMed; (h) S. H. Cho, J. Y. Kim, J. Kwak and S. Chang, Chem. Soc. Rev., 2011, 40, 5068–5083 RSC; (i) R. Giri, B.-F. Shi, K. M. Engle, N. Maugel and J.-Q. Yu, Chem. Soc. Rev., 2009, 38, 3242–3272 RSC; (j) J. F. Hartwig, Organotransition Metal Chemistry: From Bonding to Catalysis, University Science Books, Sausalito, CA, 2009 Search PubMed; (k) V. Ritleng, C. Sirlin and M. Pfeffer, Chem. Rev., 2002, 102, 1731–1770 CrossRef CAS PubMed.
- Reviews: (a) J.-Q. Yu, R. Giri and X. Chen, Org. Biomol. Chem., 2006, 4, 4041–4047 RSC; (b) O. Daugulis, V. G. Zaitsev, D. Shabashov, Q.-N. Pham and A. Lazareva, Synlett, 2006, 3382–3388 CrossRef CAS PubMed; (c) Y. J. Park, J.-W. Park and C.-H. Jun, Acc. Chem. Res., 2008, 41, 222–234 CrossRef CAS PubMed; (d) T. W. Lyons and M. S. Sanford, Chem. Rev., 2010, 110, 1147–1169 CrossRef CAS PubMed; (e) D. Balcells, E. Clot and O. Eisenstein, Chem. Rev., 2010, 110, 749–823 CrossRef CAS PubMed; (f) Top. Curr. Chem., C–H Activation, ed. J.-Q. Yu and Z. Shi, 2010, vol. 292 Search PubMed; (g) L. Ackermann, Chem. Rev., 2011, 111, 1315–1345 CrossRef CAS PubMed. Recent examples: (h) S. H. Cho and J. F. Hartwig, J. Am. Chem. Soc., 2013, 135, 8157–8160 CrossRef CAS PubMed; (i) S. Kawamorita, T. Miyazaki, T. Iwai, H. Ohmiya and M. Sawamura, J. Am. Chem. Soc., 2012, 134, 12924–12927 CrossRef CAS PubMed.
- (a) D. A. Culkin and J. F. Hartwig, Acc. Chem. Res., 2003, 36, 234–245 CrossRef CAS PubMed; (b) Modern Arylation Methods, ed. L. Ackermann, Wiley-VCH, Weinheim, 2009 Search PubMed; (c) F. Bellina and R. Rossi, Chem. Rev., 2010, 110, 1082–1146 CrossRef CAS PubMed; (d) C. C. C. Johansson and T. J. Colacot, Angew. Chem., Int. Ed., 2010, 49, 676–707 CrossRef CAS PubMed.
- Recent reviews: (a) G. Liu and Y. Wu, Top. Curr. Chem., 2010, 292, 195–209 CrossRef CAS; (b) C. J. Engelin and P. Fristrup, Molecules, 2011, 16, 951–969 CrossRef CAS PubMed. Pioneering work: (c) J. Tsuji, K. Sakai, H. Nagashima and I. Shimuzu, Tetrahedron Lett., 1981, 22, 131–134 CrossRef CAS; (d) J. E. McMurry and P. Kocovsky, Tetrahedron Lett., 1984, 25, 4187–4190 CrossRef CAS; (e) S. Hansson, A. Heumann, T. Rein and B. Åkermark, J. Org. Chem., 1990, 55, 975–984 CrossRef CAS; (f) H. Grennberg and J.-E. Bäckvall, Chem.–Eur. J., 1998, 4, 1083–1089 CrossRef CAS; (g) B. M. Trost and F. D. Toste, J. Am. Chem. Soc., 1999, 121, 9728–9729 CrossRef CAS. More recent examples: (h) J. Franzén, J. Löfstedt, J. Falk and J.-E. Bäckvall, J. Am. Chem. Soc., 2003, 125, 14140–14148 CrossRef PubMed; (i) M. S. Chen, N. Prabagaran, N. A. Labenz and M. C. White, J. Am. Chem. Soc., 2005, 127, 6970–6971 CrossRef CAS PubMed; (j) S. A. Reed and M. C. White, J. Am. Chem. Soc., 2008, 130, 3316–3318 CrossRef CAS PubMed; (k) S. Lin, C.-X. Song, G.-X. Cai, W.-H. Wang and Z.-J. Shi, J. Am. Chem. Soc., 2008, 130, 12901–12903 CrossRef CAS PubMed; (l) E. Thiery, C. Aouf, J. Belloy, D. Harakat, J. Le Bras and J. Muzart, J. Org. Chem., 2010, 75, 1771 CrossRef CAS PubMed; (m) Q. Li and Z.-X. Yu, J. Am. Chem. Soc., 2010, 132, 4542–4543 CrossRef CAS PubMed; (n) R. Alam, L. T. Pilarski, E. Pershagen and K. J. Szabó, J. Am. Chem. Soc., 2012, 134, 8778–8781 CrossRef CAS PubMed.
- (a) T. A. Boebel and J. F. Hartwig, Organometallics, 2008, 27, 6013–6019 CrossRef CAS; (b) S. Shimada, A. S. Batsanov, J. A. K. Howard and T. B. Marder, Angew. Chem., Int. Ed., 2001, 40, 2168–2171 CrossRef CAS; (c) T. Ishiyama, K. Ishida, J. Takagi and N. Miyaura, Chem. Lett., 2001, 30, 1082–1083 CrossRef.
- Reviews: (a) J. F. Hartwig, Chem. Soc. Rev., 2011, 40, 1992–2002 RSC. For selected examples, see: (b) H. Chen and J. F. Hartwig, Angew. Chem., Int. Ed., 1999, 38, 3391–3393 CrossRef CAS; (c) H. Chen, S. Schlecht, T. C. Semple and J. F. Hartwig, Science, 2000, 287, 1995–1997 CrossRef CAS; (d) J. D. Lawrence, M. Takahashi, C. Bae and J. F. Hartwig, J. Am. Chem. Soc., 2004, 126, 15334–15335 CrossRef CAS PubMed; (e) J. M. Murphy, J. D. Lawrence, K. Kawamura, C. Incarvito and J. F. Hartwig, J. Am. Chem. Soc., 2006, 128, 13684–13685 CrossRef CAS PubMed.
- (a) B. H. Brodsky and J. Du Bois, J. Am. Chem. Soc., 2005, 127, 15391–15393 CrossRef CAS PubMed; (b) M. S. Chen and M. C. White, Science, 2007, 318, 783–787 CrossRef CAS PubMed.
- T. Ohmura, T. Torigoe and M. Suginome, J. Am. Chem. Soc., 2012, 134, 17416–17419 CrossRef CAS PubMed.
- (a) T. Ishiyama and N. Miyaura, J. Organomet. Chem., 2003, 680, 3–11 CrossRef CAS; (b) I. A. I. Mkhalid, J. H. Barnard, T. B. Marder, J. M. Murphy and J. F. Hartwig, Chem. Rev., 2010, 110, 890–931 CrossRef CAS PubMed; (c) J. F. Hartwig, Chem. Soc. Rev., 2011, 40, 1992–2002 RSC.
- J. F. Hartwig, Acc. Chem. Res., 2012, 45, 864–873 CrossRef CAS PubMed.
- Recently a palladium-catalyzed C–H functionalization of a methyl group on silicon has also been reported. See: Y. Liang, W. Geng, J. Wei, K. Ouyang and Z. Xi, Org. Biomol. Chem., 2012, 10, 1537–1542 CAS.
- For selected reviews, see: (a) N. Miyaura and A. Suzuki, Chem. Rev., 1995, 95, 2457–2483 CrossRef CAS; (b) R. Jana, T. P. Pathak and M. S. Sigman, Chem. Rev., 2011, 111, 1417–1492 CrossRef CAS PubMed. For selected examples, see: (c) P. Harrisson, J. Morris, T. B. Marder and P. G. Steel, Org. Lett., 2009, 11, 3586–3589 CrossRef CAS PubMed; (d) P. Harrisson, J. Morris, P. G. Steel and T. B. Marder, Synlett, 2009, 147–150 CAS; (e) T. Ohmura, T. Awano and M. Suginome, J. Am. Chem. Soc., 2010, 132, 13191–13193 CrossRef CAS PubMed; (f) T. Awano, T. Ohmura and M. Suginome, J. Am. Chem. Soc., 2011, 133, 20738–20741 CrossRef CAS PubMed; (g) S. H. Cho and J. F. Hartwig, J. Am. Chem. Soc., 2013, 135, 8157–8160 CrossRef CAS PubMed; (h) Y. Yang and S. L. Buchwald, J. Am. Chem. Soc., 2013, 135, 10642–10645 CrossRef CAS PubMed.
- (a) T. Hiyama and E. Shirakawa, Top. Curr. Chem., 2002, 219, 61–85 CrossRef CAS; (b) S. E. Denmark and R. F. Sweis, Acc. Chem. Res., 2002, 35, 835–846 CrossRef CAS PubMed; (c) S. E. Denmark and J. D. Baird, Chem.–Eur. J., 2006, 12, 4954–4963 CrossRef CAS PubMed; (d) S. E. Denmark and C. S. Regens, Acc. Chem. Res., 2008, 41, 1486–1499 CrossRef CAS PubMed; (e) S. E. Denmark, J. Org. Chem., 2009, 74, 2915–2927 CrossRef CAS PubMed; (f) Y. Nakao and T. Hiyama, Chem. Soc. Rev., 2011, 40, 4893–4901 RSC.
- See for example: J. A. Soderquist, B. Santiago and I. Rivera, Tetrahedron Lett., 1990, 31, 4981–4984 CrossRef CAS.
- T. Ohmura, T. Torigoe and M. Suginome, Organometallics, 2013, 32, 6170–6173 CrossRef CAS.
- For selected examples, see: (a) H. Tamura, H. Yamazaki, H. Sato and S. Sakaki, J. Am. Chem. Soc., 2003, 125, 16114–16126 CrossRef CAS PubMed; (b) T. Ishiyama, J. Takagi, K. Ishida, N. Miyaura, N. R. Anastasi and J. F. Hartwig, J. Am. Chem. Soc., 2002, 124, 390–391 CrossRef CAS PubMed; (c) T. M. Boller, J. M. Murphy, M. Hapke, T. Ishiyama, N. Miyaura and J. F. Hartwig, J. Am. Chem. Soc., 2005, 127, 14263–14278 CrossRef CAS PubMed; (d) G. A. Chotana, B. A. II Vanchura, M. K. Tse, R. J. Staples, R. E. Maleczka Jr and M. R. Smith III, Chem. Commun., 2009, 5731–5733 RSC; (e) T. Ishiyama and N. Miyaura, Pure Appl. Chem., 2006, 78, 1369–1375 CrossRef CAS; (f) S. Paul, G. A. Chotana, D. Holmes, R. C. Reichle, R. E. Maleczka Jr and M. R. Smith III, J. Am. Chem. Soc., 2006, 128, 15552–15553 CrossRef CAS PubMed; (g) S. M. Preshlock, B. Ghaffari, P. E. Maligres, S. W. Krska, R. E. Maleczka Jr and M. R. Smith III, J. Am. Chem. Soc., 2013, 135, 7572–7582 CrossRef CAS PubMed; (h) J. Y. Cho, M. K. Tse, D. Holmes, R. E. Maleczka Jr and M. R. Smith III, Science, 2002, 295, 305–308 CrossRef CAS PubMed; (i) C. W. Liskey, C. S. Wei, D. R. Pahls and J. F. Hartwig, Chem. Commun., 2009, 5603–5605 RSC; (j) T. Ishiyama, J. Takagi, J. F. Hartwig and N. Miyaura, Angew. Chem., Int. Ed., 2002, 41, 3056–3058 CrossRef CAS; (k) H. Tajuddin, P. Harrisson, B. Bitterlich, J. C. Collings, N. Sim, A. S. Batsanov, M. S. Cheung, S. Kawamorita, A. C. Maxwell, L. Shukla, J. Morris, Z. Lin, T. B. Marder and P. G. Steel, Chem. Sci., 2012, 3, 3505–3515 RSC; (l) M. Larsen and J. F. Hartwig, J. Am. Chem. Soc., 2014, 136, 4287–4299 CrossRef CAS PubMed; (m) I. A. I. Mkhalid, D. N. Coventry, D. Albesa-Jove, A. S. Batsanov, J. A. K. Howard, R. N. Perutz and T. B. Marder, Angew. Chem., Int. Ed., 2006, 45, 489–491 CrossRef CAS PubMed; (n) S. Konishi, S. Kawamorita, T. Iwai, P. G. Steel, T. B. Marder and M. Sawamura, Chem.–Asian J., 2014, 9, 434–438 CrossRef CAS.
- (a) B. A. Vanchura II, S. M. Preshlock, P. C. Roosen, V. A. Kallepalli, R. J. Staples, R. E. Maleczka Jr, D. A. Singleton and M. R. Smith III, Chem. Commun., 2010, 46, 7724–7726 RSC; (b) P. C. Roosen, V. A. Kallepalli, B. Chattopadhyay, D. A. Singleton, R. E. Maleczka Jr and M. R. Smith III, J. Am. Chem. Soc., 2012, 134, 11350–11353 CrossRef CAS PubMed.
- (a) C. S. Wei, C. A. Jimenez-Hoyos, M. F. Videa, J. F. Hartwig and M. B. Hall, J. Am. Chem. Soc., 2010, 132, 3078–3091 CrossRef CAS PubMed; (b) C. E. Webster, Y. B. Fan, M. B. Hall, D. Kunz and J. F. Hartwig, J. Am. Chem. Soc., 2003, 125, 858–859 CrossRef CAS PubMed; (c) J. F. Hartwig, K. S. Cook, M. Hapke, C. D. Incarvito, Y. Fan, C. E. Webster and M. B. Hall, J. Am. Chem. Soc., 2005, 127, 2538–2552 CrossRef CAS PubMed; (d) K. R. Sawyer, J. F. Cahoon, J. E. Shanoski, E. A. Glascoe, F. K. Matthias, J. P. Schlegel, M. C. Zoerb, M. Hapke, J. F. Hartwig, C. E. Webster and C. B. Harris, J. Am. Chem. Soc., 2010, 132, 1848–1859 CrossRef CAS PubMed.
- Q. Li, C. W. Liskey and J. F. Hartwig, J. Am. Chem. Soc., 2014, 136, 8755–8765 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision C.01, Gaussian Inc., Wallingford CT, 2010 Search PubMed.
- (a) A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS PubMed; (b) C. T. Lee, W. T. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS.
- P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 270–283 CrossRef CAS PubMed.
- (a) J. Tomasi and M. Persico, Chem. Rev., 1994, 94, 2027–2094 CrossRef CAS; (b) J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3094 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104–154119 CrossRef PubMed.
- Oxidative addition taking place in an alternative complex geometry, i.e. with the C–H bond positioned trans to the nitrogen instead of the boron, was also considered, but it turned out to have the very high energy barrier of 43.9 kcal mol−1 relative to INT0. We also calculated the Si–Cl oxidative addition, and the energy barrier is 40.9 kcal mol−1 relative to INT0, which is also unfeasible. See ESI† for details.
- L. Dang, Z. Lin and T. B. Marder, Chem. Commun., 2009, 3987–3995 RSC.
- Z. Lin and I. Bytheway, Inorg. Chem., 1996, 35, 594–603 CrossRef CAS.
- HBpin elimination from INT2a was also considered, but turned to be highly unfavorable, with an energy barrier of 53.5 kcal mol−1 relative to INT0. See ESI† for details.
- J. Tomàs, A. Lledós and Y. Jean, Organometallics, 1998, 17, 190–195 CrossRef.
- An alternative pathway for the isomerization, involving changing the H and B1 positions with each other, as suggested previously,16a was also considered, and the energy barrier was found to be 1.6 kcal mol−1 higher than TSa-ISO (see ESI† for details).
- E. M. Simmons and J. F. Hartwig, Angew. Chem., Int. Ed., 2012, 51, 3066–3072 CrossRef CAS PubMed.
- A. G. Green, P. Liu, C. A. Merlic and K. N. Houk, J. Am. Chem. Soc., 2014, 136, 4575–4583 CrossRef CAS PubMed.
- (a) E. Clot, M. Besora, F. Maseras, C. Mégret, O. Eisenstein, B. Oelckers and R. N. Perutz, Chem. Commun., 2003, 490–491 RSC; (b) E. Clot, C. Mégret, O. Eisenstein and R. N. Perutz, J. Am. Chem. Soc., 2009, 131, 7817–7827 CrossRef CAS PubMed; (c) Y. Jiao, M. E. Evans, J. Morris, W. W. Brennessel and W. D. Jones, J. Am. Chem. Soc., 2013, 135, 6994–7004 CrossRef CAS PubMed.
- (a) Y. Mo, Y. Zhang and J. Gao, J. Am. Chem. Soc., 1999, 121, 5737–5742 CrossRef CAS; (b) M. Cypryk and J. Chojnowski, J. Organomet. Chem., 2002, 642, 163–170 CrossRef CAS.
- The energy barriers of ortho and para C(sp2)–H oxidative addition of 1f were calculated to be 35.2 and 27.3 kcal mol−1, respectively. See ESI† for details.
- (a) A. Pross and S. S. Shaik, Acc. Chem. Res., 1983, 16, 363–370 CrossRef CAS; (b) K. Kitaura and K. Morokuma, Int. J. Quantum Chem., 1976, 10, 325–340 CrossRef CAS; (c) S. Nagase and K. Morokuma, J. Am. Chem. Soc., 1978, 100, 1666–1672 CrossRef CAS. The distortion/interaction analysis is also named as activation-strain model, see: (d) F. M. Bickelhaupt, J. Comput. Chem., 1999, 20, 114–128 CrossRef CAS; (e) A. Diefenbach and F. M. Bickelhaupt, J. Phys. Chem. A, 2004, 108, 8460–8466 CrossRef CAS; (f) A. Diefenbach, G. T. de Jong and F. M. Bickelhaupt, J. Chem. Theory Comput., 2005, 1, 286–298 CrossRef CAS.
- A. Ariafard and Z. Lin, Organometallics, 2006, 25, 4030–4033 CrossRef CAS.
- (a) C. W. Liskey and J. F. Hartwig, J. Am. Chem. Soc., 2012, 134, 12422–12425 CrossRef CAS PubMed; (b) C. W. Liskey and J. F. Hartwig, J. Am. Chem. Soc., 2013, 135, 3375–3378 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Additional results not shown in the text, table of calculated energies, and Cartesian coordinates of all optimized structures discussed in the paper. See DOI: 10.1039/c4sc01592d |
| This journal is © The Royal Society of Chemistry 2015 |