Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
New coordination features; a bridging pyridine and the forced shortest non-covalent distance between two CO32− species†
V.
Velasco
a,
D.
Aguilà
a,
L. A.
Barrios
a,
I.
Borilovic
a,
O.
Roubeau
b,
J.
Ribas-Ariño
c,
M.
Fumanal
c,
S. J.
Teat
d and
G.
Aromí
*a
aDepartament de Química Inorgànica, Universitat de Barcelona, Diagonal 645, 08028 Barcelona, Spain. E-mail: guillem.aromi@qi.ub.es; Tel: +34 934039760
bInstituto de Ciencia de Materiales de Aragón (ICMA), CSIC and Universidad de Zaragoza, Plaza San Francisco s/n, 50009, Zaragoza, Spain
cDepartament de Química Física and IQTCUB, Universitat de Barcelona, Diagonal 645, 08028 Barcelona, Spain
dAdvanced Light Source, Berkeley Laboratory, 1 Cyclotron Road, Berkeley, California 94720, USA
First published on 29th September 2014
Abstract
The aerobic reaction of the multidentate ligand 2,6-bis-(3-oxo-3-(2-hydroxyphenyl)-propionyl)-pyridine, H4L, with Co(II) salts in strong basic conditions produces the clusters [Co4(L)2(OH)(py)7]NO3 (1) and [Co8Na4(L)4(OH)2(CO3)2(py)10](BF4)2 (2). Analysis of their structure unveils unusual coordination features including a very rare bridging pyridine ligand or two trapped carbonate anions within one coordination cage, forced to stay at an extremely close distance (dO⋯O = 1.946 Å). This unprecedented non-bonding proximity represents a meeting point between long covalent interactions and “intermolecular” contacts. These original motifs have been analysed here through DFT calculations, which have yielded interaction energies and the reduced repulsion energy experimented by both CO32− anions when located in close proximity inside the coordination cage.
1. Introduction
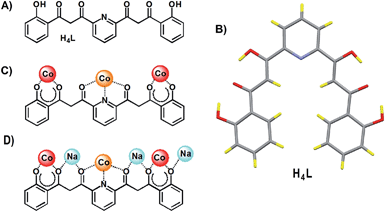
The coordination chemistry of 1,3-dicarbonyl-based multidentate ligands constitutes now an important subarea of structural molecular chemistry.1–4 The good chelating ability of β-diketonates together with a particular distribution throughout a given organic scaffold, in combination or not with additional donor groups has led to novel features in coordination chemistry. Some examples are; a whole category of oxygen based metallohelicates,4–7 an entire family of molecular platforms for the construction of supramolecular edifices,3,8 or a novel type of paddle wheel complexes.9 One subclass of this kind of ligands exhibits two β-diketone groups separated by an m-pyridinediyl spacer (Scheme 1A). Their interesting coordination chemistry is illustrated by an impressive family of heterometallic clusters with a chain-like [M–Ln–M]7+ core (M2+ = Cu, Ni; Ln3+ = any lanthanide) sandwiched by two ligands in the coordination mode shown in Scheme 1B.10,11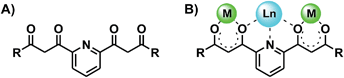 | ||
| Scheme 1 Pyridine-spaced bis-β-diketone ligands (A), and coordination mode in complexes of the type [M–Ln–M]7+ (B). | ||
We present here the unexpected (some unprecedented) features resulting from aerobic reactions of the related ligand 2,6-bis-(3-oxo-3-(2-hydroxyphenyl)-propionyl)-pyridine, H4L (Fig. 1A), with Co(II) in pyridine, under basic conditions. This ligand had only been used once in the past, also with Co(II).12 On that occasion, the chemistry was performed in the absence of any base, and the result was the formation of a cluster with formula [Co8O(OH)(H2L)6]NO3, which encapsulates a [μ3-O⋯H⋯μ3-O] moiety while the ligand H4L was found to retain its phenolic protons upon coordination. We show now that the use of strong basic conditions leads to full deprotonation of H4L, which is conducive to the oxidation of some of the Co(II) ions to Co(III) by atmospheric oxygen. This is likely the consequence of engaging the phenolate groups into coordination, thus stabilizing the latter ions. The combinations of reagents NBu4OH/Co(NO3)2 and NaH/Co(BF4)2, respectively, with H4L in pyridine have yielded the new clusters [Co4(L)2(OH)(py)7]NO3 (1) and [Co8Na4(L)4(OH)2(CO3)2(py)10](BF4)2 (2). The structural constrains resulting from this combination of metals and ligands have allowed to unveil quite remarkable features in coordination chemistry. One is a very rare example of a bridging “crevice” pyridine ligand (in complex 1). The other consists of two carbonate ligand anions, forced to stay at an extraordinarily close distance to each other within cage 2, to the point that the intermolecular O⋯O distance (1.946 Å) is found to be within 0.03 Å from the longest detected stable O–O bond (1.915 Å).13 These occurrences are studied in detail, through physical and theoretical methods.
2. Experimental
2.1 Synthesis
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.5 vol.). After two weeks, dark red crystals were collected and washed with ether and water to remove traces of the remaining ligand and salts. Final yields in the 8–21% range were obtained. IR (KBr pellet): ν/cm−1 = 3419 m, 3072 m, 1652 w, 1598 s, 1566 s, 1530 s, 1505 s, 1452 s, 1384 s, 1317 s, 1256 m, 1230 m, 1207 s, 1150 s, 1121 m, 1067 m, 1033 m, 958 w, 864 w, 754 s, 699 s, 668 m, 650 m, 584 m, 545 w, 490 m. Anal. calc. (Found) for 1·5.5H2O (−1py): C, 54.1 (53.7); H, 4.0 (3.6); N, 7.5 (7.3).
1.5 vol.). After two weeks, dark red crystals were collected and washed with ether and water to remove traces of the remaining ligand and salts. Final yields in the 8–21% range were obtained. IR (KBr pellet): ν/cm−1 = 3419 m, 3072 m, 1652 w, 1598 s, 1566 s, 1530 s, 1505 s, 1452 s, 1384 s, 1317 s, 1256 m, 1230 m, 1207 s, 1150 s, 1121 m, 1067 m, 1033 m, 958 w, 864 w, 754 s, 699 s, 668 m, 650 m, 584 m, 545 w, 490 m. Anal. calc. (Found) for 1·5.5H2O (−1py): C, 54.1 (53.7); H, 4.0 (3.6); N, 7.5 (7.3).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.5). Dark red crystals appeared after two weeks and were separated by filtration and washed with ether and water to remove traces of the remaining ligand and salts. Final yields in the 11–18% range were obtained. IR (KBr pellet): ν/cm−1 = 3431 m, 3069 m, 1652 w, 1635 w, 1599 s, 1566 s, 1531 s, 1506 s, 1455 s, 1386 m, 1317 s, 1245 w, 1207 m, 1150 s, 1122 w, 1066 m, 1032 m, 957 m, 864 w, 754 s, 697 s, 668 m, 650 m, 584 m, 547 w, 489 m. Anal. calc. (Found) for 2·3H2O·2py: C, 54.1 (53.9); H, 3.6 (3.7); N, 6.6 (7.0).
1.5). Dark red crystals appeared after two weeks and were separated by filtration and washed with ether and water to remove traces of the remaining ligand and salts. Final yields in the 11–18% range were obtained. IR (KBr pellet): ν/cm−1 = 3431 m, 3069 m, 1652 w, 1635 w, 1599 s, 1566 s, 1531 s, 1506 s, 1455 s, 1386 m, 1317 s, 1245 w, 1207 m, 1150 s, 1122 w, 1066 m, 1032 m, 957 m, 864 w, 754 s, 697 s, 668 m, 650 m, 584 m, 547 w, 489 m. Anal. calc. (Found) for 2·3H2O·2py: C, 54.1 (53.9); H, 3.6 (3.7); N, 6.6 (7.0).
2.2 X-Ray crystallography
Data for ligand H4L and for compound 1 were collected, respectively, on a yellow needle and on a red block at 150 K on a Bruker APEX II CCD diffractometer on Advanced Light Source beamline 11.3.1 at Lawrence Berkeley National Laboratory, from a silicon 111 monochromator (λ = 0.7749 Å). Data were collected for compound 2 on an orange plate at 100 K on a Bruker APEX II QUAZAR diffractometer equipped with a microfocus multilayer monochromator with Mo Kα radiation (λ = 0.71073 Å). Data reduction and absorption corrections were performed with SAINT and SADABS,15 respectively. The structures were solved with SIR9716 (H4L) and SHELX-TL15,17 (1 and 2) and refined on F2 with SHELX-TL suite.15,17 In 1, one of the oxygens of the nitrate ion is disordered over two equivalent positions. The atoms of both this nitrate ion and one pyridine molecule sitting on the symmetry operation were refined with displacement parameters restraints. In 2 one of the sodium atoms is disordered over two positions with similar occupation, while one of the coordinated pyridines is disordered over two positions sharing the same nitrogen (N7). These as well as oxygens coordinated to the disordered sodium atom and a number of carbon atoms from phenyl groups of the ligands and of coordinated pyridines were refined with displacement parameters restraints, due to disorder. Three of the four lattice pyridines also required the use of rigid body restraints for their refinement to converge, in addition to displacement parameters restraints. The tetrafluoroborate ion was refined with both distance and displacement parameters restraints. At the end of the refinement, there remained a number of weak electron diffraction peaks that seemed to form two partial and highly disordered lattice pyridine molecules. Their refinement was unstable even with strong displacement parameters restraints and the corresponding space was thus analyzed and taken into account with SQUEEZE as implemented in the PLATON package.18 A total of 310 electrons per cell were recovered by SQUEEZE, mostly over two voids of 580 cubic angstrom each. These figures are reasonable for at least six additional diffuse pyridine molecules per cell, i.e. three per [Co8] formula unit. These have been included in the formula.2.3 Physical Measurements
Variable-temperature magnetic susceptibility data were obtained with a Quantum Design MPMS5 SQUID magnetometer. Pascal's constants were used to estimate diamagnetic corrections to the molar paramagnetic susceptibility. The elemental analysis was performed with a Elemental Microanalizer (A5), model Flash 1112 at the Servei de Microanàlisi of CSIC, Barcelona, Spain. IR spectra were recorded as KBr pellet samples on a Nicolet AVATAR 330 FTIR spectrometer. Positive ion ESI TOF mass spectrometry experiments were performed on a LC/MSD-TOF (Agilent Technologies) at the Unitat d'Espectrometria de Masses de Caracterització Molecular (CCiT) of the University of Barcelona. The experimental parameters were: capillary voltage 4 kV, gas temperature 325 °C, nebulizing gas pressure 15 psi, drying gas flow 7.0 L min−1, and fragmentor voltage ranging from 175 to 300 V. The samples (μL) were introduced into the source by an HPLC system (Agilent 1100), using a mixture of H2O/MeCN (1/1) as eluent (200 μL min−1).3. Results and discussion
3.1 Synthesis
As mentioned in the Introduction, in absence of a base, H4L was found to react with a Co(II) salt leading to a cluster where the phenol groups of the ligand remain protonated and do not coordinate.12 It has now been found that the use of a strong enough base allows removing all the ionisable protons from H4L, which facilitates the involvement of the resulting phenolate groups in the coordination. This concept had been proofed previously with the related ligand H4L1, featuring an m-phenylene spacer instead of the m-pyridinediyl. In that case, the presence of AcO− allowed only removing the β-diketone protons, leading to complexes with a [M2(H2L1)2] core.19 Instead, stronger bases such as NBu4OH or NaH react also with the phenols of H4L1, serving to engage more metals to the coordination with formation of linear molecules of the type [M4(L1)2].20,21 Here the reactivity becomes richer. Full deprotonation of H4L seems to favour the oxidation of some of the Co(II) ions to Co(III) with atmospheric oxygen (see structural analysis) by stabilization of the latter ions through chelation. Thus the reaction between H4L and Co(NO3)2 in pyridine, in the presence of NBu4OH, leads to the formation of a new cluster, [Co4(L)2(OH)(py)7]NO3 (1). It must be mentioned that the procedure was originally intended to incorporate a lanthanide ion together with cobalt, therefore it was conducted in the presence of Gd(NO3)3. However, the rare earth has never been observed in the isolated product. On the other hand, the absence of gadolinium salt prevents the formation of any crystals or identifiable products. It is however not clear what the precise role of this component is in the equilibrium. While the formation of 1 involves presumably other side reactions, it can be described with a net equation as originating from the starting materials (eqn (1)).| 4Co(NO3)2·6H2O + 2H4L + 0.5O2 + 7NBu4OH + 7py → [Co4(OH)(L)2(py)7](NO3) + 7NBu4NO3 + 31H2O | (1) |
The use of NaH as a base in a very similar reaction entails profound differences to the product obtained. Thus, mixing NaH, H4L and Co(BF4)2 in pyridine allows crystallization of the assembly [Co8Na4(L)4(OH)2(CO3)2(py)10](BF4)2 (2), featuring the same Co(II) to Co(III) ratio as in complex 1. In this case, the presence of Na(I) ions plays a key role resulting in the “dimerization” of the basic [Co4L2(OH)]+ unit already observed in the tetranuclear complex (see below). The reaction involves oxidation of Co(II) by atmospheric oxygen and the capture of CO2 from air through conversion to CO32− or HCO3−. This process, favored by strong basic conditions and coordination to metals has been widely documented.22–24 In one of the few mechanistic studies performed,25 it is proposed that it occurs following the insertion of CO2 within the Ni–O coordination bond of a terminal hydroxide from a Ni(II) square planar mononuclear complex. However, this reaction has been more commonly observed on precursors containing bridged M(II)2(OH)1,2 moieties.26,27 This is likely to be also the case in complex 2 since it contains Co(II)2(μ-OH) moieties (see below). Other schemes involving three metals seem to proceed first by a nucleophilic attack of bound OH to CO2, which subsequently coordinates to the other two metals, yielding a μ3-CO32− ligand.28 The chemical process leading to complex 2, starting from the initial reagents, can be described with a balanced equation (eqn (2)).
| 8Co(BF4)2·6H2O + 4H4L + O2 + 2CO2 + 18NaH + 10py → [Co8Na4(OH)2(L)4(CO3)2(py)10](BF4)2 + 14NaBF4 + 18H2 + 46H2O | (2) |
In both reactions, the yields of isolated crystals are relatively low. Thus, eqn (1) and (2) are only means of describing the possible processes of formation of 1 and 2, respectively, without implying that other processes and equilibria are not also occurring. The main focus here is analyzing and describing the fascinating novel coordination features unveiled within these new compounds. Once isolated, the crystals could be re-dissolved in various solvents (acetone, MeOH, ACN, DMF). The nature of the systems in acetone solution was analyzed by positive ion mass spectrometry (Fig. S1–S4†). While the whole cluster cation was not observed for any of the compounds, in both cases it was possible to identify numerous forms of the [L2Co4] basic unit bearing H2O and/or pyridine ligands and also exhibiting several distributions of +2 and +3 oxidation states of the Co centers (e.g. [L2Co4]2+, [L2Co4(py)2]2+, [L2Co4(py)2]2+ [L2Co4(py)(H2O)2]2+, etc.). Some fragments lacking one of the central metal ions were also observed (such as [L2Co3] + 2H+, [L2Co3] + H+, [L2Co3(py)] + 2H+) as well as moieties incorporating a K+ into that vacant position ([L2Co3K(py)]+ + H+, [L2Co3K(py)(MeCN)]+ + H+, [L2Co3K(py)] + H+, [L2Co3K(py)(MeCN)]+, [L2Co3K(py)3(H2O)2]+, etc., the presence of K+ and MeCN being inherent to the technique and thus very common). From this point of view, complex 2 in solution is essentially no different than compound 1. These results indicate that a prevalent moiety in solution is most likely a solvated form of the [L2Co4]2+ rhombic fragment.
3.2 Description of structures
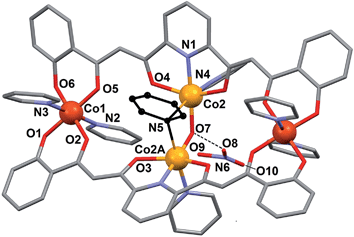
The NO3− counter ion is disordered, pivoting around the N atom over two slightly different orientations and forming a hydrogen bond with the μ-OH− ligand. The oxidation states postulated for the Co(II) ions are consistent with the charge of the cluster and were very clearly confirmed by bond valence sum (BVS) analysis (Table S5†). Of all the unusual structural features of compound 1, perhaps the most remarkable is the presence of a bridging pyridine ligand in between two Co(II) centers (see the details in Table 1). This bridge interacts with both Co(II) ions in a slightly asymmetric manner, thus featuring a shorter (2.367(5) Å) and a longer (2.700(5) Å) Co–N distance. In fact the occupation of this pyridine group within the crystal lattice is shared in equal amounts over two symmetric orientations corresponding to having the N donor closer to either one or the other Co(II) ion (Fig. 4). These two orientations form a mutual calculated angle of 20.18°. In addition, the angles of each ring with the idealized equatorial planes around the Co(II) ions are 45.48° and 65.65°, respectively. The molecule exhibits a crystallographic C2 axis passing through the donor atoms of the μ-OH ligand and bisecting the two orientations of the disordered μ-py group.
| a Symmetry operation A: 1 − x, y, 0.5 − z. | |||
|---|---|---|---|
| Co2–N5 | 2.367(4) | Co2–N5A–Co2A | 80.32(10) |
| Co2–N5A | 2.700(5) | Co2–O7–Co2A | 116.22(11) |
| Co2–O7 | 1.9300(12) | Co–N calc. | 2.214/2.861 |
| Co2⋯Co2A | 3.2774(7) | Binding energy | −38.8/−33.6 |
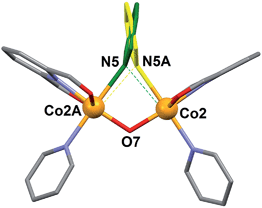 | ||
| Fig. 4 Representation of the central core of [Co4(L)2(OH)(py)7]NO3 (1) emphasizing the two positions of the disordered μ-pyridine group (yellow and green). | ||
This peculiar bridging interaction of pyridine with two metals has been termed a “crevice” interaction and is extremely rare in the literature. It originates at the exposed two-site “cleft” of a molecular scaffold in the absence of any better bridging ligand. It was observed for the first time on a dinuclear Mo(V) complex,29,30 and since then, very few further examples have been reported involving Ag(I),31 Ti(IV),32 Cs(I),33 or Cu(I).34 Here we study it by means of theoretical methods for the first time (see below).
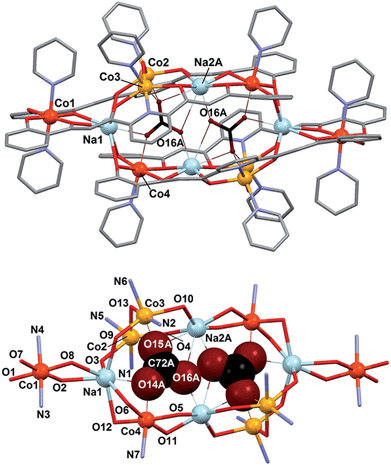
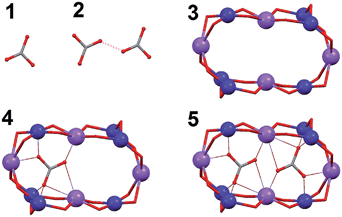
In fact, the [Co8] cages are distributed over two equally populated and very similar disordered positions (Fig. S7†). The cage offers the conditions to encapsulate two CO32− anions, which are brought to lie extremely close to each other in both disordered positions (O16A⋯O16A# = 1.946 Å and O16B⋯O16B# = 1.971 Å, respectively) considering the sum of the van der Waals radii for oxygen (rV(O) = 1.4 Å). Both CO32− groups are stabilized within the cage by interactions with the metals (see details in Table 2). In one of the disordered positions the number of interactions is six; three Na(I), two Co(II) and one Co(III) cations. In the other, the sodium atom Na2 is slightly removed away from the cage (distant by 0.912(8) Å from the first position, Fig. S7†), and thus loses contact with the internal CO32− ions. In comparison to cluster 1, the coordination geometry of the Co(II) ions (Co2 and Co3) is also distorted octahedral, replacing the μ-py group with a bridging oxygen atom from one CO32− ligand. Half of the Co(III) centers have the same environment as in 1 (Co1), whereas the other half (Co4) replace one axial pyridine ligand by one oxygen atom from CO32− on that position. Encapsulation of CO32− from atmospheric carbon dioxide under strong basic conditions by incorporation into transition metal complexes is now very well documented.35–37 Fixation of more than one carbonate unit by one molecule is much rarer. In such cases, these species usually act essentially as spacers between metals or are subtended by metal ions conforming the external surface of a cage.38–46 In lesser occasions, the incorporated CO32− moieties may be rather considered as being encapsulated inside the coordination cage.47–51 In any case, two carbonate anions have never been forced to lie so close to each other as within complex 2. To the best of our knowledge, the closest intermolecular contact between CO32− species observed to date (2.487 Å) was found within the compound [Y(H2O)]2(C2O4)(CO3)2, from a structure resolved by powder diffraction methods.52 The occurrence here is quite remarkable since the O⋯O contact now observed through single crystal X-ray diffraction methods is very close (within 0.03 Å) to the covalent O–O distance detected by spectroscopic methods on the molecule HOON, found to be stable at near 2 K. This distance was calculated to be, from the experimental data, of 1.915 Å.13 Therefore, this limiting observation and the one now reported represent the meeting point in the oxygen–oxygen distance when coming from two ends, that of covalent interactions and that of (forced) intermolecular contacts.
| a Symmetry operation #: 1 − x, 1 − y, 1 − z. | |||
|---|---|---|---|
| O14A–Na1# | 2.230(18) | Co4–O14A–Na1# | 93.7(6) |
| O14A–Co4 | 2.088(15) | Co3#–O15A–Co2# | 99.0(5) |
| O15A–Co3# | 1.958(14) | Co3#–O15A–Na2A# | 95.8(7) |
| O15A–Co2# | 2.185(16) | Co2#–O15A–Na2A# | 92.2(5) |
| O15A–Na2A# | 2.785(19) | Na2A–O16A–Na2A | 138.8(6) |
| O16A–Na2A | 2.241(14) | Co4–O14B–Na1 | 90.6(6) |
| O16A–Na2A# | 2.970(18) | Co2–O15B–Co3 | 91.6(4) |
| O14B–Na1# | 2.320(18) | Co2–O15B–Na2B | 85.9(4) |
| O14B–Co4 | 2.110(14) | Co3–O15B–Na2B | 84.0(4) |
| O15B–Co2# | 2.151(14) | ||
| O15B–Co3# | 2.248(10) | O16A⋯O16A# | 1.946 |
| O15B–Na2B# | 2.803(14) | O16B⋯O16B# | 1.971 |
| O16B–Na2B | 2.991(16) | ||
3.3 DFT calculations
The extremely rare coordination interactions observed here warrant a proper description through a theoretical treatment. For this we employed density functional theory (DFT) calculations.53The energy of the “crevice” pyridine has indeed not been studied theoretically yet. The original papers, reporting a Mo–(μ-py)–Mo moiety,29,30 speculate about the existence or not of a Mo⋯py interaction, in view of very long Mo–N distances (2.967 Å and 2.931 Å). When found bridging two Ag(I) ions,31 the pyridine group was described as “weakly coordinating”, with Ag–N of 2.71 Å. The complex involving Ti(IV),32 is the only reported example where the bridging pyridine has been crystallographically solved as disordered over two equivalent positions, showing two distinctly different (2.532 Å and 3.093 Å) Ti–N distances, as found here in complex 1. In fact, the original solution for the structure of 1 featured a symmetric μ-pyridine ligand. It was in light of the simulation procedure (see below) that the data were refined anew and the disorder unveiled. Thus, the nuclear configuration of [Co4(OH)(L)2(py)7]+ was optimized by means of DFT calculations carried out with Gaussian 09 (ref. 54) using the B3LYP55 functional within the spin unrestricted formalism, together with an Ahlrichs SVP basis set56 on all atoms and Grimme's D2 empirical dispersion correction.57 The result of this optimization showed the μ-py group in a very asymmetric configuration, with very differentiated N–Co distances (2.214 Å and 2.861 Å) and two distinct orientations of the ring with respect to the Co(II) equatorial planes (85.70° and 18.67°). This observation prompted the new refinement of the experimental crystallographic data (see above), which unveiled that this group is indeed bound unsymmetrically (Fig. 4), although not so much as suggested by the simulation. These differences could be explained to a large extent by packing effects. DFT binding energies were then computed at the B3LYP-D2/TZVP level. In these calculations, the basis set superposition error was corrected using the counterpoise method.58 A binding energy of −38.6 kcal mol−1 was first determined for the μ-py group by using as a model a truncated version of the optimized structure (Fig. S8†), chosen to avoid the inclusion of the distal metals, not relevant for this calculation, since they are too distant to have an influence on the binding energy of interest. Subsequently, calculations were performed employing the same simplified model, using now the coordinates of the experimental solid state structure for all the nuclear positions, except these from μ-py. A very similar value of −33.6 kcal mol−1 was reached. For comparison, the binding energy of terminal pyridine to the distal Co(III) ion was determined by DFT calculations on a fragment of 1 containing the relevant metal (Fig. S8†) and using the experimental coordinates of the atoms involved (with Co–N of 1.943 Å). The calculated value is −41.0 kcal mol−1. This means that the binding energy of the μ-py group in 1 is comparable to that of a true terminal py ligand. The contribution of the individual metal–ligand interactions has been analyzed by calculating the critical points around the Co ions involved in this interaction (Co2 and Co2A) using the AIM method,59 using the experimental coordinates of one of the disordered components of the structure (Fig. S9†). A list of the critical points encountered and the electron density at these points is in Table S8.† It has been found that indeed there is a critical point for both Co–N vectors featured by the μ-py ligand, which shows that the ligand interacts with each of the metals. The electron density at these critical points is 3.75 × 10−2 and 1.75 × 10−2 a.u. for the short and long interaction, respectively. Since the electron density at the bond critical points correlates with the strength of the bond,59 68% of the interaction energy (−22.8 kcal mol−1) can be attributed to the short contact and 32% (−10.8 kcal mol−1) to the long one.
The cluster cation of 2 exhibits the shortest non-covalent O⋯O distance ever observed between two CO32− species. The reason that these two species come so close to each other is the stabilization brought by the large number of interactions that they establish with the metals of 2 upon coordination. DFT calculations constitute an invaluable tool to verify and quantify this hypothesis. Thus, the absolute energy of various model systems (Fig. 6) built up using the experimental coordinates of the pertinent atoms of 2 was determined. For this, the atomic positions of the component that locates the CO32− anions closest to each other (distance O⋯O, 1.946 Å) was employed (Fig. 5). The energies associated to the other components were not expected to vary significantly (see below). First, the energy of bringing two CO32− anions at the distance observed within 2 in the same relative orientation (Edimer/out = E2 − 2E1; Fig. 6 and S10†) without considering any other interaction, is extremely high; +349.6 kcal mol−1. This renders as quite remarkable the observation of these two anions in such relative positions within the cage. The stabilization attained upon coordination of CO32− inside the cage was estimated by calculating the energy of encapsulating one such anion from the gas phase into the cluster (Ecoord1 = E4 − E3 − E1; Fig. 6 and S10†), which amounts to −773.4 kcal mol−1. This already suggests that the system is to release energy when including two CO32− inside that cavity, despite the cost of having them so close to each other. Likewise, bringing two infinitely distant carbonate molecules inside the cage (Ecoord2 = E5 − E3 − 2E1; Fig. 6 and S10†) also represents an important gain in stability, the energy of the process being calculated as −1329.4 kcal mol−1, consistent with the experimental observation. The process as calculated is not perfectly comparable with the real situation, since the species involved are not in the gas phase but in pyridine solution. Nevertheless, a medium made of pyridine molecules, which are good Lewis bases, should favor the encapsulation even further. The models studied also allow to quantify the repulsion of the CO32− groups once they are inside the cage (Edimer/in = Ecoord2 − 2Ecoord1 = E5 + E3 − 2E4; Fig. 6 and S10†). Thus the interaction involves an energy of +217.5 kcal mol−1. While this unfavorable interaction remains relatively high, it is reduced by 38% as compared to the cost of maintaining two CO32− ions at such distance in the gas phase. This is because the interactions with the metals withdraw an important part of the negative charge from the anions, diminishing the magnitude of their mutual repulsion when they are inside the cage. This last calculated value does not depend on the medium outside the cage, since the models used never involve free CO32−. The conclusions arising from these calculations are not expected to vary at all if the atomic coordinates of other disordered components present in the crystal lattice (Fig. S7†) were employed. To illustrate this, Edimer/out was calculated using the positions of CO32− in this other component and a value of +365.6 kcal mol−1 was extracted, only 16% higher than for the component chosen to illustrate the interaction energies in 2.
3.4 Bulk magnetization properties
Complexes 1 and 2 exhibit one and two [L2Co4] moieties in their molecule, respectively. The metals in these units are distributed in the form of a rhombus (Fig. 3) with two Co(III) ions (Co1 and symmetry equivalent) spanning the long diagonals and two Co(II) centres (Co2 and Co2A) at the ends of the short one. The trivalent metals are expected to be diamagnetic (S = 0) whereas the Co(II) centres, bridged by one μ-OH− and the μ-py ligand (or one O-atom from CO32−), must be paramagnetic. Variable temperature magnetization measurements were performed on powdered microcrystalline samples of both compounds under a constant magnetic field of 0.5 T. The results are shown in Fig. 7, in the form of χMT vs. T plots (χM is the molar paramagnetic susceptibility). At 300 K, the χMT product values are 7.21 and 12.45 cm3 Kmol−1, respectively, much higher than those expected for two and four uncoupled high spin (S = 3/2) Co(II) centers (expected at 3.75 and 7.5 cm3 Kmol−1, respectively, for g = 2). This means that the magnetic properties are strongly affected by the orbital angular momentum of these ions, not quenched despite the significant deviation from the octahedral geometry shown by them. χMT decreases as the temperature declines, increasingly faster towards lower temperatures, to reach 2.30 and 2.37 cm3 Kmol−1, respectively, at 2 K. This may be due to the effects of spin orbit coupling, but also to a possible interaction between the two Co(II) ions within each rhombus (Co2 and Co2A for 1 and Co2 and Co3 for 2). The magnetic data were fit by matrix diagonalization of the Hamiltonian in eqn (3), using the program PHI.60Ĥ = 2λσ![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) CoŜCo − 2J(ŜCo1ŜCo2) + 2μB(σ CoŜCo − 2J(ŜCo1ŜCo2) + 2μB(σ![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) Co + gCoŜCo) Co + gCoŜCo)![[B with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0042_20d1.gif) | (3) |
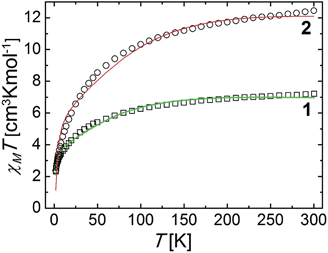 | ||
| Fig. 7 Plots of χMT vs. T for complexes 1 and 2. The solid lines are best fits to the experimental data (see text for details). | ||
In this Hamiltonian, ![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) Co and ŜCo are, respectively, the orbital and spin angular momenta of Co(II) (subscripts 1 and 2 refer to each of the two metals), while gCo is the isotropic gyromagnetic ratio for this ion. The parameters J, λ and σ correspond, respectively, to the exchange-coupling constant between both metals, the spin–orbit coupling constant of Co(II) and a combined orbital reduction parameter of this metal,61 whereas μB and
Co and ŜCo are, respectively, the orbital and spin angular momenta of Co(II) (subscripts 1 and 2 refer to each of the two metals), while gCo is the isotropic gyromagnetic ratio for this ion. The parameters J, λ and σ correspond, respectively, to the exchange-coupling constant between both metals, the spin–orbit coupling constant of Co(II) and a combined orbital reduction parameter of this metal,61 whereas μB and ![[B with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0042_20d1.gif) have the usual meanings. Reasonable fits (Fig. 7, solid lines) were obtained for the following parameters (in the 1/2 format); J = −0.40/−0.89 cm−1, g = 2.31/2.09 with fixed parameters of λ = −140/−180 cm−1 and σ = −1.0/−1.0. The discrepancies with the experimental data appear more noticeable in the temperature range between 35 and 100 K. This may be due to the approximations inherent to the model employed. In fact, treating the exchange between orbitally non-degenerate ions is very difficult. The approach used here considers only the coupling between true spin states, and not these of the orbital angular momentum.62 This is probably the reason why there are not magnetostructural correlations of exchanged coupled Co(II) ions in the literature. Nevertheless, weak couplings are generally observed between such ions when linked by oxygen monoatomic bridges.63
have the usual meanings. Reasonable fits (Fig. 7, solid lines) were obtained for the following parameters (in the 1/2 format); J = −0.40/−0.89 cm−1, g = 2.31/2.09 with fixed parameters of λ = −140/−180 cm−1 and σ = −1.0/−1.0. The discrepancies with the experimental data appear more noticeable in the temperature range between 35 and 100 K. This may be due to the approximations inherent to the model employed. In fact, treating the exchange between orbitally non-degenerate ions is very difficult. The approach used here considers only the coupling between true spin states, and not these of the orbital angular momentum.62 This is probably the reason why there are not magnetostructural correlations of exchanged coupled Co(II) ions in the literature. Nevertheless, weak couplings are generally observed between such ions when linked by oxygen monoatomic bridges.63
4. Conclusions
By employing strong basic conditions in reactions of the ligand 2,6-bis-(3-oxo-3-(2-hydroxyphenyl)-propionyl)-pyridine, H4L, with Co(II) salts, two mixed-valence Co(II)/Co(III) clusters have been obtained with unprecedented structures. The unconventional disposition of metals within these clusters prompts the isolation of one bridging, very rare “crevice” pyridine group in 1. DFT calculations reveal a binding energy to each Co(II) of approximately 40% of a regular Co–py coordination bond. The cage of 2 is seen to trap two CO32− anions that are held at the closest intermolecular distance ever seen for such species. It can be seen through calculations that the repulsion energy between these is strongly reduced inside the cage, by interaction with several Lewis acids, and that the system is very stable, thus rationalizing its formation. The very close lying CO32− groups inside 2 seem poised to easy oxidation and subsequent transformation into peroxodicarbonate. This suggests a possibility for catalytic CO2 capture from the atmosphere to form a reactive species, C2O62−, useful for chemical synthesis.Acknowledgements
G.A. thanks the Generalitat de Catalunya for the prize ICREA Academia 2008 and 2013, for excellence in research and the ERC for a Starting Grant (258060 FuncMolQIP). The authors thank the Spanish MICINN for funding through CTQ2009-06959 (GA, LAB, DA), MAT2011-24284 (OR) and a “Ramón y Cajal” Fellowship (JRA), the ERC for a Predoctoral Fellowship under grant 258060 FuncMolQIP (VV and IB) and University of Barcelona for a Ph-D grant (MF). Data for H4L and 1 were collected through access to ALS beamline 11.3.1. The Advanced Light Source is supported by the Director, Office of Science, Office of Basic Energy Sciences of the U. S. Department of Energy under contract no. DE-AC02-05CH11231.References
- G. Aromí, P. Gamez and J. Reedijk, Coord. Chem. Rev., 2008, 252, 964–989 CrossRef.
- D. J. Bray, J. K. Clegg, L. F. Lindoy and D. Schilter, in Advances in Inorganic Chemistry: Including Bioinorganic Studies, Template Effects and Molecular Organization, ed. R. Van Eldik and K. Bowman James, 2007, vol. 59, pp. 1–37 Search PubMed.
- J. K. Clegg, F. Li and L. F. Lindoy, Coord. Chem. Rev., 2013, 257, 2536–2550 CrossRef CAS.
- R. W. Saalfrank, H. Maid and A. Scheurer, Angew. Chem., Int. Ed., 2008, 47, 8794–8824 CrossRef CAS PubMed.
- V. A. Grillo, E. J. Seddon, C. M. Grant, G. Aromí, J. C. Bollinger, K. Folting and G. Christou, Chem. Commun., 1997, 1561–1562 RSC.
- M. Raja, R. G. Iyer, C. Gwengo, D. L. Reger, P. J. Pellechia, M. D. Smith and A. E. Pascui, Organometallics, 2013, 32, 95–103 CrossRef CAS.
- Y. Hou, J. Shi, W. Chu and Z. Sun, Eur. J. Inorg. Chem., 2013, 2013, 3063–3069 CrossRef CAS.
- D. Aguilà, L. A. Barrios, O. Roubeau, S. J. Teat and G. Aromí, Chem. Commun., 2011, 47, 707–709 RSC.
- L. A. Barrios, I. Borilovic, J. Salinas-Uber, D. Aguilà, O. Roubeau and G. Aromí, Dalton Trans., 2013, 42, 12185–12192 RSC.
- T. Shiga, N. Ito, A. Hidaka, H. Ōkawa, S. Kitagawa and M. Ohba, Inorg. Chem., 2007, 46, 3492–3501 CrossRef CAS PubMed.
- T. Shiga, M. Ohba and H. Ōkawa, Inorg. Chem., 2004, 43, 4435–4446 CrossRef CAS PubMed.
- J. Salinas-Uber, L. A. Barrios, O. Roubeau and G. Aromí, Polyhedron, 2013, 54, 8–12 CrossRef CAS.
- K. N. Crabtree, M. R. Talipov, O. Martinez, G. D. O'Connor, S. L. Khursan and M. C. McCarthy, Science, 2013, 342, 1354–1357 CrossRef CAS PubMed.
- G. A. Craig, L. A. Barrios, J. Sanchez Costa, O. Roubeau, E. Ruiz, S. J. Teat, C. C. Wilson, L. Thomas and G. Aromí, Dalton Trans., 2010, 39, 4874–4881 RSC.
- SAINT, SADABS and SHELXTL, Bruker AXS Inc., Madison, Wisconsin, USA Search PubMed.
- A. Altomare, M. C. Burla, M. Camalli, G. L. Cascarano, C. Giacovazzo, A. Guagliardi, A. G. G. Moliterni, G. Polidori and R. Spagna, J. Appl. Crystallogr., 1999, 115–119 CrossRef CAS.
- G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Crystallogr., 2008, 64, 112–122 CrossRef CAS PubMed.
- A. Spek, J. Appl. Crystallogr., 2003, 36, 7–13 CrossRef CAS.
- G. Aromí, C. Boldron, P. Gamez, O. Roubeau, H. Kooijman, A. L. Spek, H. Stoeckli-Evans, J. Ribas and J. Reedijk, Dalton Trans., 2004, 3586–3592 RSC.
- L. A. Barrios, D. Aguilà, S. Mellat, O. Roubeau, S. J. Teat, P. Gamez and G. Aromí, C. R. Chim., 2008, 11, 1117–1120 CrossRef CAS.
- L. A. Barrios, D. Aguilà, O. Roubeau, P. Gamez, J. Ribas-Ariño, S. J. Teat and G. Aromí, Chem.–Eur. J., 2009, 15, 11235–11243 CrossRef CAS PubMed.
- G. A. Craig, O. Roubeau, J. Ribas-Ariño, S. J. Teat and G. Aromí, Polyhedron, 2013, 52, 1369–1374 CrossRef CAS.
- S. Uozumi, H. Furutachi, M. Ohba, H. Okawa, D. E. Fenton, K. Shindo, S. Murata and D. J. Kitko, Inorg. Chem., 1998, 37, 6281–6287 CrossRef CAS.
- J. P. Wikstrom, A. S. Filatov, E. A. Mikhalyova, M. Shatruk, B. Foxman and E. V. Rybak-Akimova, Dalton Trans., 2010, 39, 2504–2514 RSC.
- D. Huang, O. V. Makhlynets, L. L. Tan, S. C. Lee, E. V. Rybak-Akimova and R. H. Holm, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 1222–1227 CrossRef CAS PubMed.
- A. Company, J.-E. Jee, X. Ribas, J. M. Lopez-Valbuena, L. Gómez, M. Corbella, A. Llobet, J. Mahía, J. Benet-Buchholz, M. Costas and R. van Eldik, Inorg. Chem., 2007, 46, 9098–9110 CrossRef CAS PubMed.
- N. Kitajima, S. Hikichi, M. Tanaka and Y. Morooka, J. Am. Chem. Soc., 1993, 115, 5496–5508 CrossRef CAS.
- P. Mateus, R. Delgado, F. Lloret, J. Cano, P. Brandão and V. Félix, Chem.–Eur. J., 2011, 17, 11193–11203 CrossRef CAS PubMed.
- M. G. B. Drew, P. C. H. Mitchell and A. R. Read, J. Chem. Soc., Chem. Commun., 1982, 238–239 RSC.
- M. G. B. Drew, P. J. Baricelli, P. C. H. Mitchell and A. R. Read, J. Chem. Soc., Dalton Trans., 1983, 649–655 RSC.
- G. A. Bowmaker, Effendy, P. J. Harvey, P. C. Healy, B. W. Skelton and A. H. White, J. Chem. Soc., Dalton Trans., 1996, 2459–2465 RSC.
- T. J. Boyle, L. A. M. Ottley, S. M. Hoppe and C. F. Campana, Inorg. Chem., 2010, 49, 10798–10808 CrossRef CAS PubMed.
- G. W. Rabe, H. Heise, G. P. A. Yap, L. M. Liable-Sands, I. A. Guzei and A. L. Rheingold, Inorg. Chem., 1998, 37, 4235–4245 CrossRef CAS PubMed.
- C. Xu, Z.-Y. Zhang, Z.-G. Ren, L.-K. Zhou, H.-X. Li, H.-F. Wang, Z.-R. Sun and J.-P. Lang, Cryst. Growth Des., 2013, 13, 2530–2539 CAS.
- A. M. Garcia-Deibe, C. Portela-Garcia, M. Fondo, A. J. Mota and J. Sanmartin-Matalobos, Chem. Commun., 2012, 48, 9915–9917 RSC.
- A. N. Georgopoulou, C. P. Raptopoulou, V. Psycharis, R. Ballesteros, B. Abarca and A. K. Boudalis, Inorg. Chem., 2009, 48, 3167–3176 CrossRef CAS PubMed.
- G. A. Craig, O. Roubeau, J. Ribas-Ariño, S. J. Teat and G. Aromí, Polyhedron, 2013, 52, 1369–1374 CrossRef CAS.
- J. Y. Liu, Z. Y. Liu, L. J. Zhang, Y. Y. Wang, P. Yang, Y. Wang, B. Ding and X. J. Zhao, CrystEngComm, 2013, 15, 6413–6423 RSC.
- M. Sarkar, G. Aromí, J. Cano, V. Bertolasi and D. Ray, Chem.–Eur. J., 2010, 16, 13825–13833 CrossRef CAS PubMed.
- L. Wang, Y. Li, Y. Peng, Z. Liang, J. Yu and R. Xu, Dalton Trans., 2012, 41, 6242–6246 RSC.
- K.-C. Xiong, F.-L. Jiang, Y.-L. Gai, D.-Q. Yuan, D. Han, J. Ma, S.-Q. Zhang and M.-C. Hong, Chem.–Eur. J., 2012, 18, 5536–5540 CrossRef CAS PubMed.
- Y. Jiang, X. Wang, X. Ying, F. Zhong, J. Cai and K. He, Inorg. Chem. Commun., 2006, 9, 1063–1066 CrossRef CAS.
- D. Armentano, N. Marino, T. F. Mastropietro, J. Martínez-Lillo, J. Cano, M. Julve, F. Lloret and G. De Munno, Inorg. Chem., 2008, 47, 10229–10231 CrossRef CAS PubMed.
- J. A. Hoshiko, G. Wang, J. W. Ziller, G. T. Yee and A. F. Heyduk, Dalton Trans., 2008, 5712–5714 RSC.
- J.-Y. Xu, H.-B. Song, G.-F. Xu, X. Qiao, S.-P. Yan, D.-Z. Liao, Y. Journaux and J. Cano, Chem. Commun., 2012, 48, 1015–1017 RSC.
- W. Lai, S. M. Berry, W. P. Kaplan, M. S. Hain, J. C. Poutsma, R. J. Butcher, R. D. Pike and D. C. Bebout, Inorg. Chem., 2013, 52, 2286–2288 CrossRef CAS PubMed.
- P. C. Andrews, T. Beck, C. M. Forsyth, B. H. Fraser, P. C. Junk, M. Massi and P. W. Roesky, Dalton Trans., 2007, 5651–5654 RSC.
- C. d. Peloux, A. Dolbecq, P. Mialane, J. Marrot and F. Sécheresse, Dalton Trans., 2004, 1259–1263 RSC.
- A. S. R. Chesman, D. R. Turner, B. Moubaraki, K. S. Murray, G. B. Deacon and S. R. Batten, Chem.–Eur. J., 2009, 15, 5203–5207 CrossRef CAS PubMed.
- K. Xiong, F. Jiang, Y. Gai, Z. He, D. Yuan, L. Chen, K. Su and M. Hong, Cryst. Growth Des., 2012, 12, 3335–3341 CAS.
- A. Dolbecq, L. Lisnard, P. Mialane, J. Marrot, M. Bénard, M.-M. Rohmer and F. Sécheresse, Inorg. Chem., 2006, 45, 5898–5910 CrossRef CAS PubMed.
- T. Bataille and D. Louer, Acta Crystallogr., Sect. B: Struct. Sci., 2000, 56, 998–1002 CrossRef.
- R. G. Parr and G. Yang, Density-Functional Theory of Atoms and Molecules, Oxford University Press, 1994 Search PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, 2009, Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford, CT Search PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- A. Schaefer, H. Horn and R. Ahlrichs, J. Chem. Phys., 1992, 97, 2571–2577 CrossRef CAS.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–566 CrossRef CAS.
- R. F. W. Bader, Atoms in Molecules: A Quantum Theory, Clarendon Press, Oxford, 1990 Search PubMed.
- N. F. Chilton, R. P. Anderson, L. D. Turner, A. Soncini and K. S. Murray, J. Comput. Chem., 2013, 34, 1164–1175 CrossRef CAS PubMed.
- F. Lloret, M. Julve, J. Cano, R. Ruiz-Garcia and E. Pardo, Inorg. Chim. Acta, 2008, 361, 3432–3445 CrossRef CAS.
- M. E. Lines, J. Chem. Phys., 1971, 55, 2977–2984 CrossRef CAS.
- G. Aromí, H. Stoeckli-Evans, S. J. Teat, J. Cano and J. Ribas, J. Mater. Chem., 2006, 16, 2635–2644 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: Mass Spectrometry and BVS analysis CCDC 996546–996548. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c4sc02491e |
| This journal is © The Royal Society of Chemistry 2015 |