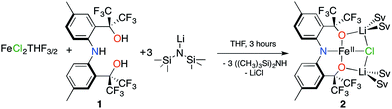A high-spin square-planar Fe(II) complex stabilized by a trianionic pincer-type ligand and conclusive evidence for retention of geometry and spin state in solution

Abstract

Square-planar high-spin Fe(II) molecular compounds are rare and the only three non-macrocyclic or sterically-driven examples reported share a common FeO₄ core. Using an easily modifiable pincer-type ligand, the successful synthesis of the first compound of this type that breaks the FeO₄ motif was achieved. In addition, we present the first evidence that geometry and spin state persist in solution. Extensive characterization includes the first high-field EPR and variable field/temperature Mössbauer spectra for this class of compounds. Analysis of the spectroscopic data indicates this complex exhibits a large and positive zero-field splitting tensor. Furthermore, the unusually small ΔE_Q value determined for this compound is rationalized on the basis of DFT calculations.

---

Chemistry students learn that inorganic complexes adopt predictable geometries and electronic structures depending on the identity of the ligands, the metal ion, and its oxidation state.¹ Examples of inorganic dogma are ubiquitous d⁸ square-planar Pd(II) and Pt(II) complexes that are predictably low-spin, or that d³–d⁷ tetrahedral complexes are inevitably high-spin. However, it is the peculiar deviations^2,3 that are most informative and stimulate curiosity. Convincing metal ions to adopt unusual geometries and electronic structures is important to realizing new chemistry. More specifically, it is appealing to expand the scope of iron chemistry because of its low toxicity, abundance, and therefore low cost relative to the noble metals.^4,5 In particular, square-planar Fe(II) complexes are abundant and virtually all adopt an S = 1 intermediate-spin state; classic examples are Fe(II) porphyrins.⁶ Gillespite (BaFeSi₄O₁₀), a mineral discovered in 1922,⁷ deviates from this norm and contains Fe(II) in a square-planar geometry with a high-spin S = 2 state; though the geometry may be due to constraint within the crystal lattice rather than an inherent electronic stabilization. The conditions that promote a high-spin square-planar geometry are: (1) charge from anionic ligands to prevent higher coordination numbers, (2) alkali metal counter cations to stabilize the anionic charge, (3) strong π-donor ligands to destabilize the sterically preferred tetrahedral geometry, and (4) weak σ-donating ligands to minimize the anti-bonding character of the d_x²−y² orbital.⁸ Until recently, the only reported molecular compounds with these characteristics employed macrocyclic^9,10 or very sterically demanding¹¹ ligands suggesting the square-planar geometry is not exclusively driven by electronic factors. Remarkably, non-macrocyclic or sterically-driven molecular square-planar Fe(II) species eluded preparation until 2011. Klüfers described the preparation and X-ray structural characterization of a square-planar high-spin Fe(II) compound,¹² and since then, two other examples appeared in the literature, all containing an anionic FeO₄ core.^13,14 In addition, Chirik reported the isolation of an S = 3/2 square-planar bis(imino)pyridine iron chloride, with an electronic structure that is best described considering a S = 2 Fe(II) center anti-ferromagnetically coupled to a ligand-based radical.^15,16 However, the structural assignment is based on DFT calculations. In addition, the assignment of a square-plane for the previously reported examples comes from data obtained from the solid state structures. An important question is whether the square-planar geometry persists in solution, or not. Since any reactivity is likely to take place in the solution phase, it is important to find complexes that feature the unique square-planar geometry and high-spin state in solution.

Herein, we present conclusive evidence of a square-planar S = 2 high-spin Fe(II) complex in both the solid, and solution state. This molecule represents an expansion beyond the FeO₄ core. Notably, frozen solution Mössbauer spectroscopy provides the first evidence that the geometry and spin state are retained in solution, highlighting that the stability of this compound is driven by electronic factors rather than constraints from the crystal lattice.

A striking feature common to the previously reported molecular species and Gillespite is the FeO₄ core. An important advance is to employ alternative donor motifs and to install a site for functionalization. Pincer ligands provide a convenient starting point for expanding square-planar S = 2 Fe(II) complexes beyond the FeO₄ unit. In particular, trianionic pincer ligands¹⁷ provide the requisite anionic charge to maintain a low coordination number and are easily modified. The tunability of trianionic pincer ligands opens the possibility of selectively accessing the S = 1 and S = 2 states for potential application as spin-crossover materials.⁸

Our group recently reported the trianionic pincer-type ligand precursor 2,2′-(azanediylbis(2,1-phenylene))bis(1,1,1,3,3,3-hexafluoropropan-2-ol) ([CF₃–ONO]H₃; 1) and its coordination chemistry with W(VI) and Ta(V).^18–20 Deprotonation of 1 using 3 equivalents of LiN(SiMe₃)₂ in THF, followed by subsequent addition to a slurry of FeCl₂(THF)_3/2 ²¹ in THF results in an immediate color change from yellow to brown. Stirring the reaction mixture for 3 h, and removing all volatiles provides 2 as an analytically pure brown microcrystalline powder in 43.6% yield (Scheme 1).

Scheme 1 Synthesis of the square-planar S = 2 complex 2. Sv: THF, Et₂O

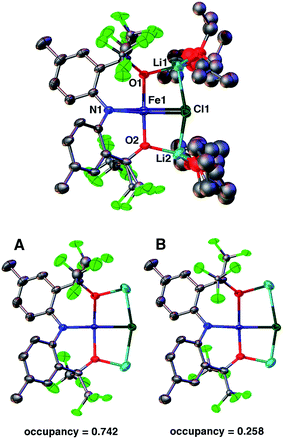
Dissolving 2 in diethyl ether and cooling to −35 °C produces red crystals suitable for single crystal X-ray diffraction analysis. Fig. 1 depicts the molecular structure of 2. In the solid state, the molecule is pseudo-C₂-symmetric (disregarding solvent molecules bound to the Li⁺ counterions) and features an Fe(II) center in a square-planar environment consisting of the [CF₃–ONO]³⁻ pincer-type ligand and a chloride. The complex is disordered in the lattice and was refined in two parts (A and B) with site occupation factors of 0.742(1) and 0.258(1). Both partitions are similar, but the less populated conformation distorts from an ideal square-plane, as revealed by the larger τ₄ value²² (0.056 vs. 0.115). The τ₄ parameter is an index of the distortion from a square-planar (τ₄ = 0) to a tetrahedral geometry (τ₄ = 1), thus the slightly higher value of 0.115 is still representative of a square-plane. These τ₄ values are comparable to the other three reported examples (0–0.214).^12–14 The [CF₃–ONO]³⁻ pincer O–Fe–O bite angles of 176.34(7)° (A) and 168.83(11)° (B) are nearly linear and much larger than observed within known Ta(V) (155.79(9)°–164.70(7)°)¹⁸ and W(VI) (147.39(8)°–147.80(7)°) complexes,²⁰ highlighting that the preference for a square-planar geometry is not enforced solely by the ligand. The Fe1–Cl1 distances of 2.3888(9) Å (A) and 2.338(3) Å (B) are longer than those typically observed for four-coordinate Fe(II) complexes,^23–26 mainly due to the strong trans influence of the amido N-atom of the pincer (N1–Fe1 = 1.9704(19) Å (A) and 1.960(2) Å (B)). For partition A, the Fe1–O1 and Fe1–O2 distances of 1.9261(19) Å and 2.0174(18) Å fall within the range reported for the three molecular Fe(II) S = 2 square-planar compounds (1.959(2)–2.0275(19) Å).¹⁴ In contrast, the Fe–O bond lengths in B are just outside this range: 2.113(2) Å and 1.848(2) Å, respectively.

Fig. 1 Molecular structure, refined into parts A and B, with ellipsoids presented at 50% probability level. Hydrogen atoms were removed for clarity. Selected bond lengths (Å) for A: Fe1–N1: 1.9704(19), Fe1–Cl1: 2.3888(9), Fe1–O1: 1.9261(19), Fe1–O2: 2.0174(18) and for B: Fe1–N1: 1.960(2), Fe1–Cl1: 2.338(3), Fe1–O1: 2.113(2), Fe1–O2: 1.848(2).

DFT calculations of 2 at the B3LYP/LANL2DZ level of theory^27,28 yield bond lengths that differ by less than 0.05 Å with respect to the X-ray structure, except for the 0.16 Å longer Fe1–Cl1 bond. Calculations using a different basis set (6-311G) also result in an overly elongated Fe1–Cl1 bond. Removing the solvent molecules from the calculation causes even further elongation of this bond (0.38 Å) and removing the Li⁺ counterions results in a large distortion towards a tetrahedral geometry (τ₄ = 0.657). Interestingly, coplanar alkali counterions are also present in the molecular structures of the previously reported compounds and are clearly important in stabilizing the square-planar geometry.^12–14 However, examples of tetrahedral Fe(II) complexes with closely bound Li atoms are known^29,30 and imply that the presence of alkali counterions alone do not impose the square-planar geometry.

SQUID measurements of microcrystalline brown 2 (Fig. 2) reveal a room temperature χ_MT value of 3.16 cm³ K mol⁻¹, which confirms its S = 2 state. The room temperature value is higher than the spin only (g = 2) value of 3.00 cm³ K mol⁻¹ expected for a high-spin complex due to spin–orbit coupling. The χ_MT value steadily decreases with decreasing temperature, reaching 1.25 cm³ K mol⁻¹ at 5 K. A good fit to the susceptibility data in the 300–5 K range can be obtained with |D| = 20.9(4) cm⁻¹, g = 2.05(3), Θ = 0.8 K, and no TIP term using eqn (S1) (see ESI†). The fitting parameters are similar to those reported by Doerrer and coworkers.¹³ The room temperature magnetic susceptibility value is also consistent with the solution value of 3.01 cm³ K mol⁻¹. SQUID measurements performed on recrystallized red 2 reflect the two partitions within the crystal lattice and a reasonable fit was accomplished, see ESI† for more details.

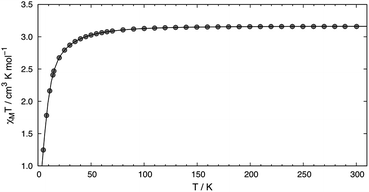Fig. 2 Temperature dependence of χ_MT for 2 measured using an applied field of 0.1 T. The line depicts the fit obtained using |D| = 20.9(4) cm⁻¹, g = 2.05(3), and Θ = 0.8 K.

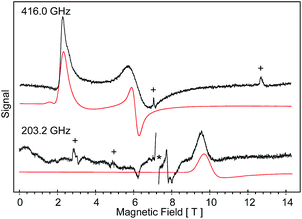
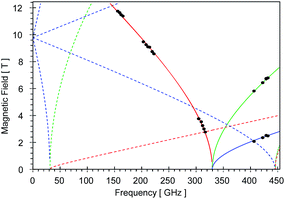
High-field, high-frequency EPR measurements on powder samples establish the magnitude of both the zero-field splitting (ZFS) and the g tensor of the quintet ground state of 2. Fig. 3 exhibits two representative 5 K EPR spectra recorded for 2 at 416.0 (top) and 203.2 GHz (bottom). The entire data set is summarized in Fig. 4 and was analysed in the framework of a standard S = 2 spin-Hamiltonian (see ESI eqn (S3)†). By using g_x = 2.19, g_y = 2.18, g_z = 2.04, D = 17.4 cm⁻¹ and E/D = 0.14 it is possible to not only simulate the individual spectra (Fig. 3), but also reproduce the field and frequency-dependent behaviour of the observed resonances (Fig. 4). In agreement with the results of the crystallographic investigation and of the Mössbauer data analysis the EPR spectra recorded on samples of recrystallized 2 as ground red crystals exhibit two distinct spectral components. While one of the components is essentially identical to that observed for microcrystalline brown 2 the other exhibits a more complicated behaviour, see ESI.†

Fig. 3 High-field EPR spectra recorded at 5 K for 2 brown, at 416.0 (top) and 203.2 GHz (bottom). The solid red traces are simulations obtained for a S = 2 with D = 17.4 cm⁻¹, E/D = 0.14, g_x = 2.19, g_y = 2.18 and g_z = 2.04. The features marked by (+) account for the molecular O₂(g) adsorbed on the surface of the sample containers. The resonance marked by (*) appears at g = 2.0023 and arises from a radical contaminant.

Fig. 4 Black dots mark the field and frequency dependencies of the prominent resonances observed for the low-temperature, high-field EPR spectra of microcrystalline brown 2. The solid lines account for the ground state resonances and the dotted lines account for the excited state resonances. The red, blue and green colors mark the z, y and x molecular orientations, respectively.

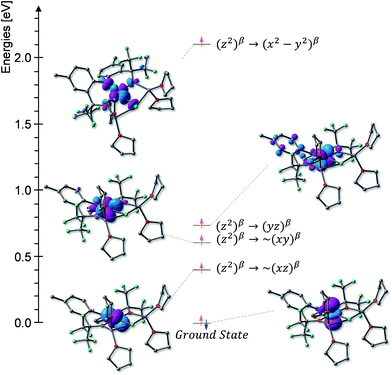
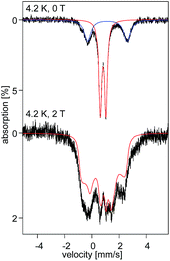
At 4.2 K, the zero-field Mössbauer spectrum of 2 consist of a sharp quadrupole doublet with an isomer shift δ = 0.83(1) mm s⁻¹ and quadrupole splitting ΔE_Q = ±0.45(1) mm s⁻¹ (Fig. 5). While the observed δ is typical of high-spin Fe²⁺ ions, the ΔE_Q is unusually small. Interestingly, this low value is similar to the only other reported data for a square-planar high-spin Fe(II) species.¹⁴ We propose that this unusually small ΔE_Q is a signature of this class of compounds. The DFT-predicted values at the UB3LYP/6-311G level of theory, δ^calc = 0.67 mm s⁻¹ and ΔE^calc_Q = −0.55 mm s⁻¹, are in good agreement with the experimental data. Furthermore, the small quadrupole splitting can be rationalized on the basis of a large ligand contribution to the electric field gradient (EFG) that essentially quenches the large valence contribution expected for a d⁶ electron configuration (see Table S8†). Interestingly, this result is a consequence of fitting a high-spin ferrous ion with a doubly occupied d_z² orbital ground state in a square-planar coordination geometry (Fig. 6).³¹

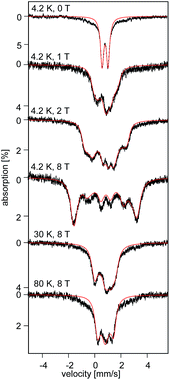Fig. 5 Field and temperature dependent ⁵⁷Fe Mössbauer spectra recorded for 2 brown. The red solid lines are spectral simulations obtained for a S = 2 using eqn (S4).† For these simulations we used the ZFS and g tensors determined from high-field EPR and A_x/g_nβ_n = −17(1) T, A_y/g_nβ_n = −13(1) T, A_z/g_nβ_n = −30(2) T, δ = 0.82 mm s⁻¹, ΔE_Q = −0.45 mm s⁻¹, η = 0.6(2), α_EFG = 0°, β_EFG = 90°, γ = 90°, see ESI.†

Fig. 6 Molecular orbital diagram derived from the TD-DFT calculations.

The uniquely small ΔE_Q offers an opportunity to examine if the square-planar geometry and spin state are retained in solution. Indeed, the zero-field spectrum recorded at 4.2 K for a ⁵⁷Fe enriched toluene solution of 2 exhibits two distinct quadrupole doublets (Fig. 7). More than 70% of the iron exhibits a quadrupole doublet that is essentially identical to that observed for 2 in the solid state. The remaining iron amount can be assigned to a high-spin ferrous species that in 0 T displays a broad quadrupole doublet characterized by δ = 1.1(1) mm s⁻¹, ΔE_Q = 2.9(1) mm s⁻¹, and Γ = 0.6 mm s⁻¹. The second species is tentatively assigned as an Fe(II) five-coordinate complex in which residual THF binds to the Fe center in solution. Support for this assignment comes from the fact that purposely increasing the amount of THF shifts the ratio of the two species. Consequently, this observation suggests that dissolving 2 in toluene does not lead to a loss of the square-planar geometry and that the electronic structure of the iron site is conserved.

Fig. 7 ⁵⁷Fe Mossbauer spectra recorded at 4.2 K in 0 (top) and 2 T (bottom) for a 5.4 nM ⁵⁷Fe enriched solution sample of 2. The solid red lines are simulations obtained using the same parameters as for 2 brown in the solid state.

Analysis of the variable-field, variable-temperature Mössbauer spectra recorded for 2 reveals the presence of an anisotropic ⁵⁷Fe hyperfine coupling tensor A that exhibits two relatively small components. Furthermore, investigation of the high-field, high-temperature data indicate that ΔE_Q < 0 and that the EFG asymmetry parameter η ≈ 0.6 (see ESI†). The A, ZFS, and g tensors are overall consistent and suggest the presence of two large, spin–orbit coupling induced, orbital contributions along their x and y directions.

The field-dependent spectra recorded for recrystallized 2 as red crystals exhibit two distinct spectral components. While one component is identical to 2 prior to recrystallization, the other can be understood only by considering axial ZFS and A tensors (E ≈ 0; A_x ≈ A_y ≠ A_z). Since in zero-field these two components exhibit identical quadrupole doublets they must originate from two distinct conformers of the same chemical species.³² Typically, an axial ZFS tensor entails a symmetric structure and thus we speculate that while the E ≈ 0 component is associated with partition A, the E/D = 0.14 component of 2 is associated with partition B of the crystal structure. We propose the two partitions arise from variable solvent (THF/Et₂O) substitution at each Li⁺ site within the lattice.

Conclusions

This work extends the set of known Fe(II) square-planar high-spin compounds beyond the limited FeO₄ motif, and presents the first high-field EPR and variable field/temperature Mössbauer characterization of this class of compounds. Moreover, the ⁵⁷Fe enriched solution phase Mössbauer confirms for the first time that the square-planar geometry is retained in solution. The results also indicate ligand 1 satisfies the prerequisites for stabilizing a square-planar high-spin Fe(II): (1) it provides three negatively charged donors, (2) it preferentially binds three meridional positions, (3) the amido and alkoxides are weak-field ligands that provide π-donation, and (4) the heavily fluorinated alkoxides are relatively weak σ-donors. We are currently analyzing approaches to modify the ligand to optimize the energy difference between the S = 2 and S = 1 states to prepare and isolate molecular spin crossover complexes.

Acknowledgements

ASV acknowledges UF and the NSF (CHE-1265993), for providing funding for this research. GC acknowledges the NSF (DMR-1213030). KAA acknowledges the NSF (CHE-0821346) for the purchase of X-ray equipment. Computational resources were provided by the University of Florida High-Performance Computing Center. NVD is an HHMI International Student Research fellow. Part of this work was performed at the National High Magnetic Field Laboratory (NHFML) which is supported by the NSF (DMR-1157490) and the State of Florida. SAS is an NHFML Jack E. Crow postdoctoral fellow.

Notes and references

1. F. A. Cotton, Advanced inorganic chemistry, Wiley, New York, 6th edn, 1999.
2. E. K. Byrne, D. S. Richeson and K. H. Theopold, J. Chem. Soc., Chem. Commun., 1986, 1491–1492.
3. J. Cirera, E. Ruiz and S. Alvarez, Inorg. Chem., 2008, 47, 2871–2889.
4. C. Bolm, J. Legros, J. Le Paih and L. Zani, Chem. Rev., 2004, 104, 6217–6254.
5. C. L. Sun, B. J. Li and Z. J. Shi, Chem. Rev., 2011, 111, 1293–1314.
6. W. R. Scheidt and C. A. Reed, Chem. Rev., 1981, 81, 543–555.
7. R. M. Hazen and C. W. Burnham, Am. Mineral., 1974, 59, 1166–1176.
8. P. L. Holland, Nat. Chem., 2011, 3, 507–508.
9. S. De Angelis, E. Solari, C. Floriani, A. Chiesi-Villa and C. Rizzoli, J. Am. Chem. Soc., 1994, 116, 5691–5701.
10. V. Esposito, E. Solari, C. Floriani, N. Re, C. Rizzoli and A. Chiesi-Villa, Inorg. Chem., 2000, 39, 2604–2613.
11. C. A. Nijhuis, E. Jellema, T. J. J. Sciarone, A. Meetsma, P. H. M. Budzelaar and B. Hessen, Eur. J. Inorg. Chem., 2005, 2005, 2089–2099.
12. X. Wurzenberger, H. Piotrowski and P. Klüfers, Angew. Chem., Int. Ed., 2011, 50, 4974–4978.
13. S. A. Cantalupo, S. R. Fiedler, M. P. Shores, A. L. Rheingold and L. H. Doerrer, Angew. Chem., Int. Ed., 2012, 51, 1000–1005.
14. D. Pinkert, S. Demeshko, F. Schax, B. Braun, F. Meyer and C. Limberg, Angew. Chem., Int. Ed., 2013, 52, 5155–5158.
15. S. C. Bart, K. Chłopek, E. Bill, M. W. Bouwkamp, E. Lobkovsky, F. Neese, K. Wieghardt and P. J. Chirik, J. Am. Chem. Soc., 2006, 128, 13901–13912.
16. M. W. Bouwkamp, S. C. Bart, E. J. Hawrelak, R. J. Trovitch, E. Lobkovsky and P. J. Chirik, Chem. Commun., 2005, 3406–3408.
17. M. E. O'Reilly and A. S. Veige, Chem. Soc. Rev., 2014, 43, 6325–6369.
18. S. VenkatRamani, M. E. Pascualini, I. Ghiviriga, K. A. Abboud and A. S. Veige, Polyhedron, 2013, 64, 377–387.
19. M. E. O'Reilly, I. Ghiviriga, K. A. Abboud and A. S. Veige, J. Am. Chem. Soc., 2012, 134, 11185–11195.
20. M. E. O'Reilly, I. Ghiviriga, K. A. Abboud and A. S. Veige, Dalton Trans., 2013, 42, 3326–3336.
21. R. J. Kern, J. Inorg. Nucl. Chem., 1962, 24, 1105.
22. L. Yang, D. R. Powell and R. P. Houser, Dalton Trans., 2007, 955–964.
23. E. J. Hawrelak, W. H. Bernskoetter, E. Lobkovsky, G. T. Yee, E. Bill and P. J. Chirik, Inorg. Chem., 2005, 44, 3103–3111.
24. A. B. Scharf and T. A. Betley, Inorg. Chem., 2011, 50, 6837–6845.
25. E. R. King, E. T. Hennessy and T. A. Betley, J. Am. Chem. Soc., 2011, 133, 4917–4923.
26. S. C. Bart, E. J. Hawrelak, A. K. Schmisseur, E. Lobkovsky and P. J. Chirik, Organometallics, 2004, 23, 237–246.
27. A. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
28. C. Lee, W. Yang and R. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
29. S. R. Foley, G. P. A. Yap and D. S. Richeson, Inorg. Chem., 2002, 41, 4149–1457.
30. G. T. Sazama and T. A. Betley, Inorg. Chem., 2010, 49, 2512–2524.
31. P. Gütlich, E. Bill and A. Trautwein, Mössbauer spectroscopy and transition metal chemistry: fundamentals and application, Springer, Berlin, Heidelberg, 2011.
32. S. A. Stoian, J. M. Smith, P. L. Holland, E. Münck and E. L. Bominaar, Inorg. Chem., 2008, 47, 8687–8695.

---

Footnote

† Electronic supplementary information (ESI) available: Detailed experimental conditions, elemental analysis, ¹H-NMR spectroscopy, magnetic susceptibility data and fitting, Mössbauer spectroscopy, high-field EPR spectroscopy of 2, and DFT calculations. CCDC 1006581. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c4sc02634a

---