Entropy driven chain effects on ligation chemistry

Abstract

We report the investigation of fundamental entropic chain effects that enable the tuning of modular ligation chemistry – for example dynamic Diels–Alder (DA) reactions in materials applications – not only classically via the chemistry of the applied reaction sites, but also via the physical and steric properties of the molecules that are being joined. Having a substantial impact on the reaction equilibrium of the reversible ligation chemistry, these effects are important when transferring reactions from small molecule studies to larger or other entropically very dissimilar systems. The effects on the DA equilibrium and thus the temperature dependent degree of debonding (%_debond) of different cyclopentadienyl (di-)functional poly(meth-)acrylate backbones (poly(methyl methacrylate), poly(iso-butyl methacrylate), poly(tert-butyl methacrylate), poly(iso-butyl acrylate), poly(n-butyl acrylate), poly(tert-butyl acrylate), poly(methyl acrylate) and poly(isobornyl acrylate)), linked via a difunctional cyanodithioester (CDTE) were examined via high temperature (HT) NMR spectroscopy as well as temperature dependent (TD) SEC measurements. A significant impact of not only chain mass and length with a difference in the degree of debonding of up to 30% for different lengths of macromonomers of the same polymer type but – remarkably – as well the chain stiffness with a difference in bonding degrees of nearly 20% for isomeric poly(butyl acrylates) is found. The results were predicted, reproduced and interpreted via quantum chemical calculations, leading to a better understanding of the underlying entropic principles.

---

Introduction

The Diels–Alder (DA) cycloaddition is long known and – especially after the introduction of the click chemistry concept by Sharpless and colleagues in 2001 – widely used due to its synthetic benefits such as readily accessible starting materials, facile handling, the lack of side products and in some cases quantitative conversion.^1,2 Consequently, DA reactions are employed in great variety in applications ranging from molecular conjugation, total synthesis, block copolymer formation, dendrimers to thermoreversible ligation and surface modification, as well as surface patterning to name only a few.^3–13 To enable such a wide field of applications, several hetero Diels–Alder (HDA) pairings such as cyclopentadiene (Cp) with different dithioester, thioaldehyde or nitrosocarbonyl functionalities have been explored to allow catalyst free reactions at ambient temperature and mild retro Diels–Alder (rDA) adduct cleavage temperatures.^4,14–16 Based on their thermoreversible character, DA reactions have gained importance in the field of self-healing materials.^17–22 These smart materials allow a change from passive to tailor-made responsive materials upon a given stimulus via extrinsic healing mechanisms as, for instance, the release of a healing agent or intrinsic ones with the aid of integrated reversible bonds to prevent material failure.^19,23 Extrinsically self-healing materials are most commonly generated via the incorporation of fibers or microcapsules filled with healing agents, for example cross-linkable monomers, catalysts or multilinkers in concrete or epoxy resins, which are released upon material damage and allow the formation of a network and prevent crack propagation while maintaining the material properties.^20,24,25 While materials with extrinsic self-healing properties can only undergo a finite number of healing cycles due to the limited amount of incorporated healing agent, intrinsic ones – in theory – enable unlimited healing as the broken covalent bonds can be reformed. To achieve intrinsic self-healing, reversible bonds such as supramolecular interactions, photo-induced metathesis or thermoreversible reactions have to be integrated in the material chemistry itself. As covalent bonds give rise to higher material strengths than non-covalent interactions, and as the temperatures needed for the reversal of the DA reactions lie in an easily accessible, yet sufficiently high range for many materials applications, more and more self-healing materials with variable DA chemistry are under investigation.¹⁹

Classically, the DA equilibrium and the associated opening or closing temperature of its adducts is tuned via the chemistry of the employed diene and dienophile functional groups and therefore their reaction enthalpy. Different electron withdrawing or donating substituents generate favorable HOMO–LUMO interactions; the application of advantageous geometries such as cyclic and thus pre-oriented dienes or the use of Lewis acids as catalysts in HDA reactions allow the adjustment of these parameters and thus also the modification of the material properties.^{4,11,14,17,26–29} In 2013, Barner-Kowollik and colleagues observed, in accordance with Gibbs equation (ΔG = ΔH − TΔS), that not only chemical factors are able to significantly affect these characteristics, but also entropic ones, thereby providing a likely explanation for the differences in published debonding temperatures of otherwise identical DA systems.^17,30,31 It could be predicted in theory and shown in multiple experiments that the chain length and mass of the moieties which are linked via DA chemistry are able to drastically influence the reaction equilibrium between open reaction sites and closed adducts.³² This behavior arises from the different mass and length specific contributions of translational and rotational entropy, which are released during chain scission events and hence the more or less favorable release of the incorporated building blocks. Such effects can be purposely used to further alter the properties and processing parameters of intrinsically self-healing materials such as cross-linked DA networks via their mesh size. Moreover, entropic effects also have to be considered when conjugation techniques are transferred from small model systems to polymer chains with considerably different entropic characteristics, as the previously expected behavior may be severely altered by the difference in entropy of the connected species.

Given the crucial role that entropy plays in determining the temperature dependent degree of debonding, an obvious question is to what extent do physical or chemical factors other than molecular mass and length including chain stiffness in general, or side chain substituents in particular, influence the equilibrium position through their effects on rotational, translational and vibrational entropy. To address this question, a set of experiments including temperature dependent characterization with ten polymeric building blocks based on eight (meth-)acrylate monomers with sterically different side-chain groups was designed.³³ Thereby, not only diverse masses (Scheme 1(a)), but also connected units of varying stiffness can be studied, as the different degrees of steric hindrance depend on the side chain substituents and lead to differing chain mobility and thus stiffness values (Scheme 1(b)).³⁴ Evidencing the effects on polymers featuring thermolabile connection units should be understood in a model sense, enabling the alteration of the molecular characteristics under investigation in a facile way. Clearly, the principle operation of entropic effects is as well valid for all other reversible connection points including supramolecular ones and not limited to synthetic polymers. A,A′-Diblock polymers connected by DA chemistry using building blocks of the same length, yet differing in either chain stiffness or mass, were synthesized and their temperature dependent debonding behavior was characterized via high temperature nuclear magnetic resonance spectroscopy (HT NMR) (Scheme 1(i)). To widen the view and systematically clarify the observed effects, DA polymers consisting of isomeric difunctional building blocks of again the same length and also mass with different chain stiffness were examined and characterized via HT NMR and temperature dependent size exclusion chromatography (TD SEC) (Scheme 1(ii)). Finally, the chain length dependent specificity of the newly observed chain stiffness effect was studied via the evaluation of DA polymers based on two building block pairs of the same basic chain segment mobility, but different lengths and thus also masses (Scheme 1(iii)). The experimental observations are compared with the results of quantum chemical calculations to explain the source of the effects via their underlying entropic principles.

Scheme 1 The examined side chain substituents with a comparison of (a) their relative masses and (b) the assumed impact of their steric hindrance on chain movement as well as approaches to investigate the chain mass, length and stiffness effect of polymer building blocks on their ligation chemistry via HT NMR and TD SEC characterization: (i) A,A′-diblockpolymers consisting of building blocks of the same length yet different mass or stiffness, (ii) DA polymers based on building blocks of the same length and mass, but different stiffness and (iii) DA polymers with different building block sizes and chain stiffness.

Experimental section

Materials

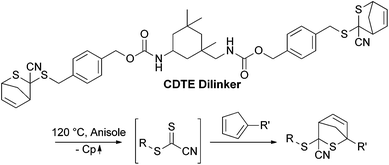
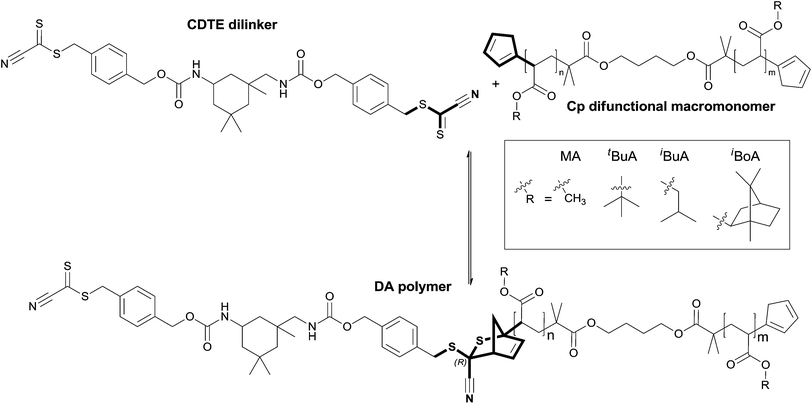
Stabilized methyl acrylate, iso-butyl acrylate (Alfa Aesar, 99%), isobornyl acrylate (ABCR, 85%), tert-butyl methacrylate (Sigma-Aldrich, 98%), iso-butyl methacrylate, methyl methacrylate (ABCR, 99%), tert-butyl acrylate and butyl acrylate (Sigma-Aldrich, 99%) were deinhibited via a short column of basic aluminum oxide. Copper(I) iodide (Sigma-Aldrich, ≥98%), tin(II)-2-ethylhexanoate (Sigma-Aldrich, 95%), tris[2-(dimethylamino)ethyl]amine (Sigma-Aldrich, 97%), butylene-bis(2-bromoisobutyrate) (provided by Evonik), ethyl-α-bromoisobutyrate (Sigma Aldrich, 98%), anisole (Acros, 99%), methanol (VWR, p.a.), triphenylphosphine and sodium iodide (ABCR, 99%) were used as received. Tetrahydrofurane (Sigma-Aldrich, anhydrous, ≥99.9%) and nickelocene (ABCR, 99%) were used as received and handled in a glovebox.

Synthesis of a cyanodithioester dilinker

The synthesis was conducted according to literature.¹⁴ The cyanodithioester (CDTE) dilinker (Scheme 3) was obtained as a yellow solid. Overall yield: 5%. ¹H NMR (400 MHz, CDCl₃) δ [ppm]: 7.41–7.29 (m, 8H, ArH), 7.22–7.20 (m, 1H, NH), 6.65–6.63 (dd, J = 5.4, 2.8 Hz, 1H, C=CH), 6.45–6.43 (dd, J = 5.1, 2.8 Hz, 1H, C=CH), 6.10–6.08 (dd, 5.2, 3.3 Hz, 1H, C=CH), 5.80–5.78 (dd, 5.2, 3.3 Hz, 1H, C=CH), 5.12–5.04 (m, 4H, NCOOCH₂), 4.82 (s, 1H, CHSC), 4.54 (s, 1H, CHSC), 4.30–4.071 (m, 4H, SCH₂Ar), 4.01–3.98 (m, 2H, CHCCN), 3.81 (br, 1H, OCONHCH), 2.97–2.87 (br, 2H, OCONHCH₂), 2.15–1.82 (m, 4H, CHCH₂CH), 1.75–1.69 (br, 2H, CH₂), 1.23–0.80 (m, 13H, CH₃, CH₂).

Scheme 2 Model DA reaction studied using quantum chemistry. Fragments in bold correspond to the core layer (reaction center) in the ONIOM-like approximation.

Scheme 3 HDA linkage of Cp functional polymers via a CDTE dilinker.

Synthesis of bromo (di-)functional polymers

Activators regenerated by electron transfer atom transfer radical polymerization (ARGET ATRP) protocols were adapted from the literature.³⁵ In a typical procedure, copper(I) bromide (13.6 mg, 0.09 mmol), tris[2-(dimethylamino)ethyl]amine (0.095 mmol, 278 μL, 0.34 mmol mL⁻¹ in anisole) and isobornyl acrylate (20 mL, 94.7 mmol) were dissolved in anisole (5 mL) in a flame dried Schlenk flask and degassed via nitrogen purging for 45 minutes. In two additional Schlenk flasks, butylene-bis(2-bromoisobutyrate) (183.7 mg, 0.95 mmol) and tin(II)-2-ethylhexanoate (153 μL, 0.47 mmol) were dissolved in anisole (7.5 mL each) and degassed. Subsequently, the solutions were transferred into the first Schlenk flask via a cannula and stirred at 60 °C for 35 minutes. The polymerization was stopped in an ice bath and quenched with air at low conversion values (∼25%) in order to control for unwanted chain termination before filtration over neutral aluminum oxide and precipitation in cold methanol. The white polymer powder was dried in vacuo and characterized via SEC and ¹H NMR, evidencing a high bromo end group fidelity of consistently between 98–99% for each synthesized polymer system via the comparison of initiator to end group signals (see Table 1 for the full list of synthesized polymers, the ESI for the characterization data in Fig. S1–S8† and the synthetic details of bromo monofunctional poly(methacrylates) in Table S1† as well as the ones of bromo difunctional polyacrylates in Table S2†).

Table 1 List of the synthesized bromo and Cp (di-)functional polymers, their number average molecular weight M_n, dispersity Đ and average number of repeating units n

Polymer	M n [g mol^−1]	Đ	n
BrPMMA	5600	1.19	52
BrP^iBuMA	7200	1.23	48
BrP^tBuMA	6800	1.19	45
Br2P^nBuA	6600	1.07	49
Br2P^iBuA	6800	1.07	50
Br2P^tBuA	6600	1.08	49
Br2PMAlarge	4600	1.07	49
Br2P^iBoAlarge	9800	1.09	45
Br2PMAsmall	1200	1.04	9
Br2P^iBoAsmall	2300	1.05	9
CpPMMA	5600	1.16	52
CpP^iBuMA	7600	1.21	51
CpP^tBuMA	7200	1.16	48
Cp2P^nBuA	6700	1.08	49
Cp2P^iBuA	7000	1.07	52
Cp2P^tBuA	6700	1.08	49
Cp2PMAlarge	4800	1.09	52
Cp2P^iBoAlarge	10 200	1.12	47
Cp2PMAsmall	1300	1.06	11
Cp2P^iBoAsmall	2900	1.13	12

---

Synthesis of Cp (di-)functional polymers

The synthetic procedure was adapted from the literature.³⁶ In a typical procedure, bromo difunctional poly(isobornyl acrylate) (3.0 g, 0.30 mmol), sodium iodide (545 mg, 3.63 mmol) and triphenyl phosphine (318 mg, 1.21 mmol) were dissolved in anhydrous THF (6.0 mL). Nickelocene (229 mg, 1.21 mmol) was added and the reaction mixture was stirred under argon at ambient temperature for 5 hours. The reaction was subsequently purged with air, filtered over basic aluminum oxide and the polymer was repeatedly precipitated in cold methanol. The off-white polymer was characterized via SEC and ¹H NMR to ensure quantitative conversion (see Table 1 for the full list of synthesized polymers, the ESI for the characterization data in Fig. S1–S8† and the synthetic details of the other Cp functionalized polymers in Table S3†).

Synthesis of Diels–Alder polymers/adducts

In a typical procedure, cyclopentadiene difunctional poly(isobornyl acrylate) (50.0 mg, 0.005 mmol) and close to equimolar amounts of CDTE dilinker (around 4.0 mg, 0.005 mmol) were dissolved in anisole (200 μL) and heated to 120 °C for 10 minutes. The reaction was then slowly cooled to ambient temperature within 1 hour to achieve the DA step growth polymer with the desired amount of repeating units. The product was characterized via SEC, temperature dependent SEC and temperature dependent ¹H NMR (see ESI for the characterization data in Fig. S1–S8† and the synthetic details for all DA polymers in Table S4†).

Characterization techniques

Offline SEC was carried out on a Polymer Laboratories/Varian PL-GPC 50 Plus system, comprising an autosampler, a Polymer Laboratories 5.0 μm bead-size guard column (50 × 7.5 mm²), followed by three PL columns and a differential refractive index detector. Measurements were performed in THF at 35 °C with a flow rate of 1 ml min⁻¹. The SEC system was calibrated using linear poly(methyl methacrylate) standards ranging from 800 g mol⁻¹ to 1.6 × 10⁶ g mol⁻¹. For analysis, appropriate Mark–Houwink–Kuhn–Sakurada parameters were employed (Table S5†) and their integrity was ensured via the comparison of initiator vs. an isolated backbone ¹H NMR signal for each respective polymer.^37–43

¹H NMR spectra were measured on a Bruker Avance III 400 spectrometer with a CryoProbe at 400 MHz in CDCl₃ with 1024 scans for standard measurements and toluene-d₈ in a pressure tube for measurements at elevated temperatures. A sample concentration of 26.7 mg mL⁻¹ was employed. Each DA polymer sample underwent the HT NMR measurements at all the desired temperatures from lower to higher ones, consecutively. After the stabilization of an adjusted temperature, the establishment of the equilibrium was ensured by repeated additional measurements with 16 scans before and after the actual measurement with 128 scans until no difference could be determined in the measured data anymore. The recyclability of the samples was checked after evaporation of the solvent and re-solvation. To compensate the varying shift of the signals at different measurement temperatures, the signals were adjusted to a polymer backbone signal. A baseline correction was conducted. The integration limits for the functional group signals were determined via the comparison with Cp functionalized polymers and DA adducts (Fig. S9†).^14,21 The temperature dependent ratio of free Cp chain end groups to DA adducts and thus the degree of debonding (%_debond) was calculated as depicted in Fig. 1.

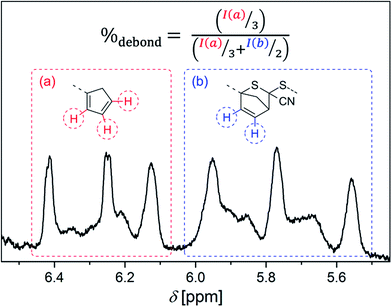Fig. 1 Calculation of the temperature dependent degree of debonding %_debondvia the ¹H NMR signal ratios of (a) free Cp chain end groups and (b) closed HDA adducts.

A typical measurement and data processing error of on average ±2% was determined via the two fold measurement of DA material from the same batch on different days.

Temperature dependent SEC was performed on a PL-GPC 220 high temperature chromatograph (Agilent Technologies), featuring a temperature controlled autosampler, column oven and dRI as well as viscosity detection. Separation was achieved through one PL ResiPore column (3 μm bead-size) and a mixture of 60% 1,2,4-tricholorobenzene (TCB) in N,N-Dimethylformamide (DMF) was employed as a solvent at a flow rate of 1 mL min⁻¹. Details regarding the evaluation of the chromatograms can be found in the ESI.†

Small-angle neutron scattering (SANS) measurements were carried out at the instrument D11 of the ILL in Grenoble with a wavelength of 6 Å and at two sample–detector distances of 8 m and 1.2 m, covering a broad q-range from 0.0083–0.0824 Å⁻¹ (at 8 m) and 0.06–0.514 Å⁻¹ (at 1.2 m) with a good overlap of the two q-regimes. The samples were measured at concentrations of approximately 1, 2, 3, 4 and 5 wt%. The solvent toluene-d₈ was additionally measured, normalized and then subtracted from the solution data. Data analysis was performed according to the procedure proposed by Casassa and Holtzer (see ESI† for further information).^44,45

Computational methods

Standard ab initio and density functional theory calculations were performed using Gaussian 09 software package.⁴⁶ The modeling was performed for a Diels–Alder reaction between the CDTE dilinker and Cp difunctional macromonomers with varying numbers of MA, ^tBuA, ⁱBuA and ⁱBoA building blocks. Calculations were based on the lowest energy isomers and conformers of the reactants and products (shown in Scheme 2), as identified by a screening carried out for the shortest difunctional macromonomers (n = m = 0 and n = m = 1). The conformational searches in the gas phase were performed using an Energy-Directed Tree Search algorithm at the M06-2X/6-31G(d) level of theory.^47,48 For the longer species (n = m = 2) the starting geometries were constructed by incorporating the next monomer unit in the lowest energy conformer of n = m = 1 and performing conformational searching only at the reaction center. For all gas-phase conformers within the lowest 10 kJ mol⁻¹, their geometries were subsequently relaxed and energies re-calculated in the presence of a solvent field (toluene), modeled using the SMD/M06-2X/6-31G(d) method. In this way the lowest-energy solution-phase conformers were obtained. Additionally, the extended chain conformers were obtained by fully unfolding the chains while keeping the conformation of the reaction center intact. Geometries of all these species were then refined at the M06-2X/6-31G(d) level of theory.

Accurate energies were calculated using two-layer ONIOM-like approximation. The electronic energy of the reaction at the core layer was calculated using high-level composite ab initio G3(MP2)-RAD method, while M06-2X/6-31G(d) method was applied to the full system.⁴⁹ Gas-phase entropic and thermal corrections were evaluated from the M06-2X/6-31G(d) frequencies, scaled by the recommended scaling factors.⁵⁰ The Gibbs free energies of solvation in toluene were calculated using the SMD/M06-2X/6-31G(d) method.⁵¹

Results and discussion

Theoretical studies

To understand the entropic contributions to debonding, we conducted a quantum chemical study of oligomeric models of acrylate DA polymers. The selection of the polymers was carried out according to the steric properties of their side chain substituents, as discussed in the experimental studies section. The enthalpic and entropic contributions to the reaction Gibbs free energy were calculated for the Diels–Alder reactions between the CDTE dilinker and Cp difunctional macromonomers of MA, ^tBuA, ⁱBuA and ⁱBoA with chain lengths up to n = m = 2 (Scheme 2).

As in our previous study, we treated these species as being in the solution phase and analyzed the entropic contributions to bonding in terms of the gas-phase vibrational, translational and rotational entropy and the remaining solvation energy contributions.³² This treatment, accurate for small molecules in solution, over-simplifies the complexities of polymer–polymer reactions but has previously been shown to be qualitatively useful in understanding the characteristic chemical trends.³² In carrying out the calculations, we considered the reactants and products in their minimum energy conformations and also in modified conformations, where the conformation of the reaction center itself was still fully optimized but the remaining polymer chains were extended into (optimized) linear conformations (Fig. 2). The extended chain structures were considered because the minimum energy conformers, while providing the best representation of the oligomeric species studied computationally, are unlikely to be realistic representations of the longer chain polymeric species, where steric hindrance would prevent such globular structures from forming.

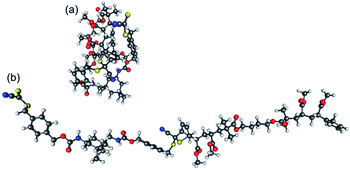Fig. 2 Optimized geometries of the DA adducts of CDTE and Cp₂PMA (with n = m = 2) corresponding to (a) the lowest energy conformation and (b) the extended chain conformation.

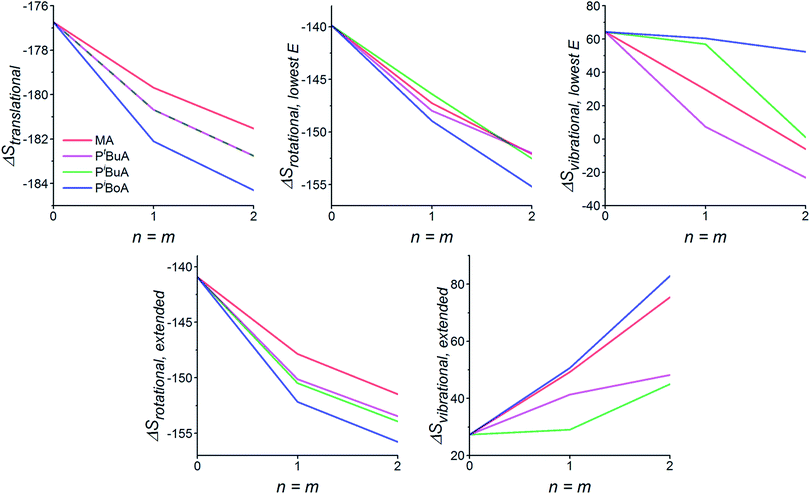
The calculated reaction entropy contributions for the various Diels–Alder reactions for both sets of conformers as a function of chain length are provided in Fig. 3, while the overall predicted %_debondvs. temperature graphs are provided in Fig. 4. Considering first Fig. 3, we note that the translational entropy, being only dependent on mass, is independent of the conformer studied. Consistent with our previous study, ΔS_trans becomes more negative (and hence bonding becomes less favored and debonding temperatures are lowered accordingly) as the side chain mass is increased (MA < ^tBuA, ⁱBuA < ⁱBoA) and as the chain length of the linkers is increased.³² The rotational entropy is dependent on both the total mass and its distribution (i.e. geometry) of the reaction participants, and hence, while a systematic trend is obtained for the linear (extended chain) conformers, results for lowest energy conformers are less coherent. For the extended conformers, the trends reinforce those for the translational entropy (i.e. MA < ^tBuA, ⁱBuA < ⁱBoA), with the heavier side chains contributing to lower debonding temperatures. For both sets of conformers, the chain length effects on ΔS_rot also reinforce those on ΔS_trans, with increasing chain length leading to lower debonding temperatures, again consistent with our earlier study.³² Interestingly, the vibrational entropy contribution, which corresponds most closely to the phenomenological concept of ‘chain stiffness’, does not appear to follow any clearly determined trends and is qualitatively different between the two conformer scenarios, as well as between the different side chain substituents. Such a complicated picture is caused by the interplay between the number and intensities of vibrational modes, corresponding to both the newly forming bonds in the DA reactions and to the intramolecular bonding modes (e.g. H-bonds), and is thus highly dependent on the conformations of the reaction participants. However, one striking observation is that for both scenarios – but especially the lowest energy conformations – ⁱBoA has the highest ΔS_vib. This counters to some extent the effect of its higher mass and bulk on ΔS_trans and ΔS_rot, both of which contribute to a greater extent of debonding compared with the other side chains.

Fig. 3 Calculated changes in the entropy (ΔS in J mol⁻¹ K⁻¹) of model DA reactions for different n, m (chain lengths) of various acrylate macromonomers in their lowest energy or extended chain conformation. In these figures, the more negative ΔS, the lower the Gibbs free energy of bonding, or the greater the extent of debonding, at a given temperature.

Fig. 4 Degree of debonding (determined from the calculated reaction energies for n = m = 2 chain lengths) vs. temperature for (a) lowest energy and (b) extended chain conformers of P^tBuA (★), PⁱBuA (▶), PMA (■) or PⁱBoA (●).

When the different entropic contributors, along with the bonding enthalpy and solvation energy, are combined to predict the effective %_debond as a function of temperature (Fig. 4), the trends are again dependent on the conformations used. In the case of the lowest energy conformations the bulkiest side chain substituent (ⁱBoA) is characterized with the highest debonding temperature. In contrast, for the extended chains, the debonding temperature decreases systematically with the bulk and mass of the side chain substituent, with ⁱBoA now having the lowest debonding temperature. As we will show below, this dramatic trend reversal is mirrored in the differing experimental results for short (10 monomer units) and longer (50 monomer units) chains. Whilst the chains studied computationally are exceptionally short (n = m = 2 units) it would appear that the lowest energy (globular) conformers provide a reasonable model for the behavior of the shorter chains, while the extended conformers provide more realistic models for the longer ones. More generally, these calculations suggest that – in addition to the mass and chain length effects demonstrated previously³² – polymer stiffness is likely to shape the polymer debonding behavior.

Experimental studies

The realization of building blocks with well-defined lengths and masses that are connected via DA chemistry for the examination of entropic chain mass and length effects on the ligation chemistry can be achieved via the application of living controlled polymerization methods or the attachment of different substituents to a core molecule.³² To also enable a choice of differently stiff polymer backbones, diverse methods were considered. As parameters such as persistence lengths, characteristic ratios or Mark–Houwink–Kuhn–Sakurada parameters are highly dependent on the given conditions and challenging in their determination – especially for short polymer chains – a more qualitative but universal approach was employed for a first selection of polymers.^52–55 The steric hindrance of the side chains of polymers, along with the backbone composition and electrostatic interactions, correlate with the polymer stiffness, as the polymer flexibility depends on the energy barriers between the different conformational states.⁵⁶ An alternative polymer characteristic, highly depending on the chain mobility and thus length and steric demand of the side chains, is the glass transition temperature T_g. Larger side chain end group volumes lead to decreasing chain mobility and thus higher T_g values, whereas an increase in free side chain length leads to facilitated chain movement and thereby to lower T_g values due to internal plasticizing effects.^34,57 Of course, T_g values are characteristics for polymer melts and cannot be transferred directly to behavior in solution where interactions between polymer and solvent are essential.⁵⁸ In addition, the chain length dependence of T_g is neglected, as only the relative differences of chains with the same amount of repeating units are of interest in the current study.⁵⁹ However, if equal polymer backbones of equal length with different homonuclear side chain substituents are investigated, their T_g values should correlate approximately with chain stiffness. Therefore, diverse polyacrylates and, in addition, some poly(methacrylates) with significantly differing T_g values were considered in the current study, as collated in Table 2.

Table 2 The different poly(meth-)acrylates investigated in the current study and the corresponding literature values for their glass transition temperatures T_g as well as measured persistence lengths (l_p) for the poly(butyl acrylates) in toluene-d₈

Polymer	T g [°C]	Ref.	l p [nm]
poly(methyl methacrylate)	105	60 and 61	—
poly(iso-butyl methacrylate)	48	62	—
poly(tert-butyl methacrylate)	118	63 and 64	—
poly(n-butyl acrylate)	−54	61	2.0
poly(iso-butyl acrylate)	−24	65	1.8
poly(tert-butyl acrylate)	43	66	2.3
poly(methyl acrylate)	8	61 and 66	—
poly(isobornyl acrylate)	95	66	—

---

To confirm the assumption of a correlation between T_g and polymer stiffness and to include solvent effects, the persistence lengths (l_p) of the three important isomeric poly(butyl acrylates) were determined via SANS measurements in the solvent that was applied for the HT NMR experiments and in the computational calculations. It can be seen in Table 2 that the solvent effects should not be underestimated, as poly(n-butyl acrylate) has a higher persistence length than its iso-butyl derivative. Still, a sufficiently large difference between the T_g values of comparable polymers can serve as a guide for their relative chain stiffness.

The diversely substituted poly(meth-)acrylates were chosen to afford polymeric building blocks varying in stiffness and mass, which can be linked to form (A,A′-) diblock or DA step growth polymers via DA chemistry. The resulting library of polymeric materials was used to study the previously reported chain mass and length effect as well as the proposed chain stiffness effect. As increasing chain mass and length could be shown to lead to substantially decreased debonding temperatures of DA adducts due to the higher amounts of released entropy during the scission of heavier and longer building blocks, different isomeric butyl (meth-)acrylates were also included in the selection to control for the entropic chain mass effect and allow an isolated investigation of a hypothetical chain stiffness effect.^32,34

Three experimental approaches were adopted to investigate the different types of entropic effects on the ligation chemistry: (i) (A,A′-) block copolymers based on building blocks of the same length, yet differing in mass or stiffness, (ii) DA polymers with building blocks of the same length and mass, but differing in stiffness and (iii) DA polymers with basic units of different chain lengths, masses and stiffness with subsequent temperature dependent characterization of their DA equilibrium (Scheme 1). Below, the three approaches and the obtained results are discussed systematically.

(A,A′-) Diblock approach with equal building block sizes

As discussed in the Introduction, we will first investigate diblock polymers of identical chain length. To compare the temperature dependent degree of debonding of polymer chains which are linked via DA chemistry and are bearing different side chain groups – which also means that the respective chains have different T_g and chain mobilities – Cp end group monofunctional poly(methyl methacrylate) (PMMA), poly(iso-butyl methacrylate) (PⁱBuMA) and poly(tert-butyl methacrylate) (P^tBuMA) building blocks with approximately 50 repeating units were synthesized. To enable the DA linkage reaction, the Cp protected CDTE dilinker was deprotected at 120 °C (Scheme 3).

The dissolution of all reaction compounds in anisole enables the evaporation of the released Cp and a dynamic protection of the exposed CDTE group with the Cp polymer end groups to prevent unwanted side reactions. During the following cooling phase, the actual HDA reaction takes place. While not being stereoselective, the more important feature for our application is its catalyst-free character. The three poly(methacrylate) blocks were each coupled to afford diblock polymers in a HDA reaction via the CDTE dilinker (see Fig. 5 for an exemplary SEC data set, Fig. S1† for the size dependent chromatograms and thus the size distributions of the other employed polymers measured via offline SEC).

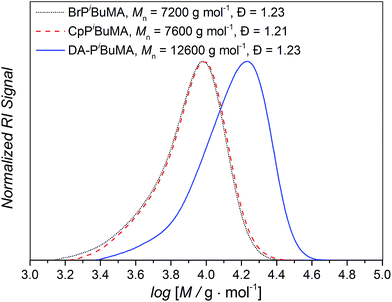Fig. 5 Exemplary SEC chromatograms of the bromo precursor polymer (⋯), Cp functional building block (----) and Diels–Alder diblock polymer (—) for 50 iso-butyl methacrylate repeating units per building block (see Fig. S1† for the chromatograms of the other employed polymers).

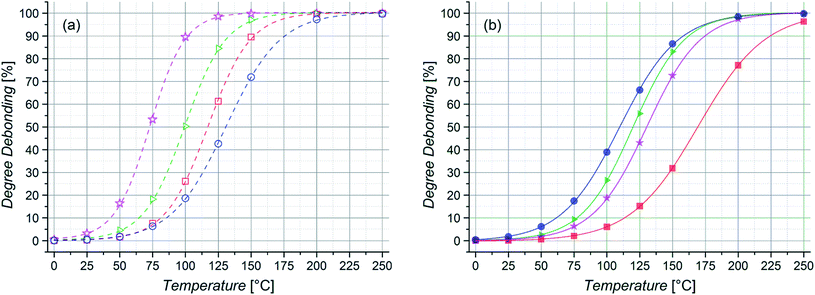
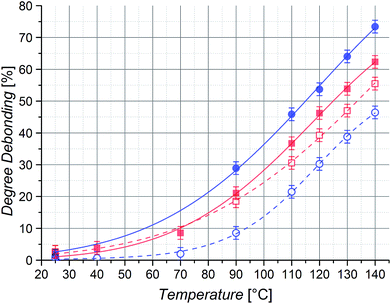
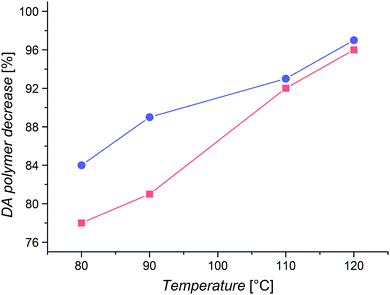
Even though there will always be a small population of unreactive species due to irreversible chain termination events during the synthesis of the utilized building blocks, the careful implementation of a living controlled polymerization technique and the quantitative subsequent functionalization in combination with a thorough characterization as well as the readily proceeding ligation chemistry allows for the conclusion that only an insignificant concentration of non-functional reactants is present. Thus, no substantial effect on the investigated reaction equilibria while guaranteeing the comparability of different samples is given. The application of monofunctional methacrylates should enable experiments without unwanted Cp–Cp self-dimerization due to their low chain mobility. Further, dimerized chains do not impair the measurements due to their lost functionality for further DA reactions and insignificant degree of debonding at the temperatures under investigation. In addition, the macromonomers can easily be precipitated and thus permit facile handling. As – in contrast to our previous study – the applied DA system enables very fast switching times between closed DA adducts and open chain ends, the resulting specimens could be characterized via high temperature (HT) ¹H NMR spectroscopy at temperatures ranging from 40 to 140 °C and the respective ratios of open Cp chain ends to HDA adduct signals were calculated as the temperature dependent degree of debonding (Fig. 1), enabling a very facile, straightforward and fast analysis.^14,32 Comparing the results of the three methacrylate diblock polymers in Fig. 6, a clear effect of the different chain nature on the degree of debonding is observed, as the sample with PⁱBuMA building blocks has the highest degree of debonding at any given temperature, followed by P^tBuMA and finally PMMA.

Fig. 6 Temperature dependent degree of debonding for Diels–Alder A,A′-type diblockcopolymers consisting of PMMA (▲), PⁱBuMA (▼) or P^tBuMA (◀) building blocks with a length of 50 repeating units assessed by HT NMR spectroscopy.

These experimental data as well as the range of the debonding values is reproduced by the quantum chemical calculations for the extended acrylate chain conformers with the same side chain substituents (Fig. 4(b)), enabling a clear assignment of the entropic causes. Considering the previously reported chain mass effect, it comes at no surprise that the two butyl methacrylate building blocks with heavier side chain groups enable a 7–14% higher degree of debonding than the methyl methacrylate ones of the same chain length.³² In contrast, the difference of 7% in debonding of the two butyl methacrylate building blocks of the same chain length and thus the same chain weight must be underpinned by yet another effect. An explanation could be the difference in chain stiffness, as the degrees of vibrational and rotational freedom of the connected chains are reduced by chain scission. When polymer chains are divided into smaller pieces, flexibility and thus rotational and vibrational entropy is lost. With PⁱBuMA having a lower T_g value than P^tBuMA – implying the PⁱBuMA building blocks have a higher chain mobility than the P^tBuMA ones of the same length – PⁱBuMA chains are less impaired by the entropic confinement and thus their debonding is less hindered (=more favored) than the one of P^tBuMA, leading to a chain stiffness effect. This is again reflected in the rotational and vibrational ΔS charts, theoretically calculated for the extended chains scenario for acrylates (Fig. 3), in which these values for DA reaction are lower in the case of ⁱBuA, corresponding to its lower debonding temperature. Remarkably, the stiffness effect is overcompensated by the mass effect when comparing PMMA and P^tBuMA samples, where the stiffer but also heavier P^tBuMA has the higher degree of debonding, allowing a first insight into the specificity of these two properties.

DA polymer approach with equal building block sizes

We next expanded our study to include DA step growth polymers of the CDTE dilinker and Cp difunctional acrylate macromonomers. Thus, a possible impact of the larger building block dispersity (ca. 1.2) and therefore the presence of a larger number of different chain lengths and masses on the results of the examined A,A′-type diblockcopolymer methacrylate systems (Fig. 6) as well as the challenging diblock formation could be addressed. The low dispersity of the polyacrylate building blocks (close to 1.1 or less, Table 1) can be utilized to achieve more accurate results. In addition, the larger size change from building block to DA polymer facilitated the analysis via SEC techniques. Furthermore, the use of DA step-growth polymers with multiple ligation sites in one molecule should lead to an enhancement of the examined effects due to the higher amount of entropy released during chain scission reactions. To achieve comparable results in the following measurements, an average degree of polymerization (DP_n) of 6 was targeted for these DA polymers under similar reaction conditions (Scheme 3) to those for the DA block copolymer formation (see Fig. 7 for an exemplary SEC data set, Fig. S2† for the chromatograms of the other employed polymers, eqn (S1)† for the calculation of the DP_n). A control sample of every macromonomer without dilinker was exposed to the same reaction conditions to ensure that the desired HDA reaction and not the unwanted Cp–Cp dimerization had occurred.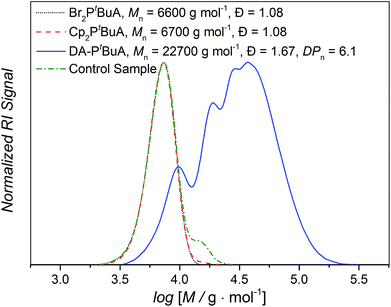

Fig. 7 Exemplary SEC chromatograms of the dibromo precursor polymer (⋯), Cp difunctional macromonomer (----), Diels–Alder polymer (—) and control sample of heated Cp difunctional macromonomer without CDTE dilinker ([dash dot, graph caption]) for 50 tert-butyl acrylate repeating units (see Fig. S2† for the chromatograms of the other employed polymers).

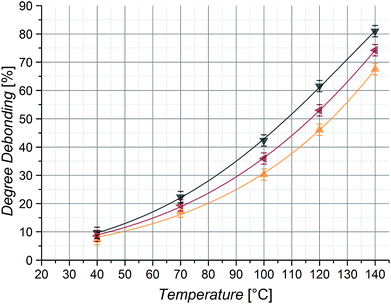
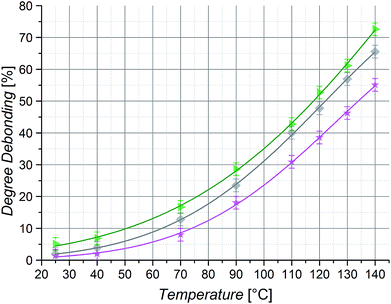
To allow a mass effect free analysis, isomeric poly(n-butyl acrylate) (PⁿBuA), poly(iso-butyl acrylate) (PⁱBuA) and poly(tert-butyl acrylate) (P^tBuA) macromonomers of the same chain length (50 repeating units) were also studied. From HT ¹H NMR characterization at temperatures ranging from 25 to 140 °C, it is evident that the stiffest polymer, P^tBuA, displays the expected lowest degree of debonding at a given temperature (Fig. 8) and the experimental results for P^tBuA and PⁱBuA are again in good agreement with the quantum chemical calculations for extended chain conformers (Fig. 4(b)).

Fig. 8 Temperature dependent degree of debonding for Diels–Alder polymers consisting of Cp difunctional PⁱBuA (▶), PⁿBuA (◆) or P^tBuA (★) building blocks with a length of 50 repeating units and CDTE dilinker assessed by HT NMR spectroscopy.

Although PⁿBuA has the lowest T_g of the three investigated poly(butyl acrylates), it has not the lowest persistence length (Table 2) and thus chain stiffness in the solvent employed for the HT NMR measurements (toluene-d₈). Indeed, Coelho et al. previously reported that in THF PⁱBuA is the least stiff of these three polymers.⁵³ Moreover, the solvent is known to affect chain conformation and the model calculations presented above clearly show the effect of chain conformation on the debonding temperature (i.e., globular chains give rise to lower debonding temperatures compared to the corresponding extended chain conformation, refer to Fig. 2 and 4). The order of the stiffness values of the examined chains and thus the hypothetically linked degrees of debonding are a consequence of solvent effects – as a result, the debonding values of PⁿBuA at 140 °C lie 11% above the ones of P^tBuA, yet 7% below the ones of PⁱBuA. Accordingly, the degree of debonding of the investigated DA polymers could be adjusted in a range of nearly 20% by merely changing the structure of the building block side chains without changing their length or mass, clearly evidencing the existence of an effect of the polymer side chain groups on the bonding reaction properties.

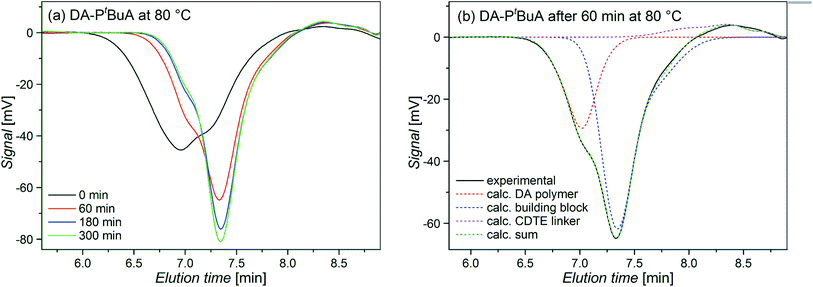
In order to investigate the debonding behavior in more detail, the rDA reaction of the DA polymers was also investigated using temperature dependent size exclusion chromatography (TD SEC). Monitoring the molar mass distribution of the polymers during the rDA reactions provides further insights into the process of the debonding reactions. Fig. 9(a) shows chromatograms of DA–P^tBuA at 80 °C at different reaction times. With increasing reaction time, the peak shifts towards lower molar masses (higher elution volume) and the width of the peak decreases and eventually converges to the shape of the building block. In Fig. 9(b) only one chromatogram is shown with the calculated individual peaks of the DA polymer, the respective building block and the CDTE dilinker molecule. Simple calculations of molar mass averages with respect to polymer standards are not possible from these chromatograms, and a different approach for their evaluation has been chosen, in which the concentration decrease of the DA polymer is being tracked during the rDA reaction. The obtained values reflect the excess of the rDA reaction but cannot be compared directly to the degree of debonding obtained by NMR as the part of the rDA reaction that only releases small linker molecules is not captured by the calculations due to the small weight and thus elution time differences as well as overlapping signals (for detailed information on the SEC analysis see the ESI†).

Fig. 9 TD SEC chromatograms, (a) DA–P^tBuA after different rDA times at 80 °C in 60% TCB and 40% DMF, (b) DA–P^tBuA after 60 min. rDA at 80 °C and distributions calculated by peak deconvolution of the individual components.

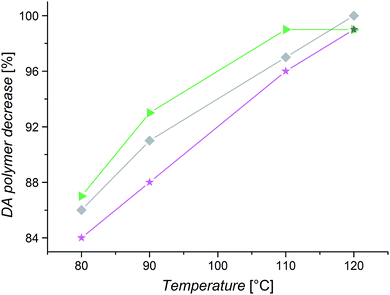
Fig. 10 shows the obtained DA–polymer concentration decreases for PⁱBuA, PⁿBuA, and P^tBuA. The graph shows that PⁿBuA exhibits the most pronounced decrease of DA polymer, followed by PⁱBuA and P^tBuA, and, thus, reproduces the trend of the T_g values observed for the three polymers. As already noted, the stiffness of polymers in solution is affected by the thermodynamic properties of the solvent and consequently the order may vary depending on the solvent. This could be a possible reason for the deviation in the debonding behavior of PⁱBuA and PⁿBuA analyzed in different solvents by TD SEC and HT NMR. Nevertheless, the significance of different side chain substituents and their impact on the ligation chemistry is again clearly illustrated, additionally emphasizing the importance of the applied solvent.

Fig. 10 TD SEC results: decrease of concentration of DA polymers due to rDA reactions of the DA polymers consisting of Cp difunctional PⁱBuA (▶), PⁿBuA (◆) or P^tBuA (★) building blocks with a length of 50 repeating units and CDTE dilinker.

DA polymer approach with differing building block sizes

To finally compare the mass and chain stiffness effects and their impact at different chain lengths, a further set of samples was prepared. Diels–Alder macromonomers with very different side chain groups, namely Cp difunctional poly(methyl acrylate) (PMA) and poly(isobornyl acrylate) (PⁱBoA), were synthesized with two chain lengths each and underwent the described DA step growth polymerization with the CDTE dilinker (see Fig. S3 and S4† for the SEC chromatograms of the employed polymers). It is expected that the stiffness effect on the chain scission of longer building blocks is less pronounced than the one of smaller building blocks, as longer chain sections still have more degrees of freedom and thus their liberation should be less hindered. Inspection of the debonding values of the DA polymers synthesized from reasonably long macromonomers with 50 repeating units (Fig. 11) indicates that the heavier macromonomer PⁱBoA_large has more than 10% higher debonding values than PMA_large, leading to the conclusion that for long chains the chain stiffness effect becomes less important and is surpassed by the mass effect.

Fig. 11 Temperature dependent degree of debonding for Diels–Alder polymers consisting of Cp difunctional PMA_large (■, 50 repeating units), PⁱBoA_large (●, 50 repeating units), PMA_small (□, 10 repeating units) or PⁱBoA_small (○, 10 repeating units) building blocks and CDTE dilinker assessed by HT NMR spectroscopy.

To decrease the freely jointed chain character of the building blocks by decreasing their contour length, DA polymers based on macromonomers with 10 acrylate repeating units (PMA_small and PⁱBoA_small) were examined.⁶⁷ The previously described chain length and mass effect is reproduced, as the observed debonding values decrease for shorter and thus also lighter chains of the same polymer type when comparing the debonding values for PMA_small/large as well as PⁱBoA_small/large (Fig. 11). Interestingly, the values for PMA_small and PⁱBoA_small macromonomers indicate that the chain mass effect is now overcompensated by the stiffness effect, as the debonding values for the lighter PMA_small even surpass the ones of the heavier PⁱBoA_small sample by nearly 10%, clearly confirming the assumption of a growing influence of the stiffness effect with decreasing chain length due to the more impaired chain mobility of the separated building blocks. Indeed, as foreshadowed above, these trends for shorter chains are in qualitative agreement with the quantum chemical trends for the calculations performed on (globular) lowest energy conformations, where such mobility is expected to be hampered (Fig. 4(b)). In contrast, the experimental trends for the longer chains qualitatively follow the quantum chemical trends based on extended chains (Fig. 4(a)). In other words, shorter chains are able to coil better, whereas longer chains stay largely extended.

Investigating the same set of DA polymers by TD SEC was not possible as in the case of PMA_small and PⁱBoA_small the peaks of the DA polymer, the building block and the CDTE dilinker overlap too strongly for a precise analysis. PMA_large and PⁱBoA_large however could be analyzed very precisely and can reproduce very well the trend that the stiffness effect is overcompensated by the mass effect and – as a consequence – the rDA reaction proceeds further for PⁱBoA than for PMA (Fig. 12).

Fig. 12 TD SEC results: decrease of concentration of DA polymer due to rDA reaction of the DA polymers consisting of Cp difunctional PMA_large (■, 50 repeating units) and PⁱBoA_large (●, 50 repeating units) building blocks and CDTE dilinker.

Conclusions

Strong entropic chain effects on chain linking and scission reactions are observed for Diels–Alder step-growth and diblock polymers via HT NMR and TD SEC experiments. Not only could the previously published chain length and mass effect be excellently reproduced with other Diels–Alder polymer systems enabling the adjustment of the temperature dependent degree of debonding by approximately 30% for the investigated PⁱBoA macromonomers of different chain lengths, but also a large chain stiffness effect could be identified, which enables the modification of the reaction equilibrium between free and linked chains by up to approximately 20% at 140 °C for different isomeric poly(butyl acrylate) chains of the same length and mass. Moreover, the impact of the chain stiffness effect was found to increase with decreasing chain length, as the chain mobility originates more and more from the local flexibility and less from the freely jointed character of a long polymer chain. While for the comparison of long chains, the heavier and stiffer PⁱBoA system has higher debonding values than PMA – overcompensating any stiffness effect via the mass effect – for short chains the much lighter, but also less stiff PMA has significantly higher debonding values. In summary, it could be experimentally shown that not only higher molecular masses and longer chains, but also lower molecular stiffness values favor the debonding of ligated species, thus evidencing the manifold molecular characteristics that have to be considered when planning and executing reversible reactions. The experimentally observed trends can be reproduced and explained via quantum chemical calculations, leading to a better understanding of the fundamental principles of entropic effects on reversible bonding/debonding systems. The complex interplay of translational, rotational and vibrational entropy and their conformational dependencies are illustrated and it is shown that the better coiling ability accounts for the increased impact of chain stiffness of shorter and thus sterically less hindered chains on bonding reactions, in addition giving an explanation for differing debonding values in solvents of different thermodynamic properties. The new insight into different chain effects in general and a chain stiffness effect in particular can be utilized to tune the processing and application temperatures of materials via the incorporation of different easily accessible backbones and their entropic effects without the need to change the underlying ligation chemistry. Our findings thus have the potential to invoke a step change in the design approach taken for self-healing or other smart materials, such as post-formable organic sheets via physical rather than chemical parameters. Further – and importantly – the entropic chain length, mass and stiffness effects have to be kept in mind when ligation chemistry is transferred from small molecules to polymers or other large systems with significantly different entropic properties, as their impact on the molecule and material properties can be substantial.

Acknowledgements

C. B.-K., A. L. and M. L. C. are grateful for continued support from and the excellent collaboration with Evonik Industries. C. B.-K. additionally acknowledges funding from the KIT via the Helmholtz association as well as the German Research Council (DFG). The authors thank A. Turkin (KIT) for his contributions to parts of the synthetic work, Dr J. Ho (Yale) for helpful discussions on the computational methods as well as Prof. Dr W. Burchard for his expertise on SANS measurements. M. L. C. and G. G. also thank the National Facility of the Australian National Computational Infrastructure for supercomputer resources.

Notes and references

1. O. Diels and K. Alder, Liebigs Ann. Chem., 1928, 460, 98–122.
2. H. C. Kolb, M. G. Finn and K. B. Sharpless, Angew. Chem., Int. Ed., 2001, 40, 2004–2021.
3. N. K. Devaraj, R. Weissleder and S. A. Hilderbrand, Bioconjugate Chem., 2008, 19, 2297–2299.
4. S. Sinnwell, A. J. Inglis, T. P. Davis, M. H. Stenzel and C. Barner-Kowollik, Chem. Commun., 2008, 2052–2054.
5. K. C. Nicolaou, S. A. Snyder, T. Montagnon and G. Vassilikogiannakis, Angew. Chem., Int. Ed., 2002, 41, 1668–1698.
6. H. Durmaz, B. Colakoglu, U. Tunca and G. Hizal, J. Polym. Sci., Part A: Polym. Chem., 2006, 44, 1667–1675.
7. M. Langer, J. Brandt, A. Lederer, A. S. Goldmann, F. H. Schacher and C. Barner-Kowollik, Polym. Chem., 2014, 5, 5330–5338.
8. J. R. McElhanon and D. R. Wheeler, Org. Lett., 2001, 3, 2681–2683.
9. A. A. Kavitha and N. K. Singha, ACS Appl. Mater. Interfaces, 2009, 1, 1427–1436.
10. A. J. Inglis, S. Sinnwell, M. H. Stenzel and C. Barner-Kowollik, Angew. Chem., Int. Ed., 2009, 48, 2411–2414.
11. M. A. Tasdelen, Polym. Chem., 2011, 2, 2133–2145.
12. A. S. Goldmann, T. Tischer, L. Barner, M. Bruns and C. Barner-Kowollik, Biomacromolecules, 2011, 12, 1137–1145.
13. T. Pauloehrl, G. Delaittre, V. Winkler, A. Welle, M. Bruns, H. G. Boerner, A. M. Greiner, M. Bastmeyer and C. Barner-Kowollik, Angew. Chem., Int. Ed., 2012, 51, 1071–1074.
14. K. K. Oehlenschlaeger, N. K. Guimard, J. Brandt, J. O. Mueller, C. Y. Lin, S. Hilf, A. Lederer, M. L. Coote, F. G. Schmidt and C. Barner-Kowollik, Polym. Chem., 2013, 4, 4348–4355.
15. M. Glassner, K. K. Oehlenschlaeger, A. Welle, M. Bruns and C. Barner-Kowollik, Chem. Commun., 2013, 49, 633–635.
16. A. V. Samoshin, C. J. Hawker and J. Read de Alaniz, ACS Macro Lett., 2014, 753–757.
17. X. Chen, M. A. Dam, K. Ono, A. Mal, H. Shen, S. R. Nutt, K. Sheran and F. Wudl, Science, 2002, 295, 1698–1702.
18. E. B. Murphy, E. Bolanos, C. Schaffner-Hamann, F. Wudl, S. R. Nutt and M. L. Auad, Macromolecules, 2008, 41, 5203–5209.
19. N. K. Guimard, K. K. Oehlenschlaeger, J. Zhou, S. Hilf, F. G. Schmidt and C. Barner-Kowollik, Macromol. Chem. Phys., 2012, 213, 131–143.
20. S. Billiet, X. K. D. Hillewaere, R. F. A. Teixeira and F. E. Du Prez, Macromol. Rapid Commun., 2013, 34, 290–309.
21. K. K. Oehlenschlaeger, J. O. Mueller, J. Brandt, S. Hilf, A. Lederer, M. Wilhelm, R. Graf, M. L. Coote, F. G. Schmidt and C. Barner-Kowollik, Adv. Mater., 2014, 26, 3561–3566.
22. S. Billiet, K. De Bruycker, F. Driessen, H. Goossens, V. Van Speybroeck, J. M. Winne and F. E. Du Prez, Nat. Chem., 2014, 6, 815–821.
23. S. D. Bergman and F. Wudl, J. Mater. Chem., 2008, 18, 41–62.
24. C. Dry, Int. J. Mod. Phys. B, 1992, 6, 2763–2771.
25. S. R. White, N. R. Sottos, P. H. Geubelle, J. S. Moore, M. R. Kessler, S. R. Sriram, E. N. Brown and S. Viswanathan, Nature, 2001, 409, 794–797.
26. J. P. Kennedy and K. F. Castner, J. Polym. Sci., Part A-1: Polym. Chem., 1979, 17, 2039–2054.
27. W. H. Binder, Self-Healing Polymers, Wiley-VCH, Weinheim, Germany, 2013.
28. J. Zhou, N. K. Guimard, A. J. Inglis, M. Namazian, C. Y. Lin, M. L. Coote, E. Spyrou, S. Hilf, F. G. Schmidt and C. Barner-Kowollik, Polym. Chem., 2012, 3, 628–639.
29. A. J. Inglis, L. Nebhani, O. Altintas, F. G. Schmidt and C. Barner-Kowollik, Macromolecules, 2010, 43, 5515–5520.
30. M. Watanabe and N. Yoshie, Polymer, 2006, 47, 4946–4952.
31. T. A. Plaisted and S. Nemat-Nasser, Acta Mater., 2007, 55, 5684–5696.
32. N. K. Guimard, J. Ho, J. Brandt, C. Y. Lin, M. Namazian, J. O. Mueller, K. K. Oehlenschlaeger, S. Hilf, A. Lederer, F. G. Schmidt, M. L. Coote and C. Barner-Kowollik, Chem. Sci., 2013, 4, 2752–2759.
33. J. Brandt, K. K. Oehlenschlaeger, F. G. Schmidt, C. Barner-Kowollik and A. Lederer, Adv. Mater., 2014, 26, 5758–5785.
34. C. Cao and Y. Lin, J. Chem. Inf. Comput. Sci., 2003, 43, 643–650.
35. W. Jakubowski and K. Matyjaszewski, Angew. Chem., Int. Ed., 2006, 45, 4482–4486.
36. A. J. Inglis, T. Paulöhrl and C. Barner-Kowollik, Macromolecules, 2009, 43, 33–36.
37. D. A. P. R. A. Hutchinson Jr, J. H. McMinn, S. Beuermann, R. E. Fuller and C. Jackson, DECHEMA Monogr., 1995, 131, 467–492.
38. B. Dervaux, T. Junkers, M. Schneider-Baumann, F. E. Du Prez and C. Barner-Kowollik, J. Polym. Sci., Part A: Polym. Chem., 2009, 47, 6641–6654.
39. H. L. Wagner, J. Phys. Chem. Ref. Data, 1985, 14, 1101–1106.
40. G. E. Roberts, T. P. Davis, J. P. A. Heuts and G. E. Ball, Macromolecules, 2002, 35, 9954–9963.
41. R. A. Hutchinson, S. Beuermann, D. A. Paquet and J. H. McMinn, Macromolecules, 1997, 30, 3490–3493.
42. S. Beuermann, D. A. Paquet, J. H. McMinn and R. A. Hutchinson, Macromolecules, 1996, 29, 4206–4215.
43. E. Penzel and N. Goetz, Angew. Makromol. Chem., 1990, 178, 191–200.
44. E. F. Casassa, J. Chem. Phys., 1955, 23, 596–597.
45. A. Holtzer, J. Polym. Sci., 1955, 17, 432–434.
46. G. W. T. M. J. Frisch, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, M. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09 (Revision C.01), Gaussian Inc., Wallingford CT, 2009.
47. E. I. Izgorodina, C. Yeh Lin and M. L. Coote, Phys. Chem. Chem. Phys., 2007, 9, 2507–2516.
48. Y. Zhao and D. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241.
49. D. J. Henry, M. B. Sullivan and L. Radom, J. Chem. Phys., 2003, 118, 4849–4860.
50. J. P. Merrick, D. Moran and L. Radom, J. Phys. Chem. A, 2007, 111, 11683–11700.
51. A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396.
52. S. Lecommandoux, F. Chécot, R. Borsali, M. Schappacher, A. Deffieux, A. Brûlet and J. P. Cotton, Macromolecules, 2002, 35, 8878–8881.
53. J. F. J. Coelho, E. Y. Carvalho, D. S. Marques, A. V. Popov, V. Percec and M. H. Gil, J. Polym. Sci., Part A: Polym. Chem., 2008, 46, 6542–6551.
54. A. P. Haehnel, M. Schneider-Baumann, L. Arens, A. M. Misske, F. Fleischhaker and C. Barner-Kowollik, Macromolecules, 2014, 47, 3483–3496.
55. J. Brandrup and E.-H. Immergut, Polymer Handbook, Wiley, Chichester, UK, 1989.
56. T. P. Lodge and M. Muthukumar, J. Phys. Chem., 1996, 100, 13275–13292.
57. F. Fleischhaker, A. P. Haehnel, A. M. Misske, M. Blanchot, S. Haremza and C. Barner-Kowollik, Macromol. Chem. Phys., 2014, 215, 1192–1200.
58. M. D. Lechner, E. H. Nordmeier and K. Gehrke, Makromolekulare Chemie, Birkhäuser, Basel, 2010.
59. J. M. G. Cown, Eur. Polym. J., 1975, 11, 297–300.
60. G. M. Martin, S. S. Rogers and L. Mandelkern, J. Polym. Sci., 1956, 20, 579–581.
61. L. J. Hughes and G. L. Brown, J. Appl. Polym. Sci., 1961, 5, 580–588.
62. S. Krause, J. J. Gormley, N. Roman, J. A. Shetter and W. H. Watanabe, J. Polym. Sci., Part A: Gen. Pap., 1965, 3, 3573–3586.
63. J. Heijboer, Proc. Intern. Conf. on Physics of Non-Crystalline Solids, North Holland Publishing, Amsterdam, 1965.
64. Z. A. Azimov, S. P. Mitsengendler and A. A. Korotkov, Polym. Sci. USSR, 1965, 7, 929–933.
65. C. E. Rehberg, W. A. Faucette and C. H. Fisher, J. Am. Chem. Soc., 1944, 66, 1723–1724.
66. J. A. Shetter, J. Polym. Sci., Part B: Polym. Lett., 1963, 1, 209–213.
67. J. E. Mark, Physical Properties of Polymers Handbook, Springer, New York, 2007.

---

Footnote

† Electronic supplementary information (ESI) available: Synthetic details, applied MHKS parameters, SEC chromatograms of all samples, (HT) NMR data, experimental debonding values, SANS measurements, computational data (energy contributions and geometries in the form of Gaussian archive entries). See DOI: 10.1039/c4sc02908a

---