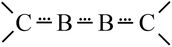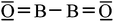Open Access Article
Open Access ArticleThe boron–boron triple bond? A thermodynamic and force field based interpretation of the N-heterocyclic carbene (NHC) stabilization procedure†
R.
Köppe
and
H.
Schnöckel
*
Institute of Inorganic Chemistry, Karlsruhe Institute of Technology (KIT), Engesserstr. 15, 76131 Karlsruhe, Germany. E-mail: hansgeorg.schnoeckel@kit.edu
First published on 25th November 2014
Abstract
Recently, the NHC→B![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) B←NHC molecule 1 has been published in Science where it is described as a stabilized B2 molecule in its 1Σ excited state (B2*) (NHC = N-heterocyclic carbene C3N2H2(C6H3Pri2-2,6)2). The bonding of 1 based on sophisticated calculations and the BB distances of the solid compound was discussed as the first example of a B2 triple bond in a stable molecule. Now we present an only experimentally based interpretation of 1via detailed thermodynamic considerations, including its fragmentation to B2 molecules. Furthermore, from the vibrational spectrum force constants (fBB for the BB bond and fBC for the BC bond) were extracted, which are classical examples to indicate single, double and triple CC bonds in organic chemistry. The consequence of both properties of 1 (ΔE and f) generates a new interpretation which is in contrast to the triple bond donor–acceptor description visualized by arrows and which casts a critical light on the interpretation of any NHC “stabilized” molecule.
B←NHC molecule 1 has been published in Science where it is described as a stabilized B2 molecule in its 1Σ excited state (B2*) (NHC = N-heterocyclic carbene C3N2H2(C6H3Pri2-2,6)2). The bonding of 1 based on sophisticated calculations and the BB distances of the solid compound was discussed as the first example of a B2 triple bond in a stable molecule. Now we present an only experimentally based interpretation of 1via detailed thermodynamic considerations, including its fragmentation to B2 molecules. Furthermore, from the vibrational spectrum force constants (fBB for the BB bond and fBC for the BC bond) were extracted, which are classical examples to indicate single, double and triple CC bonds in organic chemistry. The consequence of both properties of 1 (ΔE and f) generates a new interpretation which is in contrast to the triple bond donor–acceptor description visualized by arrows and which casts a critical light on the interpretation of any NHC “stabilized” molecule.
Introduction
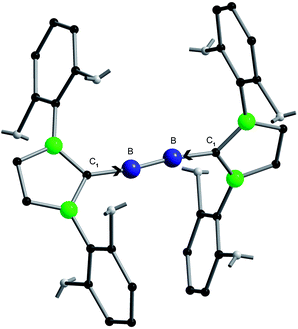
During the last two decades an unprecedented renaissance of main group chemistry has been developed.1 High-lighted areas are e.g.: nanoscaled species such as metalloid clusters as intermediates between normal valence compounds and bulk metals on one hand,2–6 and, on the other hand, reactive molecules containing multiple bonding stabilized either via bulky ligands7,8 or via N-heterocyclic carbenes (NHCs).9,10 As an outstanding example in the latter field we will concentrate here on a compound containing an unusual B–B bond.11–13Though there have already been presented some nice molecules before, which contain electron precise boron–boron bonds14,15 as well as BB bonds containing additional π-bonding,16–18 two years ago the outstanding impressive molecule NHC→B![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) B←NHC (1) (NHC = N-heterocyclic carbene C3N2H2(C6H3Pri2-2,6)2) (Fig. 1) was published in Science under the title “Ambient-Temperature Isolation of a Compound with a Boron–Boron Triple Bond”.
B←NHC (1) (NHC = N-heterocyclic carbene C3N2H2(C6H3Pri2-2,6)2) (Fig. 1) was published in Science under the title “Ambient-Temperature Isolation of a Compound with a Boron–Boron Triple Bond”.
1 has been characterized via its X-ray solid state structure exhibiting a short B–B distance which is, however, longer than expected,19via different NMR spectroscopic investigations, via three intensive IR bands, and an elemental analysis.11,12 Furthermore, detailed quantum chemical investigations, including the calculated UV/VIS spectrum have been presented. These calculations and the visualization of the orbitals involved in the multiple bonding were the basis for the interpretation summarized in the above-mentioned title11 and for a highlight article in the same issue of Science.12 Since this triple bond interpretation has also been predicted theoretically20 and was also included in recent reviews,10,21 we feel that it is time to make a cut and to give a different, only experimentally based interpretation for this nice compound 1 in order to increase our understanding of its unusual bonding and in order to prevent already beginning confusion, especially in the textbooks.22 Furthermore we will show that any mainly “orbital based” interpretation in which an NHC stabilization is involved should make us cautious. Compound 1 was chosen for this discussion as an impressive example for the NHC stabilization, since many other molecules containing B–B bonding exhibit suitable reference data because the variation of the B–B vibration indicates the degree of “stabilization”. Thus, we want to discuss 1 with respect to its thermodynamic property (Section 1) and its molecular vibrations (Section 2) for which the bond strengths (force constants) are an essential basis; i.e. we want to discuss two properties which are basic for every bonding discussion in the entire field of chemistry.23–25
Thermodynamic view
Today the thermodynamic stability of every species, even of reactive ones, is available via quantum chemical calculations.Sometimes, additional experimental data make this discussion more confident. Unfortunately, this discussion is missing for 120,28) and its interpretation as a donor–acceptor stabilized molecule visualized by two arrows (Fig. 1). In Fig. 2 the calculated and the experimentally obtained thermodynamic data of molecule 1 and of solid boron together with the hot gaseous molecules/atoms B1 [ground state 2P],27,30 B2 [ground state 3Σg−]26 and B2* [excited state 1Σg+] are summarized.
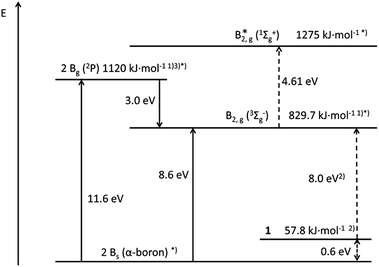 | ||
| Fig. 2 Energy diagram for solid boron, B-atoms, B2 molecules (B2, B2*) and the decomposition of 1 to B2 and 2NHC. Calculated (dashed lines) and experimentally obtained values.26 For 2 see ESI.† Footnotes to figure: *) “+2NHC” omitted for clarity; 1) ref. 26; 2) calculated for 1a: 35.7 kJ mol−1 and 8.23 eV; 3) ref. 27. | ||
Therefore, fundamental thermodynamic considerations could be the starting point for every bonding discussion before any other investigation will go into detail. The most remarkable conclusion from Fig. 2 is that, with respect to the gaseous species B atoms, B2 (3Σ) and B2* (1Σ), solid boron and the gaseous compound 1 are nearly on the same thermodynamic level: e.g. two boron atoms are 11.6 eV (1120 kJ mol−1) above solid boron and 11.0 eV above 1.29,30 However, since the boiling point of boron at 3900 °C exhibits its robustness based on strong covalent B–B bonds, it is hard to believe that the gaseous B1, B2, B2* species can be obtained from 1via heating, i.e. energy transfer from outside.31 Nevertheless, at least theoretically in a Gedanken experiment the dissociation of 1 to Bn-species and 2NHCs can be allowed. However, the observation of a similar energy transfer starting from boron and from 1 to get gaseous B1, B2 and B2* should be alarming!
Now we will discuss the reverse Gedanken experiment, i.e. we look at the gaseous species B1, B2 and B2*, and allow B2* (a) to condense to solid boron or (b) to react with 2NHC molecules to 1 in the gas phase.
At about 2000 K the following gaseous boron species are in equilibrium with solid boron: i.e. the relative concentration of B1, B2 and B2* is 1018![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1012
1012![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (see ESI†). Now we concentrate on the excited B2* molecule32 though its relative concentration in the gas phase is extremely low. Nevertheless this B2* molecule was the basis for the theoretical discussion of 1 and its triple bond character.
1 (see ESI†). Now we concentrate on the excited B2* molecule32 though its relative concentration in the gas phase is extremely low. Nevertheless this B2* molecule was the basis for the theoretical discussion of 1 and its triple bond character.
(a) When B2* is condensed to form solid boron, 13.2 eV (1275 kJ mol−1) are gained, because the multiple bond of B2* is changed to solid boron containing only single bonds like in a polymerization process. Thus, there is a dramatic exothermic rearrangement of atoms and electrons, and one of the strong covalent bonded allotropes of boron with high thermal robustness is formed. The large energy gain which is connected with this process will cause a strong heating of boron, which is no problem for this material, and which finally heats the environment. The conclusion of this Gedanken experiment is, that solid boron and its structure has nothing to do with the bonding and structure of B2*. Therefore, nobody would conclude that B2* is stabilized in solid boron!
(b) Now we look at the reaction of B2* with 2NHC molecules in the gas phase: this formation of 1 is strongly exothermic with 12.6 eV (1221 kJ mol−1) because the electrons are rearranged, new bonds are formed, and the original bonds are changed. The large energy gain of this gas-phase reaction should result in the heating of 1 and its fragmentation; i.e. this fragmentation process would start by breaking the weakest bonds: however, in principle, this fragmentation can be avoided33–38 – at least theoretically – if the heat can be transferred fast enough to the environment, e.g. via radiation. Anyway, if 1 really would survive in this exothermic reaction starting from B2* and 2NHC, one has to conclude: the final state of this reaction (i.e.1) is energetically far below the starting point (B2* + 2NHC) (12.6 eV), i.e. electron distribution and bonding of the educts and products must be extremely different. In one word, the final state 1 has nearly nothing to do with the educts (B2* and 2NHC molecules), like in the case of solid boron! Consequently, the bonding situation in 1 can hardly be symbolized as a slight modification of the educts via arrows (Fig. 1), which suggest only a weak donor (NHC)–acceptor (B2*) interaction in which the bonding of the educts is still visible.
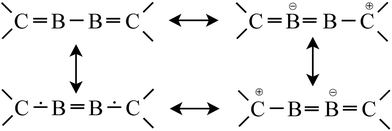
However, to look more carefully to the energetic situation of the final electron distribution within the “C–B–B–C” core, especially with respect to the BC bonding, one has to start with the ground state of B2 (8 eV (772 kJ mol−1) above 1); with its BB single bond and without BC contacts to 2NHCs. If the BB bond is not changed during the reaction with 2NHCs, the formation of two BC single bonds will consume 772 kJ mol−1, i.e. each BC bond consumes 386 kJ mol−1, nearly the expected value of the BC single bond energy 372 kJ mol−1.39 However, this intermediate electronic situation of 1 with one BB and two BC single bonds has to drop into a more stable energetic valley, if the energy of the B2 molecule is increased after its formation from B2* as starting point. Subsequently, this intermediate possessing only single bonds has to consume 445 kJ mol−1 (4.61 eV), which is nearly quantitatively possible by the formation of two BC double bonds, which are each estimated to be at 230 kJ mol−1, i.e. slightly more stable than the BC single bond.40 Thus the following situation for the central C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) B–B
B–B![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C core results, which is in line with the most prominent neutral resonance structure presented in Scheme 1. Finally, after distribution of the π electrons from the BC bonds to the whole CBBC core, this thermodynamic Gedanken experiment results in a 4-electron–4-center π bond, NHC
C core results, which is in line with the most prominent neutral resonance structure presented in Scheme 1. Finally, after distribution of the π electrons from the BC bonds to the whole CBBC core, this thermodynamic Gedanken experiment results in a 4-electron–4-center π bond, NHC![[partial double bond, top dashed]](https://www.rsc.org/images/entities/char_e12f.gif) B
B![[partial double bond, top dashed]](https://www.rsc.org/images/entities/char_e12f.gif) B
B![[partial double bond, top dashed]](https://www.rsc.org/images/entities/char_e12f.gif) NHC (Scheme 2).
NHC (Scheme 2).
In order to confirm the conclusion of a rearrangement of electrons in 1 which is completely different from that of the educts, we look at the forces between the atoms of 1 which are visible by its vibrational spectrum i.e. by its IR and Raman spectrum and compare this situation with that of the B2* molecule.
Determination and discussion of the force constants of 1
For the bonding discussion of 1, the most convincing structured property concerning the BB bond was its short distance.11,19,41–43 Much more reliable and sensitive for the experimental characterization of a bond and especially of multiple bonds are the force constants which reflect directly the situation of the bonding electrons between two nuclei. More accurately, the force constant f (spring constant: force = fΔr) represents the restoring force which resists to a small elongation (Δr) of the atoms from the equilibrium distance.44 The relevance of force constants for the discussion of bond properties has recently been shown for the Zn–Zn bond in Zn2Cp2*,45 has been highlighted for the discussion of S–S multiple bonds46 and, as a classical example, is convincingly demonstrated in fundamental organic chemistry, where the relation of the force constants of a CC single bond to a double and a triple bond is about 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3.47,48
3.47,48
Therefore, a discussion of force constants of bonds between carbon and its direct neighbor element boron should also be a convincing measure to discuss BB and BC bonds, especially whether or not multiple bonding is involved.
Unfortunately, force constants cannot directly be obtained from the vibrational spectra, because the observed spectra are the result of interactions of the hypothetical isolated motions within every bond or special entities of a molecule. However, the so-called normal-coordinate analysis52 allows extracting the force constants for every bond, if the molecule and the number of vibrations are not too large. Therefore, instead of the determination of the force constant of 1 (there are 390 vibrations) we have chosen the model compound 1a in which the NHC of 1 is substituted by the most simple NHC containing only H ligands: C(NH)2(CH)2, and only 54 vibrations are obtained. Since the vibrations and the vibrational coupling within the CBBC moieties of 1 and 1a are similar53 and since the relevant structural data of the N2CBBCN2 unit of 1a and 1 are nearly identical (cf. below), this simplification is valid. The normal coordinate analysis of the vibrations of the N2CBBCN2 core of 1a is collected in Table 1.
| ν/cm−1 | Δν (10B/11B) | Δν (12C/13C) | Δν (14N/15N) | PED | |
|---|---|---|---|---|---|
| a ν s′ means ν (symmetric) but out of phase motion. | |||||
| a1 | 1156.94 | 2.53 | 9.88 | 20.27 | 22% νS(CN2) + 60% νs(NCH) |
| b2 | 1298.74 | 11.85 | 13.55 | 20.29 | 40% νas(BC) + 30% νs′(NCH)a |
| a1 | 1450.95 | 6.93 | 8.29 | 26.56 | 20% νs(CN2) + 22% νs(NCH) |
| b2 | 1505.32 | 5.3 | 22.52 | 35.34 | 23% νas(BC) + 23% νs′(CN2) |
| a1 | 1582.80 | 0.85 | 0.04 | 2.55 | 61% νs(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C) (in phase) C) (in phase) |
| b2 | 1585.54 | 0.35 | 1.35 | 3.85 | 58% νs′(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C) C) |
| a1 | 1769.50 | 64.72 | 10.79 | 11.09 | 47% ν(BB) + 43% νs(BC) |
The potential energy distribution (PED)52 exhibits the strong coupling of the BB, BC and CN vibrations, which is a first hint for a strong BC bonding! Furthermore, the resulting force constants (mdyn Å−1) fBB, fBC and fBB/BC give a convincing picture of the bonding in the core of 1a and also of 1.54
| fBB = 6.0 (1.49 Å) |
| fBC = 5.2 (1.49 Å) |
| fBB/BC = 0.16 |
In order to get a feeling for these values and to discuss them, we will compare them with force constants of some species summarized in Table 2.
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2a
CH2a
In order to decide about the possible multiple bond strength of the BB bond in 1 we must obtain reliable reference data for a BB single bond. As far as we know, only a single experimental value with 3.4 mdyn Å−1 has been published (for B2Cl4).50 Perhaps this value represents a weak BB single bond, because the BB distance in B2Cl4 with 1.73 Å is relatively large. The value for fBB of the B2 triplet molecule (3Σ) in its ground state with 3.6 mdyn Å−1 is a little bit larger; however, the distance of the BB bond is significantly shorter (1.59 Å). Both parameters of this B2 molecule are difficult to access because of the triplet character of B2 and two “binding” electrons in orthogonal π-bonds.50,55 In order to have a BB bond situation similar to that of 1 with a linear X–B–B–X moiety,56 we have finally calculated the force constants [mdyn Å−1] within the O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) B–B
B–B![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O57 species (O
O57 species (O CH2) for which already the vibrational spectrum of the matrix isolated species was obtained two decades ago:58
CH2) for which already the vibrational spectrum of the matrix isolated species was obtained two decades ago:58
| fBB = 3.5 (rBB = 165 pm) |
| fBO = 13.9 (rBO = 121.3 pm) |
| fBB/BO = 0.05 |
The force constant fBB of 3.5 mdyn Å−1 corresponds to a BB single bond though the BB distance is shorter than in B2Cl4 and longer than in B2 (3Σ) (Table 1). However, the Lewis formula O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) B–B
B–B![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O is in accordance with the values of the BB and BC force constants. The value of the interaction force constant fBB/BO is, like that of 1a, unexpectedly low (mostly about 10% of the stretching force constants), which demonstrates that the changes (stretching/compressing) of the BB bond have only a small influence on BC bonds (1a) or BO bonds in B2O2. However, these interactions are, as expected, significantly larger for 1a than for B2O2, i.e. for a more ionic compound.
O is in accordance with the values of the BB and BC force constants. The value of the interaction force constant fBB/BO is, like that of 1a, unexpectedly low (mostly about 10% of the stretching force constants), which demonstrates that the changes (stretching/compressing) of the BB bond have only a small influence on BC bonds (1a) or BO bonds in B2O2. However, these interactions are, as expected, significantly larger for 1a than for B2O2, i.e. for a more ionic compound.
The only example for a BB multiple bond within the molecules of Table 1 is observed in the excited B2* molecule: The large value of fBB of 7.7 mdyn Å−1 is in line with a small BB distance of 1.4 Å, i.e. a strong double bond is present in this molecule. From all these data we are now able to interpret the fBB = 6.0 mdyn Å−1 and fBC = 5.2 mdyn Å−1 force constant of 1a.
The BB bond should be addressed as a strong 1.5 BB bond and the BC bond as a weak 1.5 BC one. These results are in line with the thermodynamic discussion, from which the BB bond in B2* has lost its strong double bond character and, even more important, the value of the BC force constant forbids to address it as a donor–acceptor bond. This BC bond is even significantly stronger than a 2e2c bond! Therefore, mainly the two strong BC bonds of 1 are responsible for the large energy gain of 12.6 eV discussed in the thermodynamic part.24,25,59,60
The results of the thermodynamic data and of force constant determinations of 1 both accessible by observables show that a reassessment is pending concerning the bond description of 1. For a conclusive interpretation we have to decide whether to rely, besides the measured bond distance, on the predominant occupation of selected calculated MOs,61 or – and this is the bonding description of multiple bonds we favor – to prefer an interpretation based on observed thermodynamic relationships and the force constants based on the observed vibrational spectra. These force constants reflect the slope of the potential energy curve near the equilibrium distance and are thus a confident measure of the bond strength. This argument has already been impressively demonstrated in the evaluation of CC multiple bonds in the past48 so that we had applied it also for assessing the GaGa multiple bonds that were under discussion about 20 years ago.62–65 Even at that time, we were able to show that the bond described as a GaGa triple bond was just a slightly stronger single bond.66–69
Conclusions
Thus, from the thermodynamic and the force constant discussion a new description of bonding results for 1.70 To sum up, 1 does not contain a BB triple bond and the description as a stabilization of an excited B2* molecule via “arrows” of 2NHC molecules is strongly misleading.71 Therefore a bonding situation results which can be described by the resonance structures shown in Scheme 1 containing 4 π electrons for the BB and two BC bonds; i.e. the situation for these three bonds is just between single and double ones as represented by a simpler description for this 4-electron 4-center π-bond as NHC![[partial double bond, top dashed]](https://www.rsc.org/images/entities/char_e12f.gif) B
B![[partial double bond, top dashed]](https://www.rsc.org/images/entities/char_e12f.gif) B
B![[partial double bond, top dashed]](https://www.rsc.org/images/entities/char_e12f.gif) NHC (Scheme 2).
NHC (Scheme 2).
To sum up, the bonding within 1 is determined by an overall electron transfer from the “triple” bond of B2* to the BC bonds. This partial electron transfer is completed in the isolated normal valent B2O2 molecule, and consequently a BB single bond results:72
Furthermore, from the discussion of 1 presented here a fundamental conclusion for the reaction of any NHC (cyclic (diamino) carbenes) as well as for cyclic (alkyl)(amino) carbenes such as in 2 during the “stabilization” of a reactive species X has to be drawn, in order to avoid serious problems for the description of bonding in many fields of inorganic chemistry: are the bonds between the X species and the NHC molecule – concluded from thermodynamics and from force constants as significant indicators of bond strength – weak donor–acceptor bonds symbolized by arrows, or are there strong covalent bonds which are possibly increased to have partial multiple bond character.71 The analysis of the variation of the BB vibration of 1 provides an easy indicator for the degree of its stabilization. Therefore, the bonding description of 1 presented here may also show exemplarily that the bonding discussion of any other NHC stabilized reactive species has to been seen critically. Anyway, the description of such bonding by arrows is at least strongly misleading,73 as a more general controversy has already shown.74–76 However, our critical description does not lower the excellent work of H. Braunschweig and G. Robinson, but it increases the understanding of the bonding of their unprecedented compounds.
Acknowledgements
We thank the Deutsche Forschungsgemeinschaft (DFG), the Institute of Inorganic Chemistry (KIT) and the Fonds der Chemischen Industrie for their support of this work. We want to thank the reviewers of the manuscript for their critical and helpful contributions. Many of them are directly introduced in this paper in order to make our arguments more precise.Notes and references
- Dalton Discussion 11: The Renaissance of Main Group Elements; Dalton Trans. 2008, 33, 4321–4524 Search PubMed.
- A. Ecker, E. Weckert and H. Schnöckel, Nature, 1997, 387, 379 CrossRef CAS.
- N. T. Tran, D. R. Powell and L. F. Dahl, Angew. Chem., Int. Ed., 2000, 39, 4121 CrossRef CAS.
- P. D. Jadzinsky, G. Calero, C. J. Ackerson, D. A. Bushnell and R. D. Kornberg, Science, 2007, 318, 430 CrossRef CAS PubMed.
- R. L. Whetten and R. C. Price, Science, 2007, 318, 407 CrossRef CAS PubMed.
- H. Schnöckel, Chem. Rev., 2010, 110, 4125 CrossRef PubMed.
- R. J. Wright, M. Brynda and P. P. Power, Angew. Chem., Int. Ed., 2006, 45, 5953 CrossRef CAS PubMed.
- J. R. Su, X. W. Li, R. C. Crittendon and G. H. Robinson, J. Am. Chem. Soc., 1997, 119, 5471 CrossRef CAS.
- Y. Wang and G. H. Robinson, Inorg. Chem., 2011, 50, 12326 CrossRef CAS PubMed.
- D. J. D. Wilson and J. L. Dutton, Chem.–Eur. J., 2013, 19, 13626 CrossRef CAS PubMed.
- H. Braunschweig, R. D. Dewhurst, K. Hammond, J. Mies, K. Radacki and A. Vargas, Science, 2012, 336, 1420 CrossRef CAS PubMed.
- G. Frenking and N. Holzmann, Science, 2012, 336, 1394 CrossRef CAS PubMed.
- A BB double bond has been published before: Y. Wang and G. H. Robinson, Chem. Commun., 2009, 5201 RSC.
- H. Nöth and H. Pommerening, Angew. Chem., 1980, 92, 481 ( Angew. Chem., Int. Ed. Engl. , 1980 , 19 , 482 ) CrossRef.
- T. Mennekes, P. Paetzold, R. Boese and D. Bläser, Angew. Chem., 1991, 103, 199 ( Angew. Chem., Int. Ed. Engl. , 1991 , 30 , 173 ) CrossRef CAS.
- H. Klusik and A. Berndt, Angew. Chem., Int. Ed. Engl., 1981, 20, 870 CrossRef.
- A. Moezzi, M. M. Olmstead and P. P. Power, J. Am. Chem. Soc., 1992, 114, 2715 CrossRef CAS.
- W. J. Grigsby and P. P. Power, Chem. Commun., 1996, 2235 RSC.
- The following convincing argument has been recommended by a referee: given that the covalent radii of C and B are ca. 0.76 and 0.84 Å80 and that a CC triple bond is ca. 1.18 Å in acetylene, an only slightly longer BB triple bond of ca. 1.30 Å (1.18 × 0.84 ÷ 0.76), which is roughly proportionate to the different covalent radii of B and C, might have been expected (however: r(BB) = 1.45 Å for 1) for B
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) B (Fig. 1). On the other hand, the B–C bond length (1.49 Å) is shorter than might be expected for a B–C single bond, and it lies (just) within the range known for B–C double bonds in methylene boranes (1.351–1.488 Å40) suggesting that the B–C bond has multiple character.
B (Fig. 1). On the other hand, the B–C bond length (1.49 Å) is shorter than might be expected for a B–C single bond, and it lies (just) within the range known for B–C double bonds in methylene boranes (1.351–1.488 Å40) suggesting that the B–C bond has multiple character. - L. C. Ducati, N. Takagi and G. Frenking, J. Phys. Chem. A, 2009, 113, 11693 CrossRef CAS PubMed.
- H. Braunschweig and R. D. Dewhurst, Angew. Chem., 2013, 125, 3658 ( Angew. Chem., Int. Ed. , 2013 , 52 , 3574 ) CrossRef.
- D. Steudel, Chemie der Nichtmetalle, de Gruyter GmbH, Berlin, Boston, 2014 Search PubMed.
- Even two years after the publication of 111–13 a further nice BB containing compound 2 has been published,24 just when we had finished this manuscript. However, even for 2, which does not contain the cyclic di(amino)carbene of 1 but a cyclic (alkyl)(amino)carbene (CAAC),25 a thermodynamic as well as a force constant discussion based on the vibrational spectra is missing.
- J. Böhnke, H. Braunschweig, W. C. Ewing, C. Hörl, T. Kramer, I. Krummenacher, J. Mies and A. Vargas, Angew. Chem., Int. Ed., 2014, 53, 9082 CrossRef PubMed.
- Y. Li, K. C. Mondal, J. Luebben, H. Zhu, B. Dittrich, I. Purushothaman, P. Parameswaran and H. W. Roesky, Chem. Commun., 2014, 50, 2986 RSC.
- M. Binnewies and E. Milke, Thermochemical Data of Elements and Compounds, Wiley-VCH, Weinheim, Germany, 1999 Search PubMed.
- The excited quartet state of B atoms is 314 kJ mol−1 above the ground state.
- However, some thermodynamic data are presented for the molecules COB2CO and N2B2N2 (cf.ref. 20).
- With respect to this fragmentation, compound 2 is even 1 eV more stable than boron. Obviously, there are stronger BC bonds, as can be expected from the boron carbides, which are exothermic compounds, cf. ESI† and ref. 30.
- M. W. Chase Jr, NIST-JANAF Thermochemical Tables, J. Phys. Chem. Ref. Data, Monogr., 1998, 9, 1–1951 Search PubMed.
- More realistic are fragmentation and elimination reactions within the NHC moiety.
- B2* decomposes exothermically to 2 B atoms in their ground state.
- However, in all gas phase reactions we have studied in the past, the excited intermediates lose their energy via fragmentation (cf.ref. 34–38). Furthermore, we do not know any molecular example for which a fragmentation is avoided after an excitation of more than 10 eV.
- R. Burgert, H. Schnöckel, M. Olzmann and K. H. Bowen, Angew. Chem., 2006, 118, 1505 ( Angew. Chem., Int. Ed. , 2006 , 45 , 1476 ) CrossRef.
- R. Burgert, S. Stokes, K. H. Bowen and H. Schnöckel, J. Am. Chem. Soc., 2006, 128, 7904 CrossRef CAS PubMed.
- R. Burgert, H. Schnöckel, A. Grubisic, X. Li, S. T. Stokes, G. F. Ganteför, B. Kiran, P. Jena and K. H. Bowen, Science, 2008, 319, 438 CrossRef CAS PubMed.
- R. Burgert and H. Schnöckel, Chem. Commun., 2008, 2075 RSC , Feature Article.
- M. Neumaier, M. Olzmann, B. Kiran, K. H. Bowen, B. Eichhorn, A. Buonaugurio, S. T. Stokes, R. Burgert and H. Schnöckel, J. Am. Chem. Soc., 2014, 136, 3607 CrossRef CAS PubMed.
- J. E. Huheey, E. A. Keiter and R. L. Keiter, Anorganische Chemie, Walter de Gruyter, Berlin, New York, 1995 Search PubMed.
- A. Berndt, Angew. Chem., Int. Ed. Engl., 1993, 32, 985 CrossRef.
- However, there are well-known examples that the distance between two atoms can be a misleading property for the characterization of a bond (e.g. the BB distances in B2H6 with 1.77 Å without a direct bond is similar to the 2e2c BB bond in B2Cl4 (1.72 Å); furthermore, the following NaNa distances (Å) show that there is no correlation between bonding and distance: in solid NaCl (3.44), Nametal: 3.72, Na2-molecule: 3.0, (NaCl)2-molecule: 2.81 (see ref. 42 and 43).
- A. F. Wells, Structural Inorganic Chemistry, Clarendon Press, Oxford, 5th edn, 1984 Search PubMed.
- (a) A. F. Holleman, E. Wiberg and N. Wiberg, Inorganic Chemistry, Academic Press, San Diego, London, 2001 Search PubMed; (b) A. F. Holleman, E. Wiberg and N. Wiberg, Lehrbuch der Anorganischen Chemie, Walter de Gruyter, Berlin, New York, erweiterte Auflage, 2007, vol. 102 Search PubMed.
- Larger elongation to infinity distance between the vibrating entities means the dissociation energy ΔEdiss mostly is not a representative measure of a bond, as the educt and the (fragmentation) products have different electronic and structural properties. Therefore, the force constant represents a more reliable characterization of a bond!.
- D. del Rio, I. Resa, A. Rodriguez, L. Sanchez, R. Köppe, A. J. Downs, C. Y. Tang and E. Carmona, J. Phys. Chem. A, 2008, 112, 10516 CrossRef CAS PubMed.
- S. Brownridge, T. S. Cameron, H. Du, C. Knapp, R. Köppe, J. Passmore, J. M. Rautiainen and H. Schnöckel, Inorg. Chem., 2005, 44, 1660 CrossRef CAS PubMed ; highlighted in S. K. Ritter, Chemical & Engineering News, 2005, 83, 49.
- f CC/mdyn Å−1: C2H6 (4.4); C2H4 (9.1); C2H2 (15.6) (ref. 48).
- H. Schnöckel and H. Willner, in Infrared and Raman Spectroscopy, ed. B. Schrader, VCH, Weinheim, N. Y., 1995, pp. 223–253 Search PubMed.
- K. P. Huber, G. Herzberg, Molecular Spectra and Molecular Structure: IV. Constants of Diatomic Molecules., Van Nostrand Reinhold company, New York, 1979 Search PubMed.
- H. J. Becher and H. Schnöckel, Z. Anorg. Allg. Chem., 1970, 379, 136 CrossRef CAS.
- R. C. Taylor, J. Chem. Phys., 1957, 26, 1131 CrossRef CAS.
- E. B. Wilson, J. C. Decius and P. C. Cross, Molecular Vibrations, New York, 1995, 1955, Dover ISBN 0716787598 Search PubMed.
- This is convincingly and exemplarily shown for the BB vibration and its 10B/11B and 12C/13C (in parentheses) shifts (all in cm−1) 1: 1702 (63.4; 9.5); 1a: 1770 (64.7; 10.8). Even for 2 a very similar bonding can be expected: 1686 cm−1 (60.3; 11.8 cm−1).
- f XY means the stretching force constant between the atoms X and Y. The interaction force constant fXY/WZ means the interaction between two bonds, i.e. whether or not and to which extent there is a restoring force within the XY bond if the WZ bond is elongated.
- The BB bond in B12 units of α-boron is, as expected, much smaller (about fBB 1.3 mdyn Å−1), since there is an electron deficient situation of only 13 doubly occupied orbitals and 30 equivalent BB bonds50.
- There are already published calculated78 and experimentally obtained79 examples with a central X–BB–X moiety, for which a BB triple bond has been calculated. However, our normal coordinate analysis for the most prominent example [O
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) B–B
B–B![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) B–B
B–B![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) O]2− (ref. 78) indicates that a different formula [O–B–B
O]2− (ref. 78) indicates that a different formula [O–B–B![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) B–B–O]2− has to be concluded due to the following calculated force constants: fBO = 10.26, fBB = 3.70, fBB (central) = 5.51 mdyn Å−1, i.e. the situation of B4O22− is comparable to the discussion of 1 presented here, and also contradicts the BB triple bond interpretation.
B–B–O]2− has to be concluded due to the following calculated force constants: fBO = 10.26, fBB = 3.70, fBB (central) = 5.51 mdyn Å−1, i.e. the situation of B4O22− is comparable to the discussion of 1 presented here, and also contradicts the BB triple bond interpretation. - The following results are obtained for N
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–C
C–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N isoelectronic to OBBO: r(CN) = 1, 1755, r(CC) = 1.3836 Å, fCN = 17.81, fCC = 7.29 mdyn Å−1, i.e. there is a strengthened CC single bond.
N isoelectronic to OBBO: r(CN) = 1, 1755, r(CC) = 1.3836 Å, fCN = 17.81, fCC = 7.29 mdyn Å−1, i.e. there is a strengthened CC single bond. - T. R. Burkholder and L. Andrews, J. Chem. Phys., 1991, 95, 8697 CrossRef CAS.
- J. Huheey, E. Keiter and R. Keiter, Inorganic Chemistry: Principles of Structure and Reactivity, Prentice Hall, Upper Saddle River, 4th Aufl., 1997 Search PubMed.
- The BB compound 2 containing two cyclic (alkyl)(amino)carbenes (cf.ref. 24) which has been published recently, may be just between the bonding of 1 and O
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) B–B
B–B![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O. Thus, the latter one represents an extreme situation with a BB single bond. In analogy the BB single bond may also be present if two electron withdrawing carbenes such as CCl2 are the ligands: Cl2C
O. Thus, the latter one represents an extreme situation with a BB single bond. In analogy the BB single bond may also be present if two electron withdrawing carbenes such as CCl2 are the ligands: Cl2C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) B–B
B–B![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CCl2. In this case, like for the (alkyl)(amino) carbenes of 2, the HOMO is increased and the LUMO is decreased in comparison to 1; i.e. these carbenes, e.g. in 2, are better donors and acceptors (cf.ref. 25).
CCl2. In this case, like for the (alkyl)(amino) carbenes of 2, the HOMO is increased and the LUMO is decreased in comparison to 1; i.e. these carbenes, e.g. in 2, are better donors and acceptors (cf.ref. 25). - The occupation of single MOs in principle is not directly correlated with a bond, because these separated occupation numbers are no observables. Only the sum of all MOs, their occupation numbers and energies result in observables such as the distance and the force constant.
- P. P. Power, Chem. Rev., 1999, 99, 3463 CrossRef CAS PubMed.
- G. H. Robinson, Adv. Organomet. Chem., 2001, 47, 283 CrossRef CAS.
- E. Rivard and P. P. Power, Inorg. Chem., 2007, 46, 10047 CrossRef CAS PubMed.
- Y. Wang and G. H. Robinson, Chem. Commun., 2009, 5201 RSC.
- For formal GaGa single/double/triple bonds the following GaGa force constants (mdyn Å−1) and distances (Å; in parentheses) are obtained: Ga2H62−: 0.75 (2.58); Ga2H42−: 0.98 (2.46); Ga2H22−: 1.01 (2.41). In order to show that no heavy-atom effects are responsible for this drastic difference to the situation in the first period (e.g. for organic chemistry), we have studied the situation within the following AsAs-bonded molecules, though arsenic is the element next to the neighbor of Ga in the periodic table; i.e. As and Ga differ by two electrons: As2H4: 1.38 (2.49); As2H2: 2.61 (2.27); As2: 4.22 (2.12) (ref. 67).
- R. Köppe and H. Schnöckel, Z. Anorg. Allg. Chem., 2000, 626, 1095 CrossRef.
- H.-J. Himmel, L. Manceron, A. J. Downs and P. Pullumbi, Angew. Chem., Int. Ed., 2002, 41, 796 CrossRef CAS.
- J. Grunenberg and N. Goldberg, J. Am. Chem. Soc., 2000, 122, 6045 CrossRef CAS.
- Furthermore, the here presented critical description is also in line with the convincing comments on the BB and BC distances.19.
- Even the CN2 vibrations of the NHC moiety of 1 show that they are strongly involved in the bonding and vibration to the “reactive” molecule B2* (cf.Table 1), i.e. a new covalent bonded molecule is formed with hardly any relation to the “educts” B2/B2* and 2NHCs.
- The same is valid for 2 (cf.ref. 24) which has nothing to do with B2* and the discussed threefold bonding of 1 (cf.ref. 11); i.e. all argumentation presented here for 1 and its misleading bonding discussion shall be applied to 2. However, for 2 there are slightly stronger BC bonds, which correspond to the higher stability of 2 in comparison to 1. This property is in line with the exothermic behavior of solid boron carbides (ref. 30) and their covalent BC bonds, cf. ESI.†.
- Furthermore, a description of this kind generates serious confusion for teaching inorganic chemists77.
- D. Himmel, I. Krossing and A. Schnepf, Angew. Chem., 2014, 126, 378–382 ( Angew. Chem., Int. Ed. , 2014 , 53 , 370 ) CrossRef.
- G. Frenking, Angew. Chem., 2014, 126, 6152 ( Angew. Chem., Int. Ed. , 2014 , 53 , 6040 ) CrossRef.
- D. Himmel, I. Krossing and A. Schnepf, Angew. Chem., 2014, 126, 6159 CrossRef.
- M. L. H. Green and G. Parkin, J. Chem. Educ., 2014, 91, 807 CrossRef CAS.
- S. D. Li, H. J. Zhai and L. S. Wang, J. Am. Chem. Soc., 2008, 130, 2573 CrossRef CAS PubMed.
- H. Bi, P. Xie, X. Chai, Y. Liu, Q. Li and C. Sun, J. Chem. Sok. Pak., 2014, 36, 394 CAS.
- B. Cordero, V. Gómez, A. E. Platero-Prats, M. Revés, J. Echeverría, E. Cremades, F. Barragána and S. Alvarez, Dalton Trans., 2008, 2832 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: Details of the theoretical calculations (thermodynamic data and force constants). See DOI: 10.1039/c4sc02997f |
| This journal is © The Royal Society of Chemistry 2015 |